思路:
- 设 $n$ 阶格雷码集合为 $G(n)$,则 $G(n+1)$ 阶格雷码为:
- 给 $G(n)$ 阶格雷码每个元素二进制形式前面添加 $0$,得到 $G'(n)$;
- 设 $G(n)$ 集合倒序(镜像)为 $R(n)$,给 $R(n)$ 每个元素二进制形式前面添加 $1$,得到 $R'(n)$;
- $G(n+1) = G'(n) ∪ R'(n)$ 拼接两个集合即可得到下一阶格雷码。
- 根据以上规律,可从 $0$ 阶格雷码推导致任何阶格雷码。
- 代码解析:
- 由于最高位前默认为 $0$,因此 $G'(n) = G(n)$,只需在
res(即 $G(n)$ )后添加 $R'(n)$ 即可; - 计算 $R'(n)$:执行
head = 1 << i计算出对应位数,以给 $R(n)$ 前添加 $1$ 得到对应 $R'(n)$; - 倒序遍历
res(即 $G(n)$ ):依次求得 $R'(n)$ 各元素添加至res尾端,遍历完成后res(即 $G(n+1)$)。
- 由于最高位前默认为 $0$,因此 $G'(n) = G(n)$,只需在
图解:
<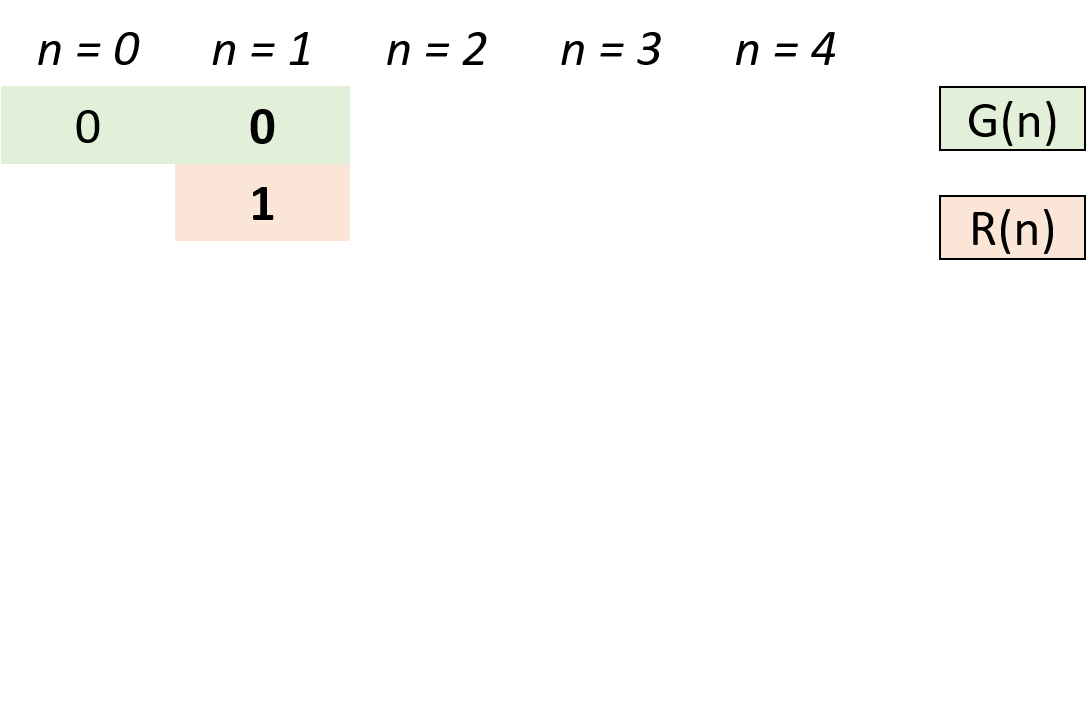 ,
,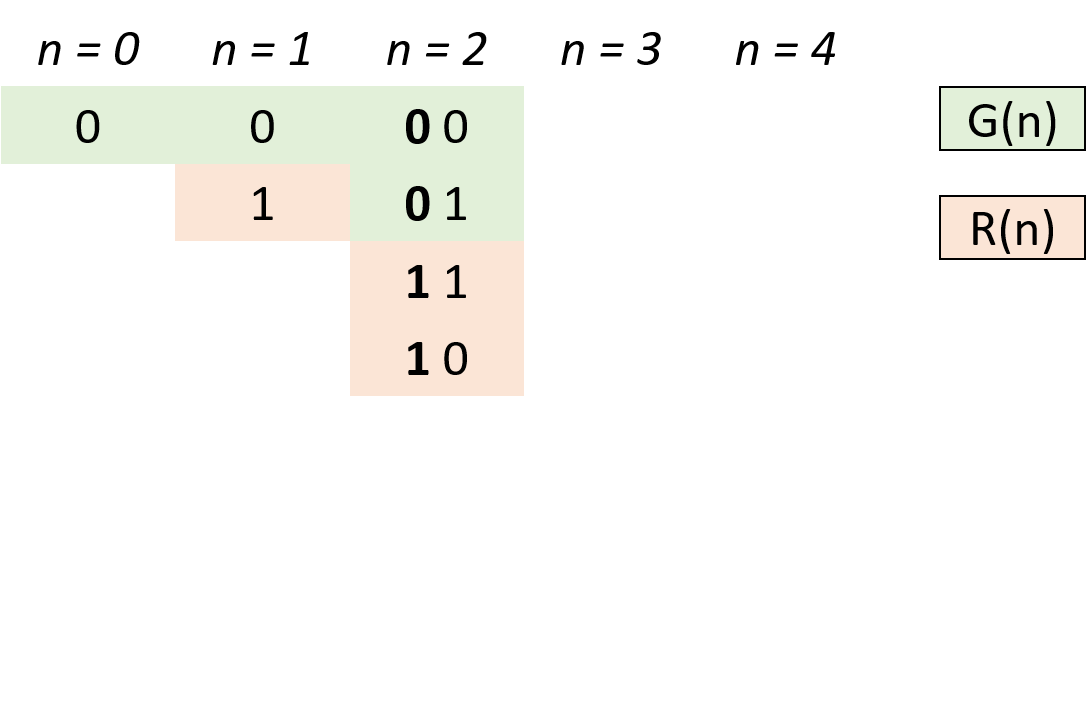 ,
,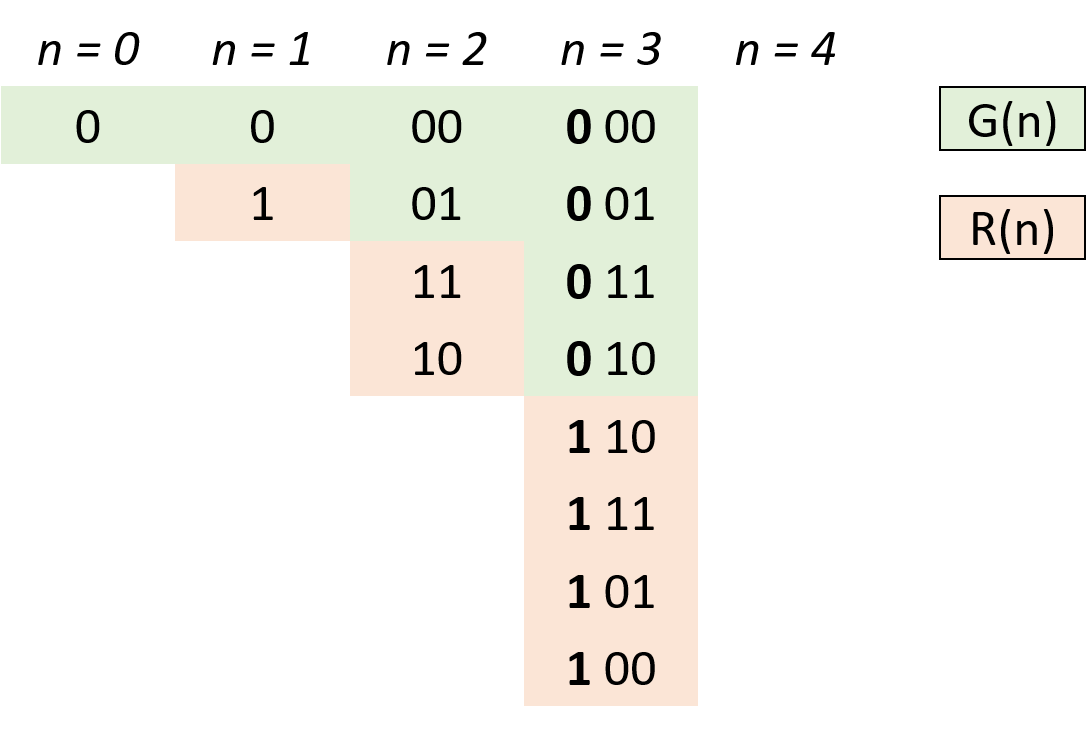 ,
,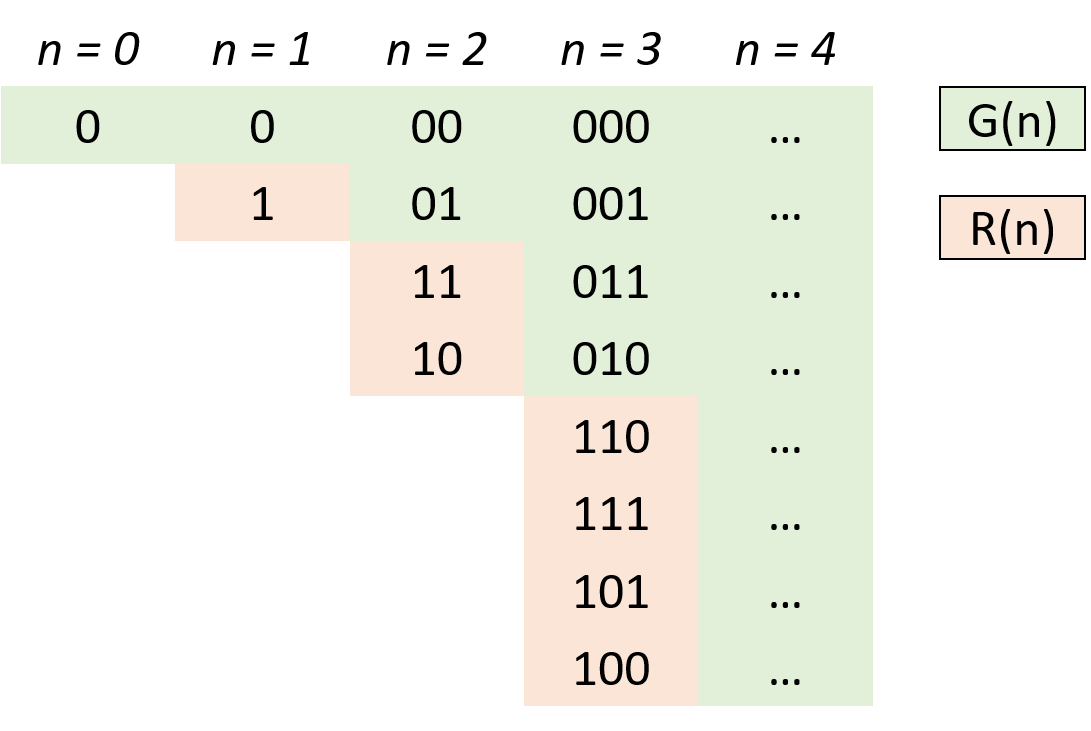 >
>
代码:
Python
class Solution:
def grayCode(self, n: int) -> List[int]:
res, head = [0], 1
for i in range(n):
for j in range(len(res) - 1, -1, -1):
res.append(head + res[j])
head <<= 1
return resJava
class Solution {
public List<Integer> grayCode(int n) {
List<Integer> res = new ArrayList<Integer>() {{ add(0); }};
int head = 1;
for (int i = 0; i < n; i++) {
for (int j = res.size() - 1; j >= 0; j--)
res.add(head + res.get(j));
head <<= 1;
}
return res;
}
}