方法一：辅助矩阵 ​

如下图所示，矩阵顺时针旋转 90º 后，可找到以下规律：

• 「第 $i$ 行」元素旋转到「第 $n - 1 - i$ 列」元素；
• 「第 $j$ 列」元素旋转到「第 $j$ 行」元素；

因此，对于矩阵任意第 $i$ 行、第 $j$ 列元素 $matrix[i][j]$ ，矩阵旋转 90º 后「元素位置旋转公式」为：

$$ \begin{aligned} matrix[i][j] & \rightarrow matrix[j][n - 1 - i] \ 原索引位置 & \rightarrow 旋转后索引位置 \end{aligned} $$

根据以上「元素旋转公式」，考虑遍历矩阵，将各元素依次写入到旋转后的索引位置。但仍存在问题：在写入一个元素 $matrix[i][j] \rightarrow matrix[j][n - 1 - i]$ 后，原矩阵元素 $matrix[j][n - 1 - i]$ 就会被覆盖（即丢失），而此丢失的元素就无法被写入到旋转后的索引位置了。

为解决此问题，考虑借助一个「辅助矩阵」暂存原矩阵，通过遍历辅助矩阵所有元素，将各元素填入「原矩阵」旋转后的新索引位置即可。

class Solution:
    def rotate(self, matrix: List[List[int]]) -> None:
        n = len(matrix)
        # 深拷贝 matrix -> tmp
        tmp = copy.deepcopy(matrix)
        # 根据元素旋转公式，遍历修改原矩阵 matrix 的各元素
        for i in range(n):
            for j in range(n):
                matrix[j][n - 1 - i] = tmp[i][j]

class Solution {
    public void rotate(int[][] matrix) {
        int n = matrix.length;
        // 深拷贝 matrix -> tmp
        int[][] tmp = new int[n][];
        for (int i = 0; i < n; i++)
            tmp[i] = matrix[i].clone();
        // 根据元素旋转公式，遍历修改原矩阵 matrix 的各元素
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                matrix[j][n - 1 - i] = tmp[i][j];
            }
        }
    }
}

class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        int n = matrix.size();
        // 深拷贝 matrix -> tmp
        vector<vector<int>> tmp = matrix;
        // 根据元素旋转公式，遍历修改原矩阵 matrix 的各元素
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                matrix[j][n - 1 - i] = tmp[i][j];
            }
        }
    }
};

如以上代码所示，遍历矩阵所有元素的时间复杂度为 $O(N^2)$ ；由于借助了一个辅助矩阵，空间复杂度为 $O(N^2)$ 。

方法二：原地修改 ​

考虑不借助辅助矩阵，通过在原矩阵中直接「原地修改」，实现空间复杂度 $O(1)$ 的解法。

以位于矩阵四个角点的元素为例，设矩阵左上角元素 $A$ 、右上角元素 $B$ 、右下角元素 $C$ 、左下角元素 $D$ 。矩阵旋转 90º 后，相当于依次先后执行 $D \rightarrow A$ , $C \rightarrow D$ , $B \rightarrow C$ , $A \rightarrow B$ 修改元素，即如下「首尾相接」的元素旋转操作：

$$ A \leftarrow D \leftarrow C \leftarrow B \leftarrow A $$

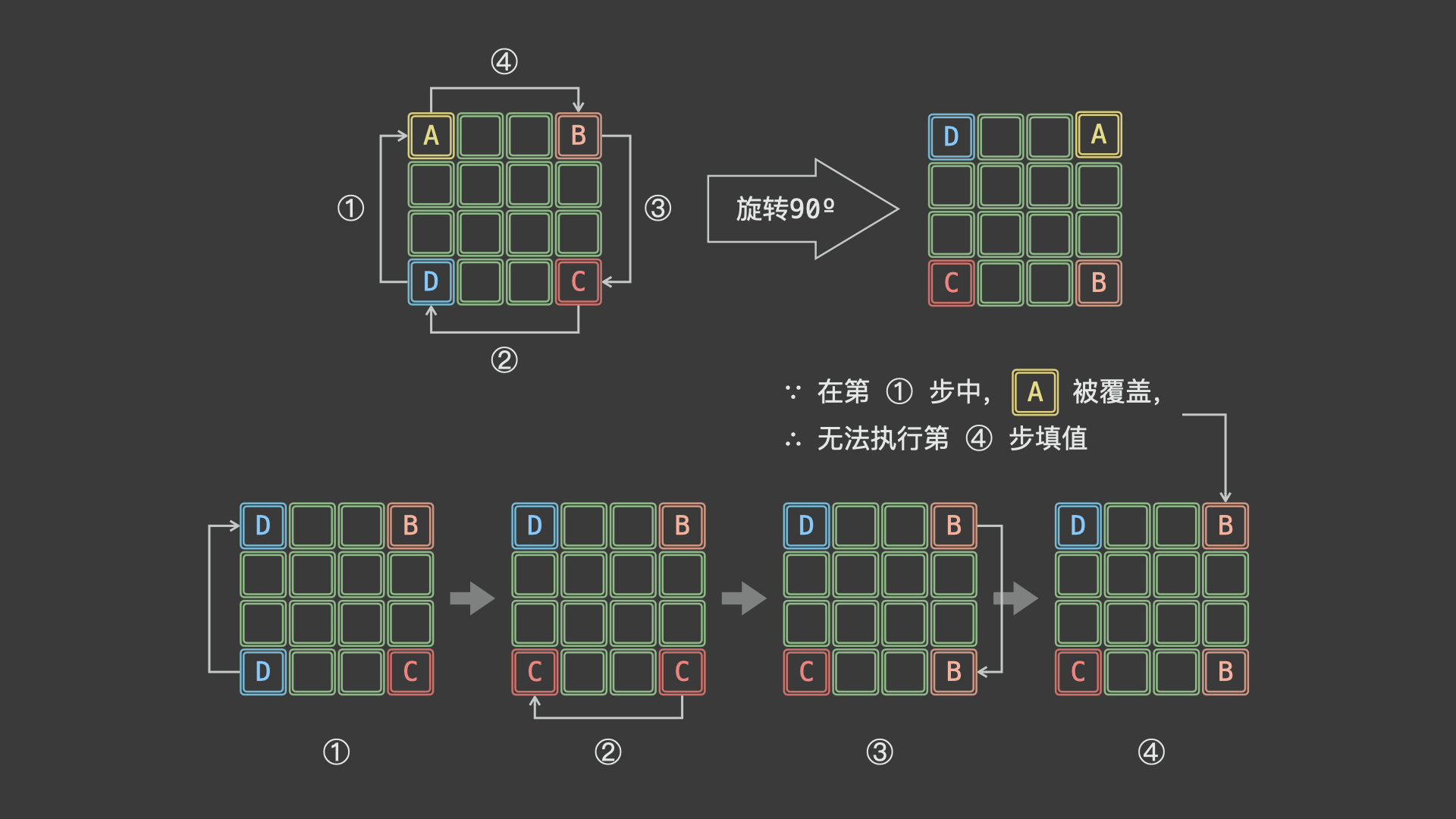
如上图所示，由于第 $1$ 步 $D \rightarrow A$ 已经将 $A$ 覆盖（导致 $A$ 丢失），此丢失导致最后第 $4$ 步 $A \rightarrow B$ 无法赋值。为解决此问题，考虑借助一个「辅助变量 $tmp$ 」预先存储 $A$ ，此时的旋转操作变为：

$$ 暂存 \ tmp = A \ A \leftarrow D \leftarrow C \leftarrow B \leftarrow tmp $$

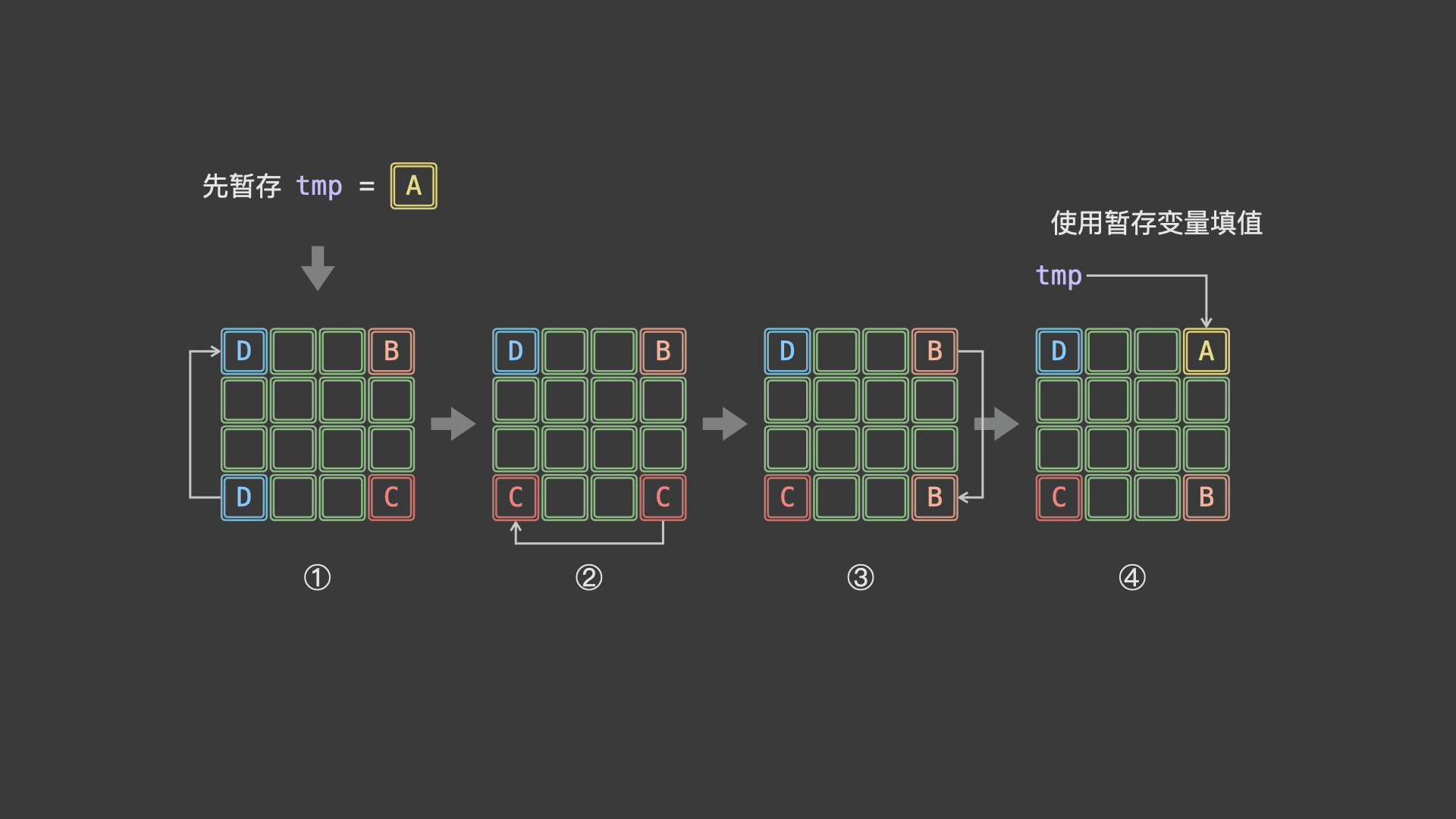
如上图所示，一轮可以完成矩阵 4 个元素的旋转。因而，只要分别以矩阵左上角 $1/4$ 的各元素为起始点执行以上旋转操作，即可完整实现矩阵旋转。

具体来看，当矩阵大小 $n$ 为偶数时，取前 $\frac{n}{2}$ 行、前 $\frac{n}{2}$ 列的元素为起始点；当矩阵大小 $n$ 为奇数时，取前 $\frac{n}{2}$ 行、前 $\frac{n + 1}{2}$ 列的元素为起始点。

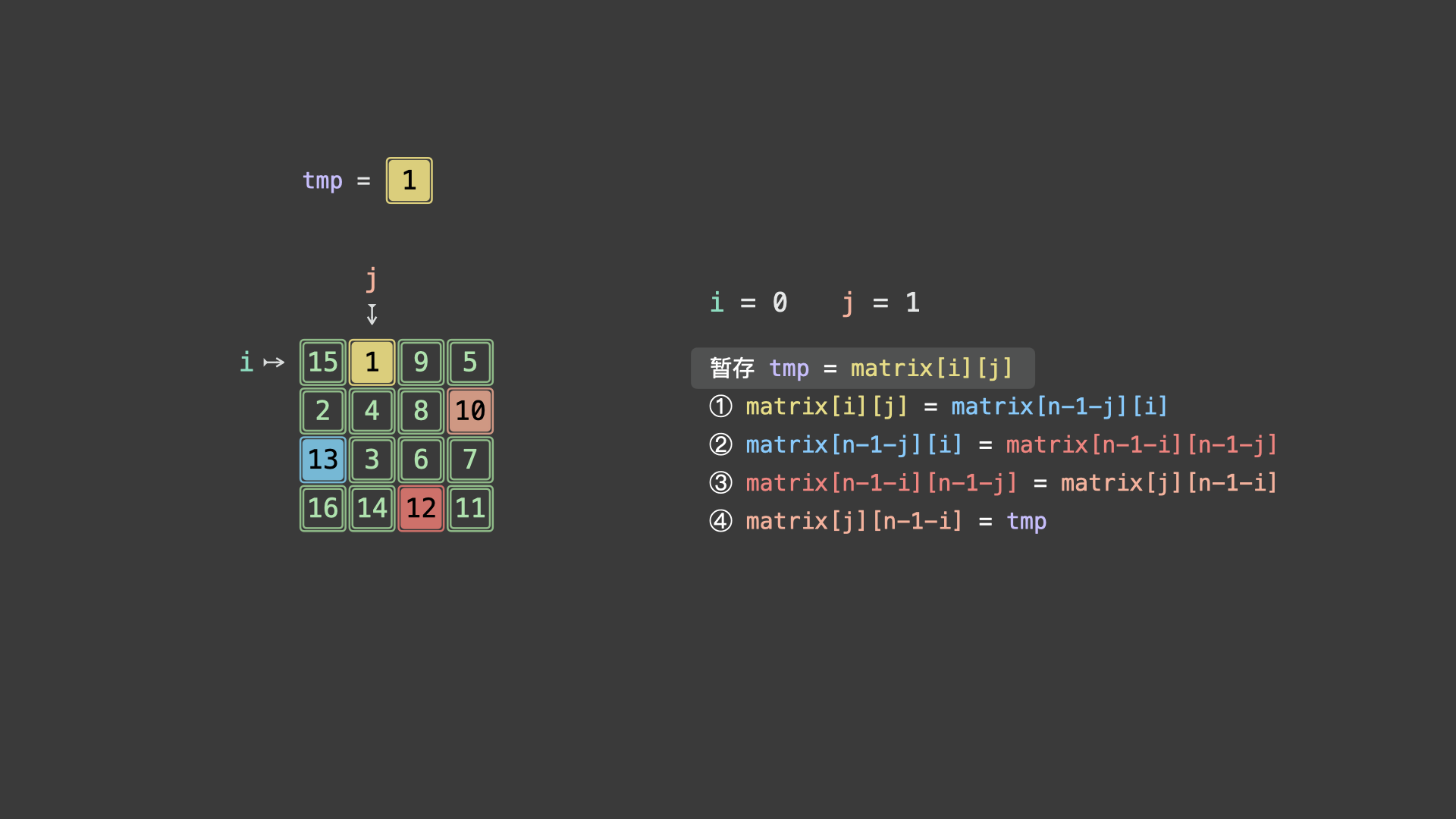
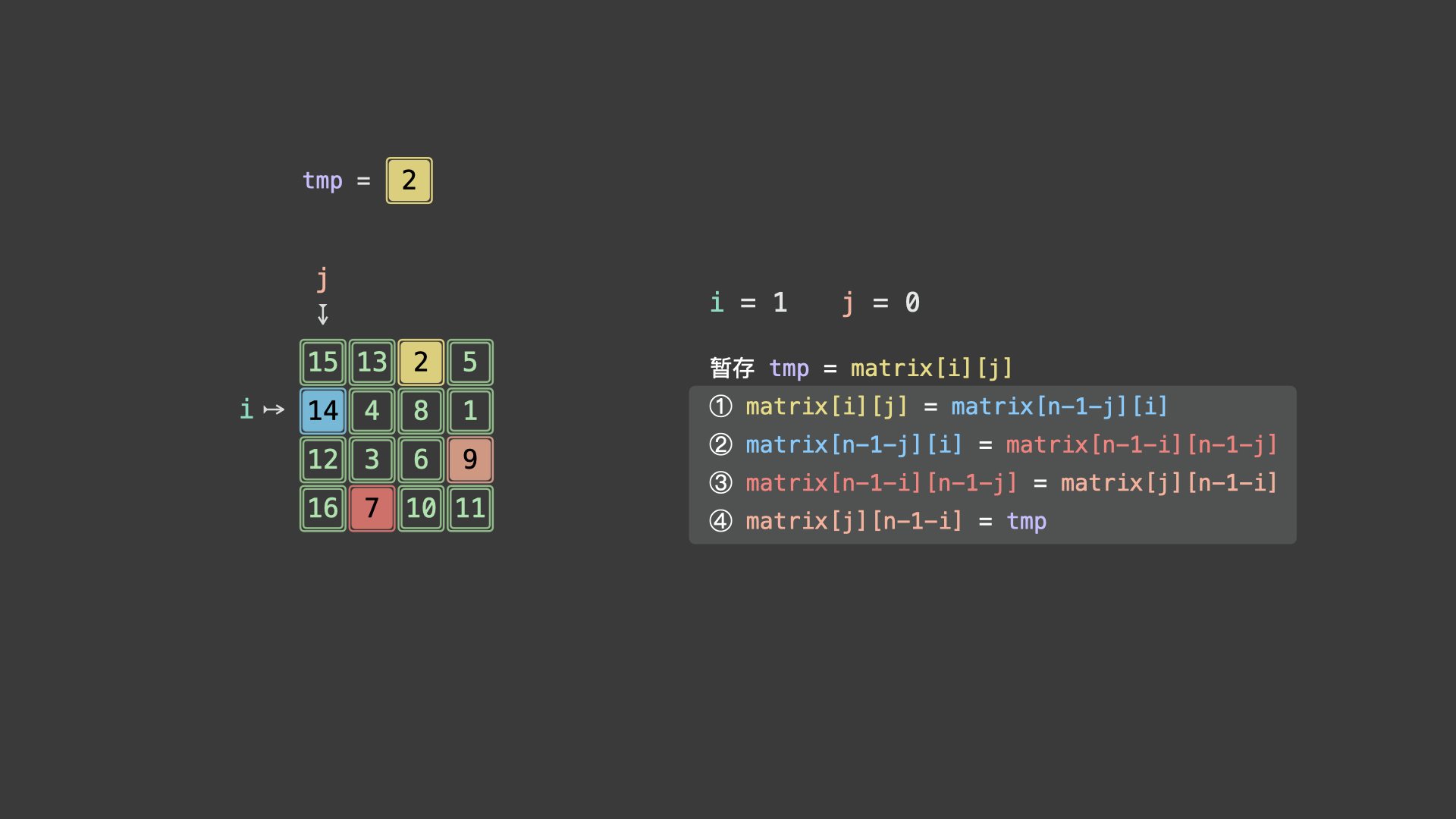
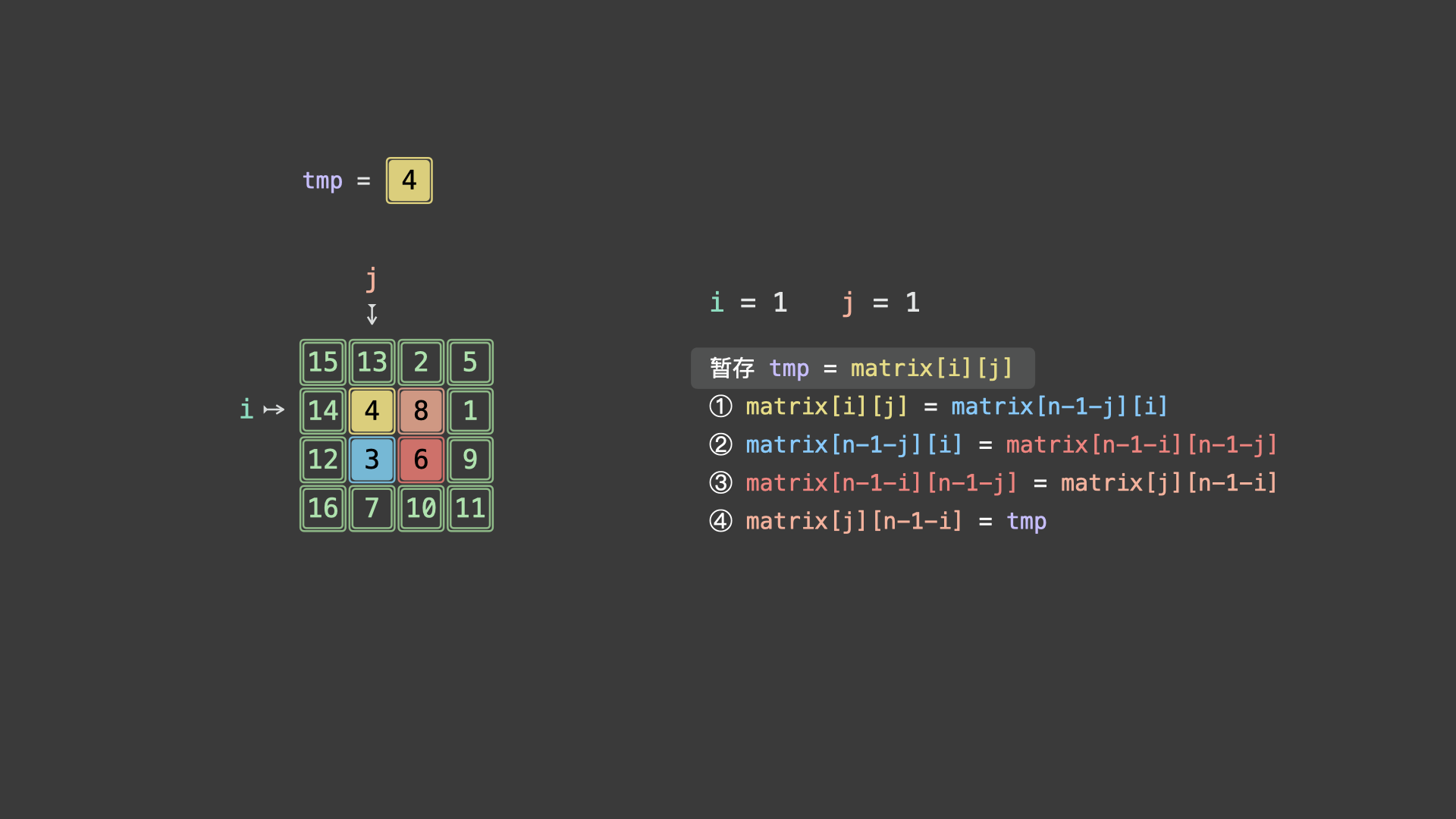
令 $matrix[i][j] = A$ ，根据文章开头的元素旋转公式，可推导得适用于任意起始点的元素旋转操作：

$$ 暂存 tmp = matrix[i][j] \ matrix[i][j] \leftarrow matrix[n - 1 - j][i] \leftarrow matrix[n - 1 - i][n - 1 - j] \leftarrow matrix[j][n - 1 - i] \leftarrow tmp $$

如下图所示，为示例矩阵的算法执行流程。

<,,,,,,,,,,,,,>

代码 ​

后三个 Tab 为「代码注释解析」。

class Solution:
    def rotate(self, matrix: List[List[int]]) -> None:
        n = len(matrix)
        for i in range(n // 2):
            for j in range((n + 1) // 2):
                tmp = matrix[i][j]
                matrix[i][j] = matrix[n - 1 - j][i]
                matrix[n - 1 - j][i] = matrix[n - 1 - i][n - 1 - j]
                matrix[n - 1 - i][n - 1 - j] = matrix[j][n - 1 - i]
                matrix[j][n - 1 - i] = tmp

class Solution {
    public void rotate(int[][] matrix) {
        int n = matrix.length;
        for (int i = 0; i < n / 2; i++) {
            for (int j = 0; j < (n + 1) / 2; j++) {
                int tmp = matrix[i][j];
                matrix[i][j] = matrix[n - 1 - j][i];
                matrix[n - 1 - j][i] = matrix[n - 1 - i][n - 1 - j];
                matrix[n - 1 - i][n - 1 - j] = matrix[j][n - 1 - i];
                matrix[j][n - 1 - i] = tmp;
            }
        }
    }
}

class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        int n = matrix.size();
        for (int i = 0; i < n / 2; i++) {
            for (int j = 0; j < (n + 1) / 2; j++) {
                int tmp = matrix[i][j];
                matrix[i][j] = matrix[n - 1 - j][i];
                matrix[n - 1 - j][i] = matrix[n - 1 - i][n - 1 - j];
                matrix[n - 1 - i][n - 1 - j] = matrix[j][n - 1 - i];
                matrix[j][n - 1 - i] = tmp;
            }
        }
    }
};

class Solution:
    def rotate(self, matrix: List[List[int]]) -> None:
        # 设矩阵行列数为 n
        n = len(matrix)
        # 起始点范围为 0 <= i < n // 2 , 0 <= j < (n + 1) // 2
        # 其中 '//' 为整数除法
        for i in range(n // 2):
            for j in range((n + 1) // 2):
                # 暂存 A 至 tmp
                tmp = matrix[i][j]
                # 元素旋转操作 A <- D <- C <- B <- tmp
                matrix[i][j] = matrix[n - 1 - j][i]
                matrix[n - 1 - j][i] = matrix[n - 1 - i][n - 1 - j]
                matrix[n - 1 - i][n - 1 - j] = matrix[j][n - 1 - i]
                matrix[j][n - 1 - i] = tmp

class Solution {
    public void rotate(int[][] matrix) {
        // 设矩阵行列数为 n
        int n = matrix.length;
        // 起始点范围为 0 <= i < n / 2 , 0 <= j < (n + 1) / 2
        // 其中 '/' 为整数除法
        for (int i = 0; i < n / 2; i++) {
            for (int j = 0; j < (n + 1) / 2; j++) {
                // 暂存 A 至 tmp
                int tmp = matrix[i][j];
                // 元素旋转操作 A <- D <- C <- B <- tmp
                matrix[i][j] = matrix[n - 1 - j][i];
                matrix[n - 1 - j][i] = matrix[n - 1 - i][n - 1 - j];
                matrix[n - 1 - i][n - 1 - j] = matrix[j][n - 1 - i];
                matrix[j][n - 1 - i] = tmp;
            }
        }
    }
}

class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        // 设矩阵行列数为 n
        int n = matrix.size();
        // 起始点范围为 0 <= i < n / 2 , 0 <= j < (n + 1) / 2
        // 其中 '/' 为整数除法
        for (int i = 0; i < n / 2; i++) {
            for (int j = 0; j < (n + 1) / 2; j++) {
                // 暂存 A 至 tmp
                int tmp = matrix[i][j];
                // 元素旋转操作 A <- D <- C <- B <- tmp
                matrix[i][j] = matrix[n - 1 - j][i];
                matrix[n - 1 - j][i] = matrix[n - 1 - i][n - 1 - j];
                matrix[n - 1 - i][n - 1 - j] = matrix[j][n - 1 - i];
                matrix[j][n - 1 - i] = tmp;
            }
        }
    }
};

复杂度分析 ​

• 时间复杂度 $O(N^2)$ ： 其中 $N$ 为输入矩阵的行（列）数。需要将矩阵中每个元素旋转到新的位置，即对矩阵所有元素操作一次，使用 $O(N^2)$ 时间。
• 空间复杂度 $O(1)$ ： 临时变量 $tmp$ 使用常数大小的额外空间。值得注意，当循环中进入下轮迭代，上轮迭代初始化的 $tmp$ 占用的内存就会被自动释放，因此无累计使用空间。