自律小屋

Appearance

当前页大纲

解题思路： ​

  • 本题可约化为： 课程安排图是否是 有向无环图(DAG)。即课程间规定了前置条件，但不能构成任何环路，否则课程前置条件将不成立。
  • 思路是通过 拓扑排序 判断此课程安排图是否是 有向无环图(DAG) 。 拓扑排序原理： 对 DAG 的顶点进行排序，使得对每一条有向边 $(u, v)$，均有 $u$（在排序记录中）比 $v$ 先出现。亦可理解为对某点 $v$ 而言，只有当 $v$ 的所有源点均出现了，$v$ 才能出现。
  • 通过课程前置条件列表 prerequisites 可以得到课程安排图的 邻接表 adjacency，以降低算法时间复杂度，以下两种方法都会用到邻接表。

方法一：入度表（广度优先遍历） ​

算法流程： ​
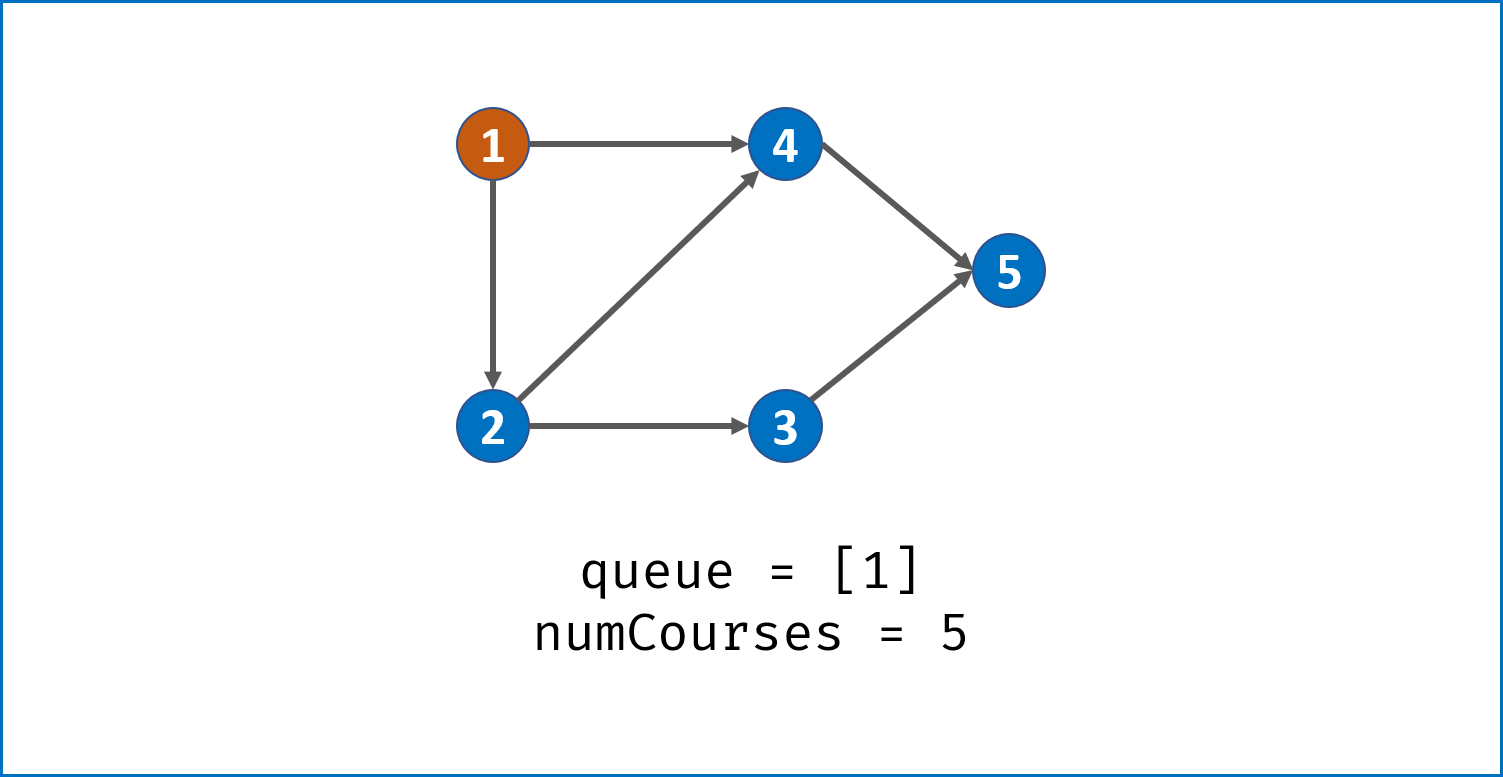
  1. 统计课程安排图中每个节点的入度，生成 入度表 indegrees。
  2. 借助一个队列 queue，将所有入度为 $0$ 的节点入队。
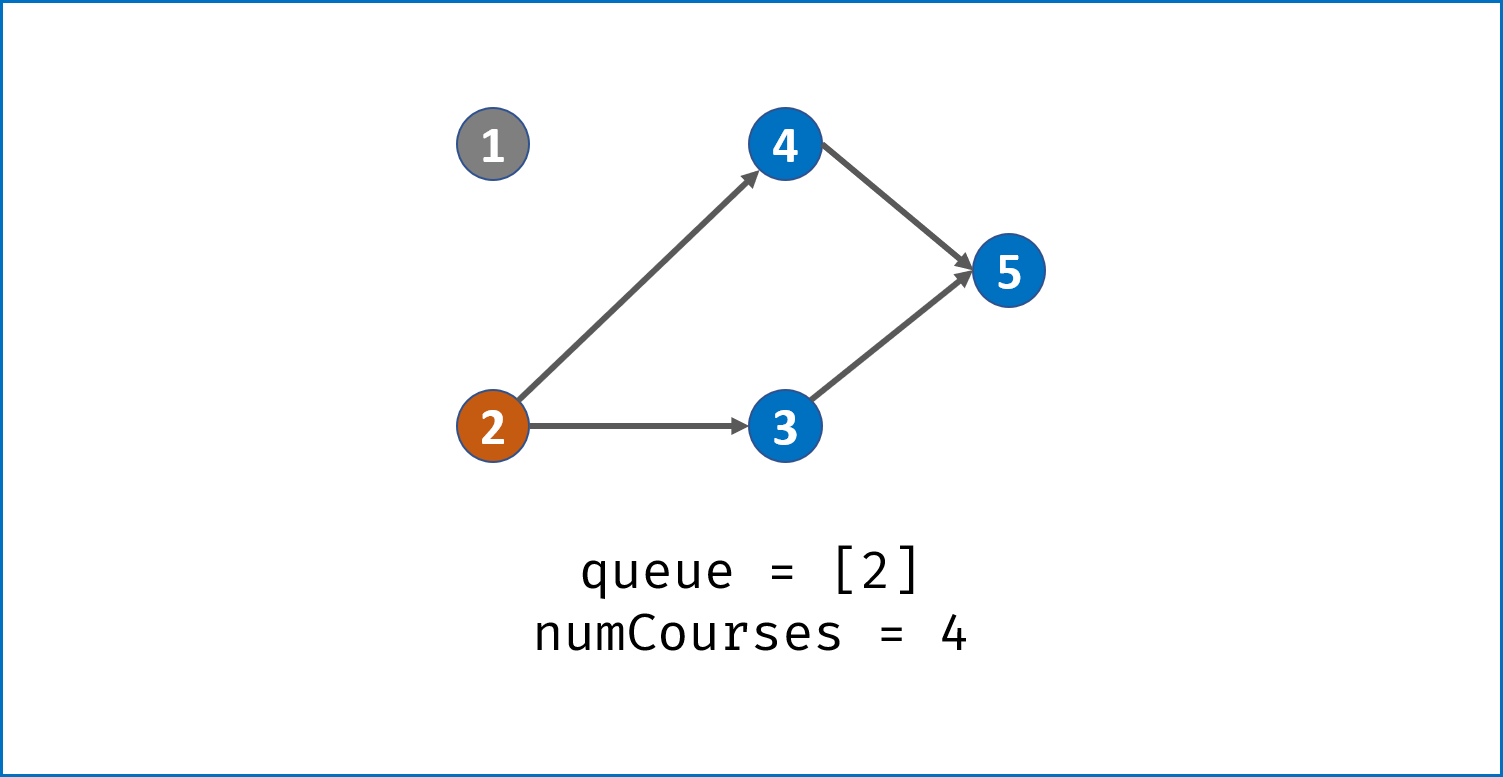
  3. 当 queue 非空时，依次将队首节点出队，在课程安排图中删除此节点 pre：
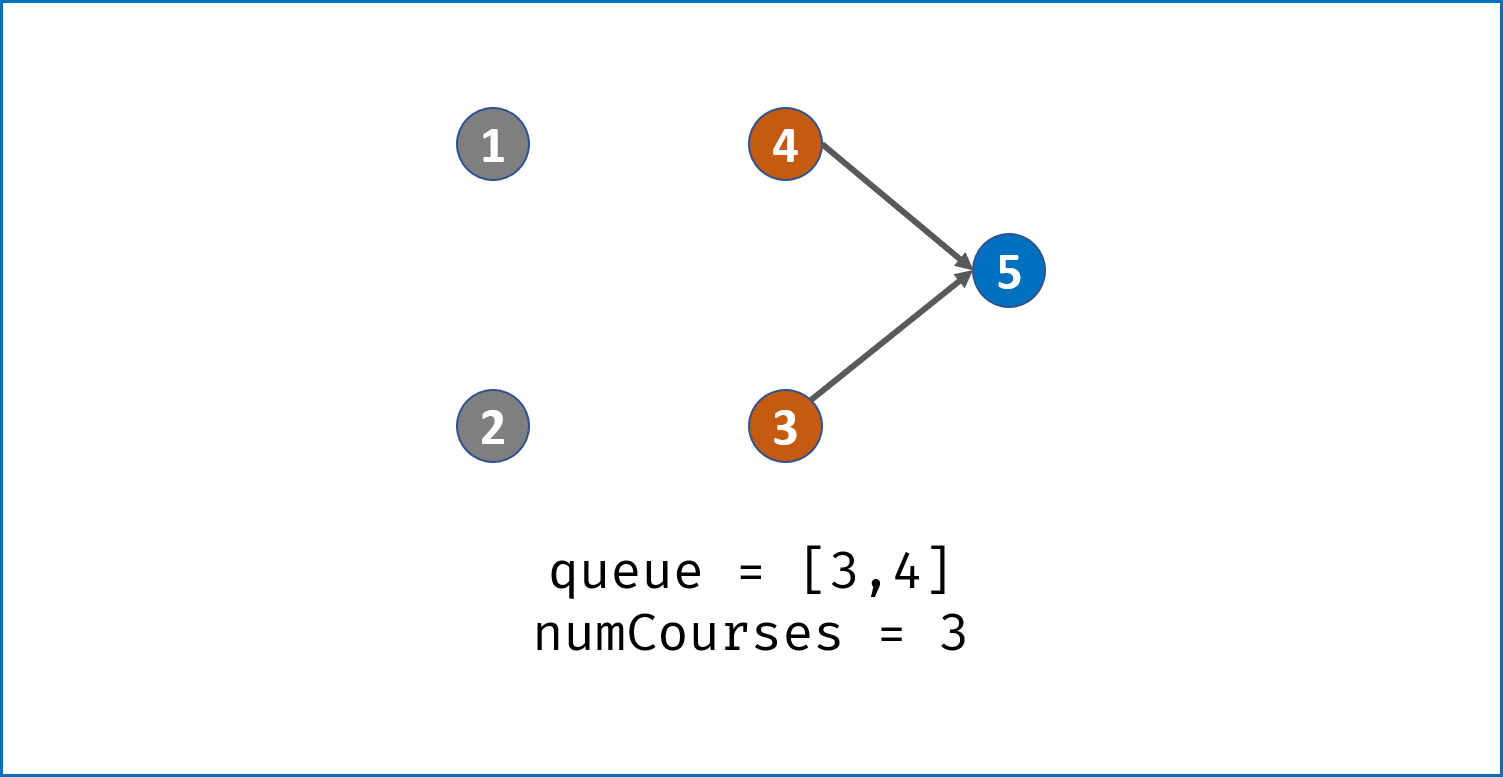
    • 并不是真正从邻接表中删除此节点 pre，而是将此节点对应所有邻接节点 cur 的入度 $-1$，即 indegrees[cur] -= 1。
    • 当入度 $-1$后邻接节点 cur 的入度为 $0$，说明 cur 所有的前驱节点已经被 “删除”，此时将 cur 入队。
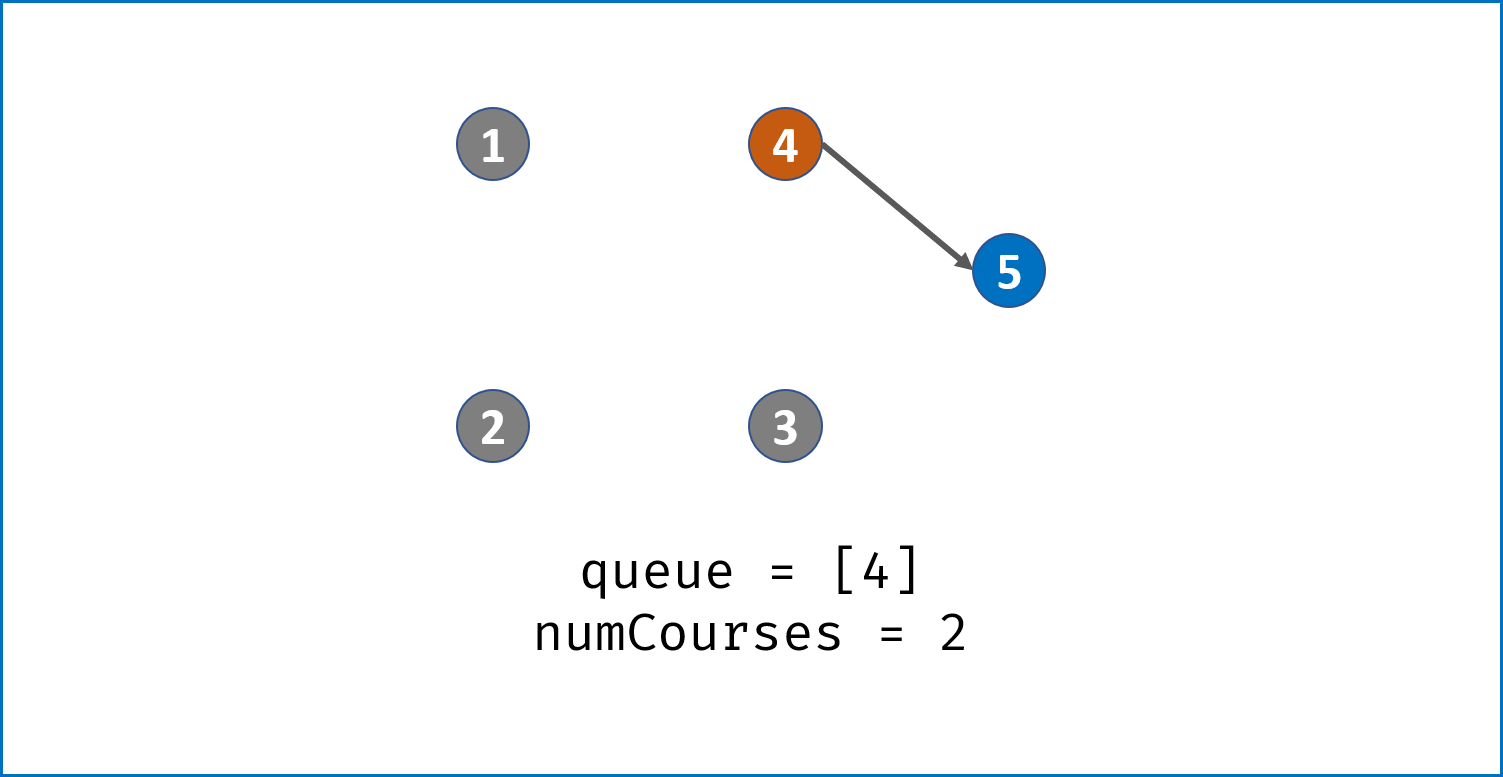
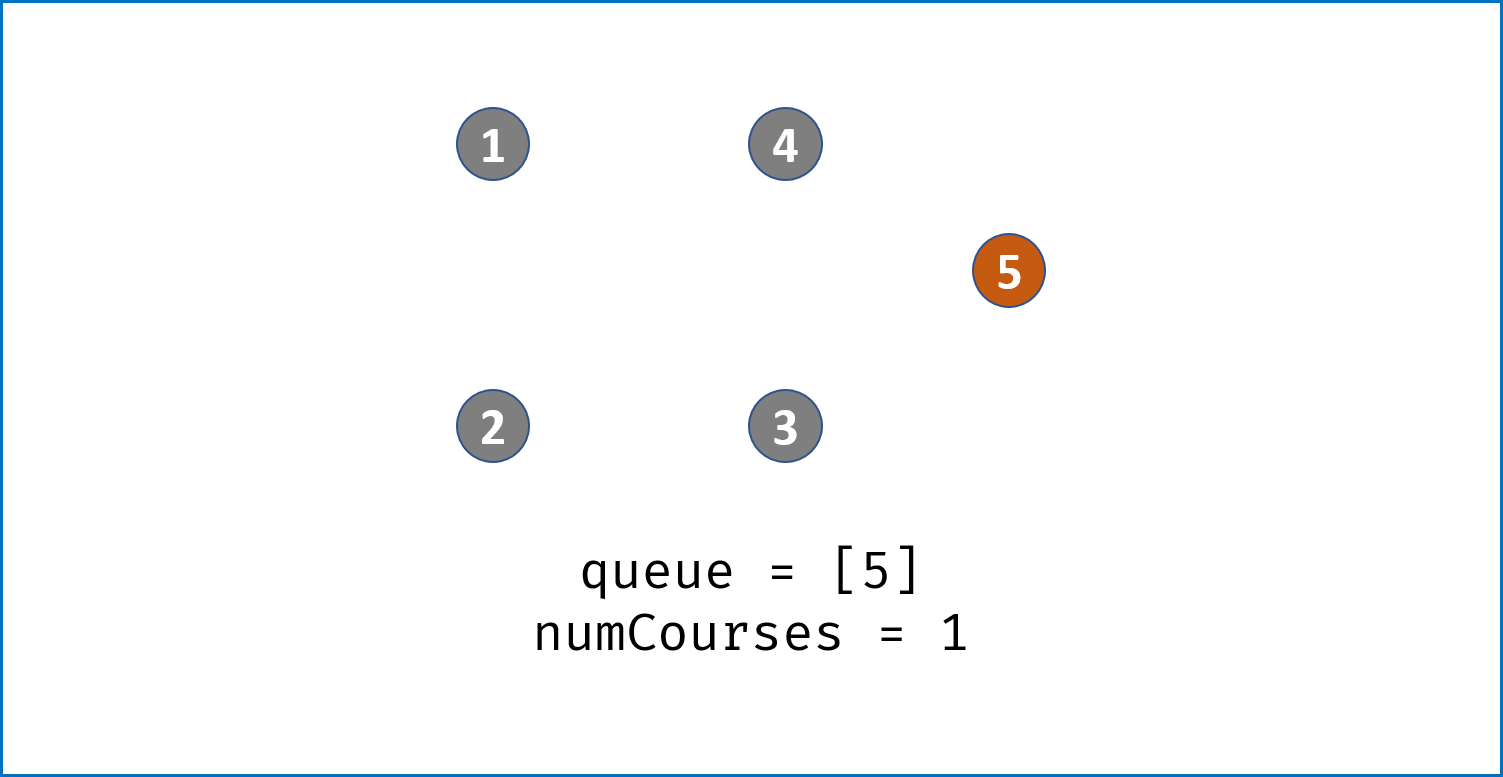
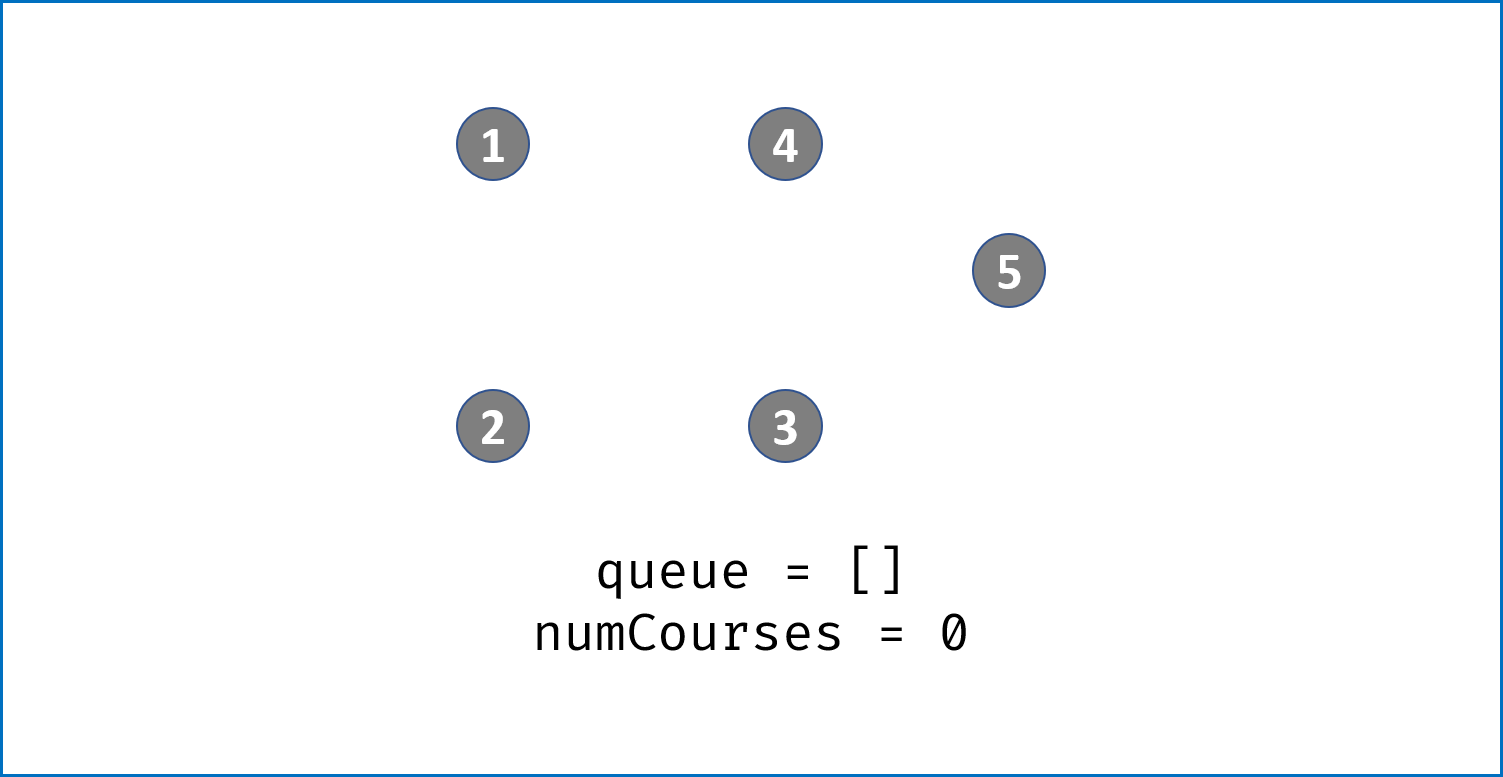
  4. 在每次 pre 出队时，执行 numCourses--；
    • 若整个课程安排图是有向无环图（即可以安排），则所有节点一定都入队并出队过，即完成拓扑排序。换个角度说，若课程安排图中存在环，一定有节点的入度始终不为 $0$。
    • 因此，拓扑排序出队次数等于课程个数，返回 numCourses == 0 判断课程是否可以成功安排。
复杂度分析： ​
  • 时间复杂度 $O(N + M)$： 遍历一个图需要访问所有节点和所有临边，$N$ 和 $M$ 分别为节点数量和临边数量；
  • 空间复杂度 $O(N + M)$： 为建立邻接表所需额外空间，adjacency 长度为 $N$ ，并存储 $M$ 条临边的数据。

<Picture1.png,Picture2.png,Picture3.png,Picture4.png,Picture5.png,Picture6.png>

代码： ​

Python
from collections import deque

class Solution:
    def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:
        indegrees = [0 for _ in range(numCourses)]
        adjacency = [[] for _ in range(numCourses)]
        queue = deque()
        # Get the indegree and adjacency of every course.
        for cur, pre in prerequisites:
            indegrees[cur] += 1
            adjacency[pre].append(cur)
        # Get all the courses with the indegree of 0.
        for i in range(len(indegrees)):
            if not indegrees[i]: queue.append(i)
        # BFS TopSort.
        while queue:
            pre = queue.popleft()
            numCourses -= 1
            for cur in adjacency[pre]:
                indegrees[cur] -= 1
                if not indegrees[cur]: queue.append(cur)
        return not numCourses
Java
class Solution {
    public boolean canFinish(int numCourses, int[][] prerequisites) {
        int[] indegrees = new int[numCourses];
        List<List<Integer>> adjacency = new ArrayList<>();
        Queue<Integer> queue = new LinkedList<>();
        for(int i = 0; i < numCourses; i++)
            adjacency.add(new ArrayList<>());
        // Get the indegree and adjacency of every course.
        for(int[] cp : prerequisites) {
            indegrees[cp[0]]++;
            adjacency.get(cp[1]).add(cp[0]);
        }
        // Get all the courses with the indegree of 0.
        for(int i = 0; i < numCourses; i++)
            if(indegrees[i] == 0) queue.add(i);
        // BFS TopSort.
        while(!queue.isEmpty()) {
            int pre = queue.poll();
            numCourses--;
            for(int cur : adjacency.get(pre))
                if(--indegrees[cur] == 0) queue.add(cur);
        }
        return numCourses == 0;
    }
}

方法二：深度优先遍历 ​

原理是通过 DFS 判断图中是否有环。

算法流程： ​
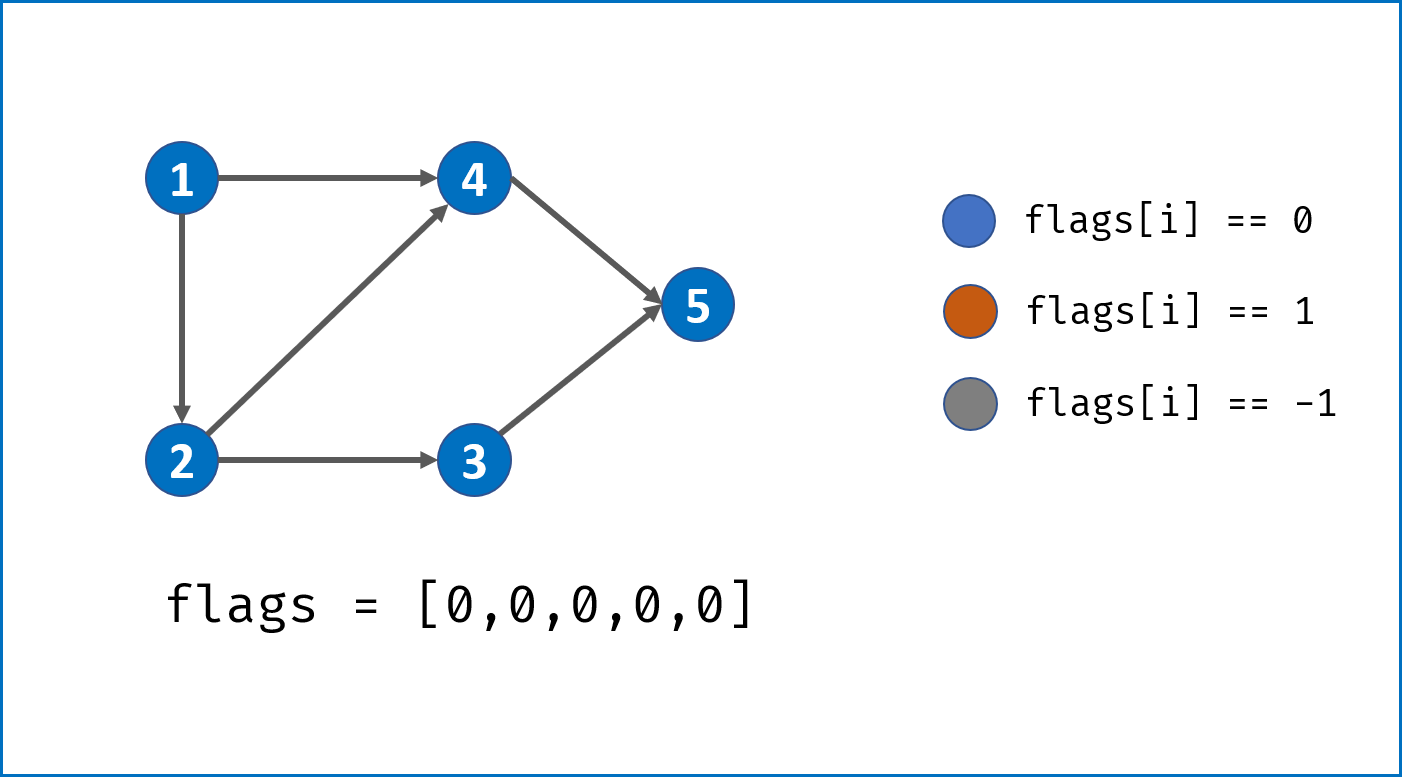
  1. 借助一个标志列表 flags，用于判断每个节点 i （课程）的状态：
    1. 未被 DFS 访问：i == 0；
    2. 已被其他节点启动的 DFS 访问：i == -1；
    3. 已被当前节点启动的 DFS 访问：i == 1。
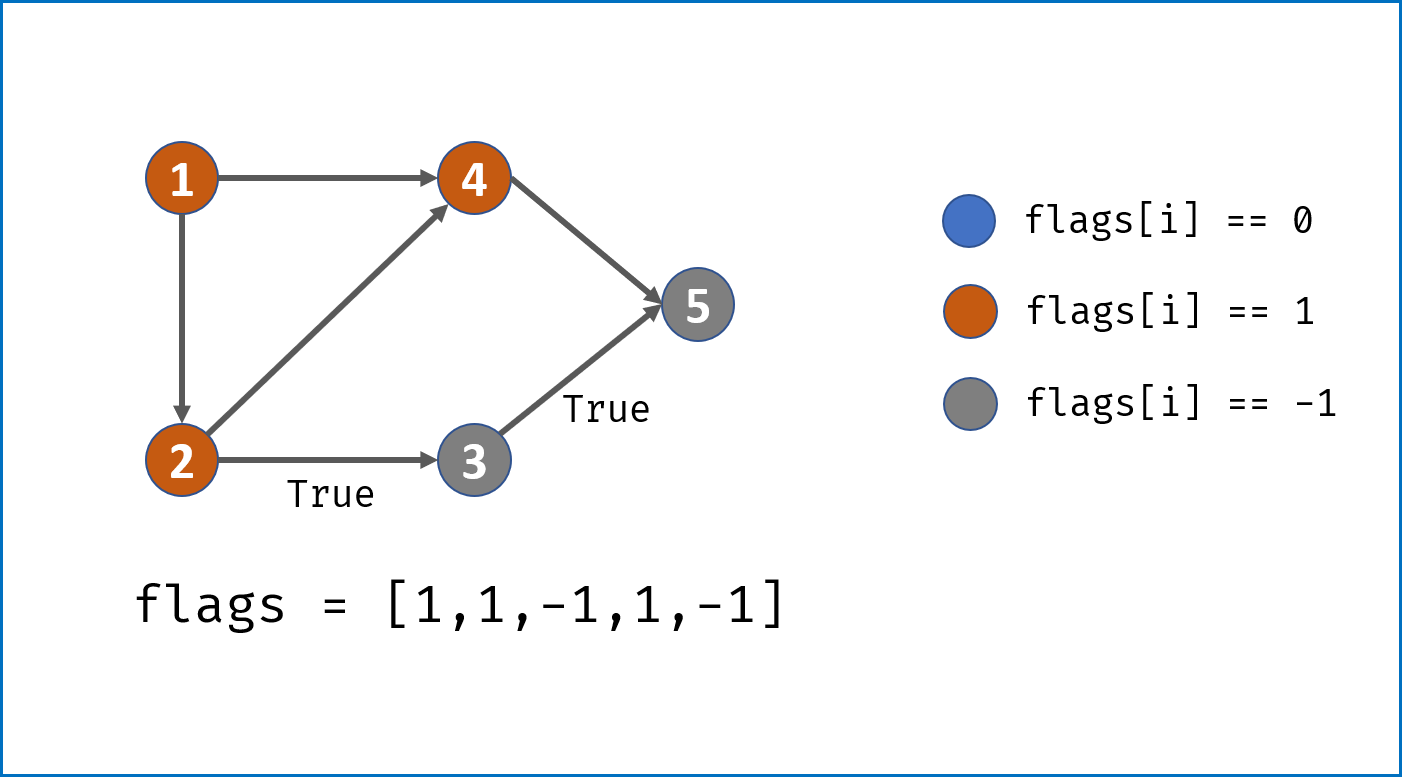
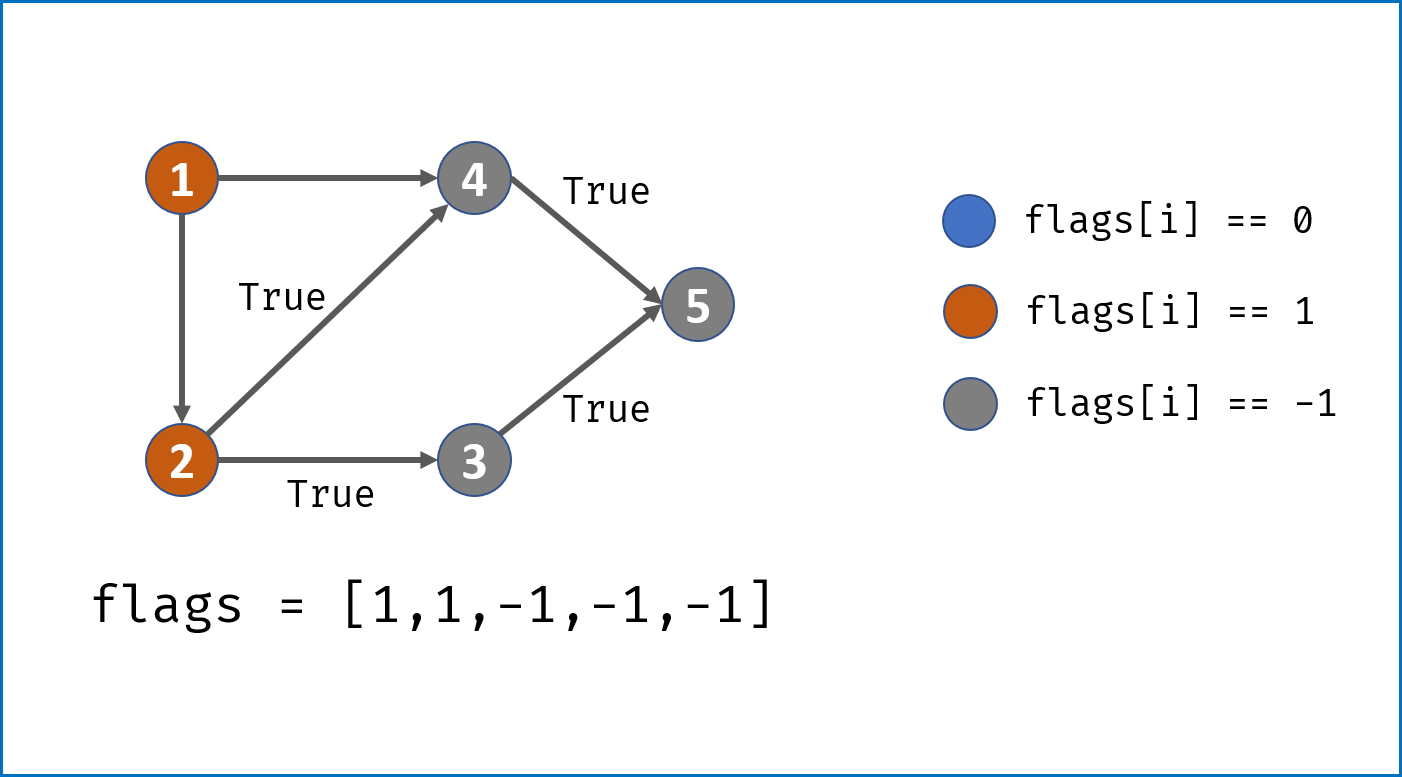
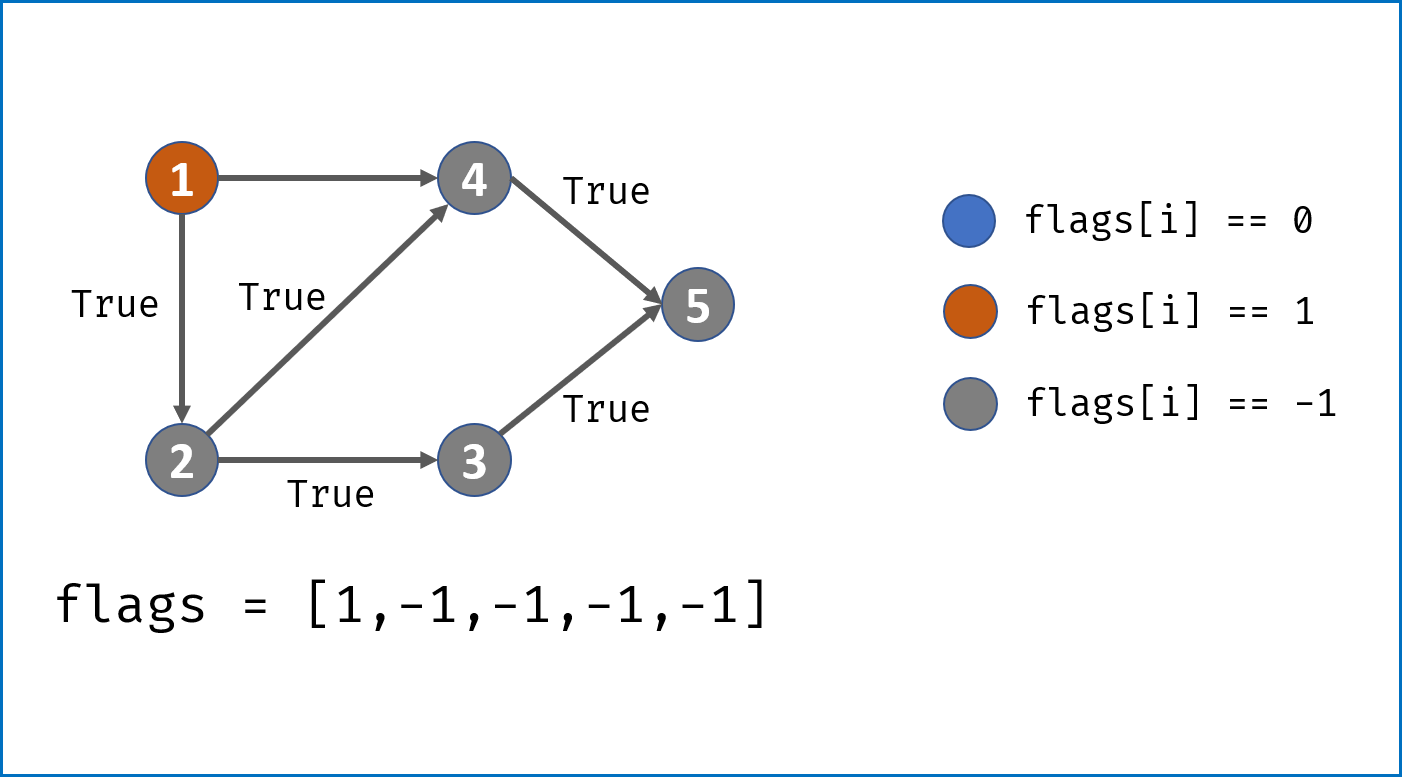
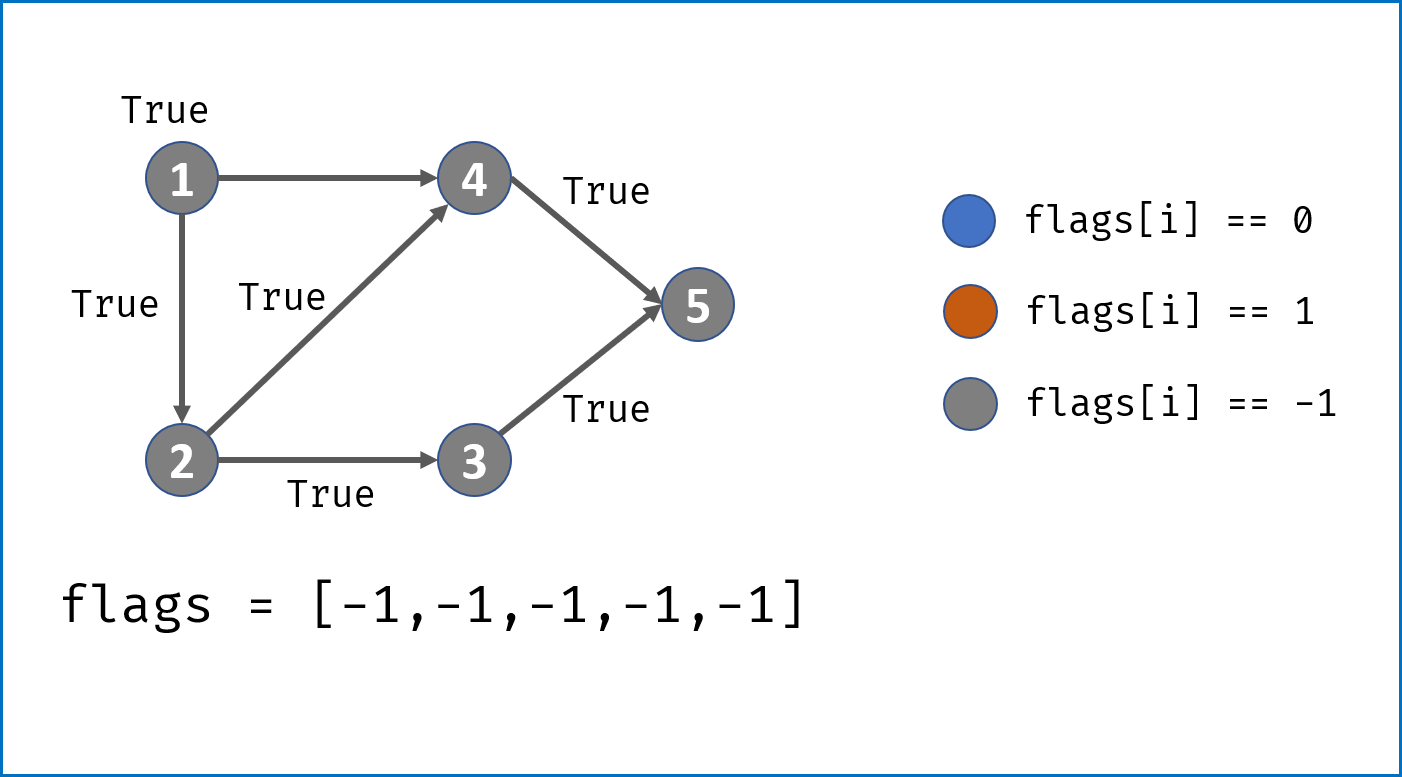
  2. 对 numCourses 个节点依次执行 DFS，判断每个节点起步 DFS 是否存在环，若存在环直接返回 $False$。DFS 流程；
    1. 终止条件：
      • 当 flag[i] == -1，说明当前访问节点已被其他节点启动的 DFS 访问，无需再重复搜索，直接返回 $True$。
      • 当 flag[i] == 1，说明在本轮 DFS 搜索中节点 i 被第 $2$ 次访问，即 课程安排图有环 ，直接返回 $False$。
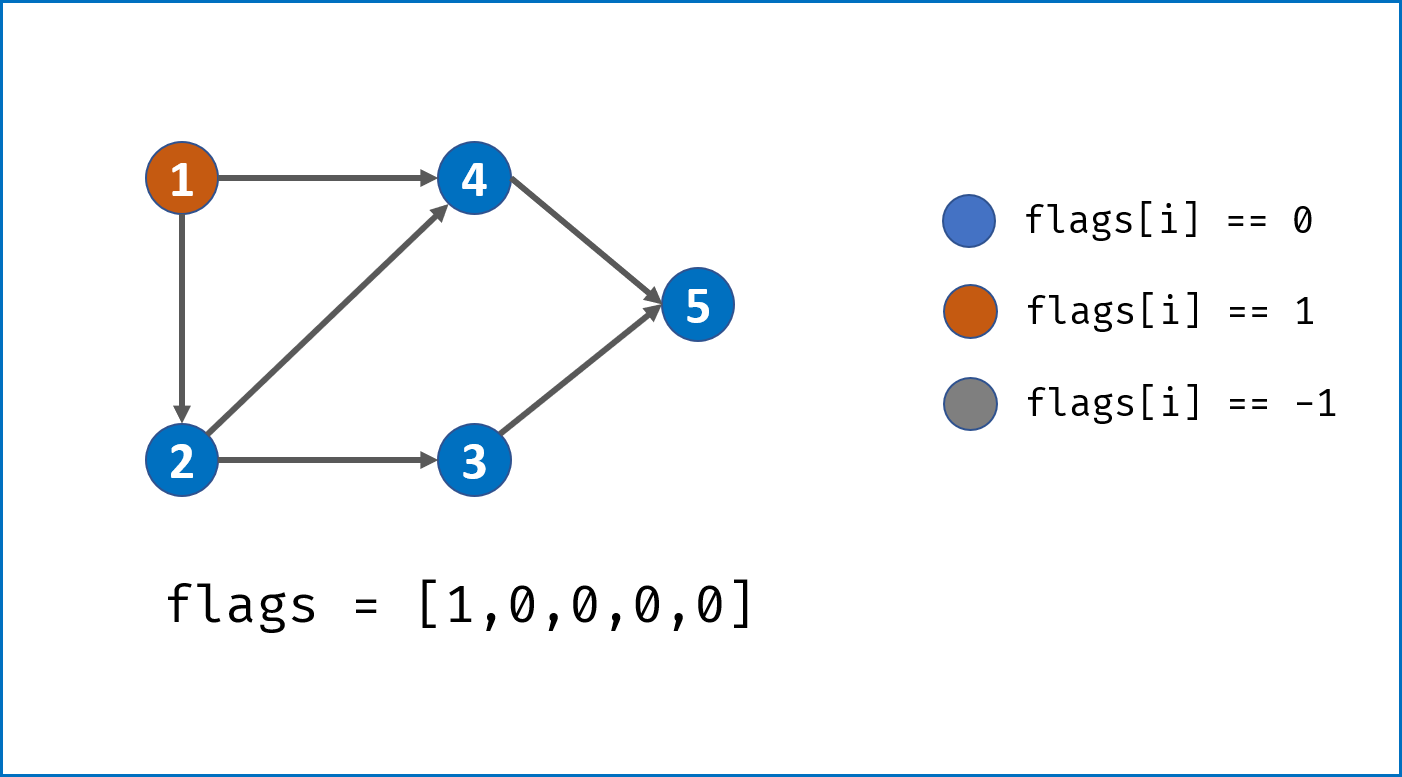
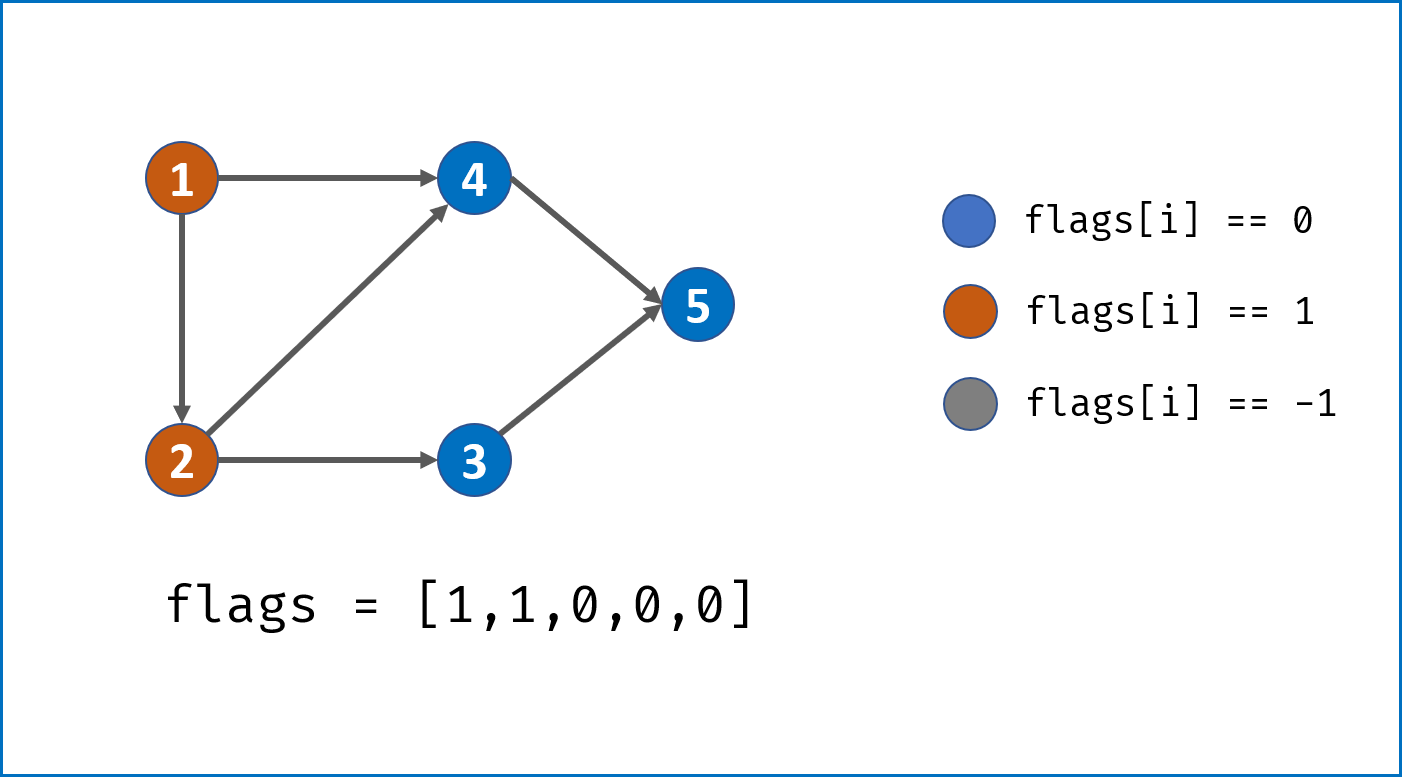
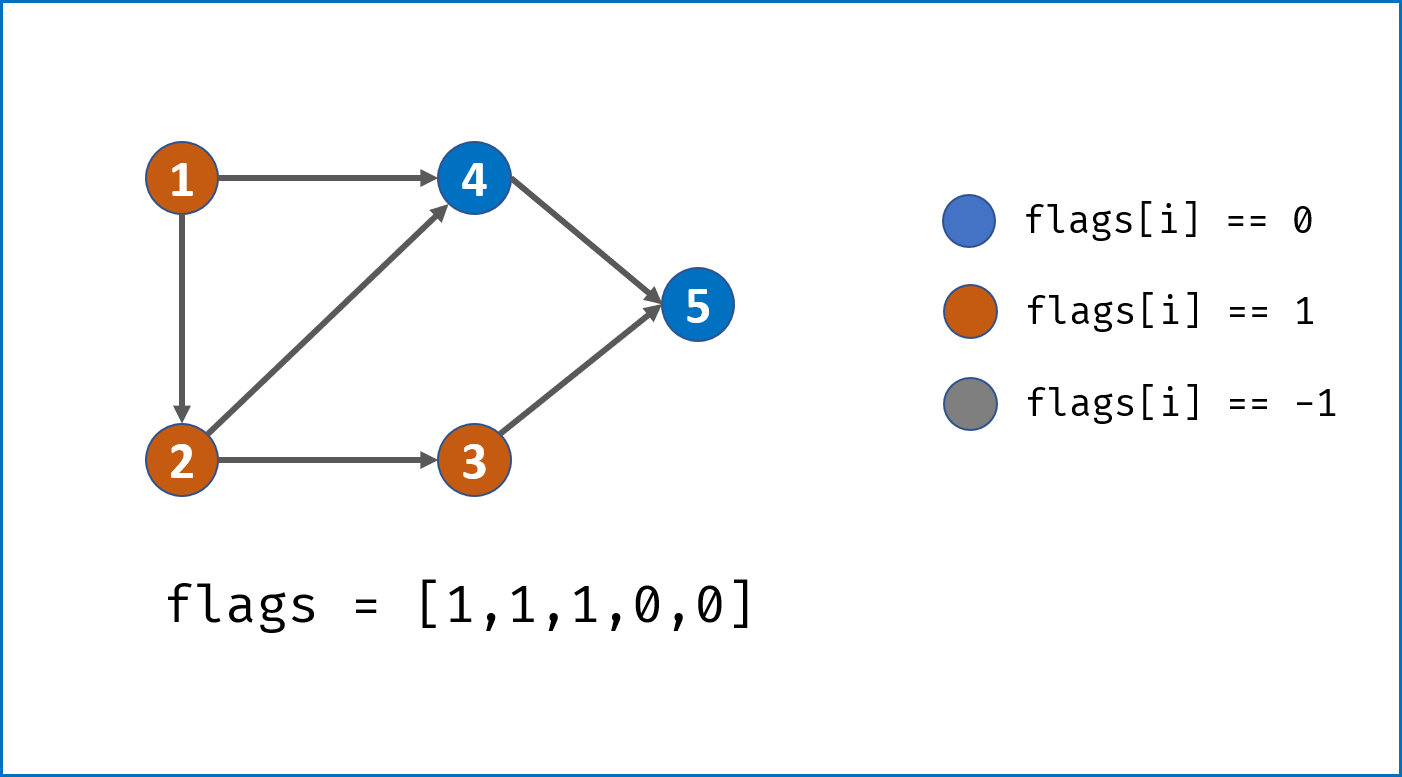
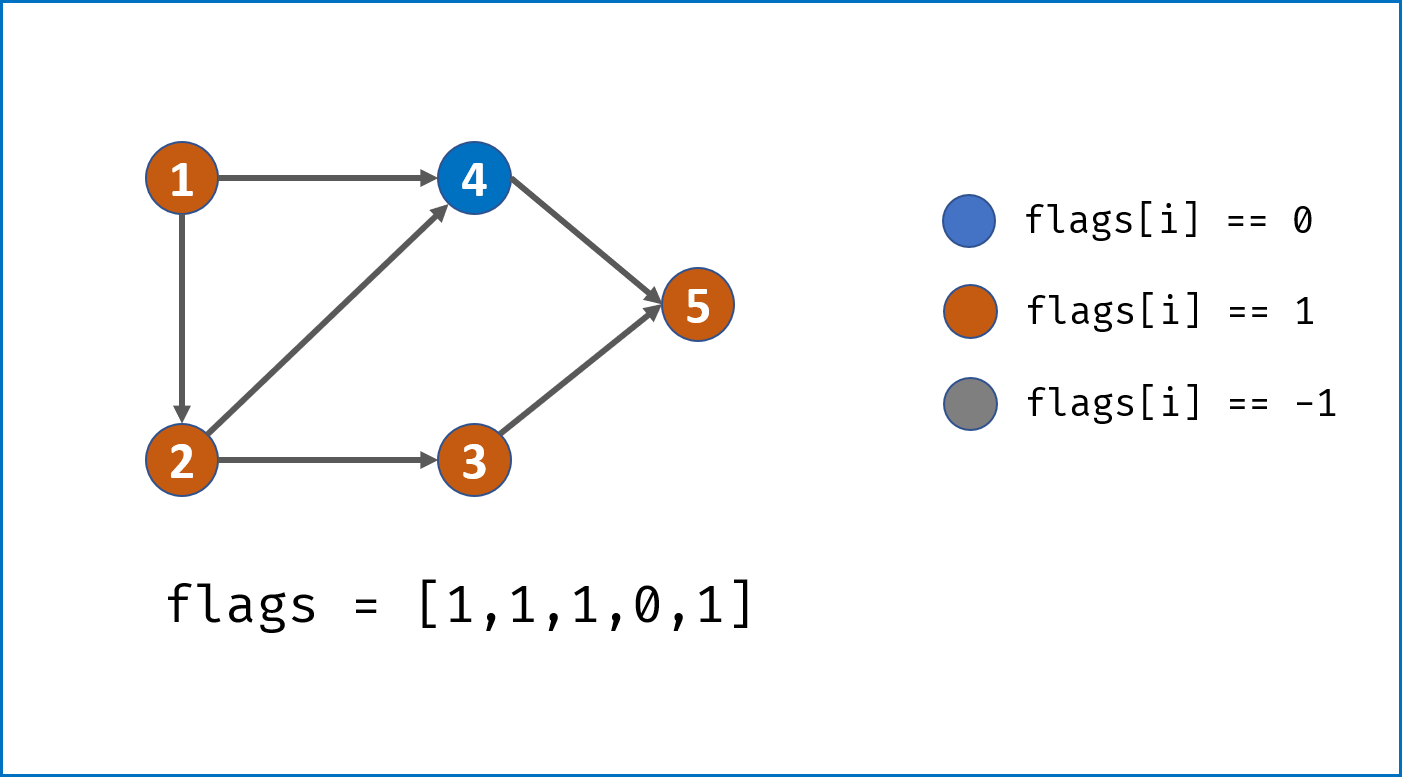
    2. 将当前访问节点 i 对应 flag[i] 置 $1$，即标记其被本轮 DFS 访问过；
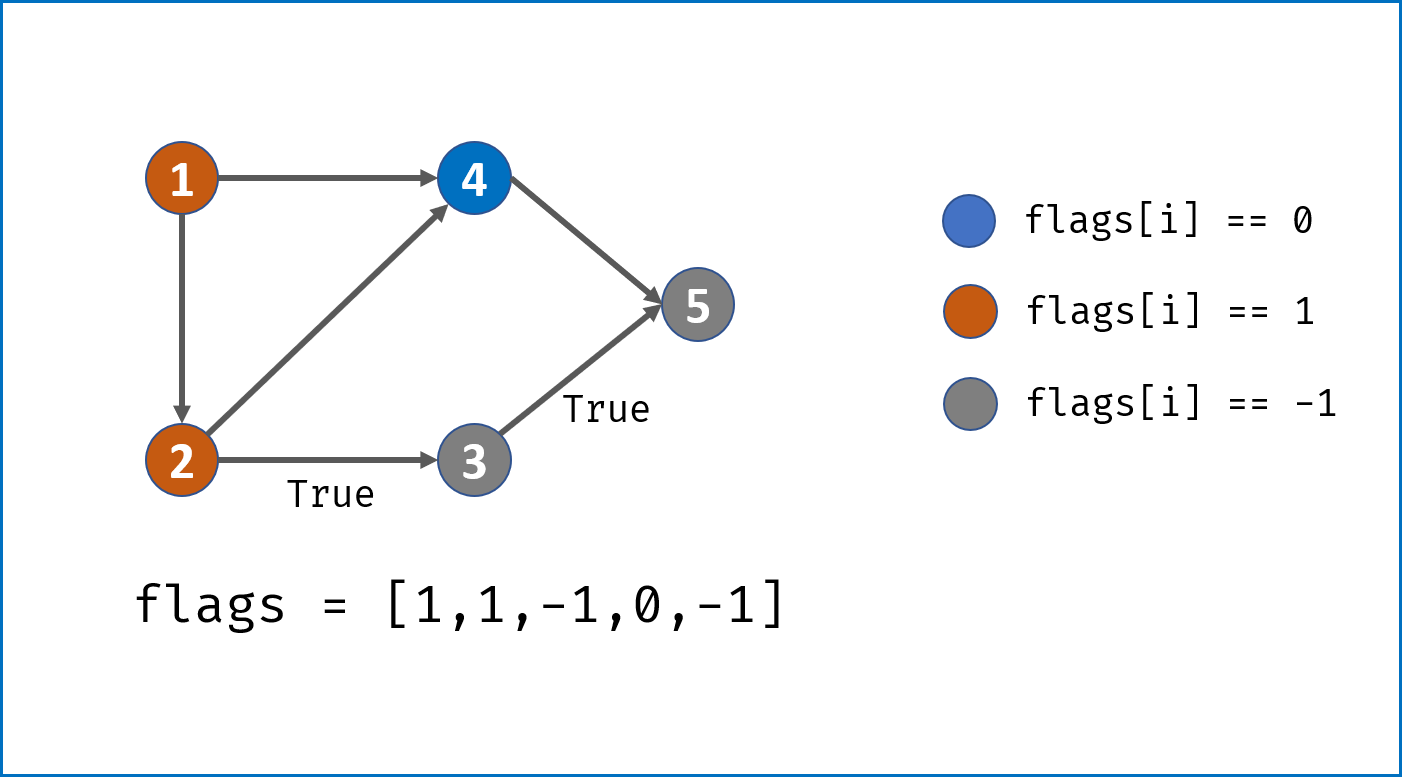
    3. 递归访问当前节点 i 的所有邻接节点 j，当发现环直接返回 $False$；
    4. 当前节点所有邻接节点已被遍历，并没有发现环，则将当前节点 flag 置为 $-1$ 并返回 $True$。
  3. 若整个图 DFS 结束并未发现环，返回 $True$。
复杂度分析： ​
  • 时间复杂度 $O(N + M)$： 遍历一个图需要访问所有节点和所有临边，$N$ 和 $M$ 分别为节点数量和临边数量；
  • 空间复杂度 $O(N + M)$： 为建立邻接表所需额外空间，adjacency 长度为 $N$ ，并存储 $M$ 条临边的数据。

<Picture1.png,Picture2.png,Picture3.png,Picture4.png,Picture5.png,Picture6.png,Picture7.png,Picture8.png,Picture9.png,Picture10.png>

代码： ​

Python
class Solution:
    def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:
        def dfs(i, adjacency, flags):
            if flags[i] == -1: return True
            if flags[i] == 1: return False
            flags[i] = 1
            for j in adjacency[i]:
                if not dfs(j, adjacency, flags): return False
            flags[i] = -1
            return True

        adjacency = [[] for _ in range(numCourses)]
        flags = [0 for _ in range(numCourses)]
        for cur, pre in prerequisites:
            adjacency[pre].append(cur)
        for i in range(numCourses):
            if not dfs(i, adjacency, flags): return False
        return True
Java
class Solution {
    public boolean canFinish(int numCourses, int[][] prerequisites) {
        List<List<Integer>> adjacency = new ArrayList<>();
        for(int i = 0; i < numCourses; i++)
            adjacency.add(new ArrayList<>());
        int[] flags = new int[numCourses];
        for(int[] cp : prerequisites)
            adjacency.get(cp[1]).add(cp[0]);
        for(int i = 0; i < numCourses; i++)
            if(!dfs(adjacency, flags, i)) return false;
        return true;
    }
    private boolean dfs(List<List<Integer>> adjacency, int[] flags, int i) {
        if(flags[i] == 1) return false;
        if(flags[i] == -1) return true;
        flags[i] = 1;
        for(Integer j : adjacency.get(i))
            if(!dfs(adjacency, flags, j)) return false;
        flags[i] = -1;
        return true;
    }
}

感谢评论区各位大佬 @马嘉利 @GSbeegnnord @mountaincode @kin @131xxxx8381 @dddong @chuwenli @JiangJian @番茄大大 @zjma 勘误。 本篇初稿错误频出，实属汗颜 Orz ，现已一一修正。再次感谢！

MIT License.

Copyright © 2024 自律小屋