自律小屋 | 自律小屋

解题思路：

排序块定义：
- 排序块 充分条件：设此块中最大数字为 $head$ , 若此块后面的所有数字都 $>= head$ ，则此块为排序块。
- 排序块 最短长度为 $1$，即单个元素可以独立看作一个排序块。
贪心法则 （划分出尽可能多的排序块）：
- 思路一：
  - 设定双指针指向数组头部，判断双指针内数字集合形成的块是否满足排序块条件，并尽量使窗口最小（贪心）。
  - 每次形成排序块时计数，并越过此排序块重新指定双指针位置，重复以上步骤直到划分完整个数组。
  - 此思路容易理解，但每次确定 $1$ 个块都需要遍历整个数组，在某些极端情况（例如如 $[1,2,3,4,5]$ ）时间复杂度达到 $O(N^2)$ 。
- 思路二（本题解采用）：
  - 判断是否是排序块只需要用到该块的 元素最大值 $head$ 。我们联想到，是否可以遍历一遍数组 $arr$ ，动态判断到目前数字 $num$ 为止最多能分出多少排序块，并保存每个排序块的最大值 $head$ 。每遍历到下个数字 $num$ ，动态判断前面所有的排序块是否成立，并更新所有排序块：
    - 当某排序块 $num < head$ ：将此排序块[A]与 num 合并，形成新排序块[A | num]，最大值仍为 $head$ ；
    - 当某排序块 $num >= head$ ：原排序块保留，并新加排序块 [num] 。
  - 而对于整个数组的排序块，其 $head$ 大小是从左到右递增的。例如：数组 $[1,2,1,3,4,7,5,6]$ 最多可划分为 $[1|2,1|3|4|7,5,6]$ ，$head$ 为 $[1,2,3,4,7]$ 。因此，若给数组尾部加入一个随机正整数 $n$ ，尾部的排序块更容易被合并（最先满足 $num < head$ ）。当 $n$ 值较小时（ $<$ 前面多个排序块的 $head$ ），则需按尾部到首部的顺序合并多个排序块。
  - 这种先入（首部到尾部添加排序块）后出（尾部到首部判断并合并排序块）的特性，让我们联想到使用栈保存排序块最大值 $head$ 。在遍历过程中，通过维护栈的 $head$ 序列，实现排序块的动态更新。
算法流程：
1. 遍历数组 $arr$ 中的每个数字 $num$ ；
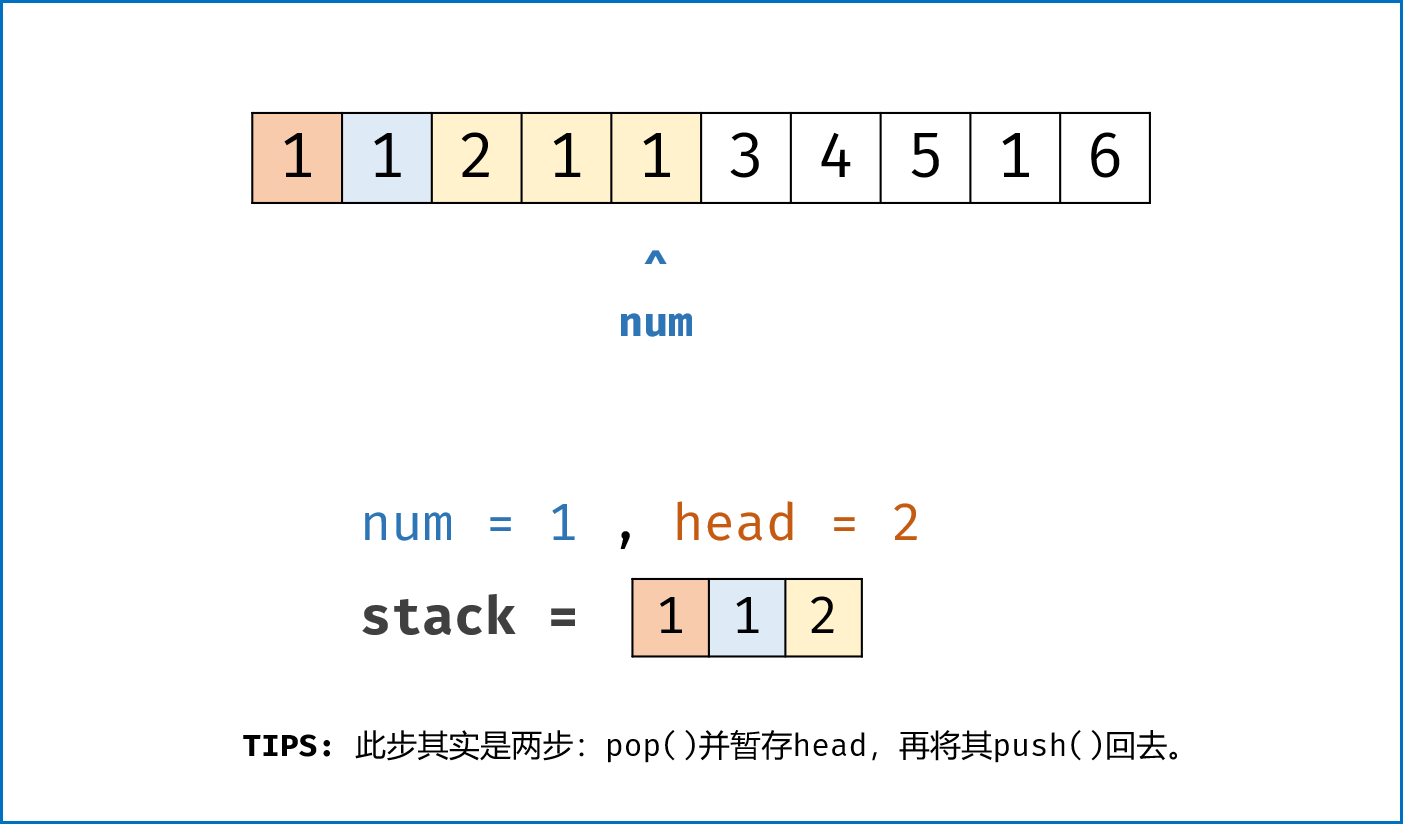
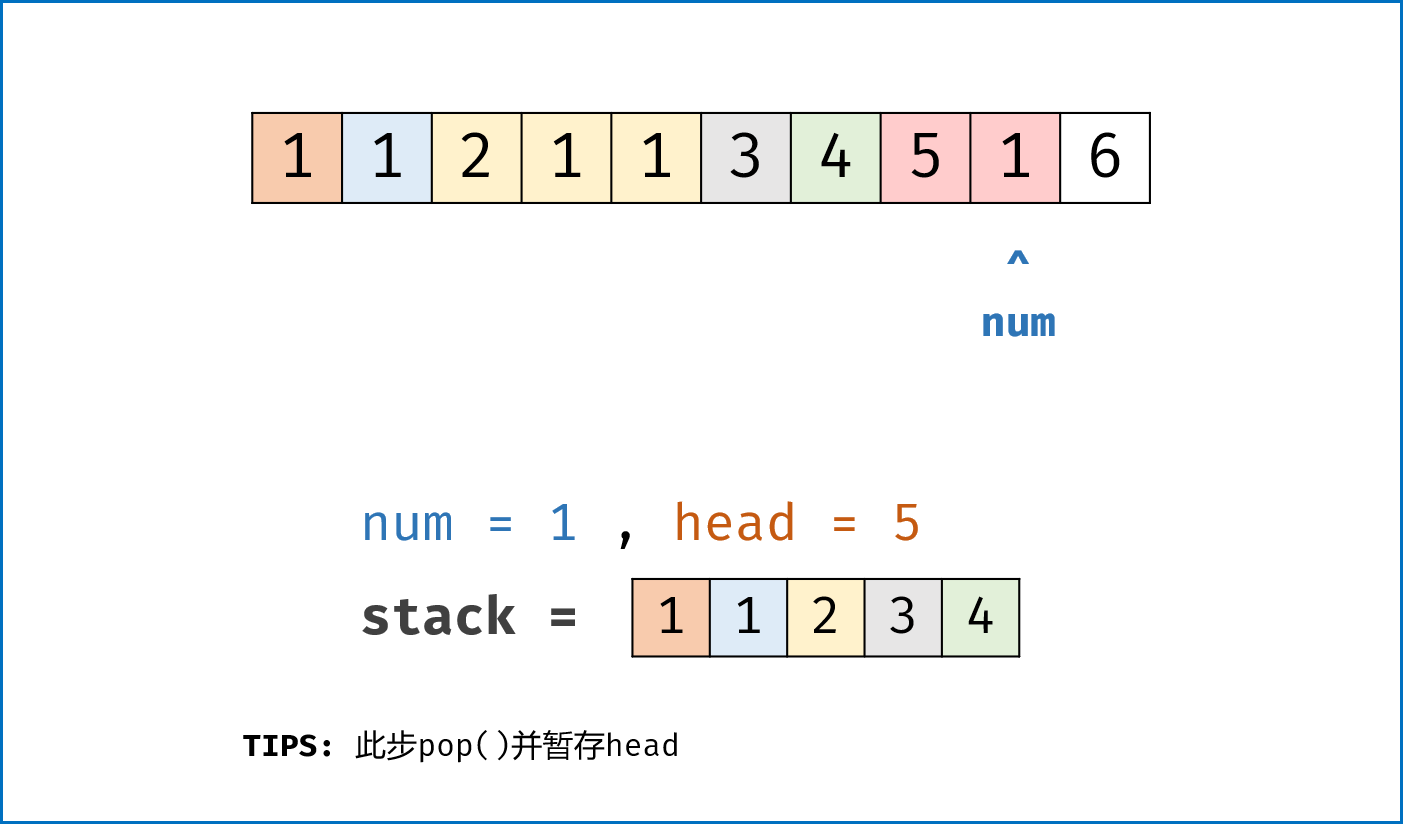
2. 当栈 $stack$ 不为空且数字 $num<$栈顶值时： （代表此 $num$ 会改变前面排序块分布）
  - 栈顶 pop() 出栈，并保存栈顶值为 $head$ 。 （此情况下，新排序块最大值还为 $head$ ，因此先暂存）
  - 当 $stack$ 不为空且数字 $num<$栈顶值时，循环栈顶 pop() 出栈。 （判断加入 $num$ 需要合并的所有排序块，每 pop() 一个 $head$ 代表合并一个块）
  - 将保存的栈顶值 $head$ 重新 push() 入栈。 （将 $head$ 重新加入，作为新排序块的最大值）
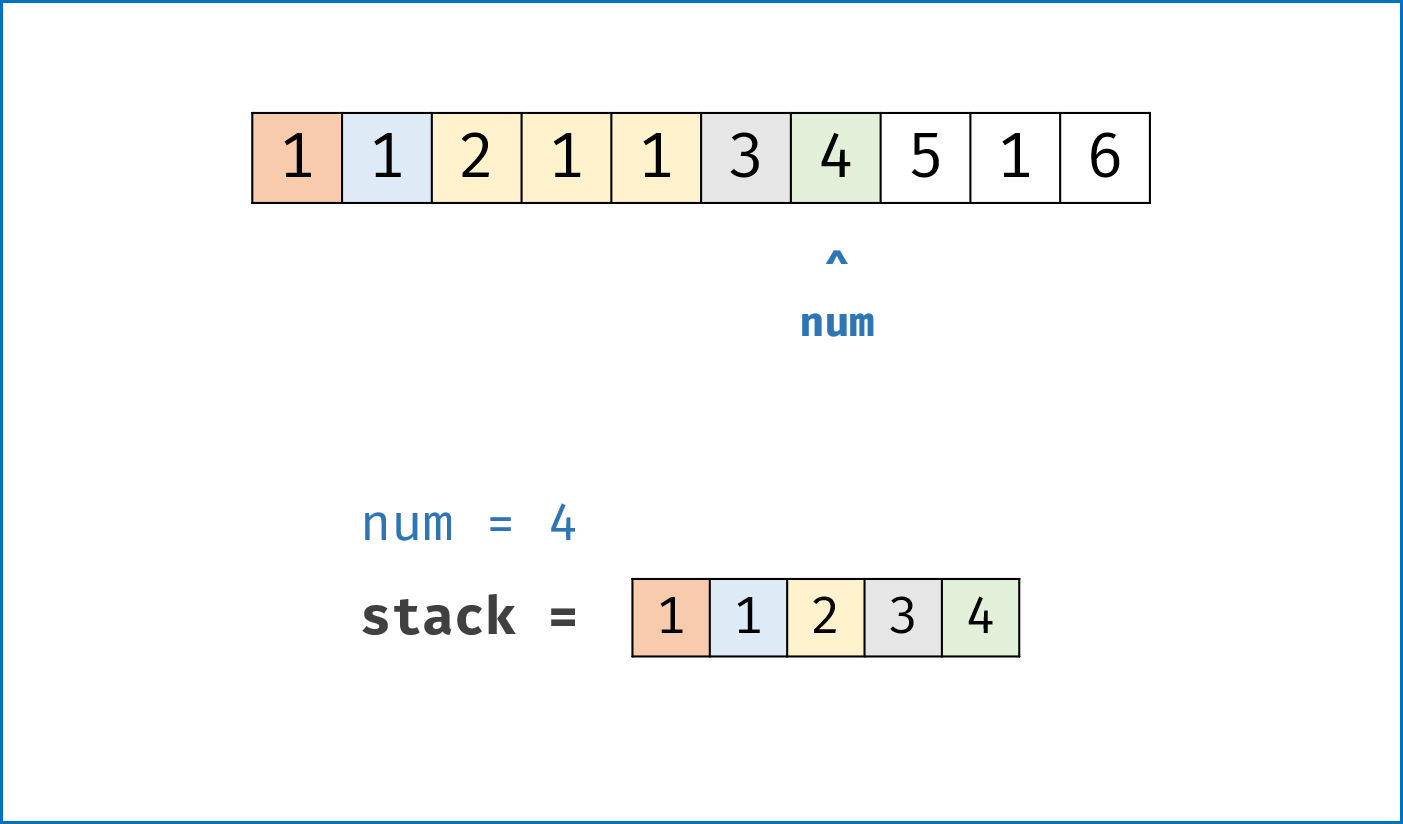
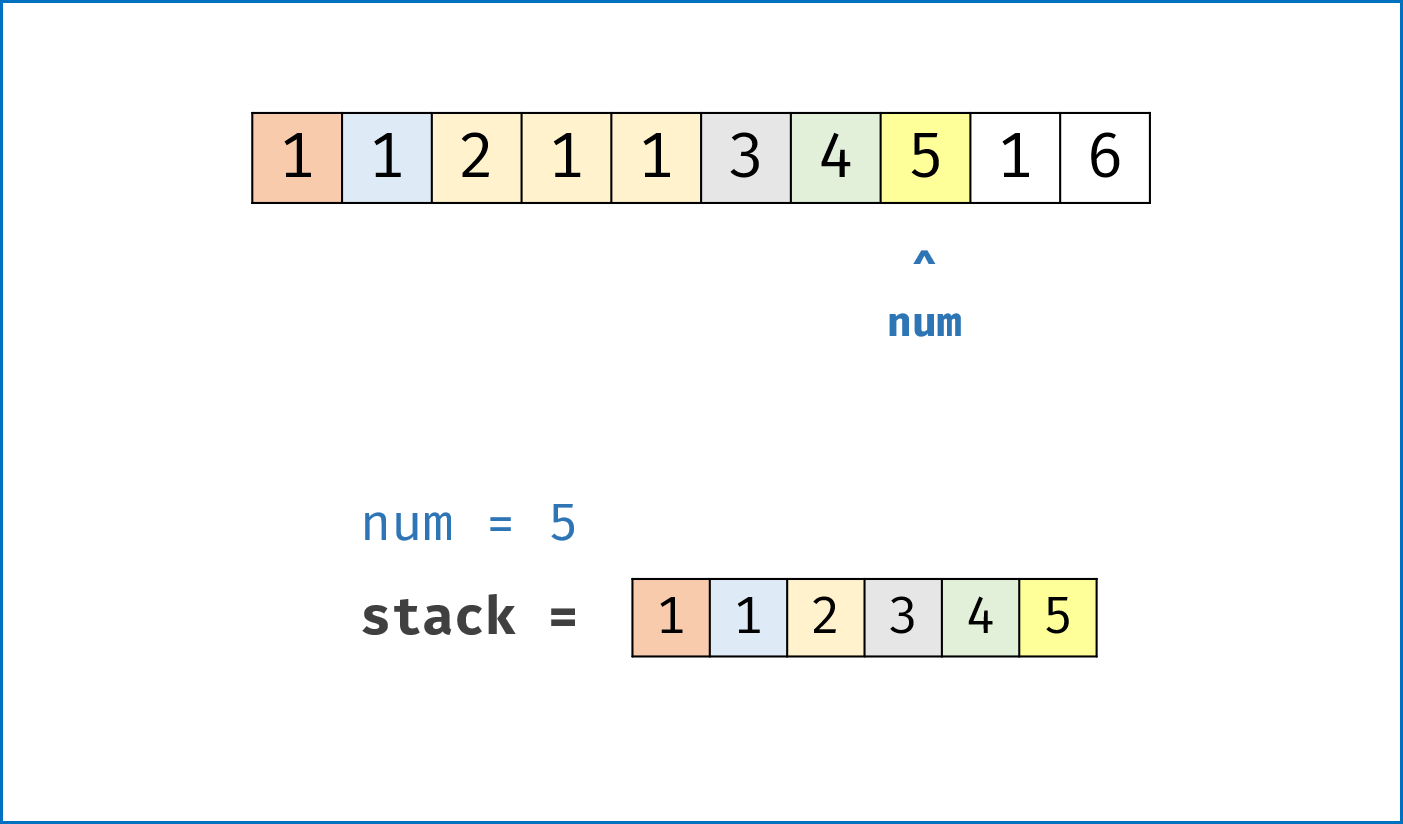
3. 当栈 $stack$ 为空或数字 $num>=$栈顶值时： （代表此 $num$ 不影响前面排序块分布）
  - 将 $num$ 数字 push() 入栈。 （加入单个元素的新排序块 [num]）
4. 遍历完成后，栈中保存 所有排序块的对应最大值 $head$ ，因此返回栈 $stack$ 长度即可获得排序块数量。
复杂度分析：
- 时间复杂度 $O(N)$ ：遍历一遍 $arr$ 为 $O(N)$，修正排序块最多遍历一遍 $arr$ 为 $O(N)$；
- 空间复杂度 $O(N)$ ：极端情况下排序块数量等于数组长度，此时 $stack$ 占用线性大小额外空间。
图解中每一种颜色代表一个排序块。

<,,,,,,,,,,,,,,>

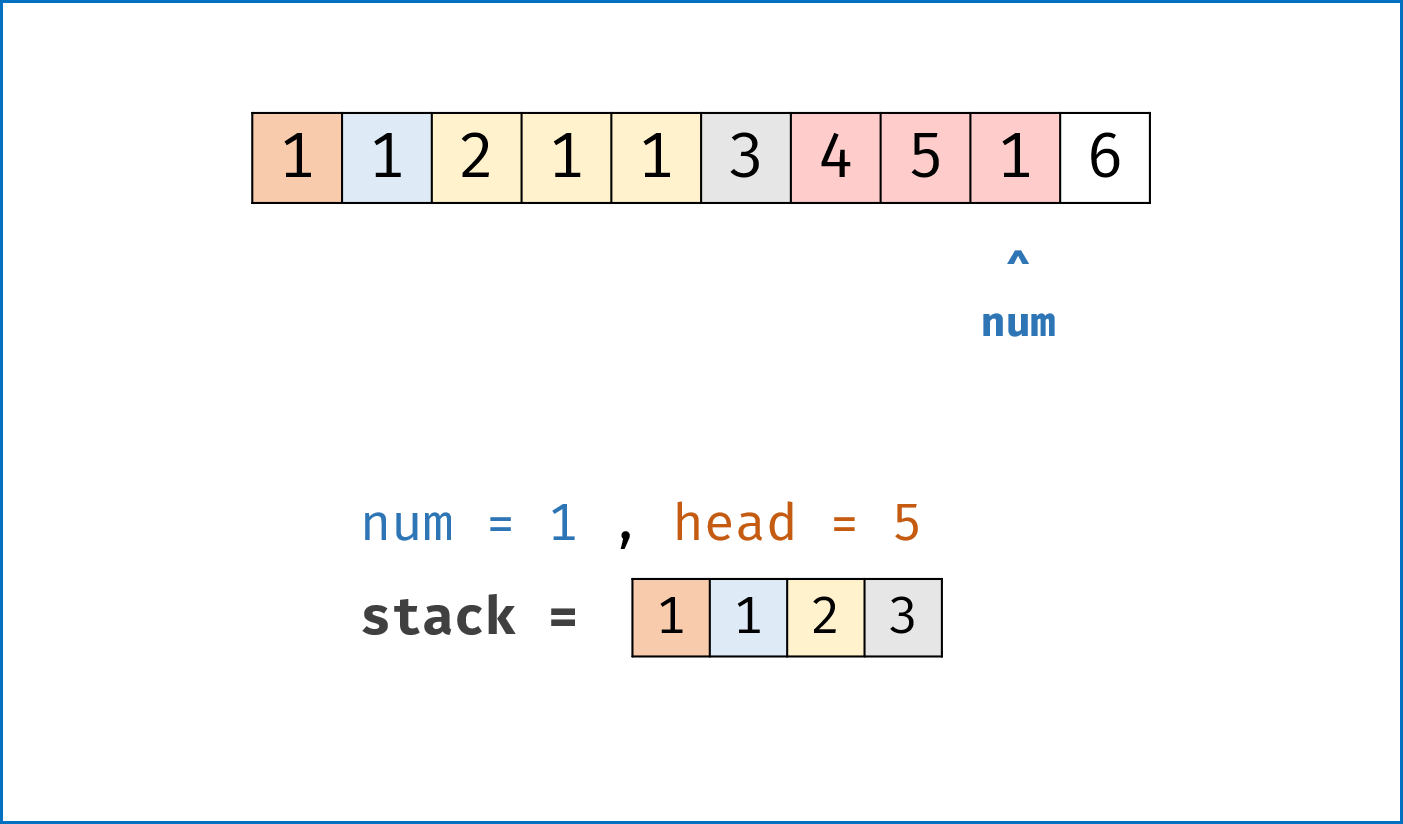代码：

python

class Solution:
    def maxChunksToSorted(self, arr: [int]) -> int:
        stack = []
        for num in arr:
            if stack and num < stack[-1]: 
                head = stack.pop()
                while stack and num < stack[-1]: stack.pop()
                stack.append(head)
            else: stack.append(num)
        return len(stack)

java

class Solution {
    public int maxChunksToSorted(int[] arr) {
        LinkedList<Integer> stack = new LinkedList<Integer>();
        for(int num : arr) {
            if(!stack.isEmpty() && num < stack.getLast()) {
                int head = stack.removeLast();
                while(!stack.isEmpty() && num < stack.getLast()) stack.removeLast();
                stack.addLast(head);
            }
            else stack.addLast(num);
        }
        return stack.size();
    }
}

解题思路： ​

代码： ​

解题思路：

代码：