解题思路:
通常使用的前序、中序、后序、层序遍历记录的二叉树的信息不完整,即唯一的输出序列可能对应着多种二叉树可能性。题目要求的 序列化 和 反序列化 是 可逆操作 。因此,序列化的字符串应携带 完整的二叉树信息 。
观察题目示例,序列化的字符串实际上是二叉树的 “层序遍历”(BFS)结果,本文也采用层序遍历。
为完整表示二叉树,考虑将叶节点下的 null 也记录。在此基础上,对于列表中任意某节点 node ,其左子节点 node.left 和右子节点 node.right 在序列中的位置都是 唯一确定 的。如下图所示:
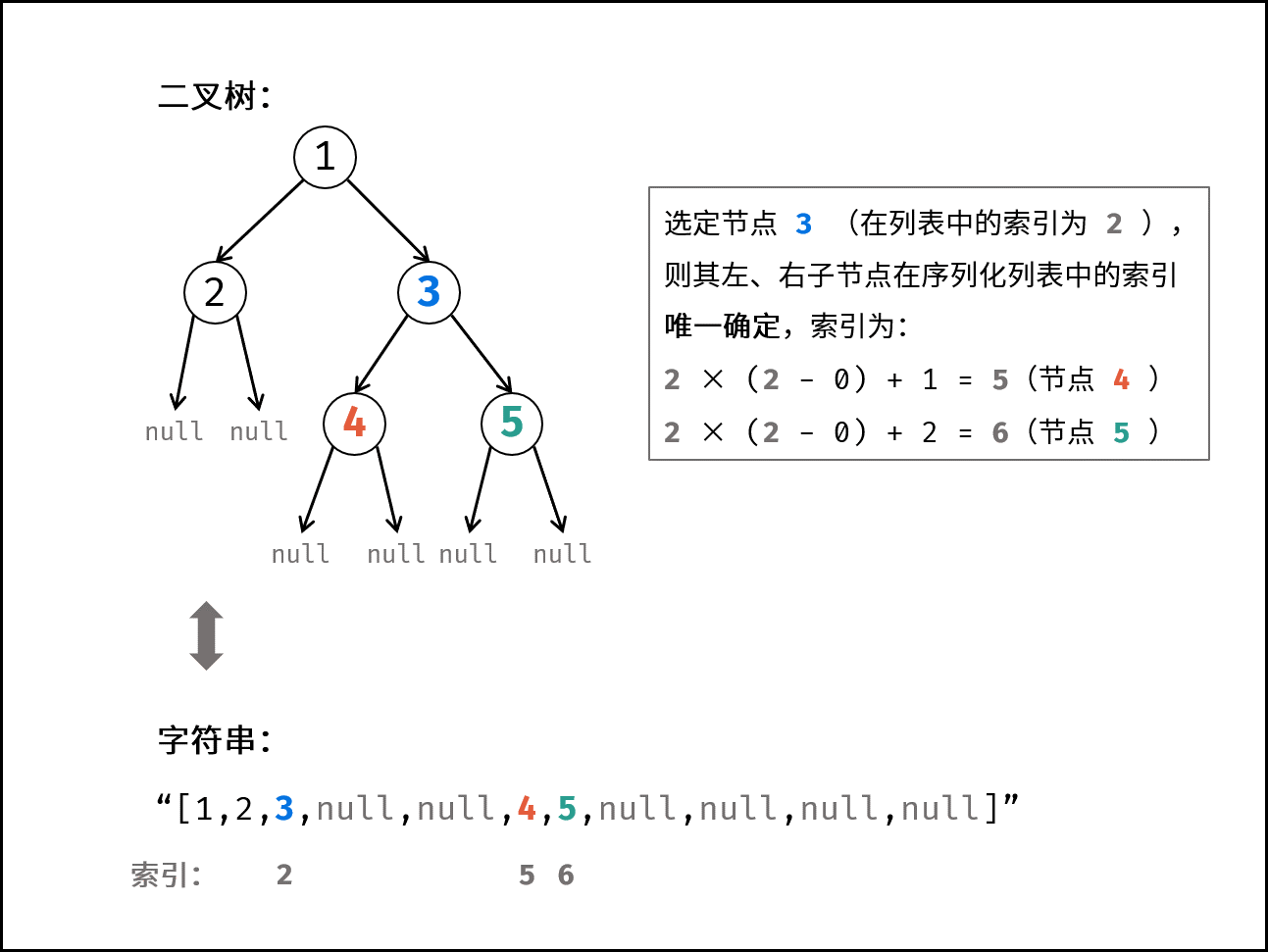
上图规律可总结为下表:
node.val | node 的索引 | node.left 的索引 | node.right 的索引 |
|---|---|---|---|
| $1$ | $0$ | $1$ | $2$ |
| $2$ | $1$ | $3$ | $4$ |
| $3$ | $2$ | $5$ | $6$ |
| $4$ | $5$ | $7$ | $8$ |
| $5$ | $6$ | $9$ | $10$ |
设 $m$ 为列表区间 $[0, n]$ 中的 null 节点个数,则可总结出根节点、左子节点、右子节点的列表索引的递推公式:
node.val | node 的列表索引 | node.left 的列表索引 | node.right 的列表索引 |
|---|---|---|---|
$\ne$ null | $n$ | $2(n-m) + 1$ | $2(n-m) + 2$ |
$=$ null | $n$ | 无 | 无 |
序列化 使用层序遍历实现。反序列化 通过以上递推公式反推各节点在序列中的索引,进而实现。
序列化 Serialize :
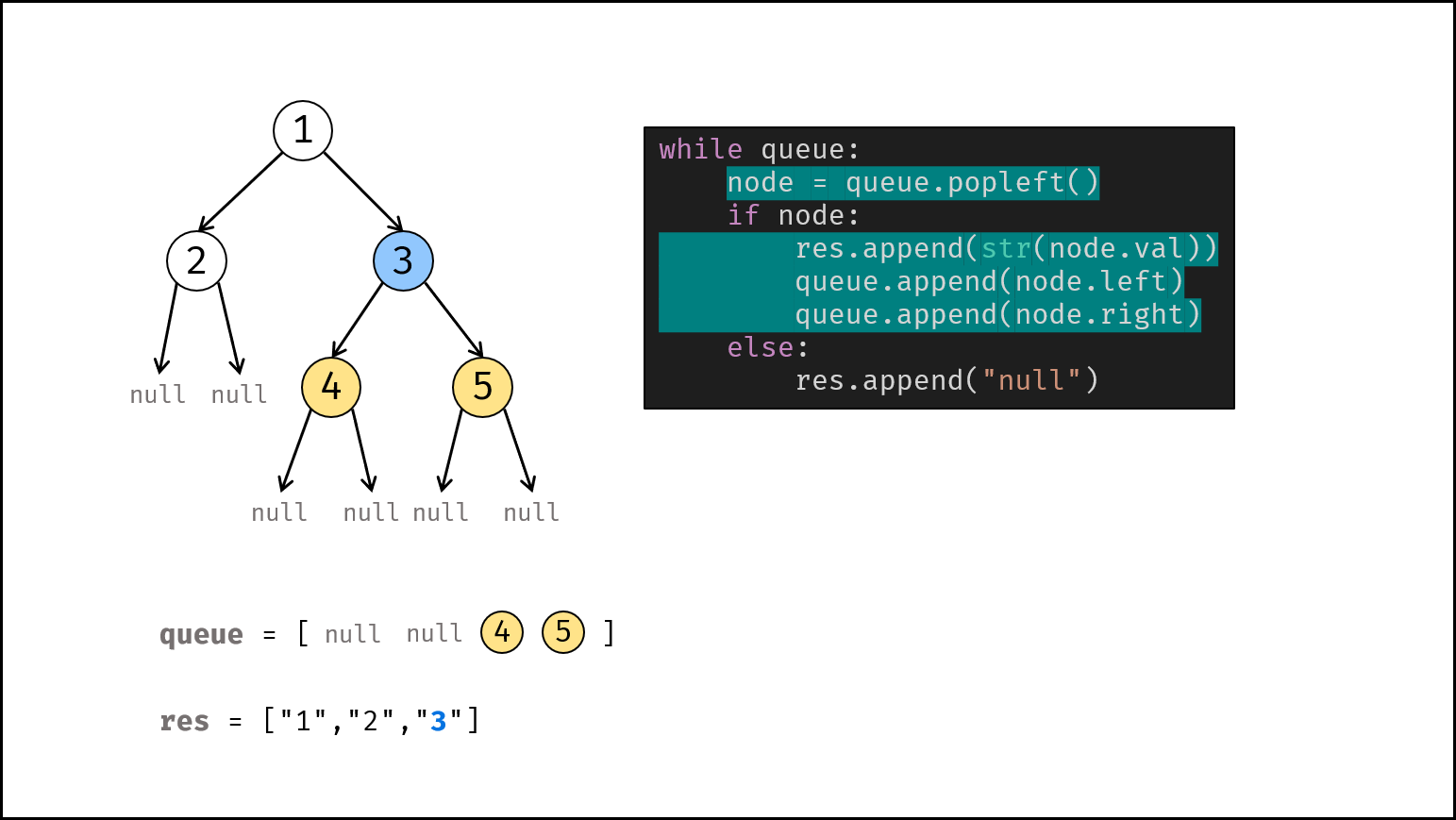
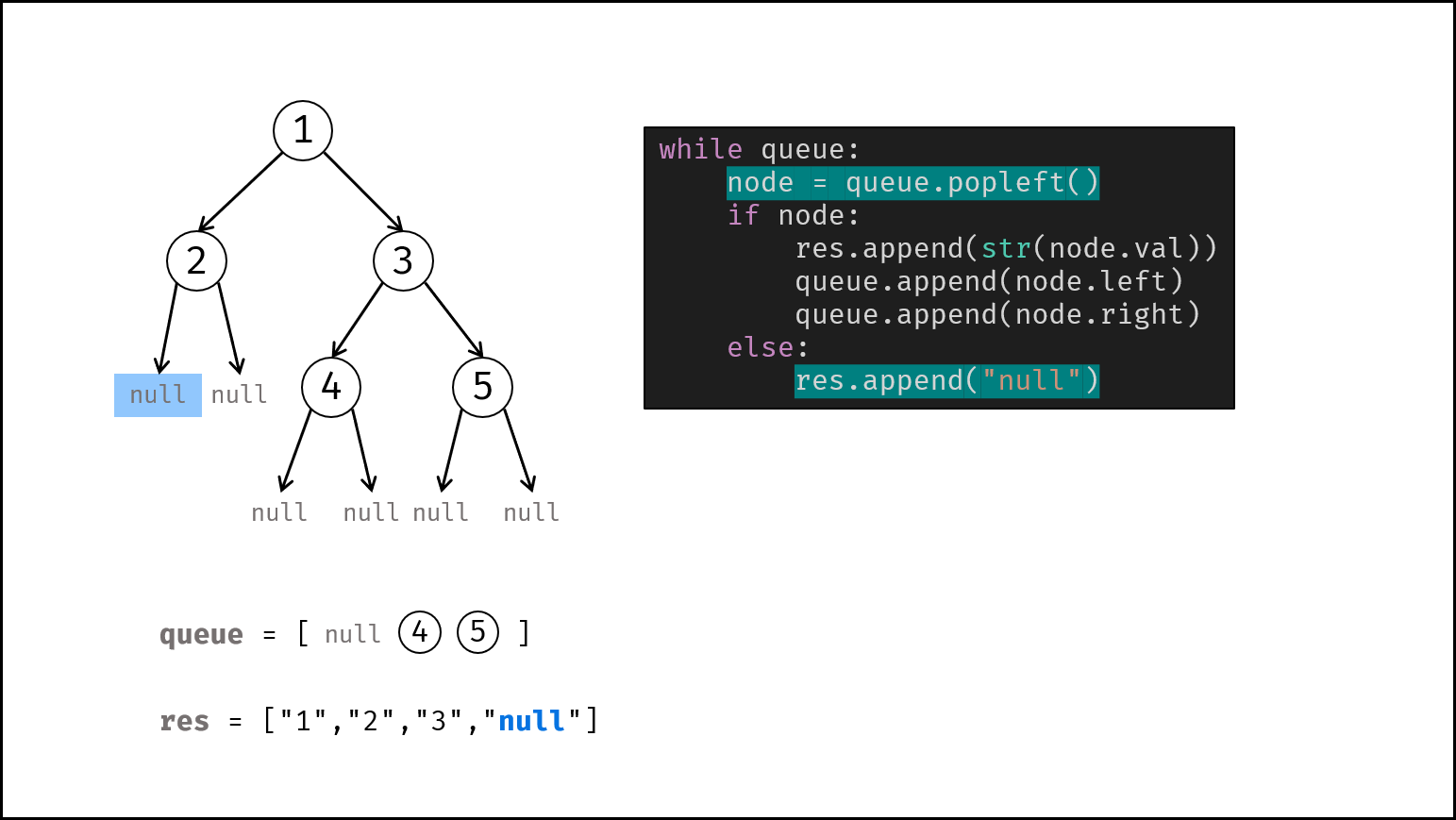
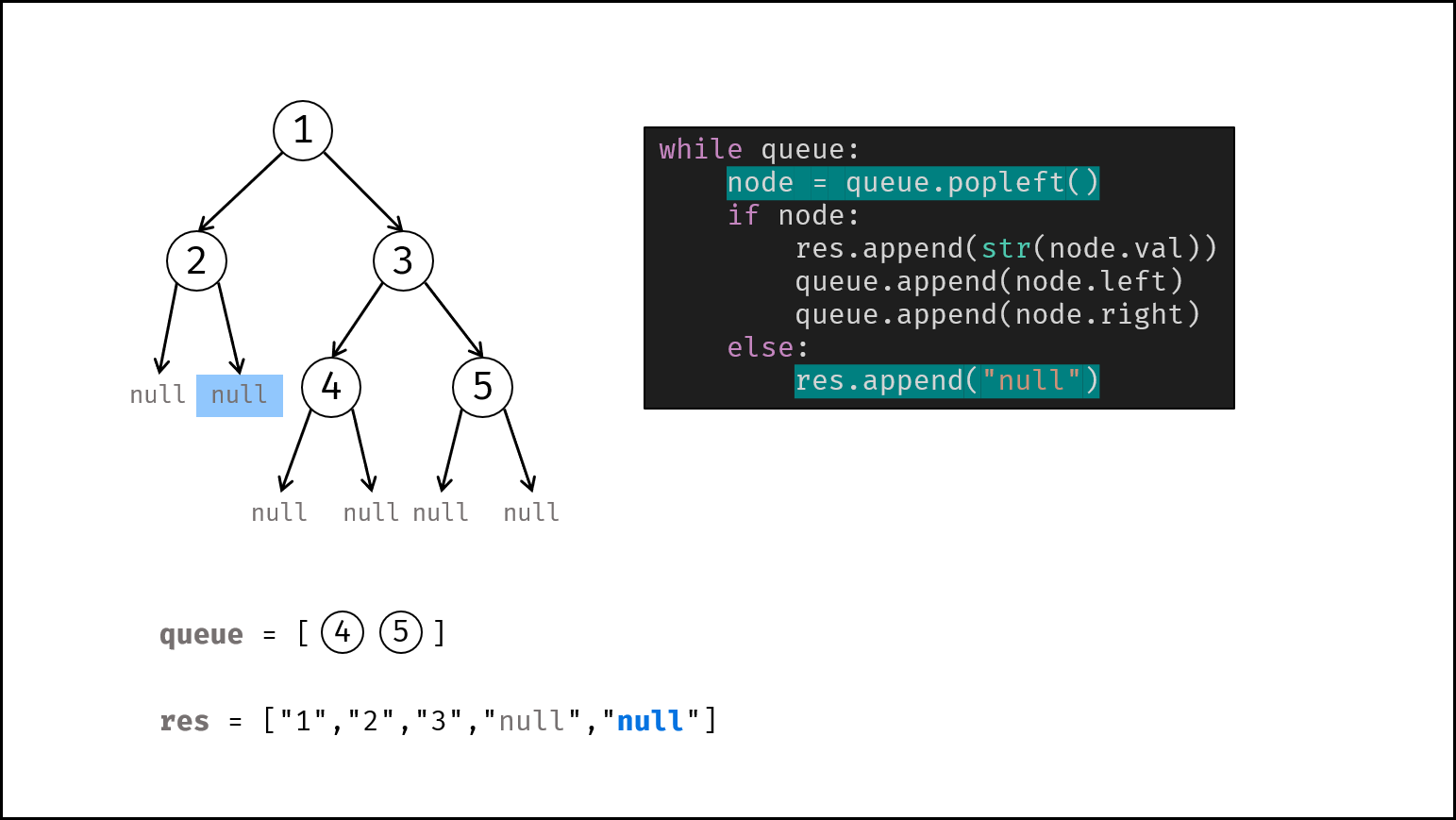
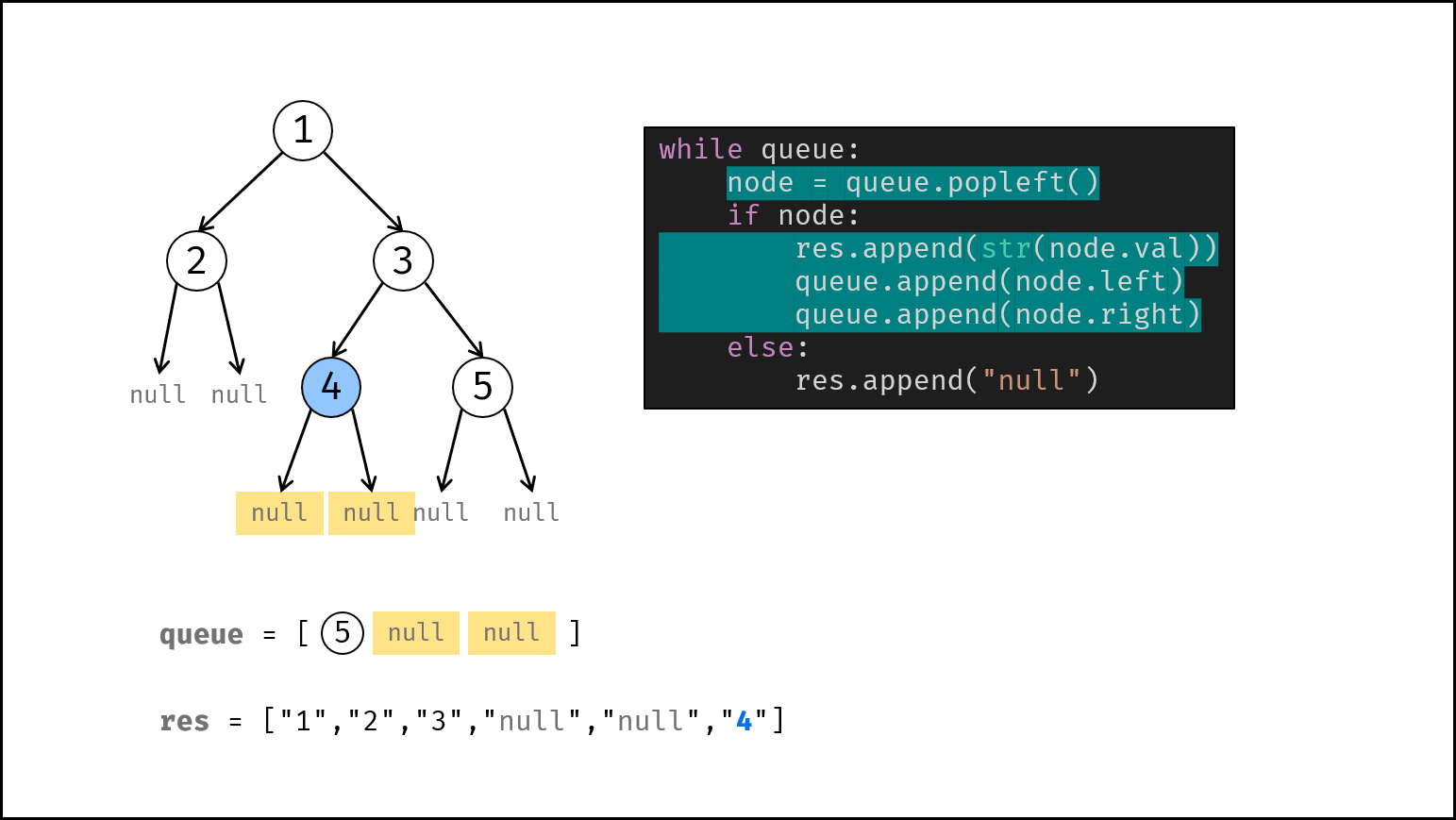
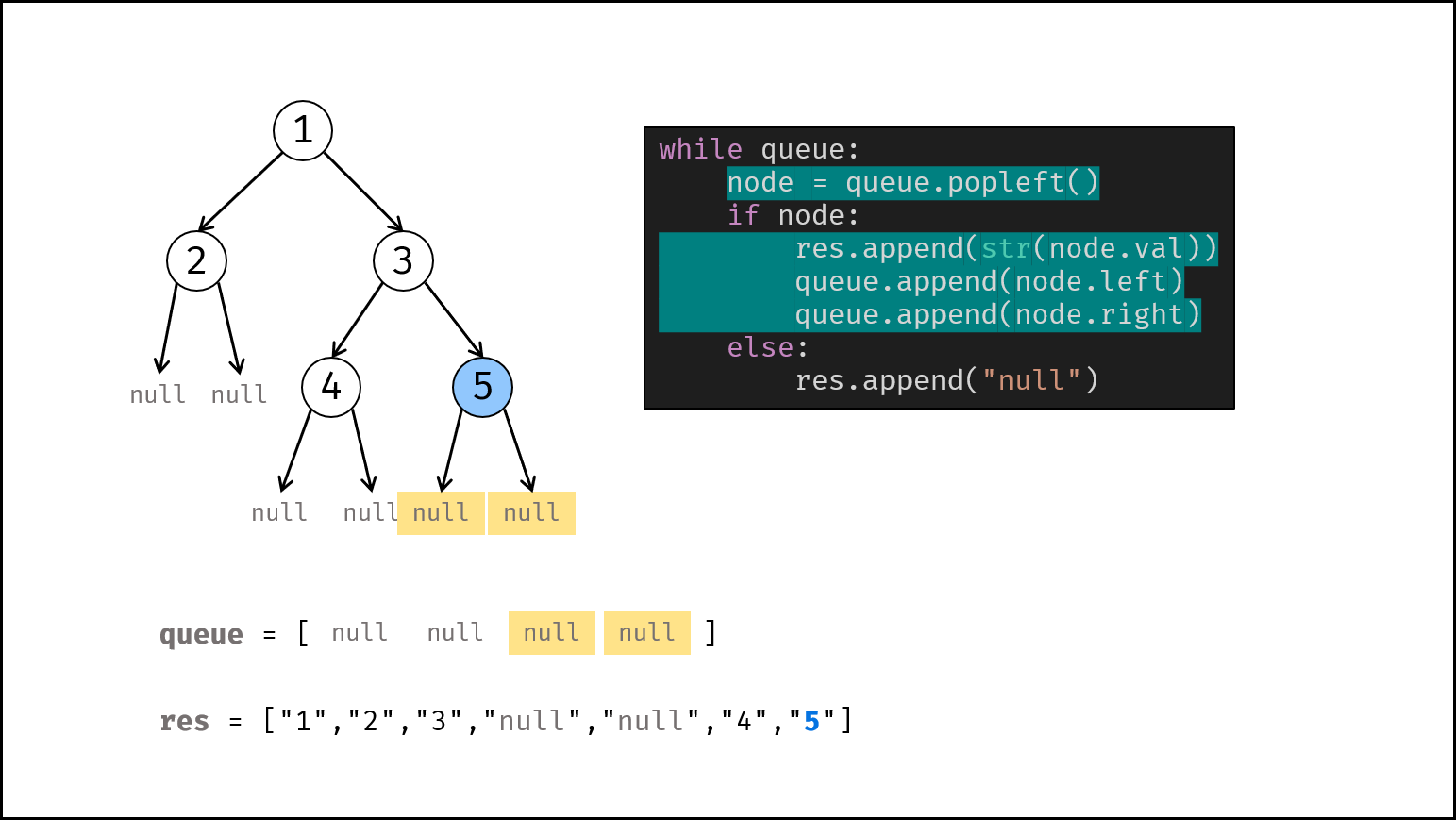
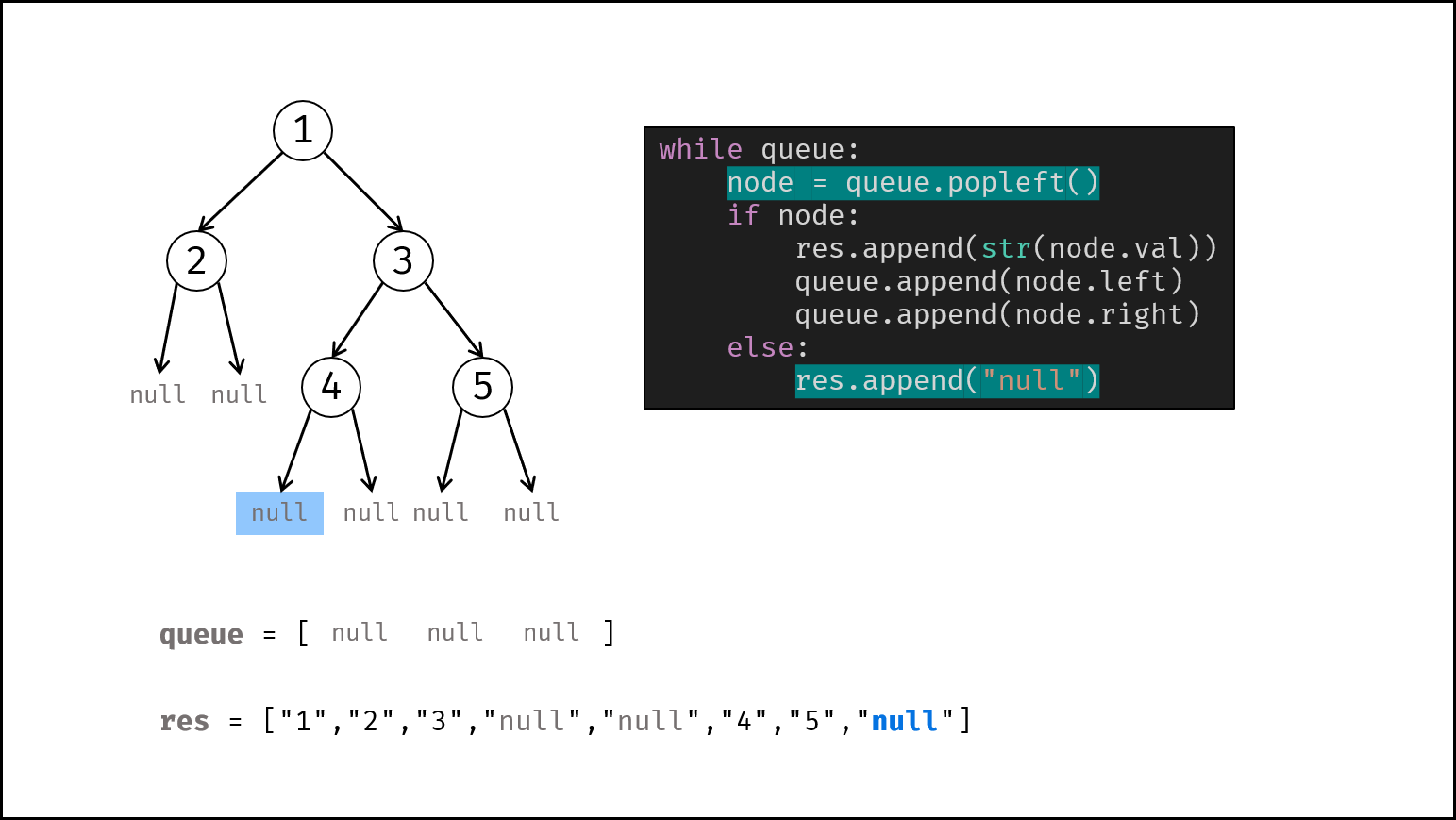
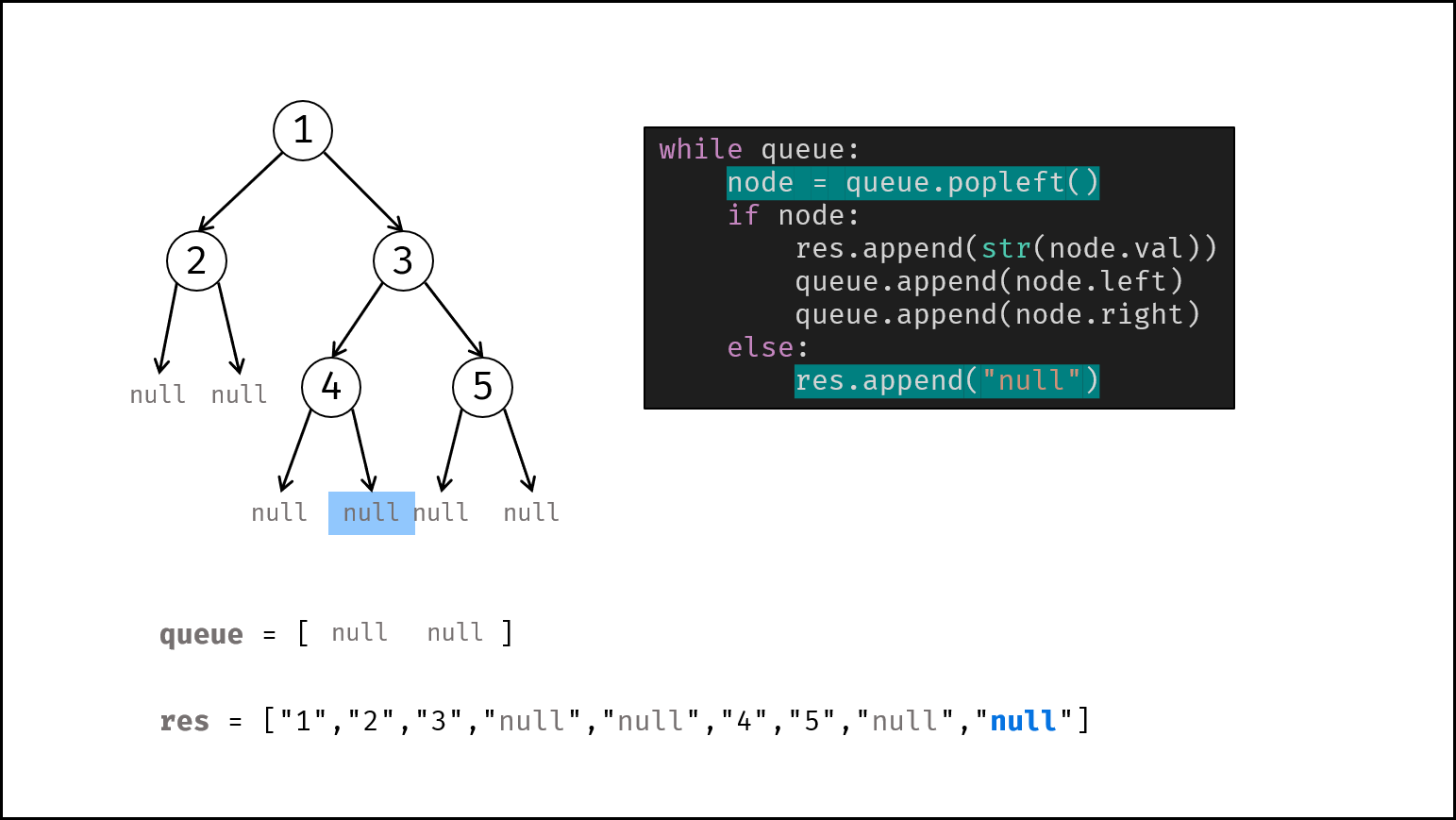
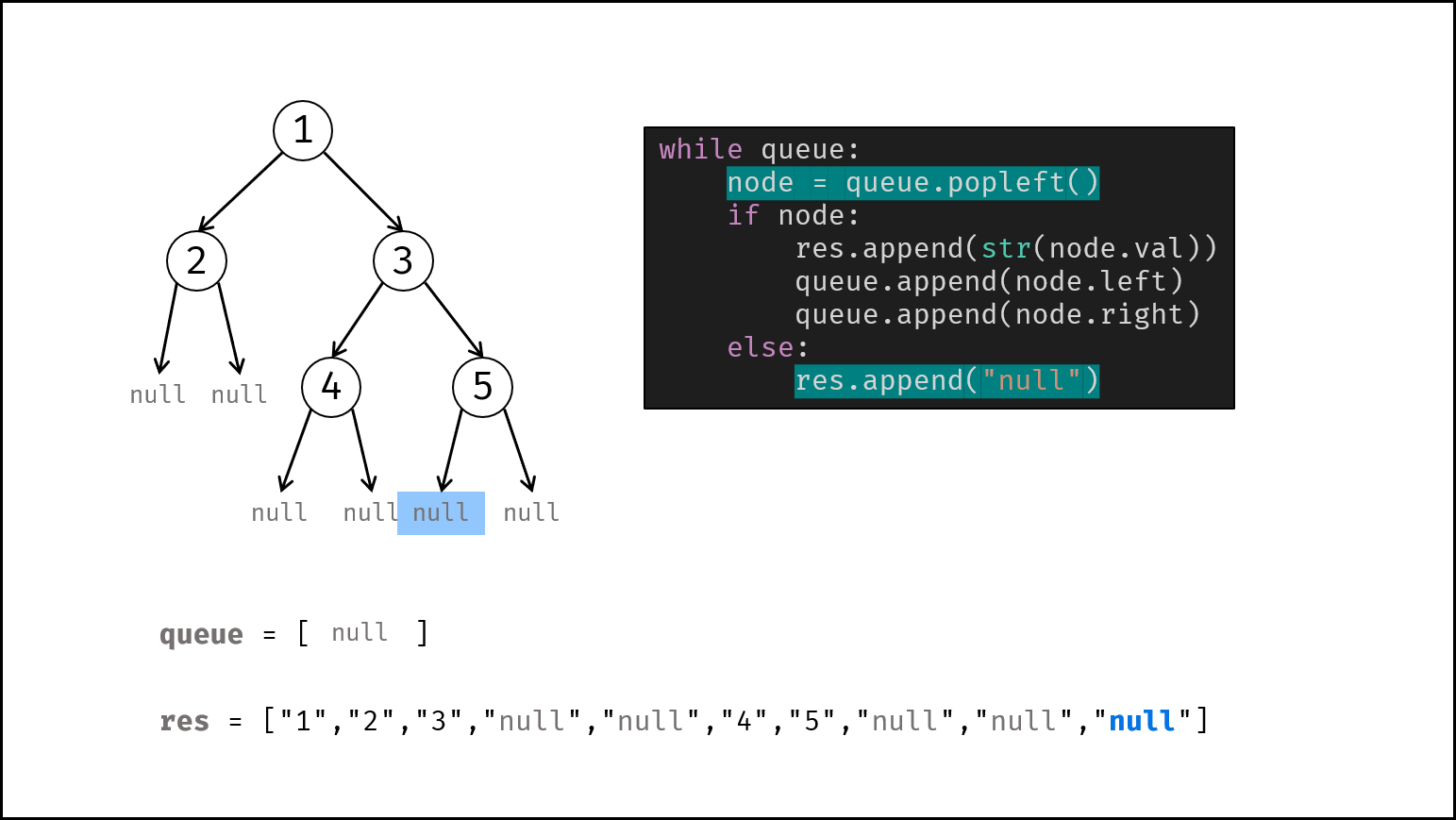
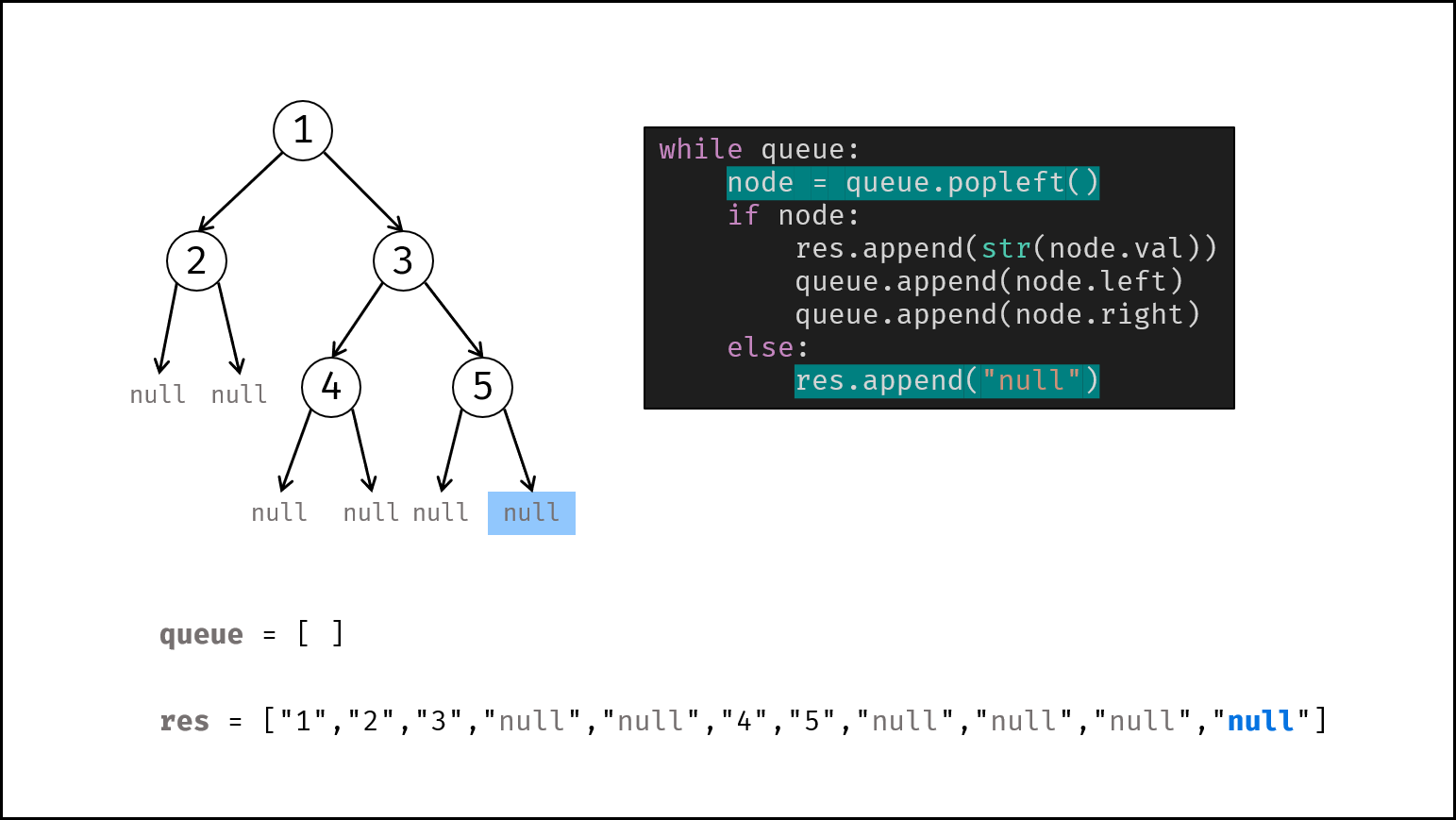
借助队列,对二叉树做层序遍历,并将越过叶节点的 null 也打印出来。
算法流程:
- 特例处理: 若
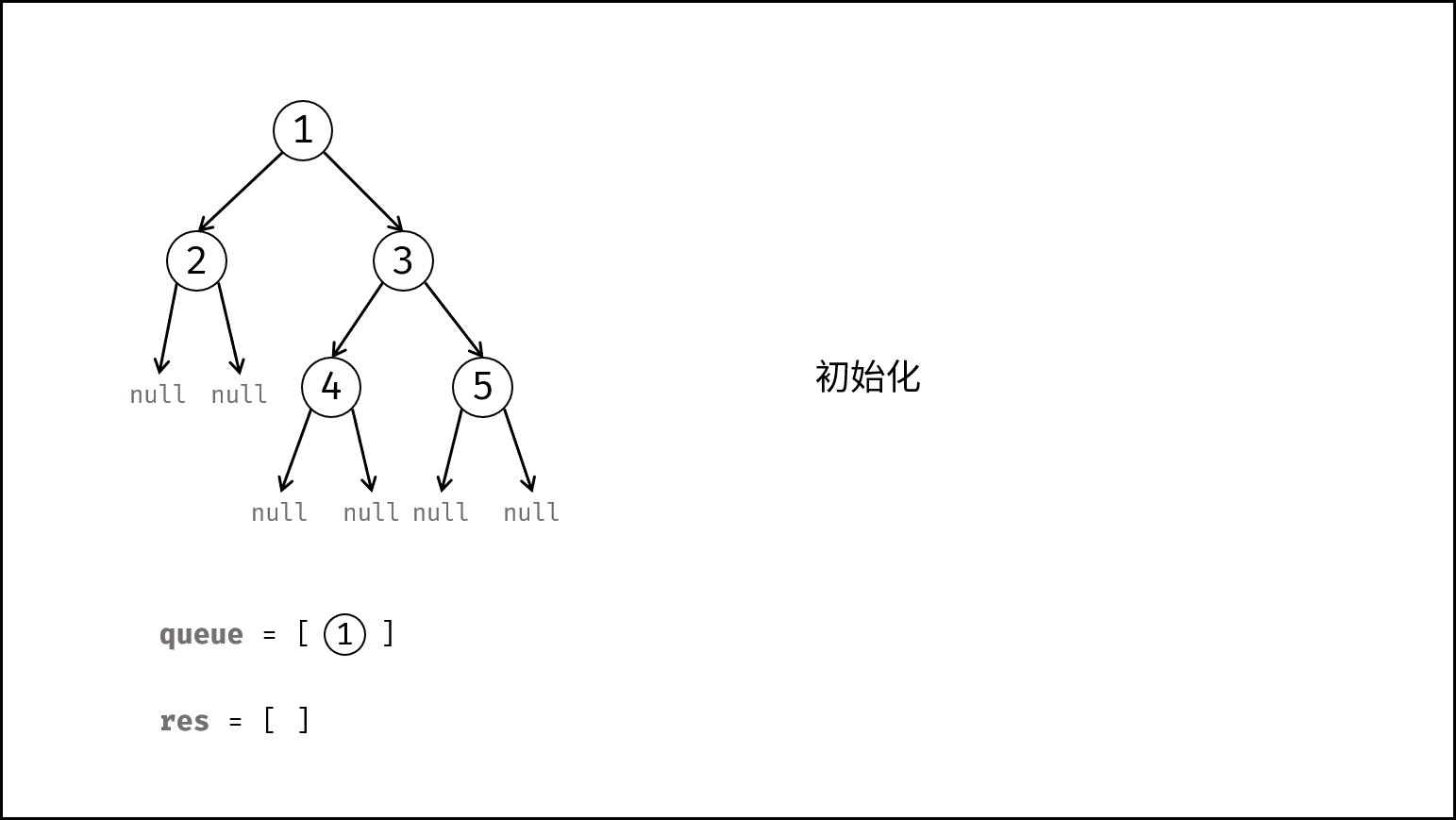
root为空,则直接返回空列表"[]"。 - 初始化: 队列
queue(包含根节点root);序列化列表res。 - 层序遍历: 当
queue为空时跳出。- 节点出队,记为
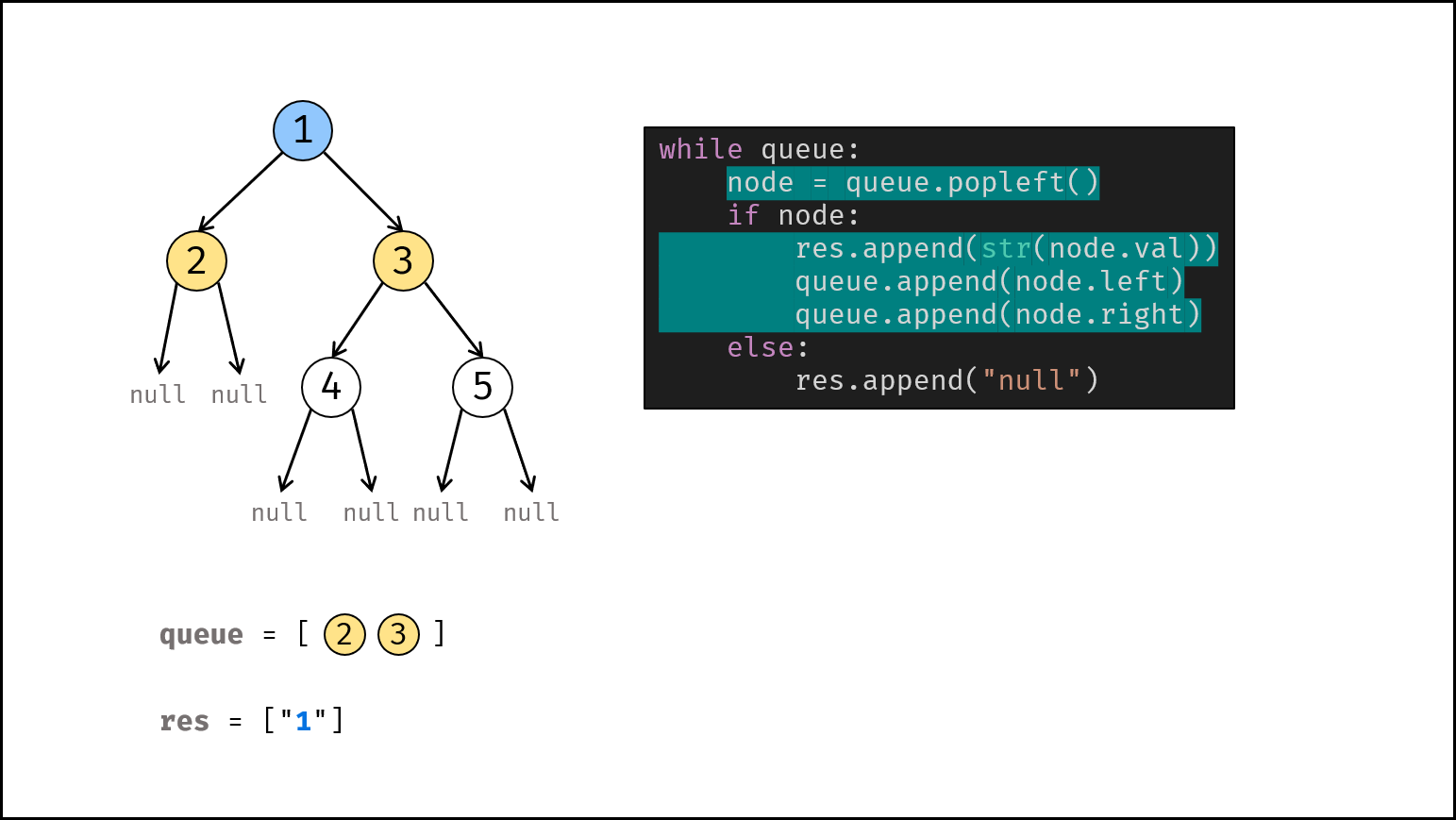
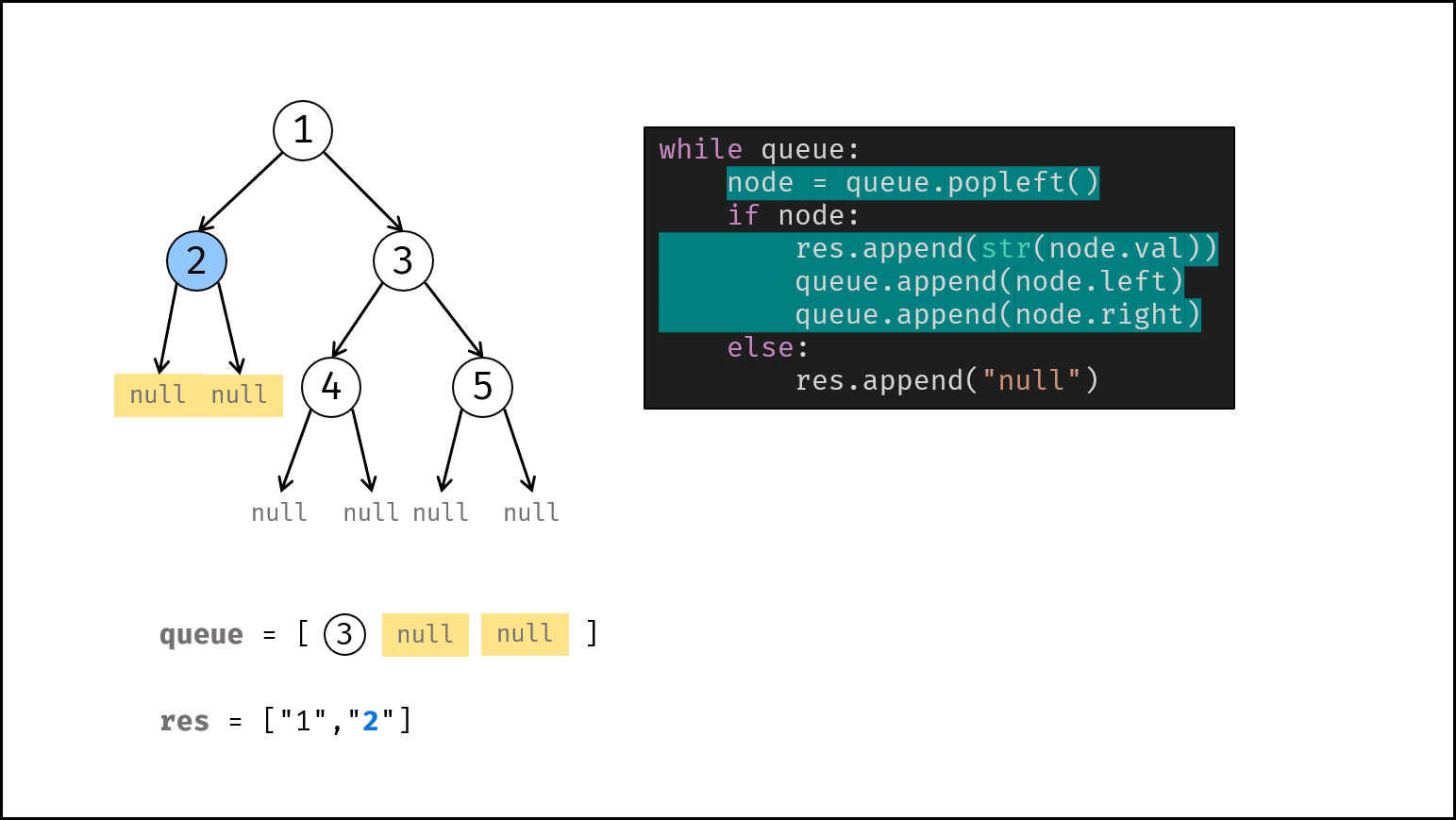
node。 - 若
node不为空:① 打印字符串node.val,② 将左、右子节点加入queue。 - 否则(若
node为空):打印字符串"null"。
- 节点出队,记为
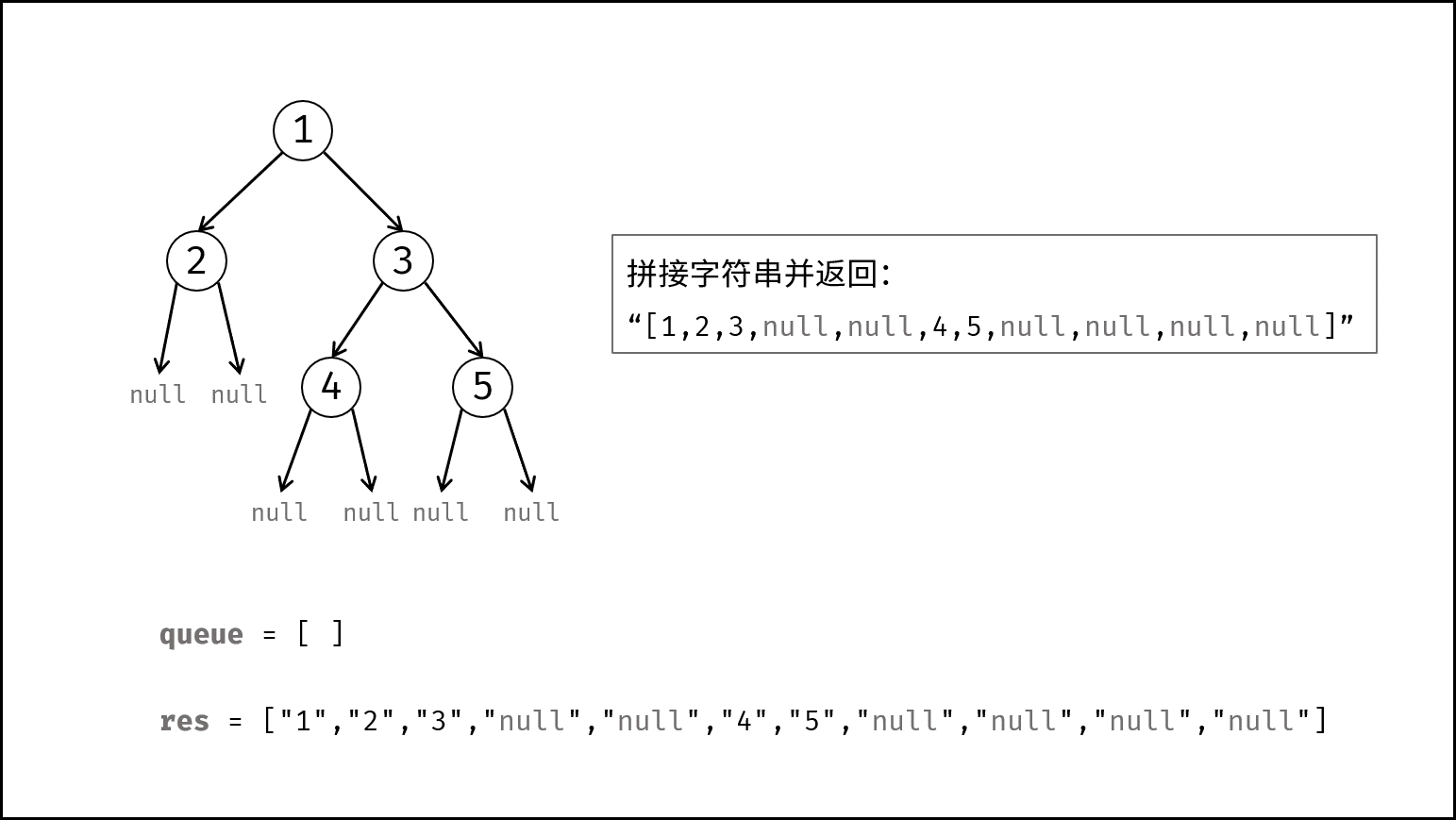
- 返回值: 拼接列表,用
','隔开,首尾添加中括号。
< ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, >
>
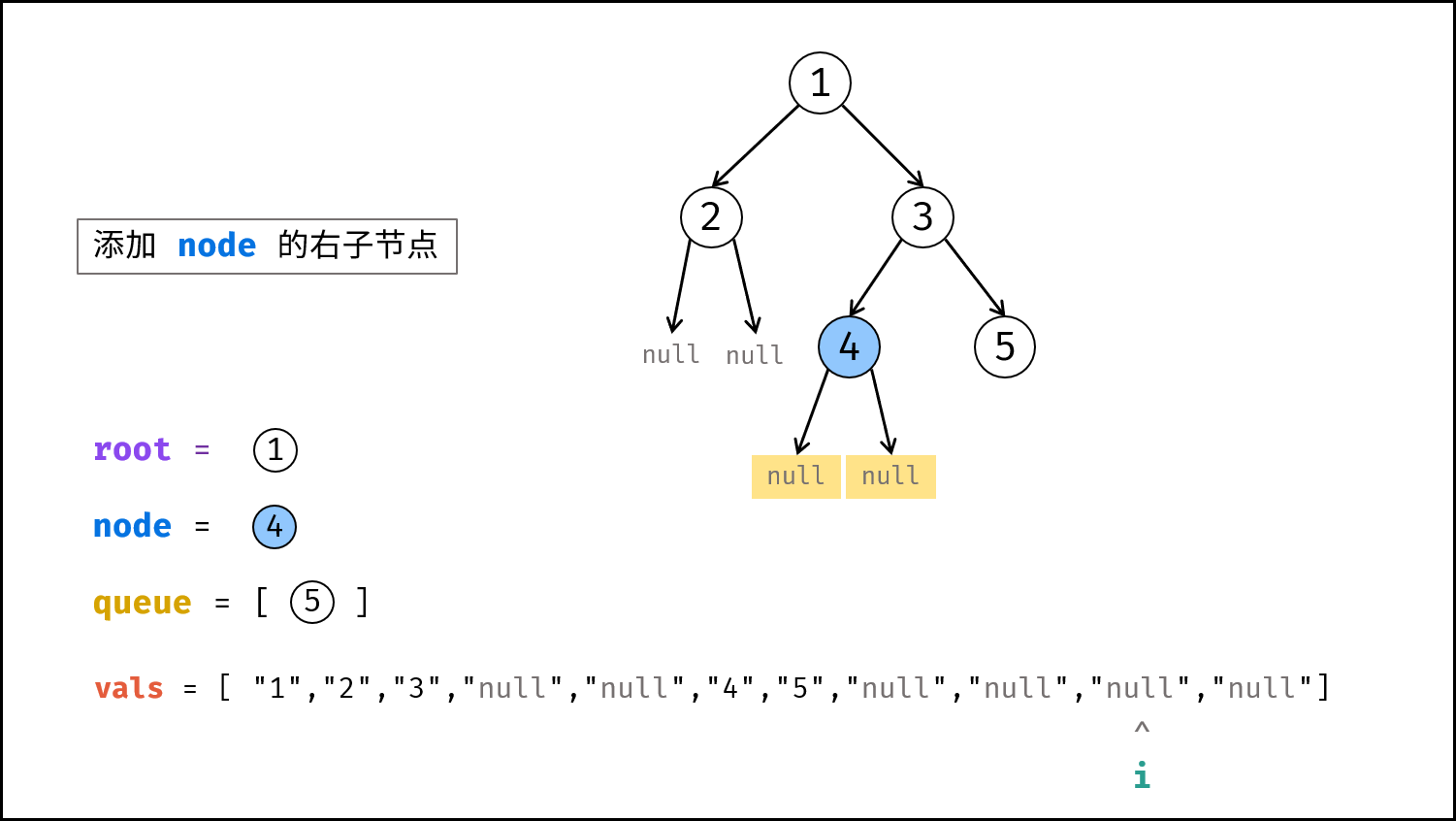
反序列化 Deserialize :
基于本文开始推出的 node , node.left , node.right 在序列化列表中的位置关系,可实现反序列化。
利用队列按层构建二叉树,借助一个指针 i 指向节点 node 的左、右子节点,每构建一个 node 的左、右子节点,指针 i 就向右移动 $1$ 位。
算法流程:
- 特例处理: 若
data为空,直接返回null。 - 初始化: 序列化列表
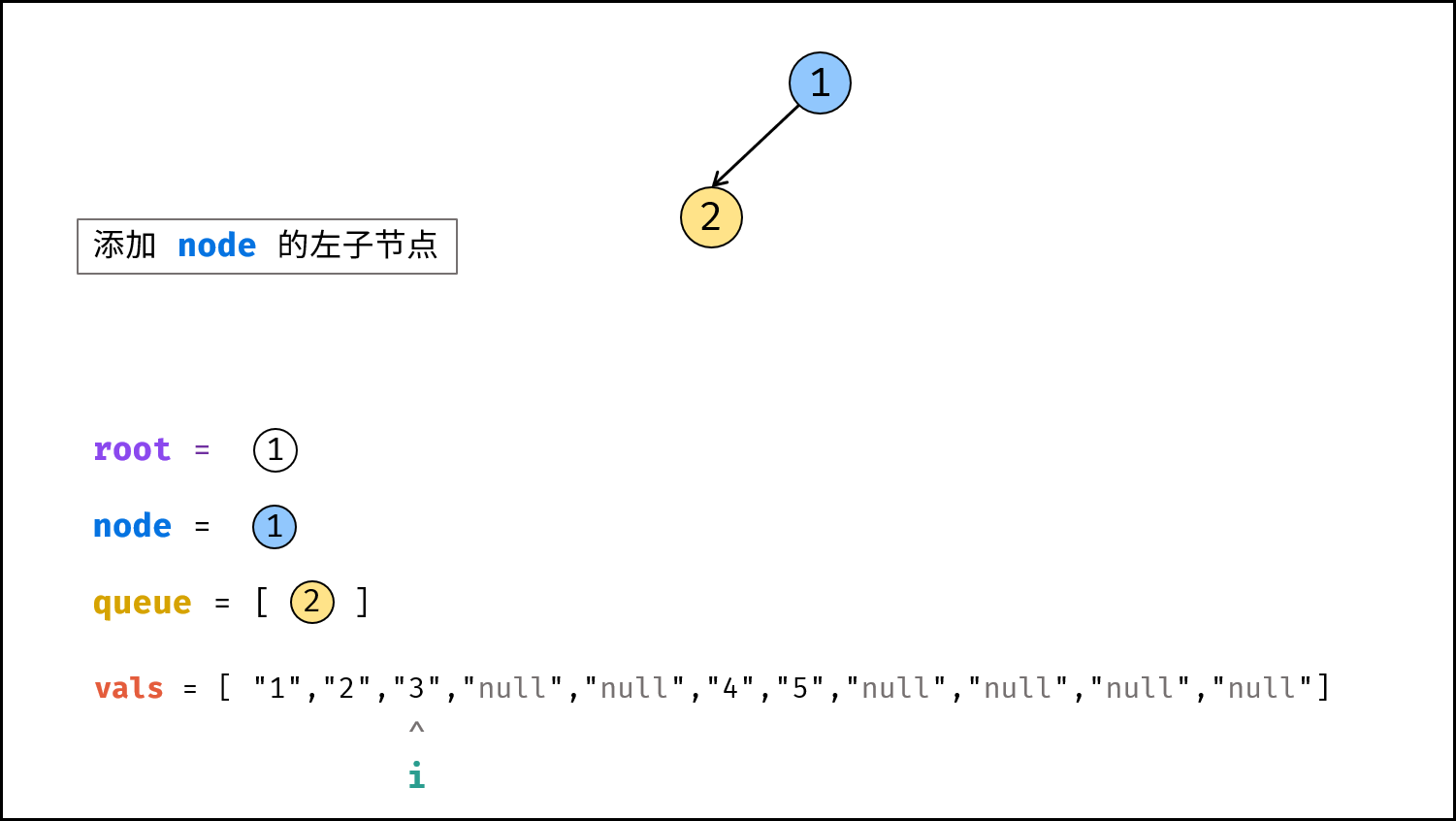
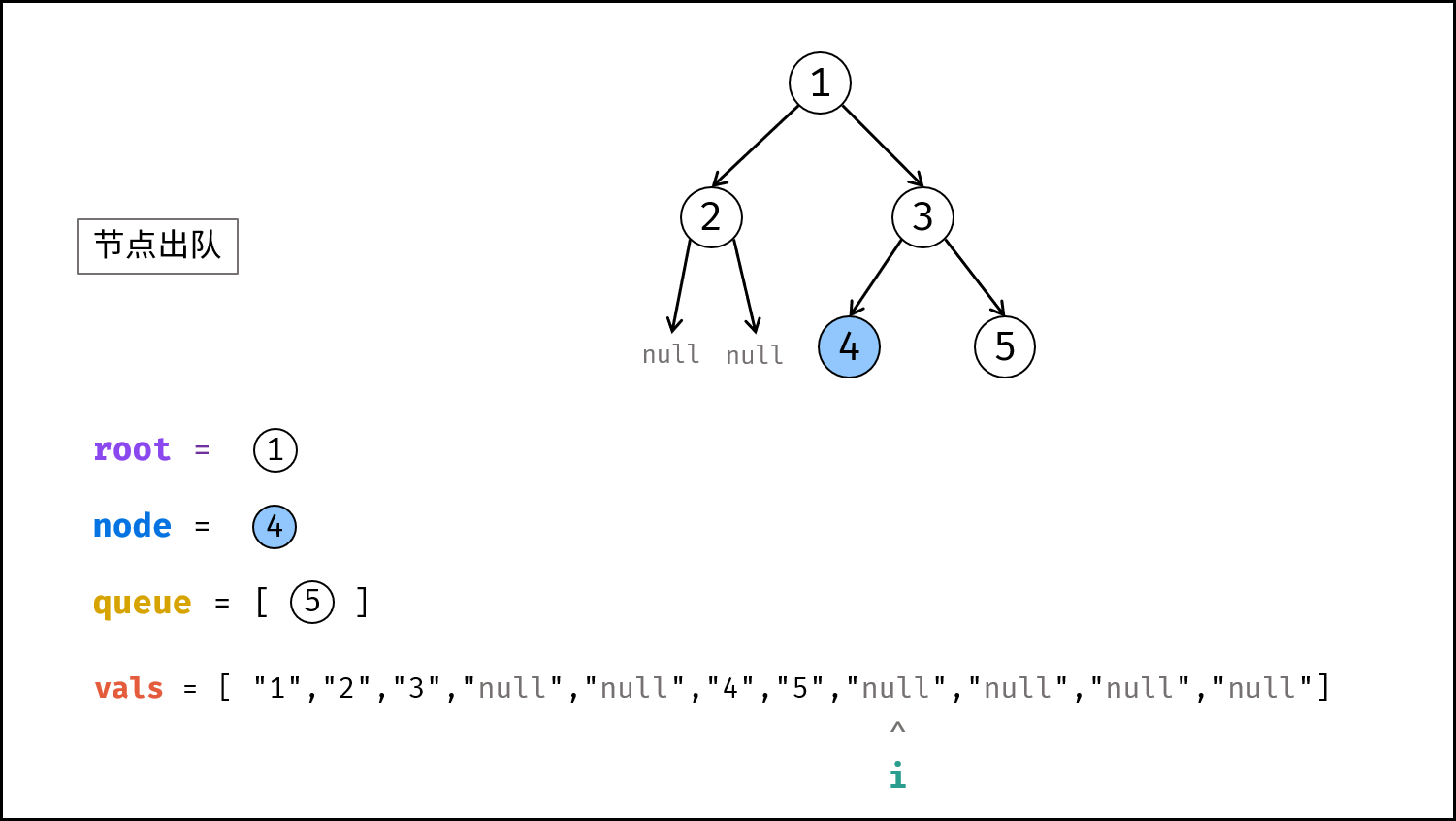
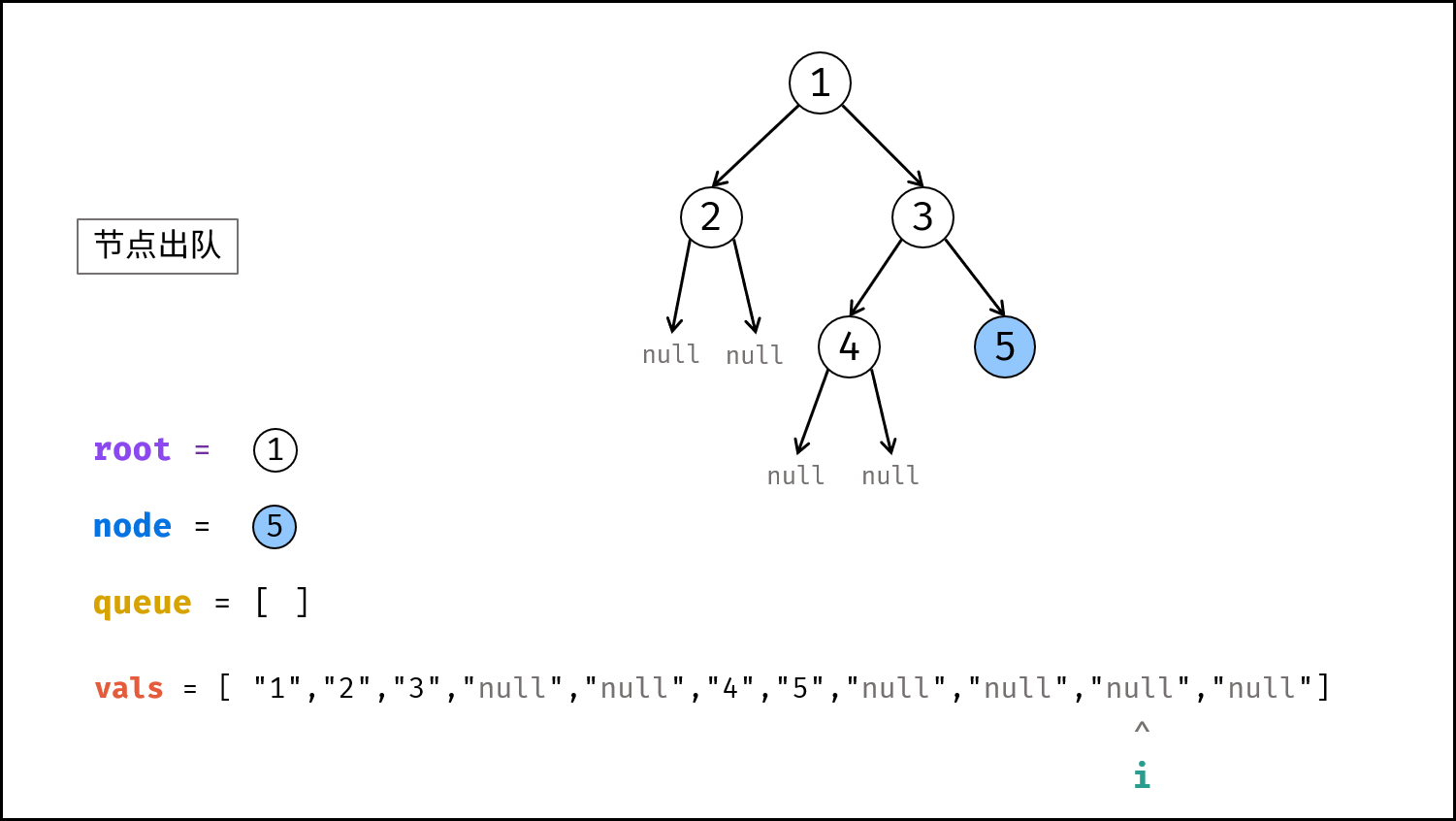
vals(先去掉首尾中括号,再用逗号隔开),指针i = 1,根节点root(值为vals[0]),队列queue(包含root)。 - 按层构建: 当
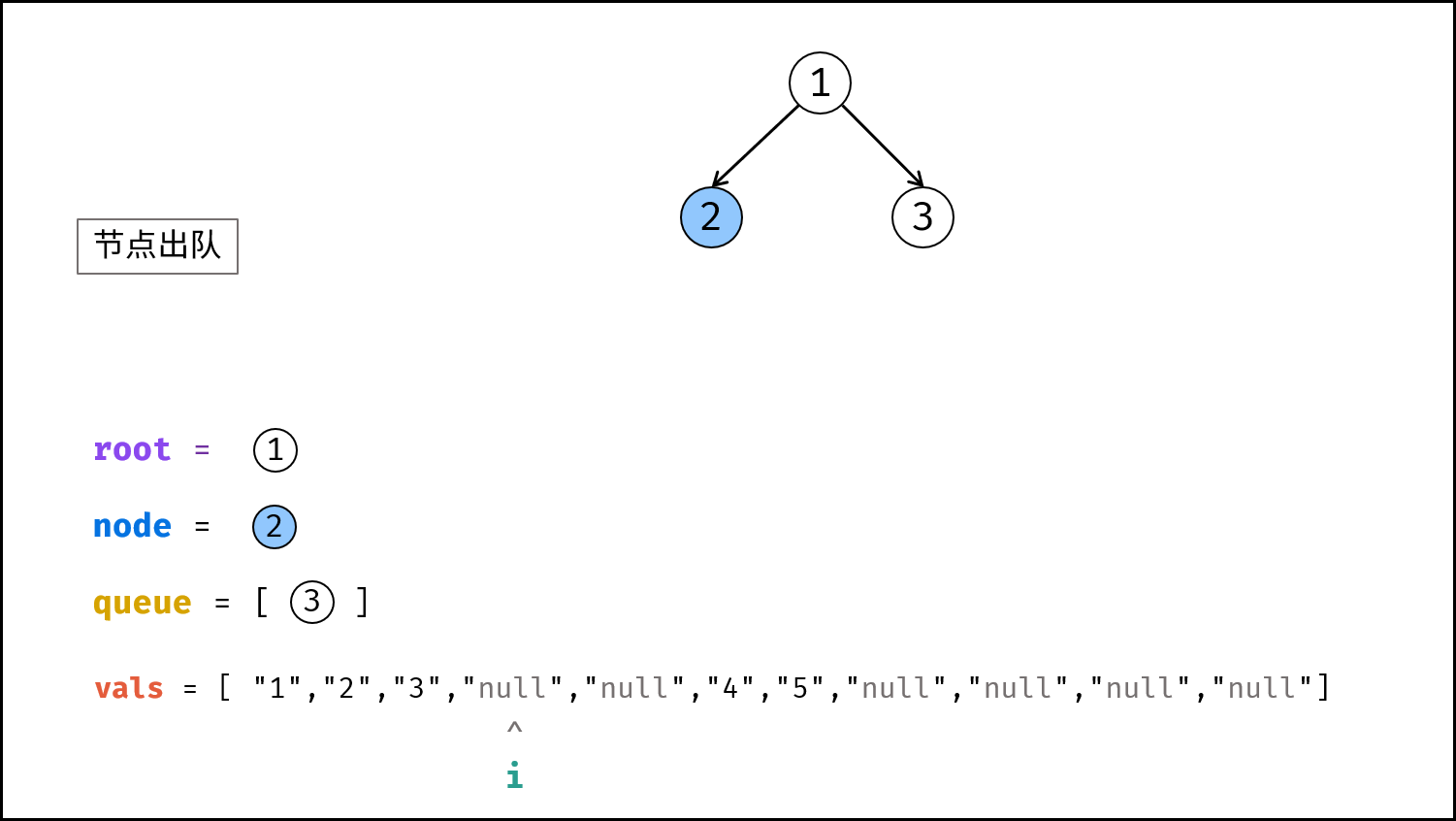
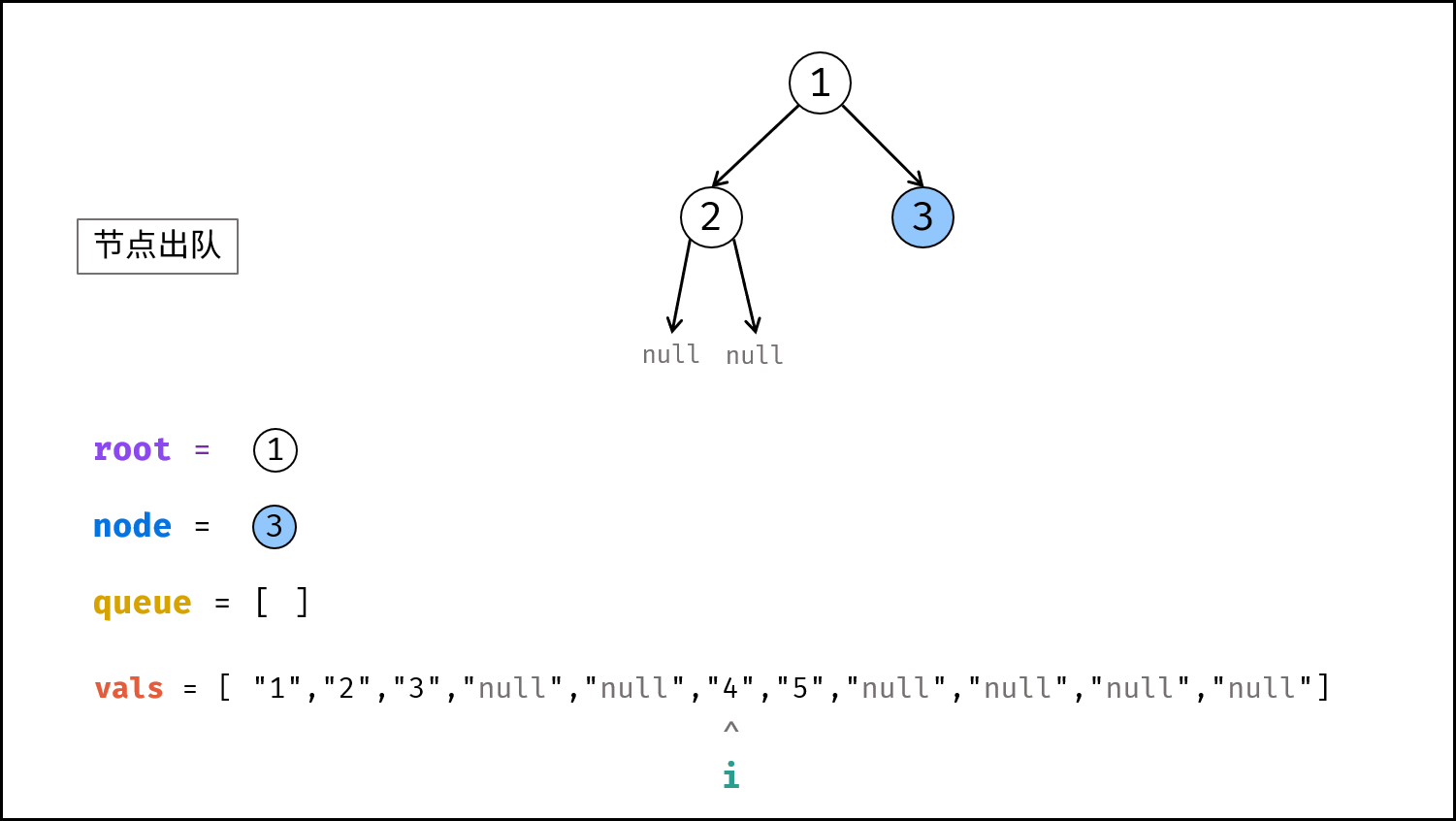
queue为空时跳出。- 节点出队,记为
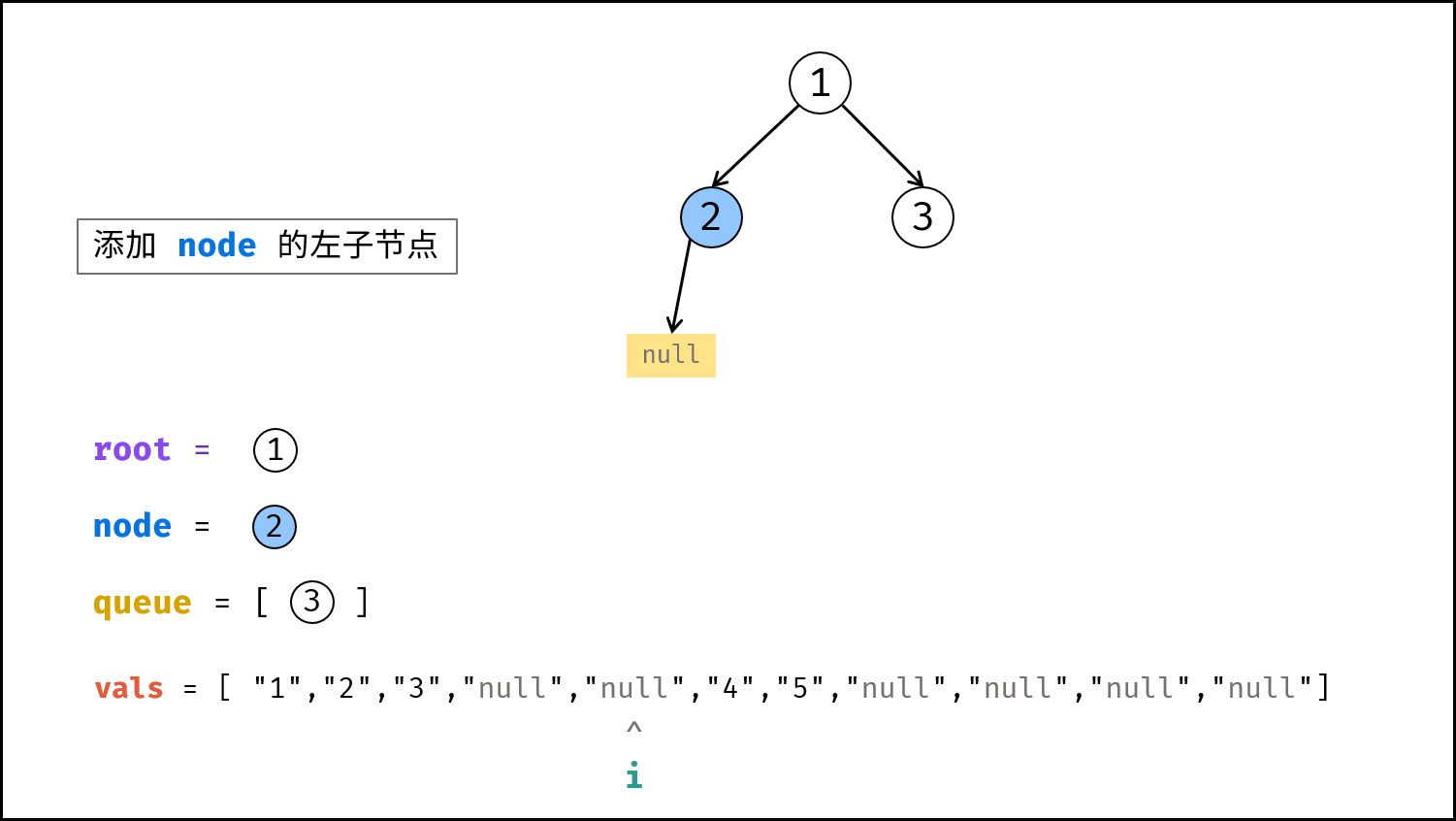
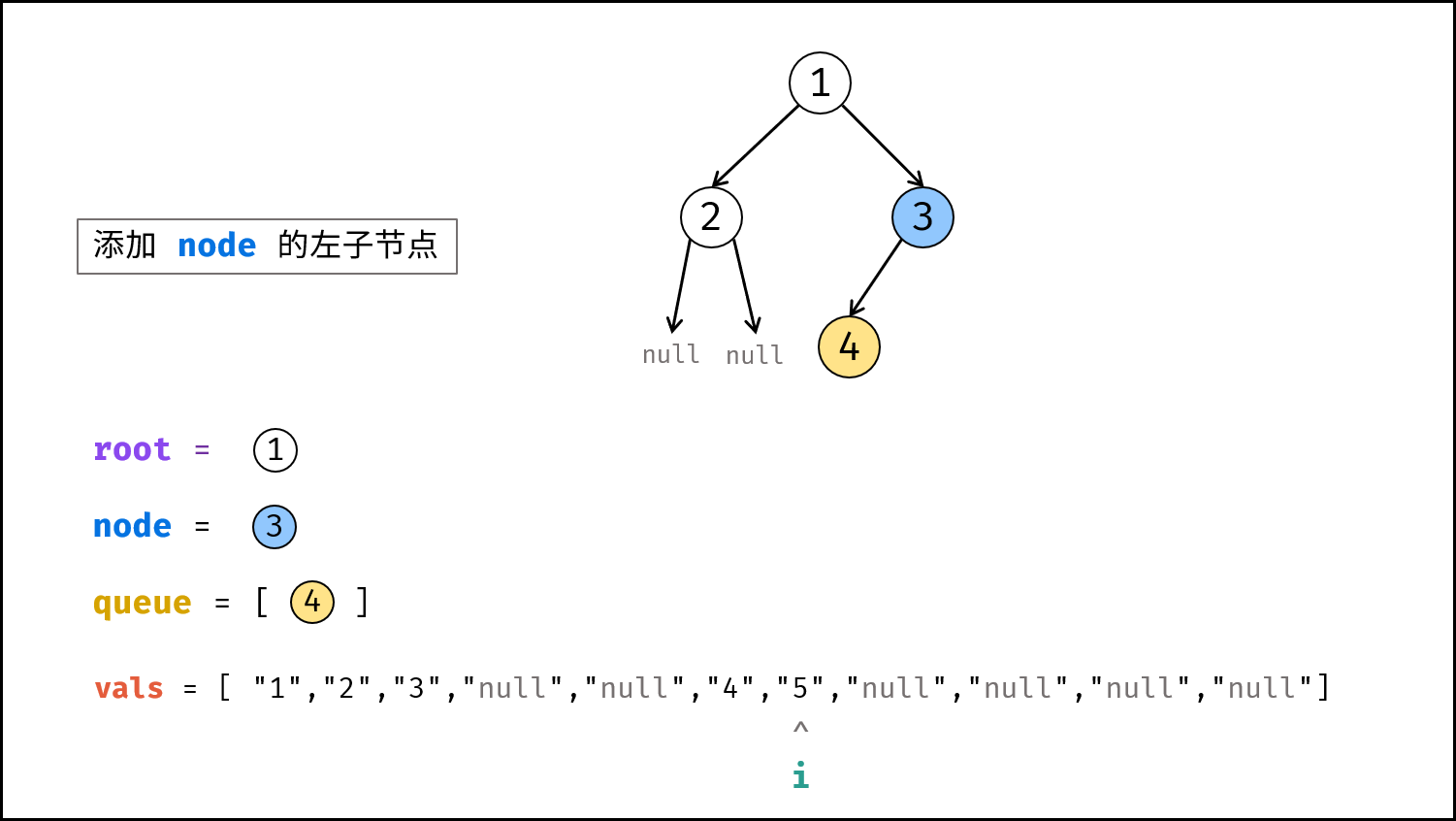
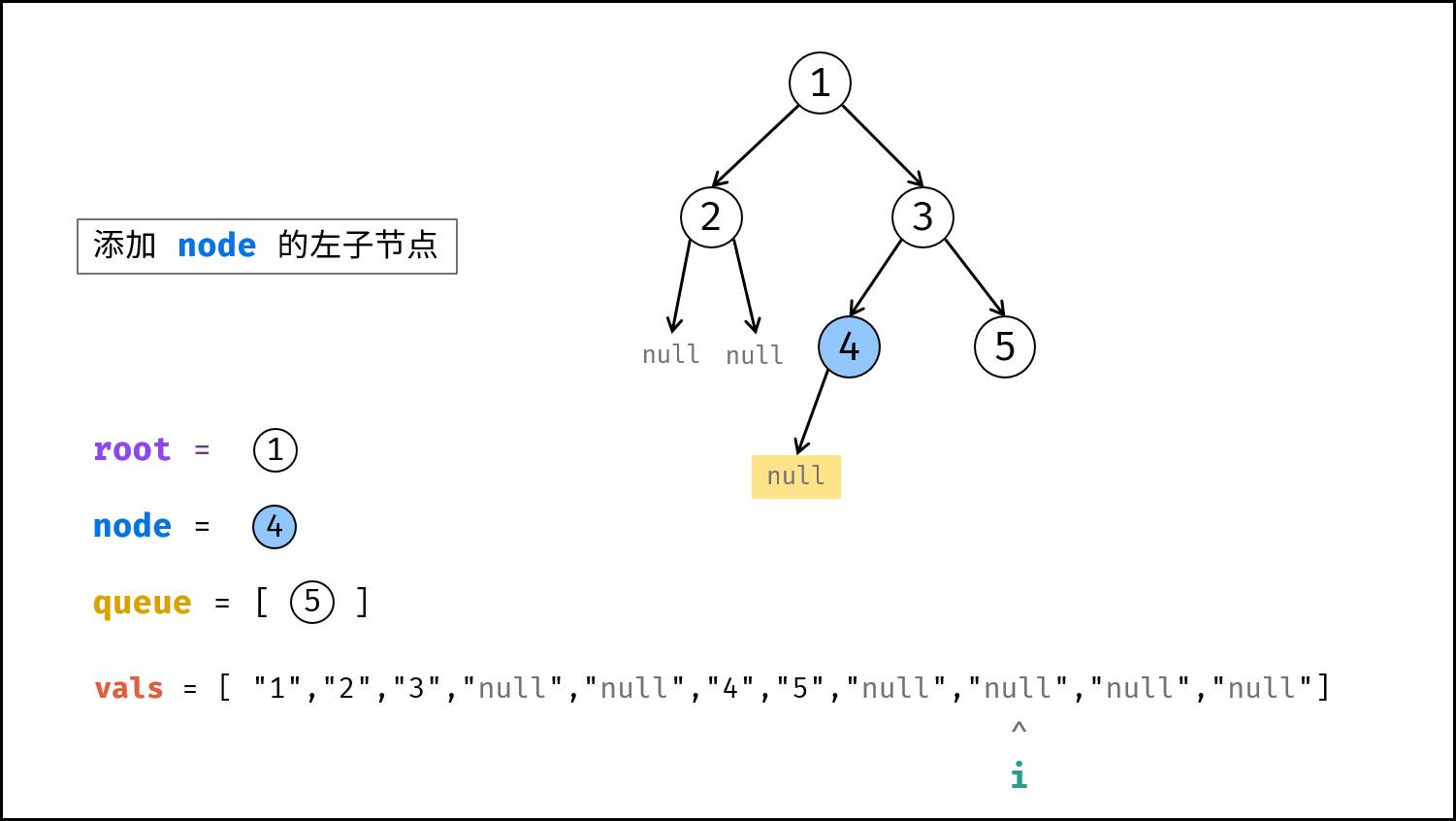
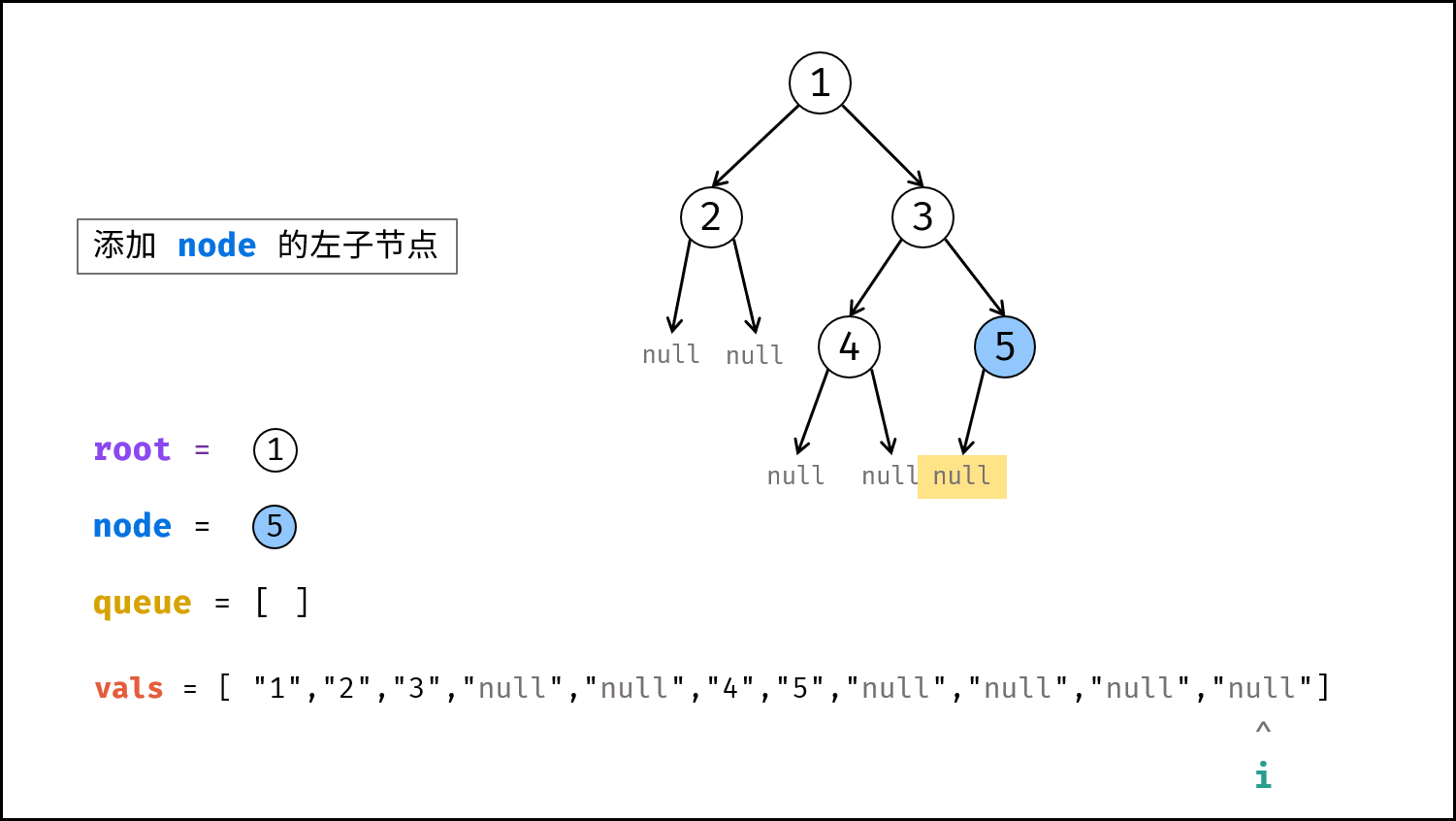
node。 - 构建
node的左子节点:node.left的值为vals[i],并将node.left入队。 - 执行
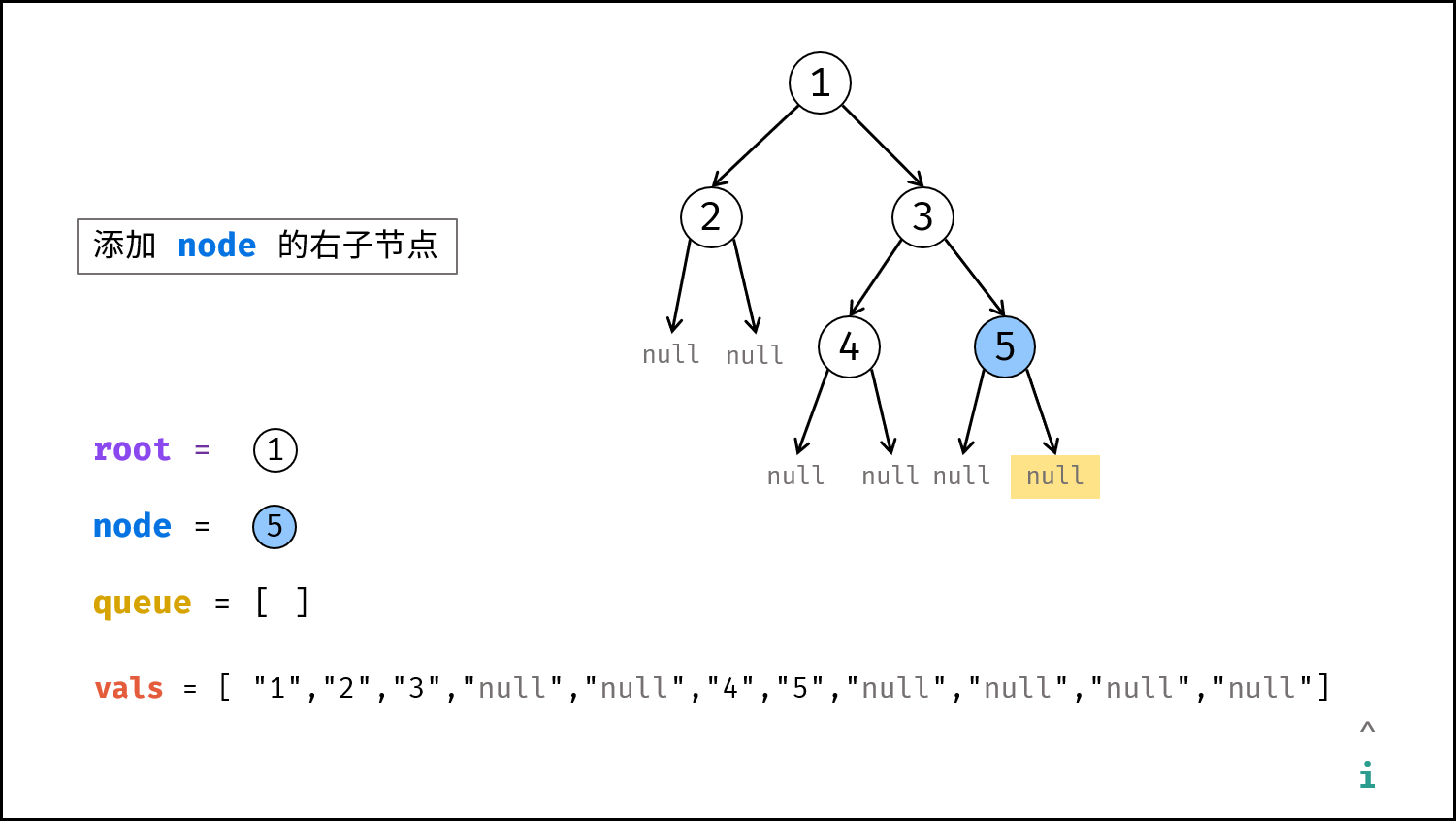
i += 1。 - 构建
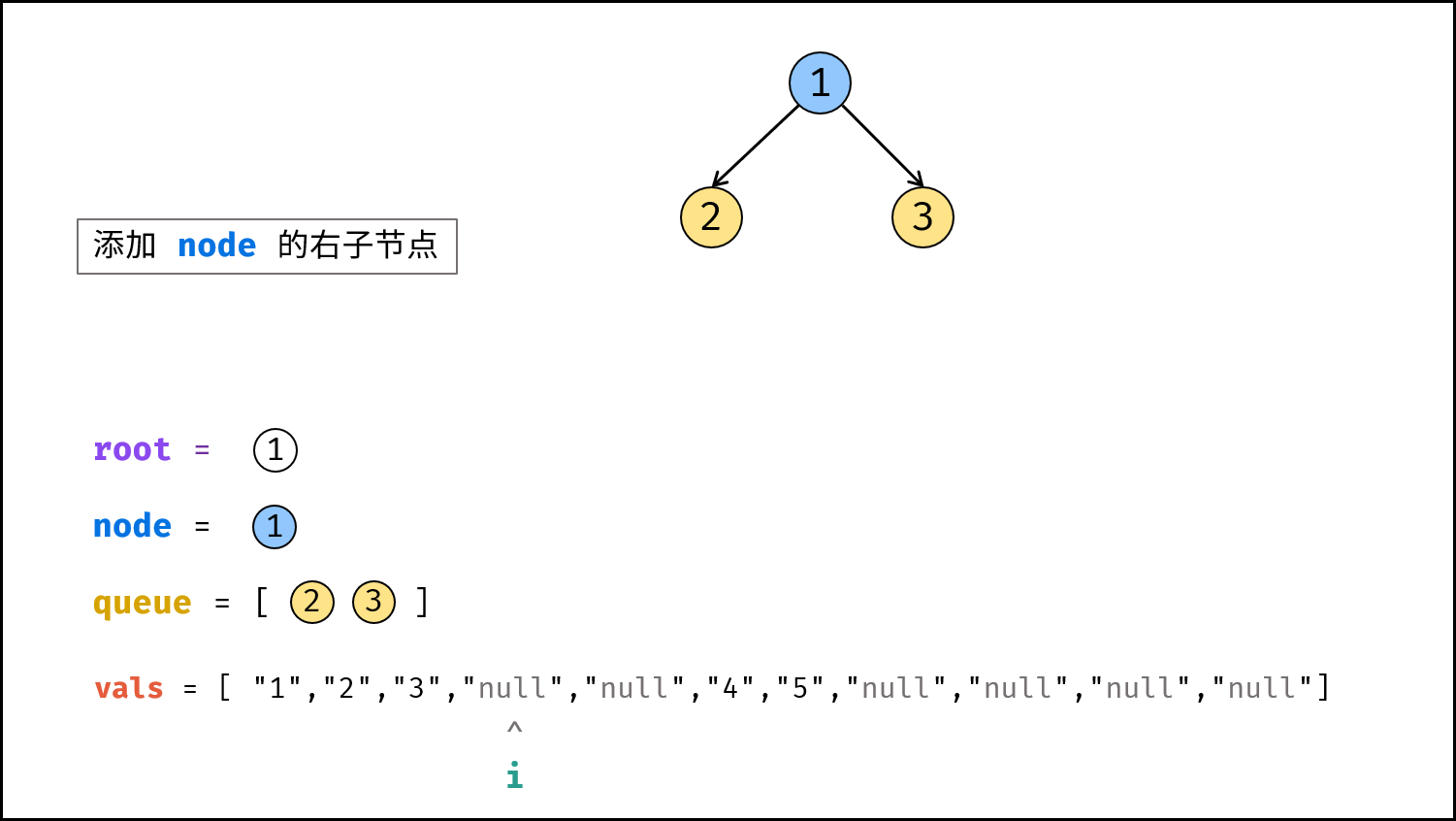
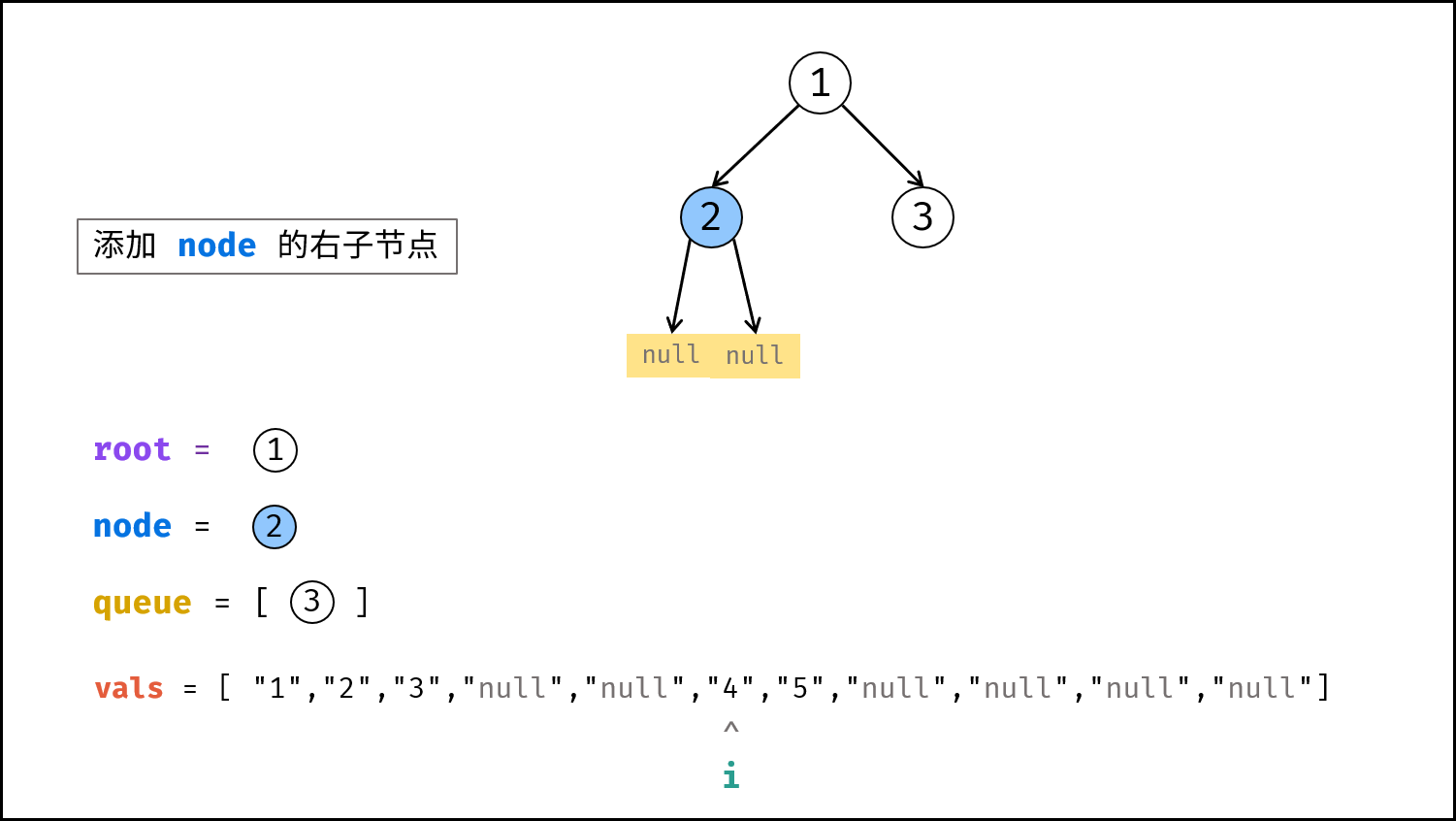
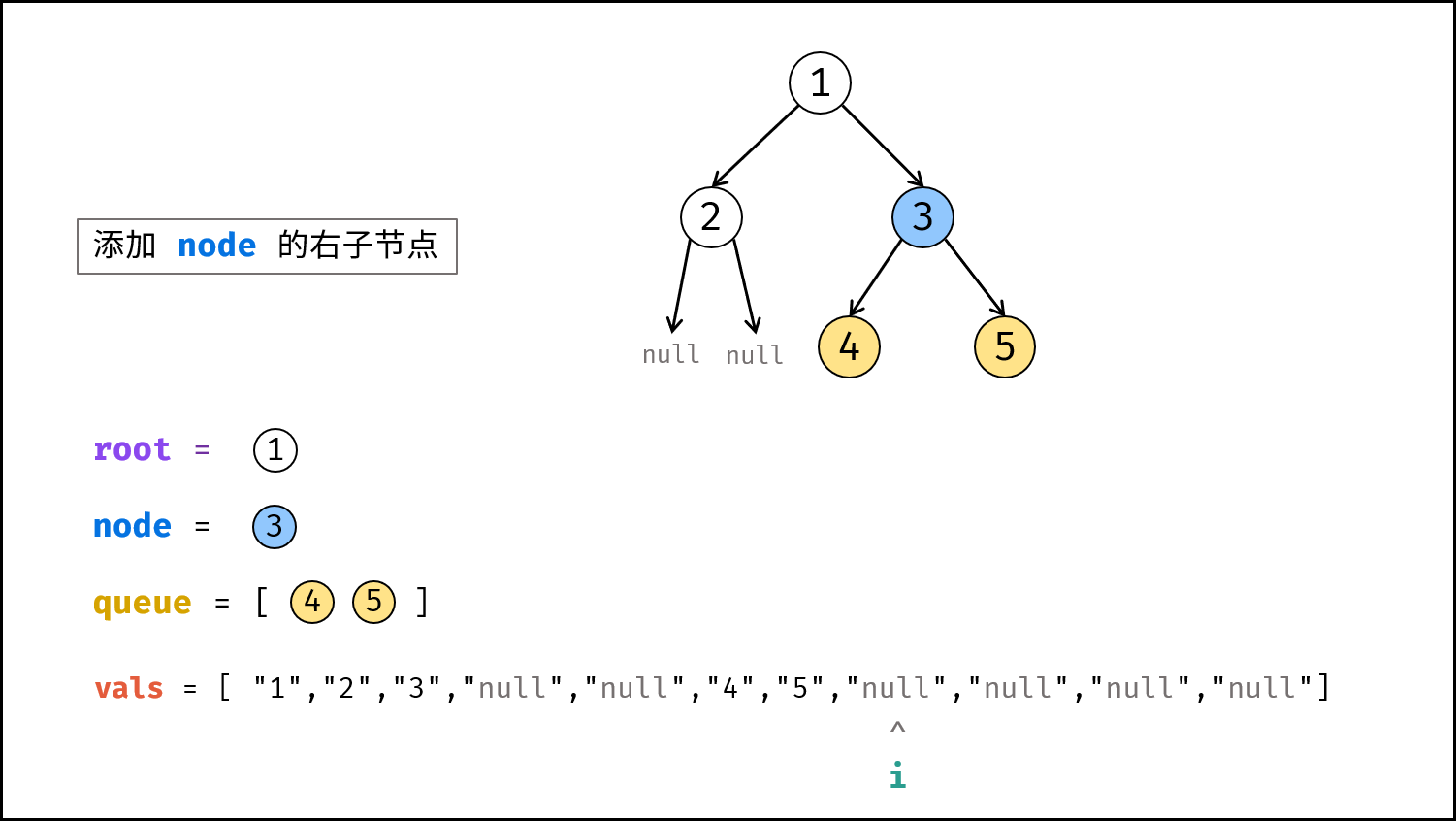
node的右子节点:node.right的值为vals[i],并将node.right入队。 - 执行
i += 1。
- 节点出队,记为
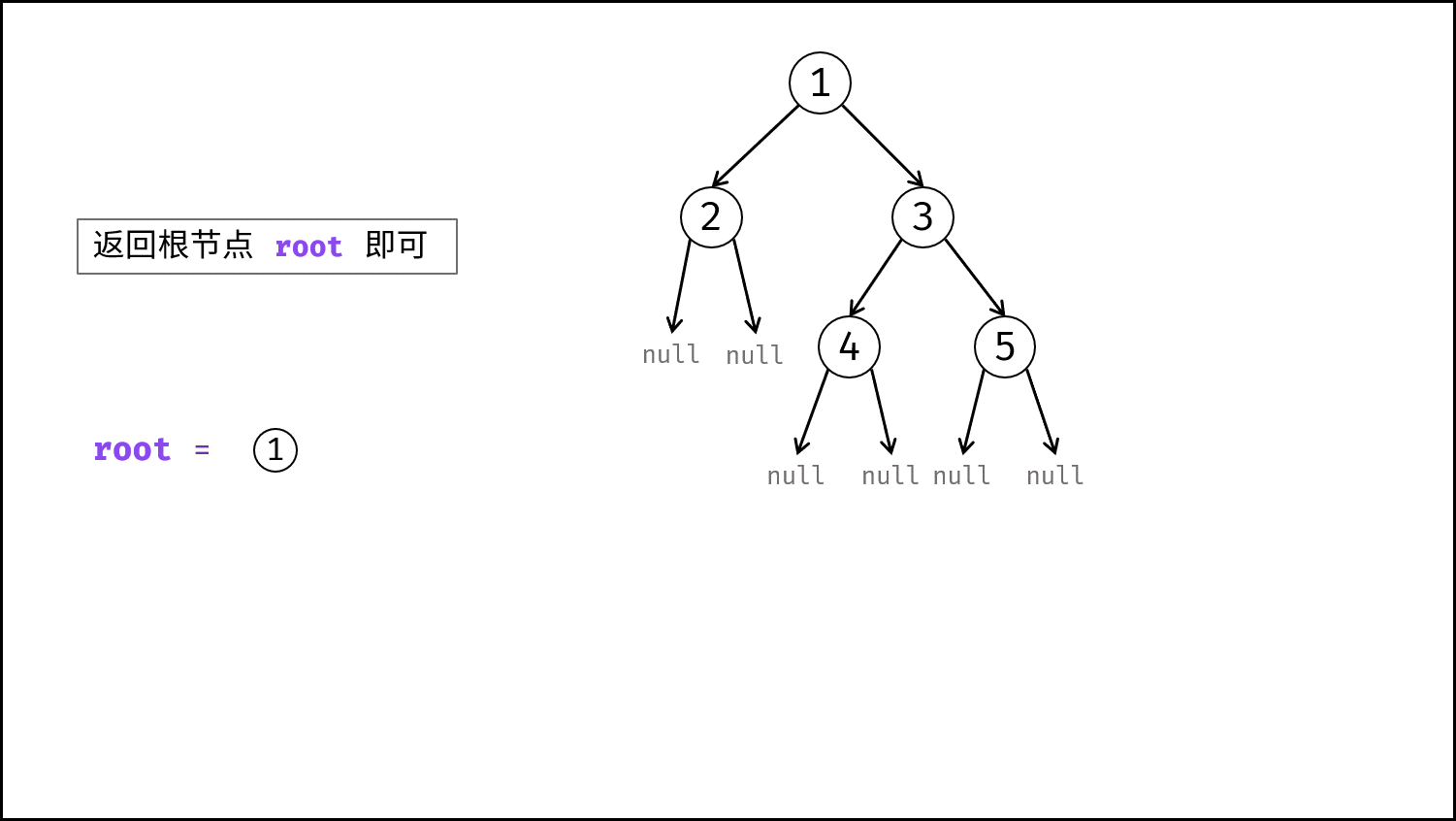
- 返回值: 返回根节点
root即可。
< ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, >
>
代码:
Python
class Codec:
def serialize(self, root):
if not root: return "[]"
queue = collections.deque()
queue.append(root)
res = []
while queue:
node = queue.popleft()
if node:
res.append(str(node.val))
queue.append(node.left)
queue.append(node.right)
else: res.append("null")
return '[' + ','.join(res) + ']'
def deserialize(self, data):
if data == "[]": return
vals, i = data[1:-1].split(','), 1
root = TreeNode(int(vals[0]))
queue = collections.deque()
queue.append(root)
while queue:
node = queue.popleft()
if vals[i] != "null":
node.left = TreeNode(int(vals[i]))
queue.append(node.left)
i += 1
if vals[i] != "null":
node.right = TreeNode(int(vals[i]))
queue.append(node.right)
i += 1
return rootJava
public class Codec {
public String serialize(TreeNode root) {
if (root == null) return "[]";
StringBuilder res = new StringBuilder("[");
Queue<TreeNode> queue = new LinkedList<>() {{ add(root); }};
while (!queue.isEmpty()) {
TreeNode node = queue.poll();
if (node != null) {
res.append(node.val + ",");
queue.add(node.left);
queue.add(node.right);
}
else res.append("null,");
}
res.deleteCharAt(res.length() - 1);
res.append("]");
return res.toString();
}
public TreeNode deserialize(String data) {
if (data.equals("[]")) return null;
String[] vals = data.substring(1, data.length() - 1).split(",");
TreeNode root = new TreeNode(Integer.parseInt(vals[0]));
Queue<TreeNode> queue = new LinkedList<>() {{ add(root); }};
int i = 1;
while (!queue.isEmpty()) {
TreeNode node = queue.poll();
if (!vals[i].equals("null")) {
node.left = new TreeNode(Integer.parseInt(vals[i]));
queue.add(node.left);
}
i++;
if (!vals[i].equals("null")) {
node.right = new TreeNode(Integer.parseInt(vals[i]));
queue.add(node.right);
}
i++;
}
return root;
}
}复杂度分析:
序列化:
- 时间复杂度 $O(N)$ : $N$ 为二叉树的节点数,层序遍历需要访问所有节点,最差情况下需要访问 $N + 1$ 个
null,总体复杂度为 $O(2N + 1) = O(N)$ 。 - 空间复杂度 $O(N)$ : 最差情况下,队列
queue同时存储 $\frac{N + 1}{2}$ 个节点(或 $N+1$ 个null),使用 $O(N)$ ;列表res使用 $O(N)$ 。
反序列化:
- 时间复杂度 $O(N)$ : $N$ 为二叉树的节点数,按层构建二叉树需要遍历整个 $vals$ ,其长度最大为 $2N+1$ 。
- 空间复杂度 $O(N)$ : 最差情况下,队列
queue同时存储 $\frac{N + 1}{2}$ 个节点,因此使用 $O(N)$ 额外空间。