解题思路： ​

• 规则定义： 设学生 $A$ 和学生 $B$ 左右相邻，$A$ 在 $B$ 左边；
  • 左规则： 当 $ratings_B>ratings_A$时，$B$ 的糖比 $A$ 的糖数量多。
  • 右规则： 当 $ratings_A>ratings_B$时，$A$ 的糖比 $B$ 的糖数量多。

相邻的学生中，评分高的学生必须获得更多的糖果 等价于 所有学生满足左规则且满足右规则。

• 算法流程：

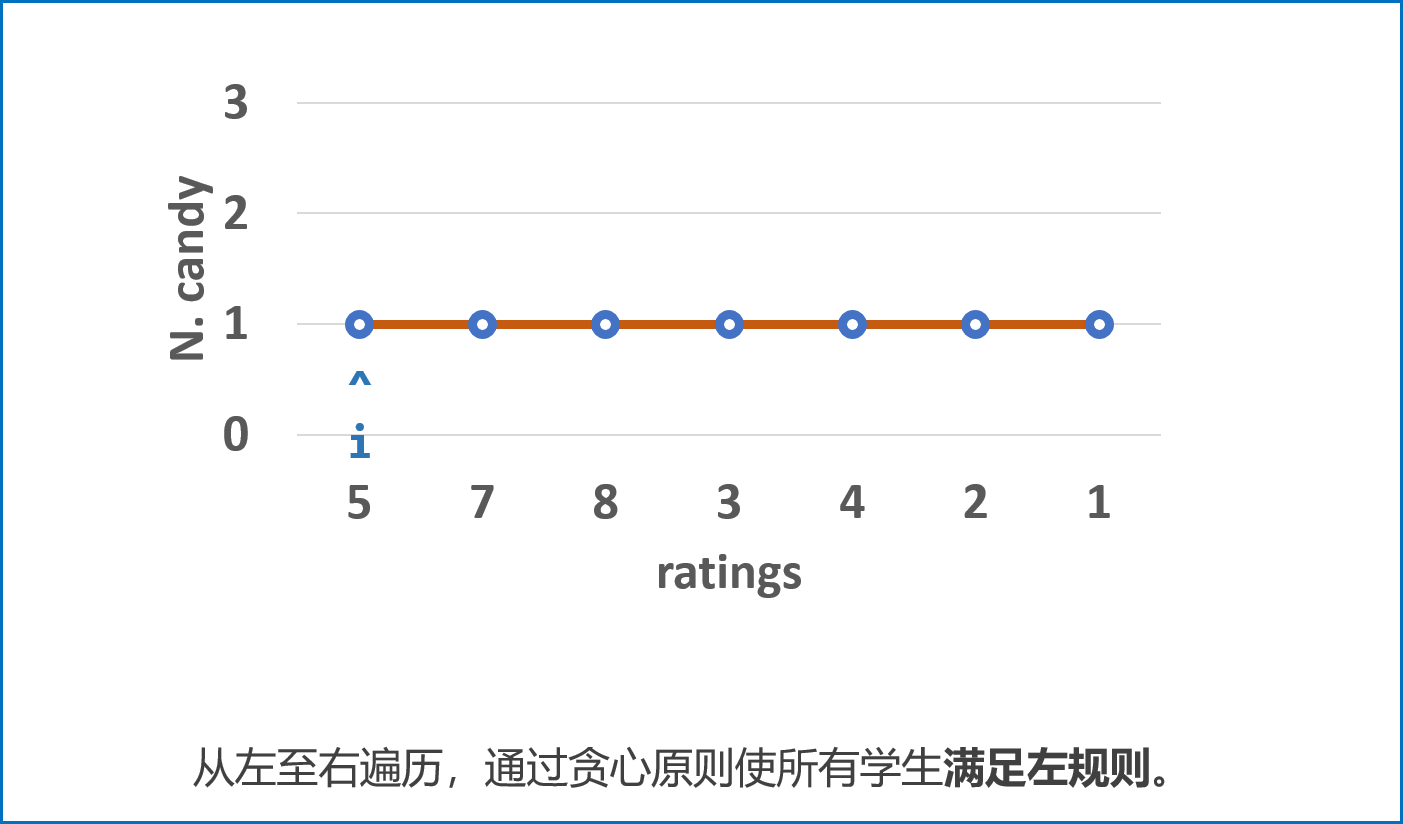
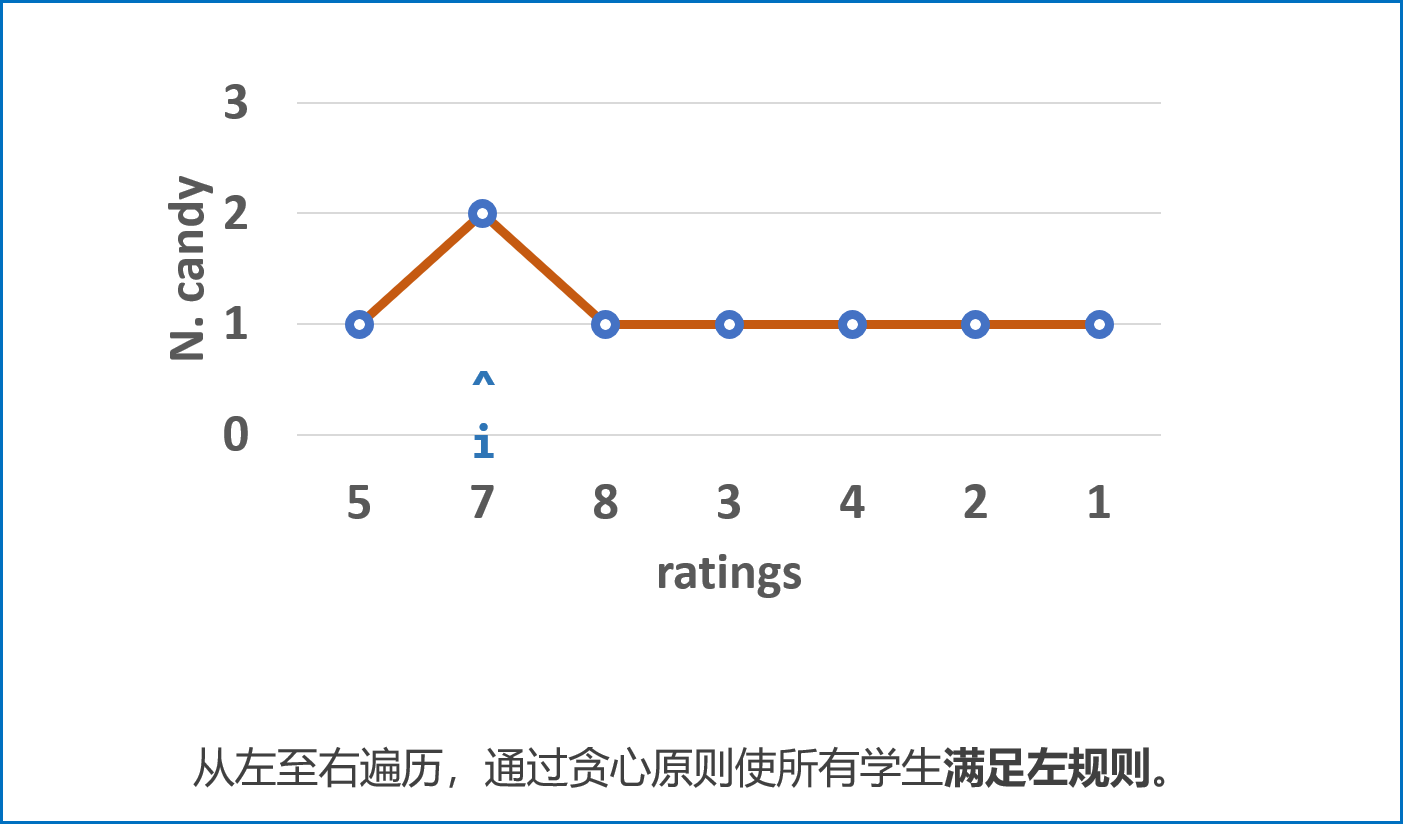
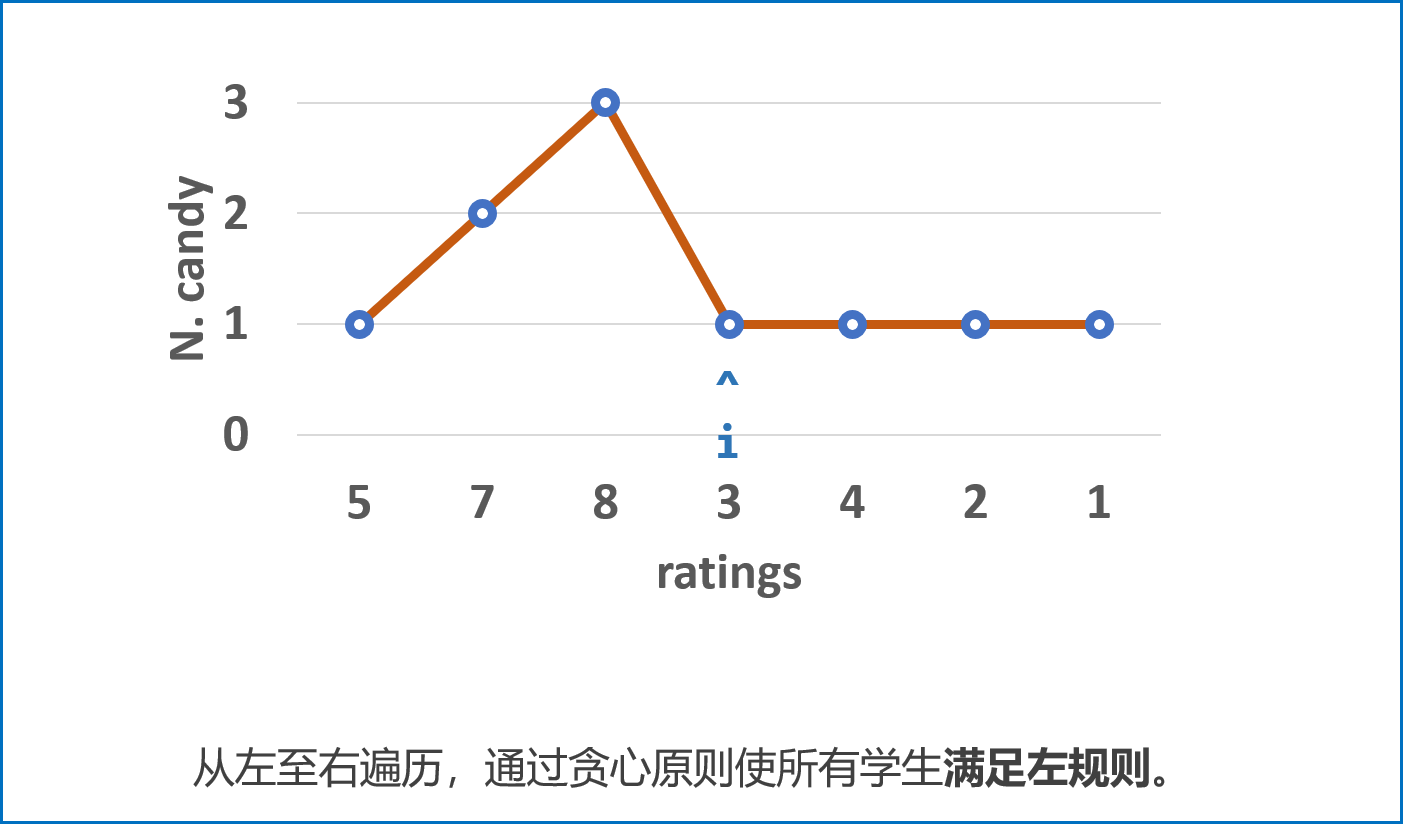
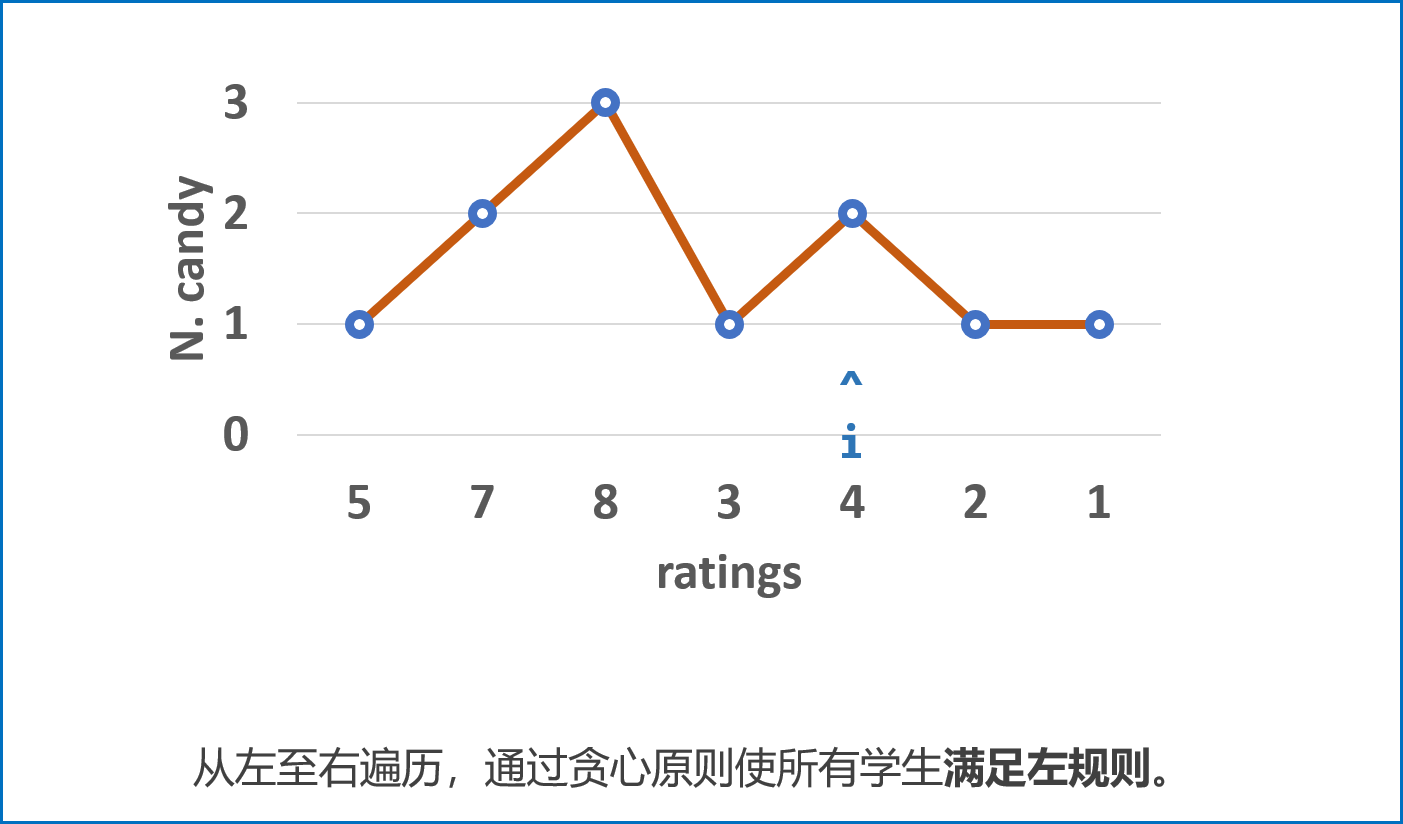
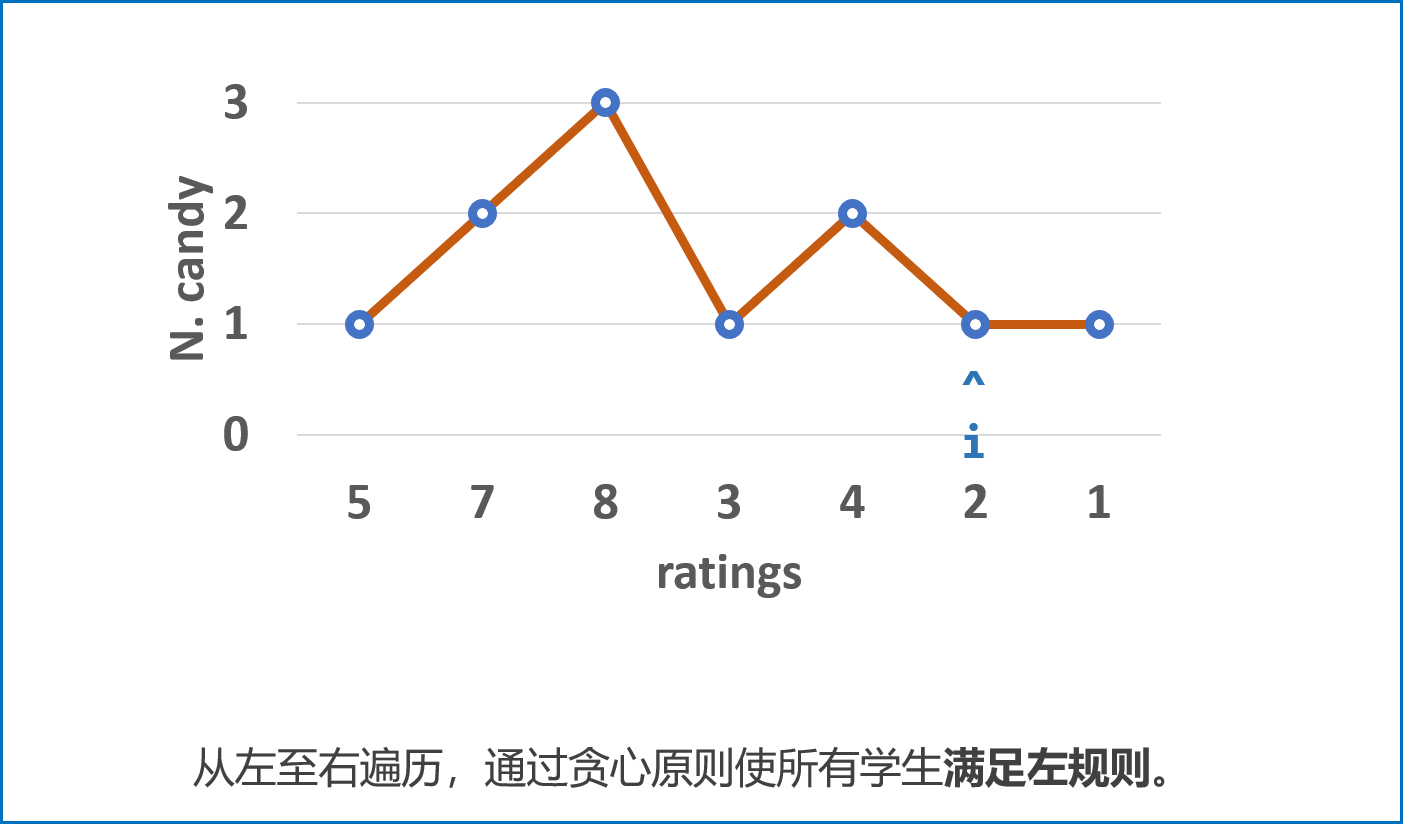
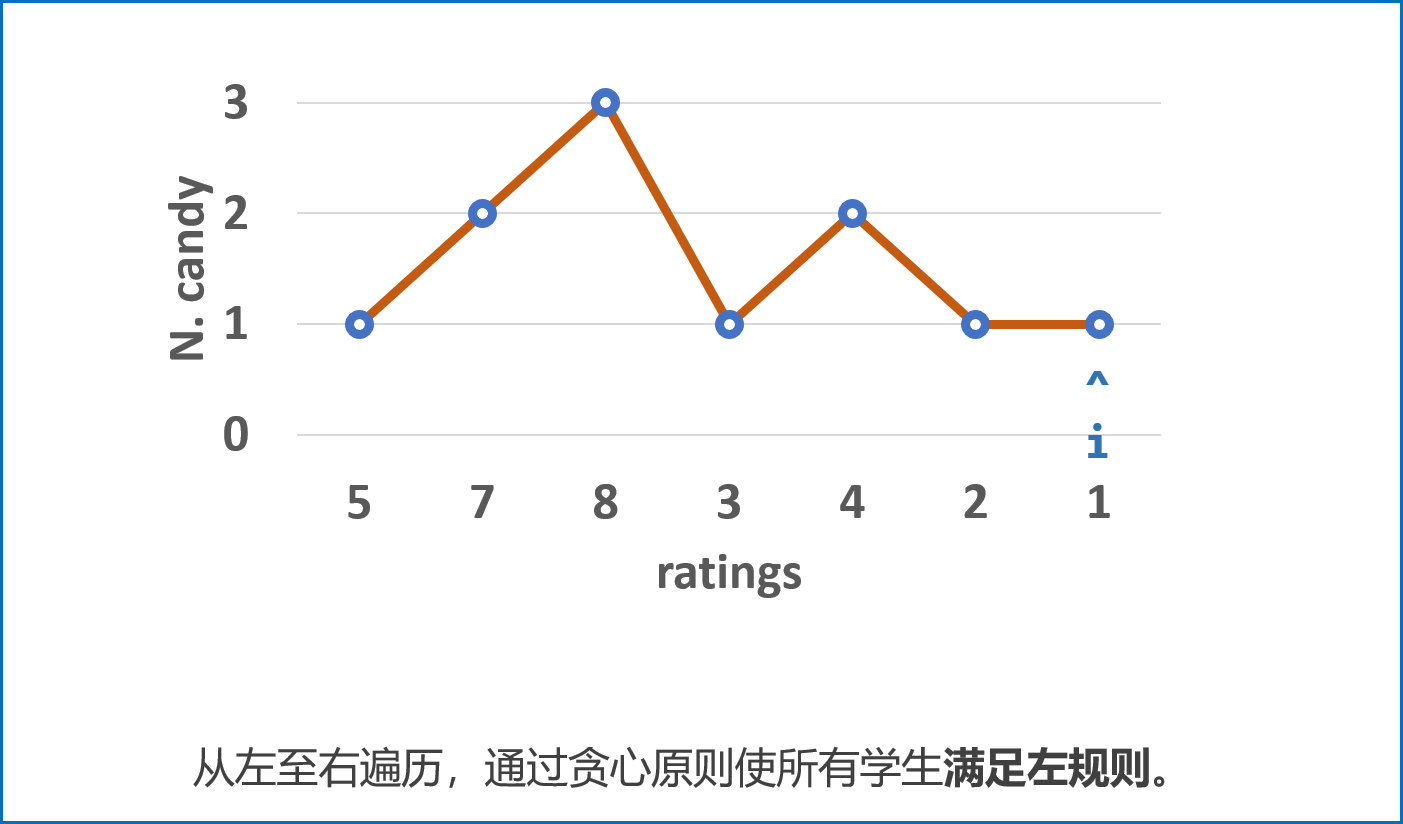
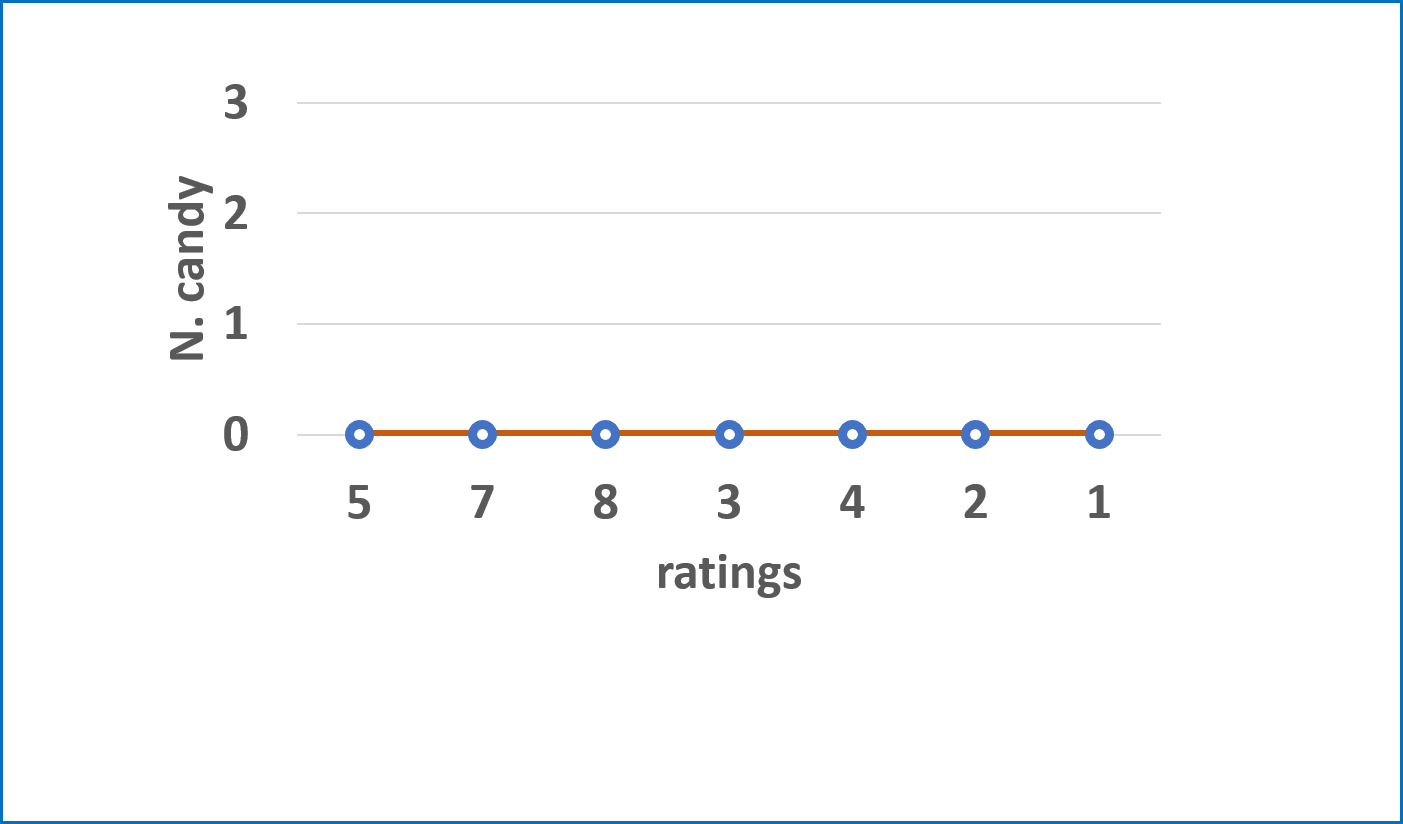
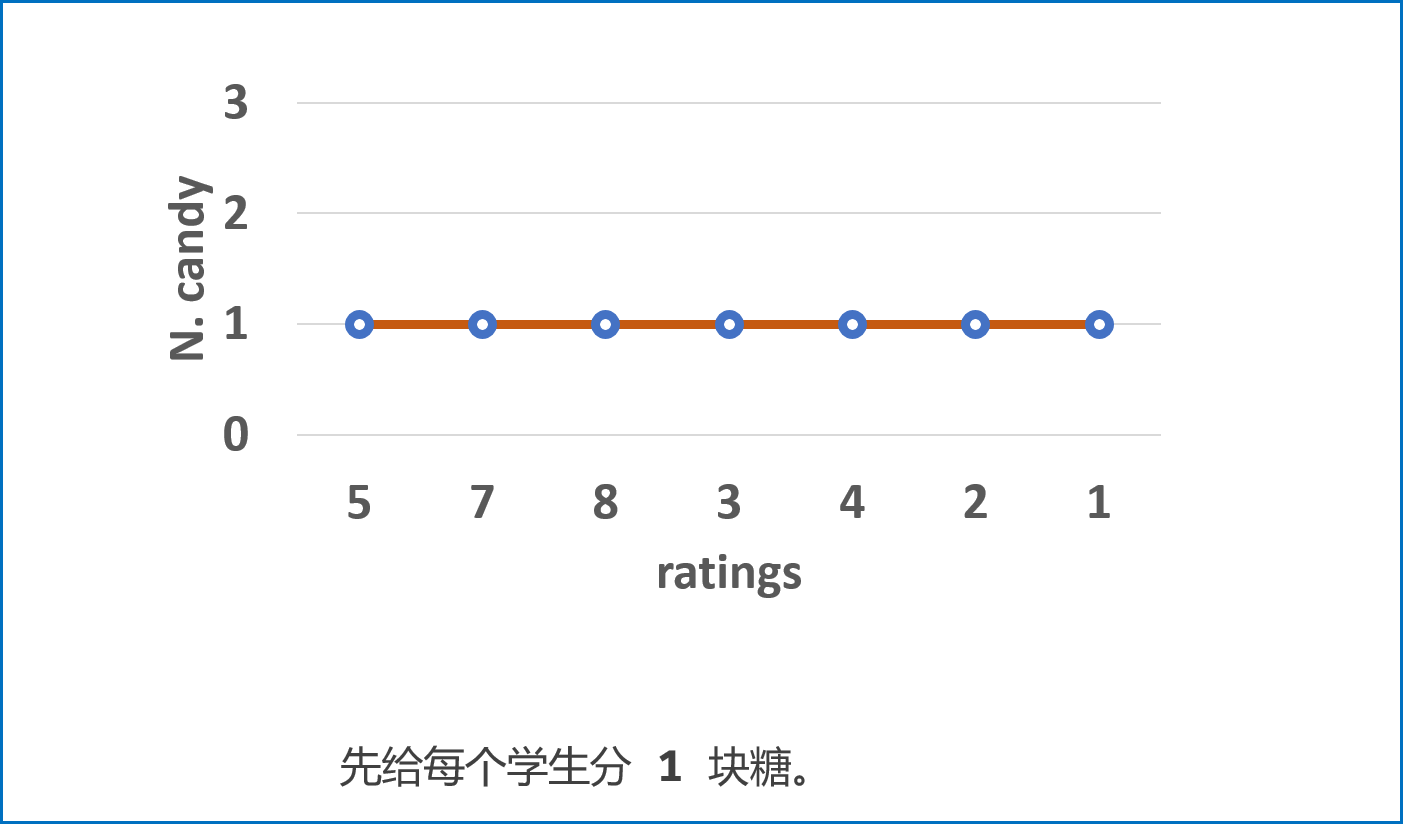
  1. 先从左至右遍历学生成绩 ratings，按照以下规则给糖，并记录在 left 中：

     1. 先给所有学生 $1$ 颗糖；
     2. 若 $ratings_i>ratings_{i-1}$，则第 $i$ 名学生糖比第 $i - 1$ 名学生多 $1$ 个。
     3. 若 $ratings_i<=ratings_{i-1}$，则第 $i$ 名学生糖数量不变。（交由从右向左遍历时处理。）
     • 经过此规则分配后，可以保证所有学生糖数量 满足左规则 。

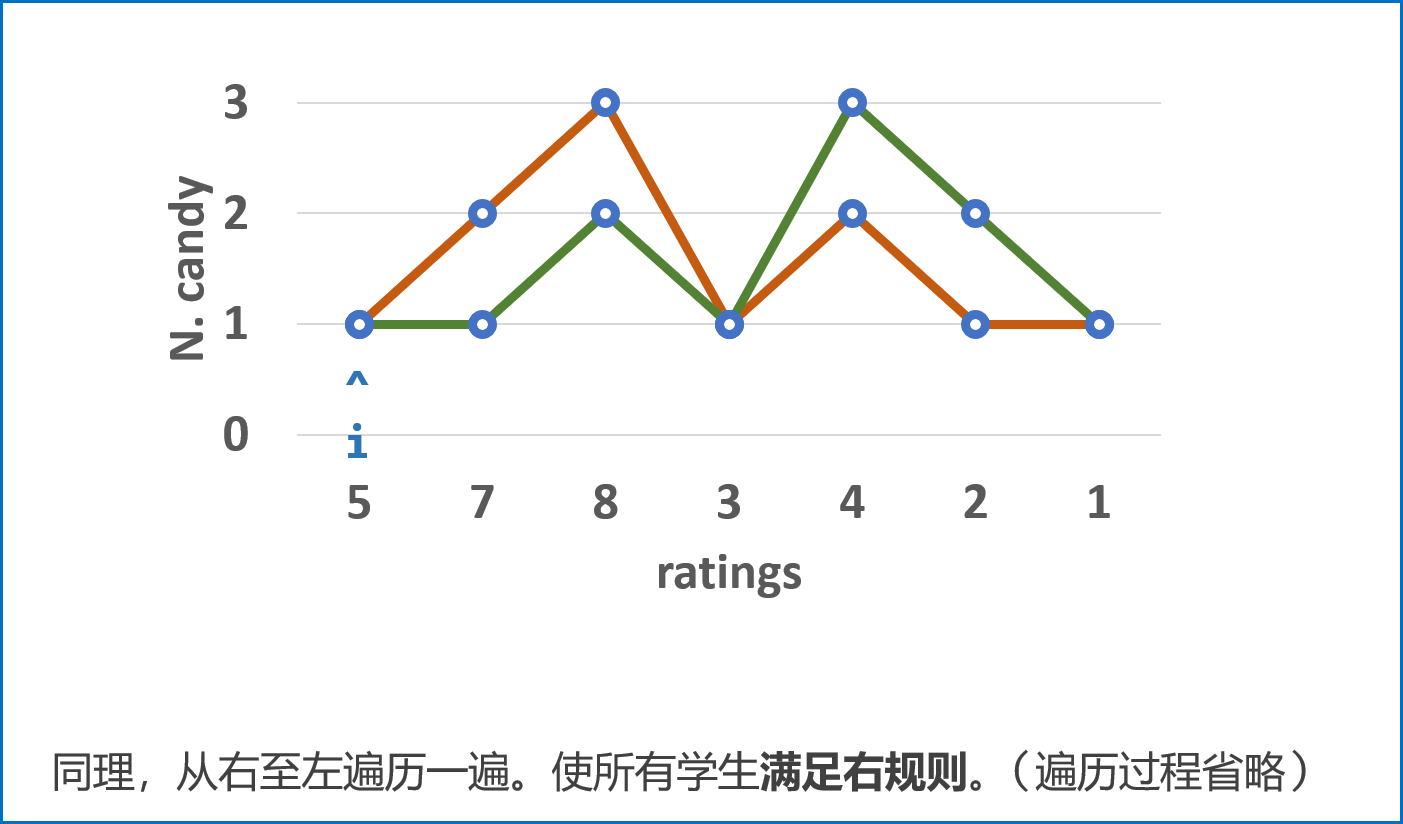
  2. 同理，在此规则下从右至左遍历学生成绩并记录在 right 中，可以保证所有学生糖数量 满足右规则 。

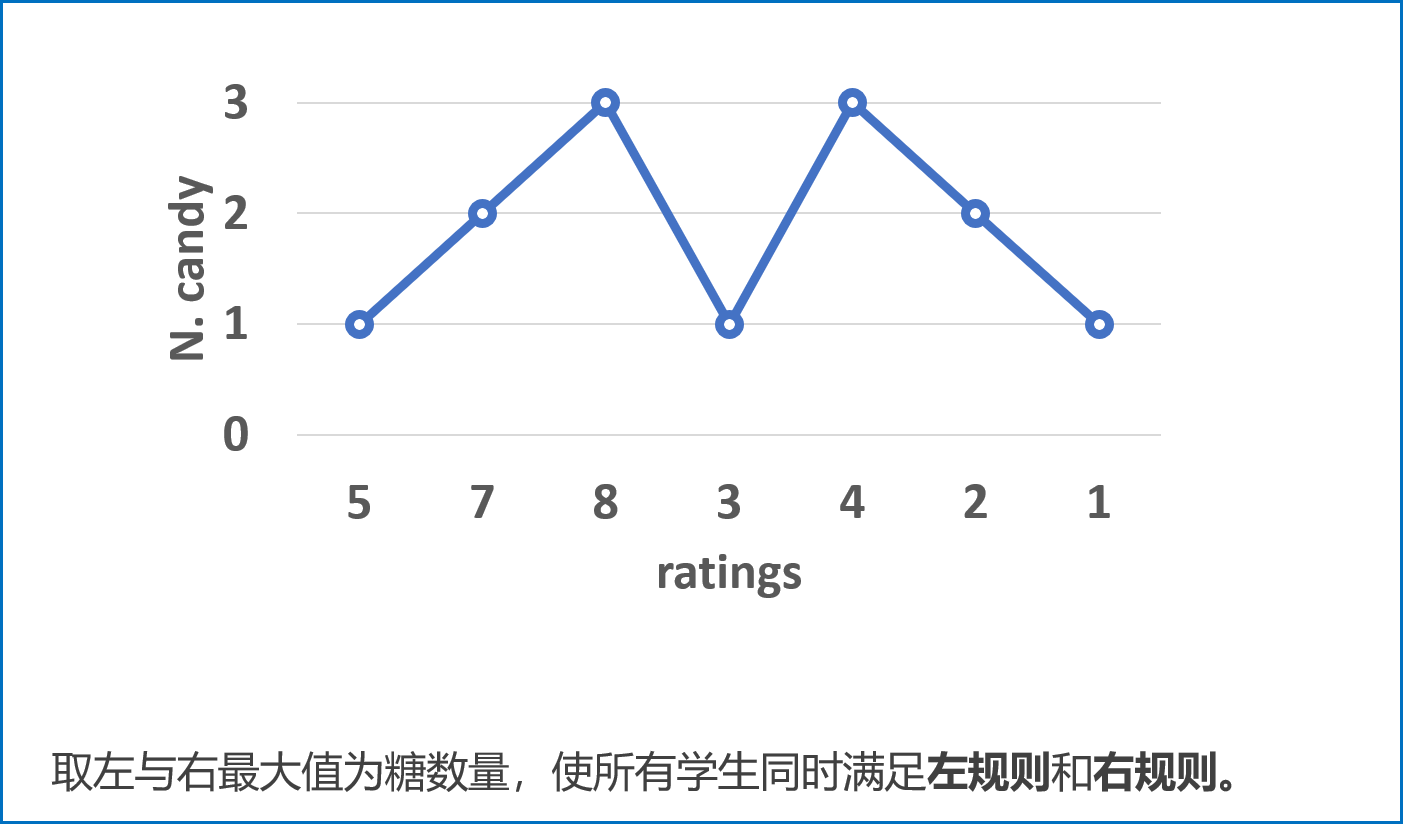
  3. 最终，取以上 $2$ 轮遍历 left 和 right 对应学生糖果数的 最大值 ，这样则 同时满足左规则和右规则 ，即得到每个同学的最少糖果数量。

• 复杂度分析：

  • 时间复杂度 $O(N)$ ： 遍历两遍数组即可得到结果；
  • 空间复杂度 $O(N)$ ： 需要借用 left，right 的线性额外空间。

<,,,,,,,,,,>

代码： ​

class Solution:
    def candy(self, ratings: List[int]) -> int:
        left = [1 for _ in range(len(ratings))]
        right = left[:]
        for i in range(1, len(ratings)):
            if ratings[i] > ratings[i - 1]: left[i] = left[i - 1] + 1
        count = left[-1]
        for i in range(len(ratings) - 2, -1, -1):
            if ratings[i] > ratings[i + 1]: right[i] = right[i + 1] + 1
            count += max(left[i], right[i])
        return count

class Solution {
    public int candy(int[] ratings) {
        int[] left = new int[ratings.length];
        int[] right = new int[ratings.length];
        Arrays.fill(left, 1);
        Arrays.fill(right, 1);
        for(int i = 1; i < ratings.length; i++)
            if(ratings[i] > ratings[i - 1]) left[i] = left[i - 1] + 1;
        int count = left[ratings.length - 1];
        for(int i = ratings.length - 2; i >= 0; i--) {
            if(ratings[i] > ratings[i + 1]) right[i] = right[i + 1] + 1;
            count += Math.max(left[i], right[i]);
        }
        return count;
    }
}