自律小屋 | 自律小屋

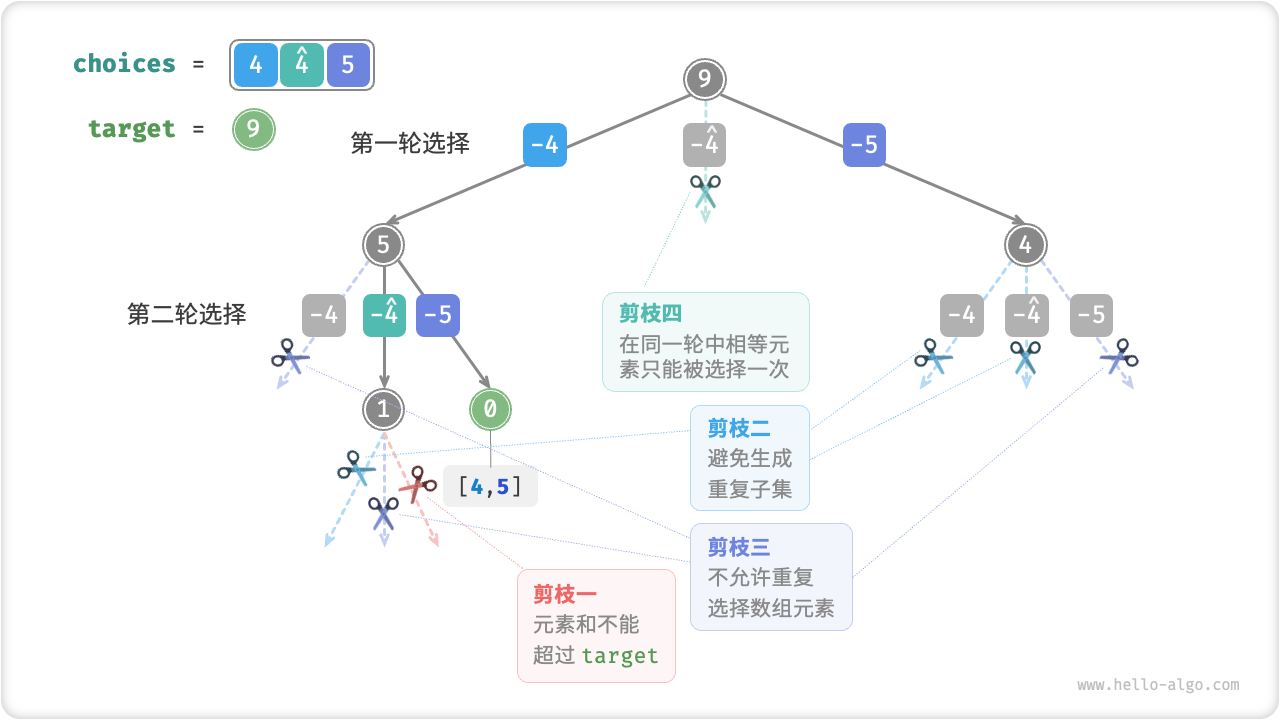
解题思路：

请先做前置题目「39. 组合总和」。

相比于上题，本题的输入数组可能包含重复元素，这引入了新的问题。例如，给定数组 $[4, \hat{4}, 5]$ 和目标元素 $9$ ，则现有代码的输出结果为 $[4, 5], [\hat{4}, 5]$ ，出现了重复子集。

造成这种重复的原因是相等元素在某轮中被多次选择。如下图所示，第一轮共有三个选择，其中两个都为 $4$ ，会产生两个重复的搜索分支，从而输出重复子集；同理，第二轮的两个 $4$ 也会产生重复子集。

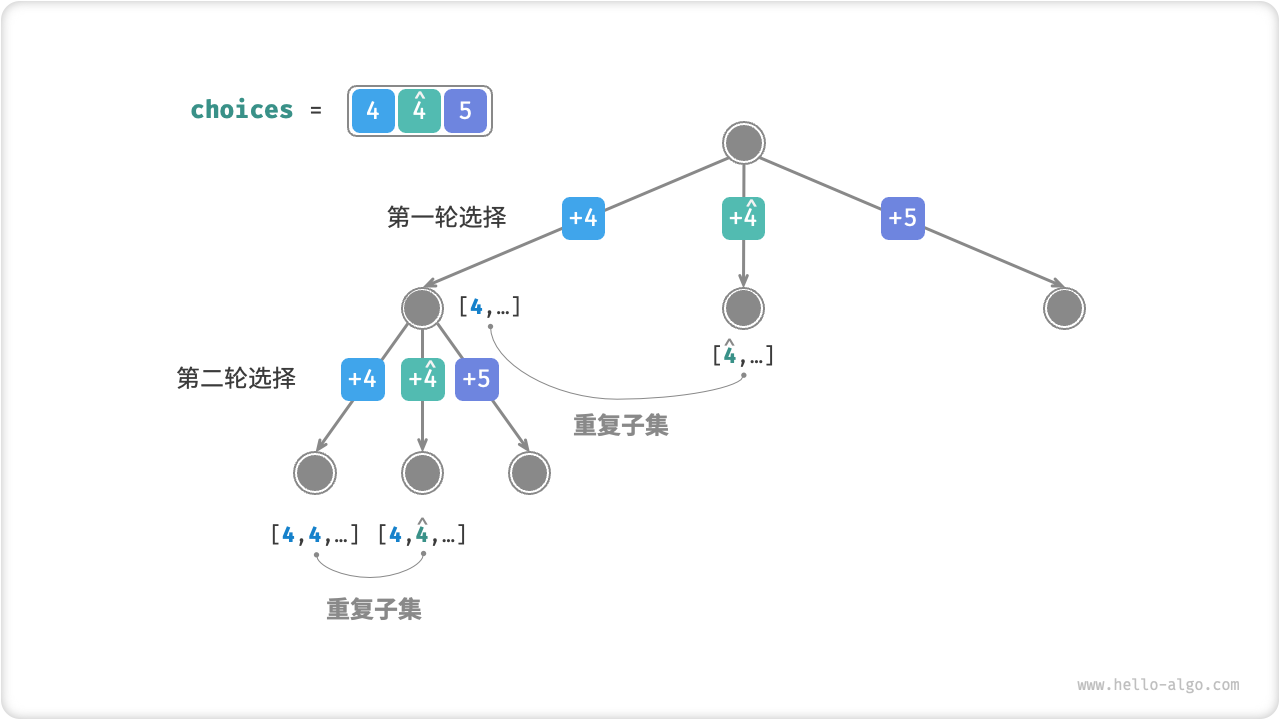
相等元素剪枝：

为解决此问题，我们需要限制相等元素在每一轮中只被选择一次。实现方式比较巧妙：由于数组是已排序的，因此相等元素都是相邻的。这意味着在某轮选择中，若当前元素与其左边元素相等，则说明它已经被选择过，因此直接跳过当前元素。

与此同时，本题规定中的每个数组元素只能被选择一次。幸运的是，我们也可以利用变量 start 来满足该约束：当做出选择 $x_{i}$ 后，设定下一轮从索引 $i + 1$ 开始向后遍历。这样即能去除重复子集，也能避免重复选择元素。

代码：

python

class Solution:
    def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
        def backtrack(
            state: list[int], target: int, choices: list[int], start: int, res: list[list[int]]
        ):
            """回溯算法：子集和 II"""
            # 子集和等于 target 时，记录解
            if target == 0:
                res.append(list(state))
                return
            # 遍历所有选择
            # 剪枝二：从 start 开始遍历，避免生成重复子集
            # 剪枝三：从 start 开始遍历，避免重复选择同一元素
            for i in range(start, len(choices)):
                # 剪枝一：若子集和超过 target ，则直接结束循环
                # 这是因为数组已排序，后边元素更大，子集和一定超过 target
                if target - choices[i] < 0:
                    break
                # 剪枝四：如果该元素与左边元素相等，说明该搜索分支重复，直接跳过
                if i > start and choices[i] == choices[i - 1]:
                    continue
                # 尝试：做出选择，更新 target, start
                state.append(choices[i])
                # 进行下一轮选择
                backtrack(state, target - choices[i], choices, i + 1, res)
                # 回退：撤销选择，恢复到之前的状态
                state.pop()

        state = []  # 状态（子集）
        candidates.sort()  # 对 candidates 进行排序
        start = 0  # 遍历起始点
        res = []  # 结果列表（子集列表）
        backtrack(state, target, candidates, start, res)
        return res

java

class Solution {
    void backtrack(List<Integer> state, int target, int[] choices, int start, List<List<Integer>> res) {
        // 子集和等于 target 时，记录解
        if (target == 0) {
            res.add(new ArrayList<>(state));
            return;
        }
        // 遍历所有选择
        // 剪枝二：从 start 开始遍历，避免生成重复子集
        // 剪枝三：从 start 开始遍历，避免重复选择同一元素
        for (int i = start; i < choices.length; i++) {
            // 剪枝一：若子集和超过 target ，则直接结束循环
            // 这是因为数组已排序，后边元素更大，子集和一定超过 target
            if (target - choices[i] < 0) {
                break;
            }
            // 剪枝四：如果该元素与左边元素相等，说明该搜索分支重复，直接跳过
            if (i > start && choices[i] == choices[i - 1]) {
                continue;
            }
            // 尝试：做出选择，更新 target, start
            state.add(choices[i]);
            // 进行下一轮选择
            backtrack(state, target - choices[i], choices, i + 1, res);
            // 回退：撤销选择，恢复到之前的状态
            state.remove(state.size() - 1);
        }
    }

    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        List<Integer> state = new ArrayList<>(); // 状态（子集）
        Arrays.sort(candidates); // 对 candidates 进行排序
        int start = 0; // 遍历起始点
        List<List<Integer>> res = new ArrayList<>(); // 结果列表（子集列表）
        backtrack(state, target, candidates, start, res);
        return res;
    }
}

cpp

class Solution {
public:
    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
        vector<int> state;              // 状态（子集）
        sort(candidates.begin(), candidates.end()); // 对 candidates 进行排序
        int start = 0;                  // 遍历起始点
        vector<vector<int>> res;        // 结果列表（子集列表）
        backtrack(state, target, candidates, start, res);
        return res;
    }
private:
    void backtrack(vector<int> &state, int target, vector<int> &choices, int start, vector<vector<int>> &res) {
        // 子集和等于 target 时，记录解
        if (target == 0) {
            res.push_back(state);
            return;
        }
        // 遍历所有选择
        // 剪枝二：从 start 开始遍历，避免生成重复子集
        // 剪枝三：从 start 开始遍历，避免重复选择同一元素
        for (int i = start; i < choices.size(); i++) {
            // 剪枝一：若子集和超过 target ，则直接结束循环
            // 这是因为数组已排序，后边元素更大，子集和一定超过 target
            if (target - choices[i] < 0) {
                break;
            }
            // 剪枝四：如果该元素与左边元素相等，说明该搜索分支重复，直接跳过
            if (i > start && choices[i] == choices[i - 1]) {
                continue;
            }
            // 尝试：做出选择，更新 target, start
            state.push_back(choices[i]);
            // 进行下一轮选择
            backtrack(state, target - choices[i], choices, i + 1, res);
            // 回退：撤销选择，恢复到之前的状态
            state.pop_back();
        }
    }
};

下图展示了数组 $[4, 4, 5]$ 和目标元素 $9$ 的回溯过程，共包含四种剪枝操作。请你将图示与代码注释相结合，理解整个搜索过程，以及每种剪枝操作是如何工作的。

解题思路： ​

相等元素剪枝： ​

代码： ​

解题思路：

相等元素剪枝：

代码：