解题思路:
设 $s$ 的长度为 $n$ , $p$ 的长度为 $m$ ;将 $s$ 的第 $i$ 个字符记为 $s_i$ ,$p$ 的第 $j$ 个字符记为 $p_j$ ,将 $s$ 的前 $i$ 个字符组成的子字符串记为 $s[:i]$ , 同理将 $p$ 的前 $j$ 个字符组成的子字符串记为 $p[:j]$ 。本题可转化为求 $s[:n]$ 是否能和 $p[:m]$ 匹配。
总体思路是从 $s[:1]$ 和 $p[:1]$ 开始判断是否能匹配,每轮添加一个字符并判断是否能匹配,直至添加完整个字符串 $s$ 和 $p$ 。展开来看,假设 $s[:i]$ 与 $p[:j]$ 可以匹配,那么下一状态有两种:
- 添加一个字符 $s_{i+1}$ 后是否能匹配?
- 添加字符 $p_{j+1}$ 后是否能匹配?
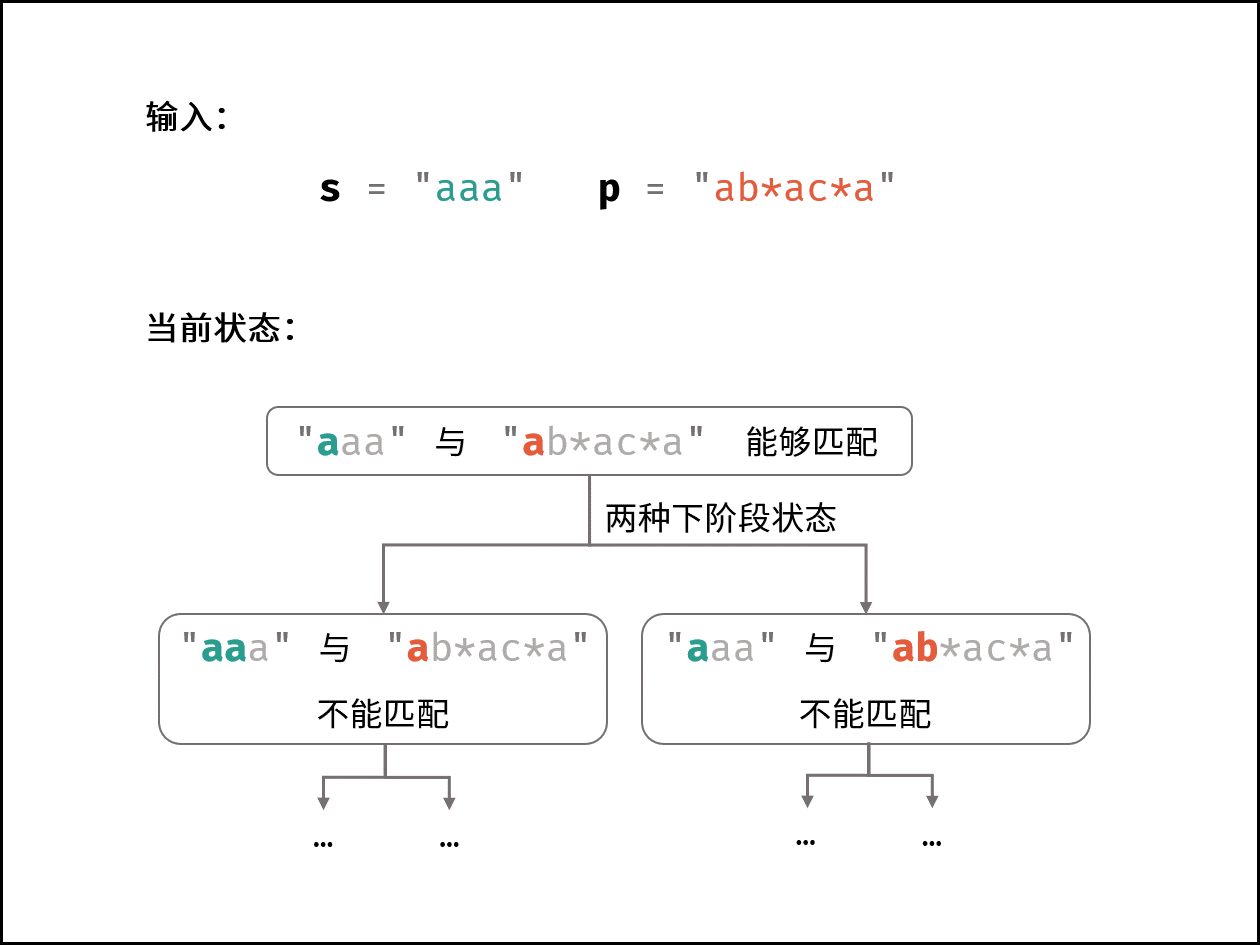
因此,本题的状态共有 $m \times n$ 种,应定义状态矩阵 $dp$ ,$dp[i][j]$ 代表 $s[:i]$ 与 $p[:j]$ 是否可以匹配。
做好状态定义,接下来就是根据 「普通字符」 , 「.」 , 「*」三种字符的功能定义,分析出动态规划的转移方程。
状态定义: 设动态规划矩阵
dp,dp[i][j]代表字符串s的前i个字符和p的前j个字符能否匹配。转移方程: 需要注意,由于
dp[0][0]代表的是空字符的状态, 因此dp[i][j]对应的添加字符是s[i - 1]和p[j - 1]。当
p[j - 1] = '*'时,dp[i][j]在当以下任一情况为 $true$ 时等于 $true$ :dp[i][j - 2]: 即将字符组合p[j - 2] *看作出现 0 次时,能否匹配。dp[i - 1][j]且s[i - 1] = p[j - 2]: 即让字符p[j - 2]多出现 1 次时,能否匹配。dp[i - 1][j]且p[j - 2] = '.': 即让字符'.'多出现 1 次时,能否匹配。
当
p[j - 1] != '*'时,dp[i][j]在当以下任一情况为 $true$ 时等于 $true$ :dp[i - 1][j - 1]且s[i - 1] = p[j - 1]: 即让字符p[j - 1]多出现一次时,能否匹配。dp[i - 1][j - 1]且p[j - 1] = '.': 即将字符.看作字符s[i - 1]时,能否匹配。
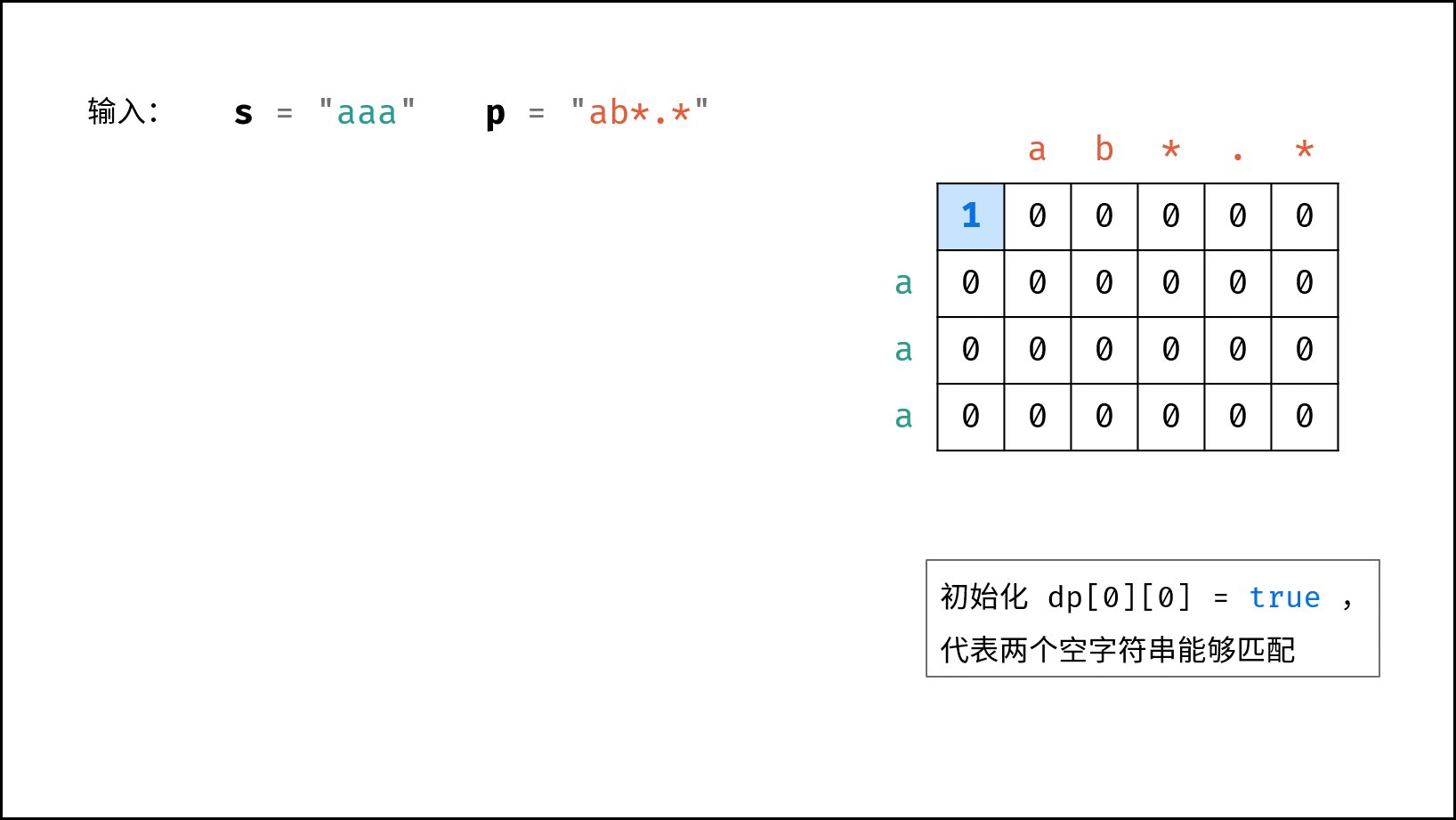
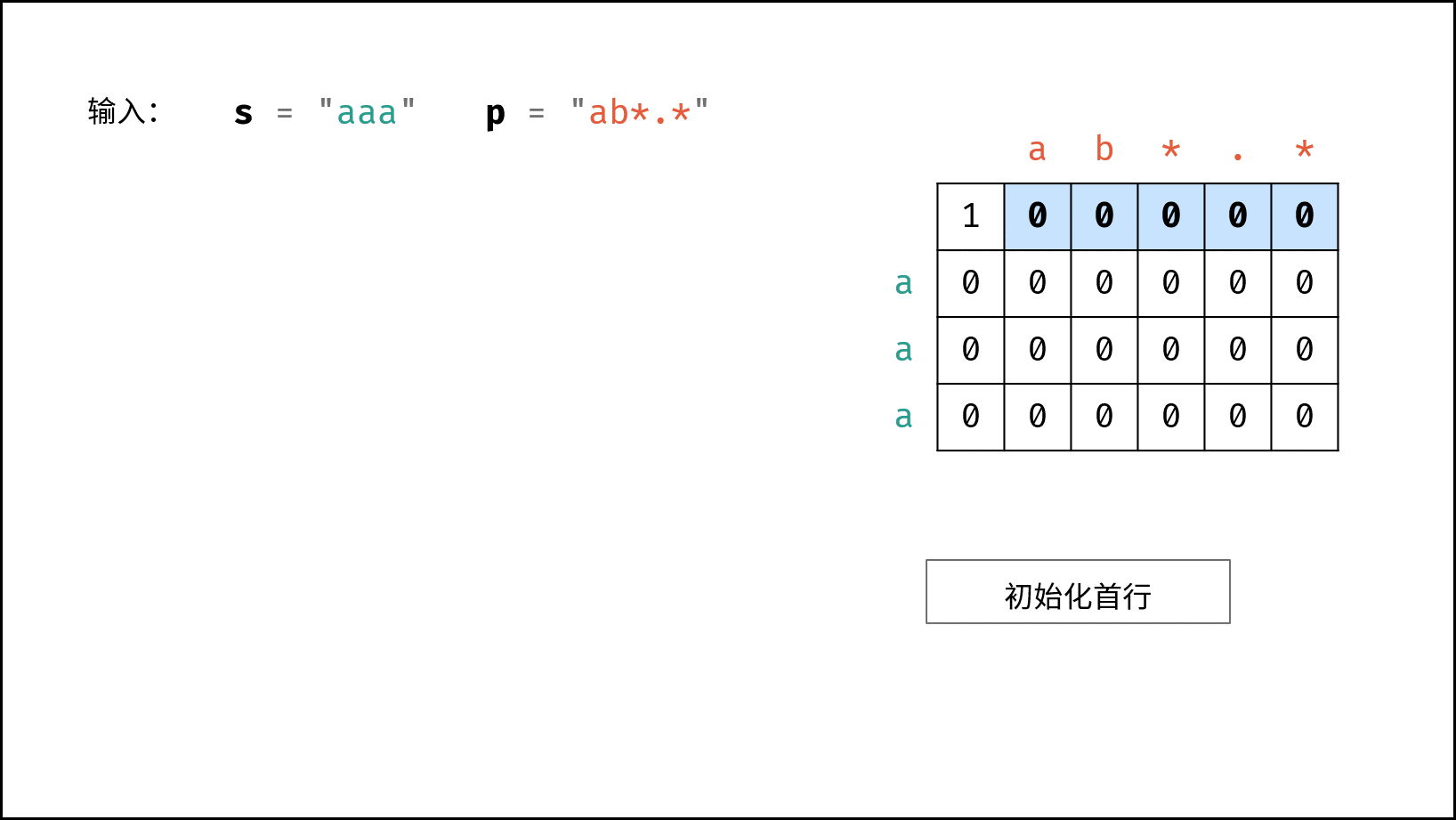
初始化: 需要先初始化
dp矩阵首行,以避免状态转移时索引越界。dp[0][0] = true: 代表两个空字符串能够匹配。dp[0][j] = dp[0][j - 2]且p[j - 1] = '*': 首行s为空字符串,因此当p的偶数位为*时才能够匹配(即让p的奇数位出现 0 次,保持p是空字符串)。因此,循环遍历字符串p,步长为 2(即只看偶数位)。
返回值:
dp矩阵右下角字符,代表字符串s和p能否匹配。
< ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, >
>
代码:
class Solution:
def isMatch(self, s: str, p: str) -> bool:
m, n = len(s) + 1, len(p) + 1
dp = [[False] * n for _ in range(m)]
dp[0][0] = True
for j in range(2, n, 2):
dp[0][j] = dp[0][j - 2] and p[j - 1] == '*'
for i in range(1, m):
for j in range(1, n):
dp[i][j] = dp[i][j - 2] or dp[i - 1][j] and (s[i - 1] == p[j - 2] or p[j - 2] == '.') \
if p[j - 1] == '*' else \
dp[i - 1][j - 1] and (p[j - 1] == '.' or s[i - 1] == p[j - 1])
return dp[-1][-1]class Solution {
public boolean isMatch(String s, String p) {
int m = s.length() + 1, n = p.length() + 1;
boolean[][] dp = new boolean[m][n];
dp[0][0] = true;
for(int j = 2; j < n; j += 2)
dp[0][j] = dp[0][j - 2] && p.charAt(j - 1) == '*';
for(int i = 1; i < m; i++) {
for(int j = 1; j < n; j++) {
dp[i][j] = p.charAt(j - 1) == '*' ?
dp[i][j - 2] || dp[i - 1][j] && (s.charAt(i - 1) == p.charAt(j - 2) || p.charAt(j - 2) == '.') :
dp[i - 1][j - 1] && (p.charAt(j - 1) == '.' || s.charAt(i - 1) == p.charAt(j - 1));
}
}
return dp[m - 1][n - 1];
}
}class Solution {
public:
bool isMatch(string s, string p) {
int m = s.size() + 1, n = p.size() + 1;
vector<vector<bool>> dp(m, vector<bool>(n, false));
dp[0][0] = true;
for(int j = 2; j < n; j += 2)
dp[0][j] = dp[0][j - 2] && p[j - 1] == '*';
for(int i = 1; i < m; i++) {
for(int j = 1; j < n; j++) {
dp[i][j] = p[j - 1] == '*' ?
dp[i][j - 2] || dp[i - 1][j] && (s[i - 1] == p[j - 2] || p[j - 2] == '.'):
dp[i - 1][j - 1] && (p[j - 1] == '.' || s[i - 1] == p[j - 1]);
}
}
return dp[m - 1][n - 1];
}
};以上代码利用布尔运算实现简短长度,若阅读不畅,可先理解以下代码,与文中内容一一对应:
class Solution:
def isMatch(self, s: str, p: str) -> bool:
m, n = len(s) + 1, len(p) + 1
dp = [[False] * n for _ in range(m)]
dp[0][0] = True
# 初始化首行
for j in range(2, n, 2):
dp[0][j] = dp[0][j - 2] and p[j - 1] == '*'
# 状态转移
for i in range(1, m):
for j in range(1, n):
if p[j - 1] == '*':
if dp[i][j - 2]: dp[i][j] = True # 1.
elif dp[i - 1][j] and s[i - 1] == p[j - 2]: dp[i][j] = True # 2.
elif dp[i - 1][j] and p[j - 2] == '.': dp[i][j] = True # 3.
else:
if dp[i - 1][j - 1] and s[i - 1] == p[j - 1]: dp[i][j] = True # 1.
elif dp[i - 1][j - 1] and p[j - 1] == '.': dp[i][j] = True # 2.
return dp[-1][-1]class Solution {
public boolean isMatch(String s, String p) {
int m = s.length() + 1, n = p.length() + 1;
boolean[][] dp = new boolean[m][n];
dp[0][0] = true;
// 初始化首行
for(int j = 2; j < n; j += 2)
dp[0][j] = dp[0][j - 2] && p.charAt(j - 1) == '*';
// 状态转移
for(int i = 1; i < m; i++) {
for(int j = 1; j < n; j++) {
if (p.charAt(j - 1) == '*') {
if (dp[i][j - 2]) dp[i][j] = true; // 1.
else if (dp[i - 1][j] && s.charAt(i - 1) == p.charAt(j - 2)) dp[i][j] = true; // 2.
else if (dp[i - 1][j] && p.charAt(j - 2) == '.') dp[i][j] = true; // 3.
} else {
if (dp[i - 1][j - 1] && s.charAt(i - 1) == p.charAt(j - 1)) dp[i][j] = true; // 1.
else if (dp[i - 1][j - 1] && p.charAt(j - 1) == '.') dp[i][j] = true; // 2.
}
}
}
return dp[m - 1][n - 1];
}
}class Solution {
public:
bool isMatch(string s, string p) {
int m = s.size() + 1, n = p.size() + 1;
vector<vector<bool>> dp(m, vector<bool>(n, false));
dp[0][0] = true;
// 初始化首行
for(int j = 2; j < n; j += 2)
dp[0][j] = dp[0][j - 2] && p[j - 1] == '*';
// 状态转移
for(int i = 1; i < m; i++) {
for(int j = 1; j < n; j++) {
if (p[j - 1] == '*') {
if (dp[i][j - 2]) dp[i][j] = true; // 1.
else if (dp[i - 1][j] && s[i - 1] == p[j - 2]) dp[i][j] = true; // 2.
else if (dp[i - 1][j] && p[j - 2] == '.') dp[i][j] = true; // 3.
} else {
if (dp[i - 1][j - 1] && s[i - 1] == p[j - 1]) dp[i][j] = true; // 1.
else if (dp[i - 1][j - 1] && p[j - 1] == '.') dp[i][j] = true; // 2.
}
}
}
return dp[m - 1][n - 1];
}
};复杂度分析:
- 时间复杂度 $O(MN)$ : 其中 $M, N$ 分别为
s和p的长度,状态转移需遍历整个dp矩阵。 - 空间复杂度 $O(MN)$ : 状态矩阵
dp使用 $O(MN)$ 的额外空间。