解题思路 ​

此题使用求和公式暴力求解的效率较低，因为包含大量重复计算。考虑借助「前一个动态和 $f(i-1)$ 」来计算得到「当前动态和 $f(i)$ 」，此题被约化为一个简单动态规划问题。

• 状态定义： 设前 $i + 1$ 个数字的和为 $f(i)$ ；
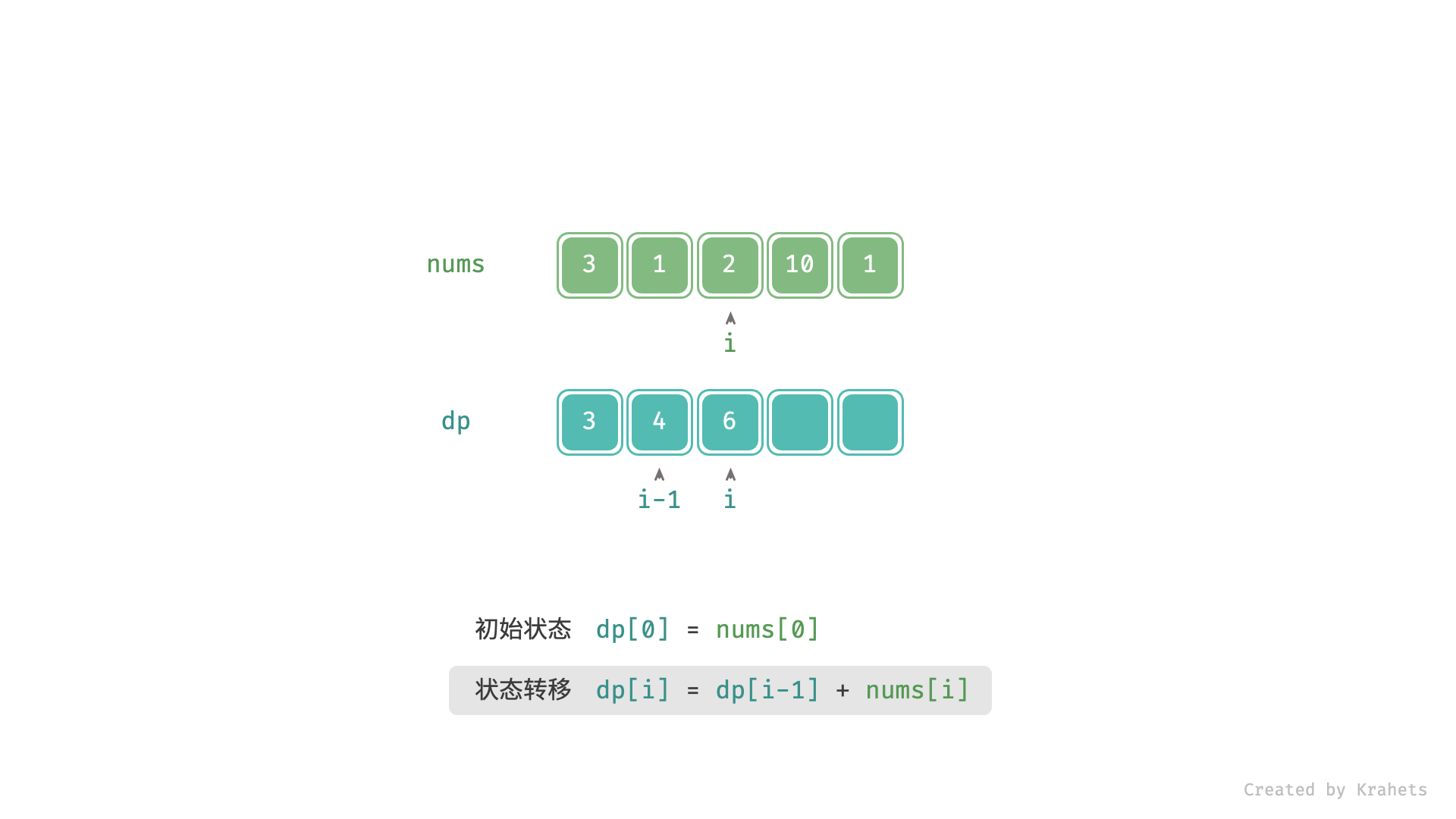
• 初始状态： $f(0) = nums[0]$ ；
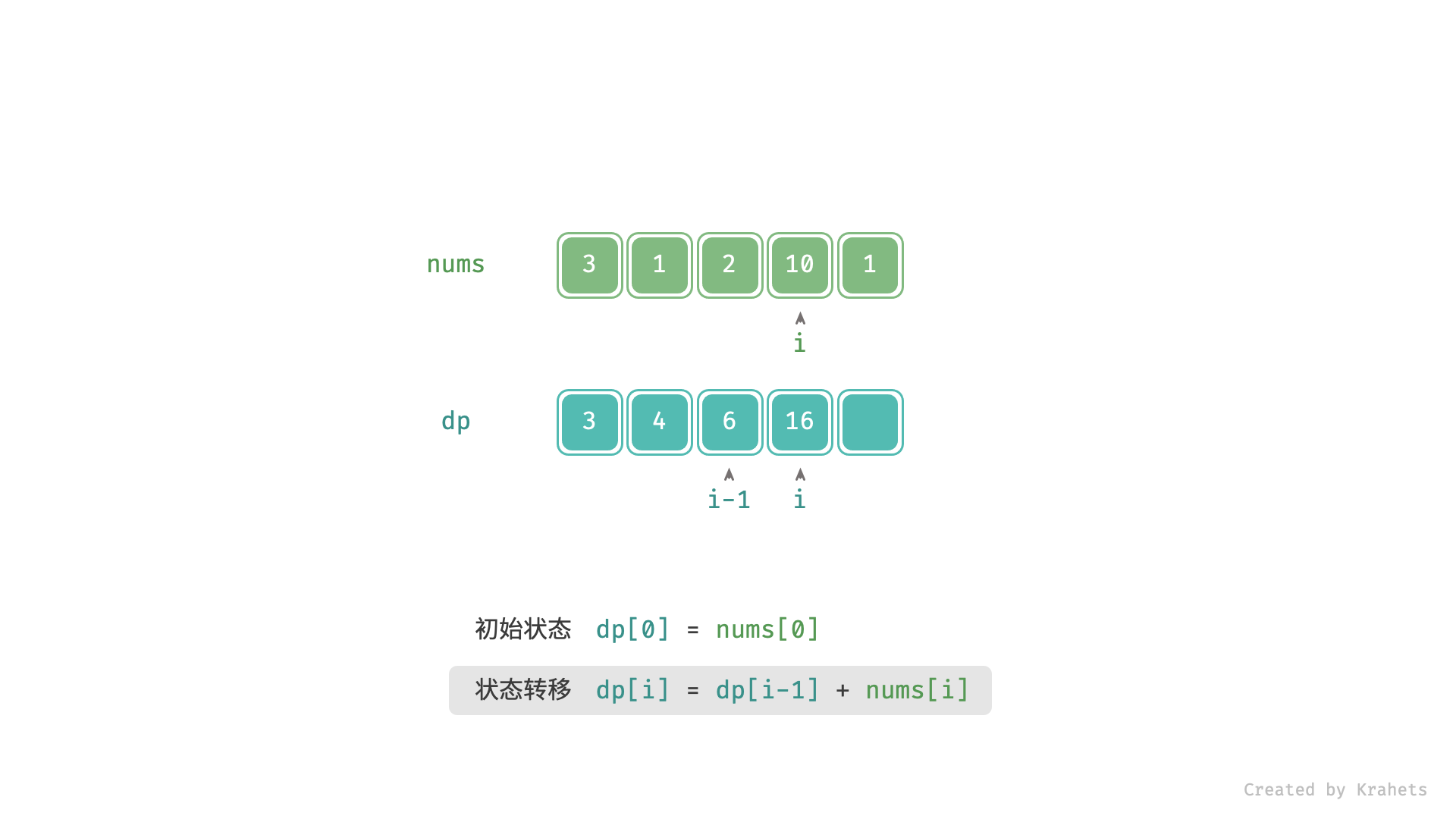
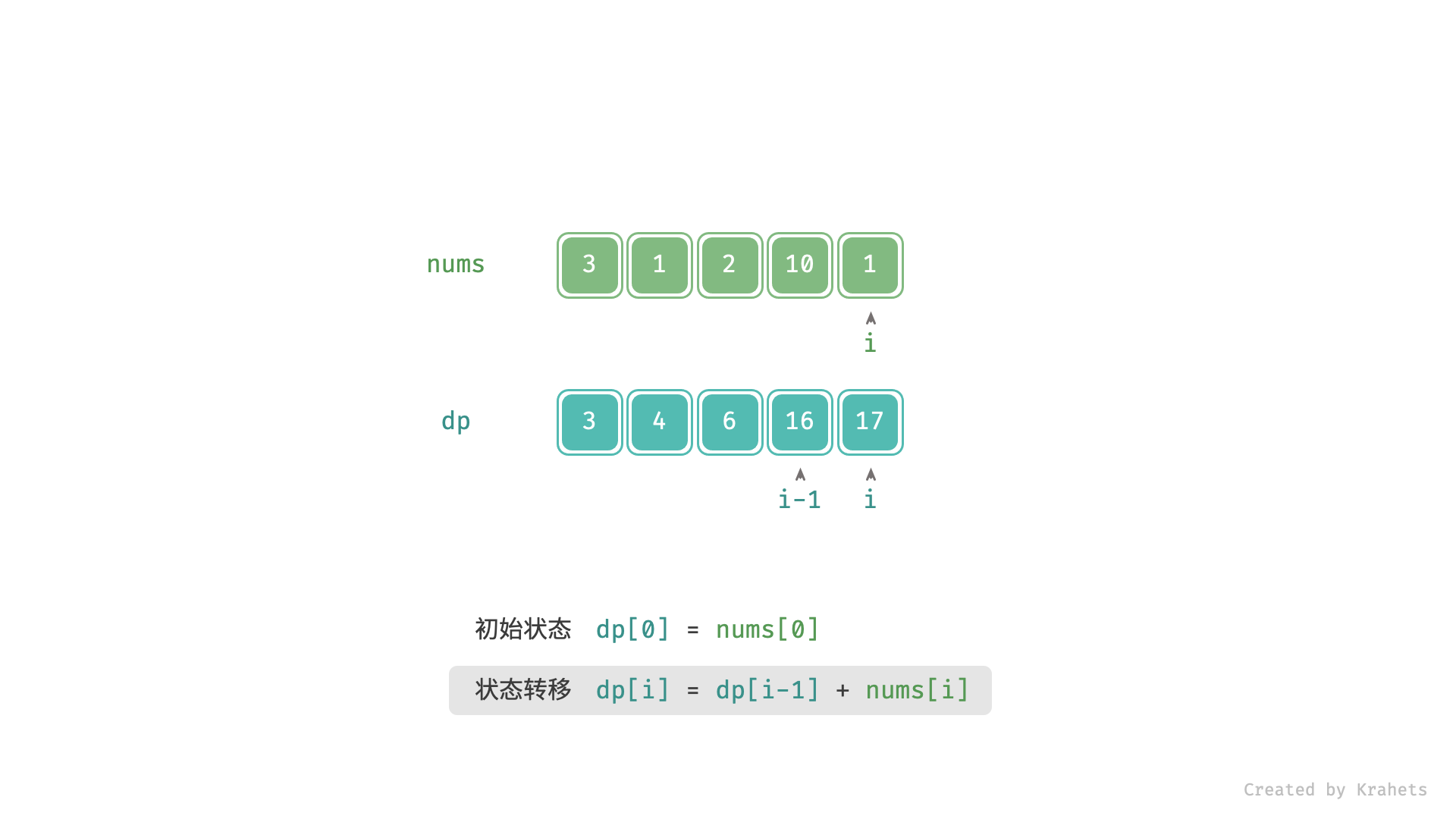
• 转移方程： $f(i) = f(i - 1) + nums[i]$ ；
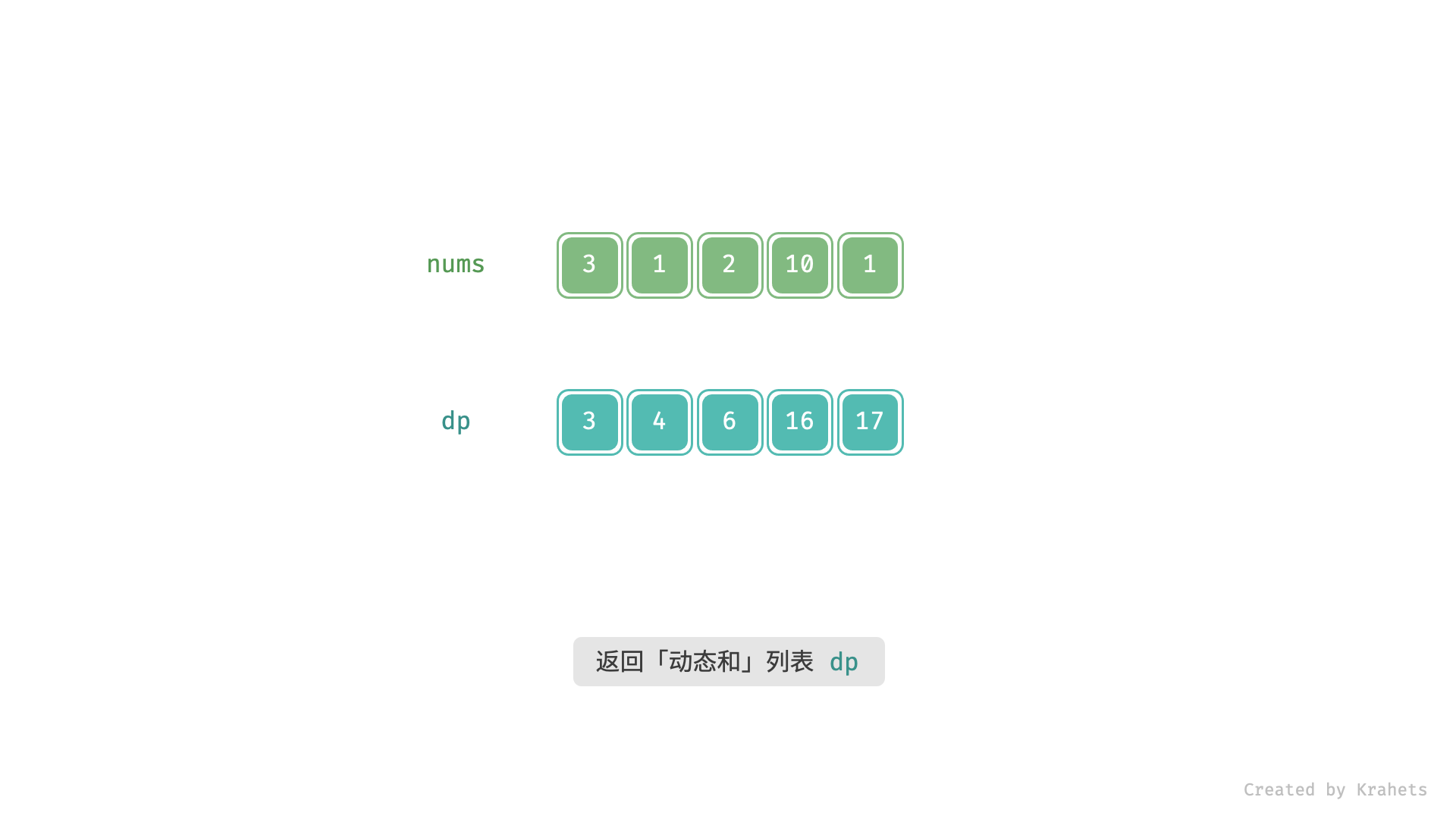
• 待求数值： $f(n - 1)$ ，其中 $n$ 为数组 $nums$ 长度；

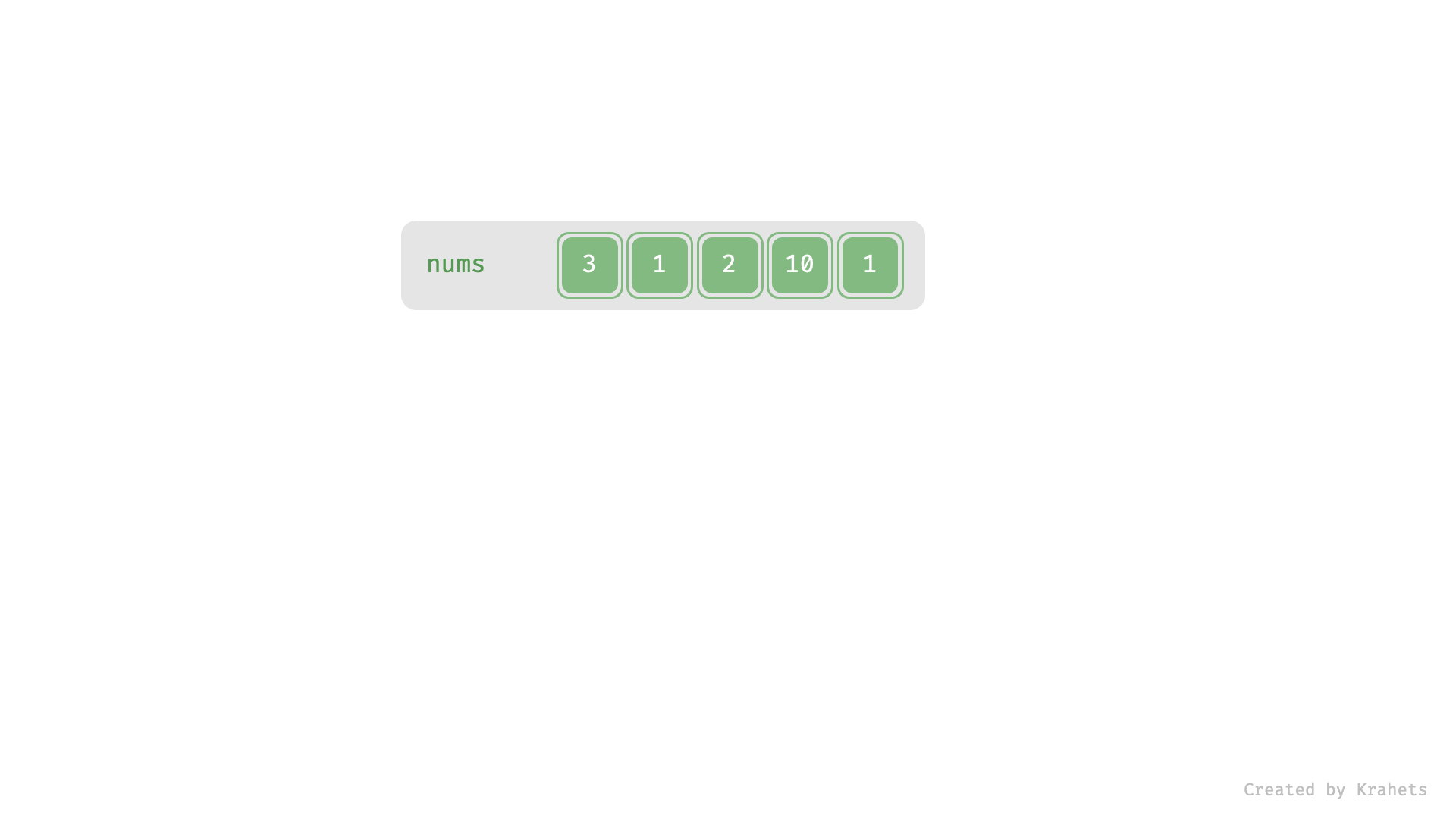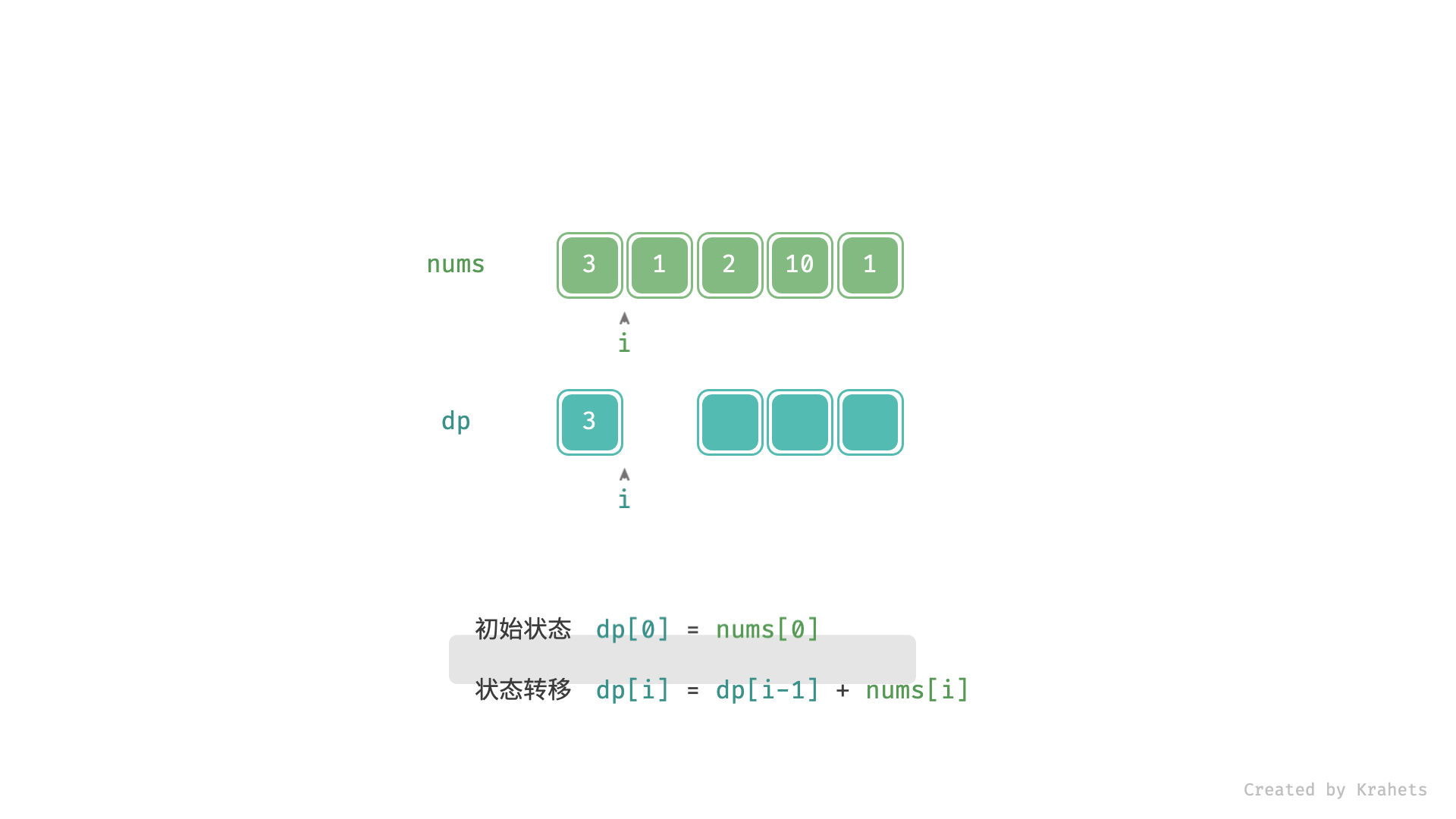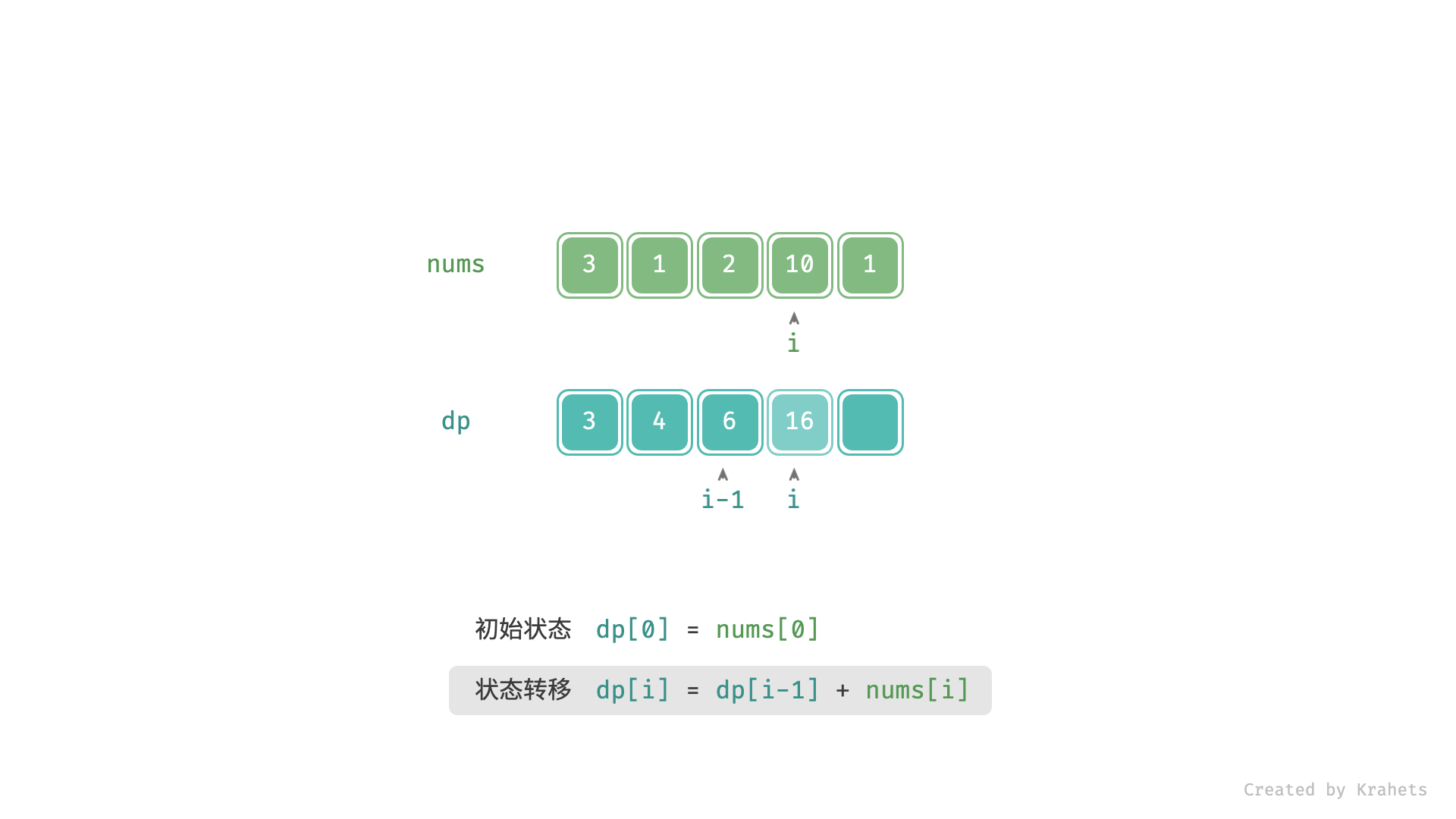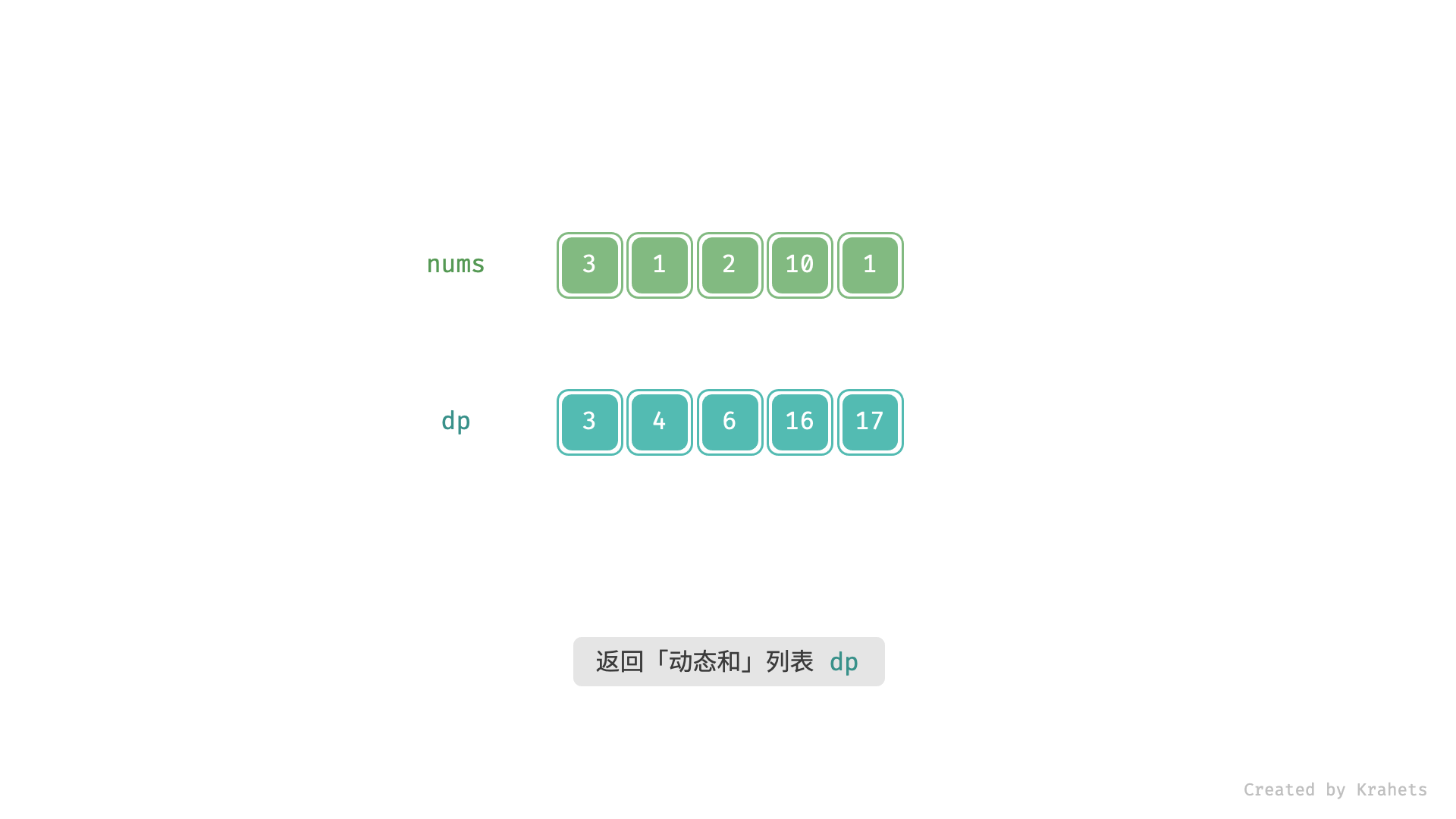
上为动态图，下为静态图，内容一致。

<,,,,,,,>

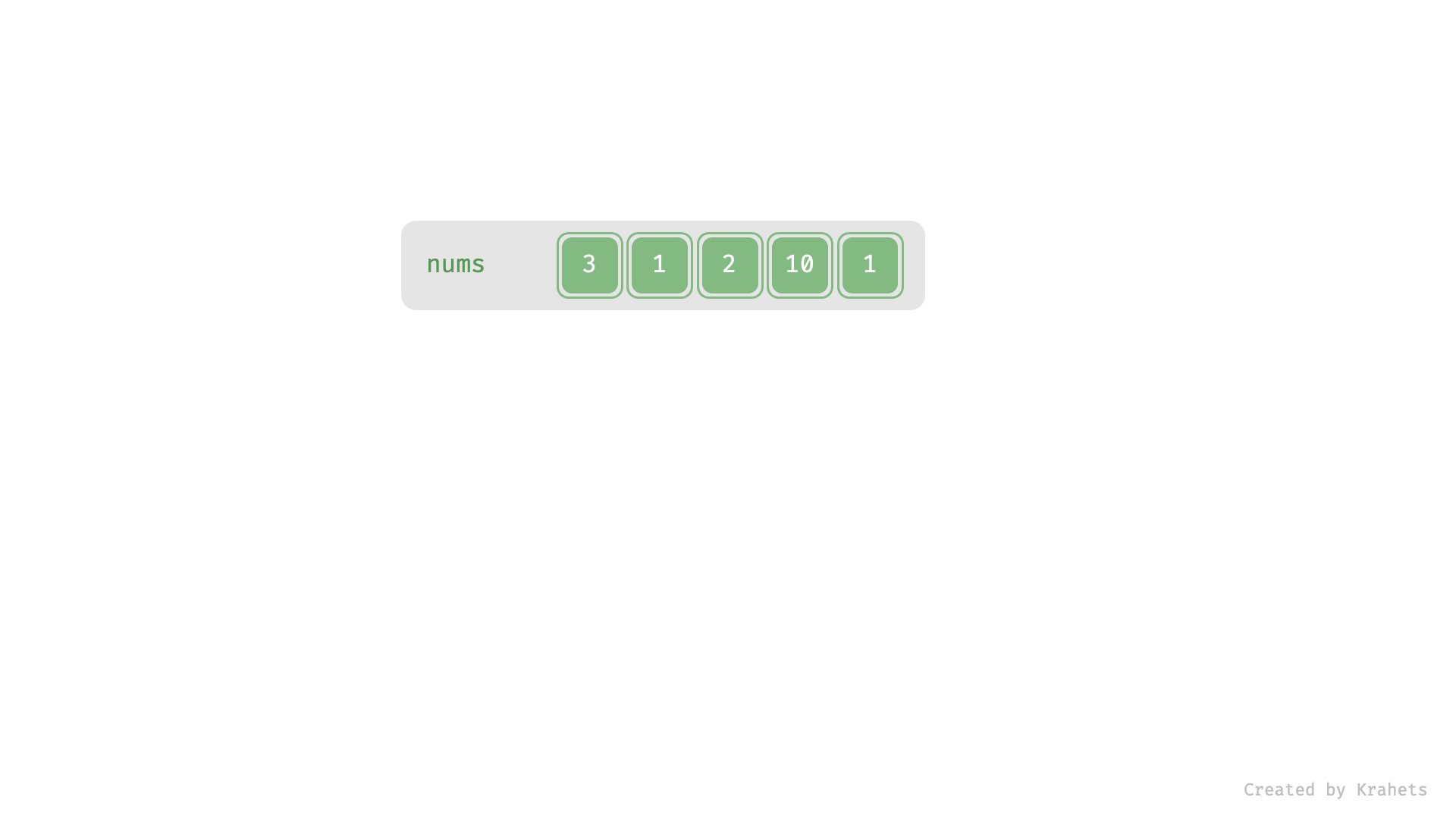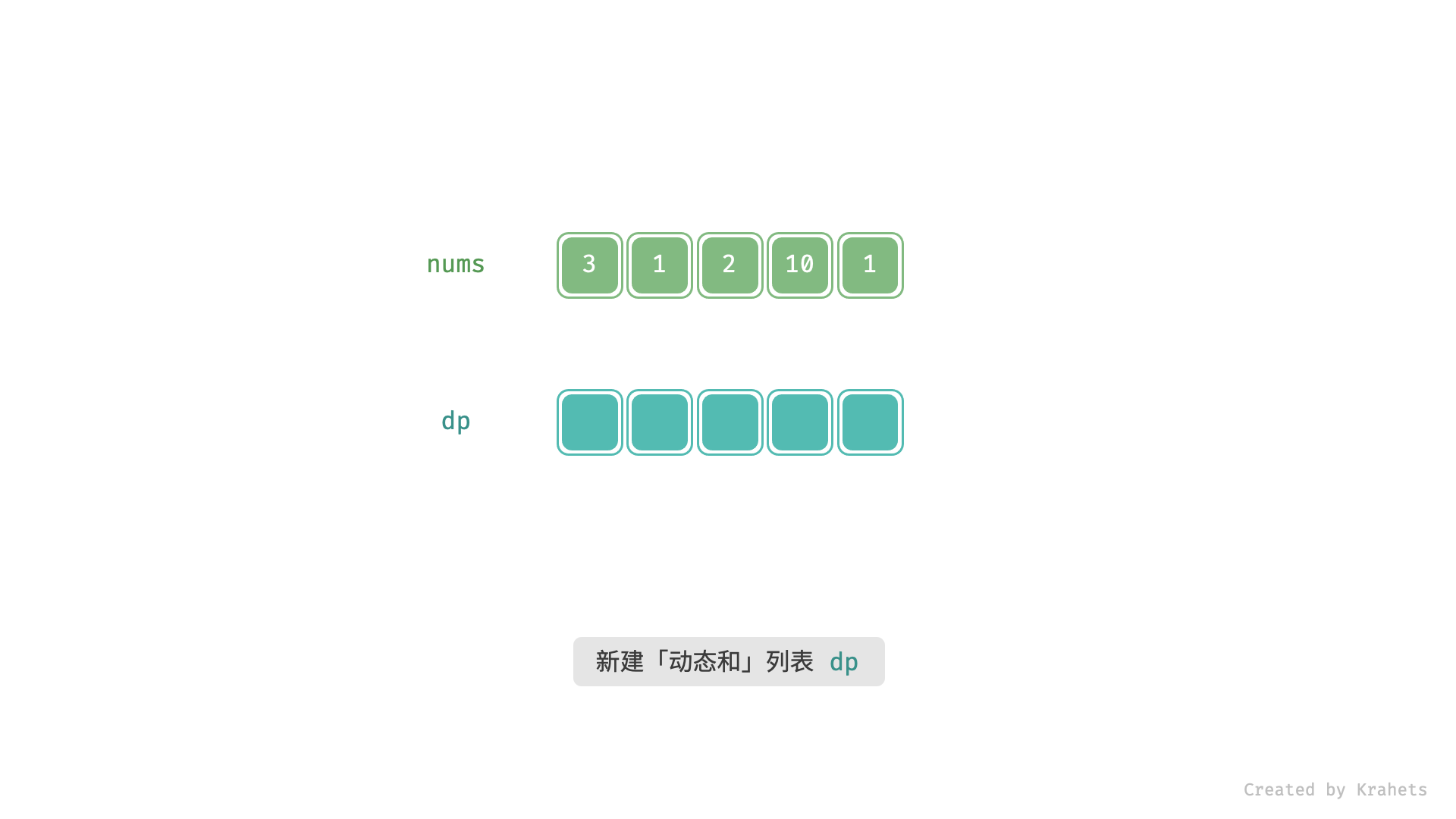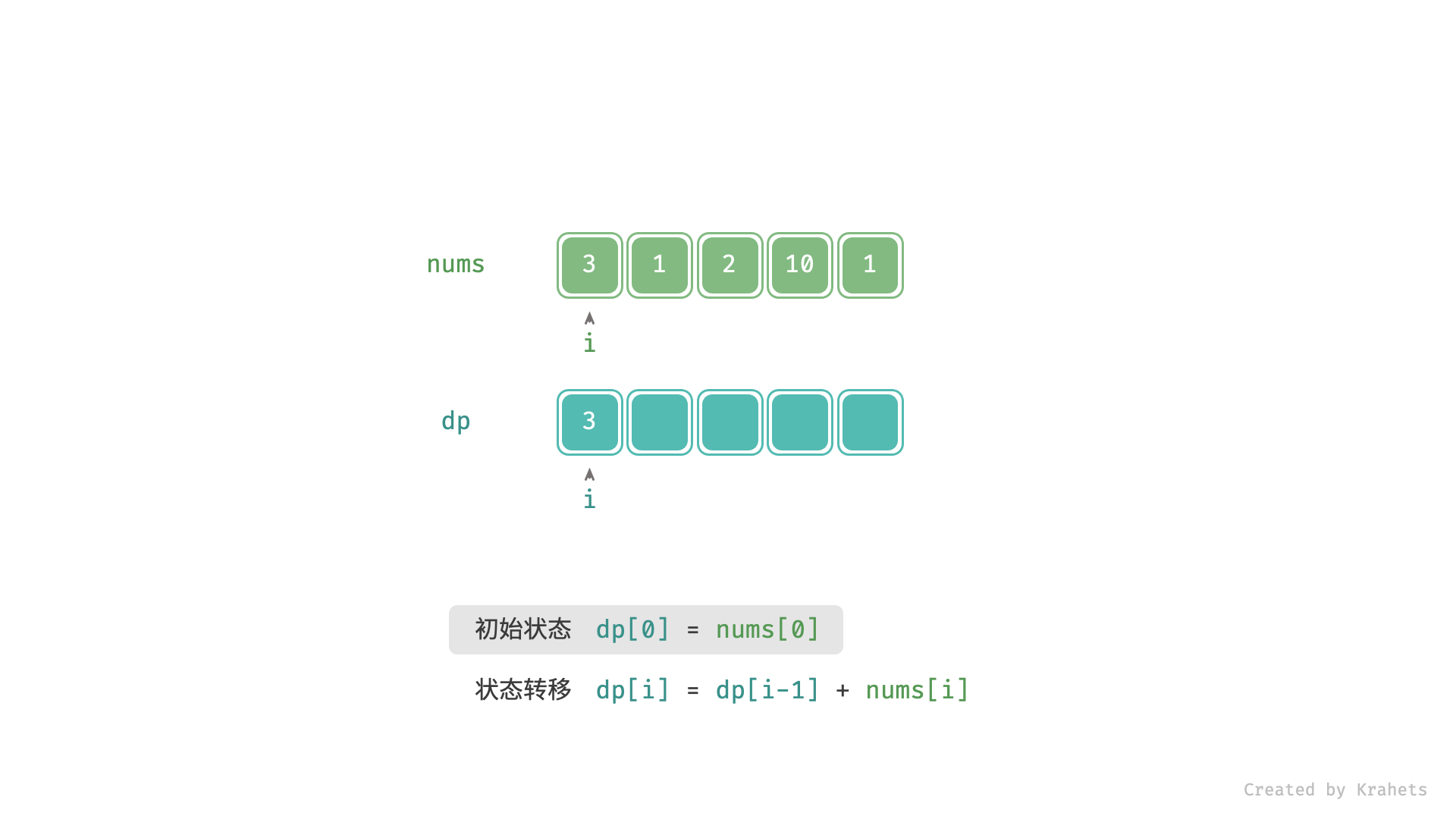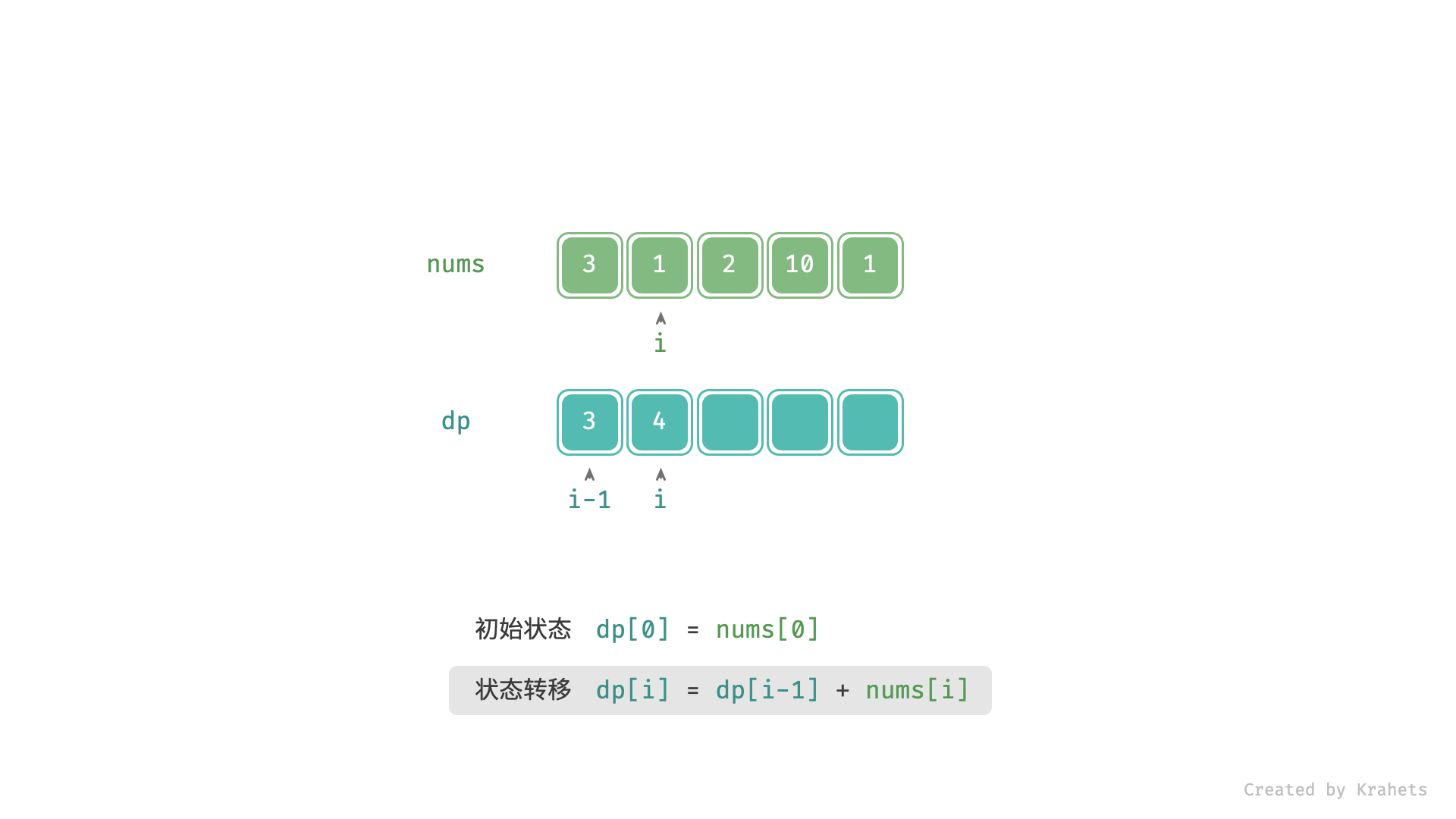代码 ​

细心的我们发现，如果原地修改 nums ，可以避免新建 dp 带来的内存开销。但通常情况下，不应改变输入变量，因此不建议原地修改 nums 数组。

class Solution:
    def runningSum(self, nums: List[int]) -> List[int]:
        dp = [0] * len(nums)
        dp[0] = nums[0]
        for i in range(1, len(nums)):
            dp[i] = dp[i - 1] + nums[i]
        return dp

class Solution {
    public int[] runningSum(int[] nums) {
        int[] dp = new int[nums.length];
        dp[0] = nums[0];
        for (int i = 1; i < nums.length; i++) {
            dp[i] = dp[i - 1] + nums[i];
        }
        return dp;
    }
}

class Solution {
public:
    vector<int> runningSum(vector<int>& nums) {
        vector<int> dp(nums.size());
        dp[0] = nums[0];
        for (int i = 1; i < nums.size(); i++) {
            dp[i] = dp[i - 1] + nums[i];
        }
        return dp;
    }
};

复杂度分析 ​

• 时间复杂度 $O(N)$ ： 遍历 nums 使用线性时间。
• 空间复杂度 $O(1)$ ： 用于保存结果的 dp 是必须使用的空间，此处不计入。