解题思路： ​

典型的动态规划，以下按照标准流程解题。

• 状态定义：

  • 设动态规划列表 $dp$ ，$dp[i]$ 代表前 $i$ 个房子在满足条件下的能偷窃到的最高金额。

• 转移方程：

  • 设： 有 $n$ 个房子，前 $n$ 间能偷窃到的最高金额是 $dp[n]$ ，前 $n-1$ 间能偷窃到的最高金额是 $dp[n-1]$ ，此时向这些房子后加一间房，此房间价值为 $num$ ；

  • 加一间房间后： 由于不能抢相邻的房子，意味着抢第 $n+1$ 间就不能抢第 $n$ 间；那么前 $n+1$ 间房能偷取到的最高金额 $dp[n+1]$ 一定是以下两种情况的 较大值 ：

    1. 不抢第 $n+1$ 个房间，因此等于前 $n$ 个房子的最高金额，即 $dp[n+1] = dp[n]$ ；
    2. 抢第 $n+1$ 个房间，此时不能抢第 $n$ 个房间；因此等于前 $n-1$ 个房子的最高金额加上当前房间价值，即 $dp[n+1] = dp[n-1] + num$ ；

  • 细心的我们发现： 难道在前 $n$ 间的最高金额 $dp[n]$ 情况下，第 $n$ 间一定被偷了吗？假设没有被偷，那 $n+1$ 间的最大值应该也可能是 $dp[n+1] = dp[n] + num$ 吧？其实这种假设的情况可以被省略，这是因为：

    1. 假设第 $n$ 间没有被偷，那么此时 $dp[n] = dp[n-1]$ ，此时 $dp[n+1] = dp[n] + num = dp[n-1] + num$ ，即两种情况可以 合并为一种情况 考虑；
    2. 假设第 $n$ 间被偷，那么此时 $dp[n+1] = dp[n] + num$ 不可取 ，因为偷了第 $n$ 间就不能偷第 $n+1$ 间。

  • 最终的转移方程： $dp[n+1] = max(dp[n],dp[n-1]+num)$

• 初始状态：

  • 前 $0$ 间房子的最大偷窃价值为 $0$ ，即 $dp[0] = 0$ 。

• 返回值：

  • 返回 $dp$ 列表最后一个元素值，即所有房间的最大偷窃价值。

• 简化空间复杂度：

  • 我们发现 $dp[n]$ 只与 $dp[n-1]$ 和 $dp[n-2]$ 有关系，因此我们可以设两个变量 cur和 pre 交替记录，将空间复杂度降到 $O(1)$ 。

复杂度分析： ​

• 时间复杂度 $O(N)$ ： 遍历 nums 需要线性时间；
• 空间复杂度 $O(1)$ ： cur和 pre 使用常数大小的额外空间。

<,,,,,,>

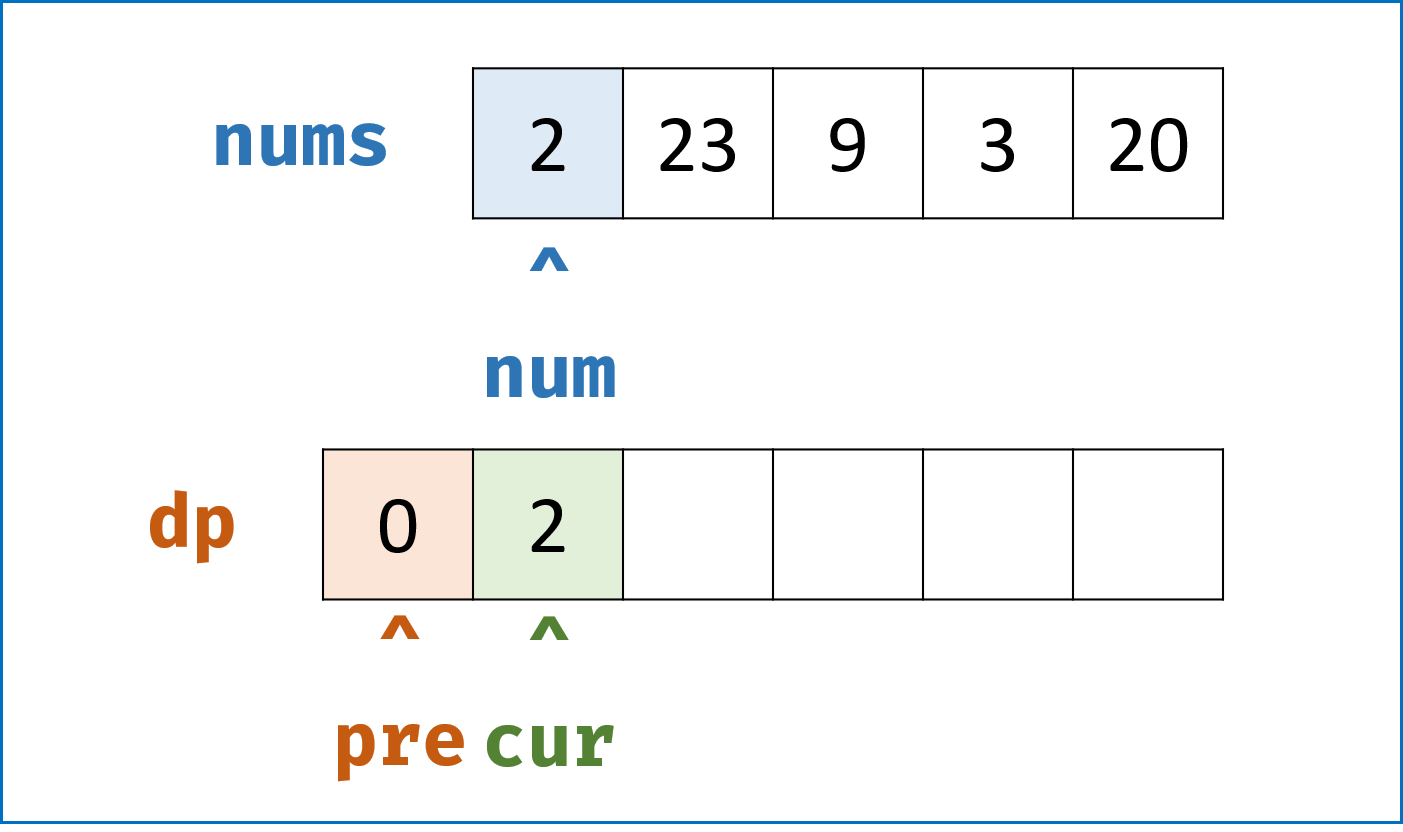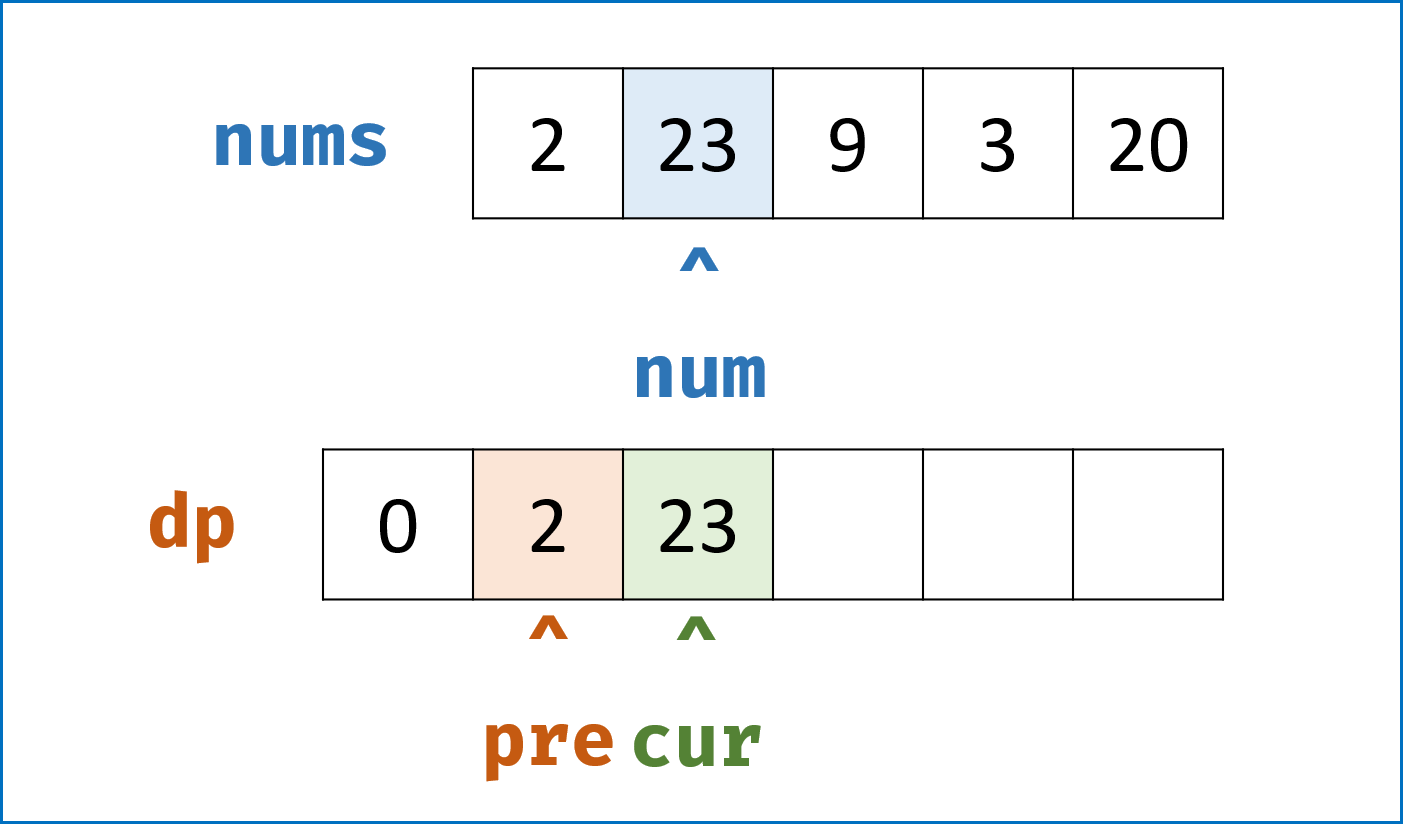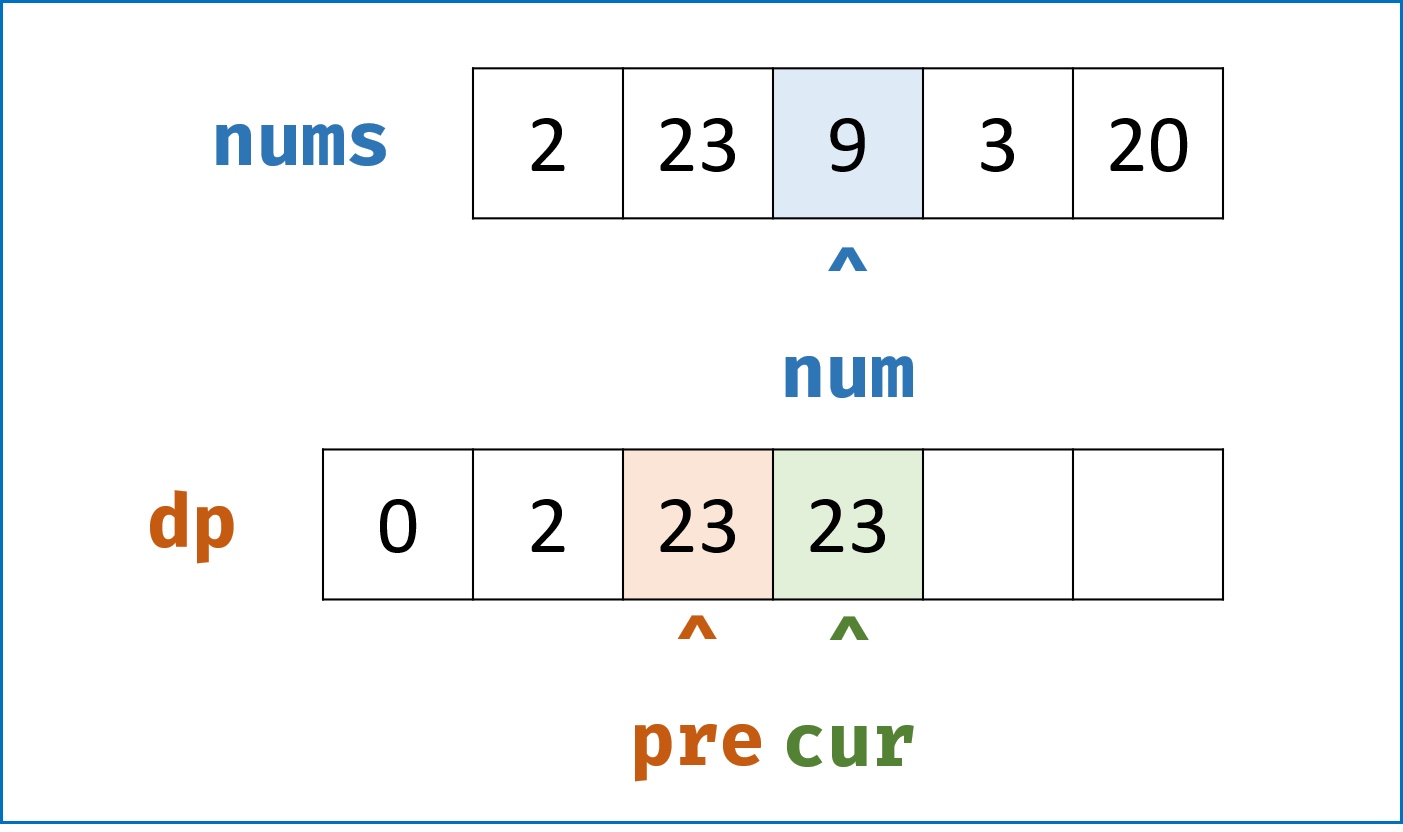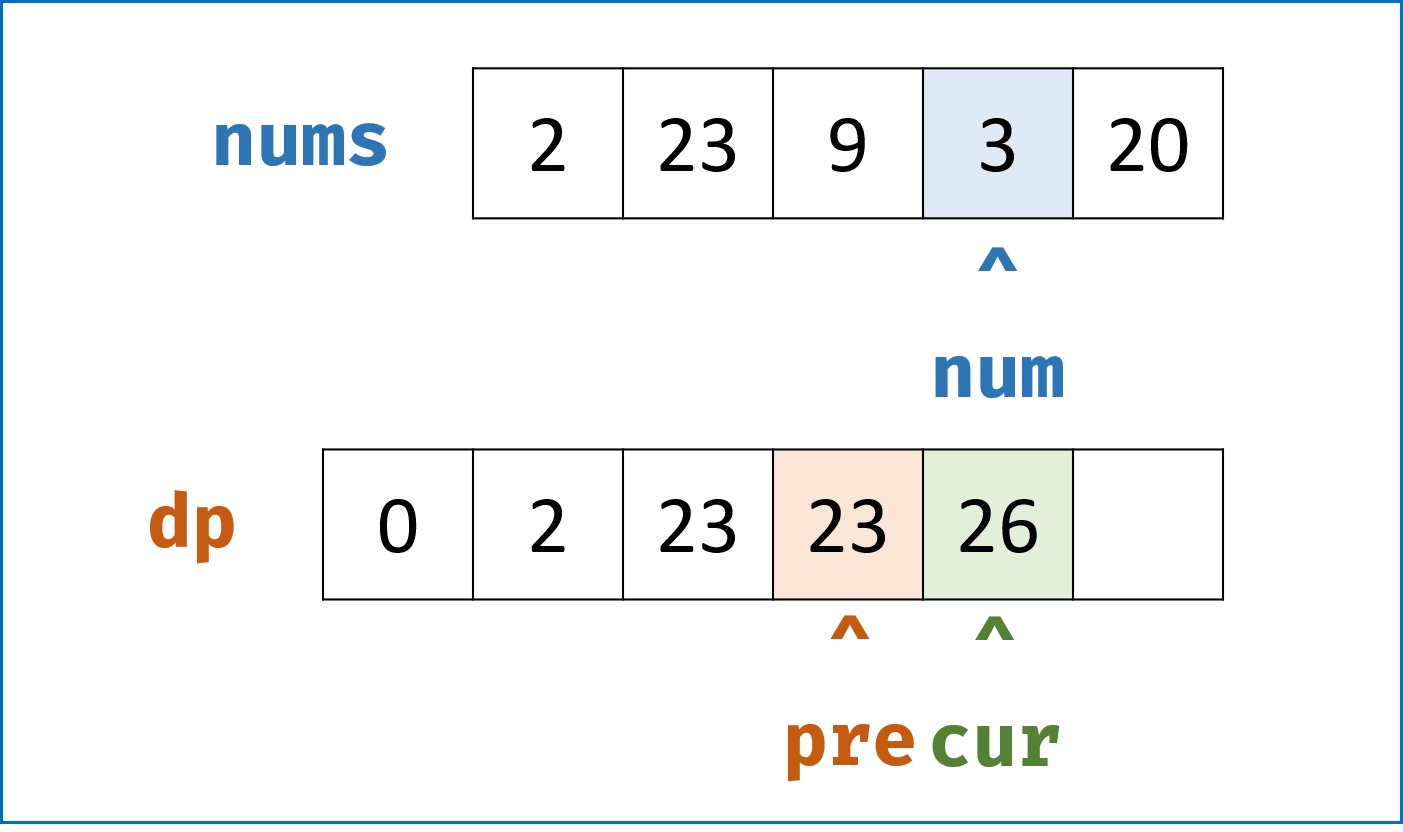代码： ​

class Solution:
    def rob(self, nums: List[int]) -> int:
        cur, pre = 0, 0
        for num in nums:
            cur, pre = max(pre + num, cur), cur
        return cur

class Solution {
    public int rob(int[] nums) {
        int pre = 0, cur = 0, tmp;
        for(int num : nums) {
            tmp = cur;
            cur = Math.max(pre + num, cur);
            pre = tmp;
        }
        return cur;
    }
}