解题思路： ​

根据题意，每个丑数都可以由其他较小的丑数通过乘以 $2$ 或 $3$ 或 $5$ 得到。

所以，可以考虑使用一个优先队列保存所有的丑数，每次取出最小的那个，然后乘以 $2$ , $3$ , $5$ 后放回队列。然而，这样做会出现重复的丑数。例如：

初始化丑数列表 [1]
第一轮： 1 -> 2, 3, 5 ，丑数列表变为 [1, 2, 3, 5]
第二轮： 2 -> 4, 6, 10 ，丑数列表变为 [1, 2, 3, 4, 6, 10]
第三轮： 3 -> 6, 9, 15 ，出现重复的丑数 6

为了避免重复，我们可以用三个指针 $a$ , $b$, $c$ ，分别表示下一个丑数是当前指针指向的丑数乘以 $2$ , $3$ , $5$ 。

利用三个指针生成丑数的算法流程：

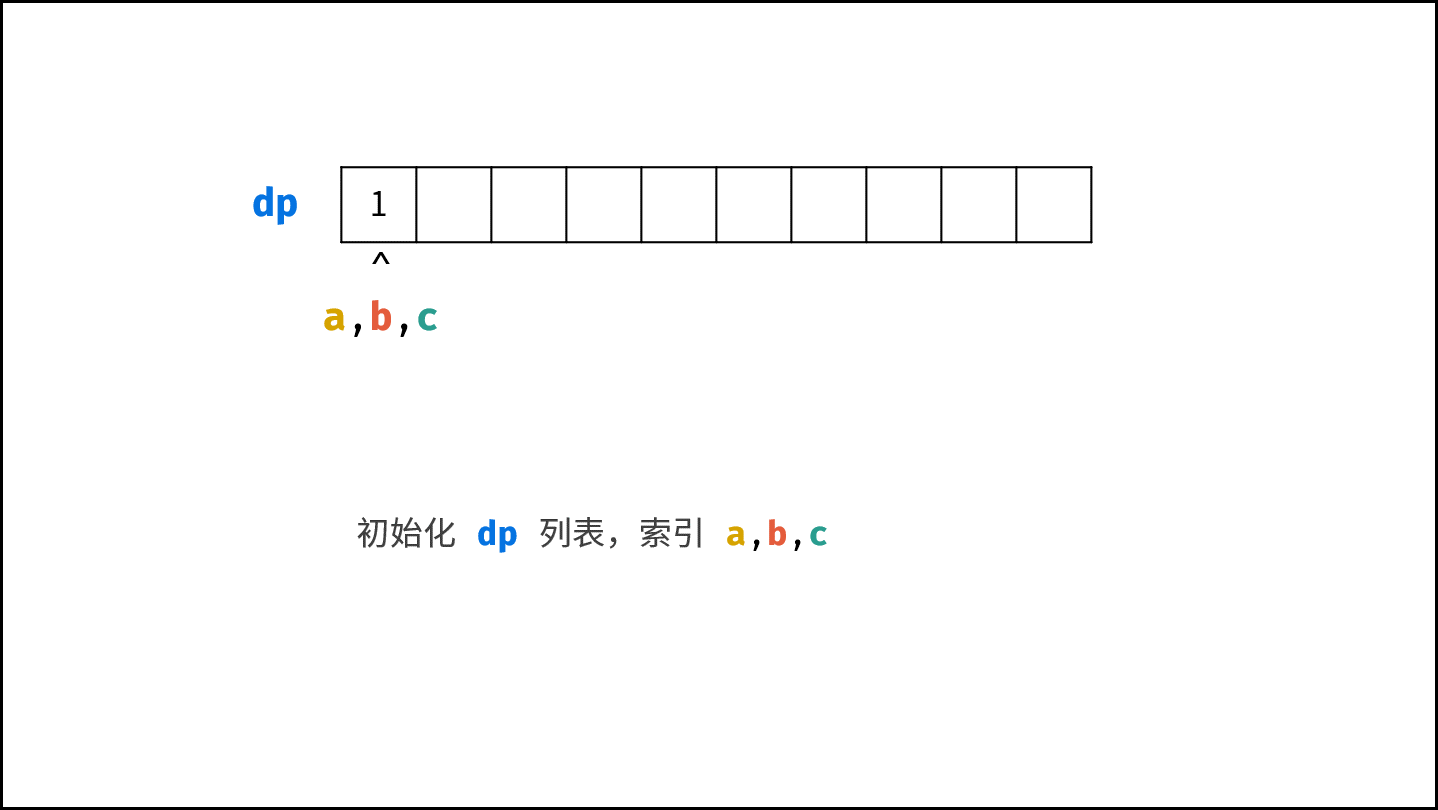
1. 初始化丑数列表 $res$ ，首个丑数为 $1$ ，三个指针 $a$ , $b$, $c$ 都指向首个丑数。
2. 开启循环生成丑数：
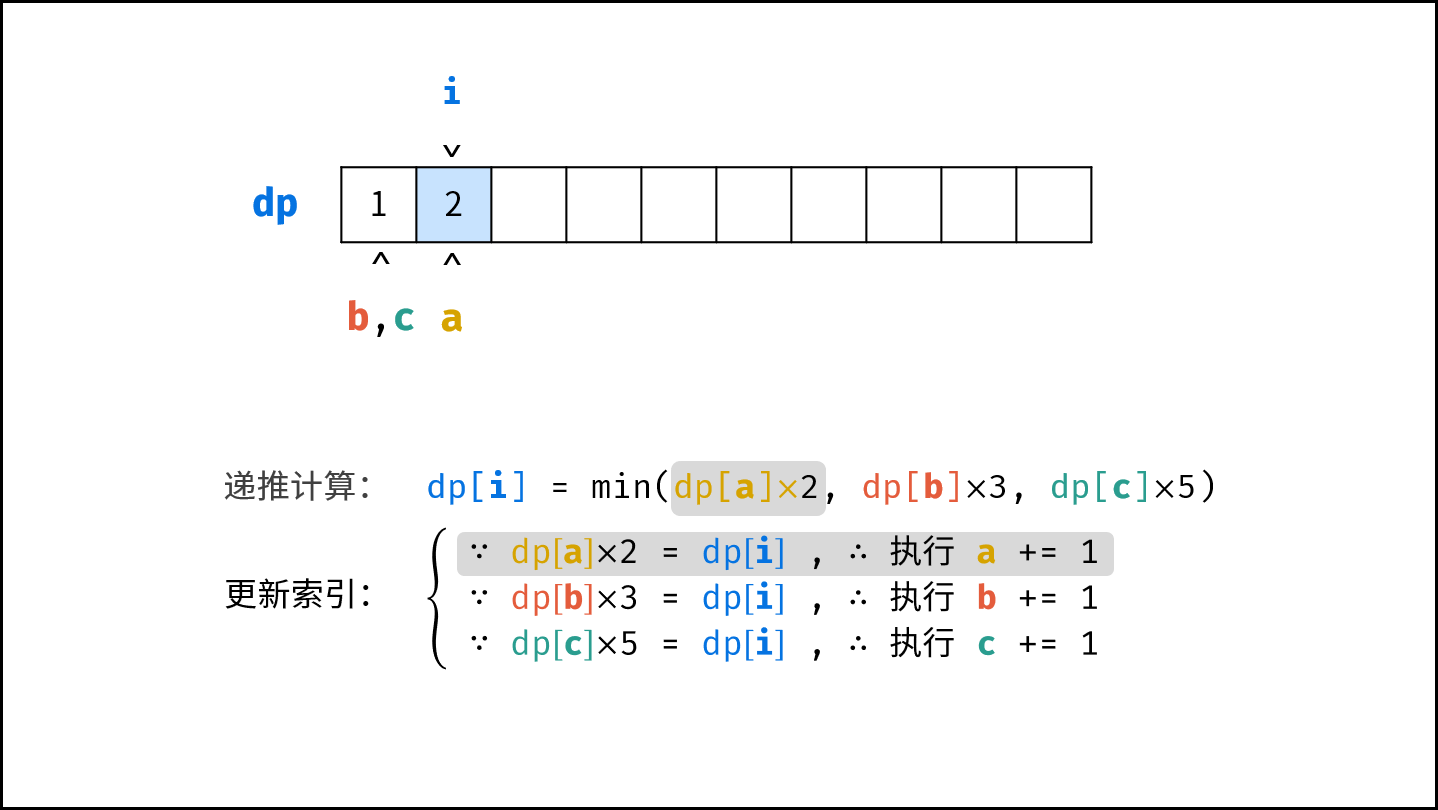
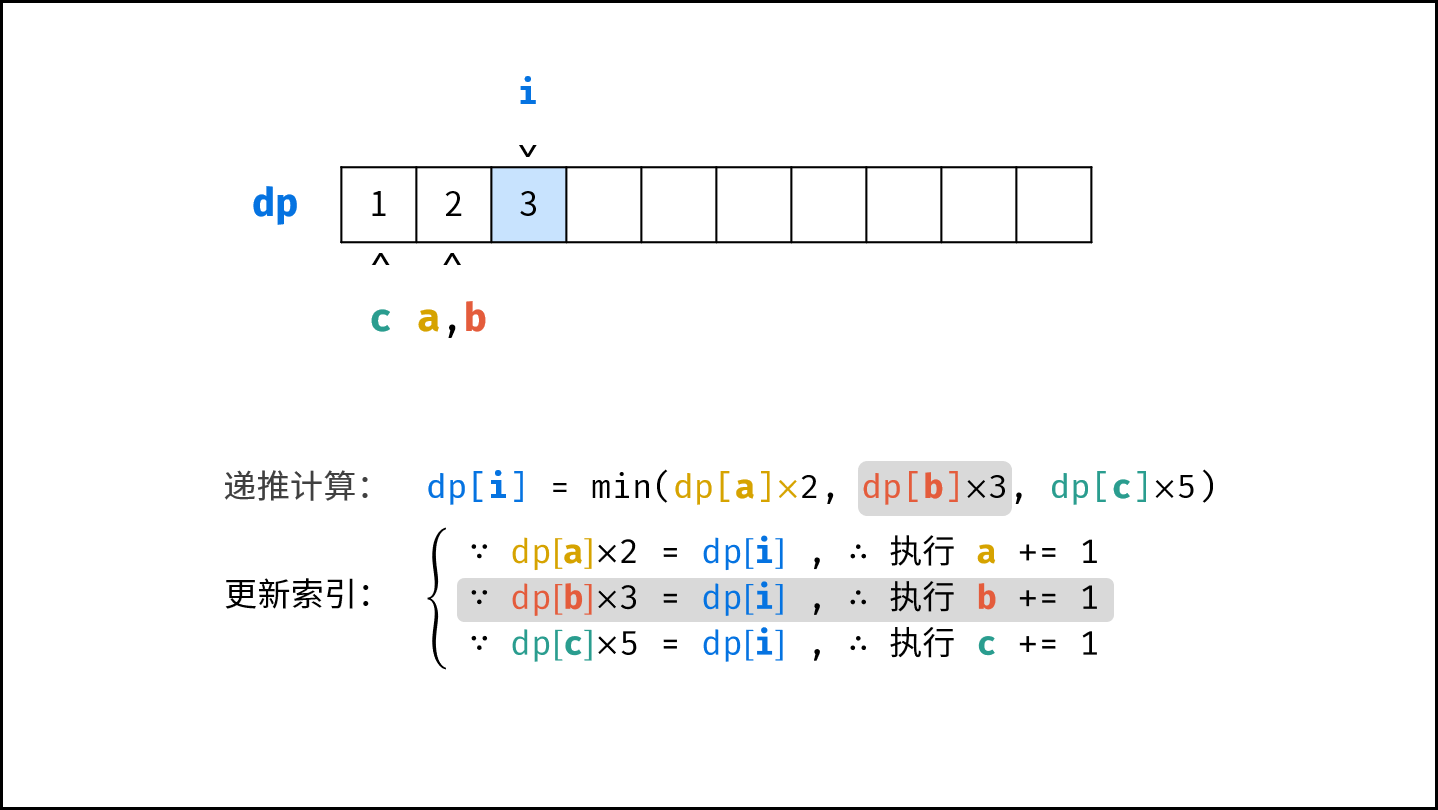
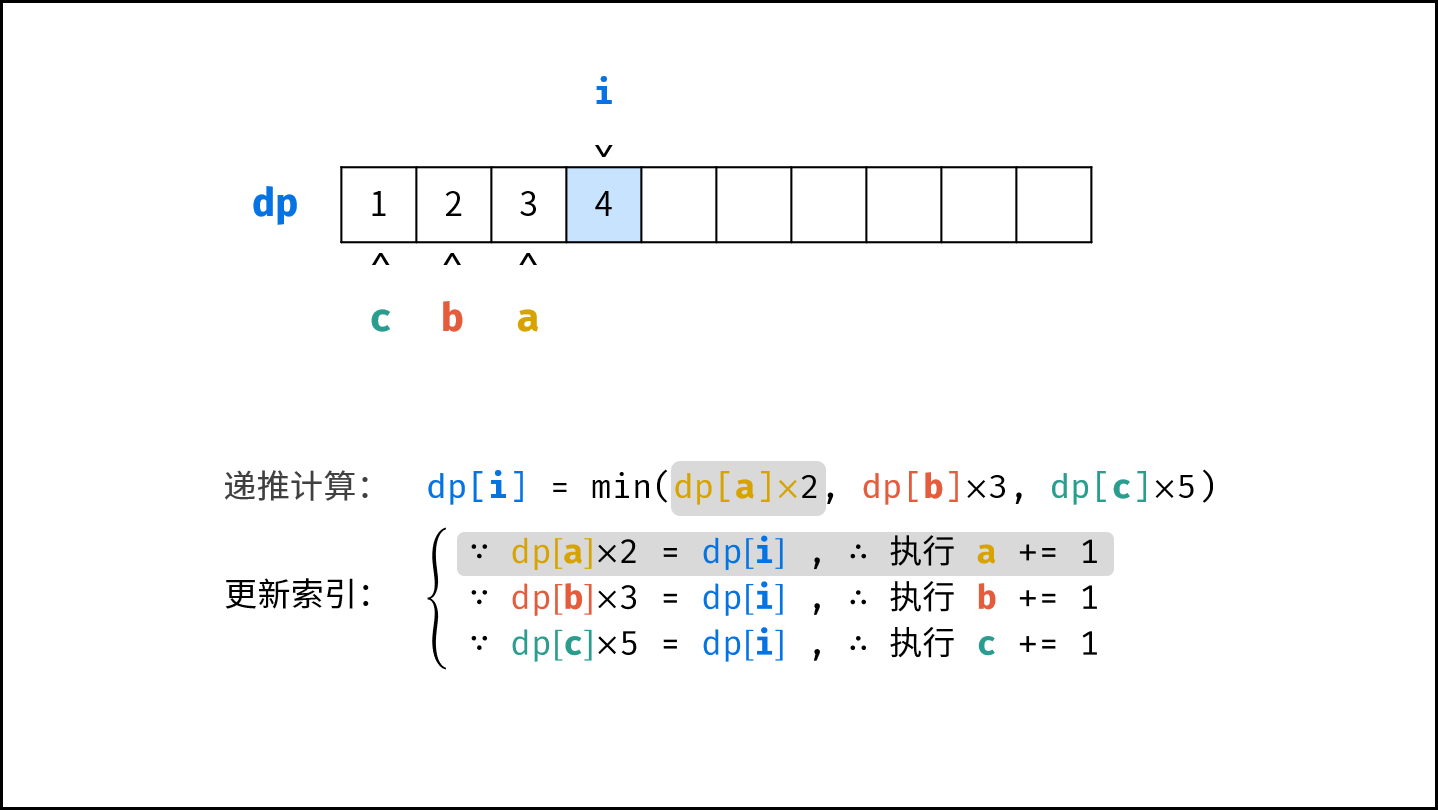
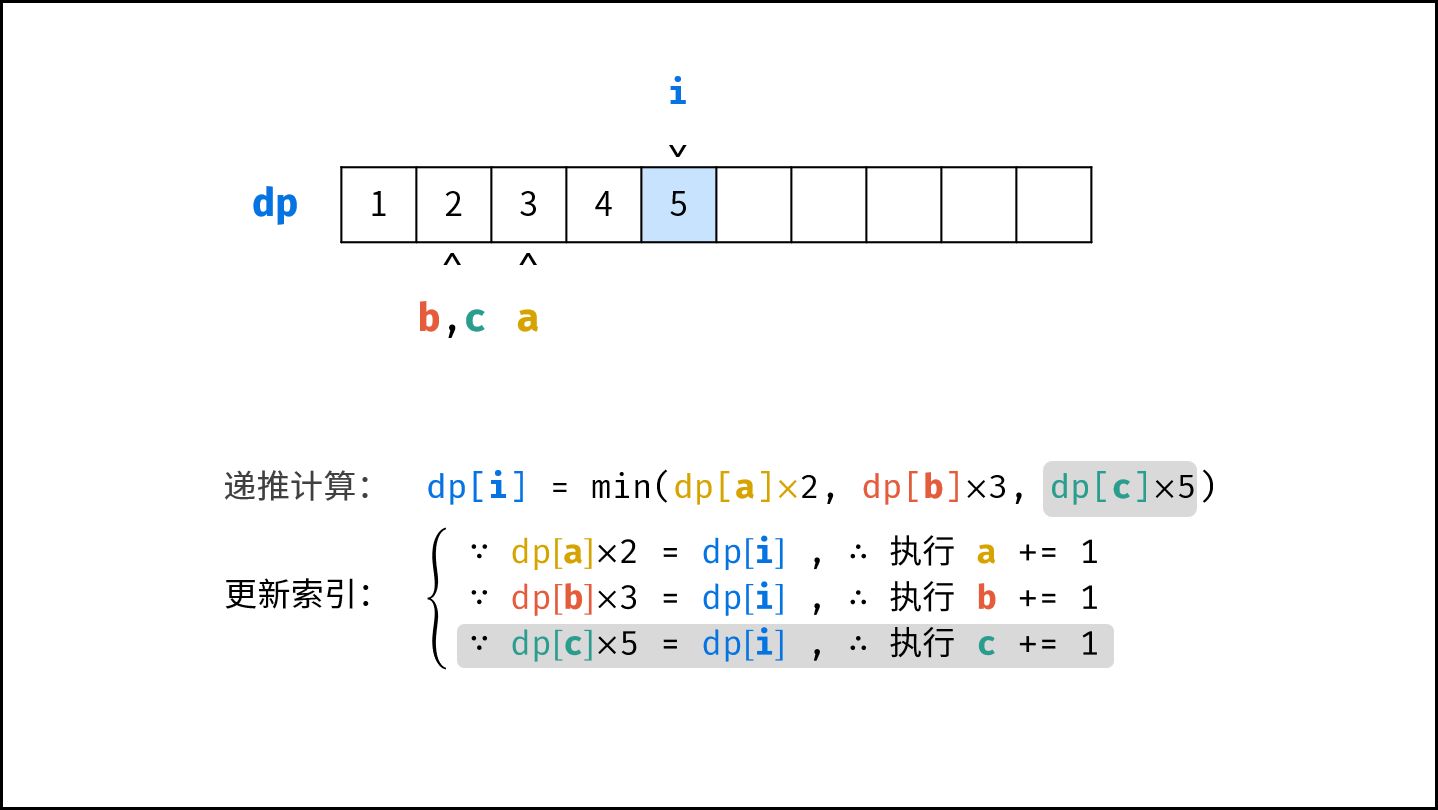
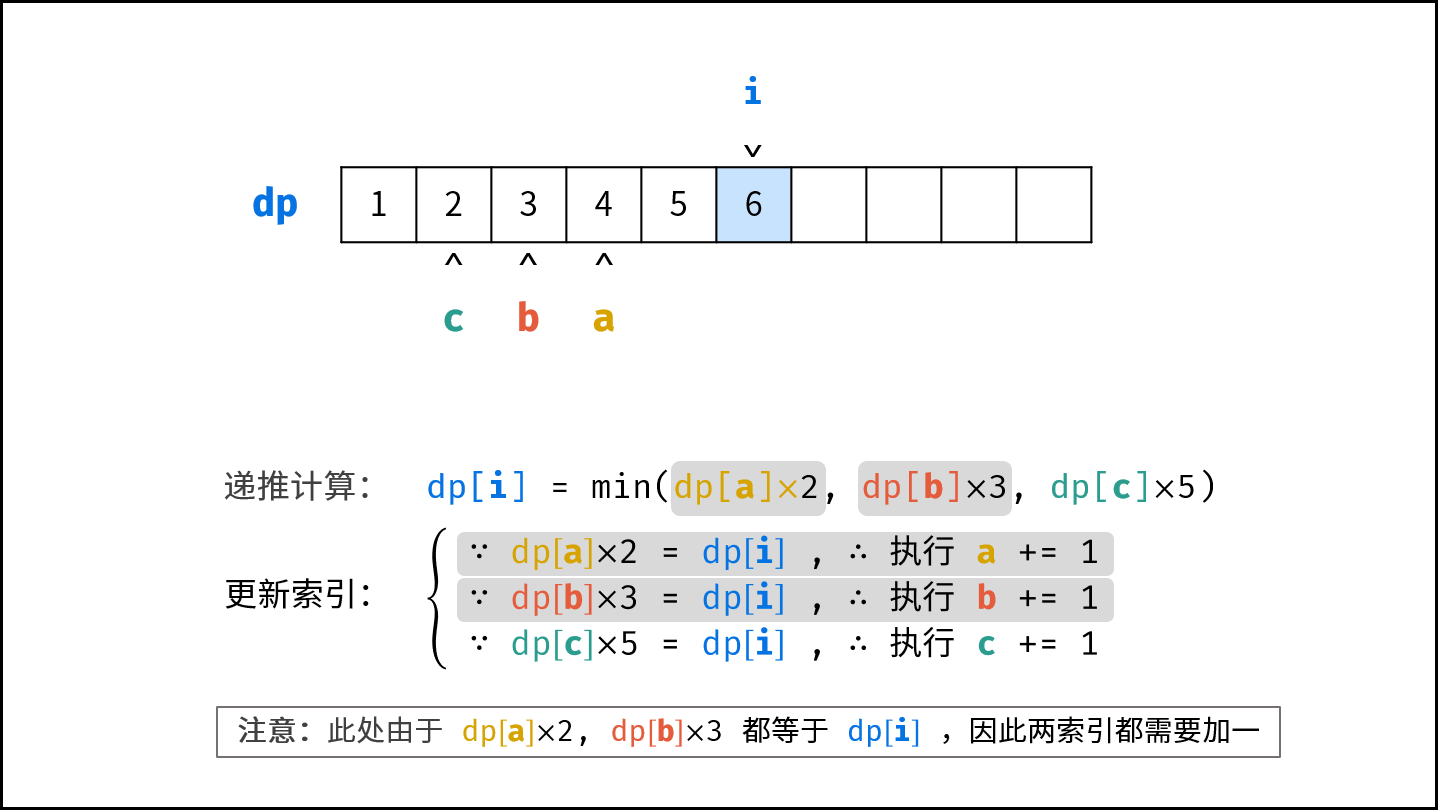
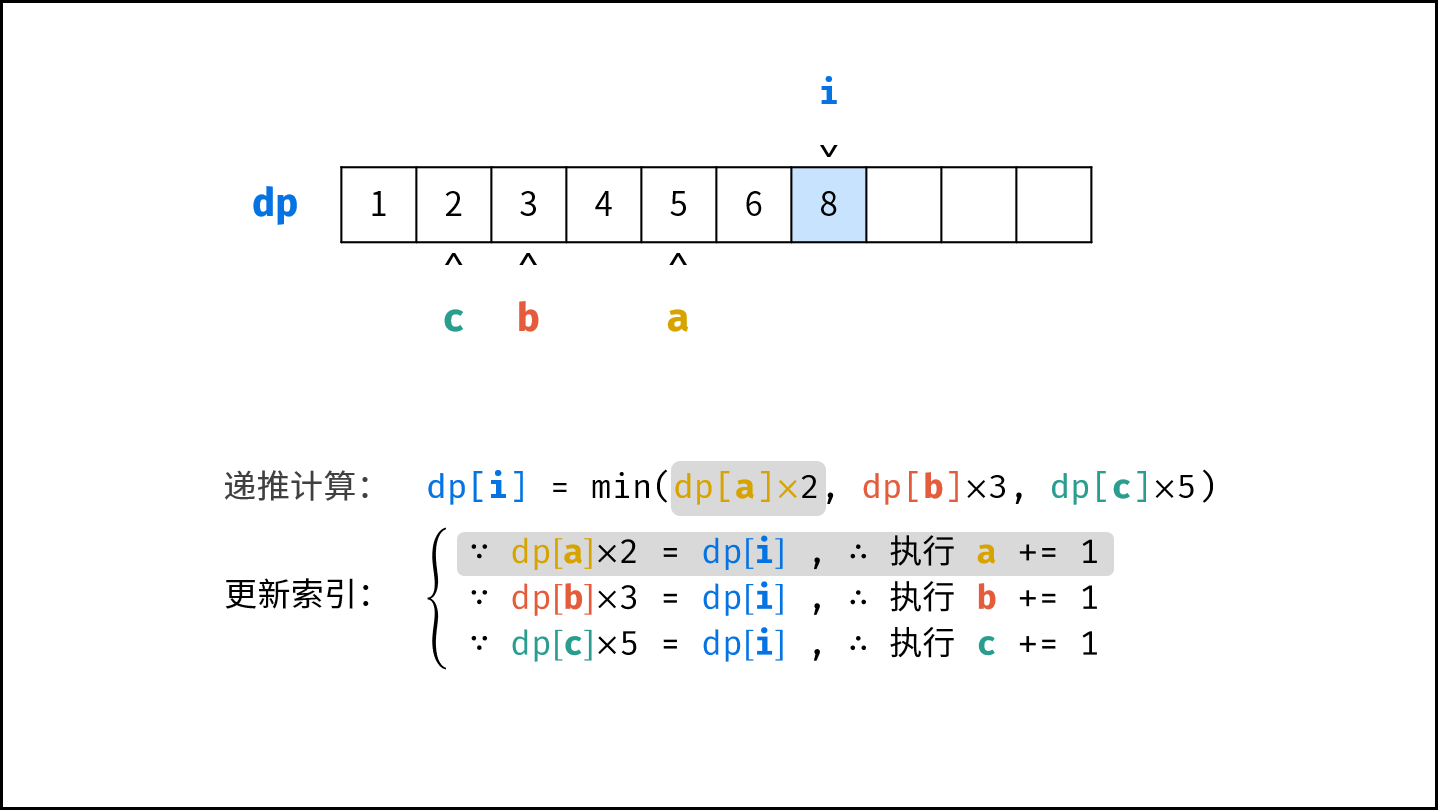
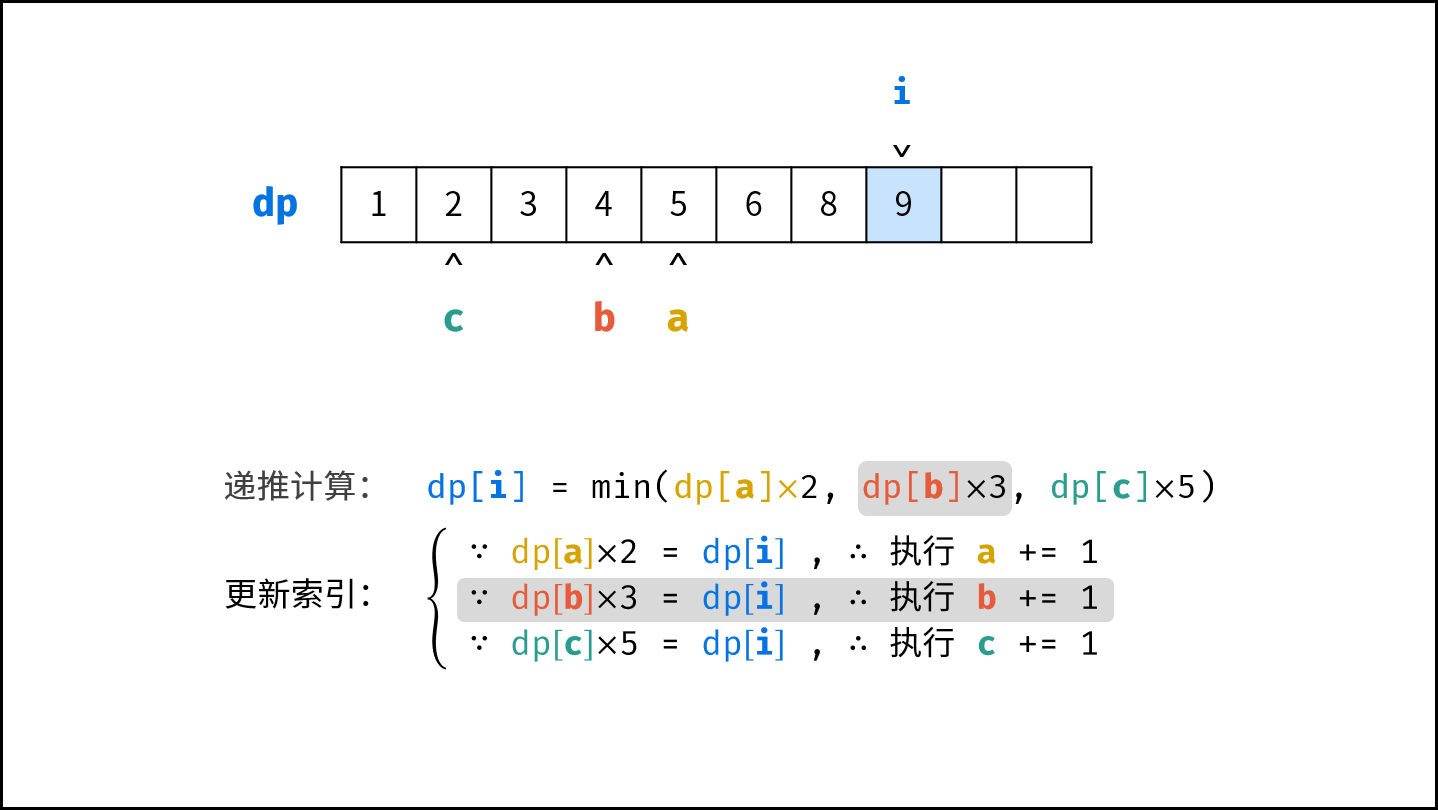
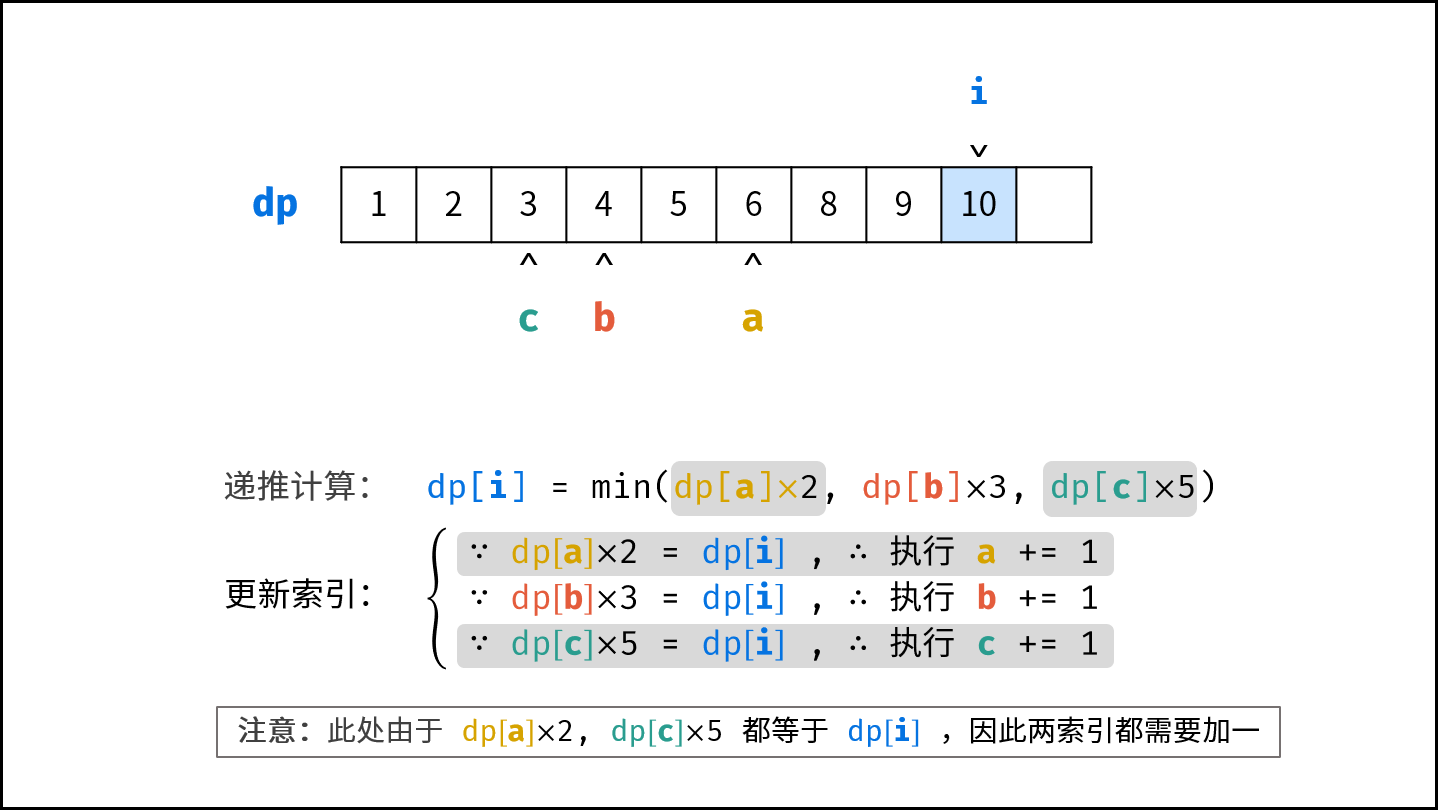
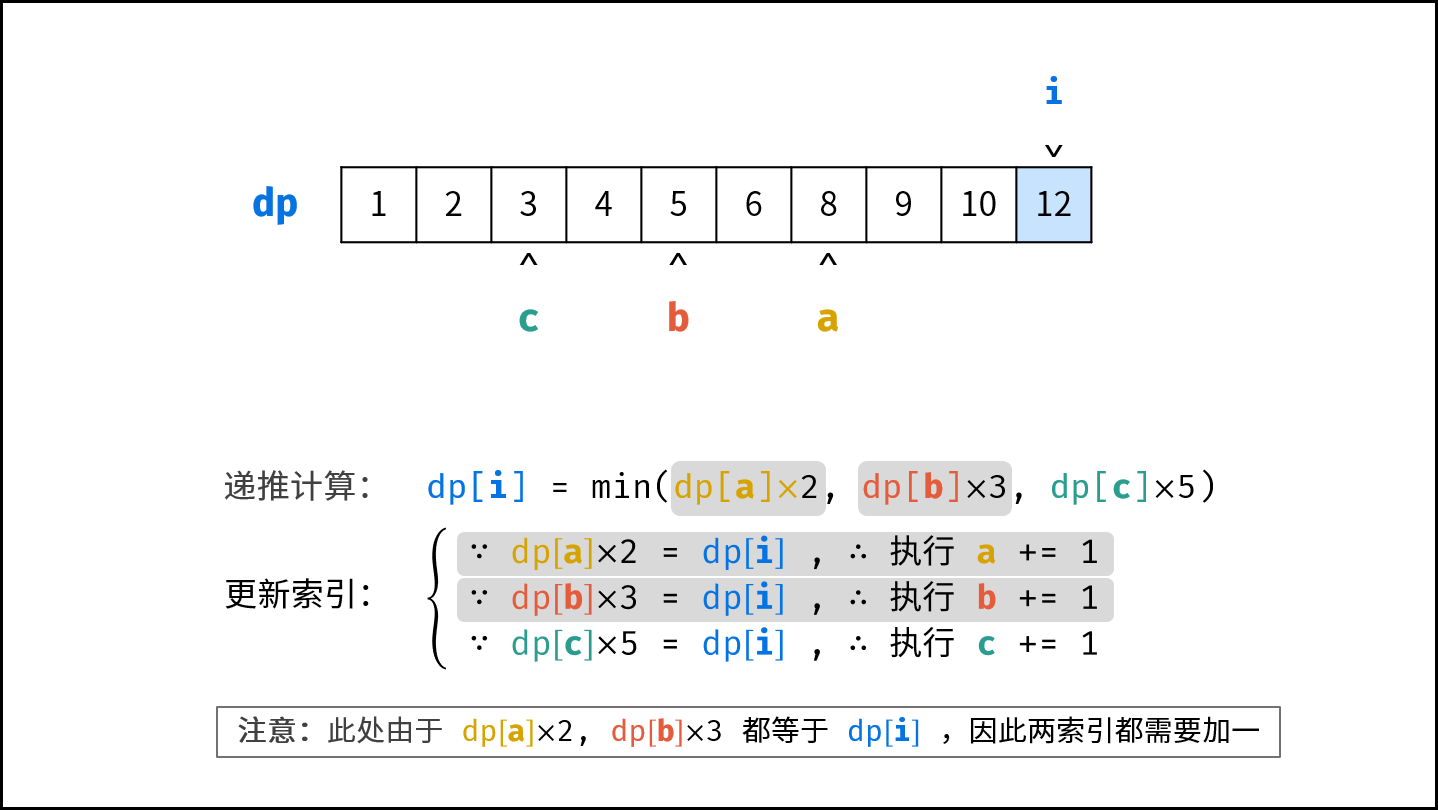
   1. 计算下一个丑数的候选集 $res[a] \cdot 2$ , $res[b] \cdot 3$ , $res[c] \cdot 5$ 。
   2. 选择丑数候选集中最小的那个作为下一个丑数，填入 $res$ 。
   3. 将被选中的丑数对应的指针向右移动一格。
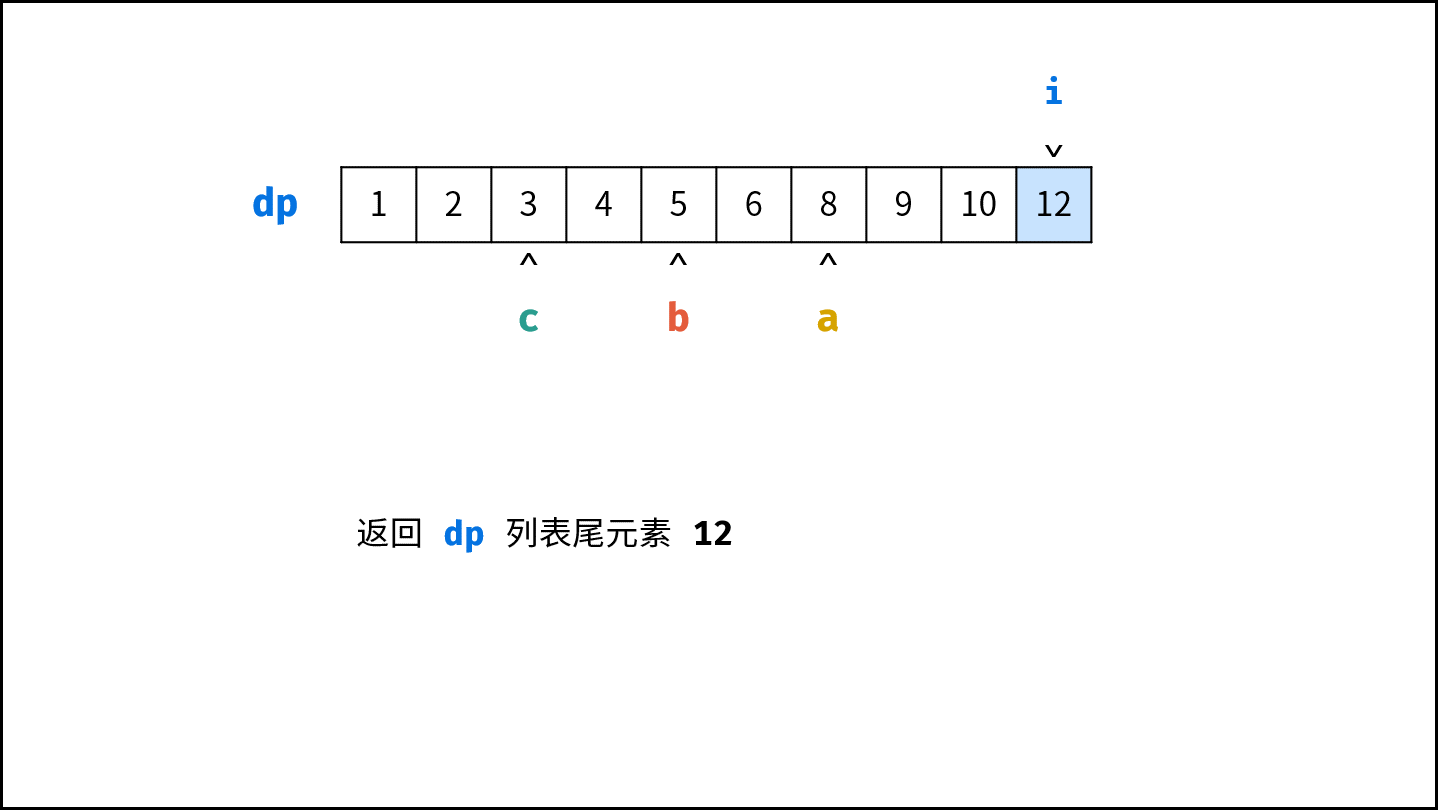
3. 返回 $res$ 的最后一个元素即可。

<,,,,,,,,,,>

代码： ​

class Solution:
    def nthUglyNumber(self, n: int) -> int:
        res, a, b, c = [1] * n, 0, 0, 0
        for i in range(1, n):
            n2, n3, n5 = res[a] * 2, res[b] * 3, res[c] * 5
            res[i] = min(n2, n3, n5)
            if res[i] == n2: a += 1
            if res[i] == n3: b += 1
            if res[i] == n5: c += 1
        return res[-1]

class Solution {
    public int nthUglyNumber(int n) {
        int a = 0, b = 0, c = 0;
        int[] res = new int[n];
        res[0] = 1;
        for(int i = 1; i < n; i++) {
            int n2 = res[a] * 2, n3 = res[b] * 3, n5 = res[c] * 5;
            res[i] = Math.min(Math.min(n2, n3), n5);
            if (res[i] == n2) a++;
            if (res[i] == n3) b++;
            if (res[i] == n5) c++;
        }
        return res[n - 1];
    }
}

class Solution {
public:
    int nthUglyNumber(int n) {
        int a = 0, b = 0, c = 0;
        int res[n];
        res[0] = 1;
        for(int i = 1; i < n; i++) {
            int n2 = res[a] * 2, n3 = res[b] * 3, n5 = res[c] * 5;
            res[i] = min(min(n2, n3), n5);
            if (res[i] == n2) a++;
            if (res[i] == n3) b++;
            if (res[i] == n5) c++;
        }
        return res[n - 1];
    }
};

复杂度分析： ​

• 时间复杂度 $O(n)$ ： 计算 $res$ 列表需遍历 $n-1$ 轮。
• 空间复杂度 $O(n)$ ： 长度为 $n$ 的 $res$ 列表使用 $O(n)$ 的额外空间。