解题思路： ​

• 股票买卖策略：

  • 单独交易日： 设今天价格 $p_1$、明天价格 $p_2$，则今天买入、明天卖出可赚取金额 $p_2 - p_1$ （负值代表亏损）。
  • 连续上涨交易日： 设此上涨交易日股票价格分别为 $p_1, p_2, ... , p_n$，则第一天买最后一天卖收益最大，即 $p_n - p_1$；等价于每天都买卖，即 $p_n - p_1=(p_2 - p_1)+(p_3 - p_2)+...+(p_n - p_{n-1})$。
  • 连续下降交易日： 则不买卖收益最大，即不会亏钱。

• 算法流程：

  • 遍历整个股票交易日价格列表 price，策略是所有上涨交易日都买卖（赚到所有利润），所有下降交易日都不买卖（永不亏钱）。
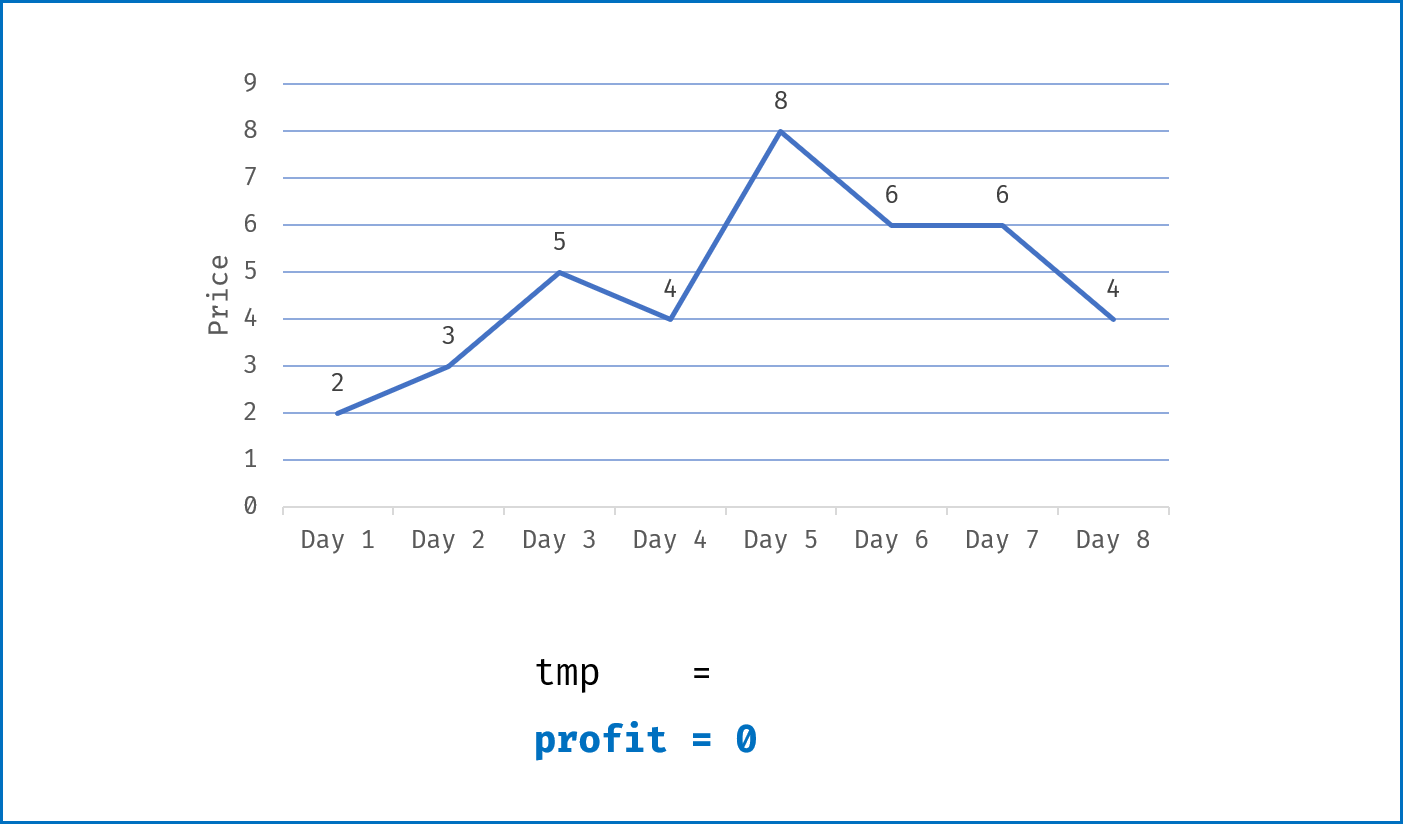
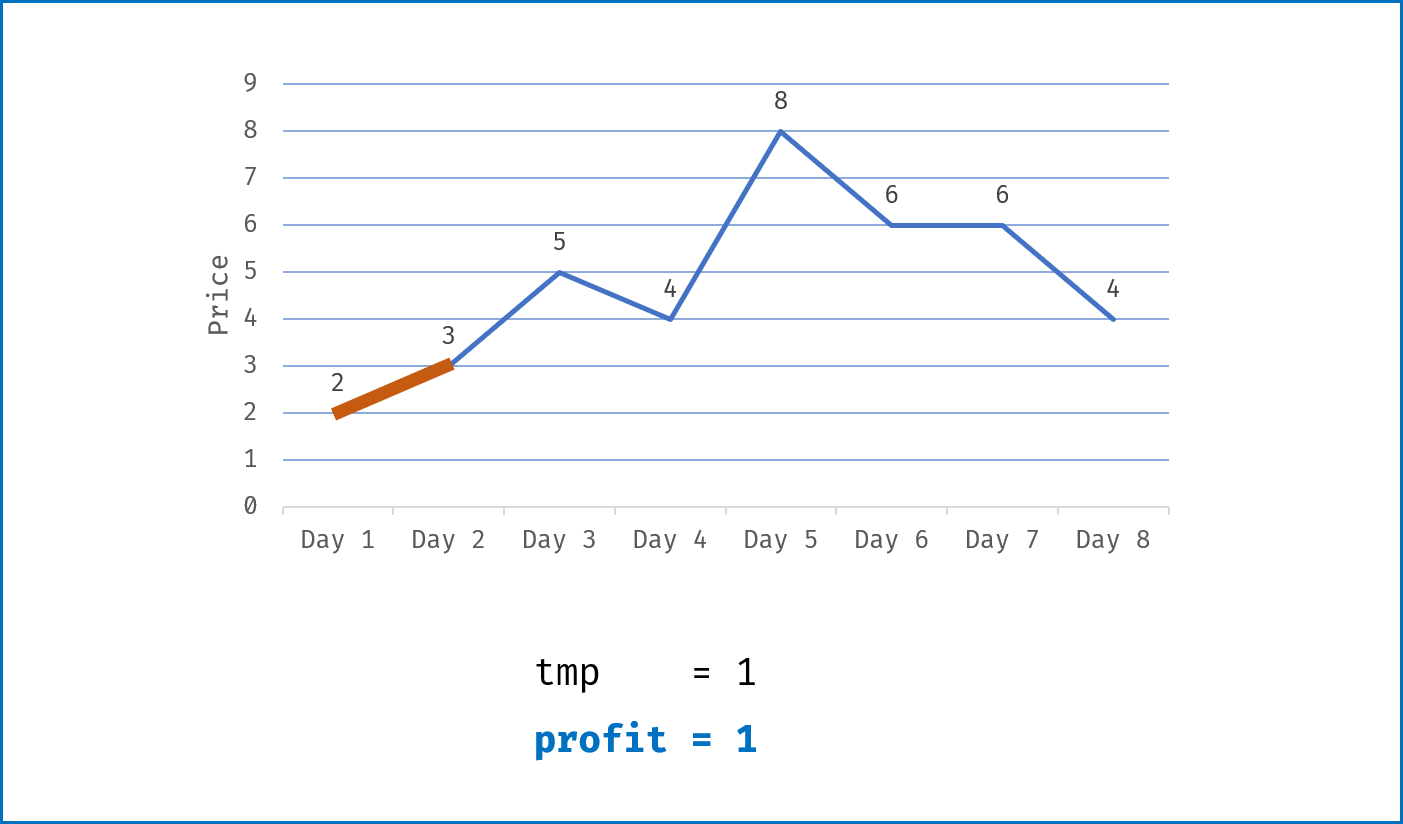
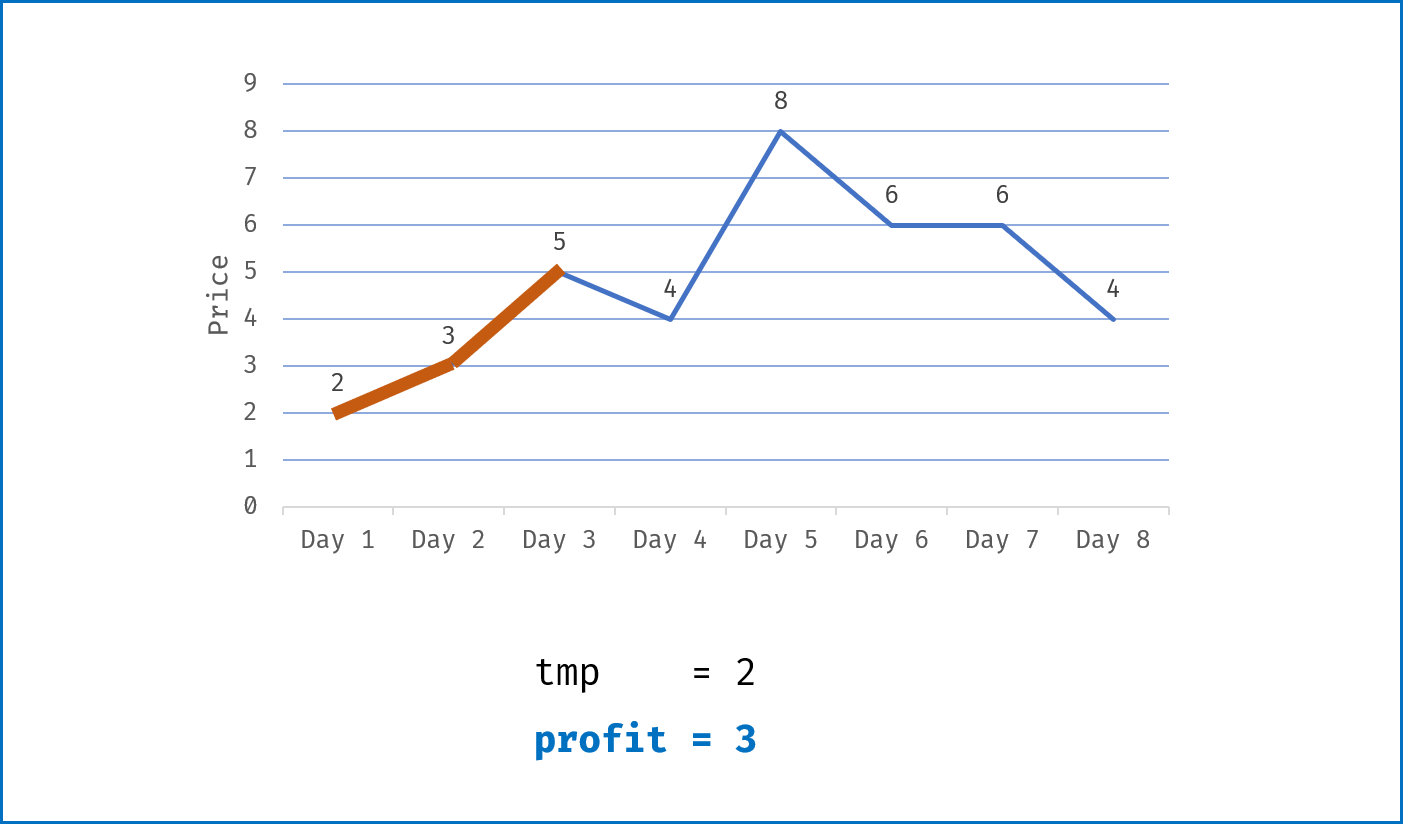
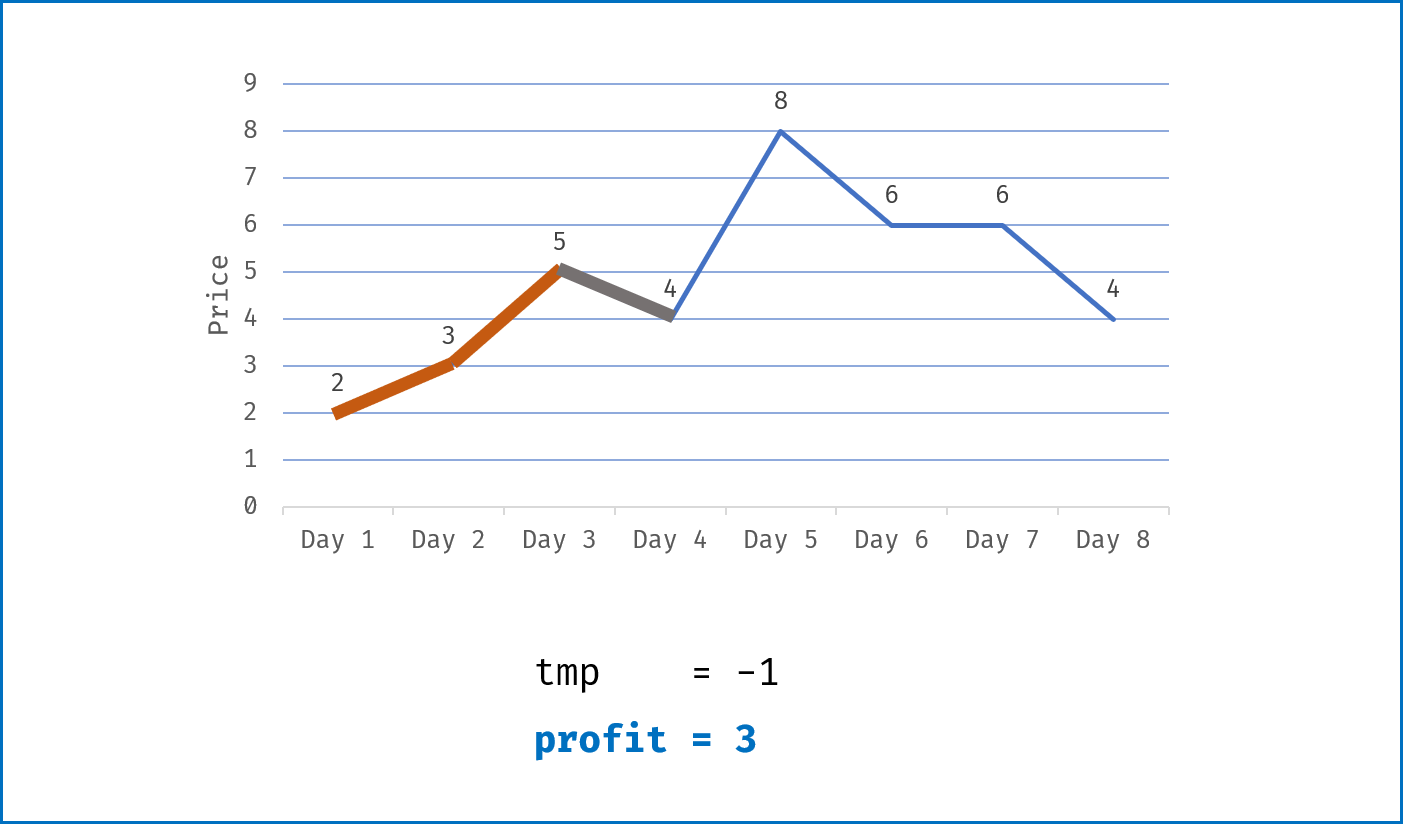
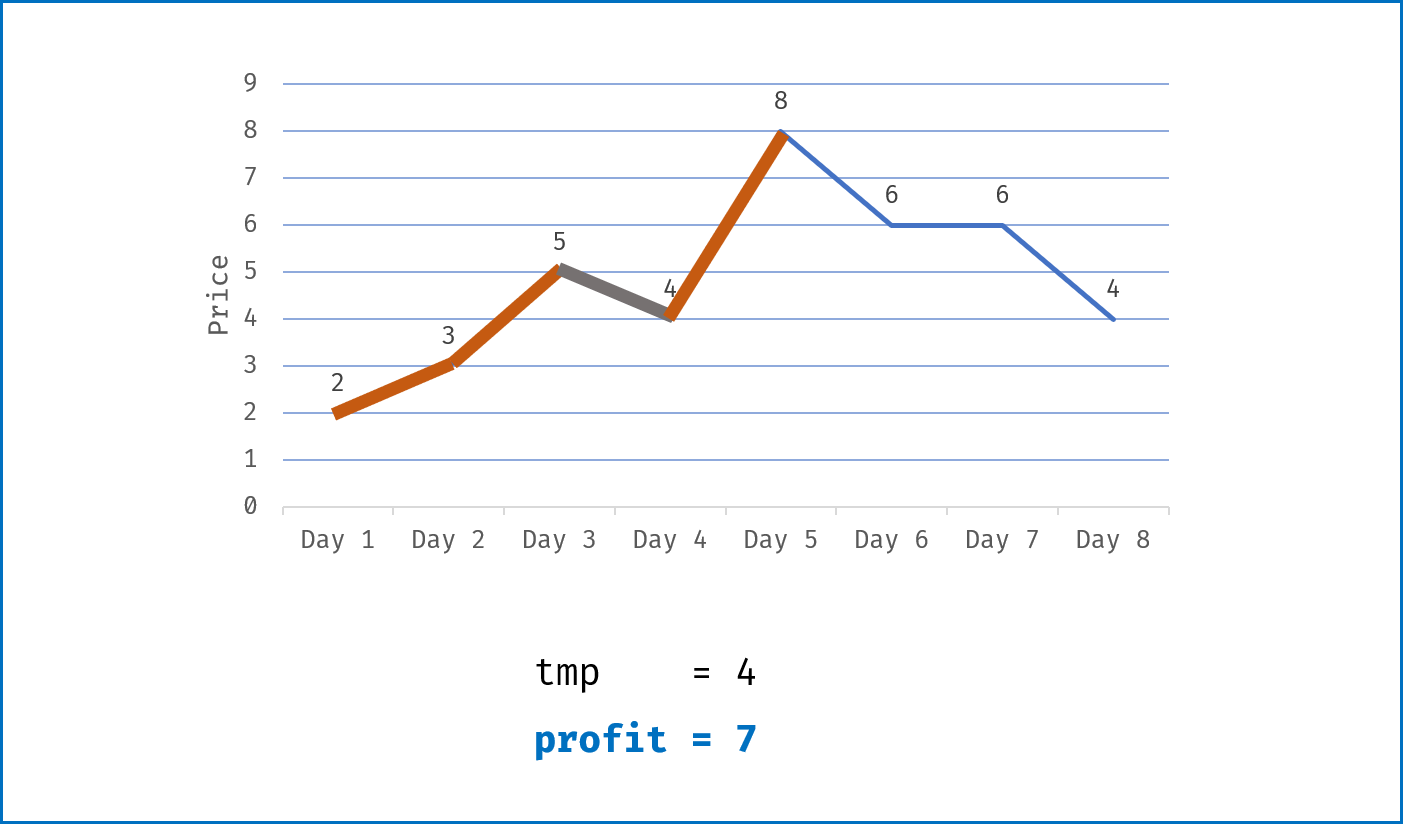
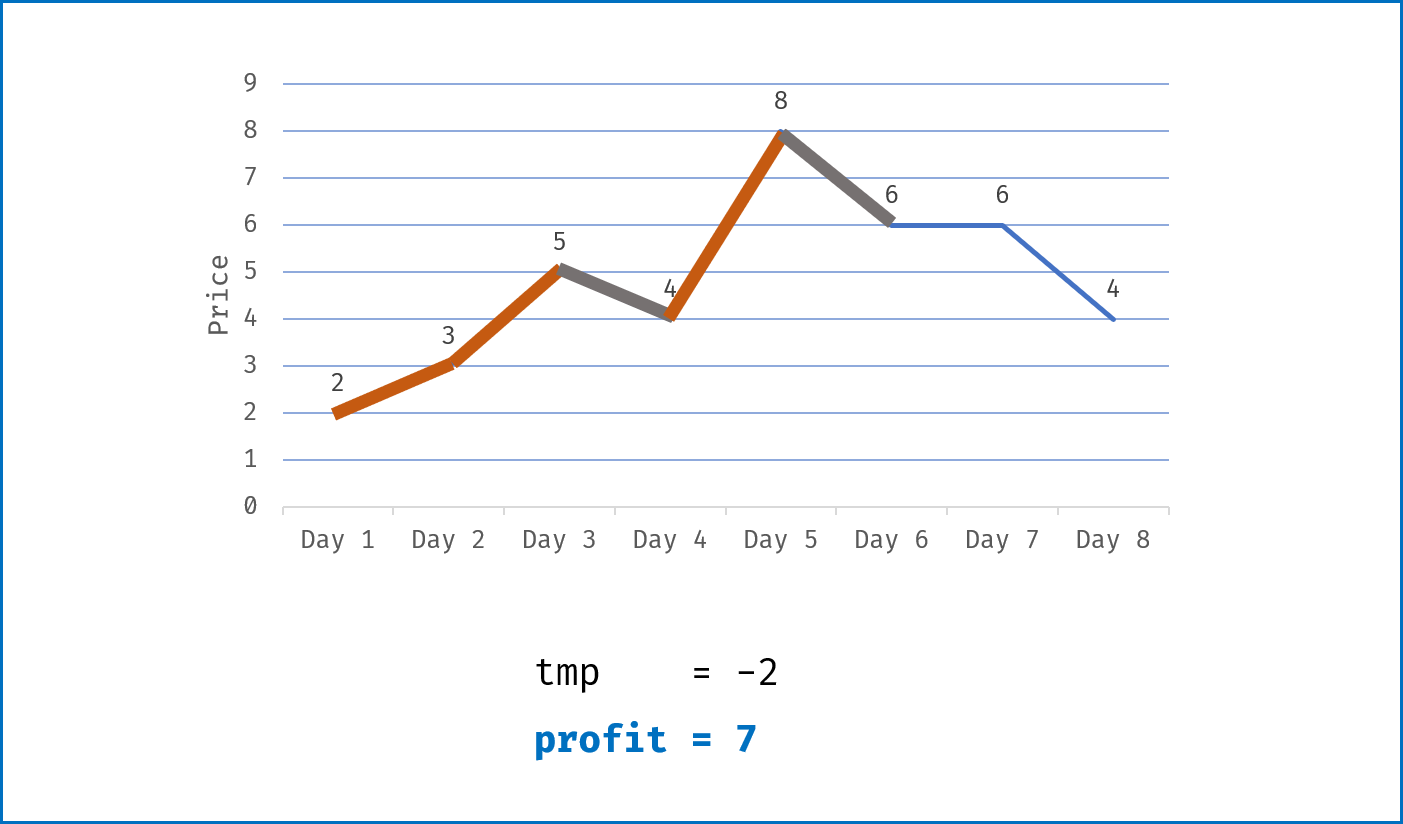
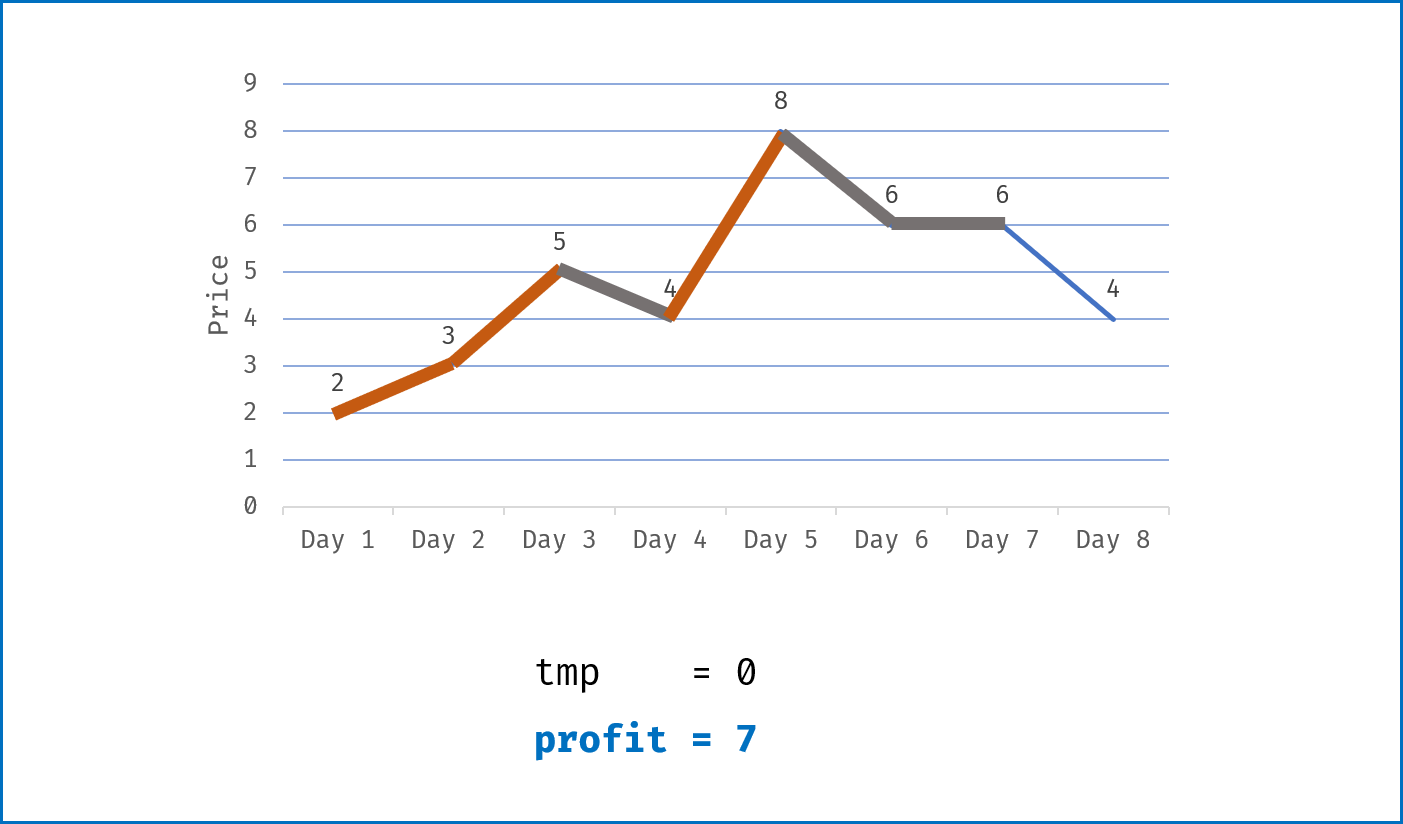
  1. 设 tmp 为第 i-1 日买入与第 i 日卖出赚取的利润，即 tmp = prices[i] - prices[i - 1] ；
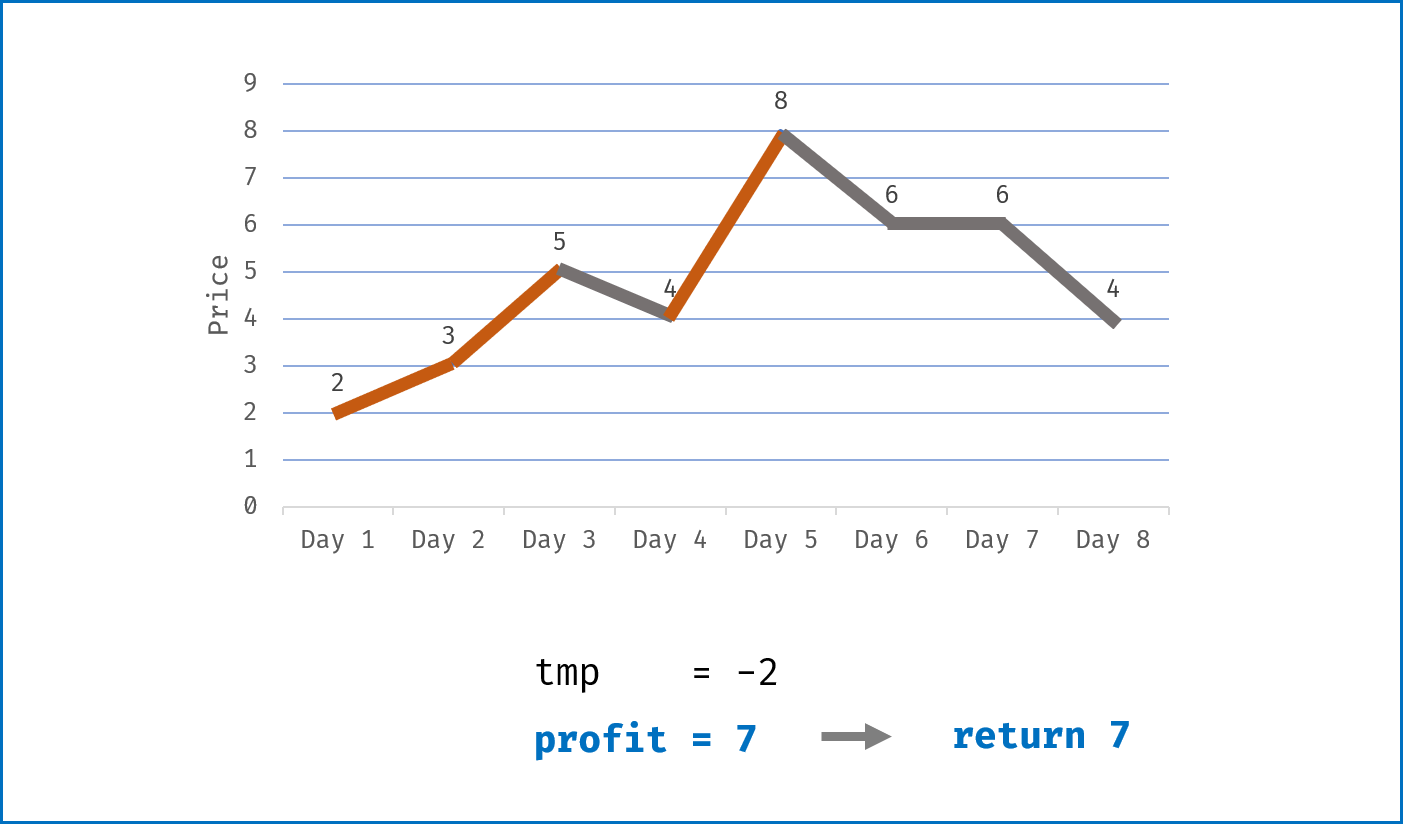
  2. 当该天利润为正 tmp > 0，则将利润加入总利润 profit；当利润为 $0$ 或为负，则直接跳过；
  3. 遍历完成后，返回总利润 profit。

• 复杂度分析：

  • 时间复杂度 $O(N)$ ： 只需遍历一次price；
  • 空间复杂度 $O(1)$ ： 变量使用常数额外空间。

<,,,,,,,>

代码： ​

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        profit = 0
        for i in range(1, len(prices)):
            tmp = prices[i] - prices[i - 1]
            if tmp > 0: profit += tmp
        return profit

class Solution {
    public int maxProfit(int[] prices) {
        int profit = 0;
        for (int i = 1; i < prices.length; i++) {
            int tmp = prices[i] - prices[i - 1];
            if (tmp > 0) profit += tmp;
        }
        return profit;
    }
}