自律小屋 | 自律小屋

解题思路：

借用一个辅助栈 min_stack，用于存获取 stack 中最小值。
算法流程：
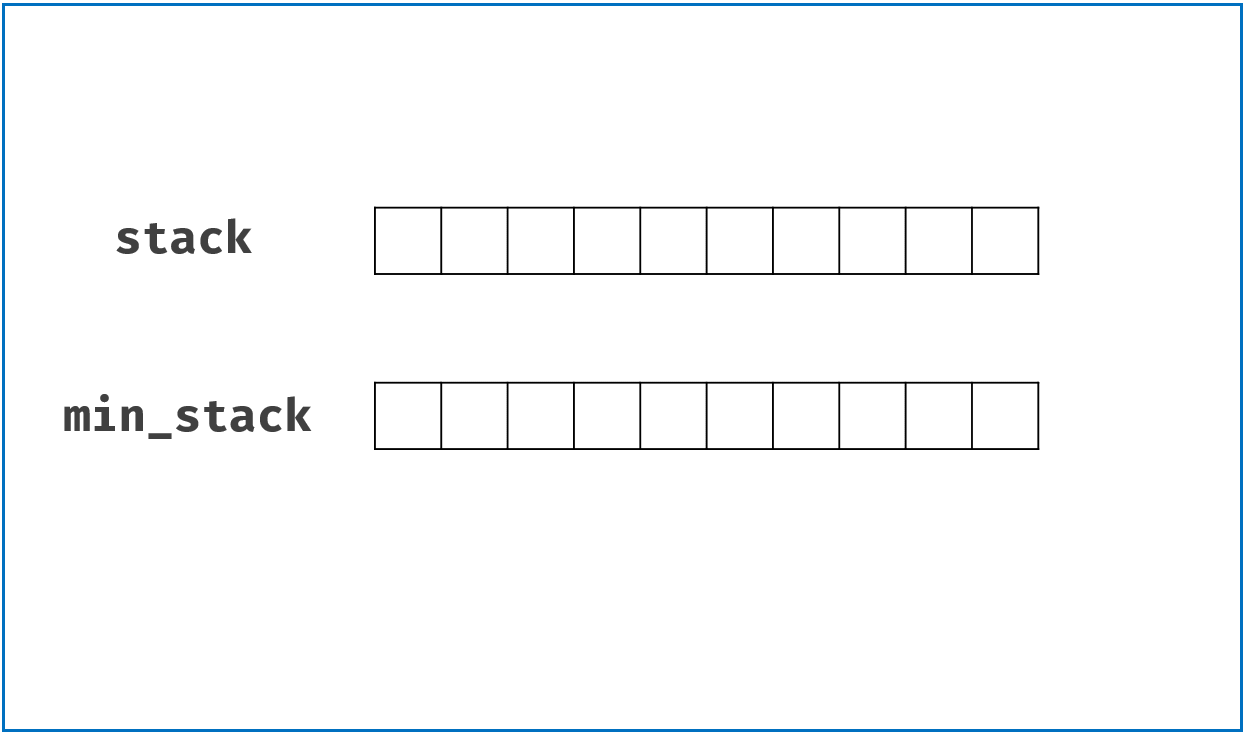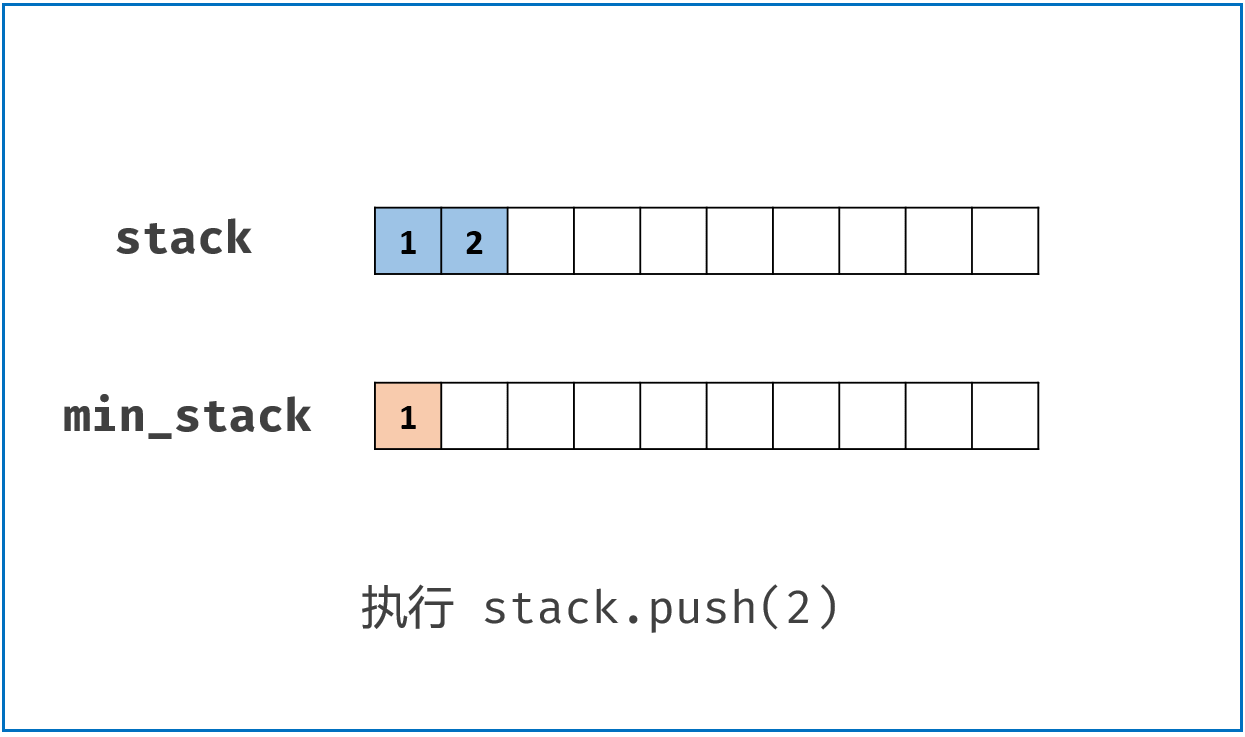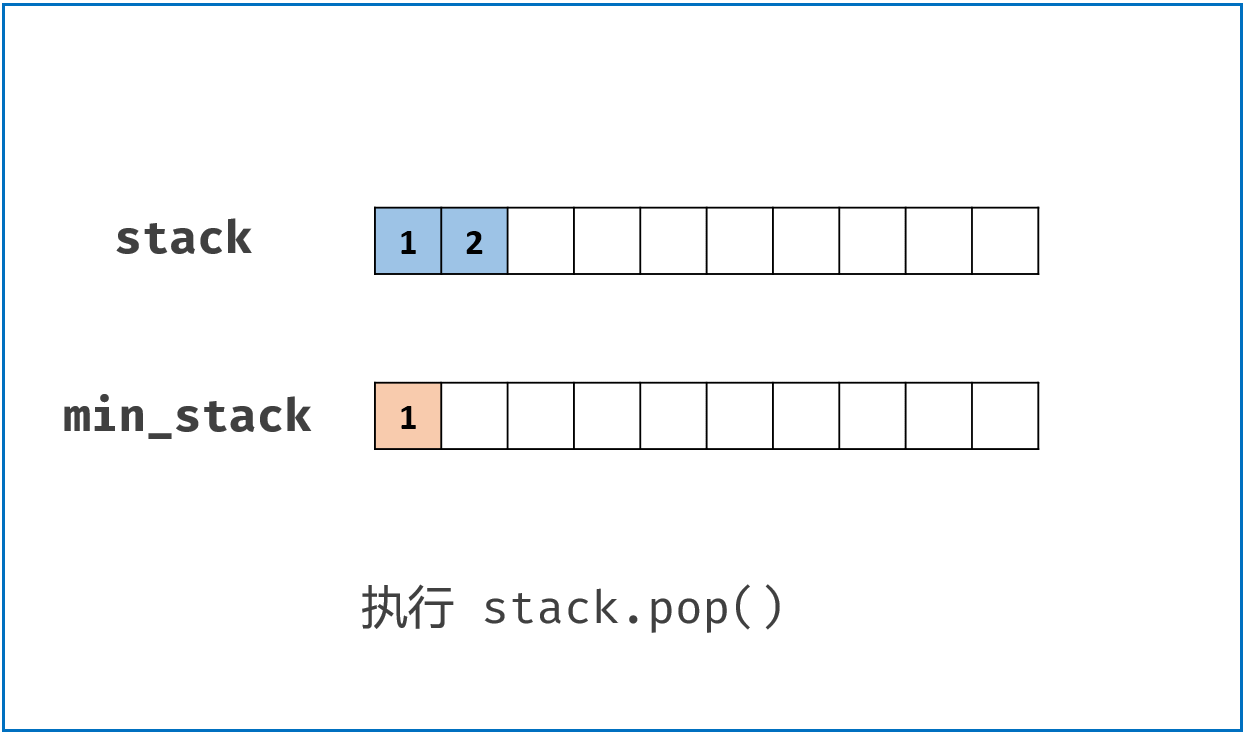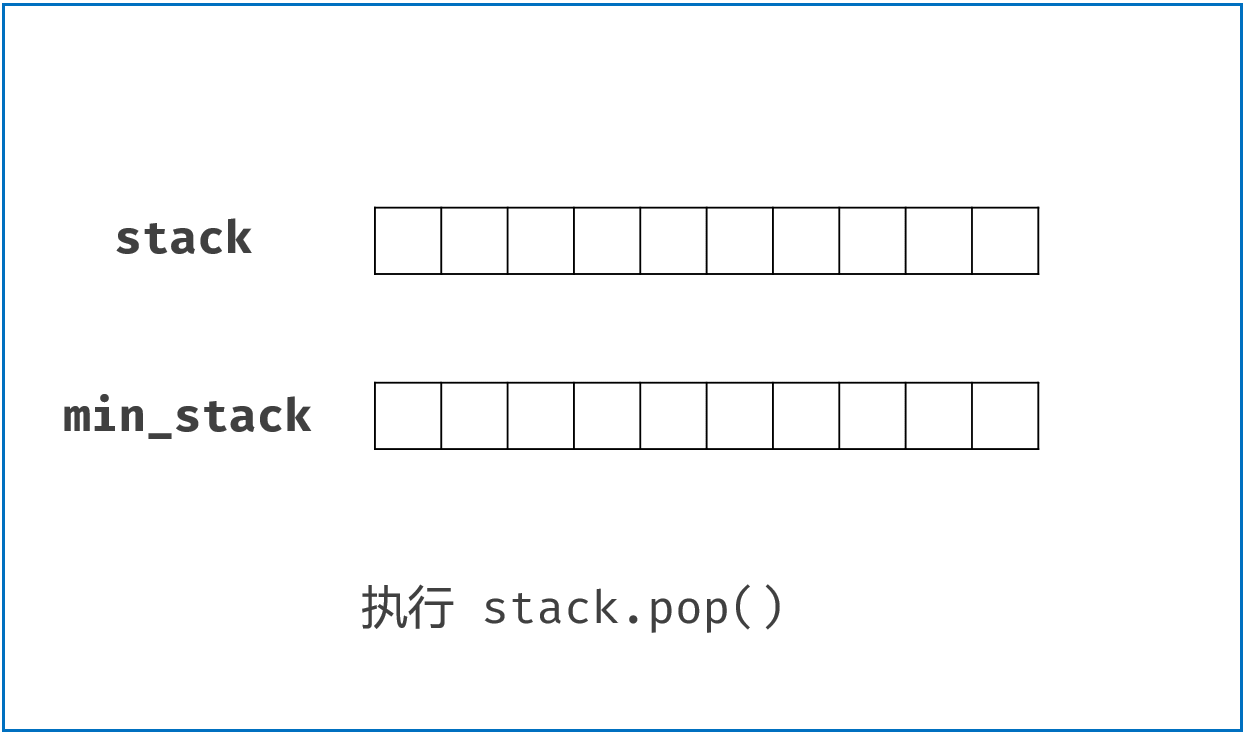
- push() 方法： 每当push()新值进来时，如果 小于等于 min_stack 栈顶值，则一起 push() 到 min_stack，即更新了栈顶最小值；
- pop() 方法： 判断将 pop() 出去的元素值是否是 min_stack 栈顶元素值（即最小值），如果是则将 min_stack 栈顶元素一起 pop()，这样可以保证 min_stack 栈顶元素始终是 stack 中的最小值。
- getMin()方法： 返回 min_stack 栈顶即可。
min_stack 作用分析：
- min_stack 等价于遍历 stack所有元素，把升序的数字都删除掉，留下一个从栈底到栈顶降序的栈。
- 相当于给 stack 中的降序元素做了标记，每当 pop() 这些降序元素，min_stack 会将相应的栈顶元素 pop() 出去，保证其栈顶元素始终是 stack 中的最小元素。
复杂度分析：
- 时间复杂度 $O(1)$ ：压栈，出栈，获取最小值的时间复杂度都为 $O(1)$ 。
- 空间复杂度 $O(N)$ ：包含 $N$ 个元素辅助栈占用线性大小的额外空间。

代码：

Python

class MinStack:
    def __init__(self):
        self.stack = []
        self.min_stack = []
    def push(self, x: int) -> None:
        self.stack.append(x)
        if not self.min_stack or x <= self.min_stack[-1]: 
            self.min_stack.append(x)
    def pop(self) -> None:
        if self.stack.pop() == self.min_stack[-1]:
            self.min_stack.pop()
    def top(self) -> int:
        return self.stack[-1]
    def getMin(self) -> int:
        return self.min_stack[-1]

Java

class MinStack {
    private Stack<Integer> stack;
    private Stack<Integer> min_stack;
    public MinStack() {
        stack = new Stack<>();
        min_stack = new Stack<>();
    }
    public void push(int x) {
        stack.push(x);
        if(min_stack.isEmpty() || x <= min_stack.peek())
            min_stack.push(x);
    }
    public void pop() {
        if(stack.pop().equals(min_stack.peek()))
            min_stack.pop();
    }
    public int top() {
        return stack.peek();
    }
    public int getMin() {
        return min_stack.peek();
    }
}

解题思路： ​

代码： ​

解题思路：

代码：