自律小屋 | 自律小屋

解题思路

「回文串」是指倒序后和自身完全相同的字符串，即具有关于中心轴对称的性质。观察发现，

当回文串长度为偶数时，则所有字符都出现了偶数次；
当回文串长度为奇数时，则位于中心的字符出现了奇数次，其余所有字符出现偶数次；

根据以上分析，字符串能被构造成回文串的充要条件为：除了一种字符出现奇数次外，其余所有字符出现偶数次。判别流程如下：

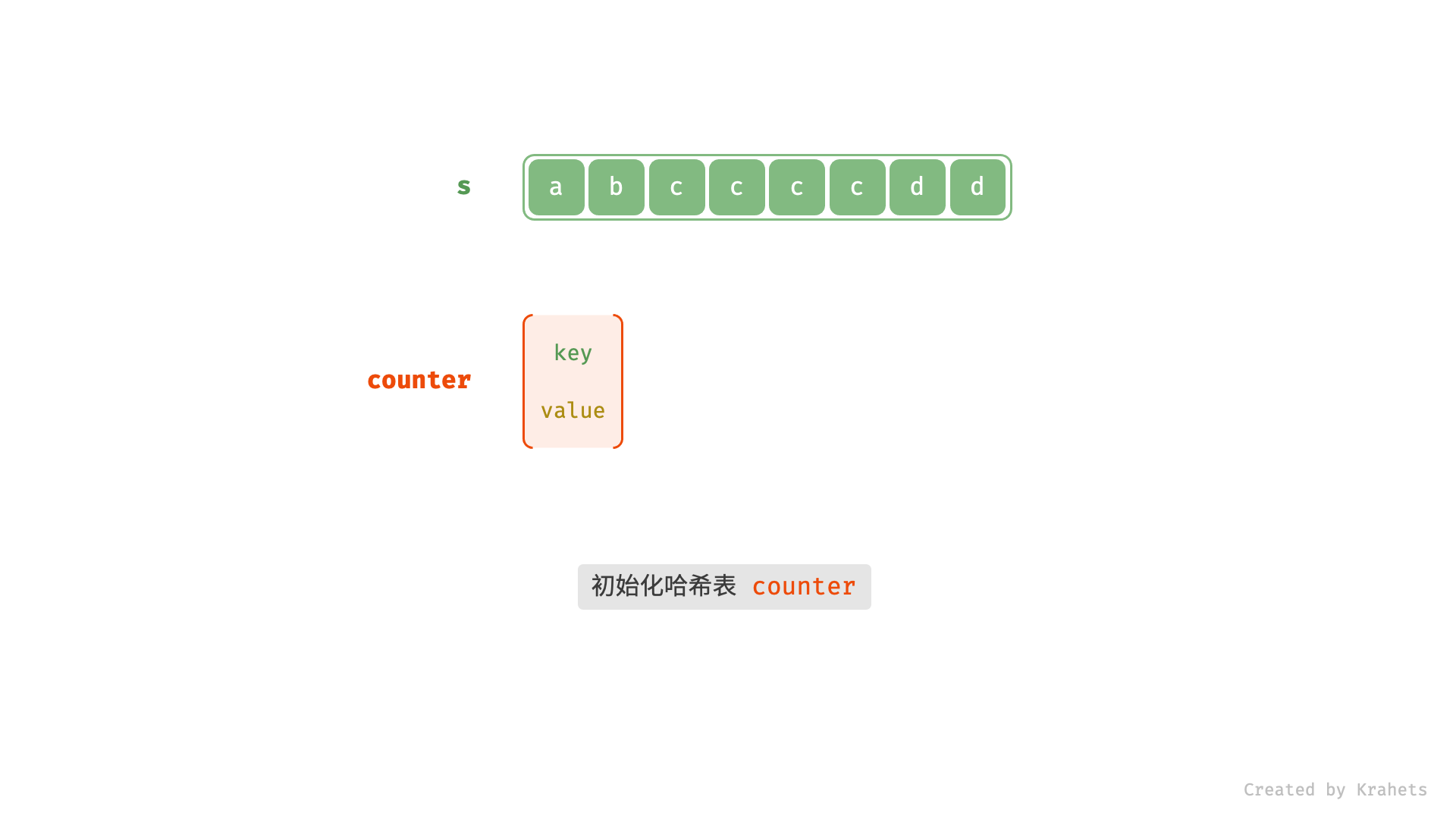
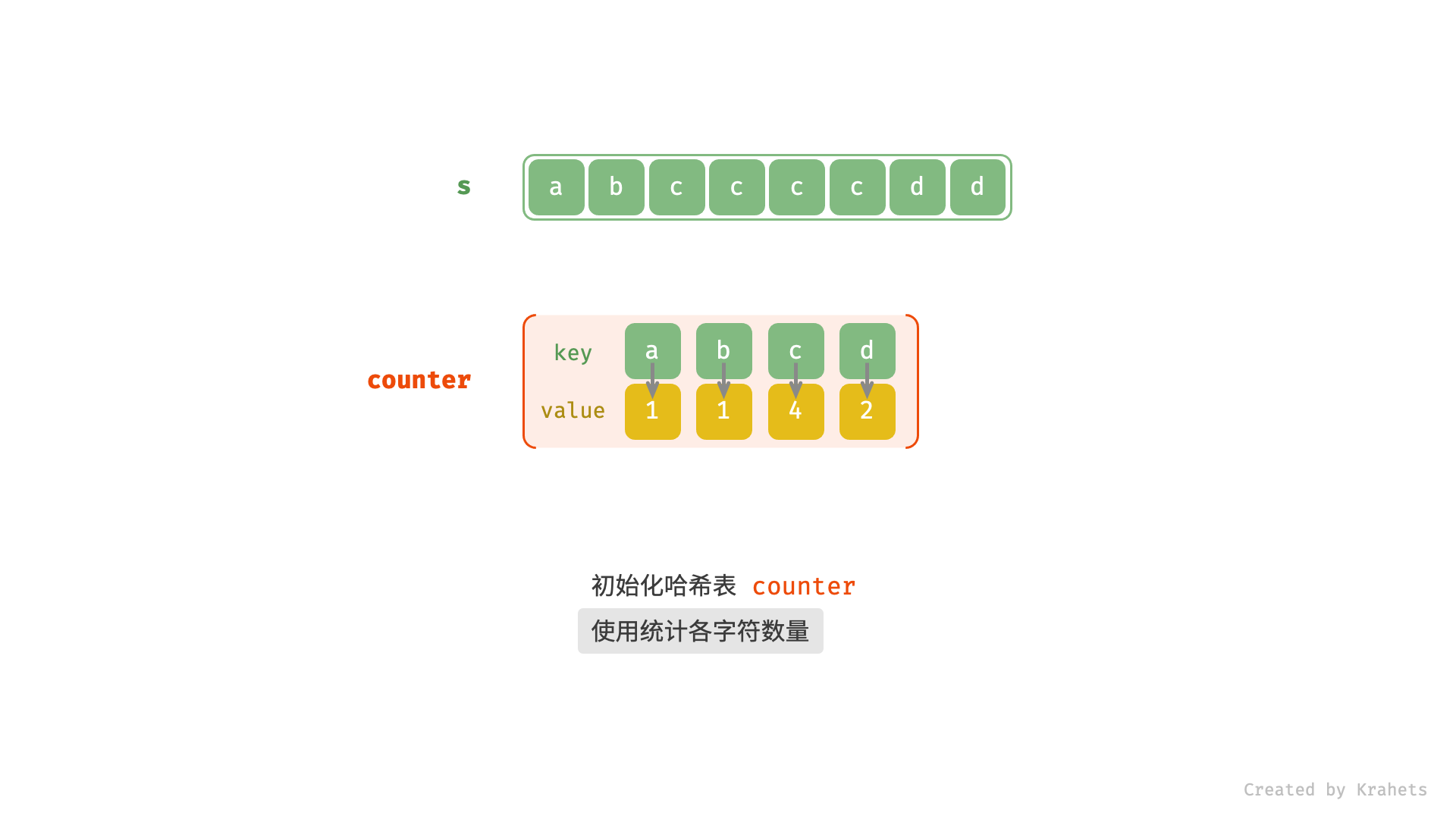
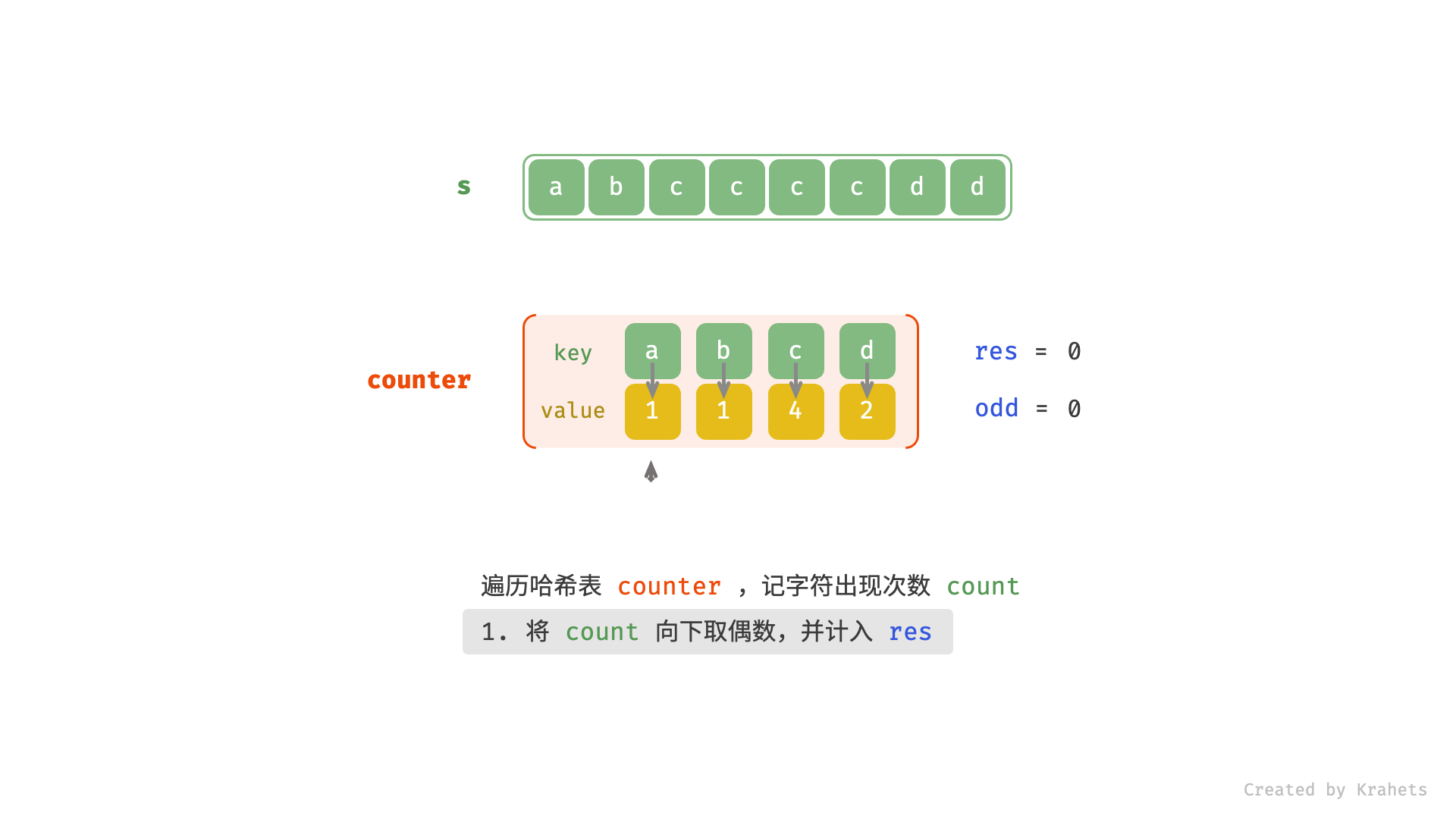
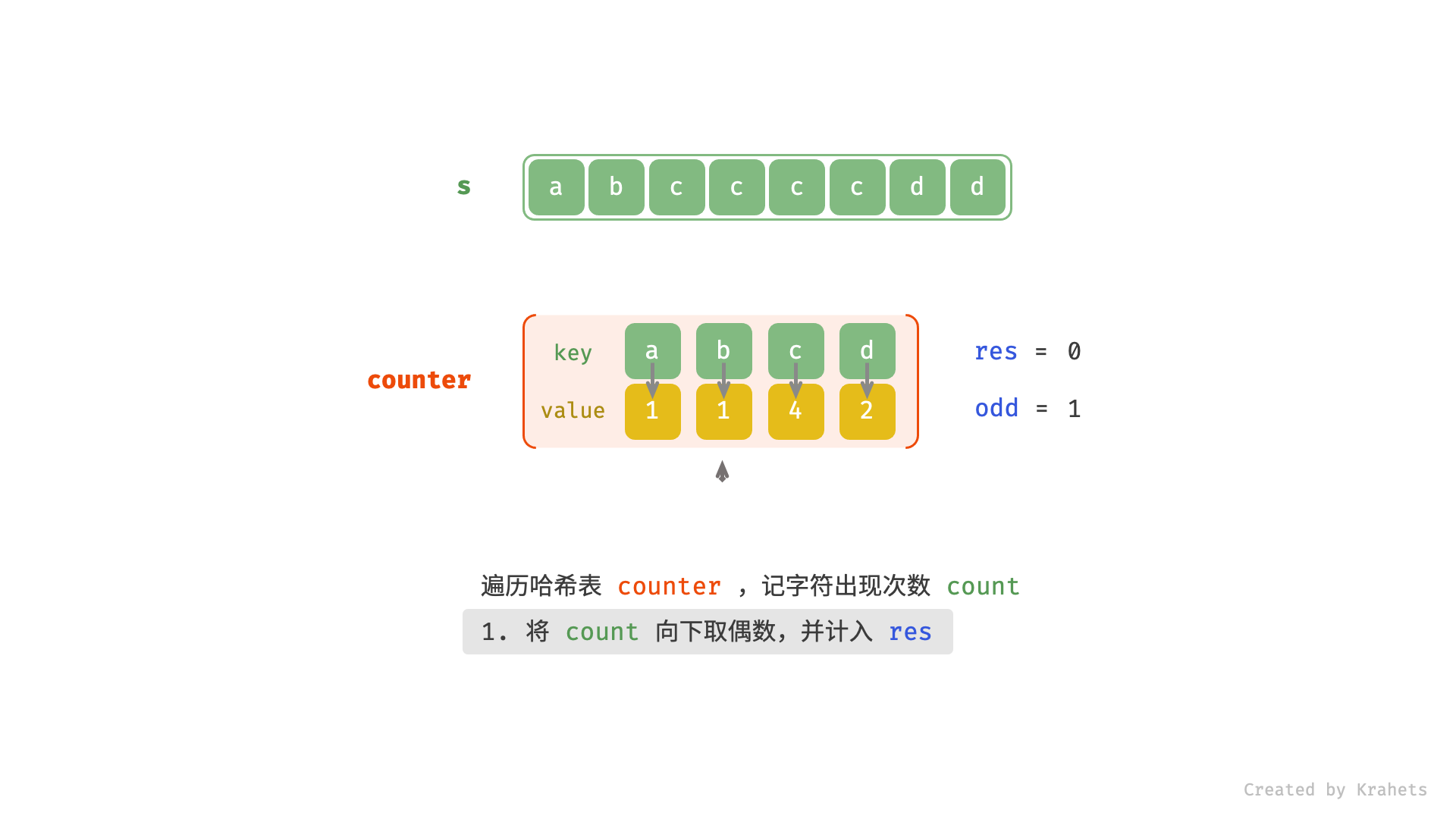
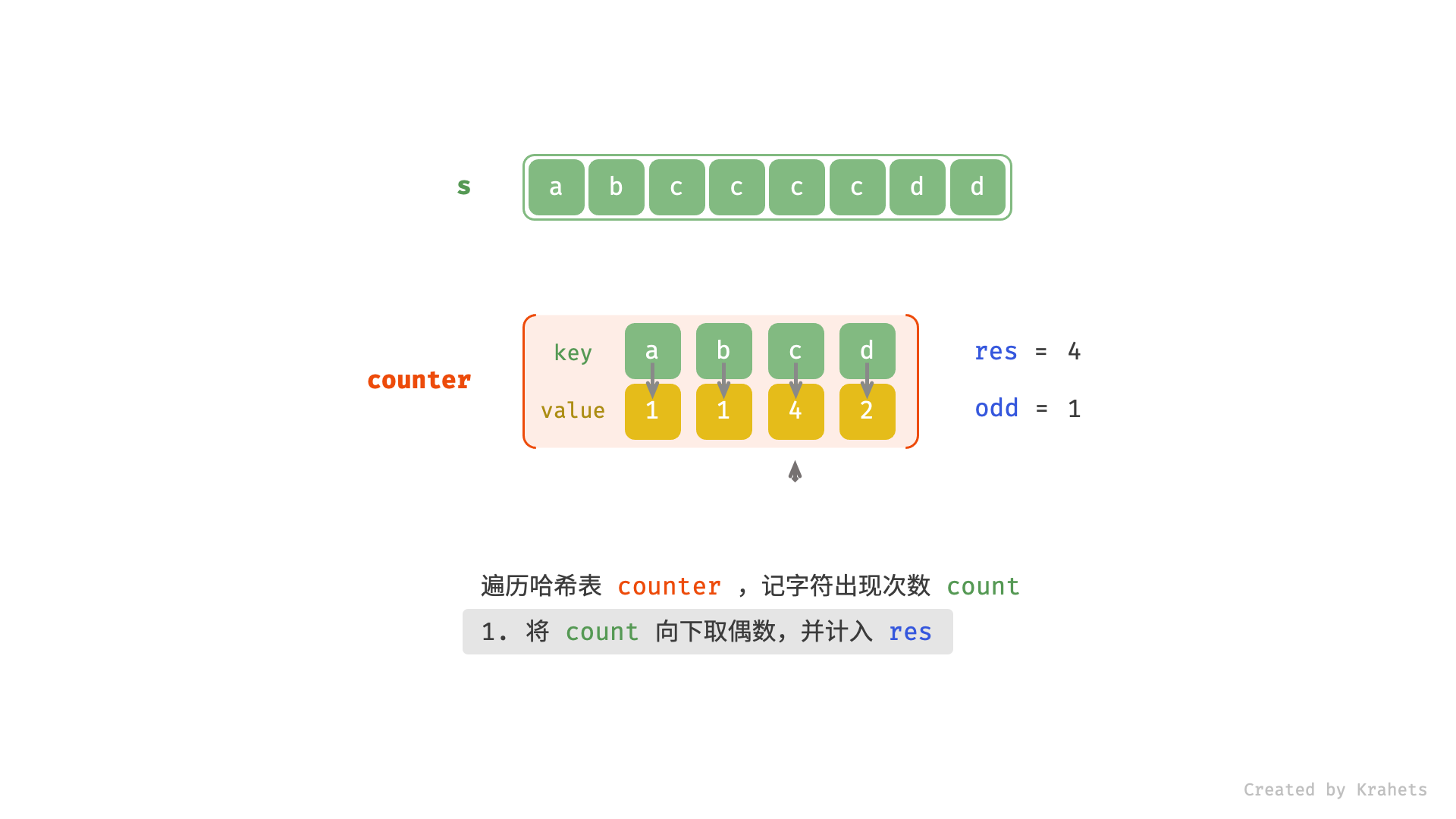
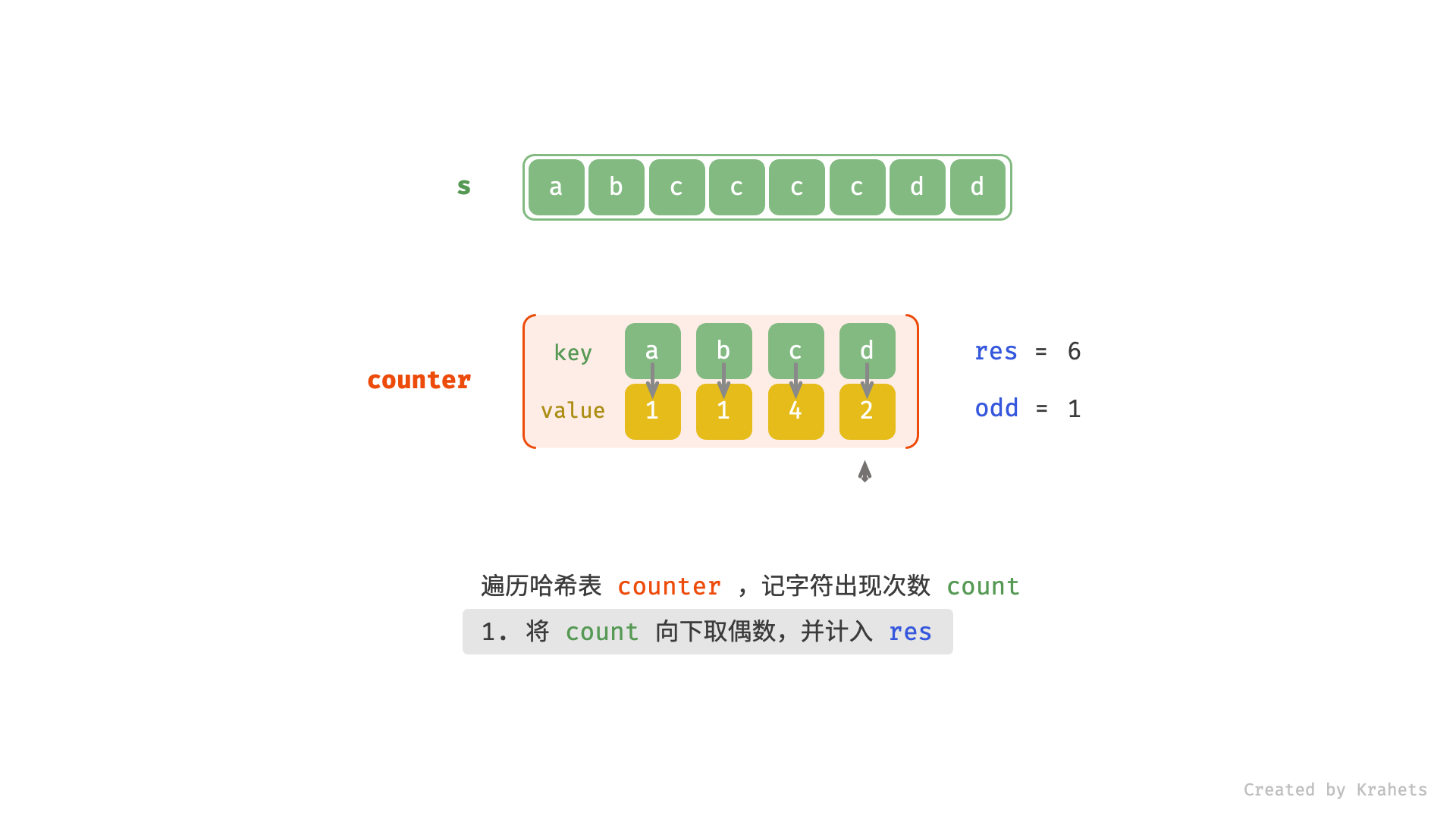
借助一个 HashMap ，统计字符串 s 中各字符的出现次数；
遍历 HashMap ，统计构造回文串的最大长度，
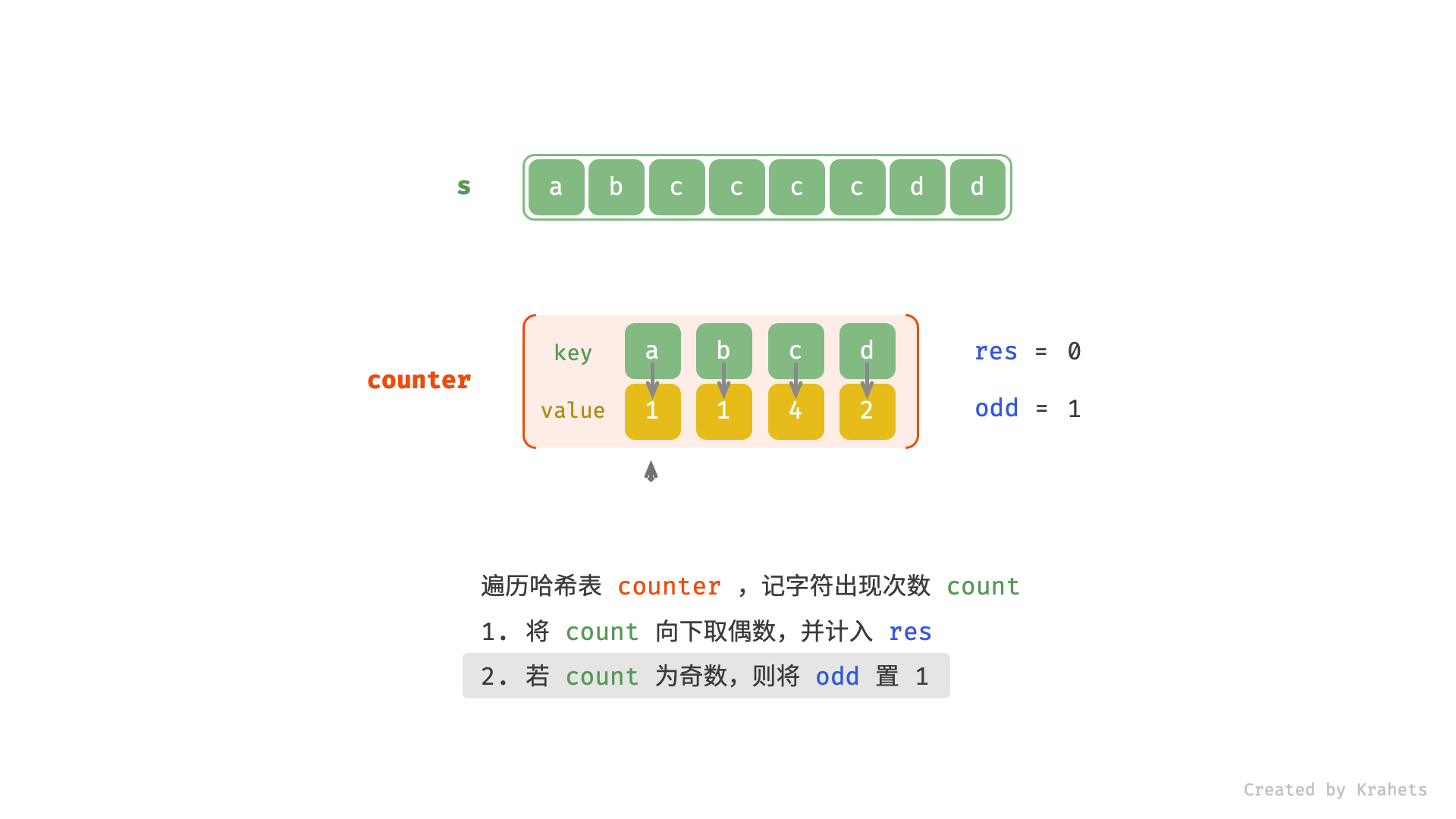
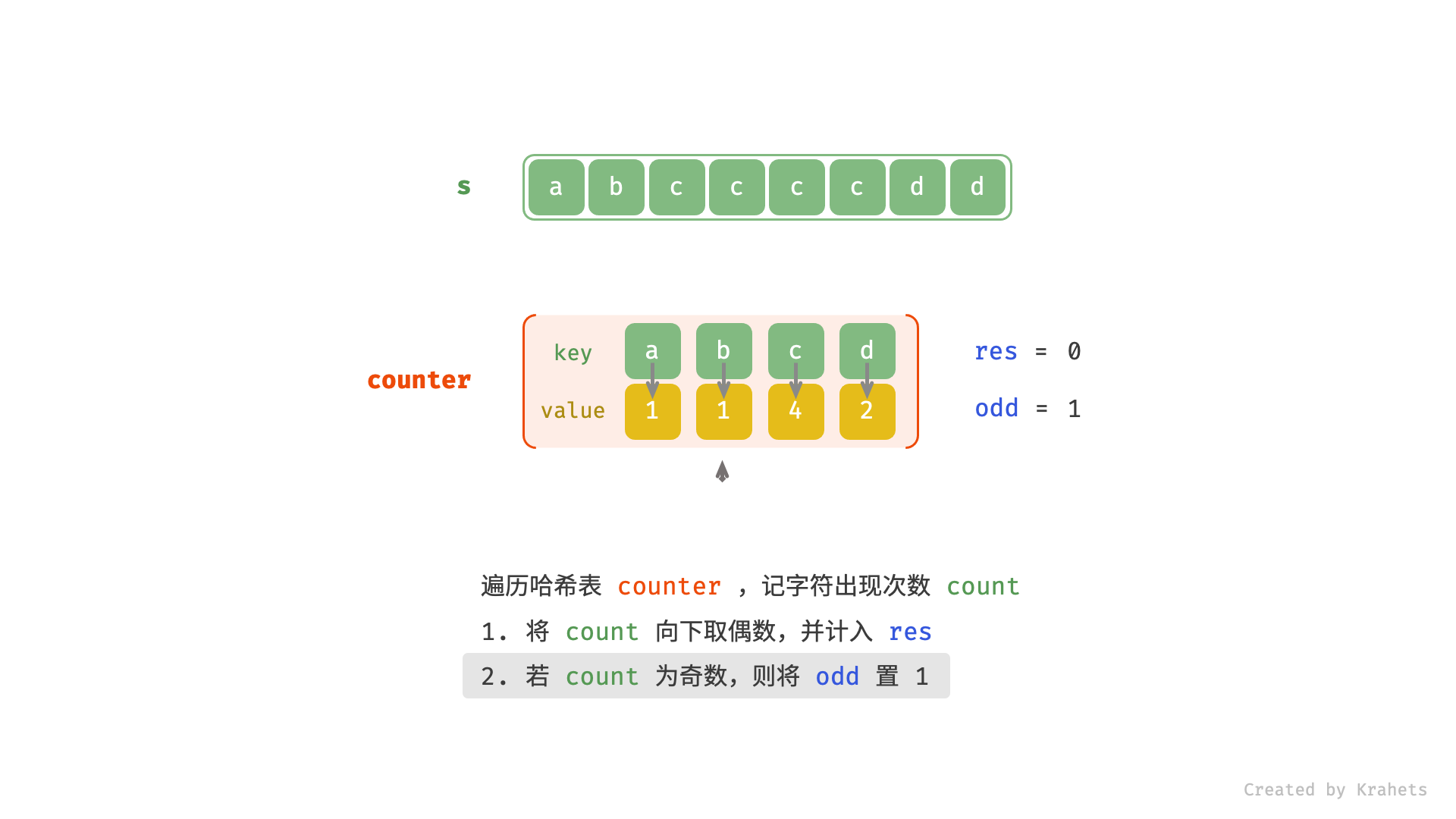
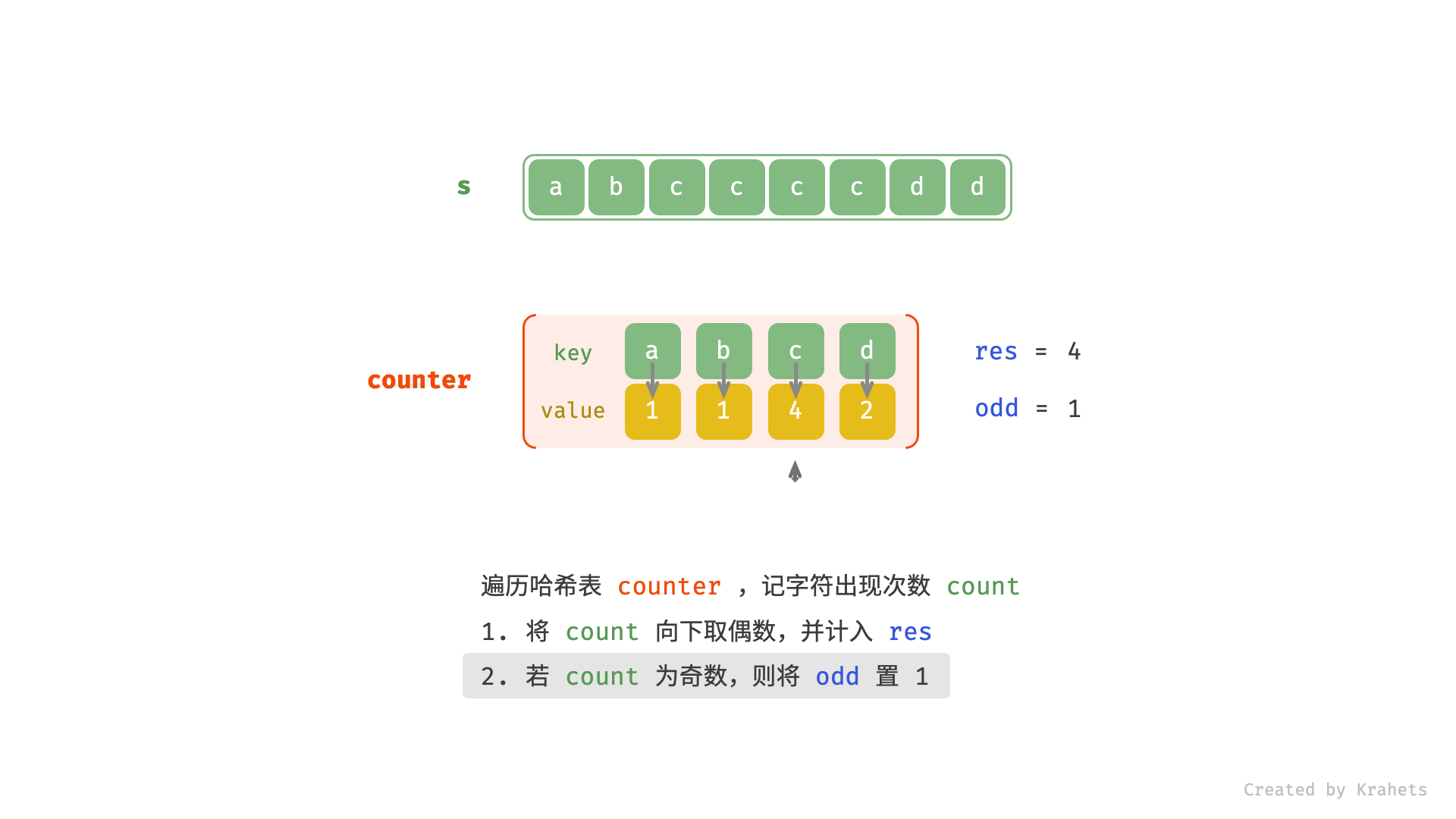
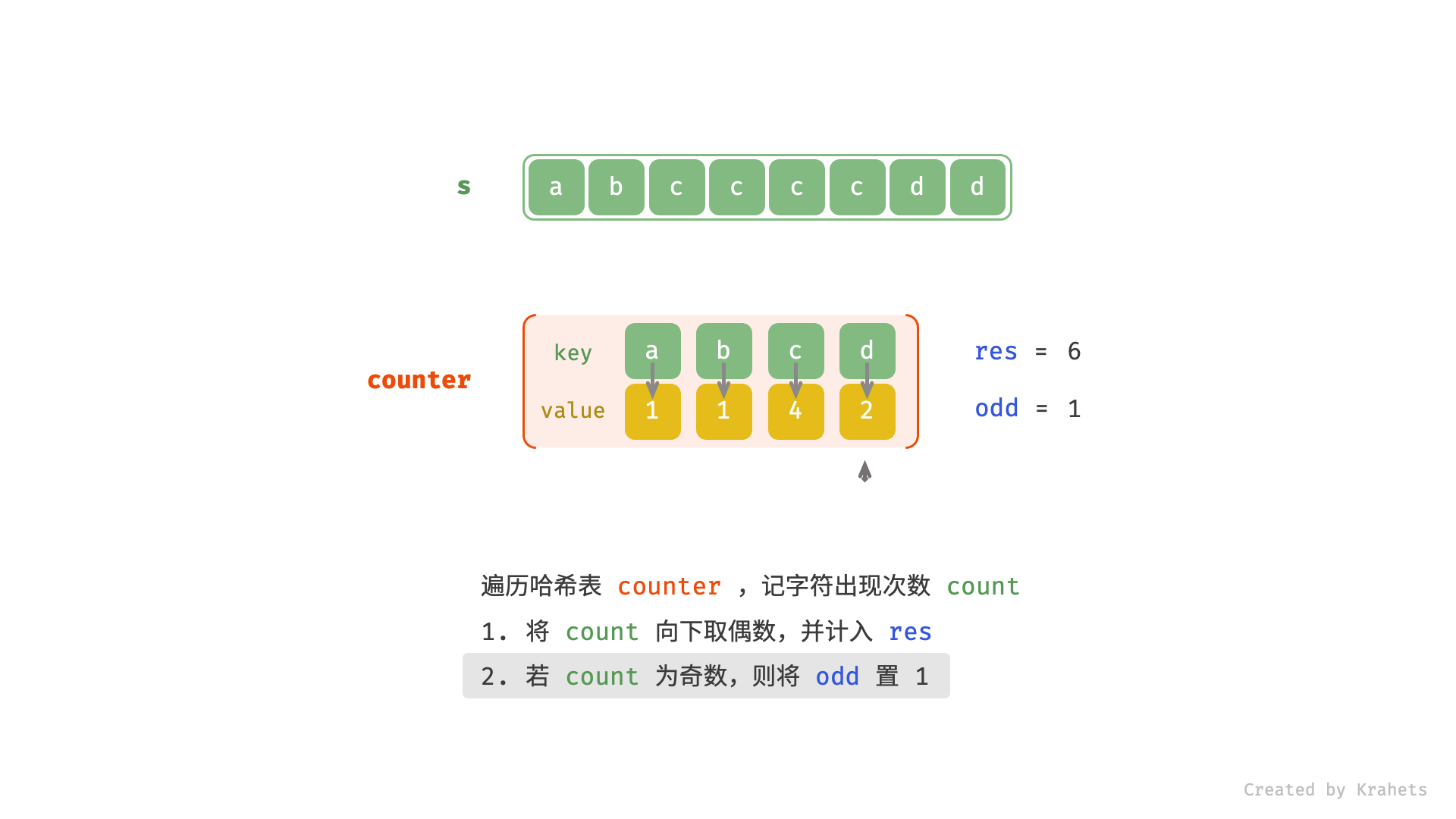
1. 将当前字符的出现次数向下取偶数（即若为偶数则不变，若为奇数则减 1 ），出现偶数次则都可组成回文串，因此计入 res ；
2. 若此字符出现次数为奇数，则可将此字符放到回文串中心，因此将 odd 置 1 ；
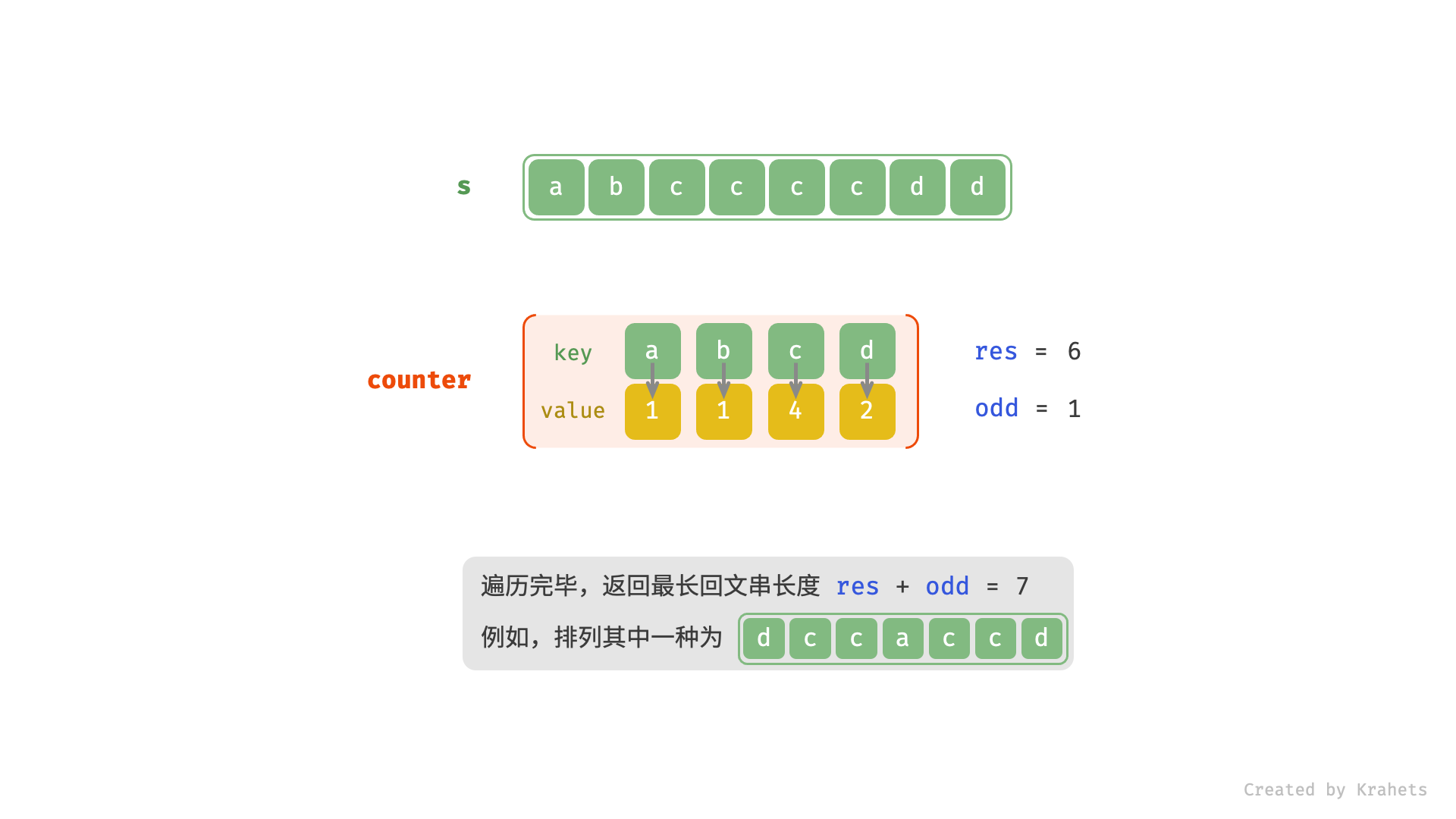
返回 res + odd 即可。

<,,,,,,,,,,,>

代码

Python

class Solution:
    def longestPalindrome(self, s: str) -> int:
        # 统计各字符数量
        counter = collections.defaultdict(int)
        for c in s:
            counter[c] += 1
        res, odd = 0, 0
        # 统计构造回文串的最大长度
        for count in counter.values():
            # 将当前字符出现次数向下取偶数，并计入 res
            rem = count % 2
            res += count - rem
            # 若当前字符出现次数为奇数，则将 odd 置 1
            if rem == 1: odd = 1
        return res + odd

Java

class Solution {
    public int longestPalindrome(String s) {
        // 统计各字符数量
        HashMap<Character, Integer> counter = new HashMap<>();
        for (int i = 0; i < s.length(); i++)
            counter.merge(s.charAt(i), 1, (a, b) -> a + b);
        // 统计构造回文串的最大长度
        int res = 0, odd = 0;
        for (Map.Entry<Character, Integer> kv : counter.entrySet()) {
            // 将当前字符出现次数向下取偶数，并计入 res
            int count = kv.getValue();
            int rem = count % 2;
            res += count - rem;
            // 若当前字符出现次数为奇数，则将 odd 置 1
            if (rem == 1) odd = 1;
        }
        return res + odd;
    }
}

C++

class Solution {
public:
    int longestPalindrome(string s) {
        // 统计各字符数量
        unordered_map<char, int> counter;
        for (char c : s)
            counter[c]++;
        // 统计构造回文串的最大长度
        int res = 0, odd = 0;
        for (auto kv : counter) {
            // 将当前字符出现次数向下取偶数，并计入 res
            int count = kv.second;
            int rem = count % 2;
            res += count - rem;
            // 若当前字符出现次数为奇数，则将 odd 置 1
            if (rem == 1) odd = 1;
        }
        return res + odd;
    }
};

复杂度分析

时间复杂度 $O(N)$ ： 其中 $N$ 为字符串 s 长度。遍历字符串 s 和哈希表 counter 皆使用线性时间。
空间复杂度 $O(1)$ ： 由于 ASCII 字符数量为 128 ，哈希表 counter 最多使用 $O(128) = O(1)$ 空间。

解题思路 ​

代码 ​

复杂度分析 ​

解题思路

代码

复杂度分析