解题思路： ​

题目要求时间复杂度 $O(N)$ ，空间复杂度 $O(1)$ ，因此首先排除 暴力法 和 辅助哈希表法 。

设整型数组 $nums$ 中出现一次的数字为 $x$ ，出现两次的数字为 $a, a, b, b, ...$ ，即：

$$ nums = [a, a, b, b, ..., x] $$

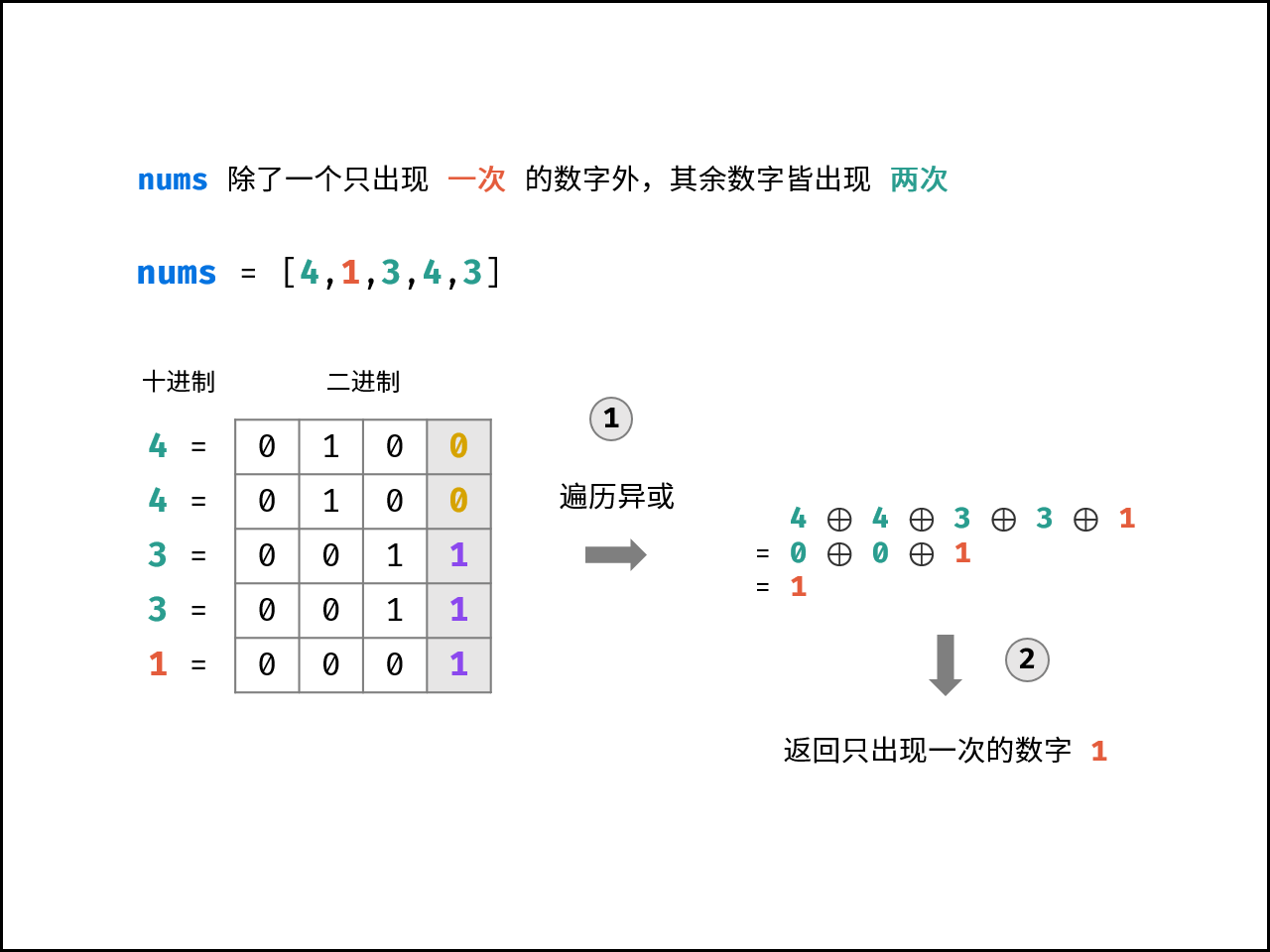
异或运算有个重要的性质，两个相同数字异或为 $0$ ，即对于任意整数 $a$ 有 $a \oplus a = 0$ 。因此，若将 $nums$ 中所有数字执行异或运算，留下的结果则为 出现一次的数字 $x$ ，即：

$$ \begin{aligned} & \ \ a \oplus a \oplus b \oplus b \oplus ... \oplus x \ = & \ \ 0 \oplus 0 \oplus ... \oplus x \ = & \ \ x \end{aligned} $$

代码： ​

异或运算满足交换律 $a \oplus b = b \oplus a$ ，即以上运算结果与 $nums$ 的元素顺序无关。代码如下：

class Solution:
    def singleNumber(self, nums: List[int]) -> List[int]:
        x = 0
        for num in nums:  # 1. 遍历 nums 执行异或运算
            x ^= num      
        return x;         # 2. 返回出现一次的数字 x

class Solution {
    public int singleNumber(int[] nums) {
        int x = 0;
        for (int num : nums)  // 1. 遍历 nums 执行异或运算
            x ^= num;
        return x;            // 2. 返回出现一次的数字 x
    }
}

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int x = 0;
        for (int num : nums)  // 1. 遍历 nums 执行异或运算
            x ^= num;
        return x;            // 2. 返回出现一次的数字 x
    }
};

复杂度分析： ​

• 时间复杂度 $O(N)$ ： 线性遍历 $nums$ 使用 $O(N)$ 时间，异或操作使用 $O(1)$ 时间。
• 空间复杂度 $O(1)$ ： 辅助变量 $a$ , $b$ , $x$ , $y$ 使用常数大小额外空间。