解题思路： ​

二叉树镜像定义： 对于二叉树中任意节点 $root$ ，设其左 / 右子节点分别为 $left, right$ ；则在二叉树的镜像中的对应 $root$ 节点，其左 / 右子节点分别为 $right, left$ 。

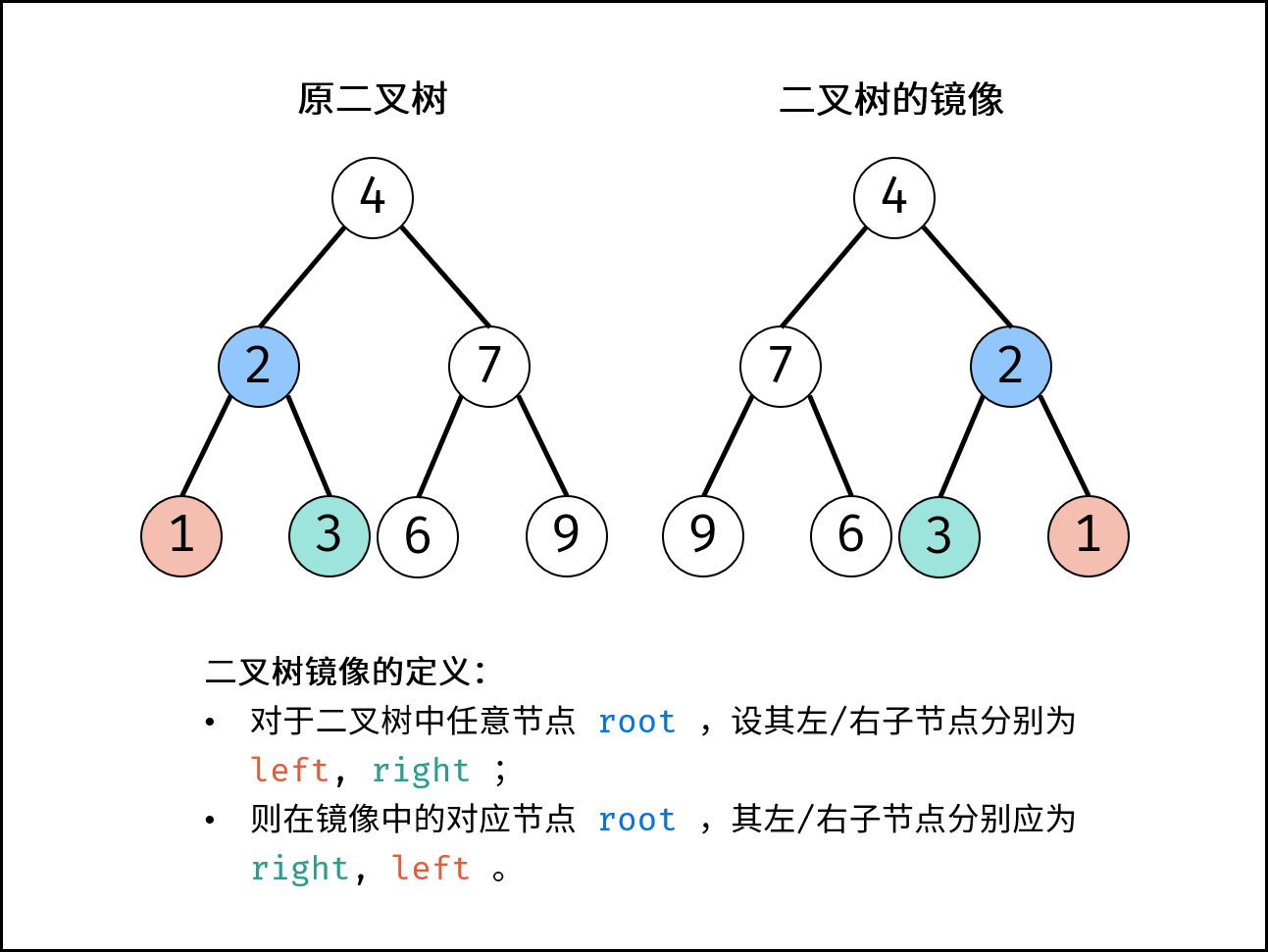
方法一：递归法 ​

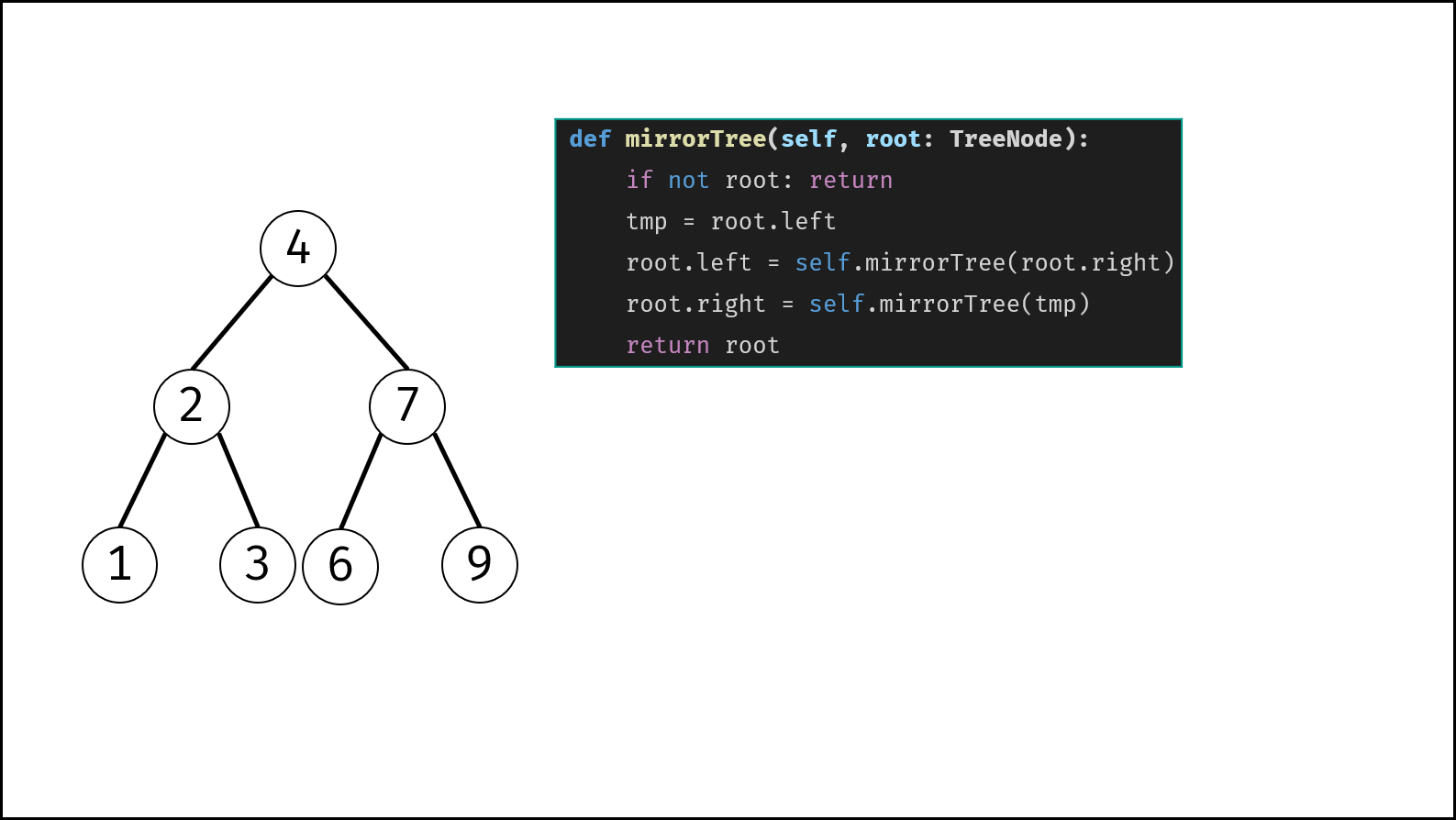
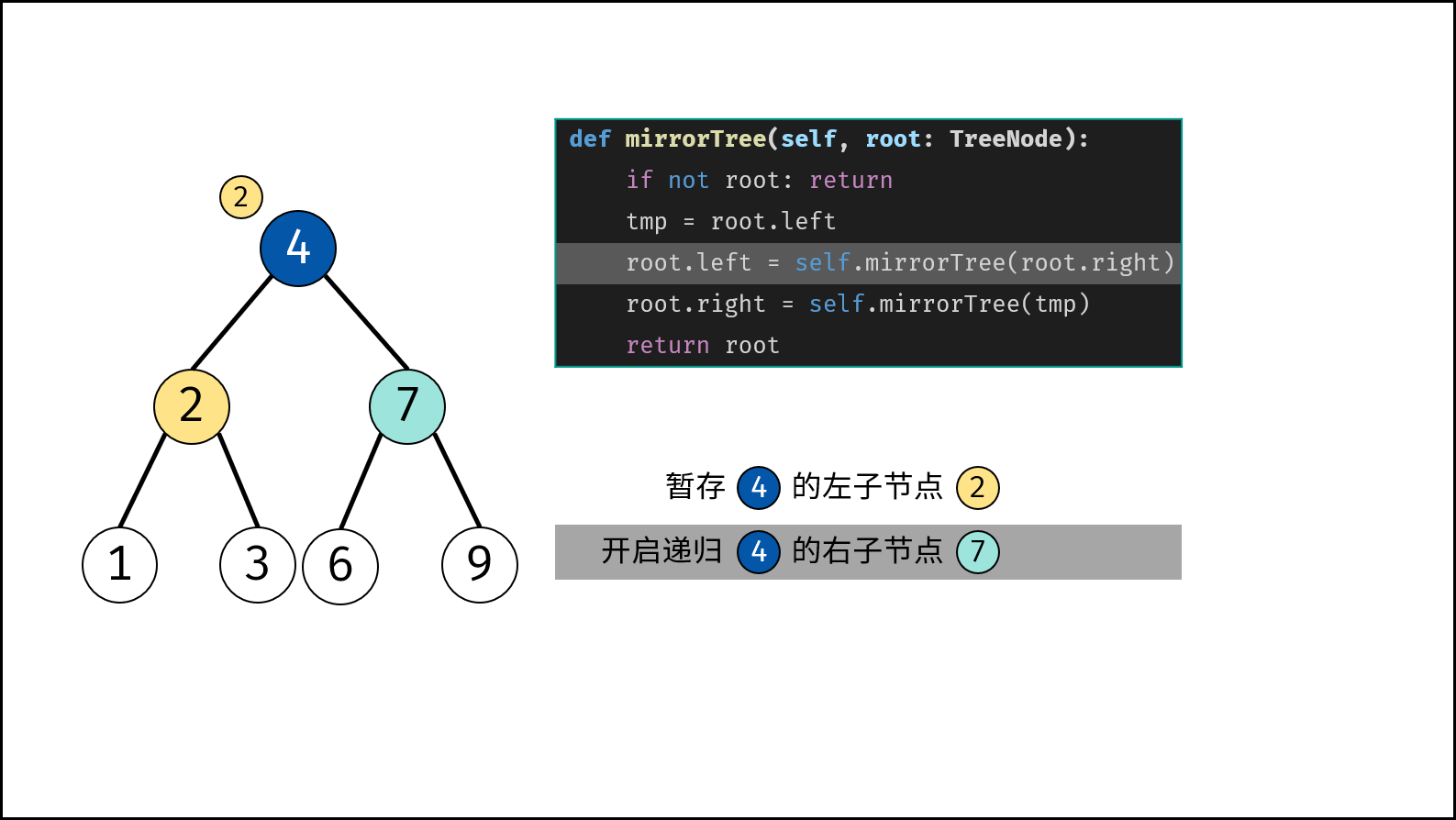
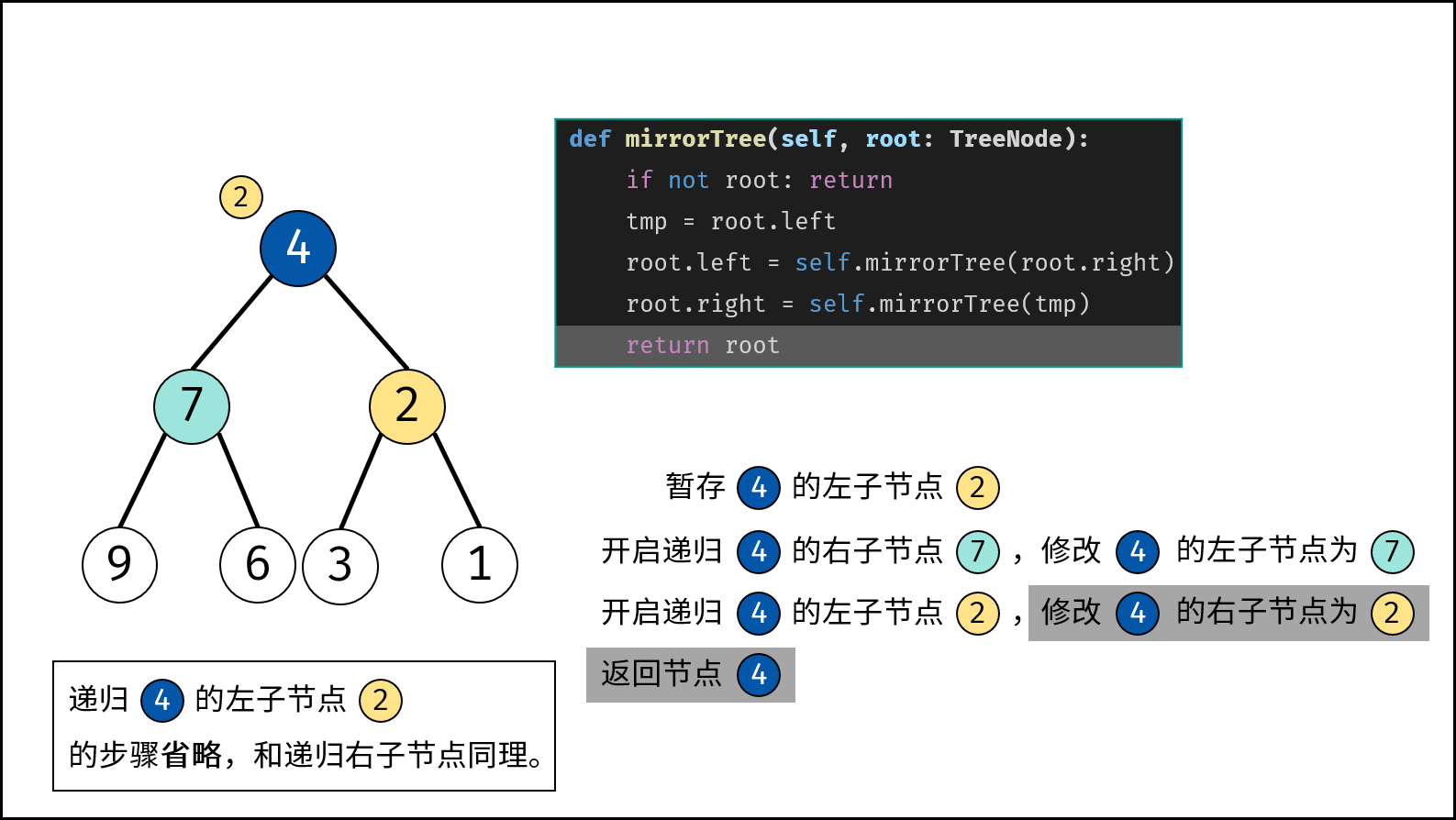
根据二叉树镜像的定义，考虑递归遍历（dfs）二叉树，交换每个节点的左 / 右子节点，即可生成二叉树的镜像。

递归解析： ​

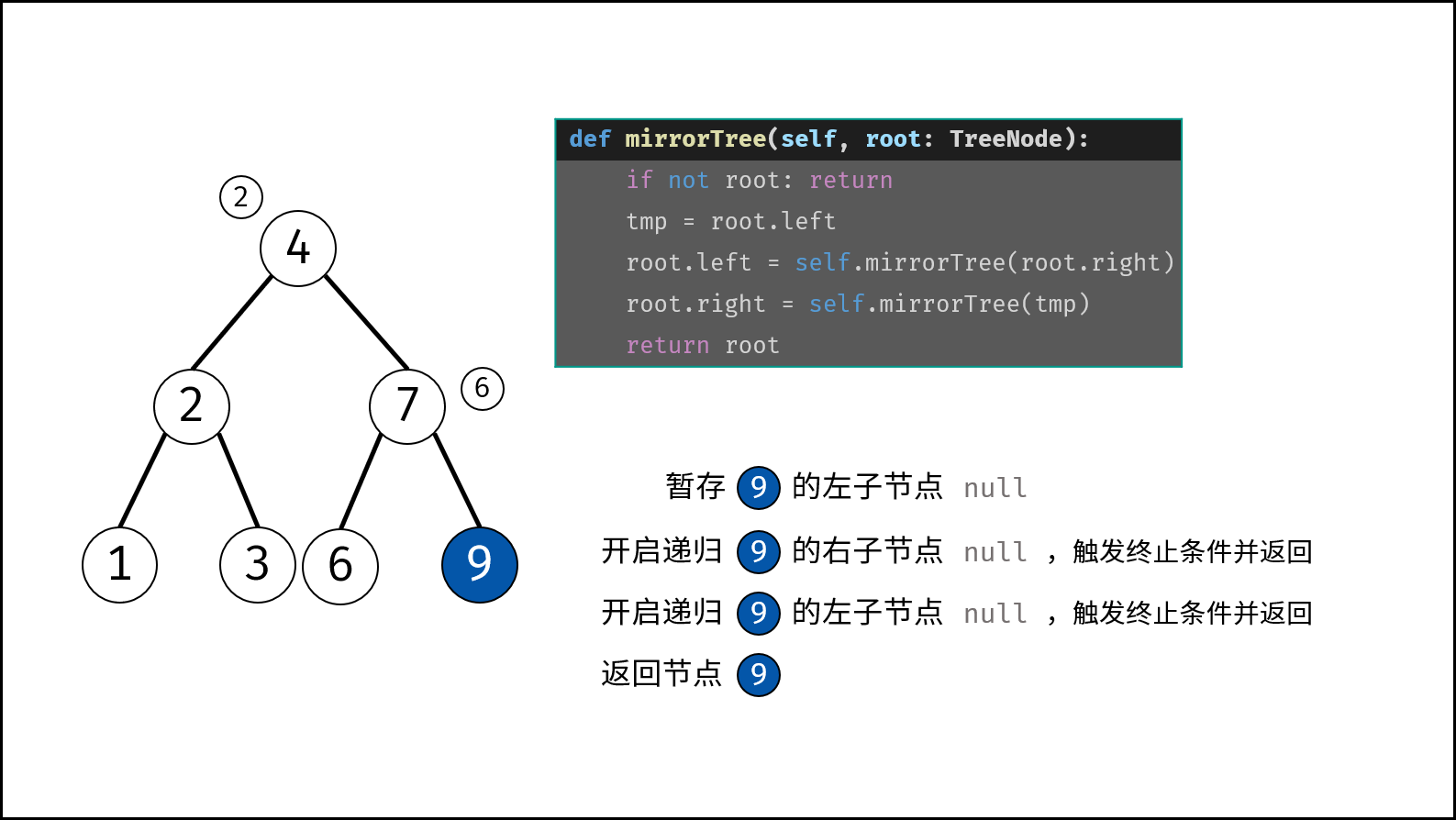
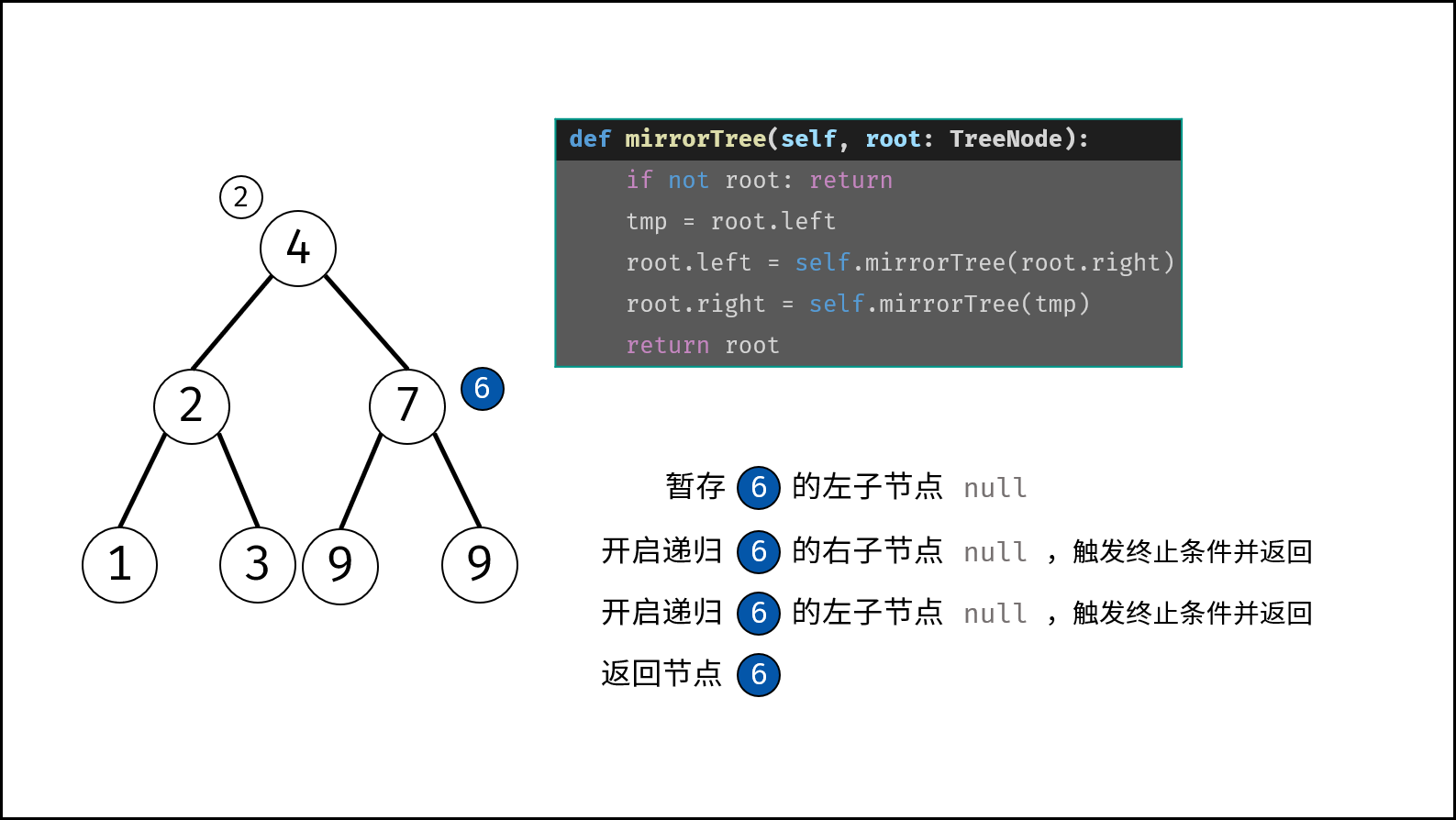
1. 终止条件： 当节点 $root$ 为空时（即越过叶节点），则返回 $null$ 。
2. 递推工作：
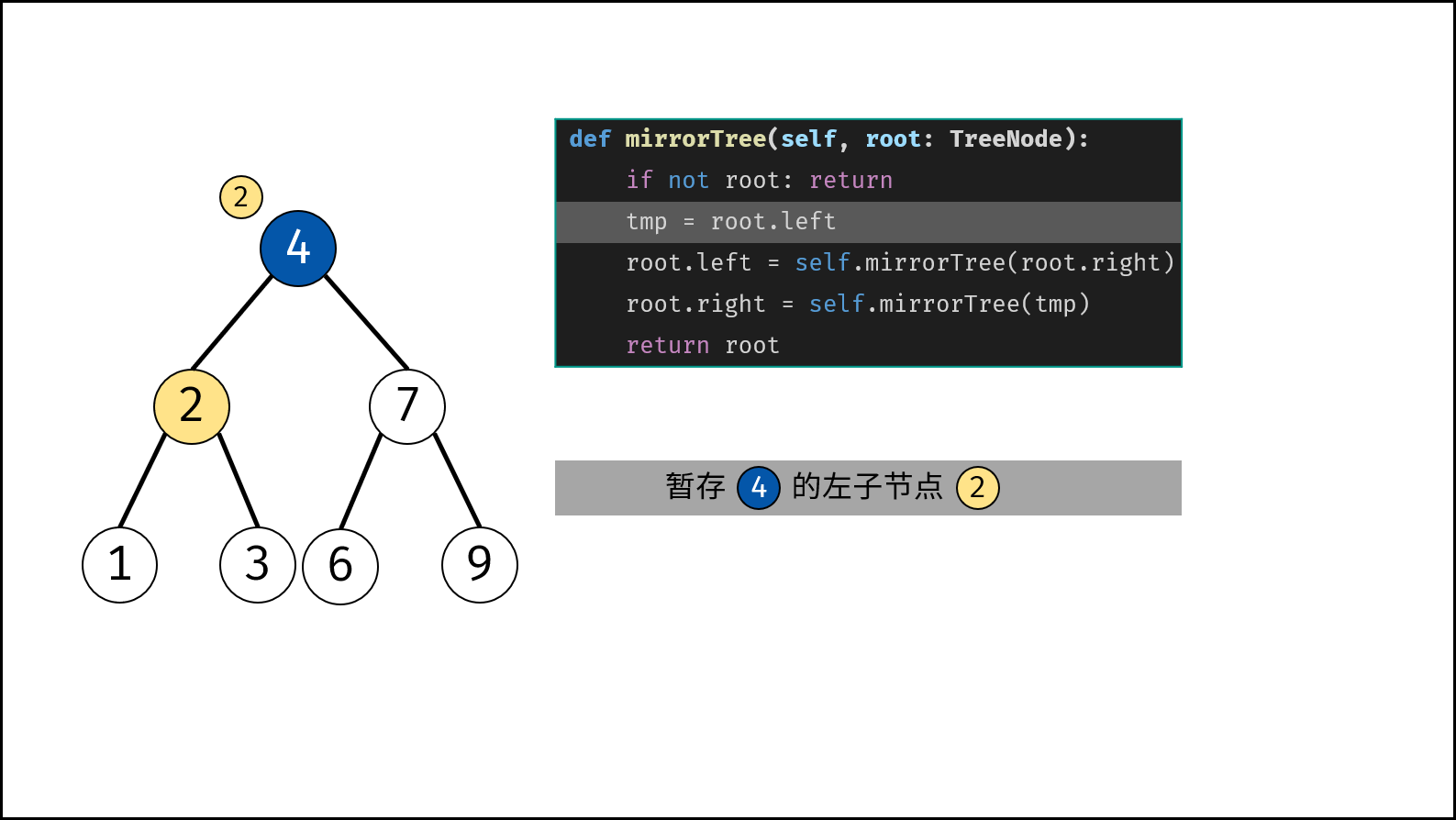
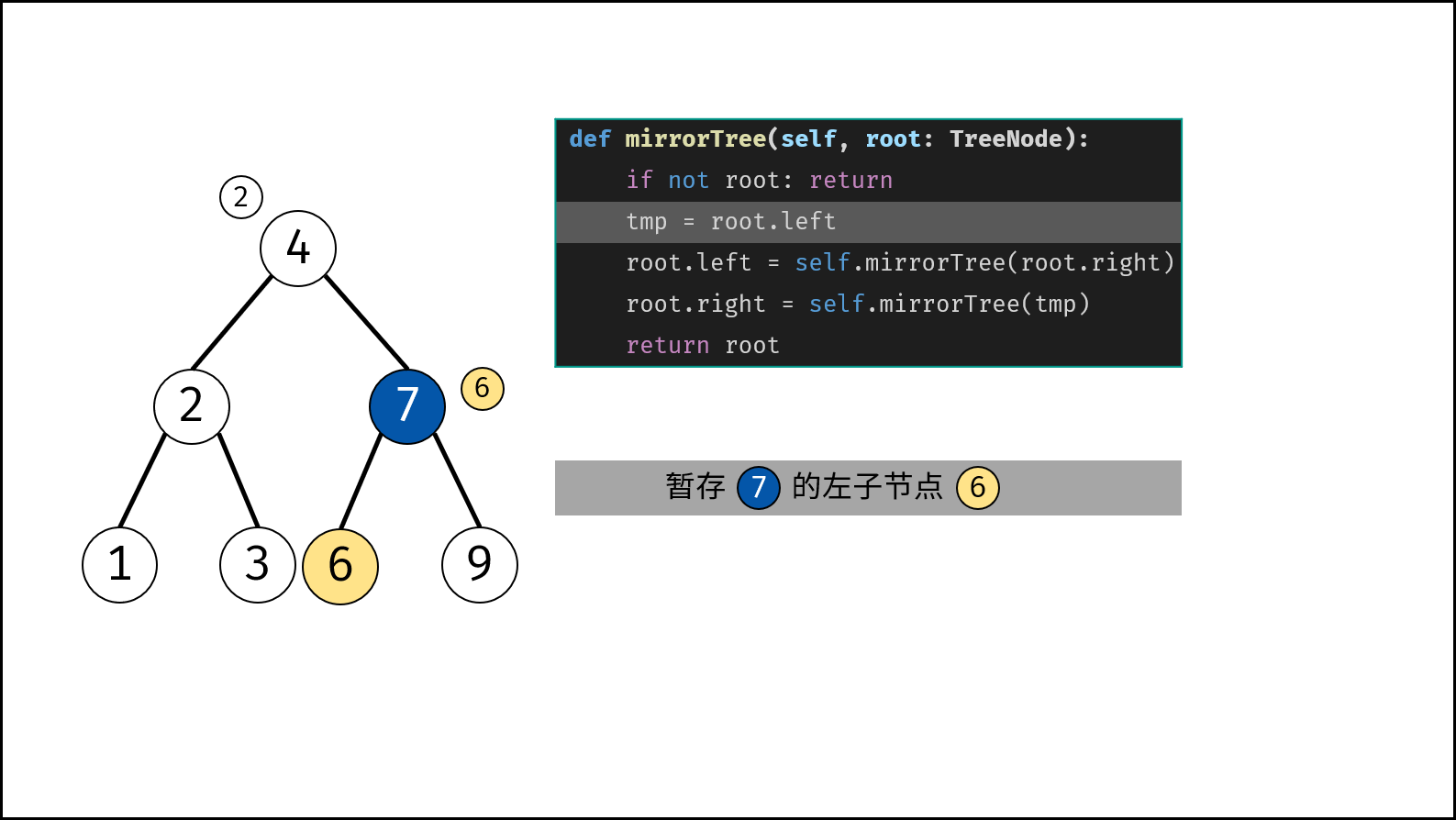
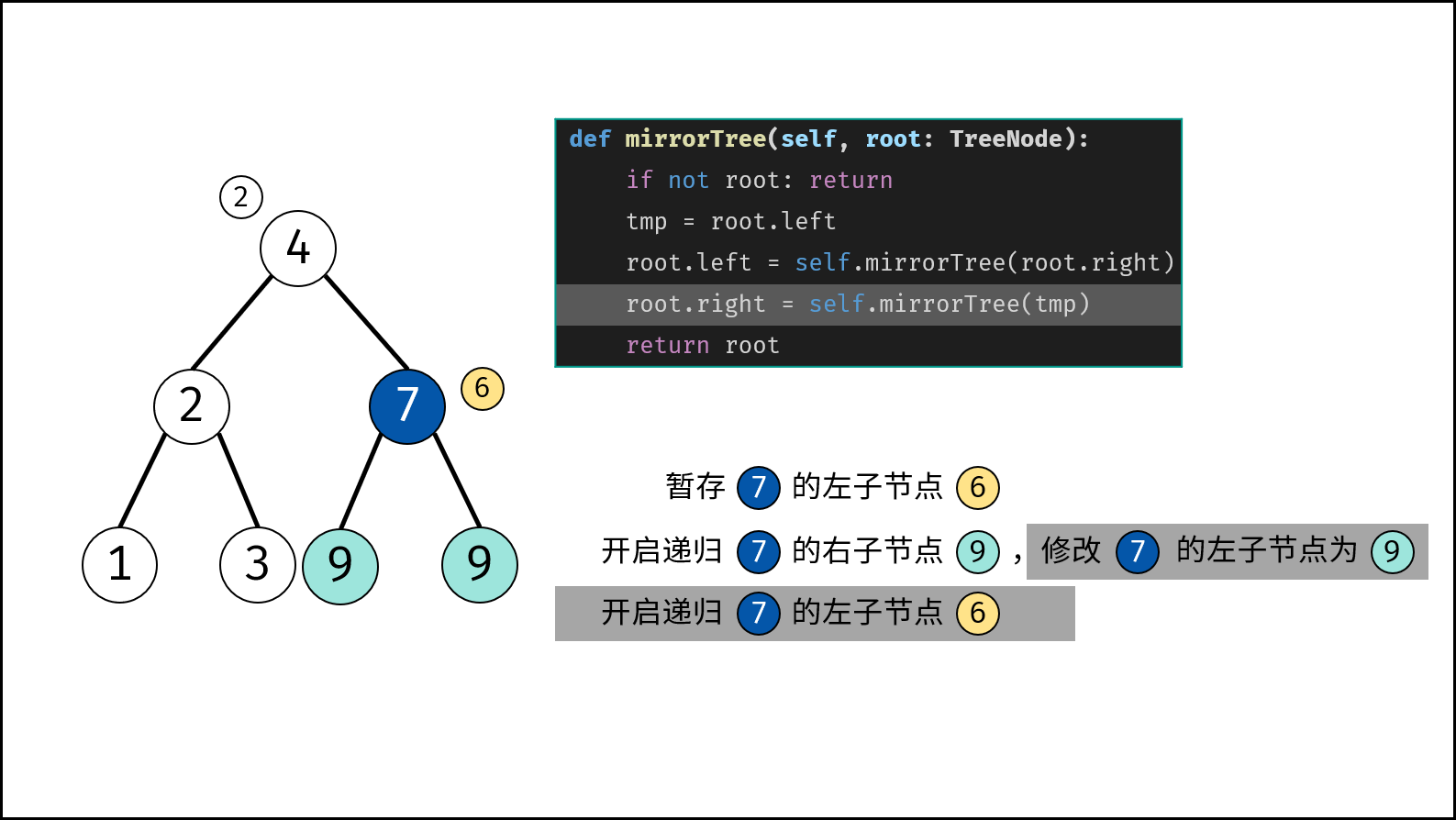
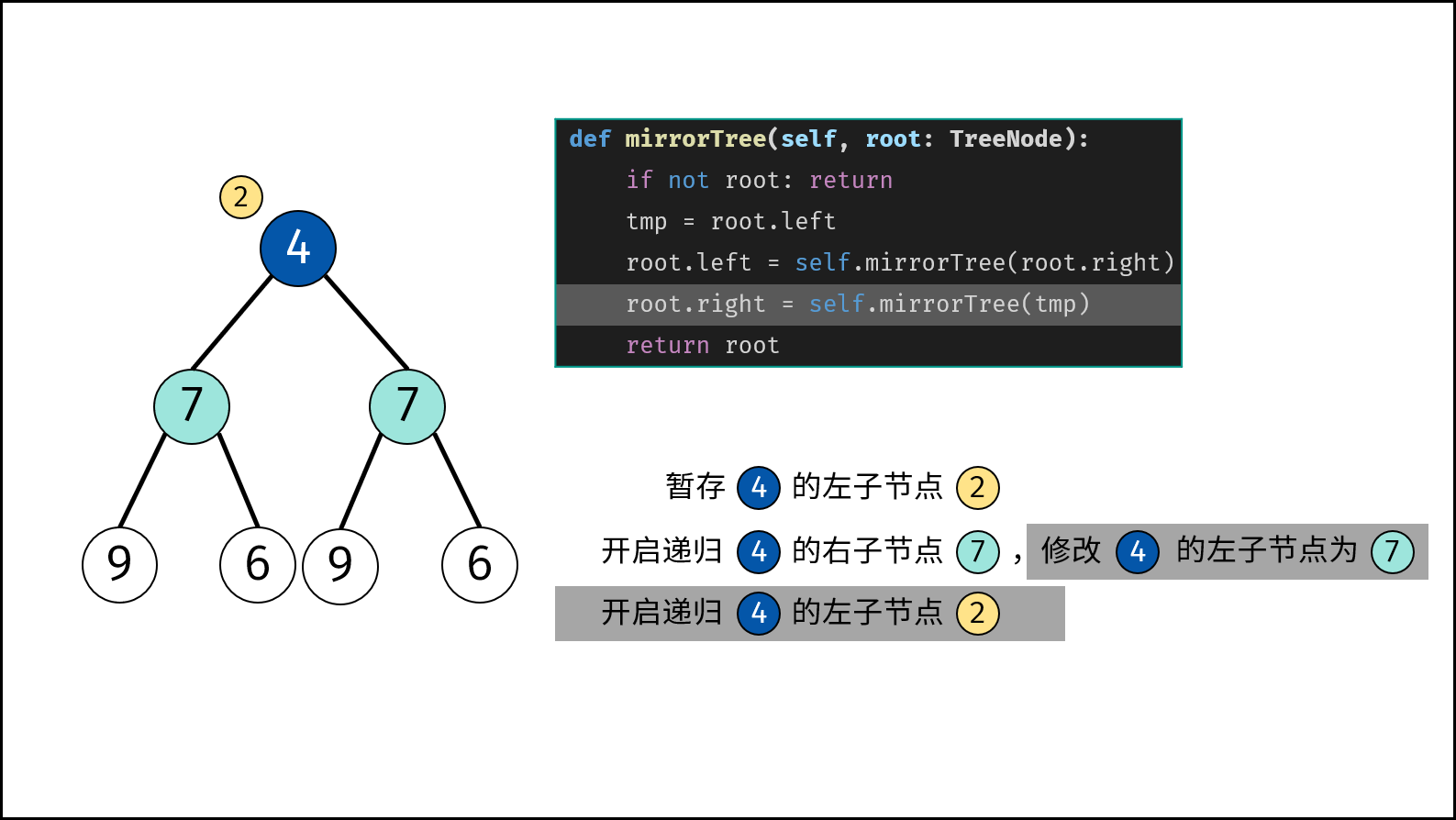
   1. 初始化节点 $tmp$ ，用于暂存 $root$ 的左子节点。
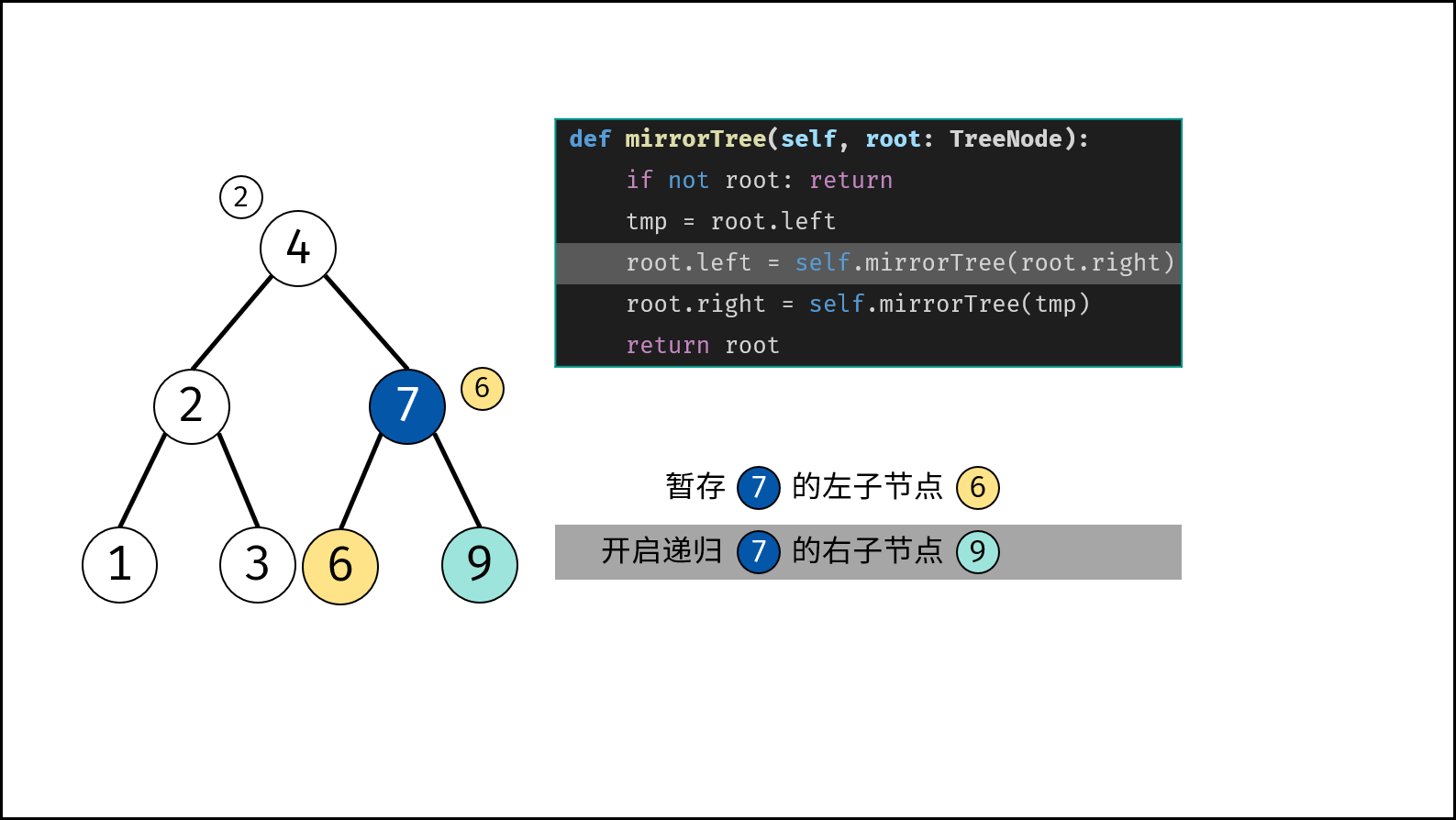
   2. 开启递归 右子节点 $invertTree(root.right)$ ，并将返回值作为 $root$ 的 左子节点 。
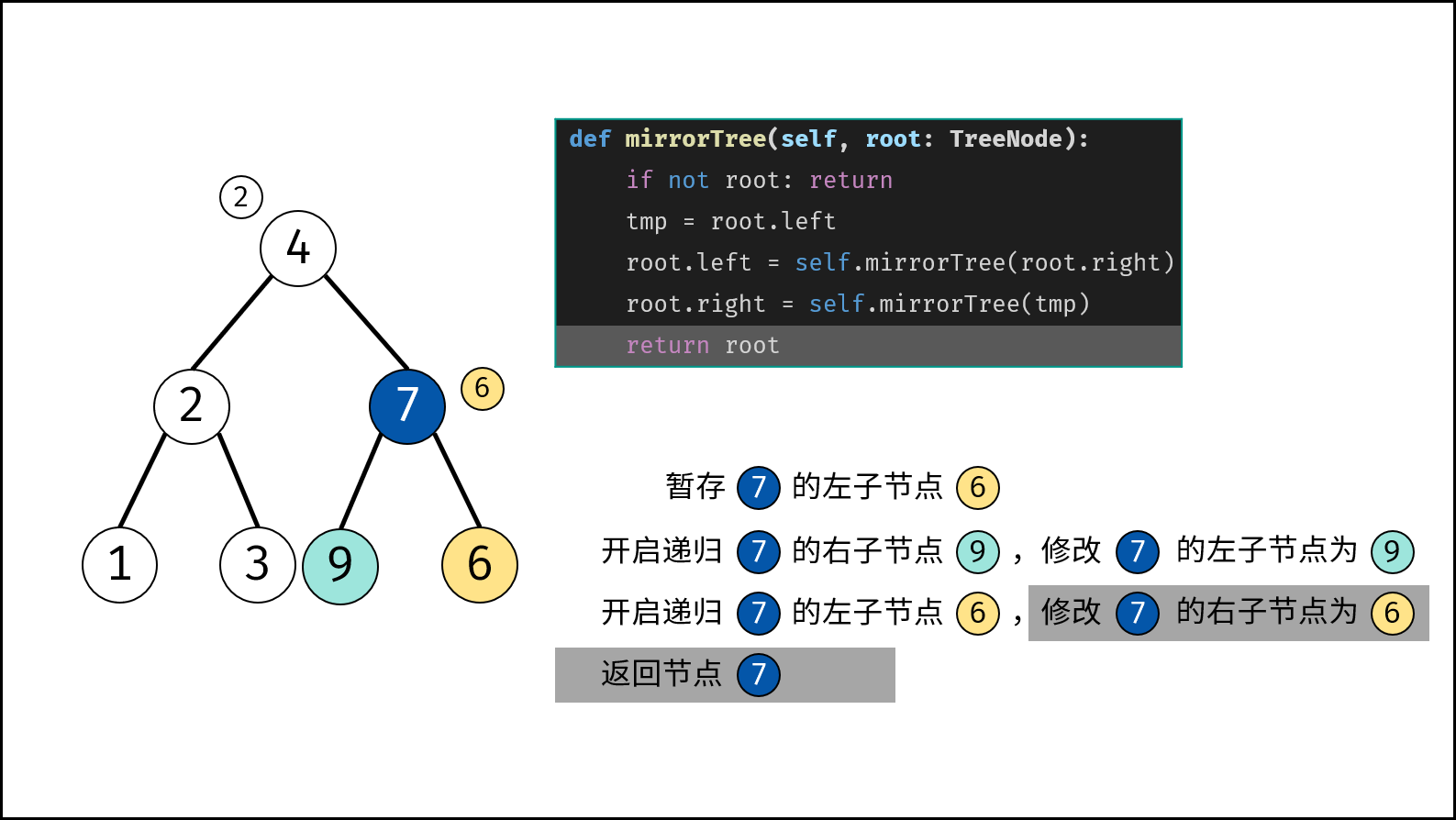
   3. 开启递归 左子节点 $invertTree(tmp)$ ，并将返回值作为 $root$ 的 右子节点 。
3. 返回值： 返回当前节点 $root$ 。

Q： 为何需要暂存 $root$ 的左子节点？ A： 在递归右子节点 “$root.left = invertTree(root.right);$” 执行完毕后， $root.left$ 的值已经发生改变，此时递归左子节点 $invertTree(root.left)$ 则会出问题。

<,,,,,,,,,,>

代码： ​

Python 利用平行赋值的写法（即 $a, b = b, a$ ），可省略暂存操作。其原理是先将等号右侧打包成元组 $(b,a)$ ，再序列地分给等号左侧的 $a, b$ 序列。

class Solution:
    def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        if not root: return
        tmp = root.left
        root.left = self.invertTree(root.right)
        root.right = self.invertTree(tmp)
        return root

class Solution:
    def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        if not root: return
        root.left, root.right = self.invertTree(root.right), self.invertTree(root.left)
        return root

class Solution {
    public TreeNode invertTree(TreeNode root) {
        if (root == null) return null;
        TreeNode tmp = root.left;
        root.left = invertTree(root.right);
        root.right = invertTree(tmp);
        return root;
    }
}

class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if (root == nullptr) return nullptr;
        TreeNode* tmp = root->left;
        root->left = invertTree(root->right);
        root->right = invertTree(tmp);
        return root;
    }
};

复杂度分析： ​

• 时间复杂度 $O(N)$ ： 其中 $N$ 为二叉树的节点数量，建立二叉树镜像需要遍历树的所有节点，占用 $O(N)$ 时间。
• 空间复杂度 $O(N)$ ： 最差情况下（当二叉树退化为链表），递归时系统需使用 $O(N)$ 大小的栈空间。

方法二：辅助栈（或队列） ​

利用栈（或队列）遍历树的所有节点 $node$ ，并交换每个 $node$ 的左 / 右子节点。

算法流程： ​

1. 特例处理： 当 $root$ 为空时，直接返回 $null$ 。
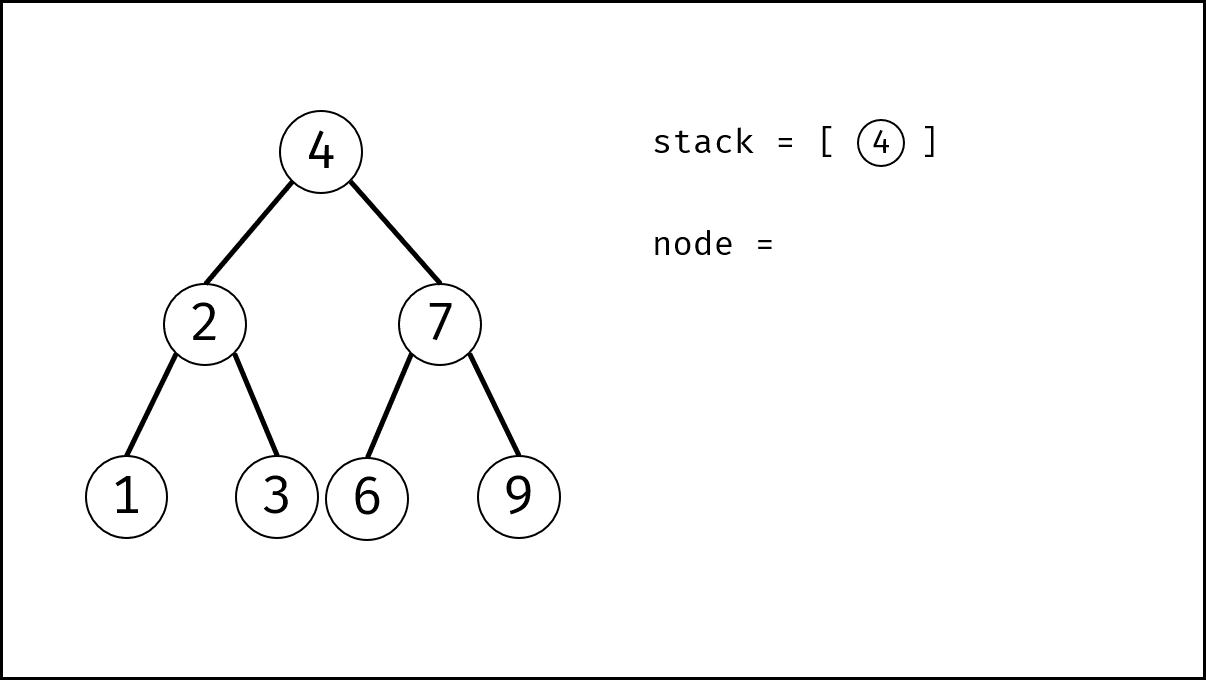
2. 初始化： 栈（或队列），本文用栈，并加入根节点 $root$ 。
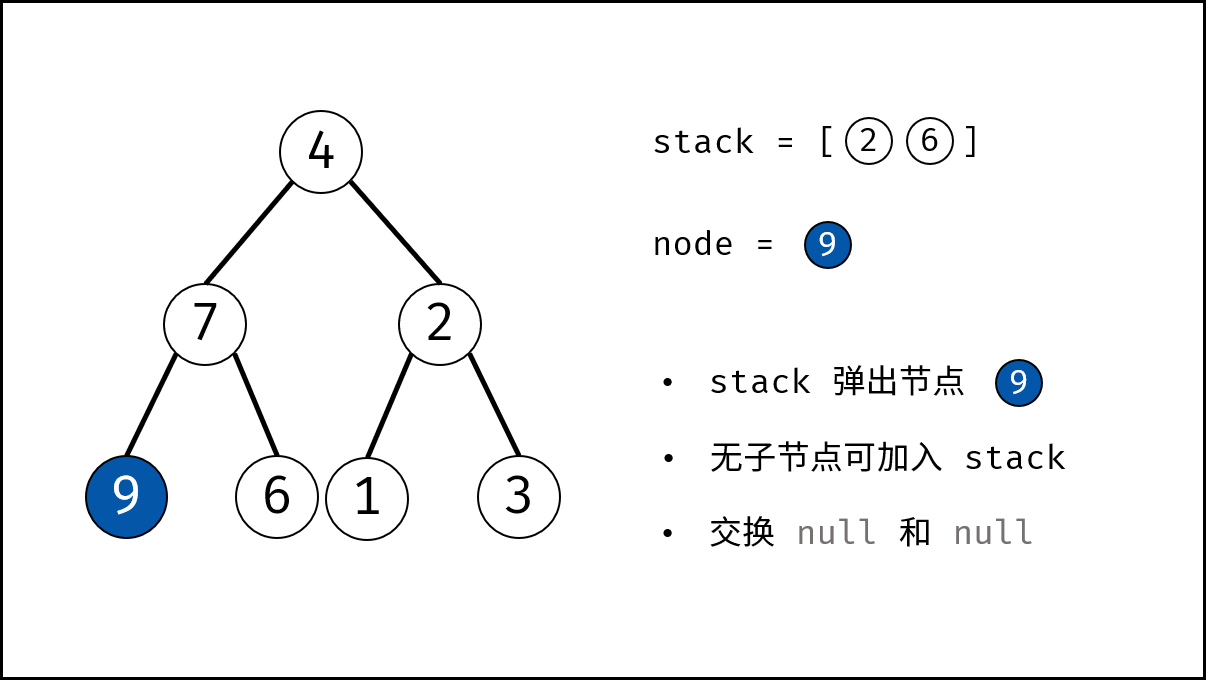
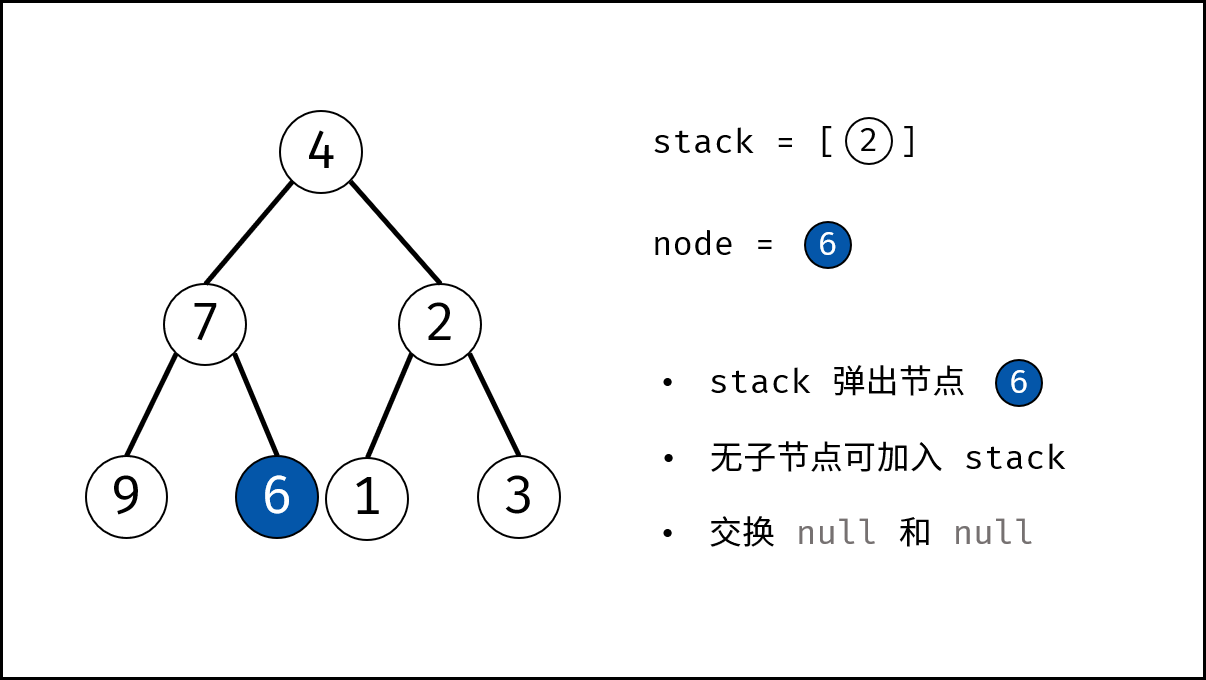
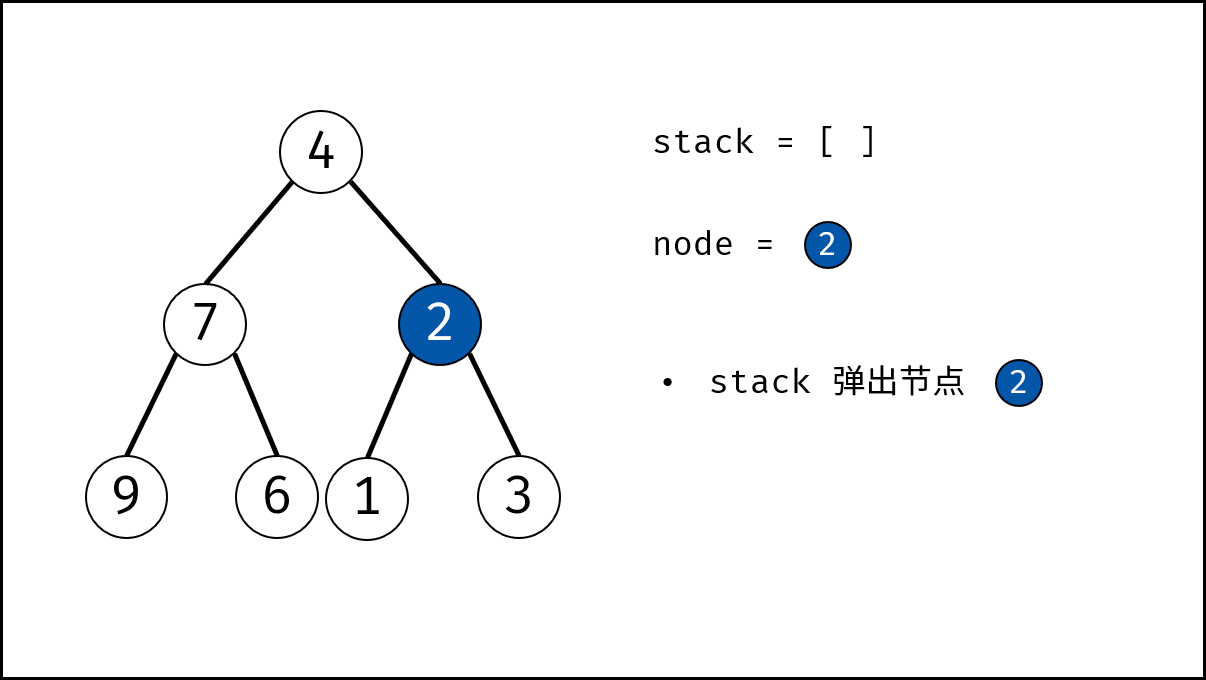
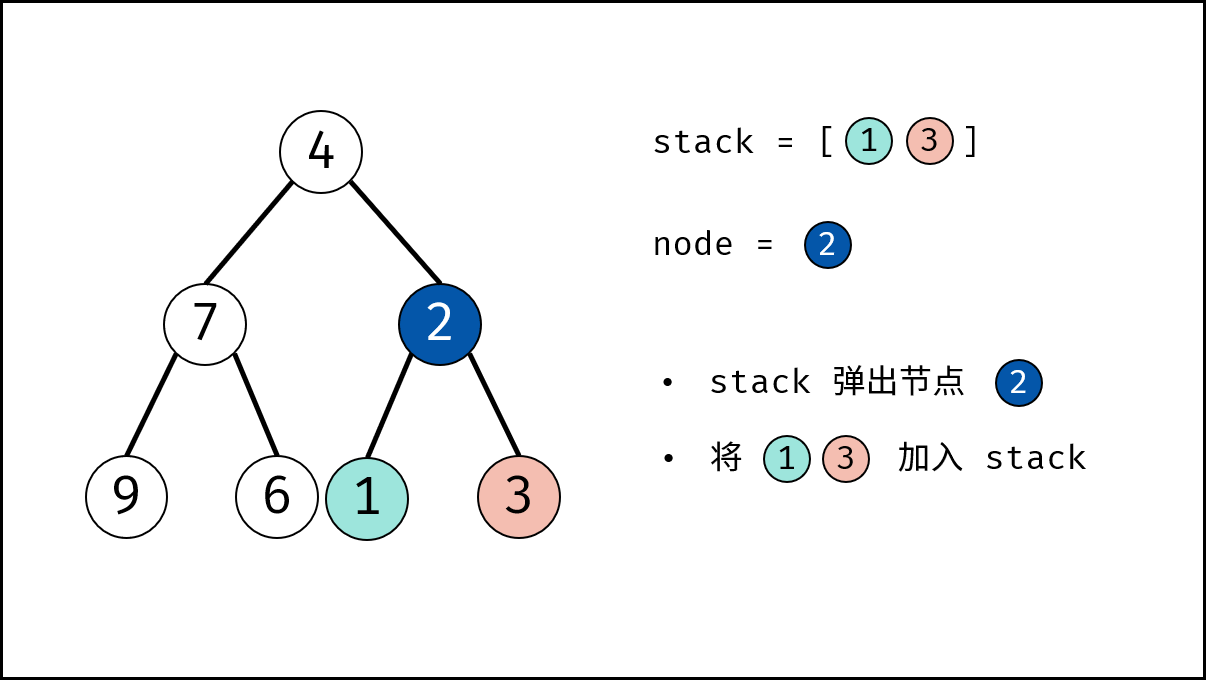
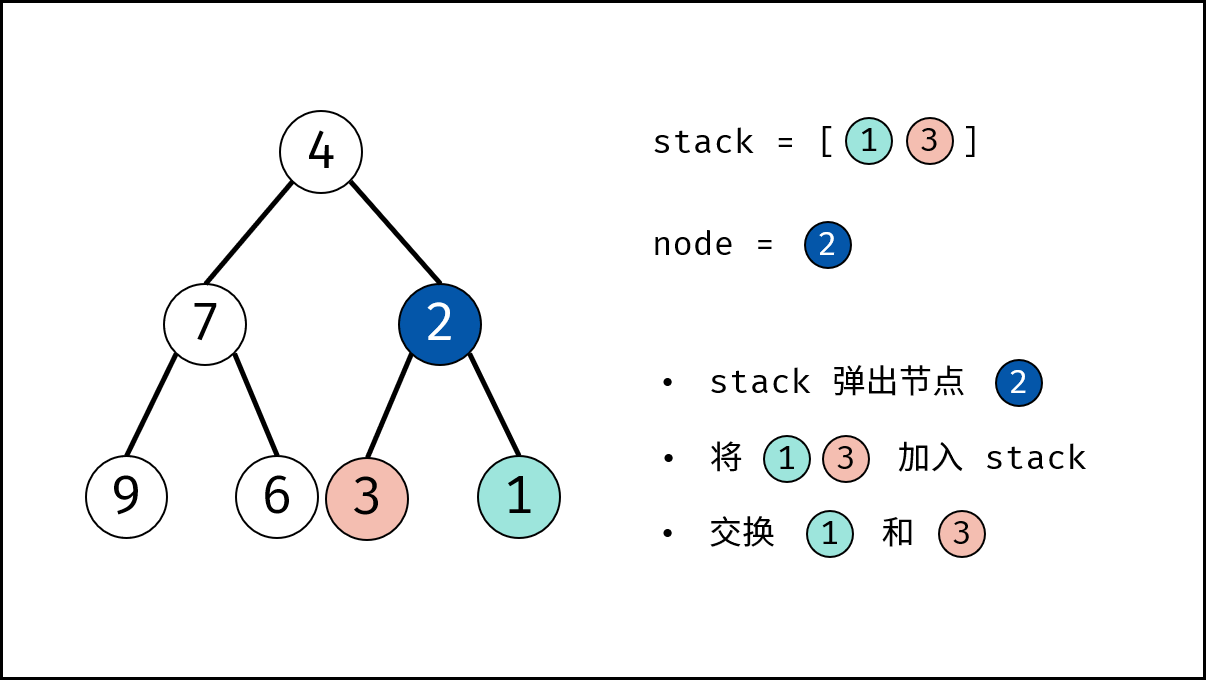
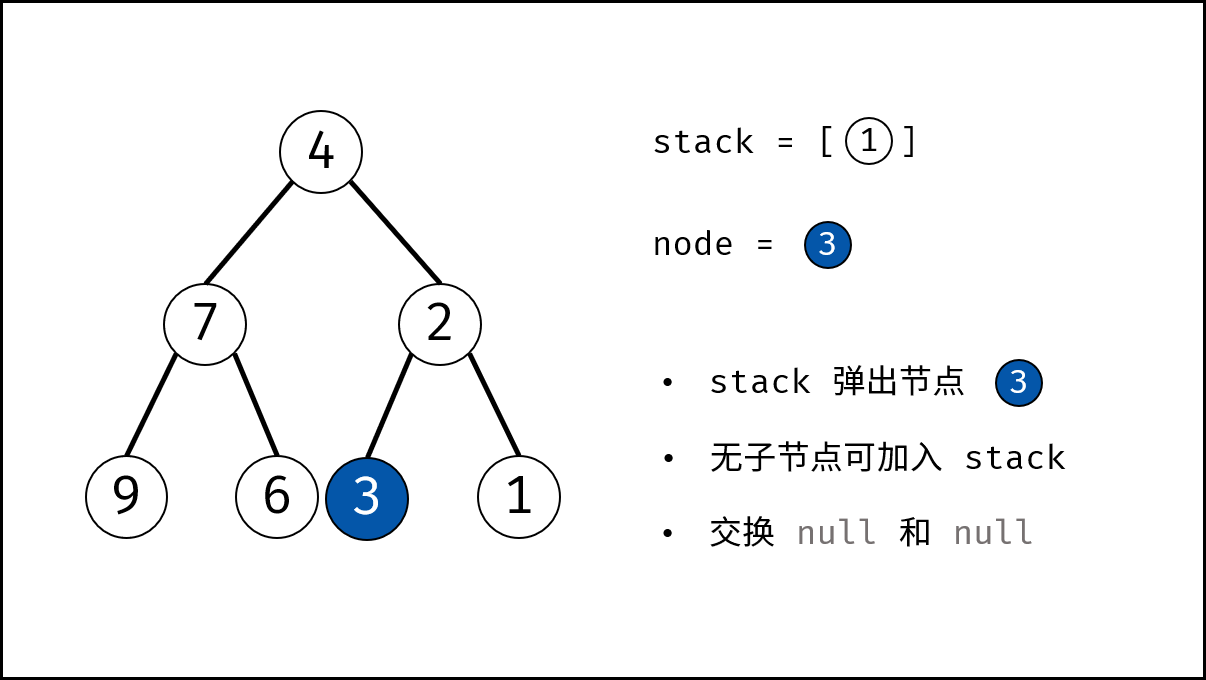
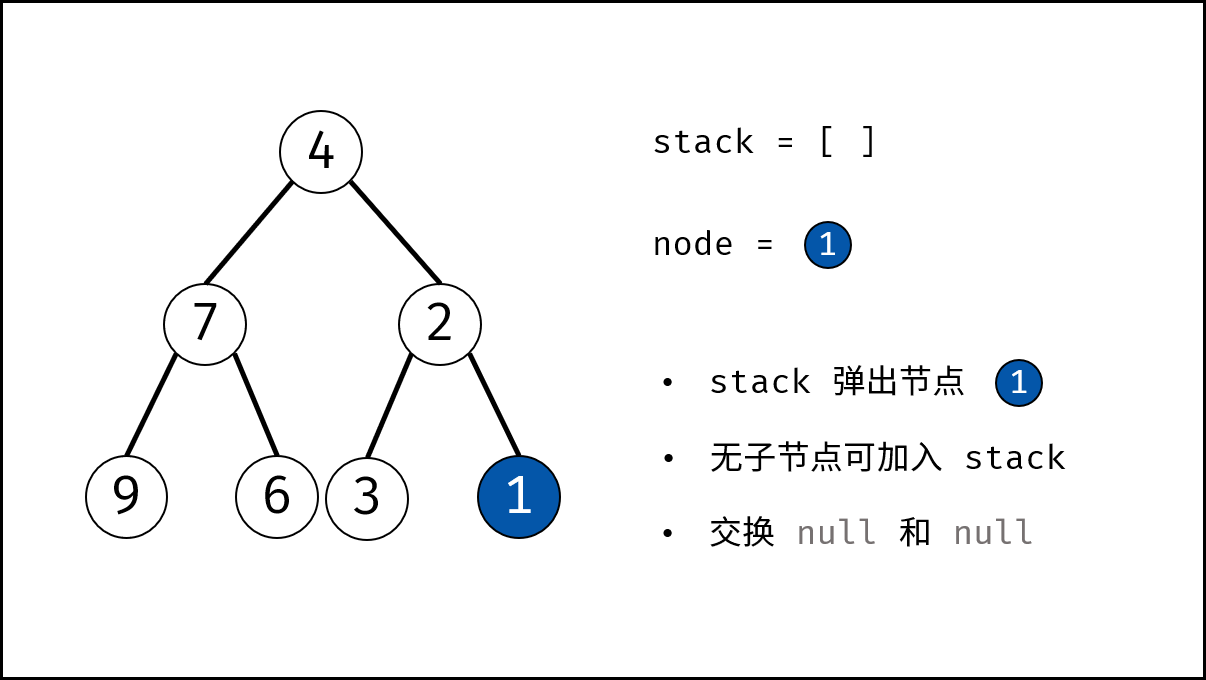
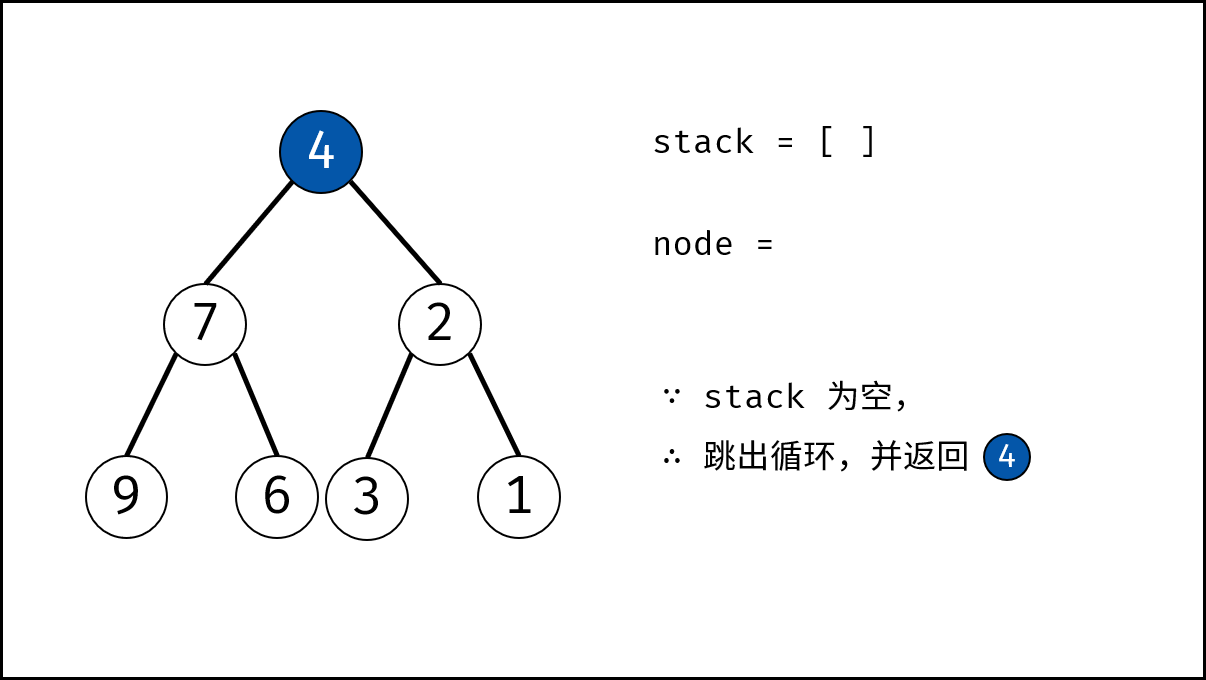
3. 循环交换： 当栈 $stack$ 为空时跳出。
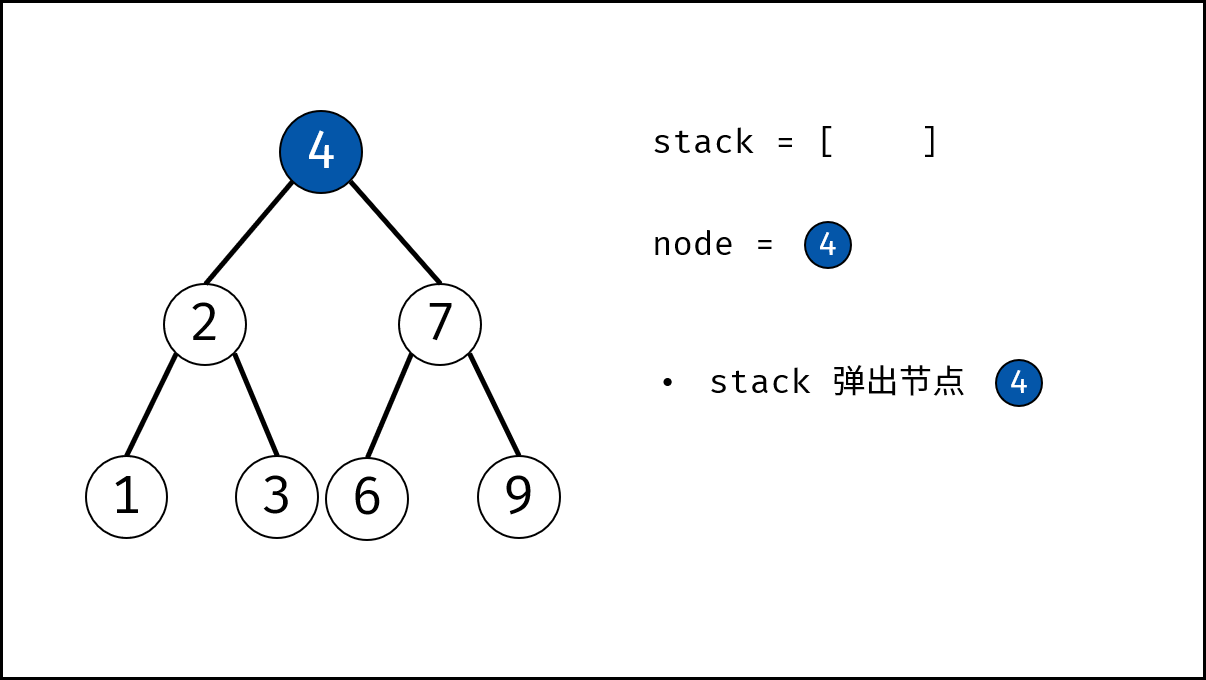
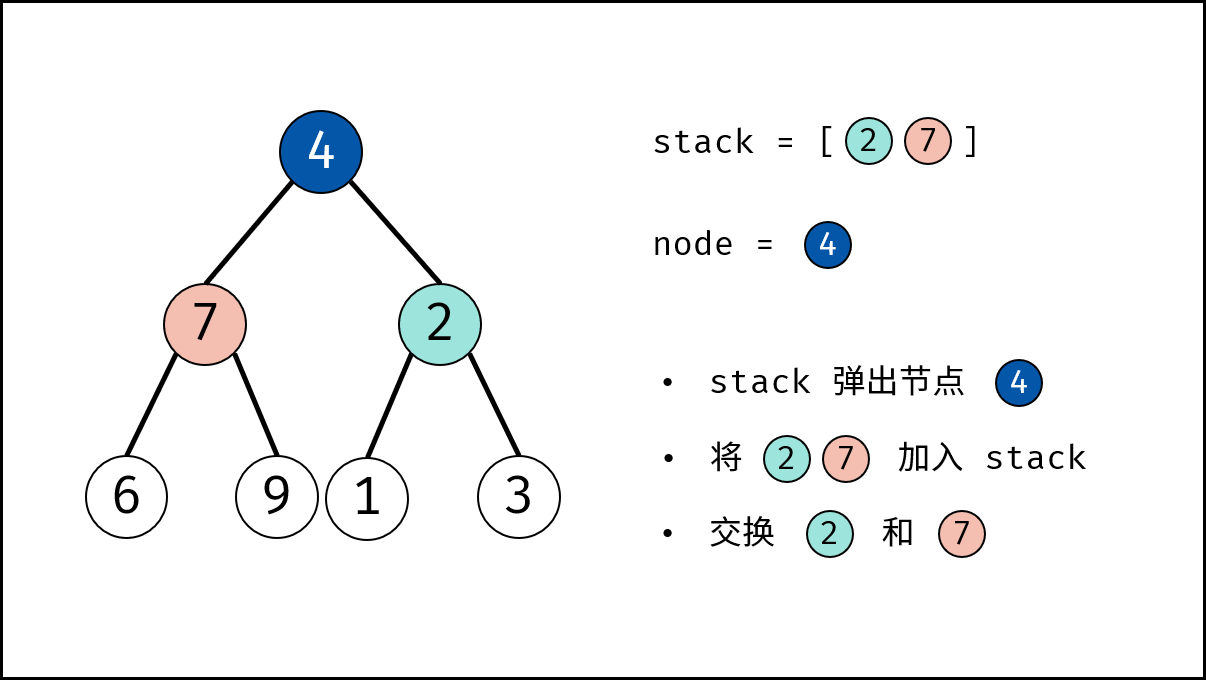
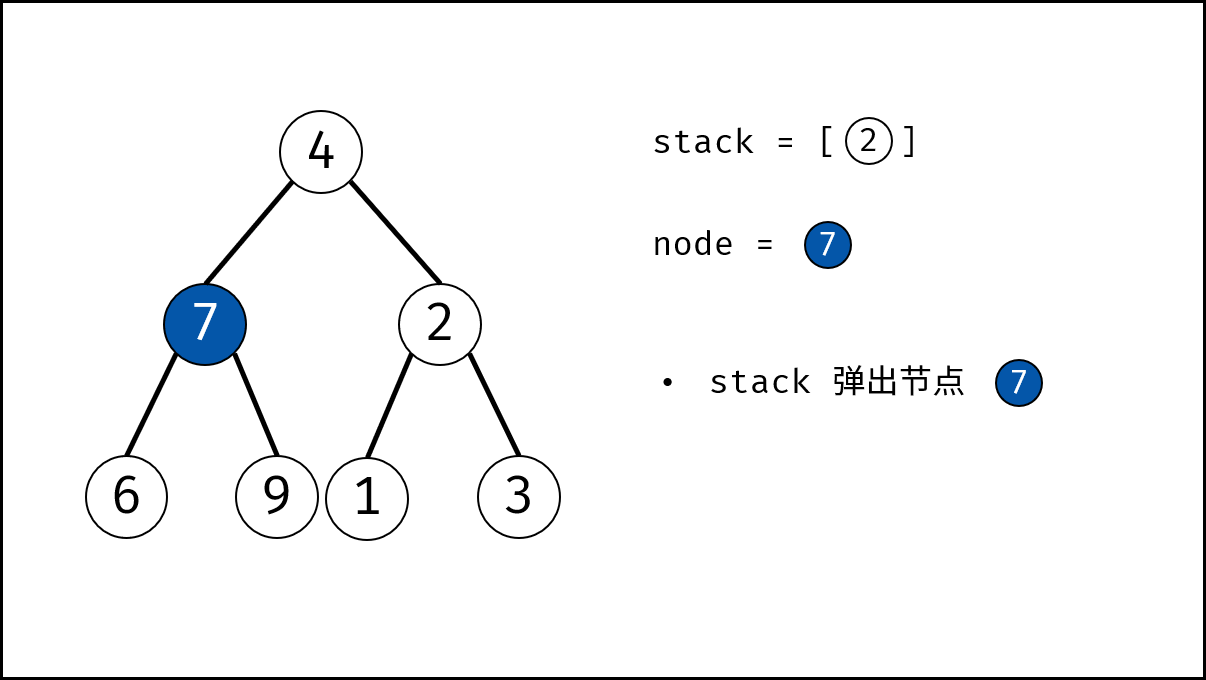
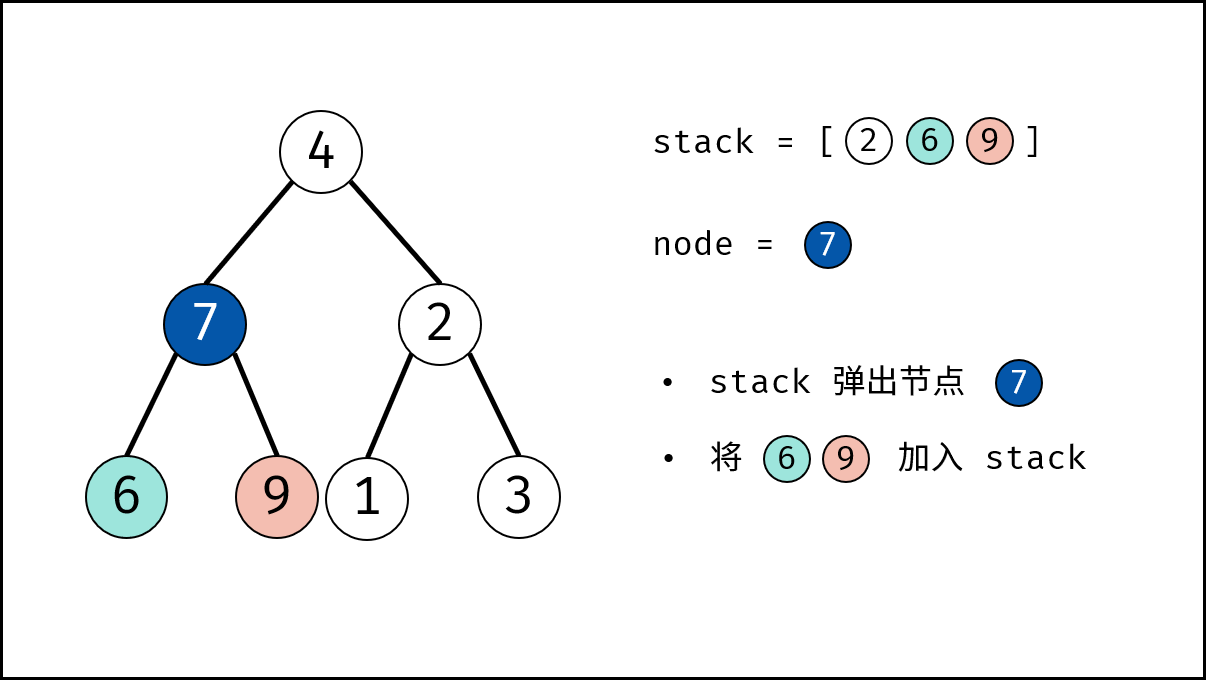
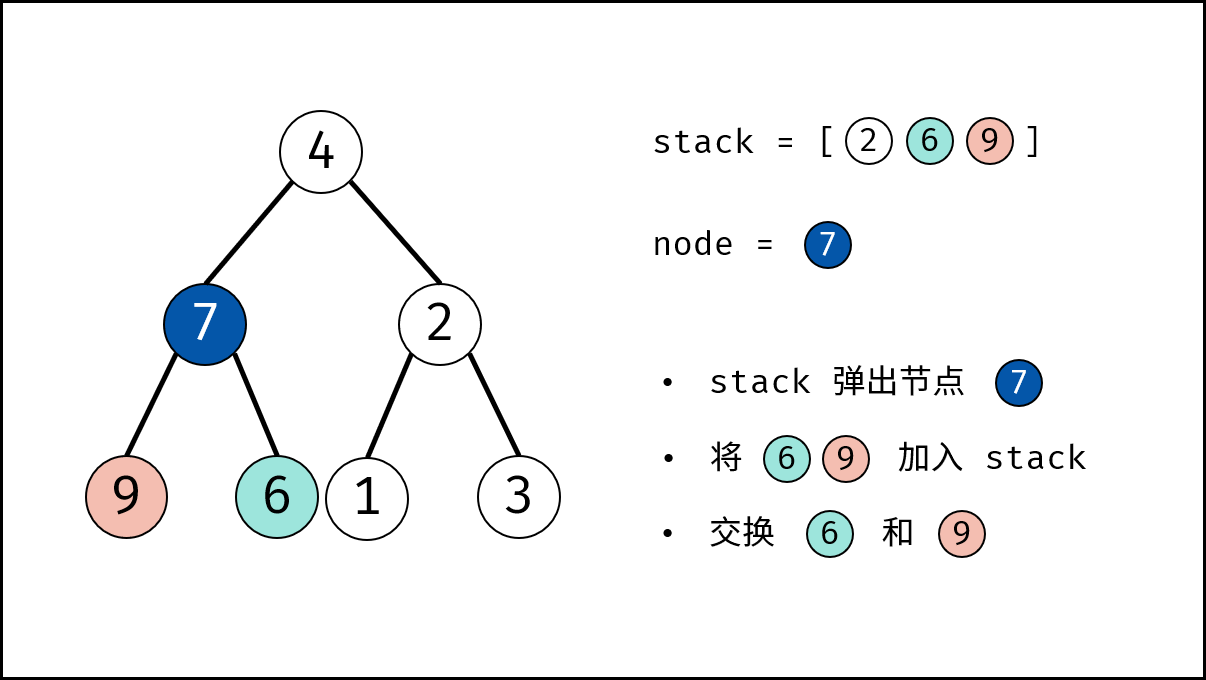
   1. 出栈： 记为 $node$ 。
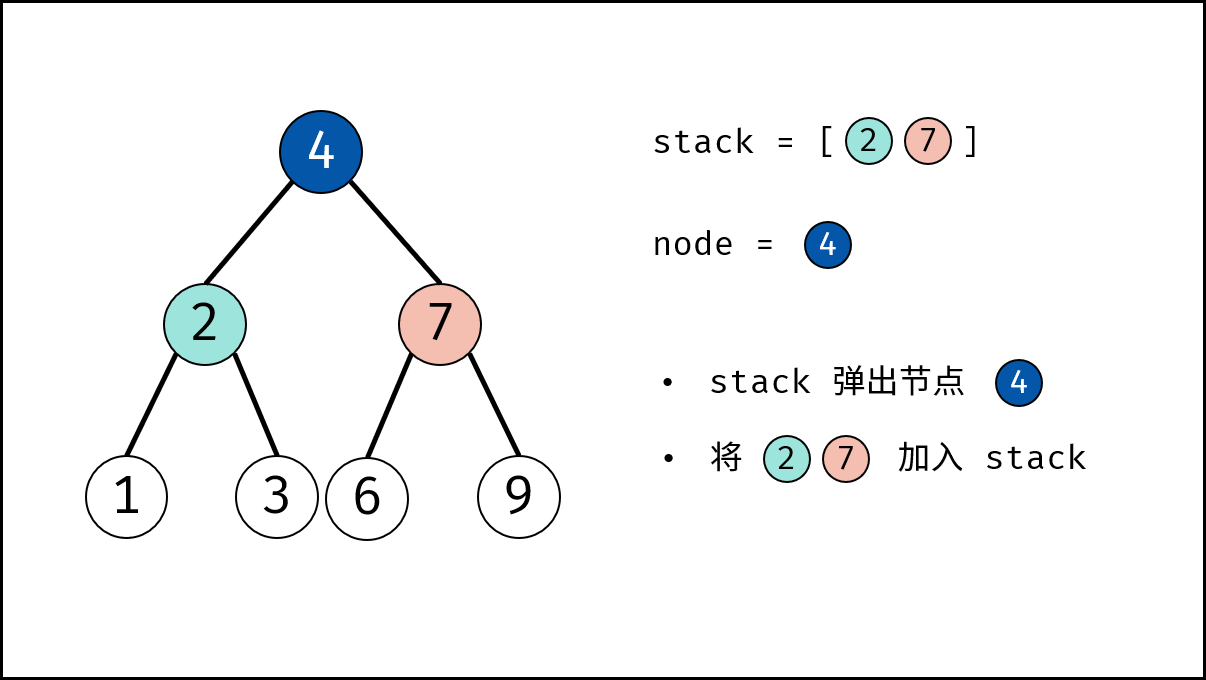
   2. 添加子节点： 将 $node$ 左和右子节点入栈。
   3. 交换： 交换 $node$ 的左 / 右子节点。
4. 返回值： 返回根节点 $root$ 。

<,,,,,,,,,,,,,,>

代码： ​

class Solution:
    def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        if not root: return
        stack = [root]
        while stack:
            node = stack.pop()
            if node.left: stack.append(node.left)
            if node.right: stack.append(node.right)
            node.left, node.right = node.right, node.left
        return root

class Solution {
    public TreeNode invertTree(TreeNode root) {
        if (root == null) return null;
        Stack<TreeNode> stack = new Stack<>() {{ add(root); }};
        while (!stack.isEmpty()) {
            TreeNode node = stack.pop();
            if (node.left != null) stack.add(node.left);
            if (node.right != null) stack.add(node.right);
            TreeNode tmp = node.left;
            node.left = node.right;
            node.right = tmp;
        }
        return root;
    }
}

class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if (root == nullptr) return nullptr;
        stack<TreeNode*> stack;
        stack.push(root);
        while (!stack.empty())
        {
            TreeNode* node = stack.top();
            stack.pop();
            if (node->left != nullptr) stack.push(node->left);
            if (node->right != nullptr) stack.push(node->right);
            TreeNode* tmp = node->left;
            node->left = node->right;
            node->right = tmp;
        }
        return root;
    }
};

复杂度分析： ​

• 时间复杂度 $O(N)$ ： 其中 $N$ 为二叉树的节点数量，建立二叉树镜像需要遍历树的所有节点，占用 $O(N)$ 时间。
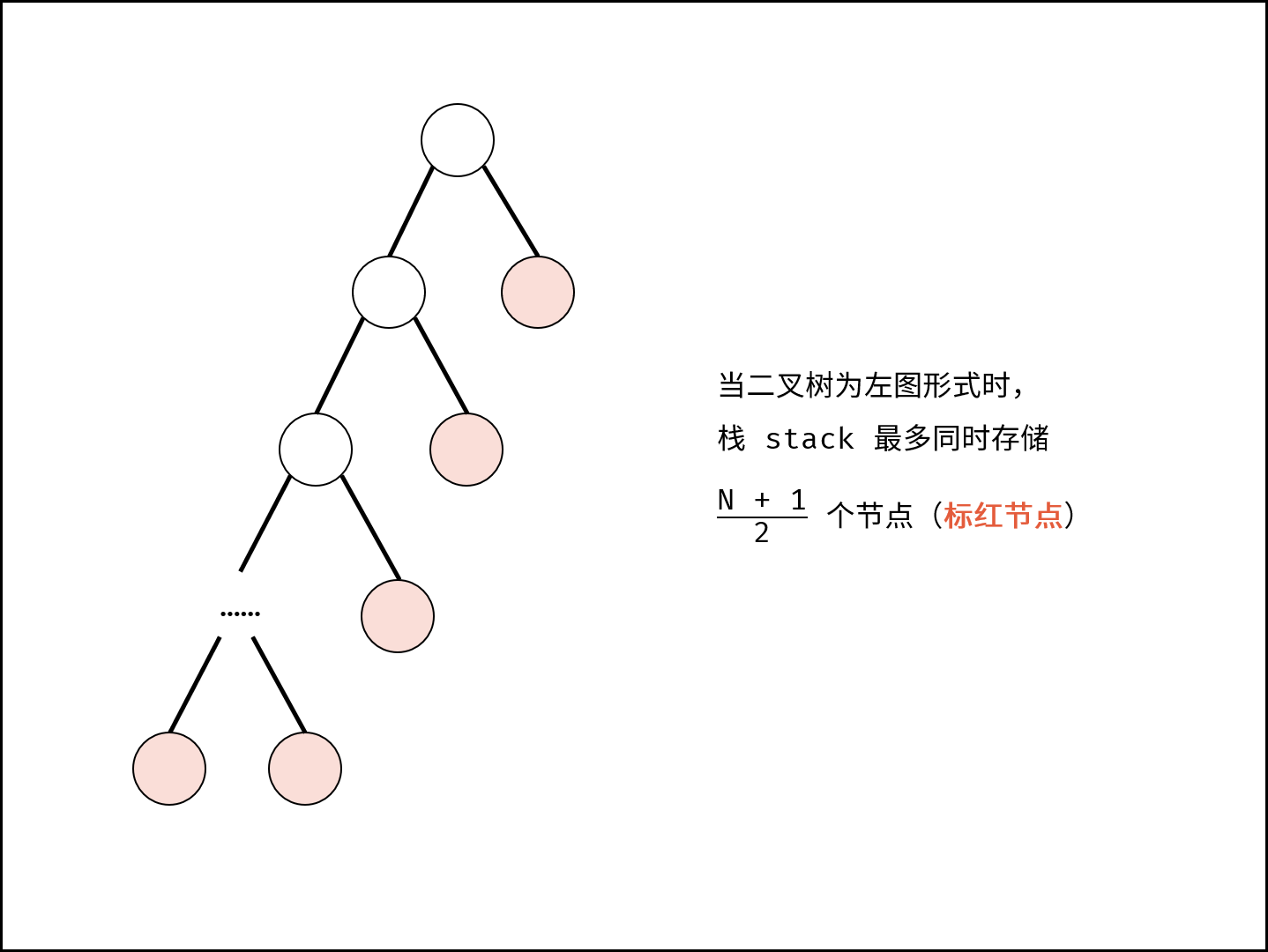
• 空间复杂度 $O(N)$ ： 如下图所示，最差情况下，栈 $stack$ 最多同时存储 $\frac{N + 1}{2}$ 个节点，占用 $O(N)$ 额外空间。