自律小屋 | 自律小屋

解题思路：

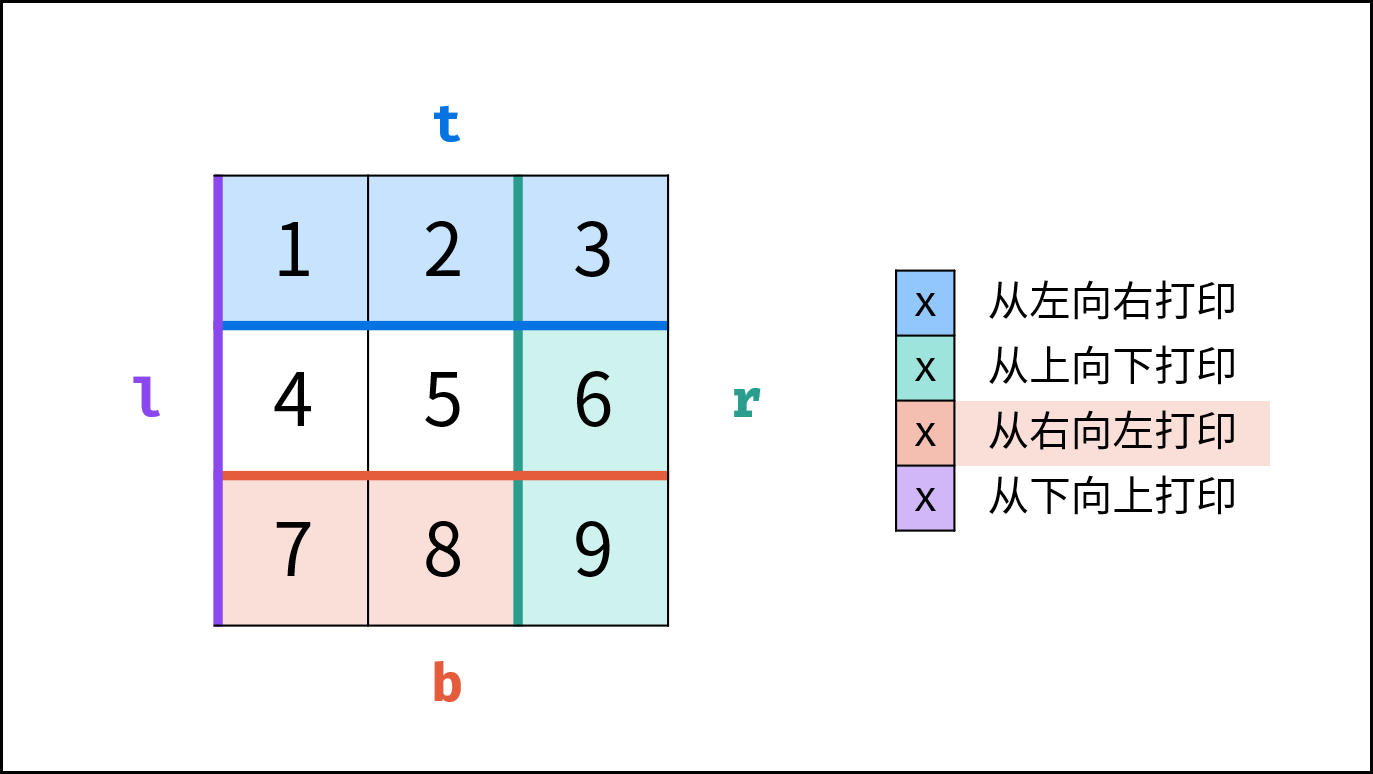
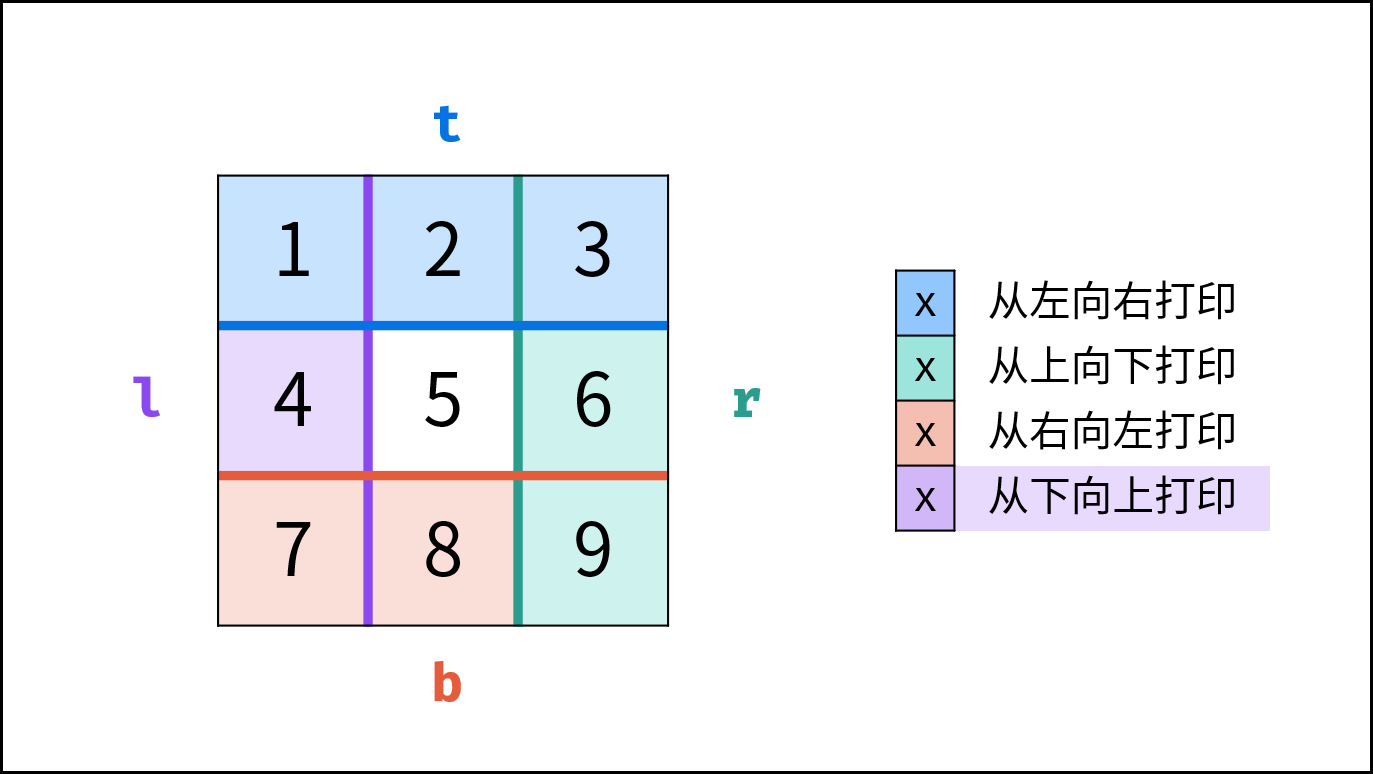
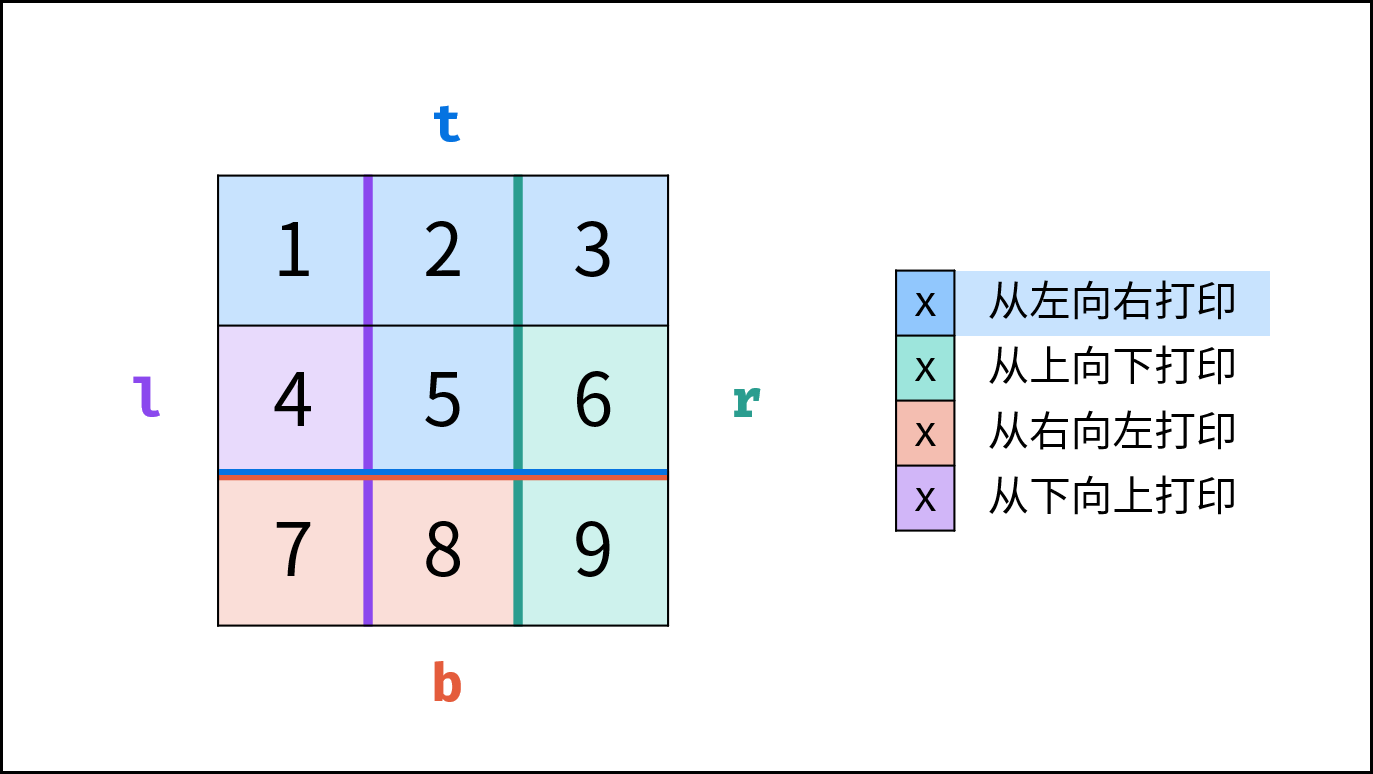
根据题目示例 matrix = [[1,2,3],[4,5,6],[7,8,9]] 的对应输出 [1,2,3,6,9,8,7,4,5] 可以发现，顺时针打印矩阵的顺序是 “从左向右、从上向下、从右向左、从下向上” 循环。

因此，考虑设定矩阵的 “左、上、右、下” 四个边界，模拟以上矩阵遍历顺序。

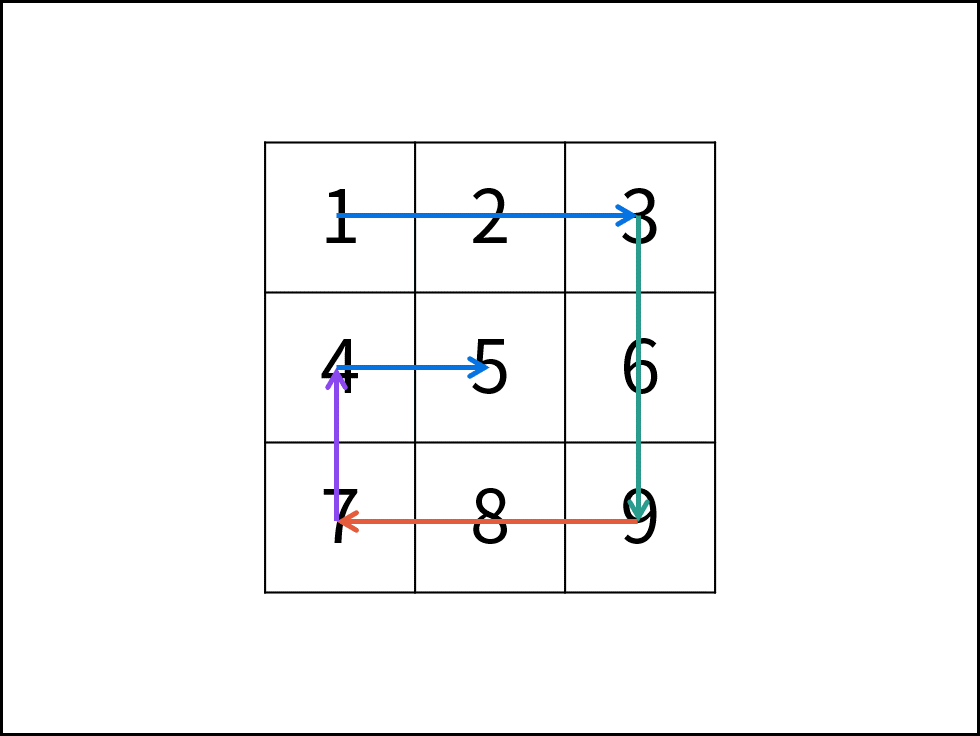
算法流程：

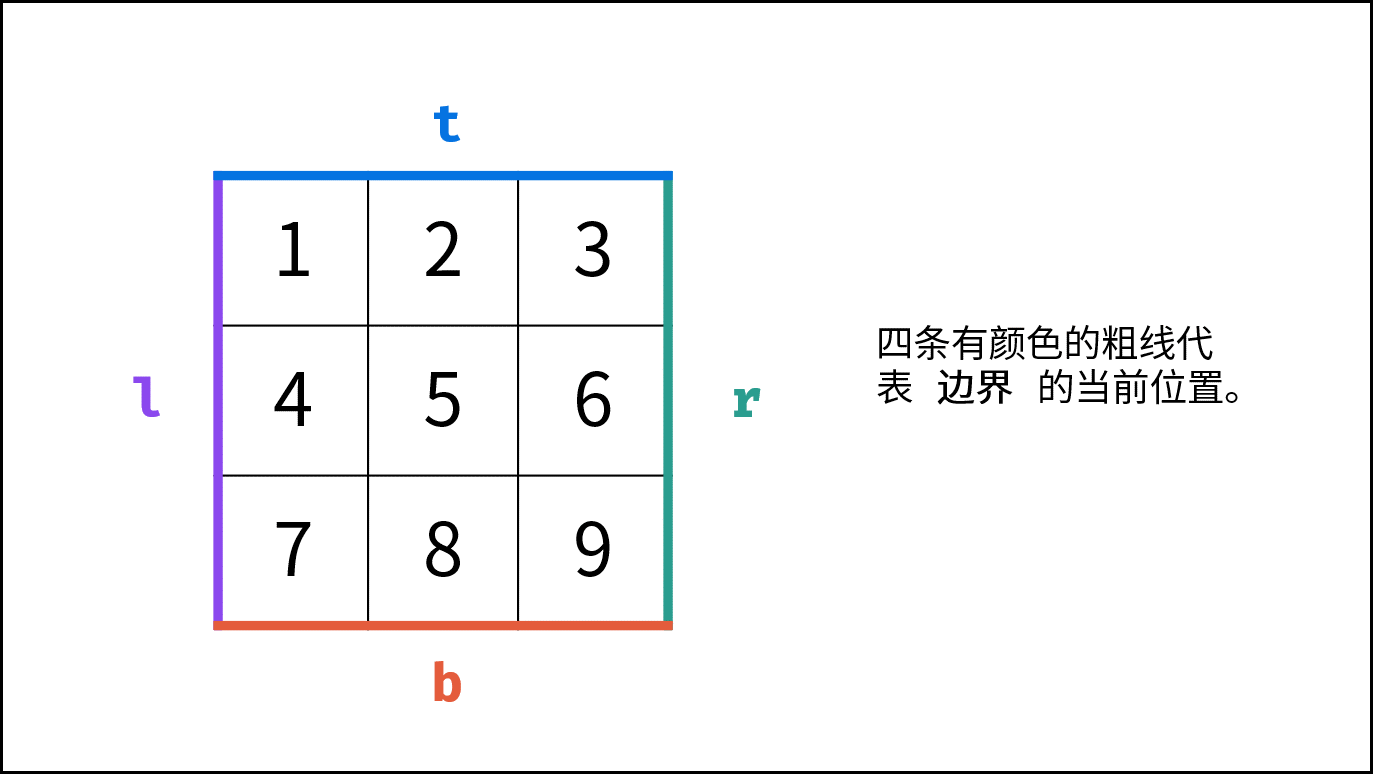
空值处理： 当 matrix 为空时，直接返回空列表 [] 即可。
初始化： 矩阵左、右、上、下四个边界 l , r , t , b ，用于打印的结果列表 res 。
循环打印： “从左向右、从上向下、从右向左、从下向上” 四个方向循环打印。
1. 根据边界打印，即将元素按顺序添加至列表 res 尾部。
2. 边界向内收缩 1 （代表已被打印）。
3. 判断边界是否相遇（是否打印完毕），若打印完毕则跳出。
返回值： 返回 res 即可。

打印方向	1. 根据边界打印	2. 边界向内收缩	3. 是否打印完毕
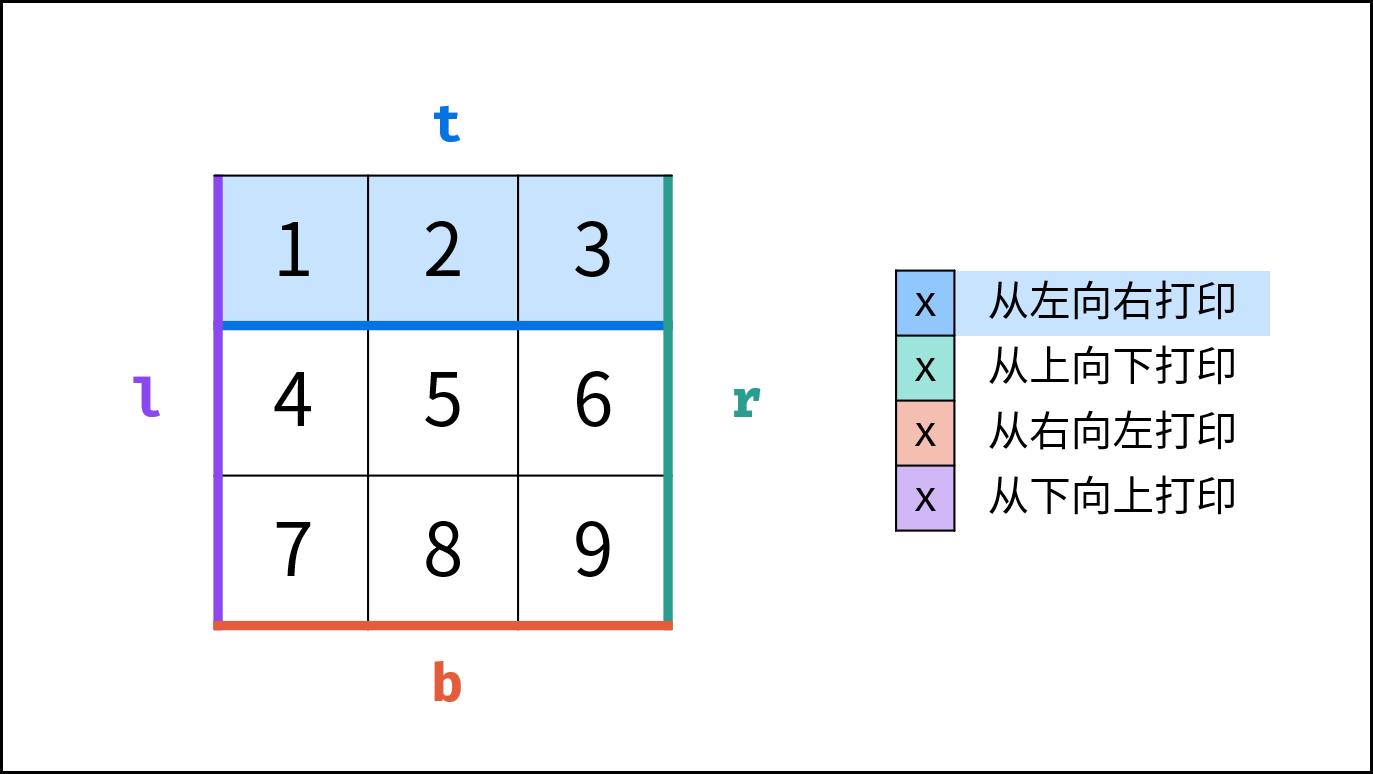
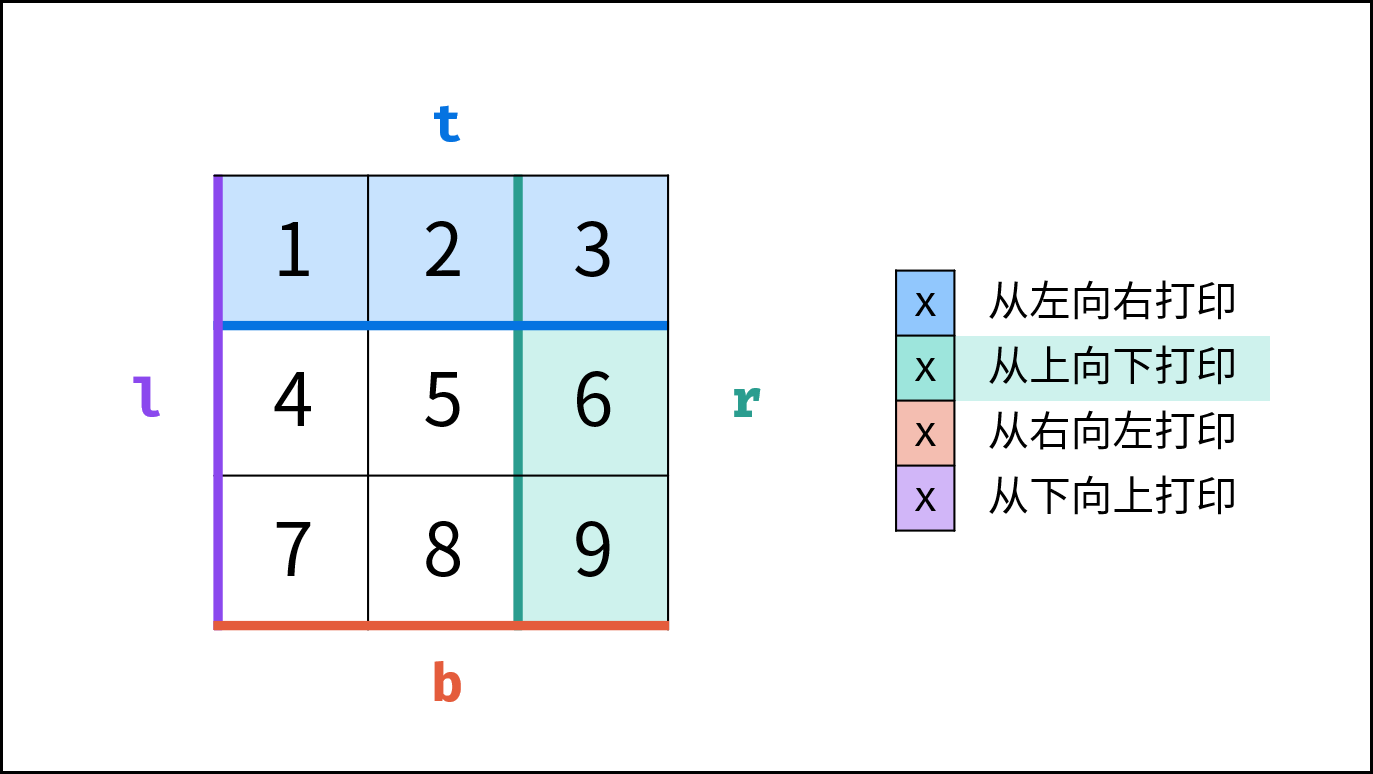
从左向右	左边界`l` ，右边界 `r`	上边界 `t` 加 $1$	是否 `t > b`
从上向下	上边界 `t` ，下边界`b`	右边界 `r` 减 $1$	是否 `l > r`
从右向左	右边界 `r` ，左边界`l`	下边界 `b` 减 $1$	是否 `t > b`
从下向上	下边界 `b` ，上边界`t`	左边界 `l` 加 $1$	是否 `l > r`

<,,,,,>

代码：

Java, C++ 代码利用了 ++ 操作的便利性，详情可见 ++i 和 i++ 的区别。

res[x++] 等价于先给 res[x] 赋值，再给 x 自增 $1$ 。
++t > b 等价于先给 t 自增 $1$ ，再判断 t > b 逻辑表达式。

TIPS：请注意区分数字 1 和字母 l 。

Python

class Solution:
    def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
        if not matrix: return []
        l, r, t, b, res = 0, len(matrix[0]) - 1, 0, len(matrix) - 1, []
        while True:
            for i in range(l, r + 1): res.append(matrix[t][i]) # left to right
            t += 1
            if t > b: break
            for i in range(t, b + 1): res.append(matrix[i][r]) # top to bottom
            r -= 1
            if l > r: break
            for i in range(r, l - 1, -1): res.append(matrix[b][i]) # right to left
            b -= 1
            if t > b: break
            for i in range(b, t - 1, -1): res.append(matrix[i][l]) # bottom to top
            l += 1
            if l > r: break
        return res

Java

class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        if (matrix.length == 0)
            return new ArrayList<Integer>();
        int l = 0, r = matrix[0].length - 1, t = 0, b = matrix.length - 1, x = 0;
        Integer[] res = new Integer[(r + 1) * (b + 1)];
        while (true) {
            for (int i = l; i <= r; i++) res[x++] = matrix[t][i]; // left to right
            if (++t > b) break;
            for (int i = t; i <= b; i++) res[x++] = matrix[i][r]; // top to bottom
            if (l > --r) break;
            for (int i = r; i >= l; i--) res[x++] = matrix[b][i]; // right to left
            if (t > --b) break;
            for (int i = b; i >= t; i--) res[x++] = matrix[i][l]; // bottom to top
            if (++l > r) break;
        }
        return Arrays.asList(res);
    }
}

C++

class Solution {
public:
    vector<int> spiralOrder(vector<vector<int>>& matrix) {
        if (matrix.empty()) return {};
        int l = 0, r = matrix[0].size() - 1, t = 0, b = matrix.size() - 1;
        vector<int> res;
        while (true) {
            for (int i = l; i <= r; i++) res.push_back(matrix[t][i]); // left to right
            if (++t > b) break;
            for (int i = t; i <= b; i++) res.push_back(matrix[i][r]); // top to bottom
            if (l > --r) break;
            for (int i = r; i >= l; i--) res.push_back(matrix[b][i]); // right to left
            if (t > --b) break;
            for (int i = b; i >= t; i--) res.push_back(matrix[i][l]); // bottom to top
            if (++l > r) break;
        }
        return res;
    }
};

复杂度分析：

时间复杂度 $O(MN)$ ： $M, N$ 分别为矩阵行数和列数。
空间复杂度 $O(1)$ ： 四个边界 l , r , t , b 使用常数大小的额外空间。

解题思路： ​

算法流程： ​

代码： ​

复杂度分析： ​

解题思路：

算法流程：

代码：

复杂度分析：