自律小屋

Appearance

当前页大纲

解题思路： ​

设窗口区间为 $[i, j]$ ，最大值为 $x_j$ 。当窗口向前移动一格，则区间变为 $[i+1,j+1]$ ，即添加了 $nums[j + 1]$ ，删除了 $nums[i]$ 。

若只向窗口 $[i, j]$ 右边添加数字 $nums[j + 1]$ ，则新窗口最大值可以 通过一次对比 使用 $O(1)$ 时间得到，即：

$$ x_{j+1} = \max(x_{j}, nums[j + 1]) $$

而由于删除的 $nums[i]$ 可能恰好是窗口内唯一的最大值 $x_j$ ，因此不能通过以上方法计算 $x_{j+1}$ ，而必须使用 $O(j-i)$ 时间， 遍历整个窗口区间 获取最大值，即：

$$ x_{j+1} = \max(nums(i+1), \cdots , num(j+1)) $$

根据以上分析，可得 暴力法 的时间复杂度为 $O((n-k+1)k) \approx O(nk)$ 。

  • 设数组 $nums$ 的长度为 $n$ ，则共有 $(n-k+1)$ 个窗口；
  • 获取每个窗口最大值需线性遍历，时间复杂度为 $O(k)$ 。

Picture1.png

本题难点： 如何在每次窗口滑动后，将 “获取窗口内最大值” 的时间复杂度从 $O(k)$ 降低至 $O(1)$ 。

回忆 最小栈 ，其使用 单调栈 实现了随意入栈、出栈情况下的 $O(1)$ 时间获取 “栈内最小值” 。本题同理，不同点在于 “出栈操作” 删除的是 “列表尾部元素” ，而 “窗口滑动” 删除的是 “列表首部元素” 。

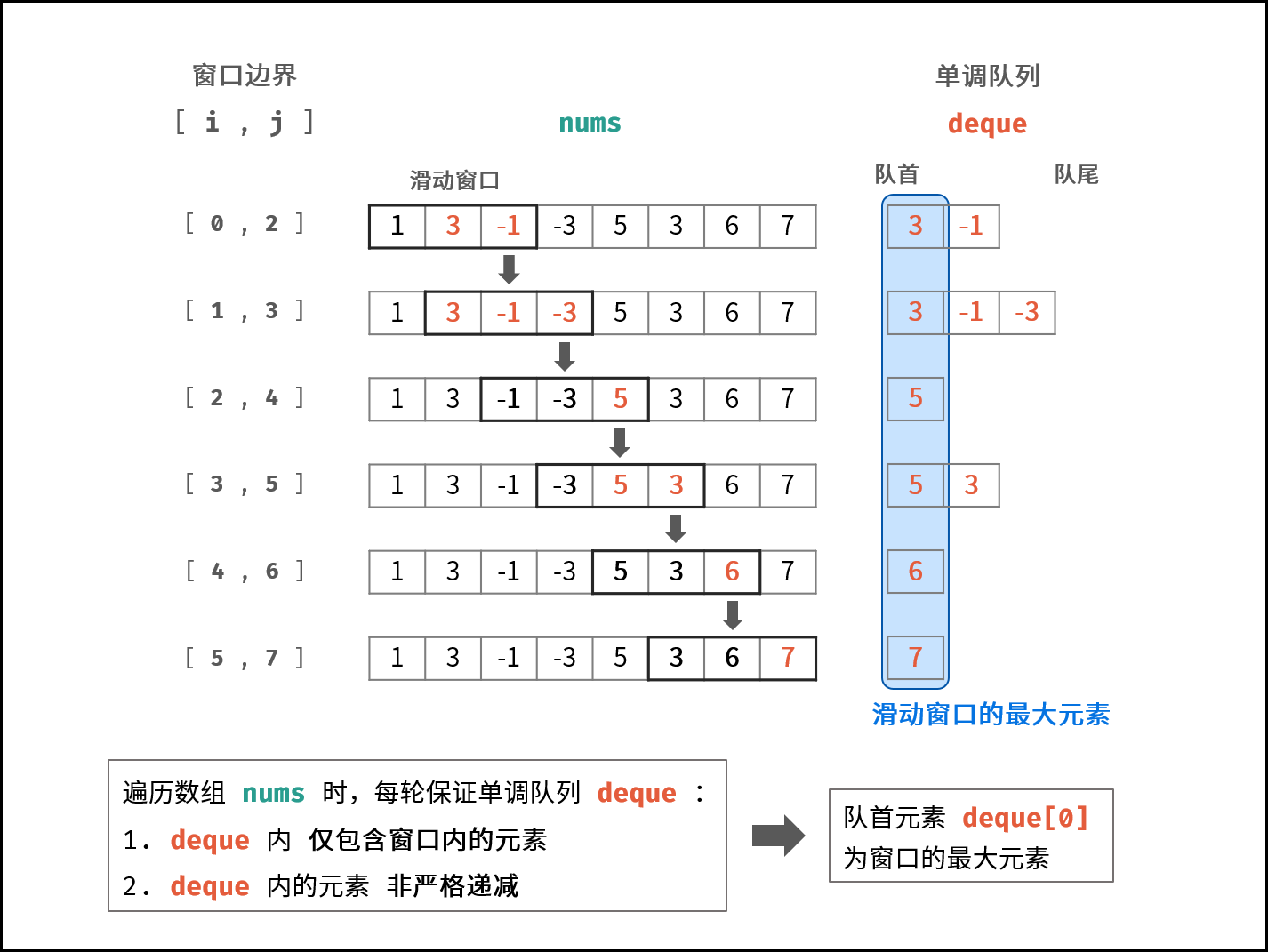
窗口对应的数据结构为 双端队列 ，本题使用 单调队列 即可解决以上问题。遍历数组时，每轮保证单调队列 $deque$ ：

  1. $deque$ 内 仅包含窗口内的元素 $\Rightarrow$ 每轮窗口滑动移除了元素 $nums[i - 1]$ ，需将 $deque$ 内的对应元素一起删除。
  2. $deque$ 内的元素 非严格递减 $\Rightarrow$ 每轮窗口滑动添加了元素 $nums[j + 1]$ ，需将 $deque$ 内所有 $< nums[j + 1]$ 的元素删除。

算法流程： ​

  1. 初始化： 双端队列 $deque$ ，结果列表 $res$ ，数组长度 $n$ ；
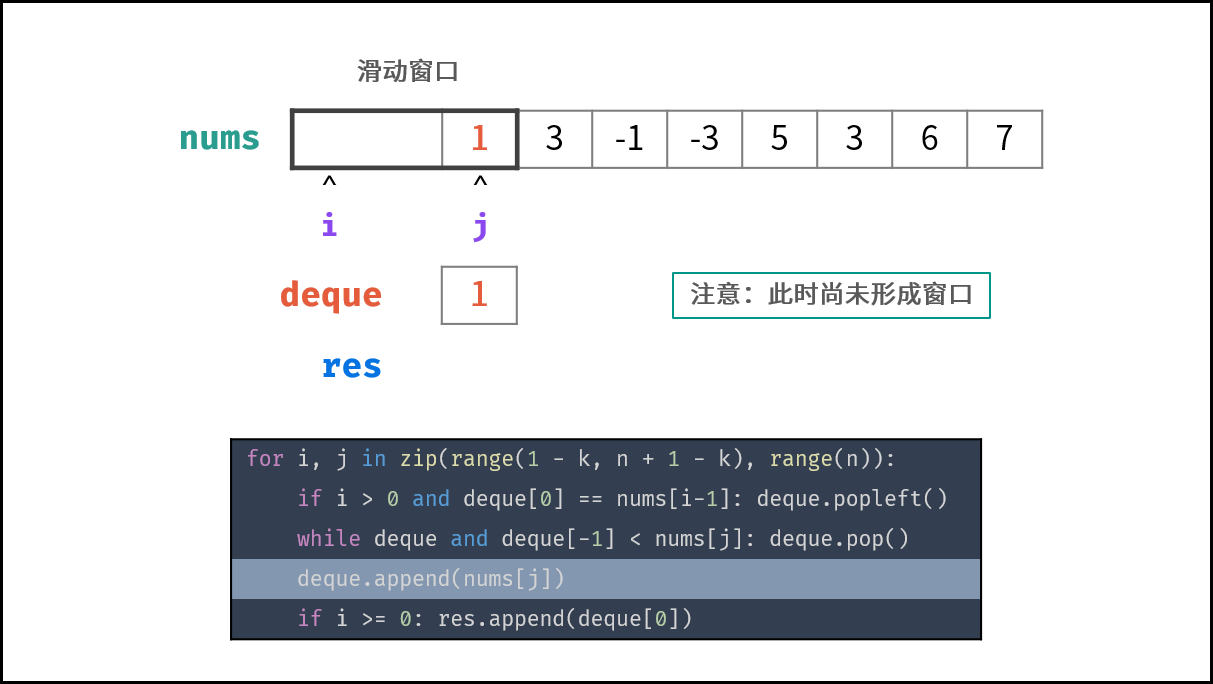
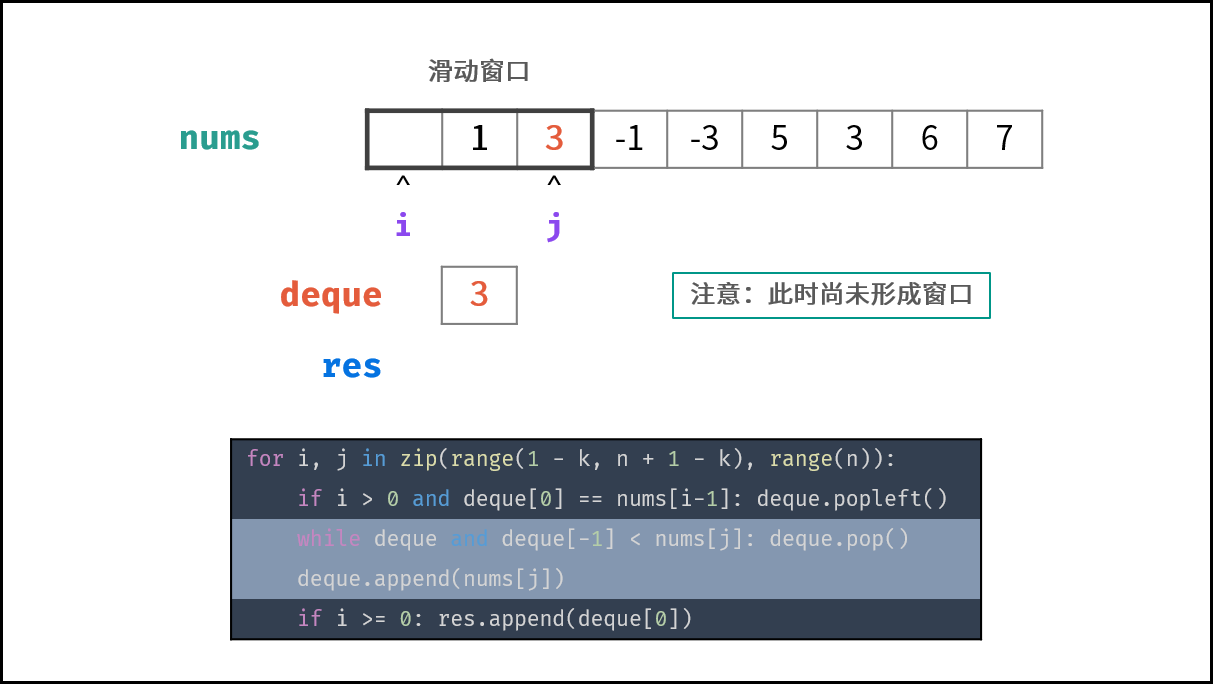
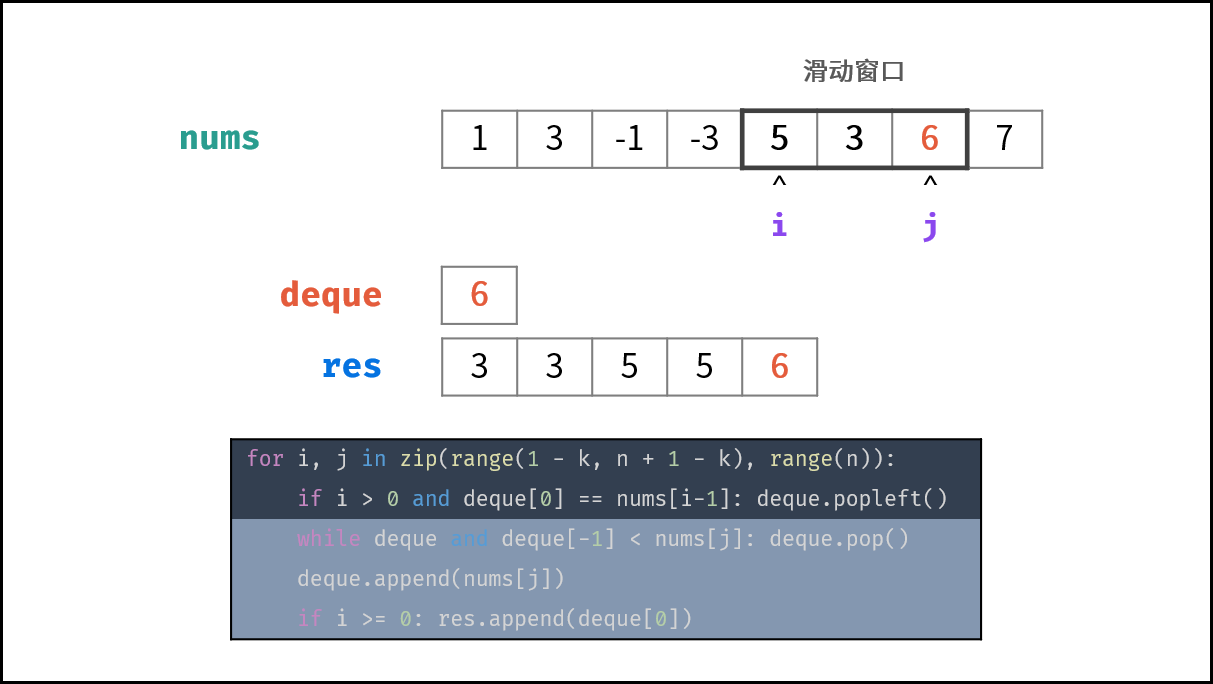
  2. 滑动窗口： 左边界范围 $i \in [1 - k, n - k]$ ，右边界范围 $j \in [0, n - 1]$ ；
    1. 若 $i > 0$ 且 队首元素 $deque[0]$ $=$ 被删除元素 $nums[i - 1]$ ：则队首元素出队；
    2. 删除 $deque$ 内所有 $< nums[j]$ 的元素，以保持 $deque$ 递减；
    3. 将 $nums[j]$ 添加至 $deque$ 尾部；
    4. 若已形成窗口（即 $i \geq 0$ ）：将窗口最大值（即队首元素 $deque[0]$ ）添加至列表 $res$ ；
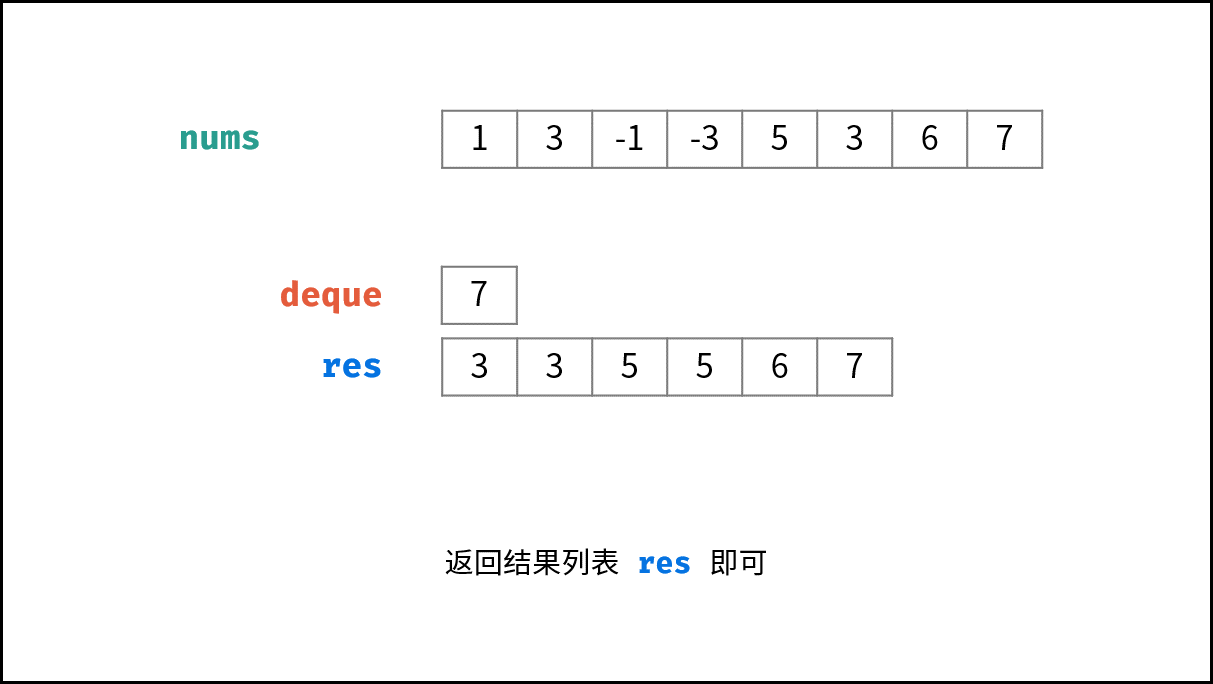
  3. 返回值： 返回结果列表 $res$ ；

<Picture2.png,Picture3.png,Picture4.png,Picture5.png,Picture6.png,Picture7.png,Picture8.png,Picture9.png,Picture10.png,Picture11.png>

代码： ​

Python 通过 zip(range(), range()) 可实现滑动窗口的左右边界 i, j 同时遍历。

Python
class Solution:
    def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
        deque = collections.deque()
        res, n = [], len(nums)
        for i, j in zip(range(1 - k, n + 1 - k), range(n)):
            # 删除 deque 中对应的 nums[i-1]
            if i > 0 and deque[0] == nums[i - 1]:
                deque.popleft()
            # 保持 deque 递减
            while deque and deque[-1] < nums[j]:
                deque.pop()
            deque.append(nums[j])
            # 记录窗口最大值
            if i >= 0:
                res.append(deque[0])
        return res
Java
class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        if(nums.length == 0 || k == 0) return new int[0];
        Deque<Integer> deque = new LinkedList<>();
        int[] res = new int[nums.length - k + 1];
        for(int j = 0, i = 1 - k; j < nums.length; i++, j++) {
            // 删除 deque 中对应的 nums[i-1]
            if(i > 0 && deque.peekFirst() == nums[i - 1])
                deque.removeFirst();
            // 保持 deque 递减
            while(!deque.isEmpty() && deque.peekLast() < nums[j])
                deque.removeLast();
            deque.addLast(nums[j]);
            // 记录窗口最大值
            if(i >= 0)
                res[i] = deque.peekFirst();
        }
        return res;
    }
}
C++
class Solution {
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        if(nums.size() == 0 || k == 0) return {};
        deque<int> deque;
        vector<int> res(nums.size() - k + 1);
        for(int j = 0, i = 1 - k; j < nums.size(); i++, j++) {
            // 删除 deque 中对应的 nums[i-1]
            if(i > 0 && deque.front() == nums[i - 1])
                deque.pop_front();
            // 保持 deque 递减
            while(!deque.empty() && deque.back() < nums[j])
                deque.pop_back();
            deque.push_back(nums[j]);
            // 记录窗口最大值
            if(i >= 0)
                res[i] = deque.front();
        }
        return res;
    }
    }
};

可以将 “未形成窗口” 和 “形成窗口后” 两个阶段拆分到两个循环里实现。代码虽变长，但减少了冗余的判断操作。

Python
class Solution:
    def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
        if not nums or k == 0: return []
        deque = collections.deque()
        # 未形成窗口
        for i in range(k):
            while deque and deque[-1] < nums[i]:
                deque.pop()
            deque.append(nums[i])
        res = [deque[0]]
        # 形成窗口后
        for i in range(k, len(nums)):
            if deque[0] == nums[i - k]:
                deque.popleft()
            while deque and deque[-1] < nums[i]:
                deque.pop()
            deque.append(nums[i])
            res.append(deque[0])
        return res
Java
class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        if(nums.length == 0 || k == 0) return new int[0];
        Deque<Integer> deque = new LinkedList<>();
        int[] res = new int[nums.length - k + 1];
        // 未形成窗口
        for(int i = 0; i < k; i++) {
            while(!deque.isEmpty() && deque.peekLast() < nums[i])
                deque.removeLast();
            deque.addLast(nums[i]);
        }
        res[0] = deque.peekFirst();
        // 形成窗口后
        for(int i = k; i < nums.length; i++) {
            if(deque.peekFirst() == nums[i - k])
                deque.removeFirst();
            while(!deque.isEmpty() && deque.peekLast() < nums[i])
                deque.removeLast();
            deque.addLast(nums[i]);
            res[i - k + 1] = deque.peekFirst();
        }
        return res;
    }
}
C++
class Solution {
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        if(nums.size() == 0 || k == 0) return {};
        deque<int> deque;
        vector<int> res(nums.size() - k + 1);
        // 未形成窗口
        for(int i = 0; i < k; i++) {
            while(!deque.empty() && deque.back() < nums[i])
                deque.pop_back();
            deque.push_back(nums[i]);
        }
        res[0] = deque.front();
        // 形成窗口后
        for(int i = k; i < nums.size(); i++) {
            if(deque.front() == nums[i - k])
                deque.pop_front();
            while(!deque.empty() && deque.back() < nums[i])
                deque.pop_back();
            deque.push_back(nums[i]);
            res[i - k + 1] = deque.front();
        }
        return res;
    }
};

复杂度分析： ​

  • 时间复杂度 $O(n)$ ： 其中 $n$ 为数组 $nums$ 长度；线性遍历 $nums$ 占用 $O(n)$ ；每个元素最多仅入队和出队一次，因此单调队列 $deque$ 占用 $O(2n)$ 。
  • 空间复杂度 $O(k)$ ： 双端队列 $deque$ 中最多同时存储 $k$ 个元素（即窗口大小）。

MIT License.

Copyright © 2024 自律小屋