解题思路:
如下图所示,寻找旋转数组的最小元素即为寻找 右排序数组 的首个元素 $nums[x]$ ,称 $x$ 为 旋转点 。
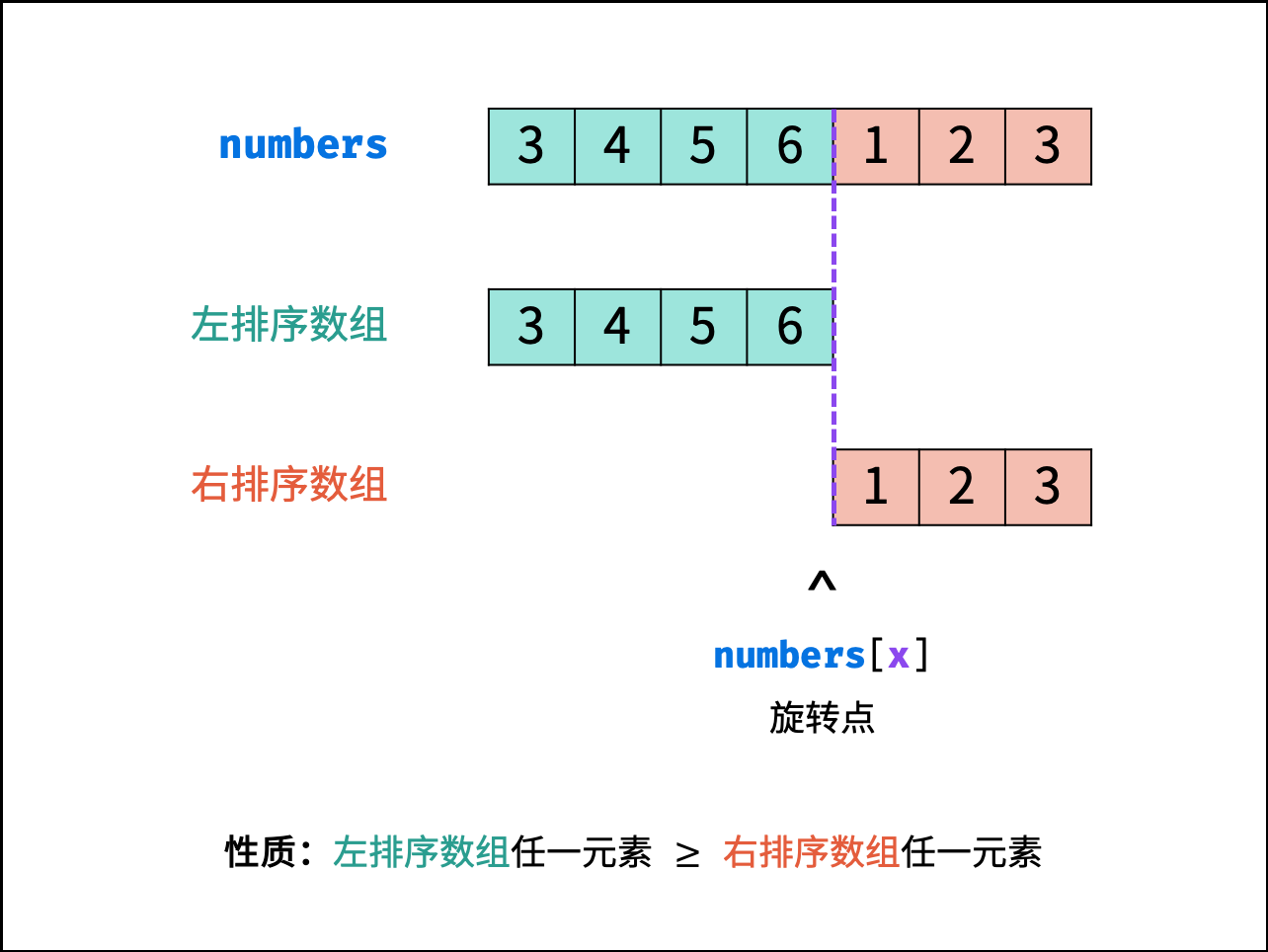
排序数组的查找问题首先考虑使用 二分法 解决,其可将 遍历法 的 线性级别 时间复杂度降低至 对数级别 。
算法流程:
- 初始化: 声明 $i$, $j$ 双指针分别指向 $nums$ 数组左右两端。
- 循环二分: 设 $m = (i + j) / 2$ 为每次二分的中点( "
/" 代表向下取整除法,因此恒有 $i \leq m < j$ ),可分为以下三种情况:- 当 $nums[m] > nums[j]$ 时: $m$ 一定在 左排序数组 中,即旋转点 $x$ 一定在 $[m + 1, j]$ 闭区间内,因此执行 $i = m + 1$。
- 当 $nums[m] < nums[j]$ 时: $m$ 一定在 右排序数组 中,即旋转点 $x$ 一定在$[i, m]$ 闭区间内,因此执行 $j = m$。
- 当 $nums[m] = nums[j]$ 时: 无法判断 $m$ 在哪个排序数组中,即无法判断旋转点 $x$ 在 $[i, m]$ 还是 $[m + 1, j]$ 区间中。解决方案: 执行 $j = j - 1$ 缩小判断范围,分析见下文。
- 返回值: 当 $i = j$ 时跳出二分循环,并返回 旋转点的值 $nums[i]$ 即可。
正确性证明:
当 $nums[m] = nums[j]$ 时,无法判定 $m$ 在左(右)排序数组,自然也无法通过二分法安全地缩小区间,因为其会导致旋转点 $x$ 不在区间 $[i, j]$ 内。举例如下:
设以下两个旋转点值为 $0$ 的示例数组,则当 $i = 0$, $j = 4$ 时 $m = 2$ ,两示例结果不同。 示例一 $[1, 0, 1, 1, 1]$ :旋转点 $x = 1$ ,因此 $m = 2$ 在 右排序数组 中。 示例二 $[1, 1, 1, 0, 1]$ :旋转点 $x = 3$ ,因此 $m = 2$ 在 左排序数组 中。
而证明 $j = j - 1$ 正确(缩小区间安全性),需分为两种情况:
当 $x < j$ 时: 易得执行 $j = j - 1$ 后,旋转点 $x$ 仍在区间 $[i, j]$ 内。
当 $x = j$ 时: 执行 $j = j - 1$ 后越过(丢失)了旋转点 $x$ ,但最终返回的元素值 $nums[i]$ 仍等于旋转点值 $nums[x]$ 。
- 由于 $x = j$ ,因此 $nums[x] = nums[j] = nums[m] \leq number[i]$ ;
- 又由于 $i \leq m <j$ 恒成立,因此有 $m < x$ ,即此时 $m$ 一定在左排序数组中,因此 $nums[m] \geq nums[i]$ ;
综合 1. , 2. ,可推出 $nums[i] = nums[m]$ ,且区间 $[i, m]$ 内所有元素值相等,即有:
$$ nums[i] = nums[i+1] = \cdots = nums[m] = nums[x] $$
此时,执行 $j = j - 1$ 后虽然丢失了旋转点 $x$ ,但之后区间 $[i, j]$ 只包含左排序数组,二分下去返回的一定是本轮的 $nums[i]$ ,而其与 $nums[x]$ 相等。
综上所述,此方法可以保证返回值 $nums[i]$ 等于旋转点值 $nums[x]$ ,但在少数特例下 $i \ne x$ ;而本题目只要求返回 “旋转点的值” ,因此本方法正确。
补充思考: 为什么本题二分法不用 $nums[m]$ 和 $nums[i]$ 作比较?
二分目的是判断 $m$ 在哪个排序数组中,从而缩小区间。而在 $nums[m] > nums[i]$情况下,无法判断 $m$ 在哪个排序数组中。本质上是由于 $j$ 初始值肯定在右排序数组中; $i$ 初始值无法确定在哪个排序数组中。举例如下:
对于以下两示例,当 $i = 0, j = 4, m = 2$ 时,有
nums[m] > nums[i],而结果不同。 $[1, 2, 3, 4 ,5]$ 旋转点 $x = 0$ : $m$ 在右排序数组(此示例只有右排序数组)。 $[3, 4, 5, 1 ,2]$ 旋转点 $x = 3$ : $m$ 在左排序数组。
< ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, >
>
代码:
class Solution:
def findMin(self, nums: [int]) -> int:
i, j = 0, len(nums) - 1
while i < j:
m = (i + j) // 2
if nums[m] > nums[j]: i = m + 1
elif nums[m] < nums[j]: j = m
else: j -= 1
return nums[i]class Solution {
public int findMin(int[] nums) {
int i = 0, j = nums.length - 1;
while (i < j) {
int m = (i + j) / 2;
if (nums[m] > nums[j]) i = m + 1;
else if (nums[m] < nums[j]) j = m;
else j--;
}
return nums[i];
}
}class Solution {
public:
int findMin(vector<int>& nums) {
int i = 0, j = nums.size() - 1;
while (i < j) {
int m = (i + j) / 2;
if (nums[m] > nums[j]) i = m + 1;
else if (nums[m] < nums[j]) j = m;
else j--;
}
return nums[i];
}
};实际上,当出现 $nums[m] = nums[j]$ 时,一定有区间 $[i, m]$ 内所有元素相等 或 区间 $[m, j]$ 内所有元素相等(或两者皆满足)。对于寻找此类数组的最小值问题,可直接放弃二分查找,而使用线性查找替代。
class Solution:
def findMin(self, nums: [int]) -> int:
i, j = 0, len(nums) - 1
while i < j:
m = (i + j) // 2
if nums[m] > nums[j]: i = m + 1
elif nums[m] < nums[j]: j = m
else: return min(nums[i:j])
return nums[i]class Solution {
public int findMin(int[] nums) {
int i = 0, j = nums.length - 1;
while (i < j) {
int m = (i + j) / 2;
if (nums[m] > nums[j]) i = m + 1;
else if (nums[m] < nums[j]) j = m;
else {
int x = i;
for(int k = i + 1; k < j; k++) {
if(nums[k] < nums[x]) x = k;
}
return nums[x];
}
}
return nums[i];
}
}class Solution {
public:
int findMin(vector<int>& nums) {
int i = 0, j = nums.size() - 1;
while (i < j) {
int m = (i + j) / 2;
if (nums[m] > nums[j]) i = m + 1;
else if (nums[m] < nums[j]) j = m;
else {
int x = i;
for(int k = i + 1; k < j; k++) {
if(nums[k] < nums[x]) x = k;
}
return nums[x];
}
}
return nums[i];
}
};复杂度分析:
- 时间复杂度 $O(\log_2 N)$ : 在特例情况下(例如 $[1, 1, 1, 1]$),会退化到 $O(N)$。
- 空间复杂度 $O(1)$ : $i$ , $j$ , $m$ 变量使用常数大小的额外空间。