解题思路： ​

斐波那契数列的定义是 $f(n + 1) = f(n) + f(n - 1)$ ，生成第 $n$ 项的做法有以下几种：

1. 暴力搜索：
   • 原理： 把 $f(n)$ 问题的计算拆分成 $f(n-1)$ 和 $f(n-2)$ 两个子问题的计算，并递归，以 $f(0)$ 和 $f(1)$ 为终止条件。
   • 缺点： 大量重复的递归计算，例如 $f(n)$ 和 $f(n - 1)$ 两者向下递归需要 各自计算 $f(n - 2)$ 的值。
2. 记忆化递归：
   • 原理： 在递归法的基础上，新建一个长度为 $n$ 的数组，用于在递归时存储 $f(0)$ 至 $f(n)$ 的数字值，重复遇到某数字则直接从数组取用，避免了重复的递归计算。
   • 缺点： 记忆化存储需要使用 $O(N)$ 的额外空间。
3. 动态规划：
   • 原理： 以斐波那契数列性质 $f(n + 1) = f(n) + f(n - 1)$ 为转移方程。
   • 从计算效率、空间复杂度上看，动态规划是本题的最佳解法。

下图帮助理解暴力搜索中的“重叠子问题”概念。

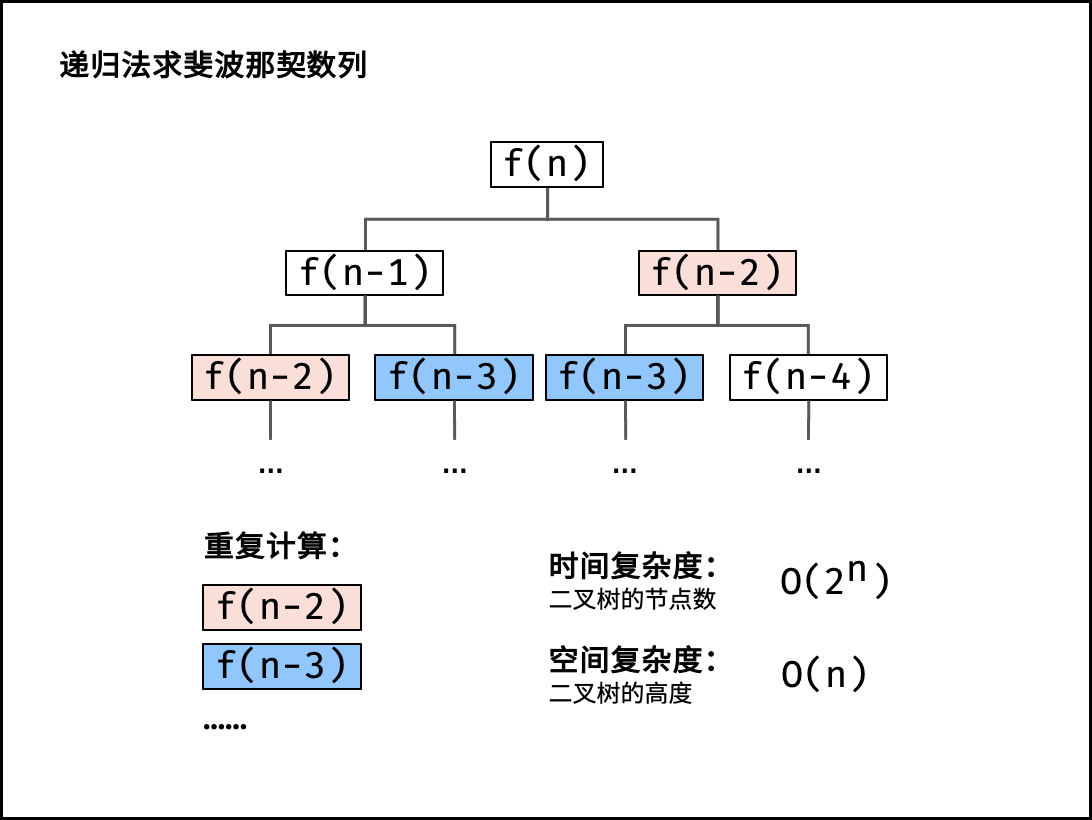
动态规划解析： ​

• 状态定义： 设 $dp$ 为一维数组，其中 $dp[i]$ 的值代表 斐波那契数列第 $i$ 个数字 。
• 转移方程： $dp[i + 1] = dp[i] + dp[i - 1]$ ，即对应数列定义 $f(n + 1) = f(n) + f(n - 1)$ 。
• 初始状态： $dp[0] = 0$, $dp[1] = 1$ ，即初始化前两个数字。
• 返回值： $dp[n]$ ，即斐波那契数列的第 $n$ 个数字。

状态压缩： ​

若新建长度为 $n$ 的 $dp$ 列表，则空间复杂度为 $O(N)$ 。

• 由于 $dp$ 列表第 $i$ 项只与第 $i-1$ 和第 $i-2$ 项有关，因此只需要初始化三个整形变量 sum, a, b ，利用辅助变量 $sum$ 使 $a, b$ 两数字交替前进即可 （具体实现见代码） 。
• 节省了 $dp$ 列表空间，因此空间复杂度降至 $O(1)$ 。

代码： ​

class Solution:
    def fib(self, n: int) -> int:
        a, b = 0, 1
        for _ in range(n):
            a, b = b, a + b
        return a

class Solution {
    public int fib(int n) {
        int a = 0, b = 1, sum;
        for(int i = 0; i < n; i++){
            sum = a + b;
            a = b;
            b = sum;
        }
        return a;
    }
}

class Solution {
public:
    int fib(int n) {
        int a = 0, b = 1, sum;
        for(int i = 0; i < n; i++){
            sum = a + b;
            a = b;
            b = sum;
        }
        return a;
    }
};

复杂度分析： ​

• 时间复杂度 $O(n)$ ： 计算 $f(n)$ 需循环 $n$ 次，每轮循环内计算操作使用 $O(1)$ 。
• 空间复杂度 $O(1)$ ： 几个标志变量使用常数大小的额外空间。