自律小屋 | 自律小屋

解题思路

根据题目描述 “错误的版本之后的所有版本都是错的” ，说明给定的版本正确性列表是「有序的」，即以某个版本为分界点，左边（右边）都是正确（错误）版本。因此，考虑使用「二分查找」来查找首个错误版本。

本文使用与 704. 二分查找相同的写法，二分查找缩窄区间的含义请参考代码注释。

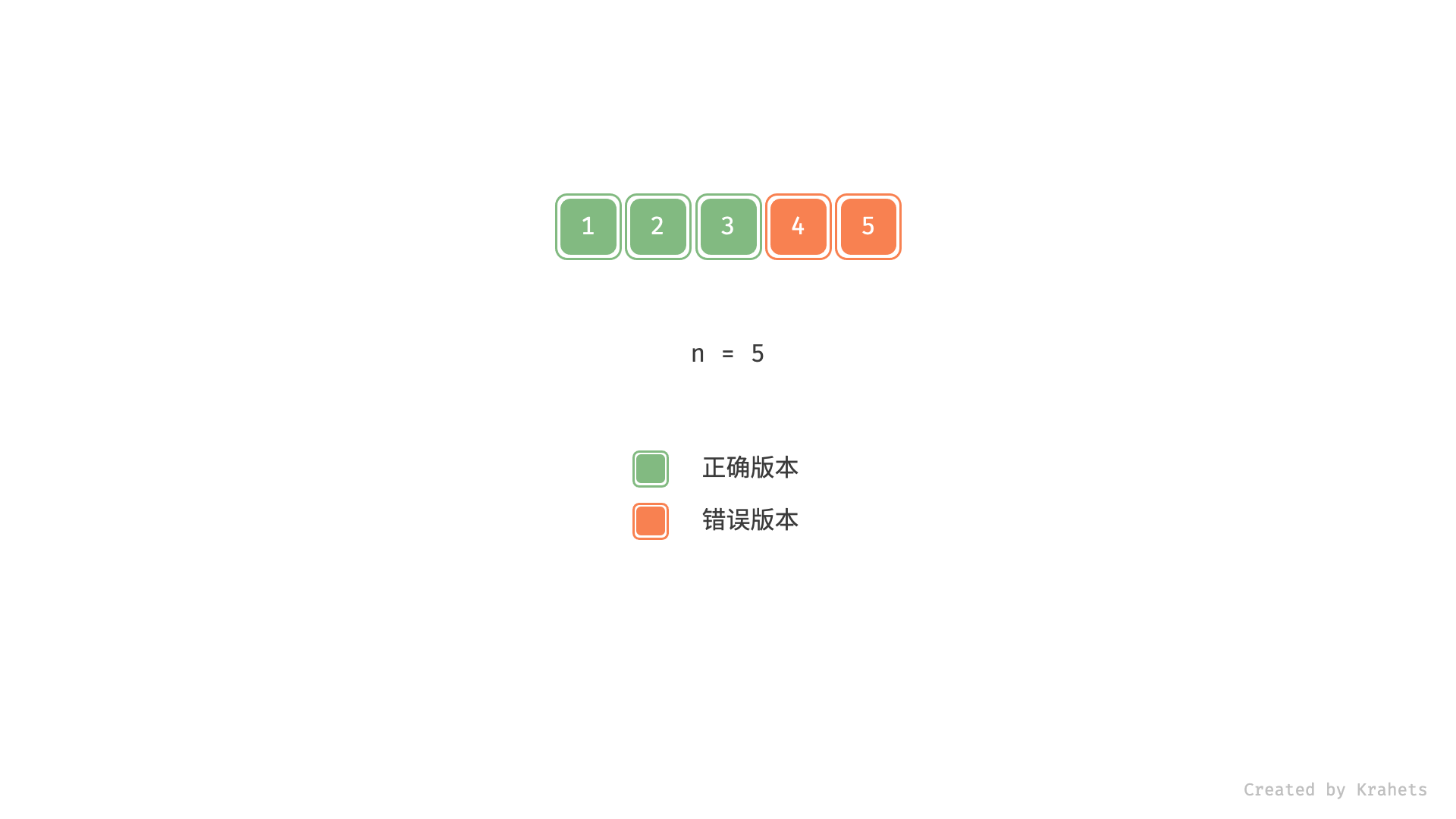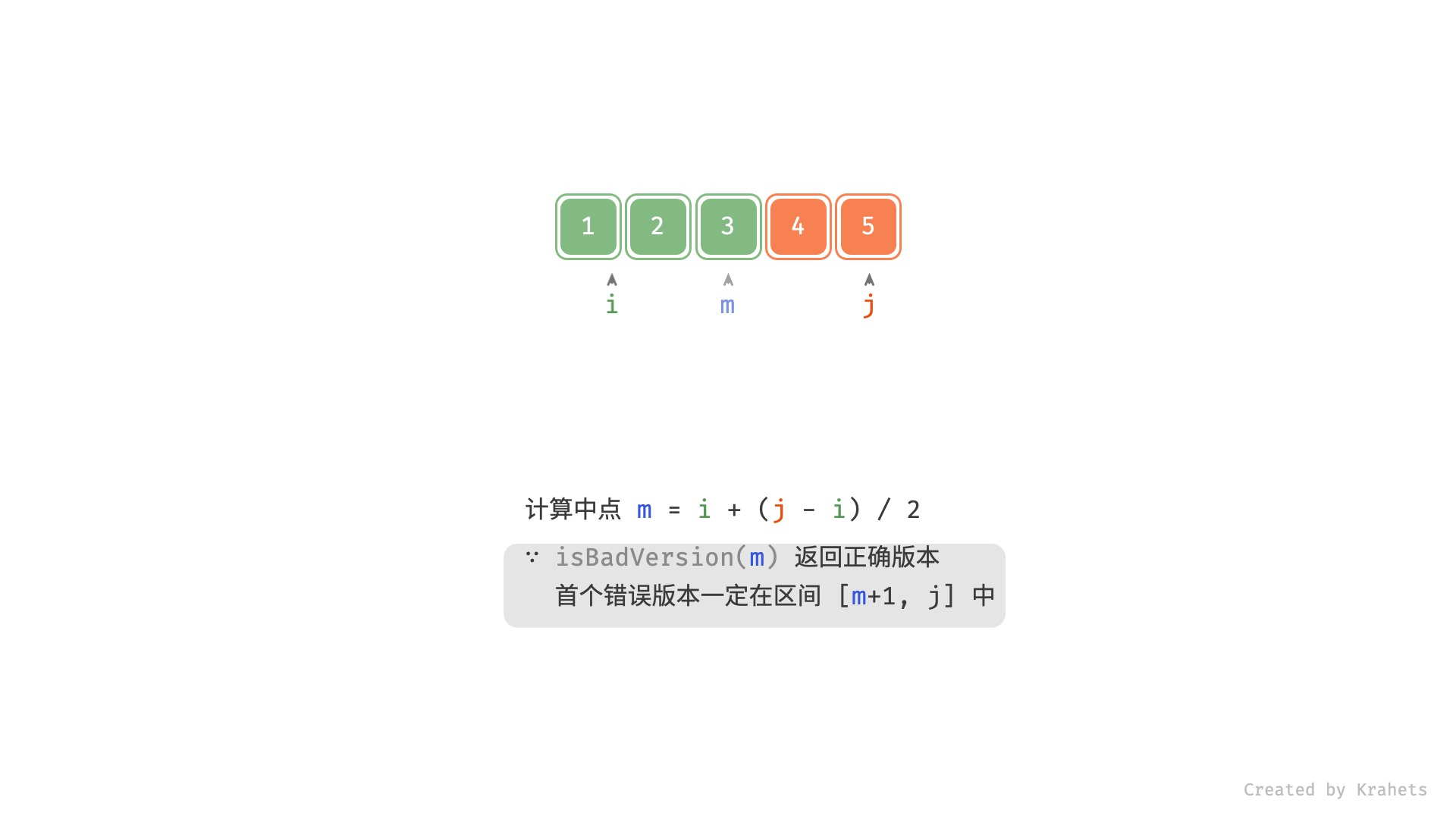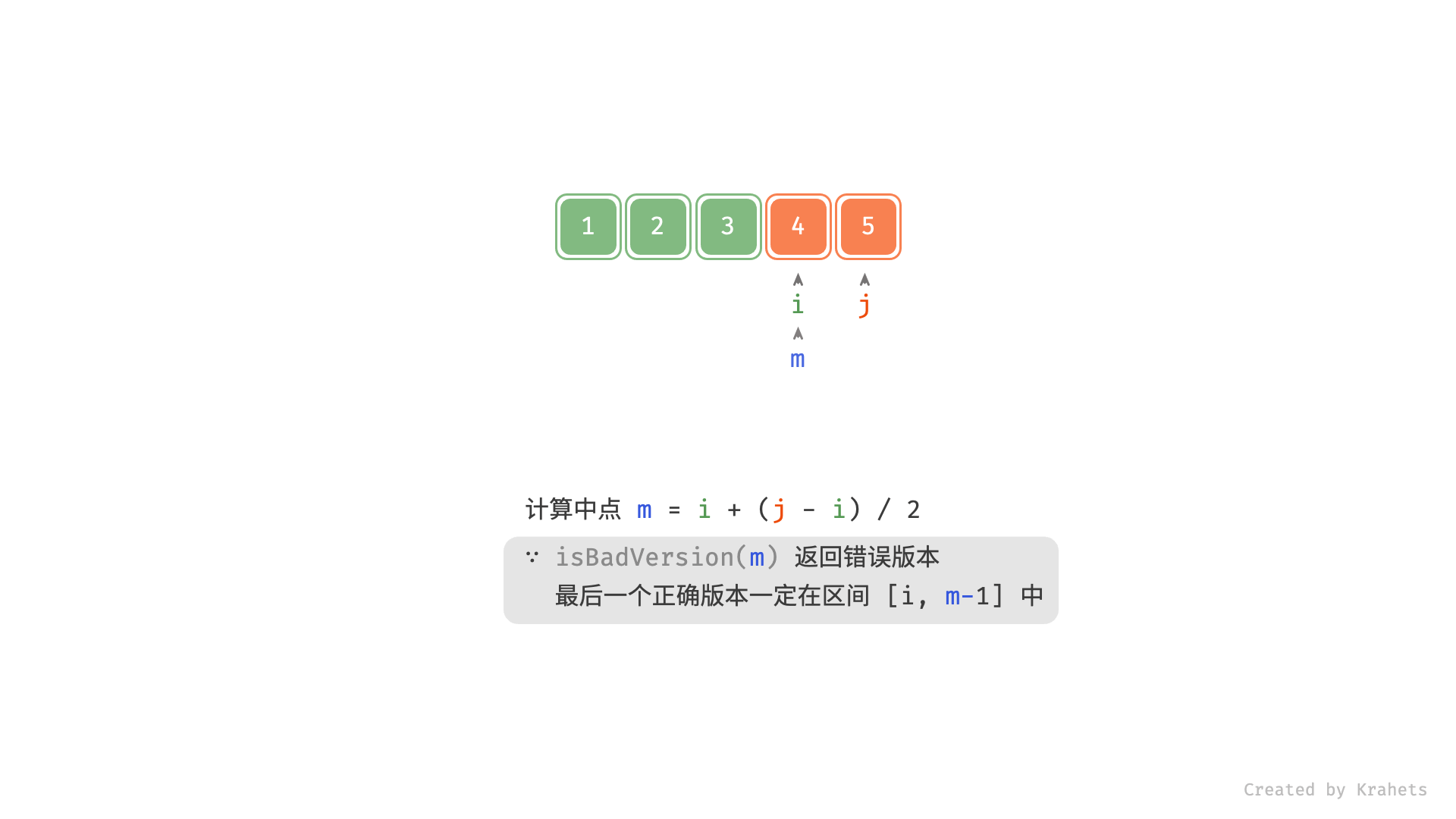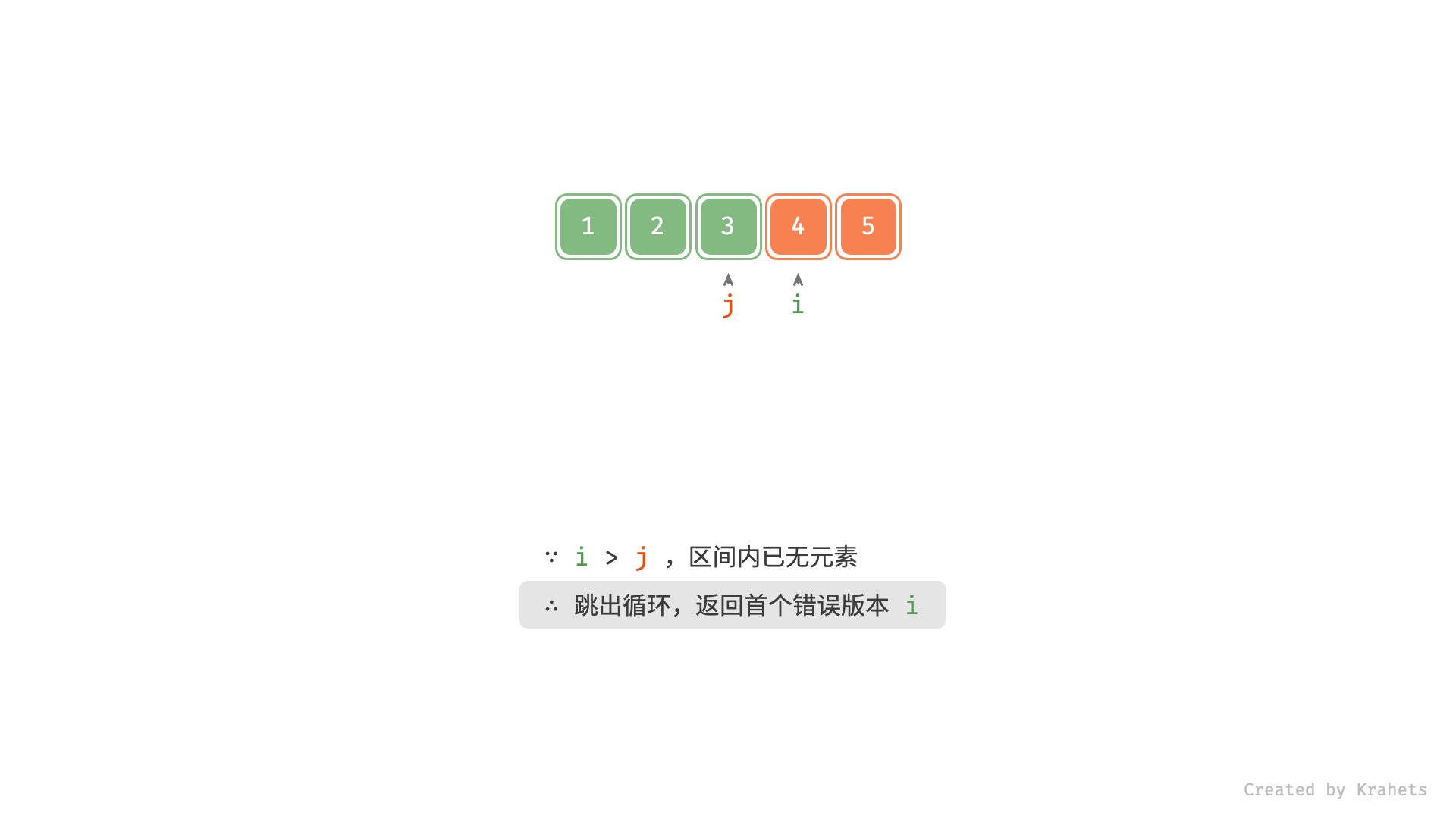
若感觉动图播放太快，可以一页页看 $\downarrow$

<,,,,,,,,,>

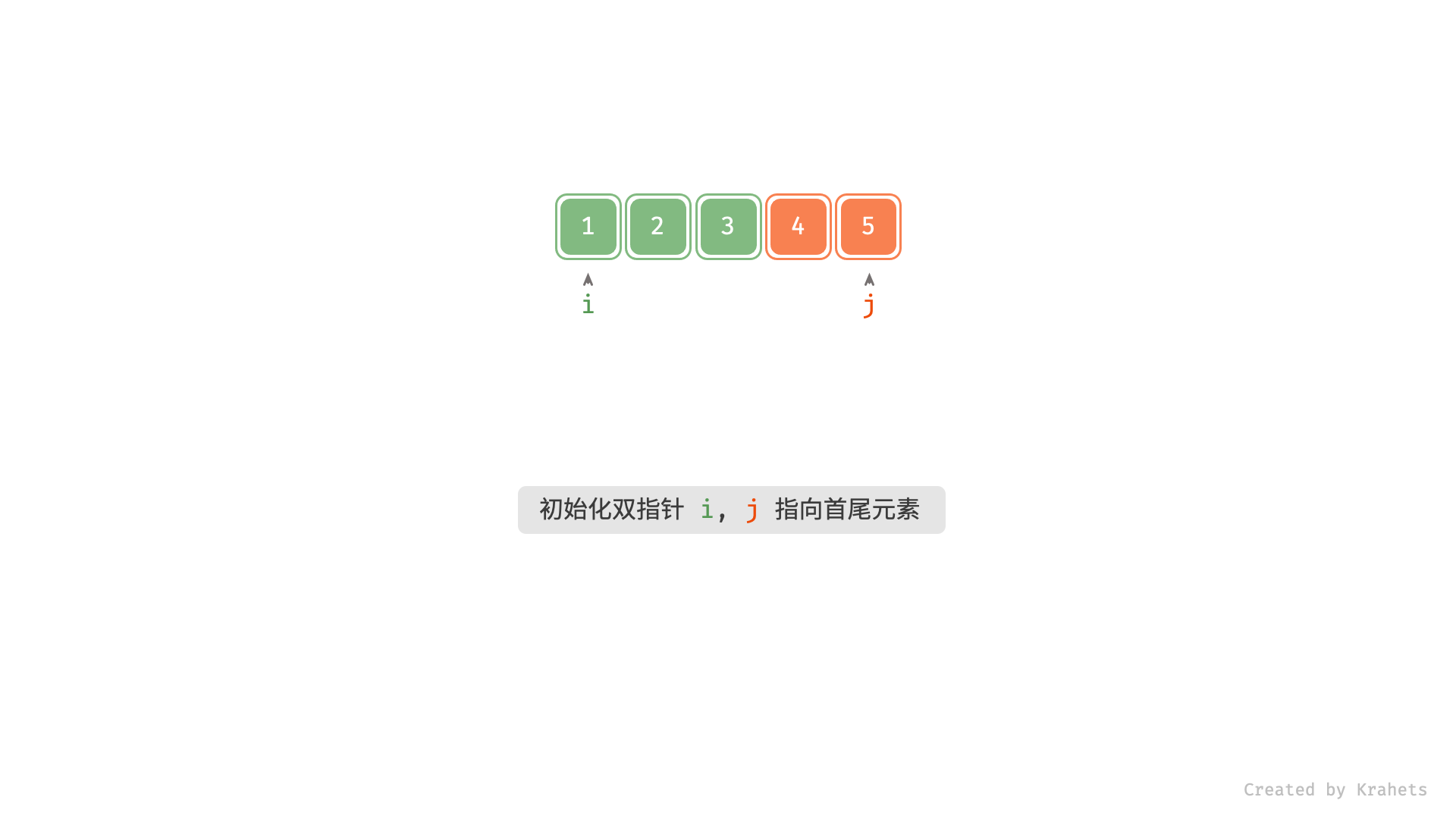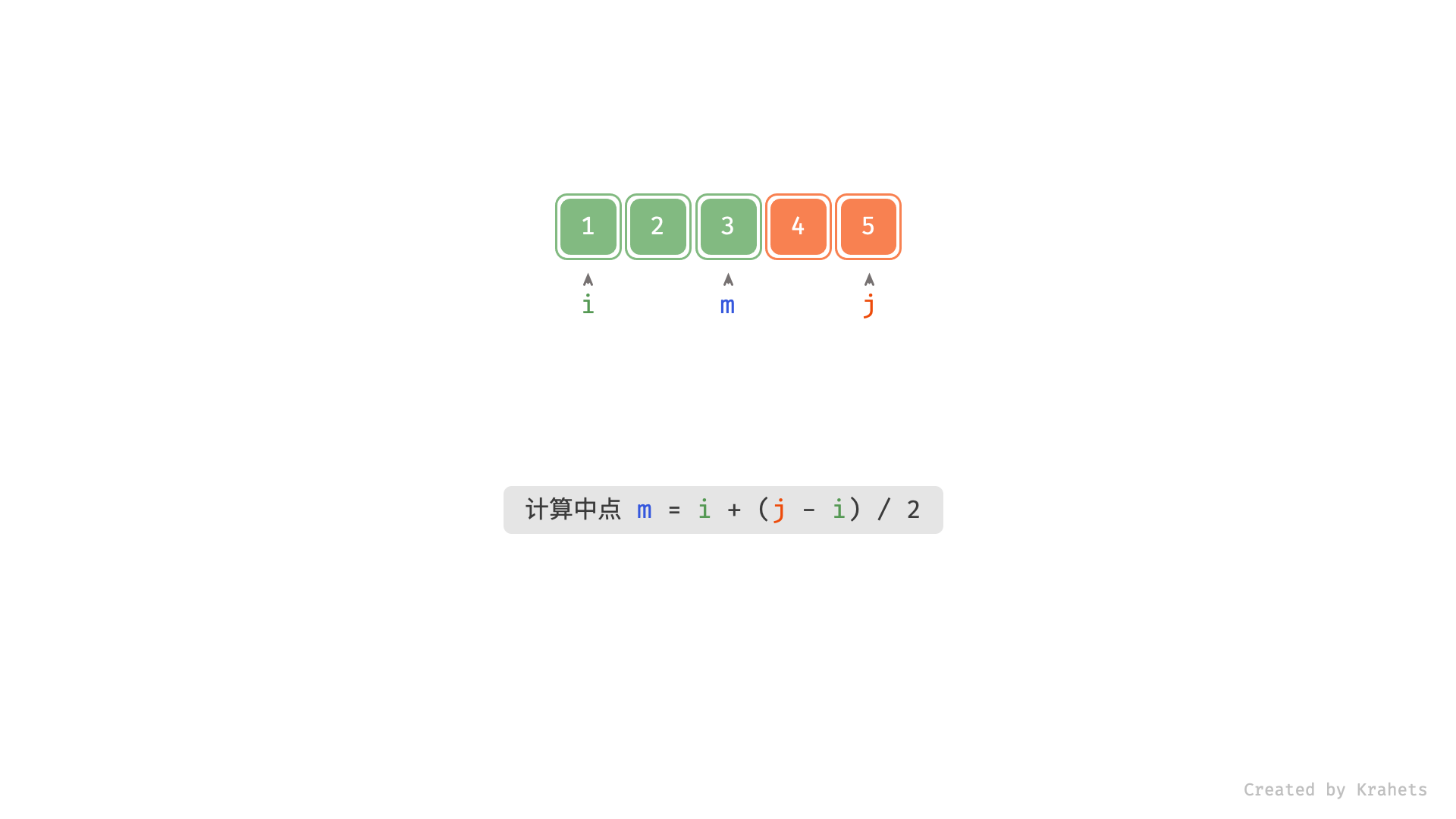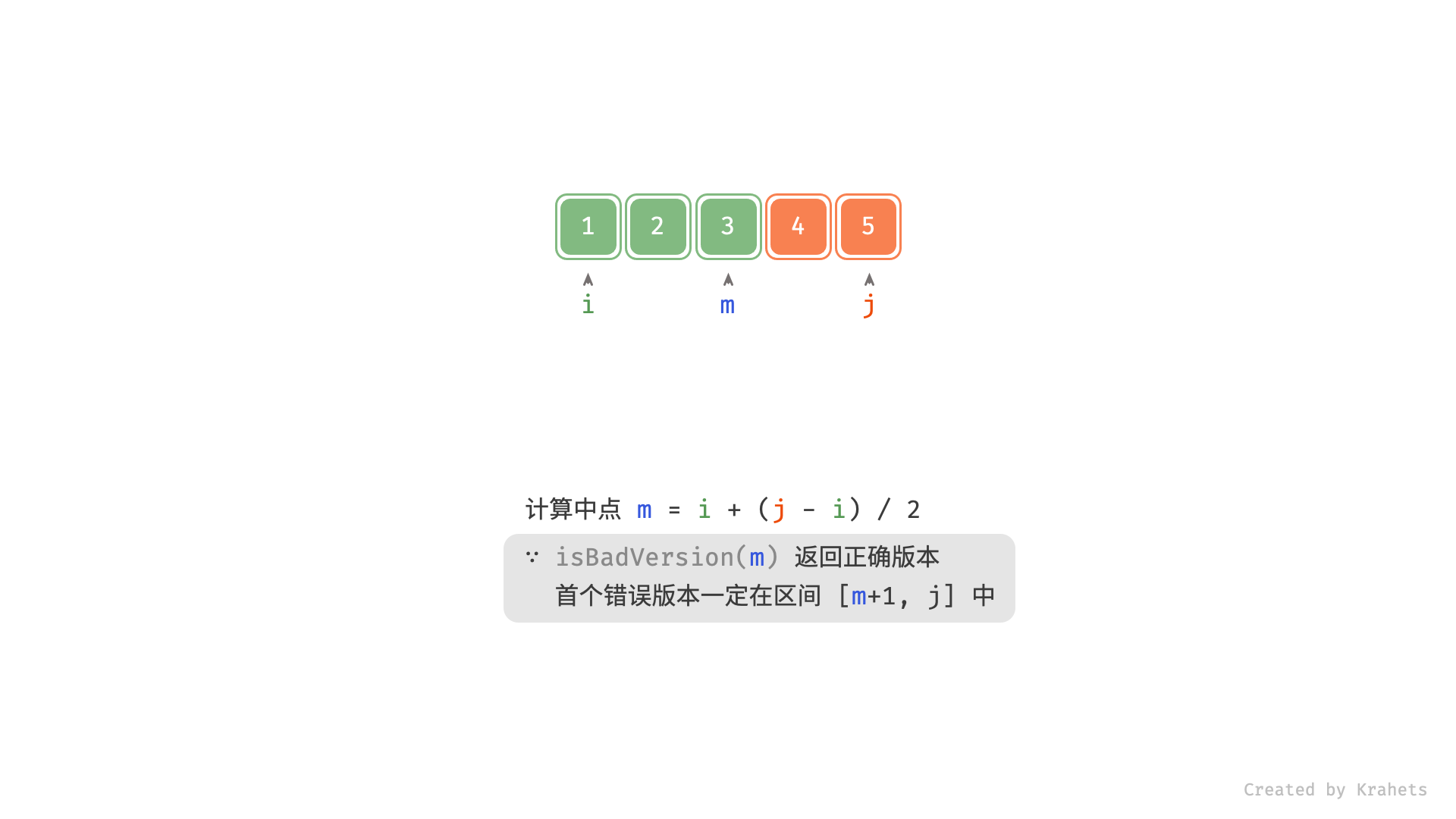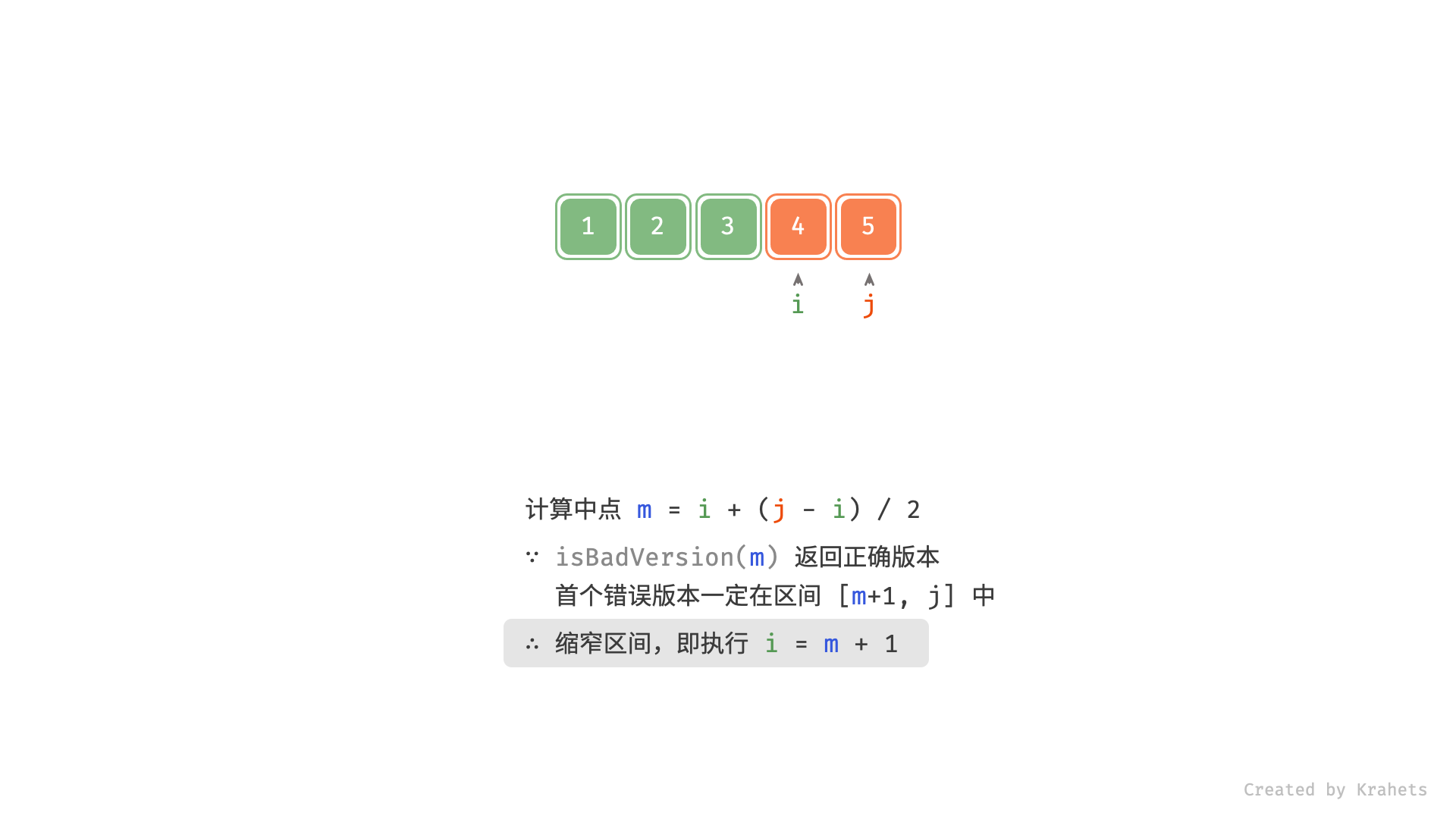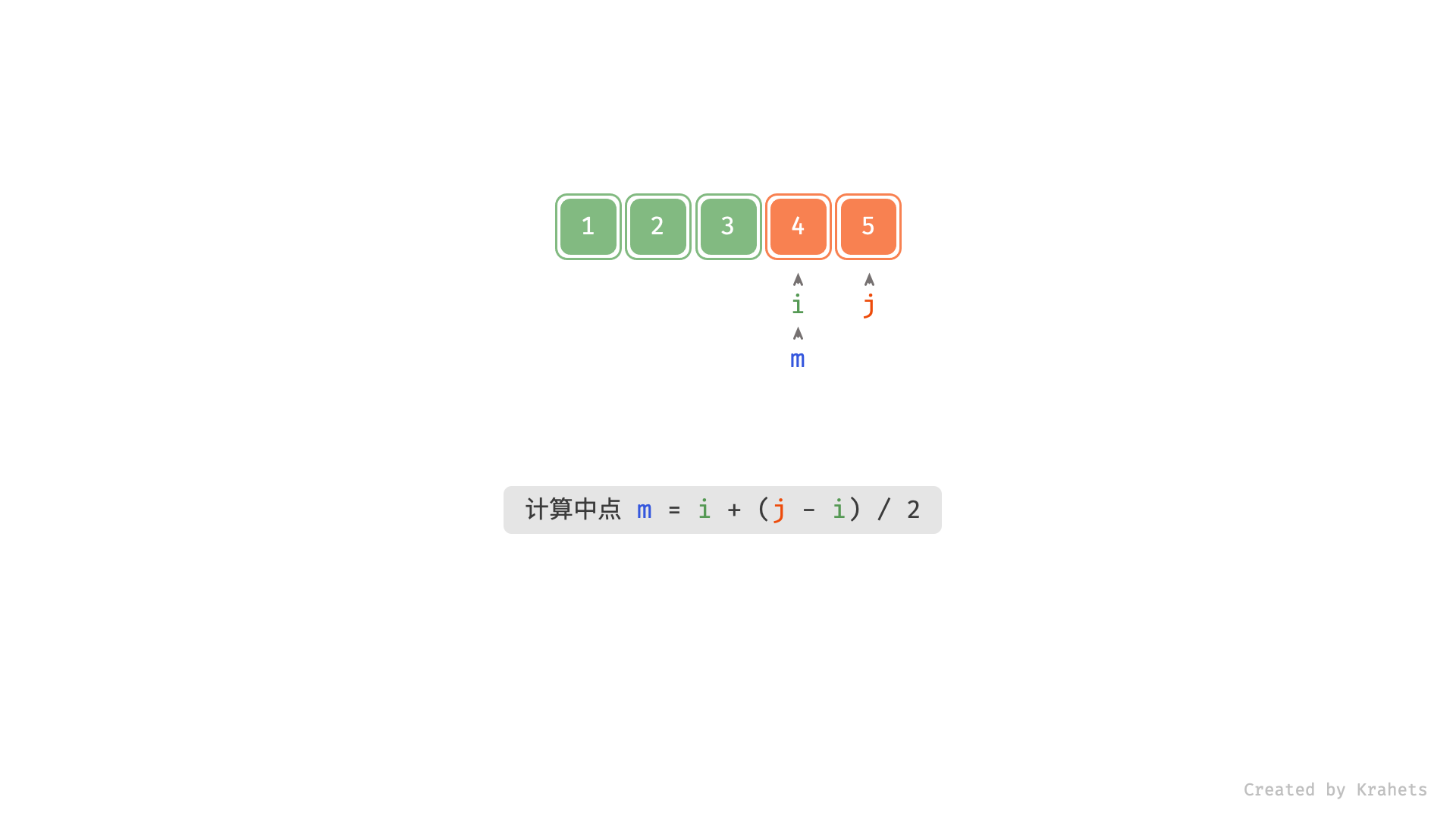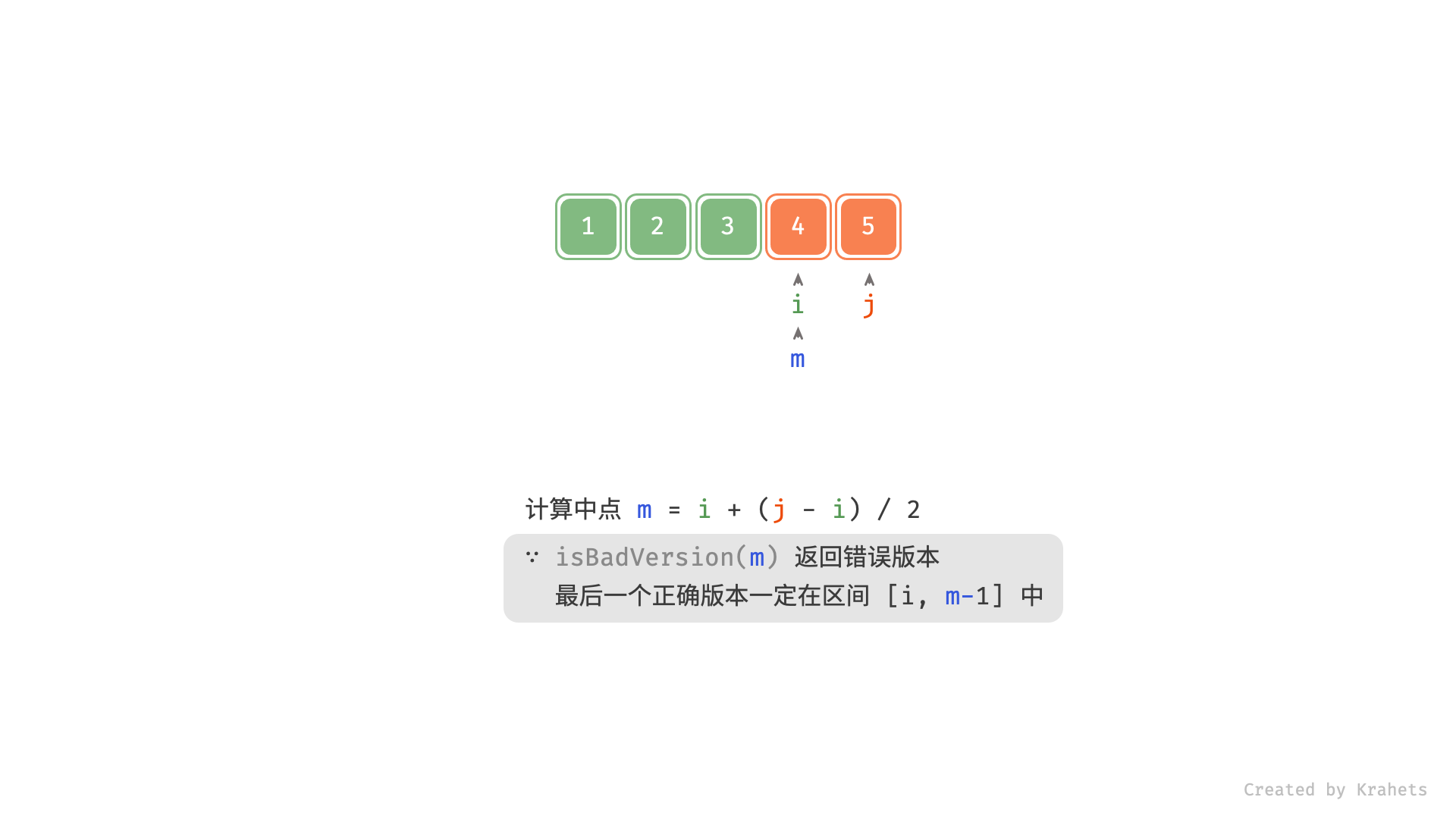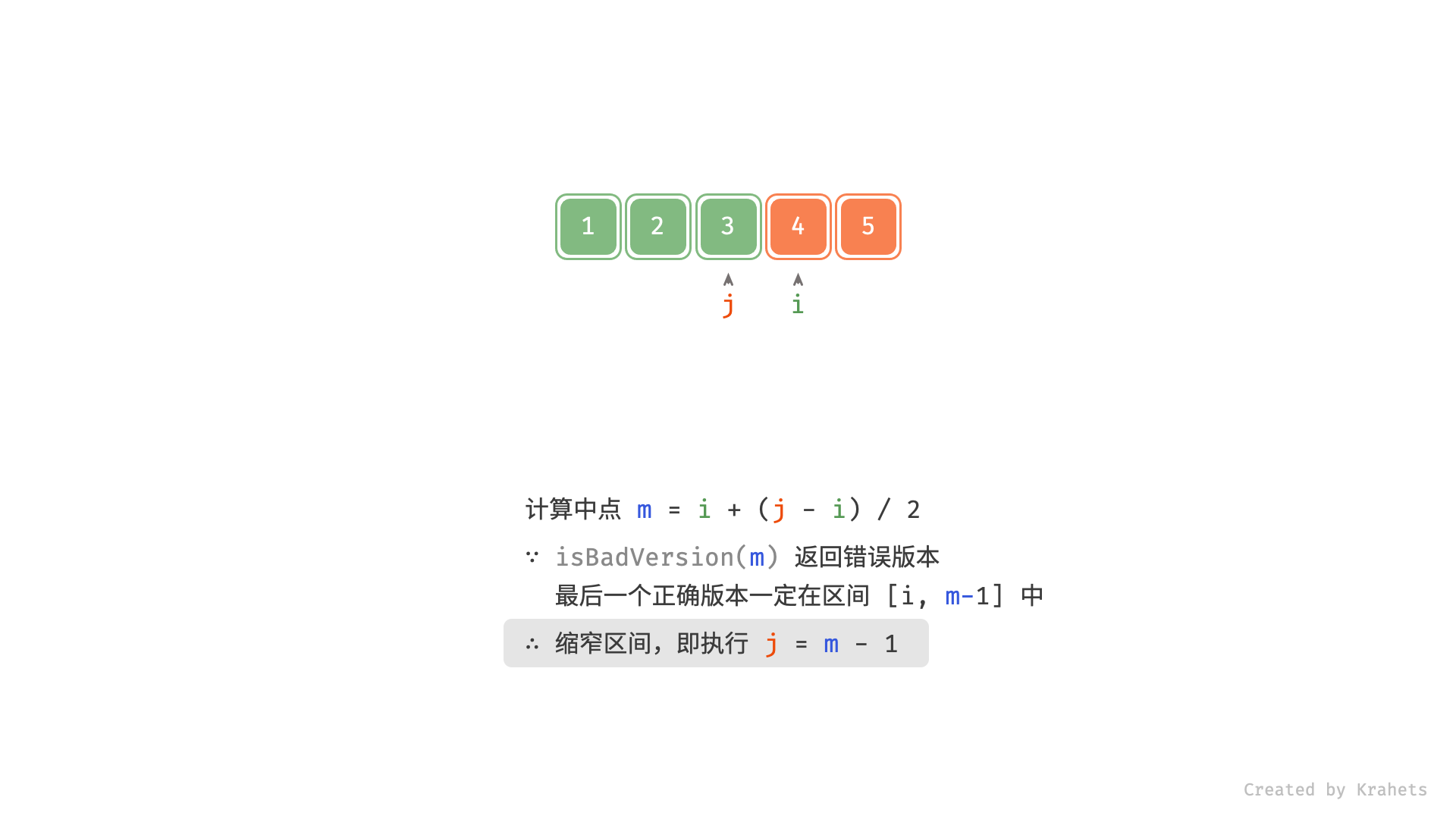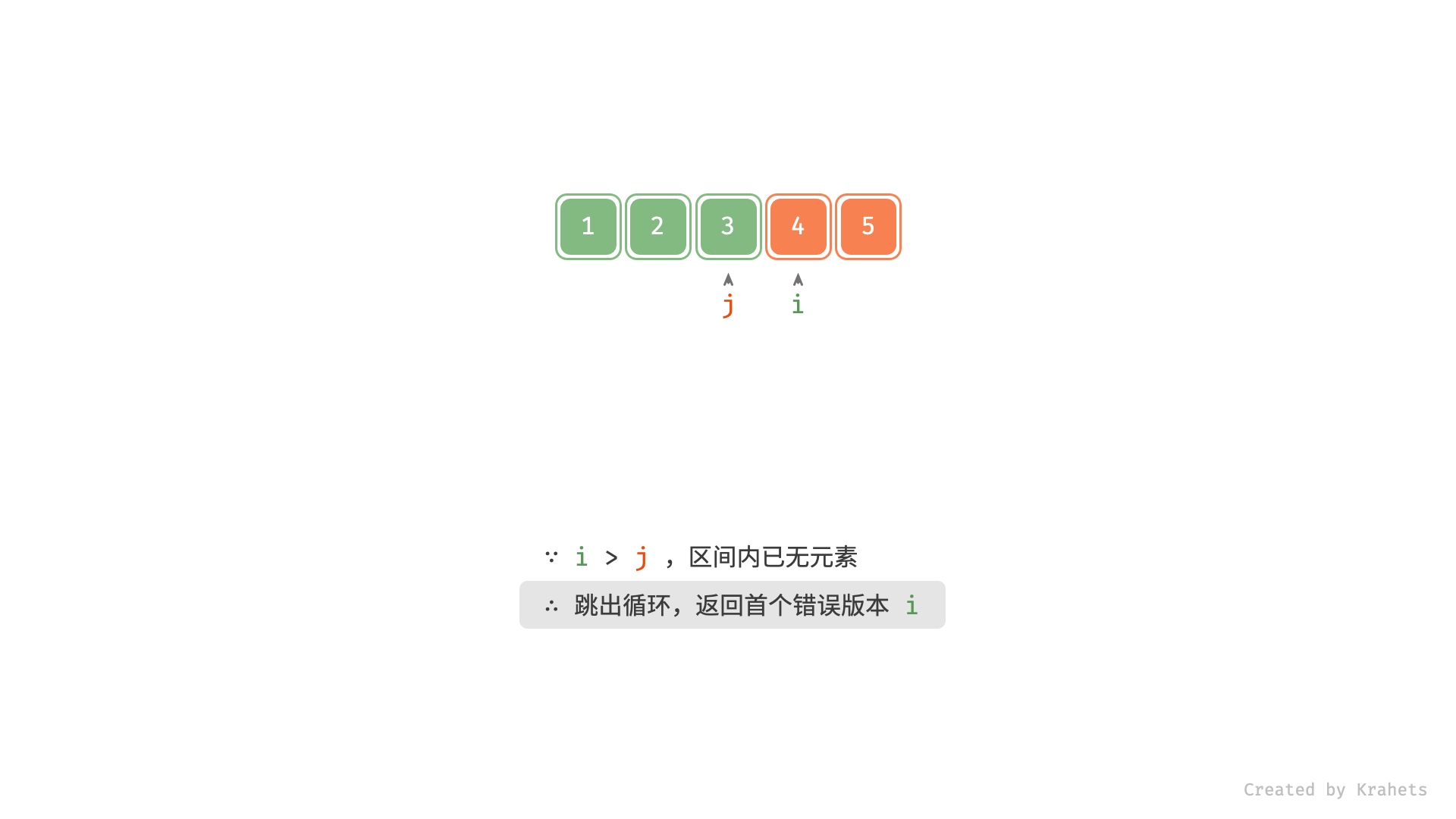代码

Python

class Solution:
    def firstBadVersion(self, n: int) -> int:
        i, j = 1, n
        while i <= j:
            # 向下取整除法计算中点 m 
            m = (i + j) // 2
            # 若 m 是错误版本，则最后一个正确版本一定在闭区间 [i, m - 1]
            if isBadVersion(m): j = m - 1
            # 若 m 是正确版本，则首个错误版本一定在闭区间 [m + 1, j]
            else: i = m + 1
        # i 指向首个错误版本，j 指向最后一个正确版本
        return i

Java

public class Solution extends VersionControl {
    public int firstBadVersion(int n) {
        int i = 1, j = n;
        while (i <= j) {
            // 向下取整除法计算中点 m 
            int m = i + (j - i) / 2;
            // 若 m 是错误版本，则最后一个正确版本一定在闭区间 [i, m - 1]
            if (isBadVersion(m)) j = m - 1;
            // 若 m 是正确版本，则首个错误版本一定在闭区间 [m + 1, j]
            else i = m + 1;
        }
        // i 指向首个错误版本，j 指向最后一个正确版本
        return i;
    }
}

C++

class Solution {
public:
    int firstBadVersion(int n) {
        int i = 1, j = n;
        while (i <= j) {
            // 向下取整除法计算中点 m 
            int m = i + (j - i) / 2;
            // 若 m 是错误版本，则最后一个正确版本一定在闭区间 [i, m - 1]
            if (isBadVersion(m)) j = m - 1;
            // 若 m 是正确版本，则首个错误版本一定在闭区间 [m + 1, j]
            else i = m + 1;
        }
        // i 指向首个错误版本，j 指向最后一个正确版本
        return i;
    }
};

复杂度分析

时间复杂度 $O(\log n)$ ： 其中 $n$ 为版本数；二分查找使用对数级别时间。
空间复杂度 $O(1)$ ： 变量 $i$ , $j$ 使用常数大小空间。

解题思路 ​

代码 ​

复杂度分析 ​

解题思路

代码

复杂度分析