解题思路:
根据字符串长度,「回文串」可分为两种情况:
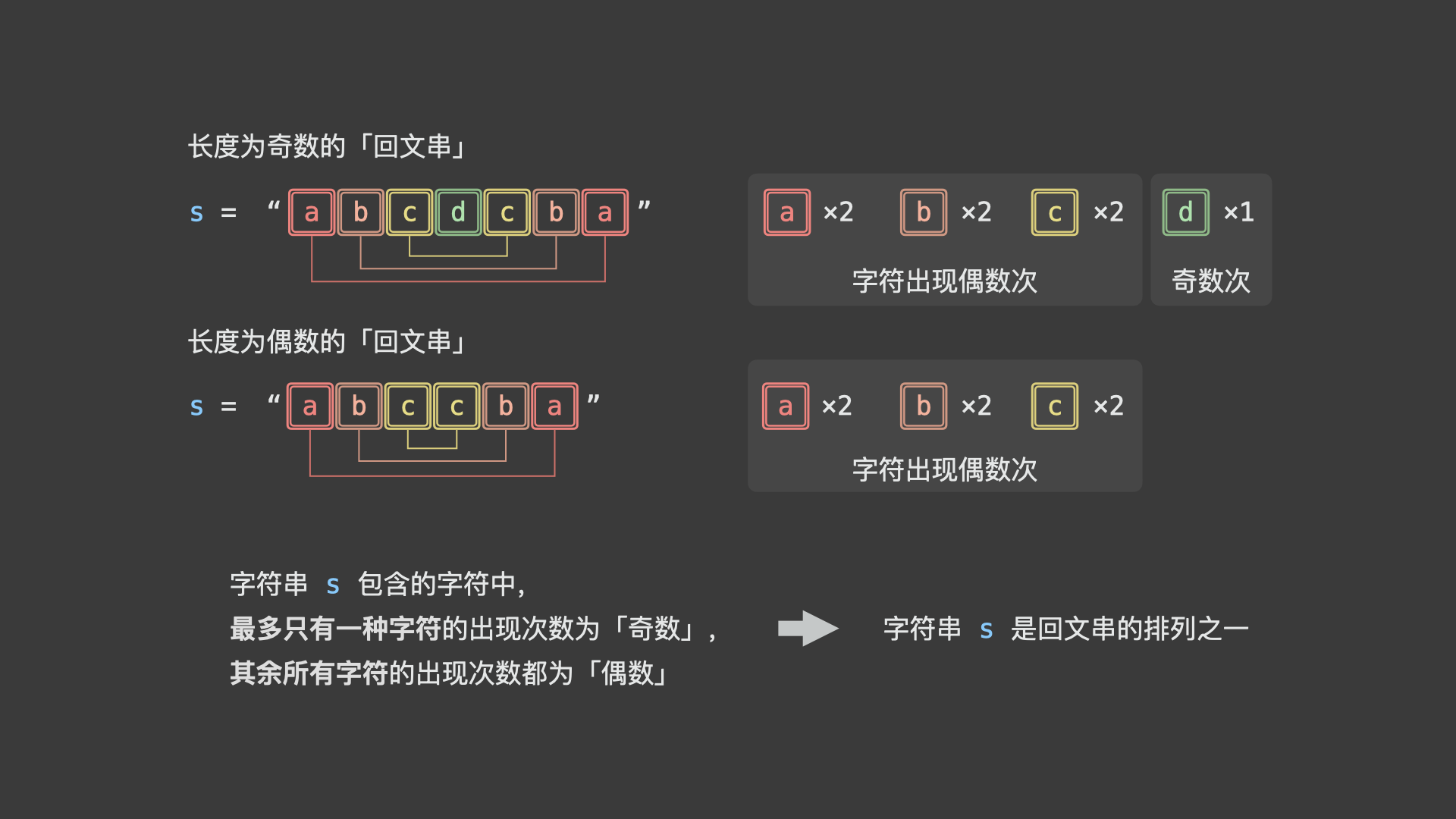
- 「回文串」长度为偶数:所有不同字符的出现次数都为「偶数」;
- 「回文串」长度为奇数:位于中点的字符出现「奇数」次,其余字符出现「偶数」次;
因此,某字符串是回文串排列之一的「充要条件」为:此字符串中,最多只有一种字符的出现次数为「奇数」,其余所有字符的出现次数都为「偶数」。
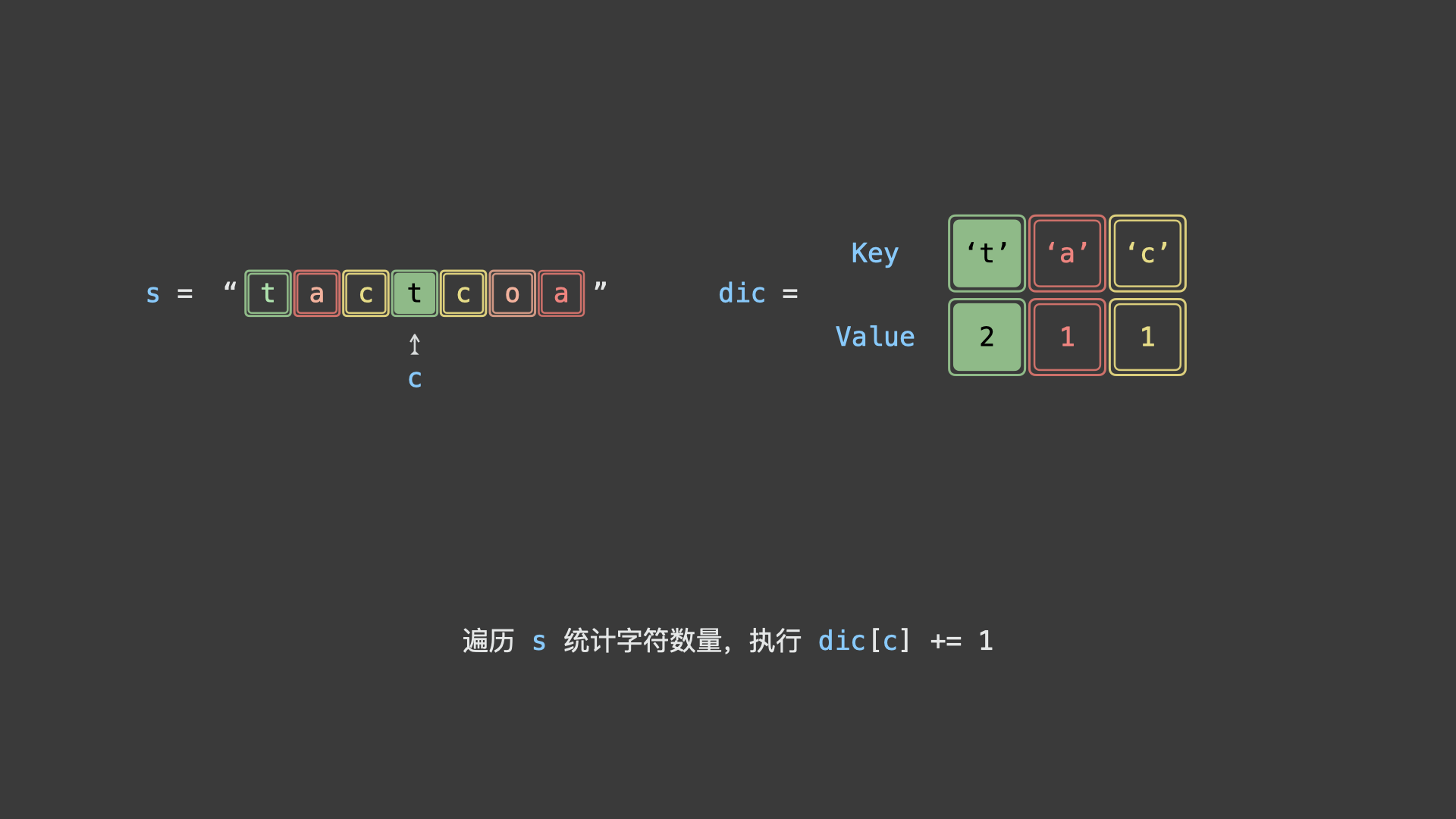
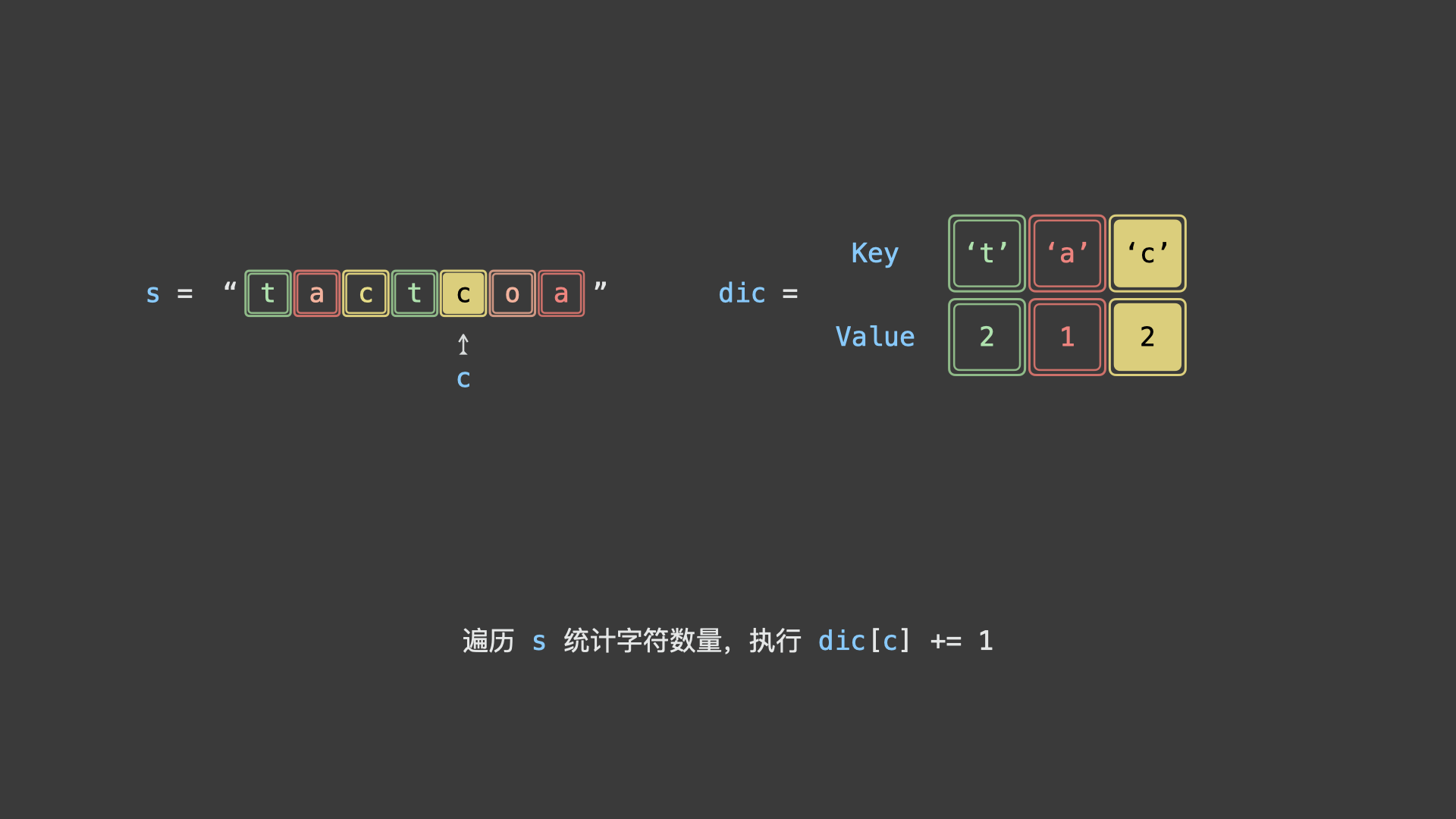
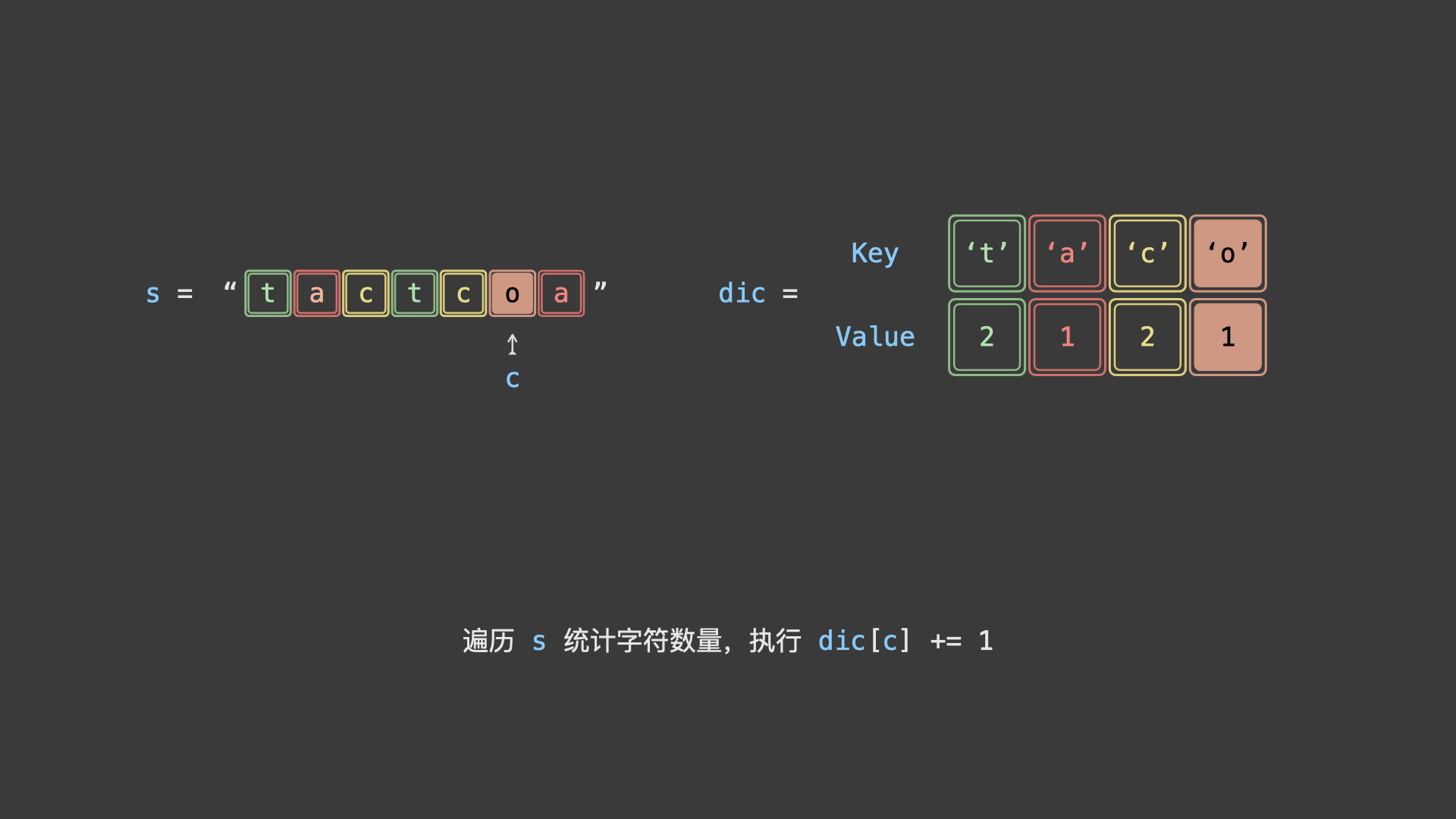
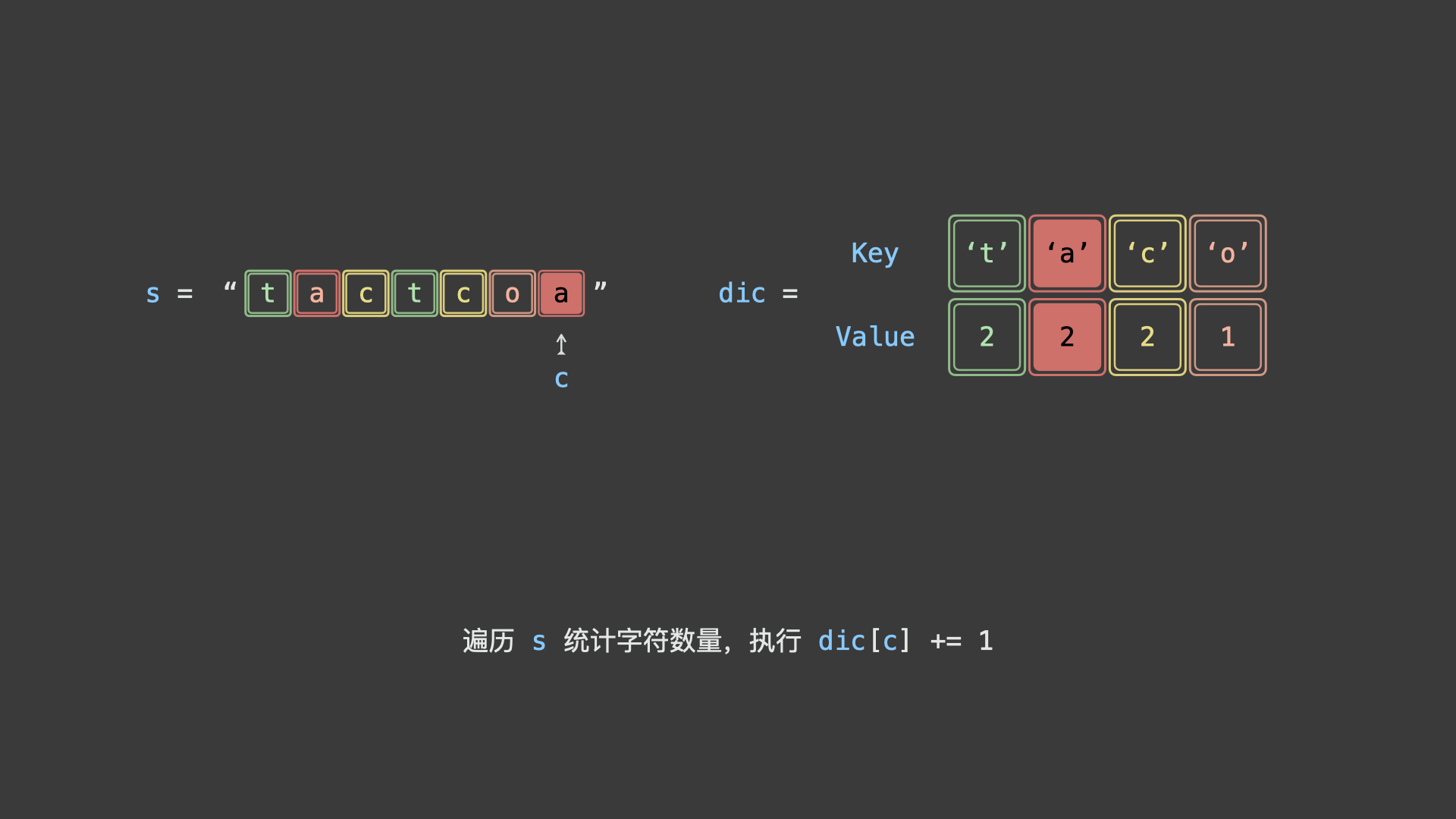
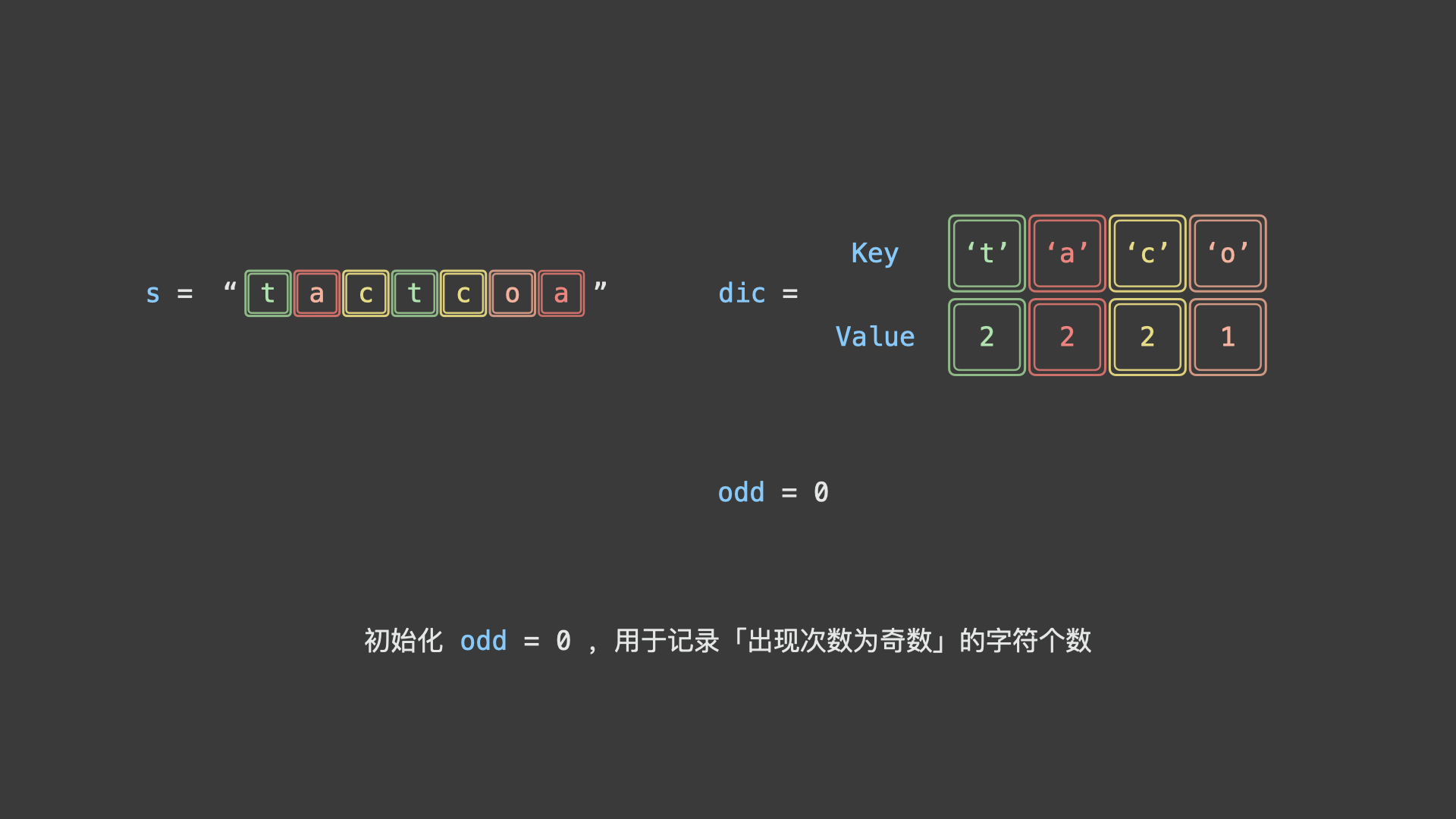
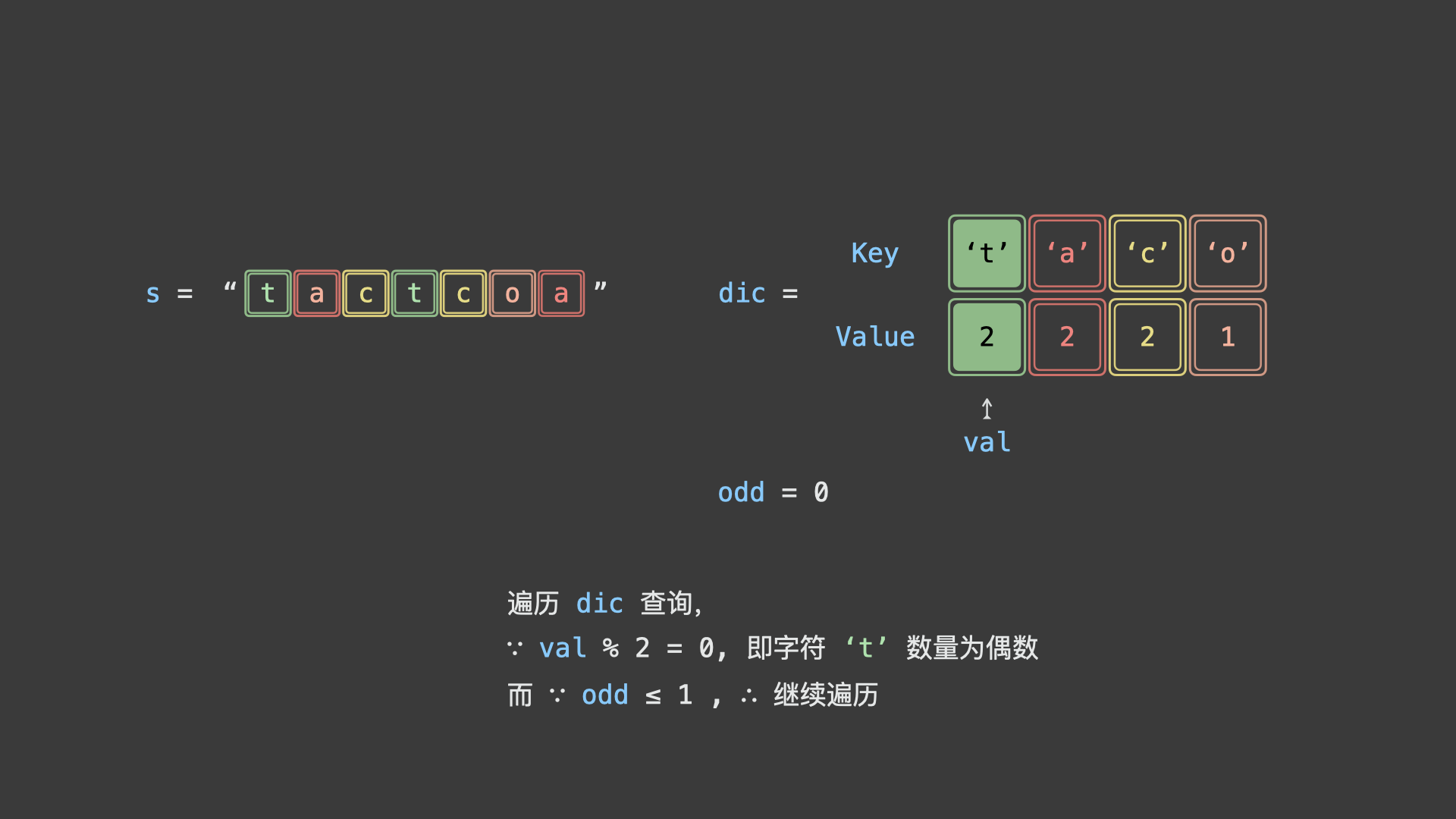
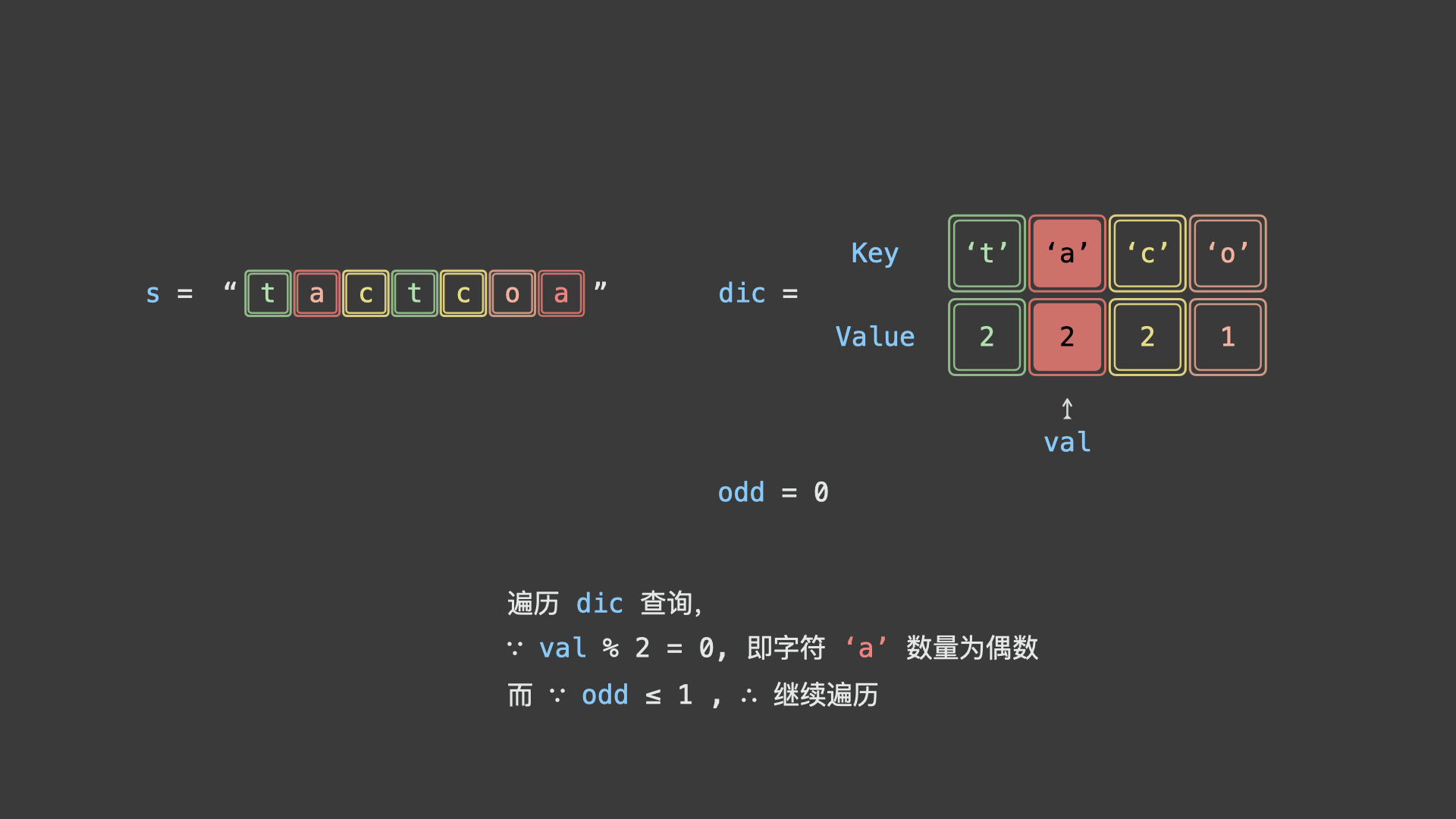
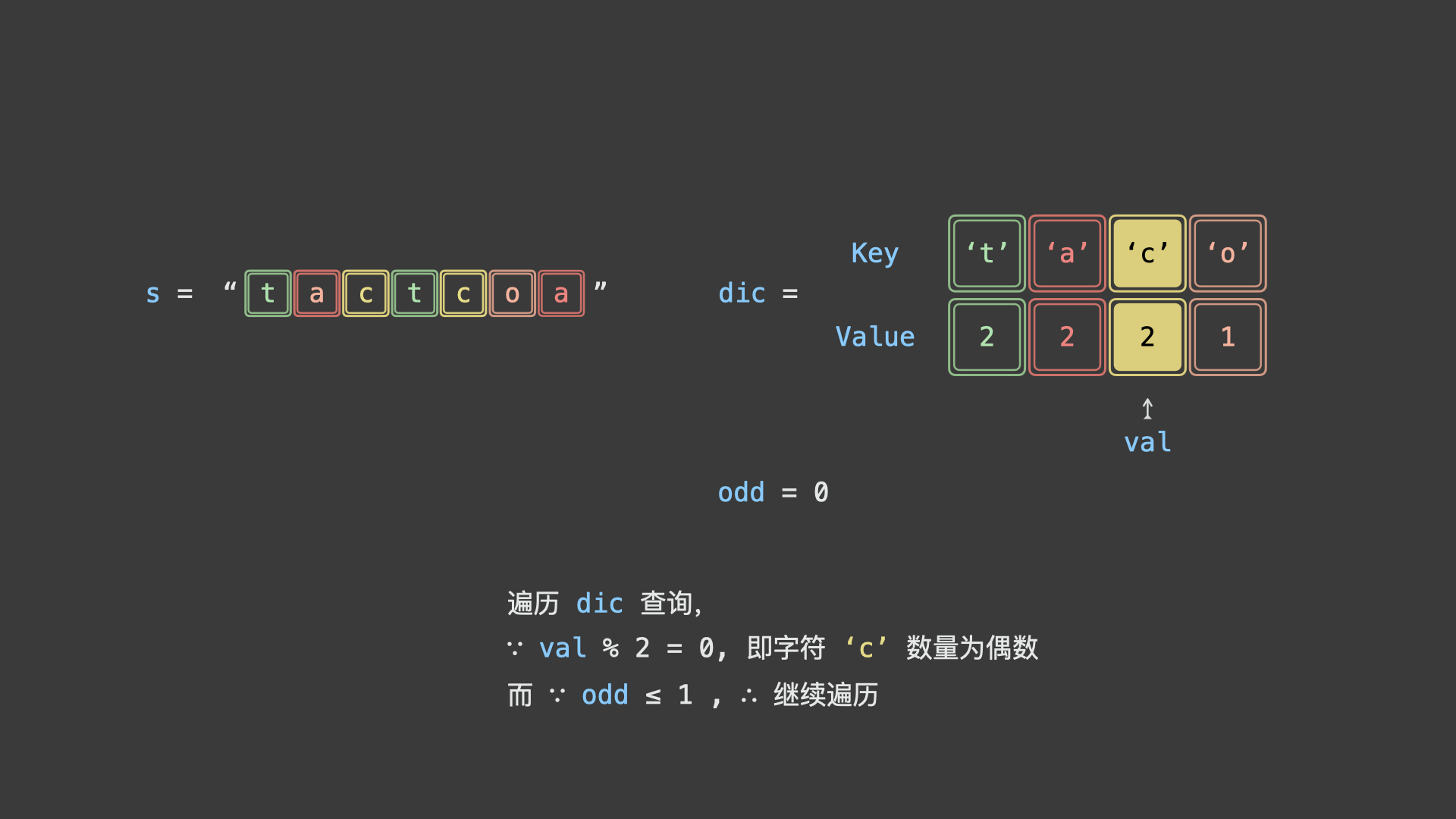
考虑使用「哈希表」统计给定字符串中各字符的数量,再根据以上规则判断字符串是否为回文串排列之一。
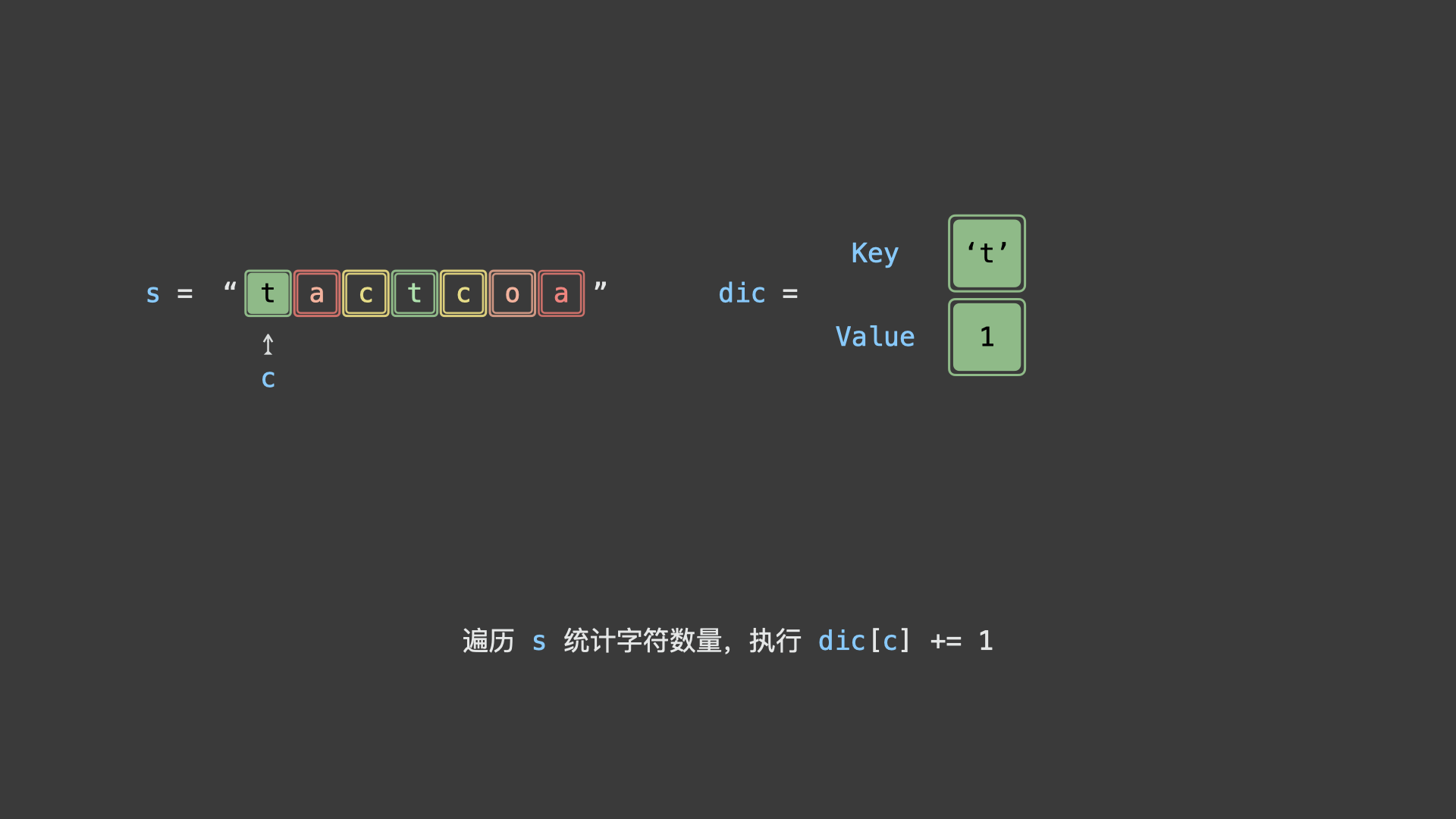
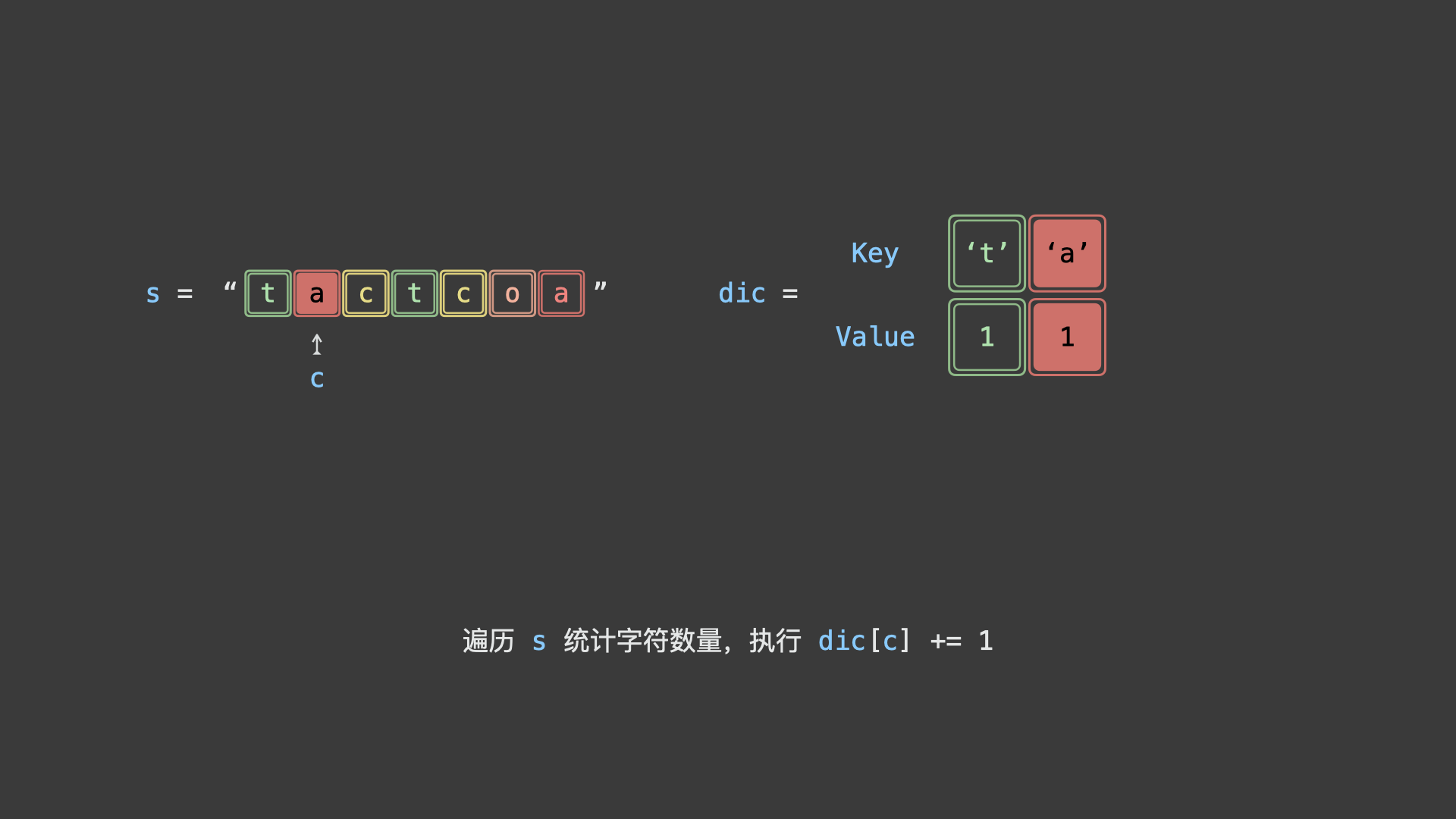
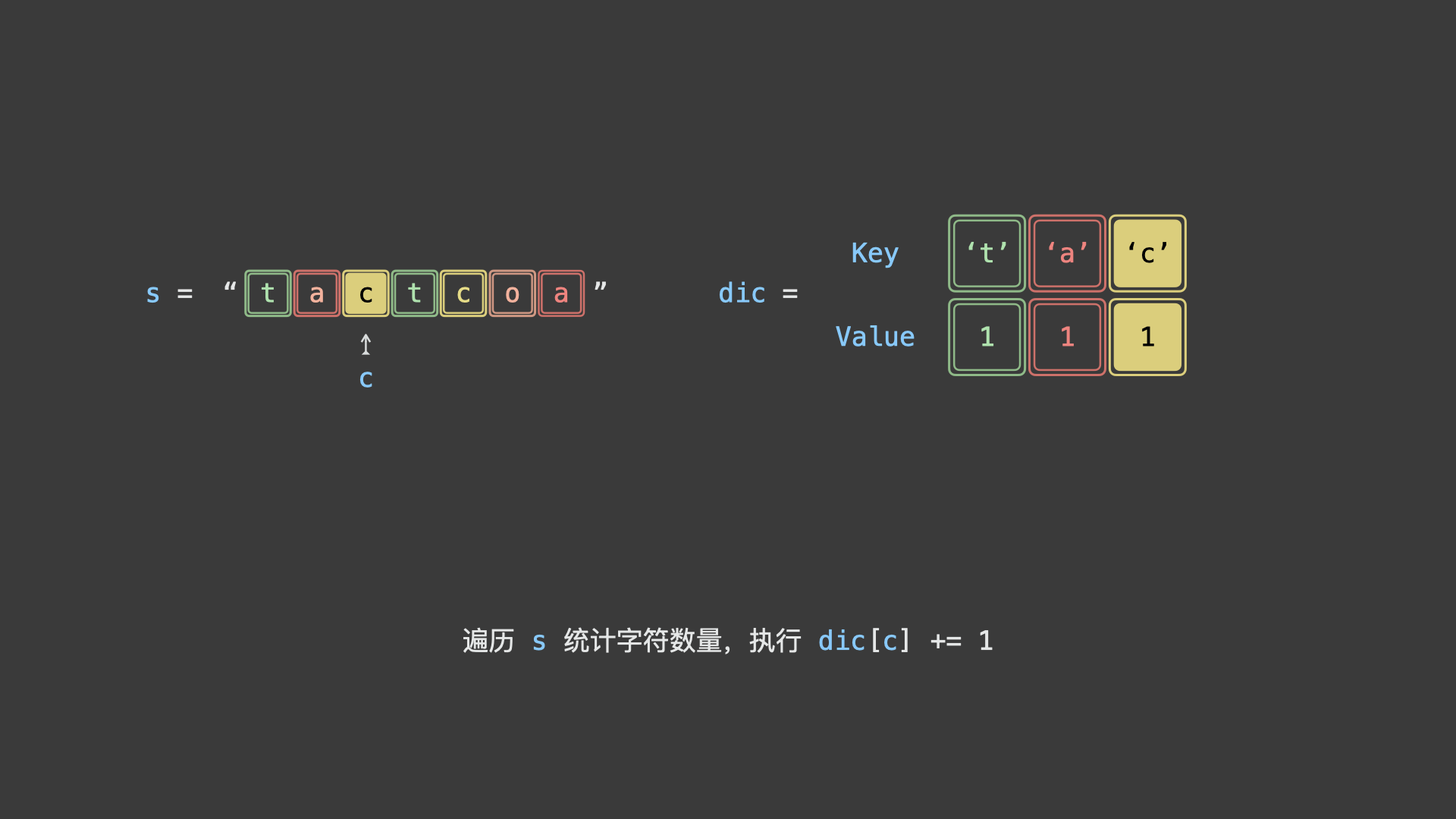
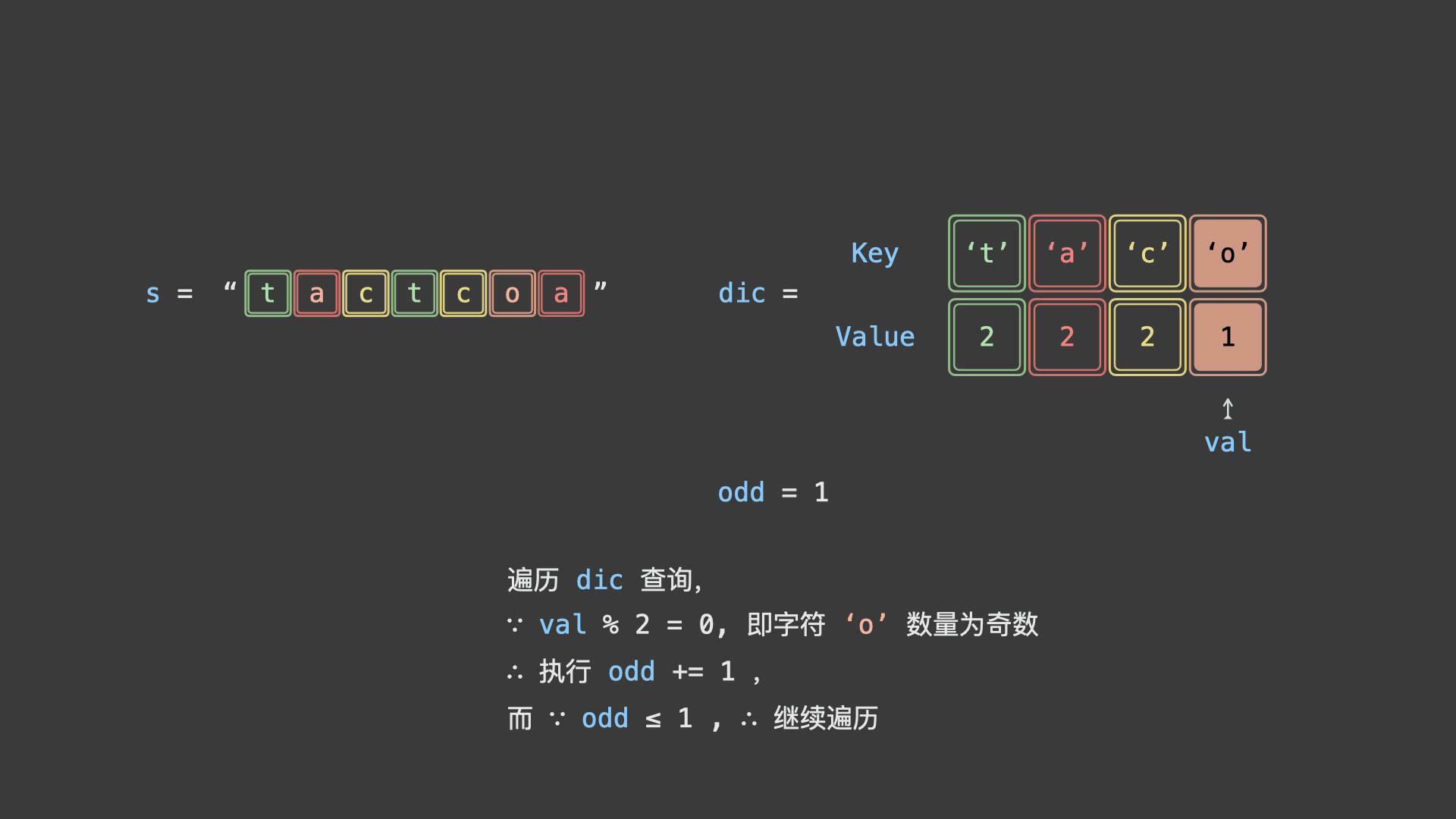
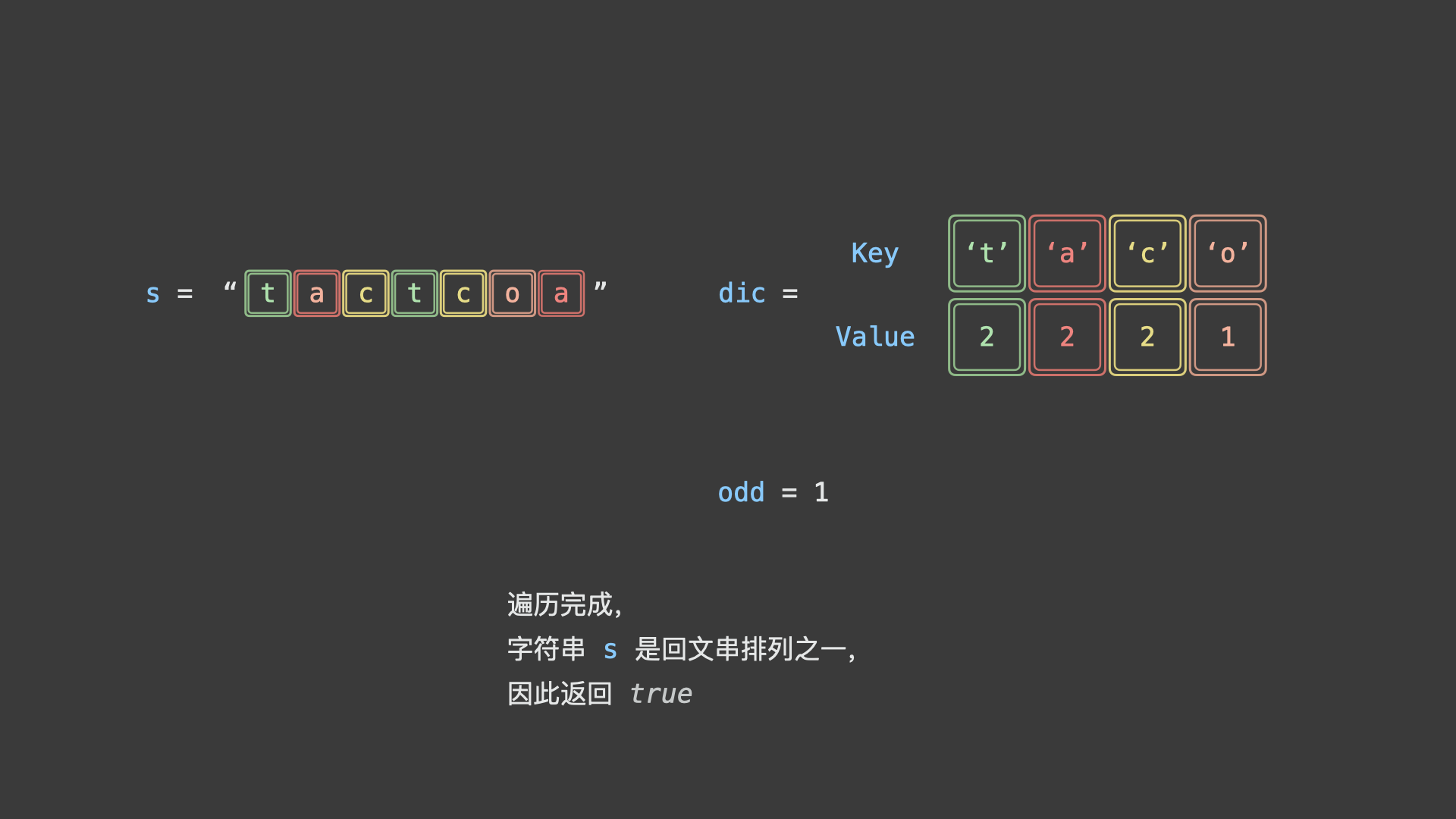
如下图所示,为判断示例字符串
"tactcoa"是否为回文串排列之一的算法执行流程。
< ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, >
>
代码:
Python 代码使用 collections.defaultdict() 类,可指定所有 key 对应的默认 value 。
后三个 Tab 的代码包括注释解析。
Python
class Solution:
def canPermutePalindrome(self, s: str) -> bool:
dic = defaultdict(int)
for c in s:
dic[c] += 1
odd = 0
for val in dic.values():
if val % 2 == 1:
odd += 1
if odd > 1:
return False
return TrueJava
class Solution {
public boolean canPermutePalindrome(String s) {
HashMap<Character, Integer> dic = new HashMap<>();
for (int i = 0; i < s.length(); i++) {
dic.put(s.charAt(i), dic.getOrDefault(s.charAt(i), 0) + 1);
}
int odd = 0;
for (int val : dic.values()) {
if (val % 2 == 1) {
if (++odd > 1)
return false;
}
}
return true;
}
}C++
class Solution {
public:
bool canPermutePalindrome(string s) {
unordered_map<char, int> dic;
for (char c : s) {
dic[c] += 1;
}
int odd = 0;
for (auto kv : dic) {
if (kv.second % 2 == 1) {
if (++odd > 1)
return false;
}
}
return true;
}
};Python
class Solution:
def canPermutePalindrome(self, s: str) -> bool:
# 初始化哈希表
dic = defaultdict(int)
# 统计字符串中各字符的数量
for c in s:
dic[c] += 1
odd = 0
for val in dic.values():
# 统计“数量为奇数”字符的个数
if val % 2 == 1:
odd += 1
# 若“数量为奇数”的字符个数 > 1 ,则不是回文串排列
if odd > 1:
return False
# 若“数量为奇数”的字符个数 <= 1 ,则是回文串排列
return TrueJava
class Solution {
public boolean canPermutePalindrome(String s) {
// 初始化哈希表
HashMap<Character, Integer> dic = new HashMap<>();
// 统计字符串中各字符的数量
for (int i = 0; i < s.length(); i++) {
dic.put(s.charAt(i), dic.getOrDefault(s.charAt(i), 0) + 1);
}
int odd = 0;
for (int val : dic.values()) {
// 统计“数量为奇数”字符的个数
if (val % 2 == 1) {
// 若“数量为奇数”的字符个数 > 1 ,则不是回文串排列
if (++odd > 1) // 注意 ++odd > 1 是先执行 odd 自增,再执行逻辑判断; odd++ 的顺序反之
return false;
}
}
// 若“数量为奇数”的字符个数 <= 1 ,则是回文串排列
return true;
}
}C++
class Solution {
public:
bool canPermutePalindrome(string s) {
// 初始化哈希表
unordered_map<char, int> dic;
// 统计字符串中各字符的数量
for (char c : s) {
dic[c] += 1;
}
int odd = 0;
for (auto kv : dic) {
// 统计“数量为奇数”字符的个数
if (kv.second % 2 == 1) {
// 若“数量为奇数”的字符个数 > 1 ,则不是回文串排列
if (++odd > 1) // 注意 ++odd > 1 是先执行 odd 自增,再执行逻辑判断; odd++ 的顺序反之
return false;
}
}
// 若“数量为奇数”的字符个数 <= 1 ,则是回文串排列
return true;
}
};复杂度分析:
时间复杂度 $O(N)$ : 其中 $N$ 为字符串长度;哈希表统计字符数量迭代 $N$ 次,判断是否为回文串最多迭代 $N$ 次,总体使用 $O(N + N) = O(N)$ 时间。
空间复杂度 $O(N)$ : 哈希表 dic 使用 $O(N)$ 大小的额外空间。