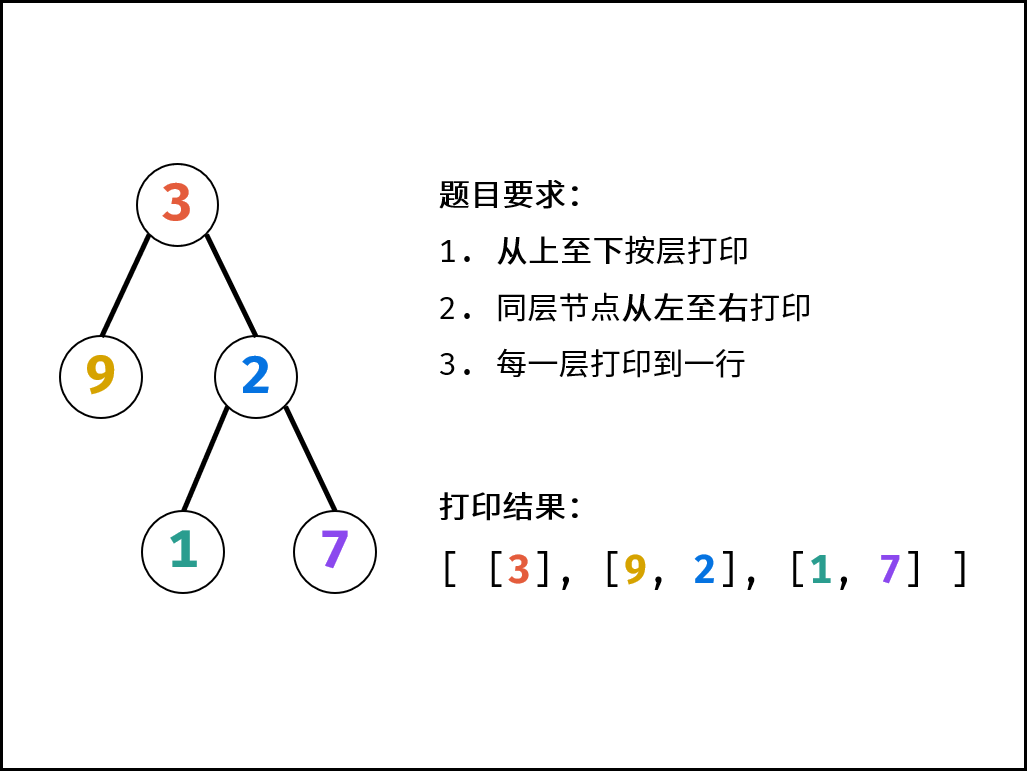
解题思路： ​

I. 按层打印： 题目要求的二叉树的 从上至下 打印（即按层打印），又称为二叉树的 广度优先搜索（BFS）。BFS 通常借助 队列 的先入先出特性来实现。

II. 每层打印到一行： 将本层全部节点打印到一行，并将下一层全部节点加入队列，以此类推，即可分为多行打印。

算法流程： ​

1. 特例处理： 当根节点为空，则返回空列表 [] 。
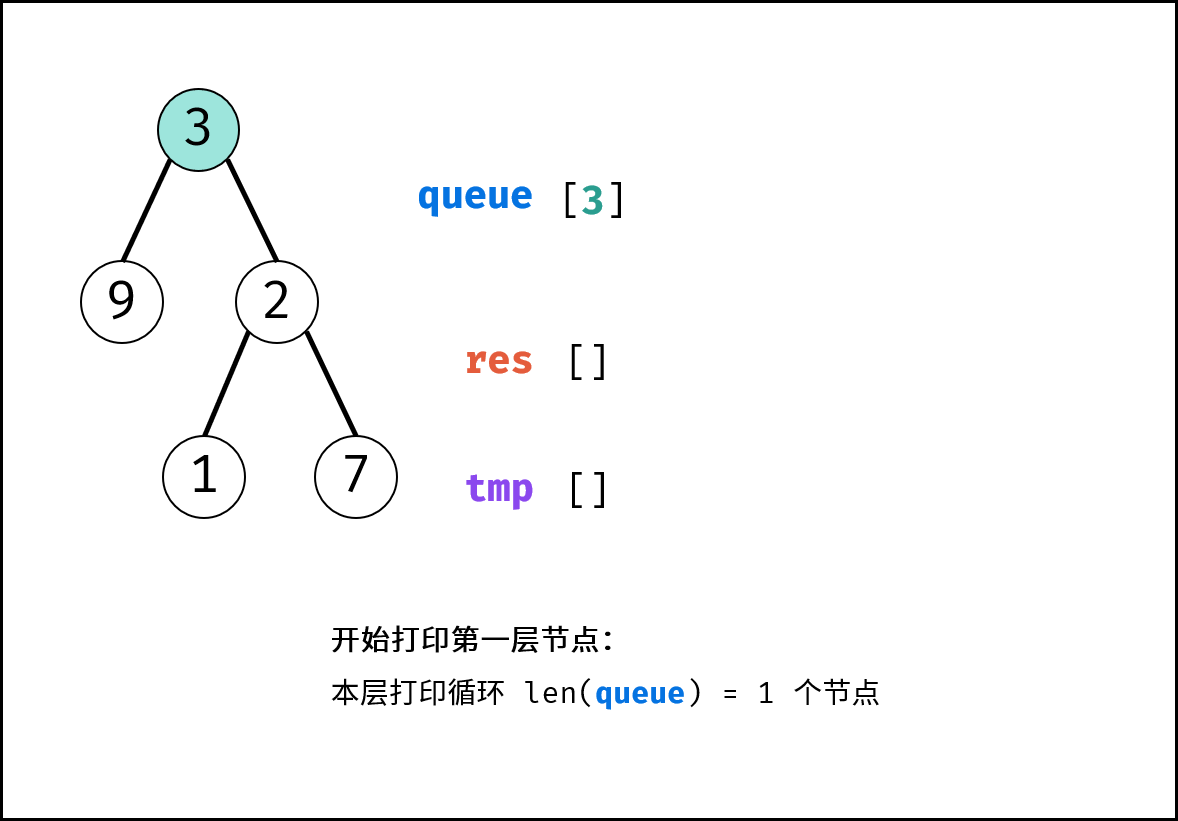
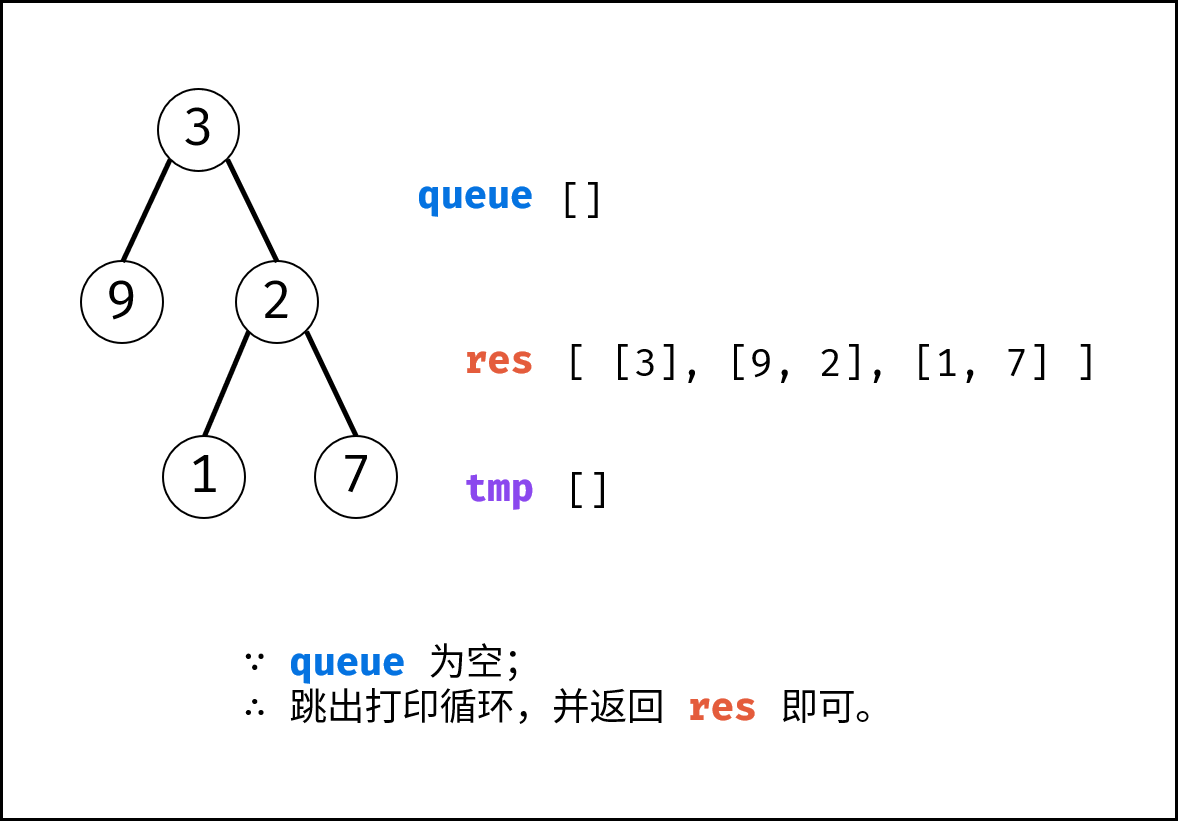
2. 初始化： 打印结果列表 res = [] ，包含根节点的队列 queue = [root] 。
3. BFS 循环： 当队列 queue 为空时跳出。
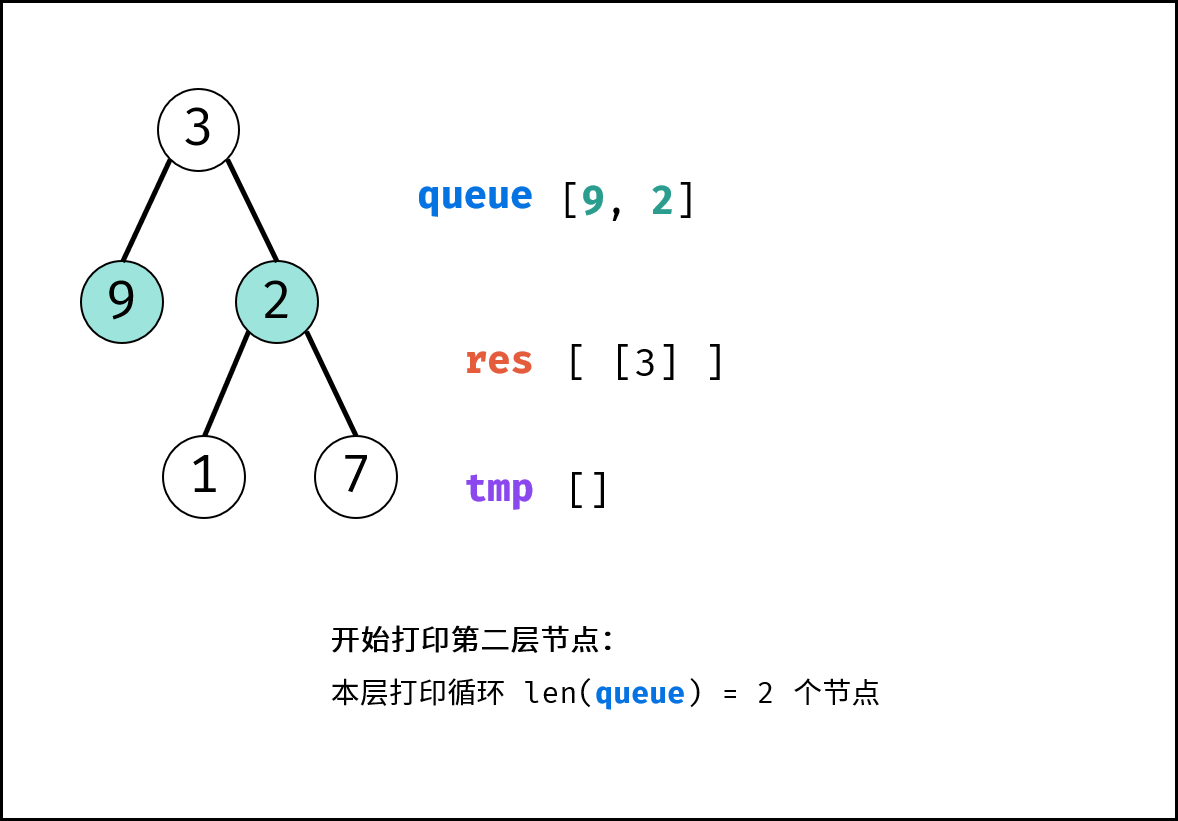
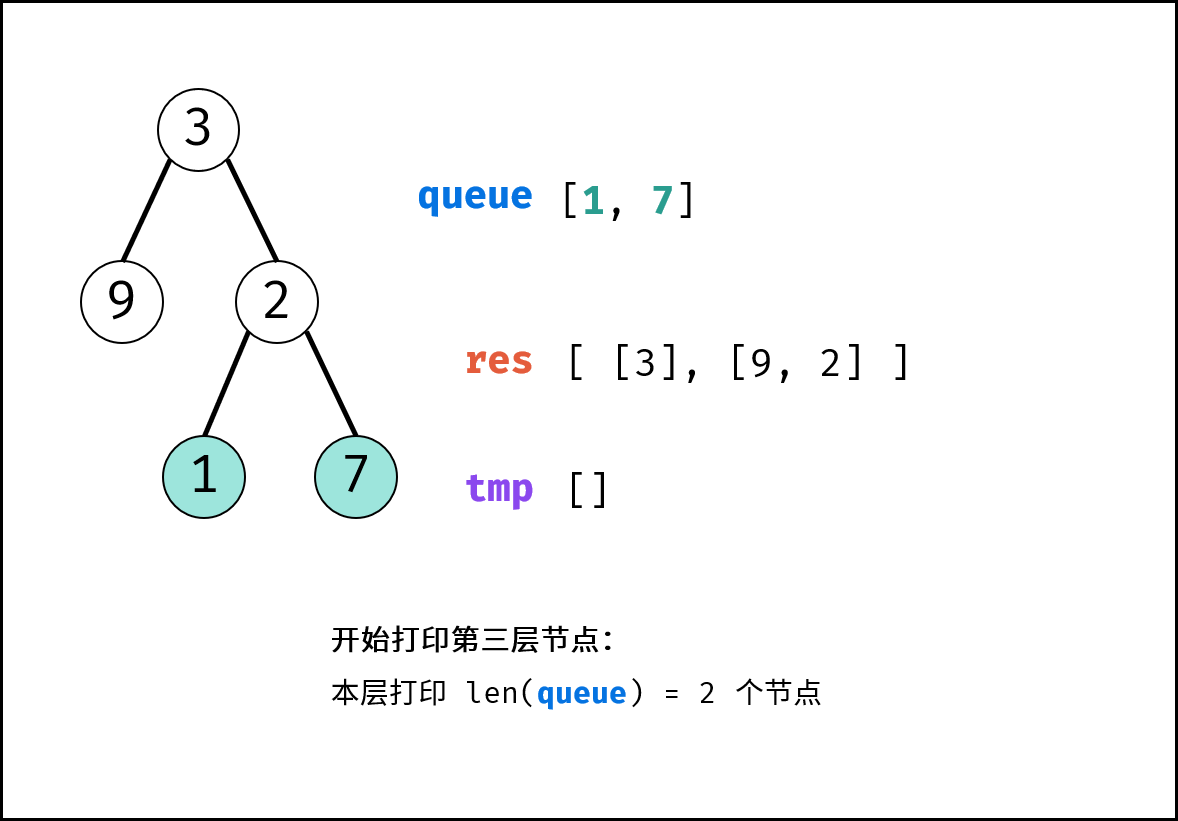
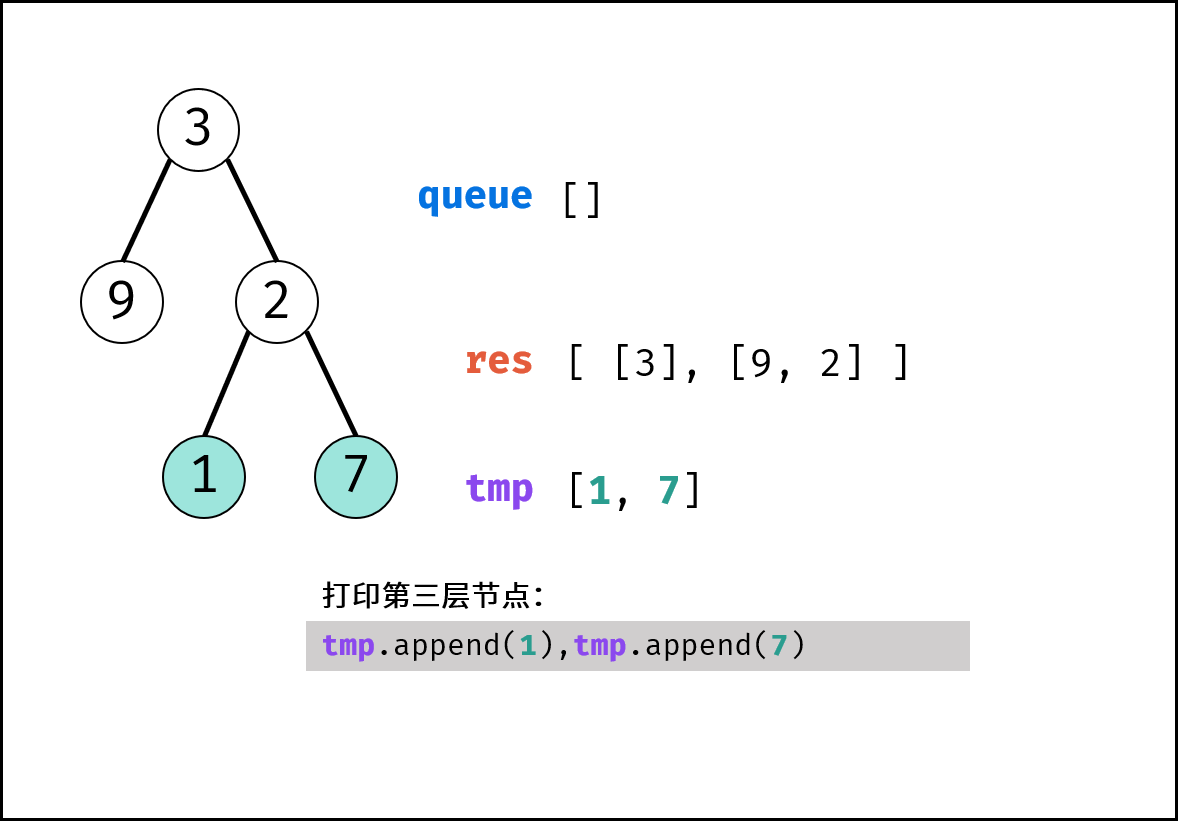
   1. 新建一个临时列表 tmp ，用于存储当前层打印结果。
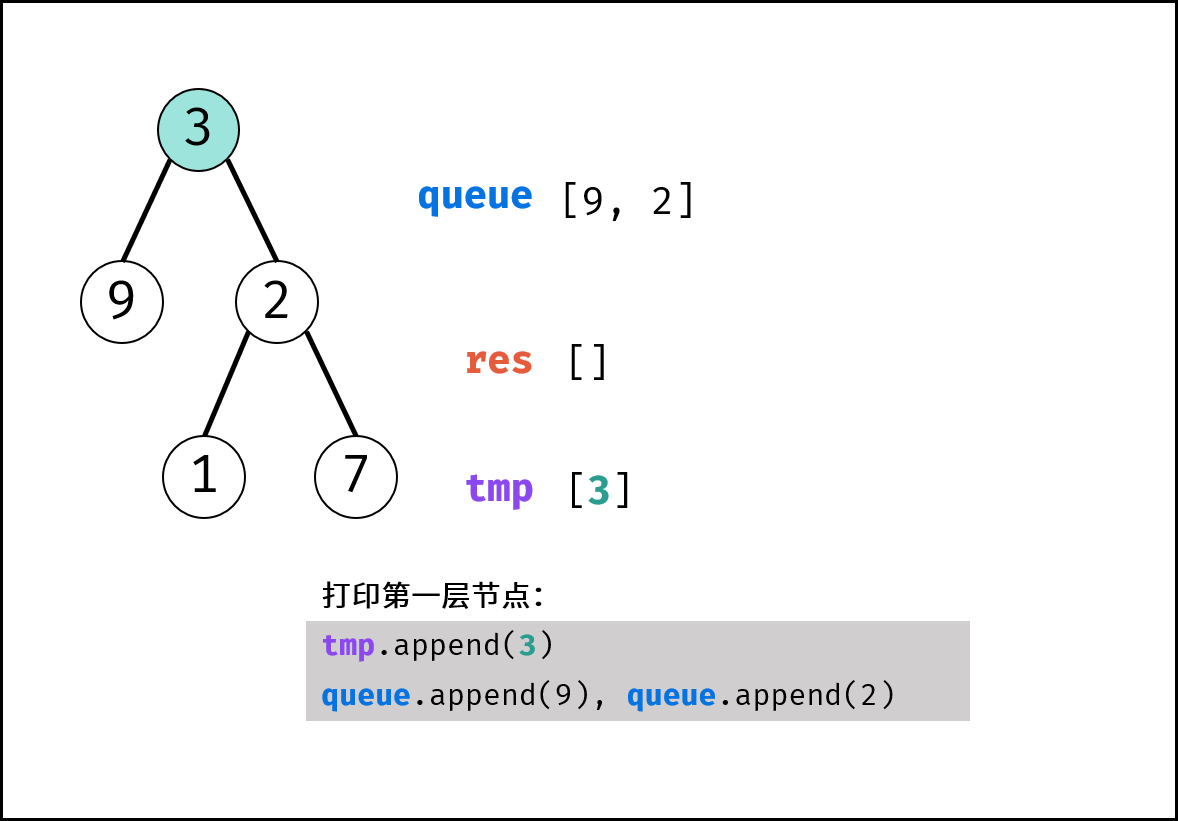
   2. 当前层打印循环： 循环次数为当前层节点数（即队列 queue 长度）。
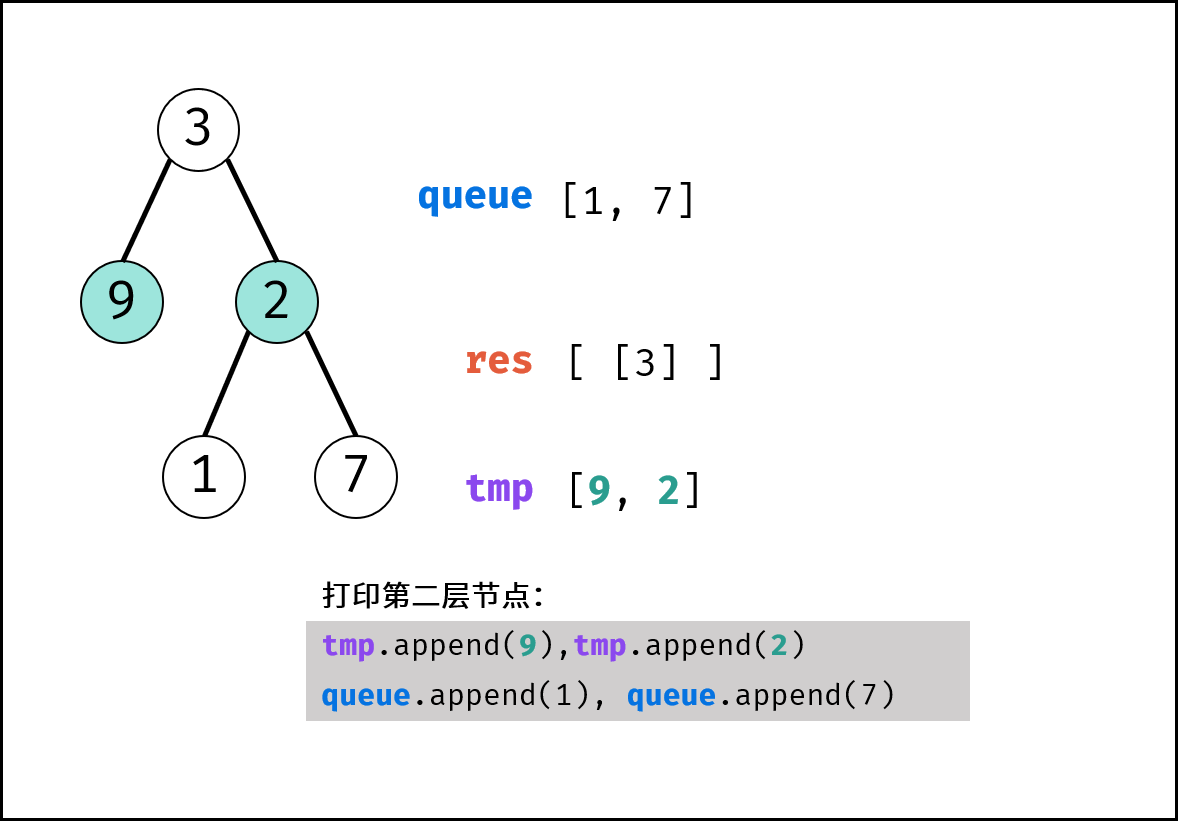
      1. 出队： 队首元素出队，记为 node。
      2. 打印： 将 node.val 添加至 tmp 尾部。
      3. 添加子节点： 若 node 的左（右）子节点不为空，则将左（右）子节点加入队列 queue 。
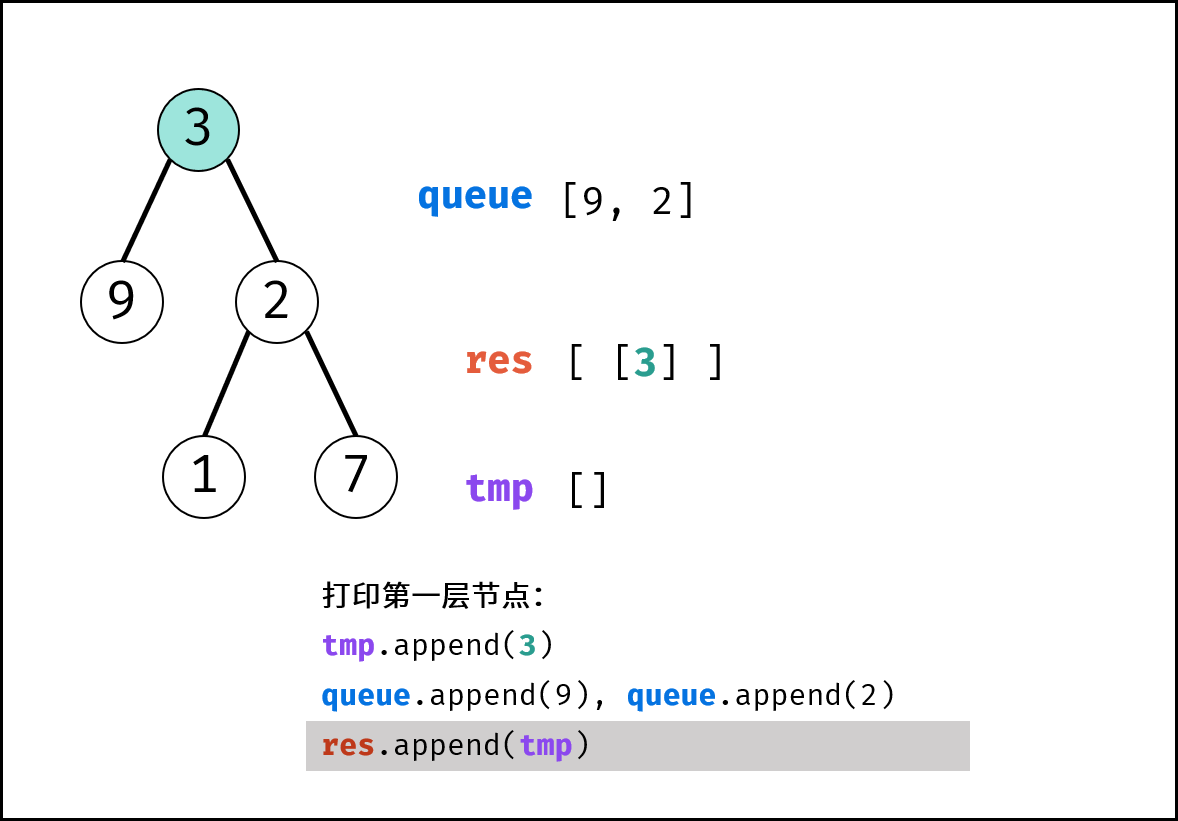
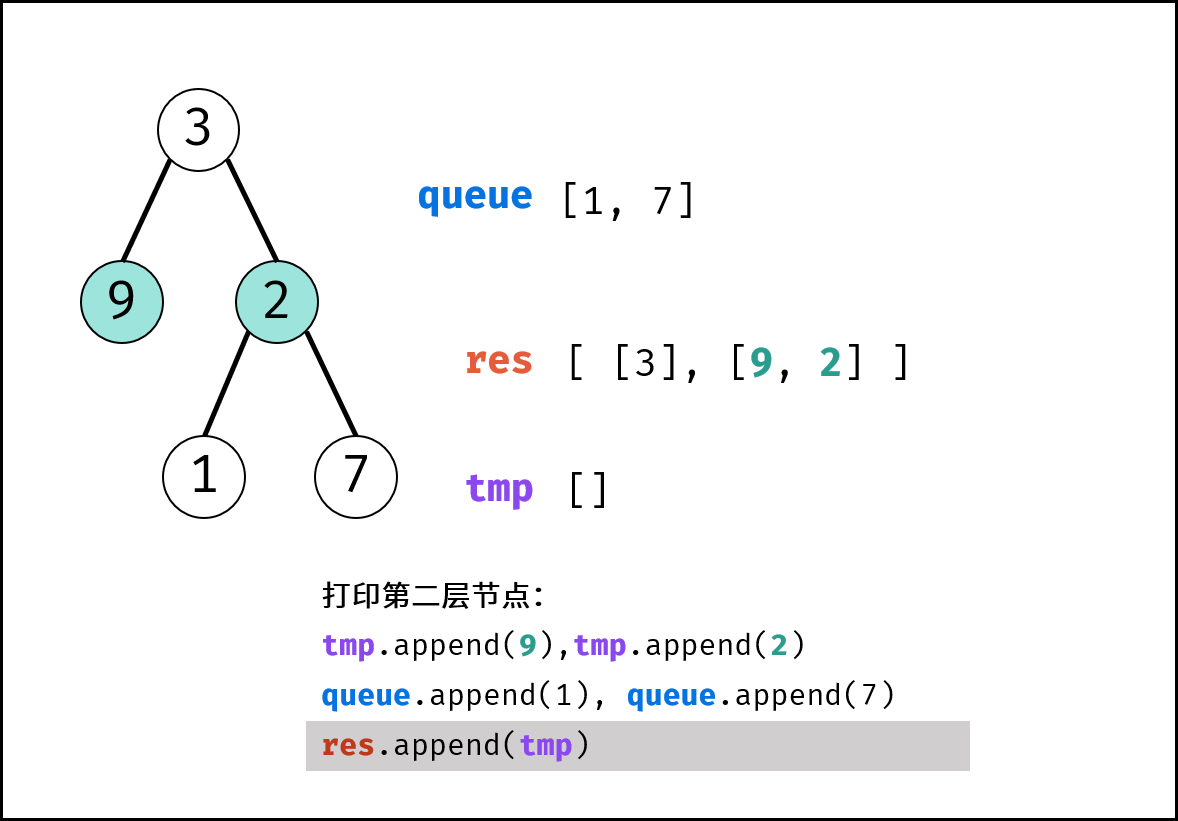
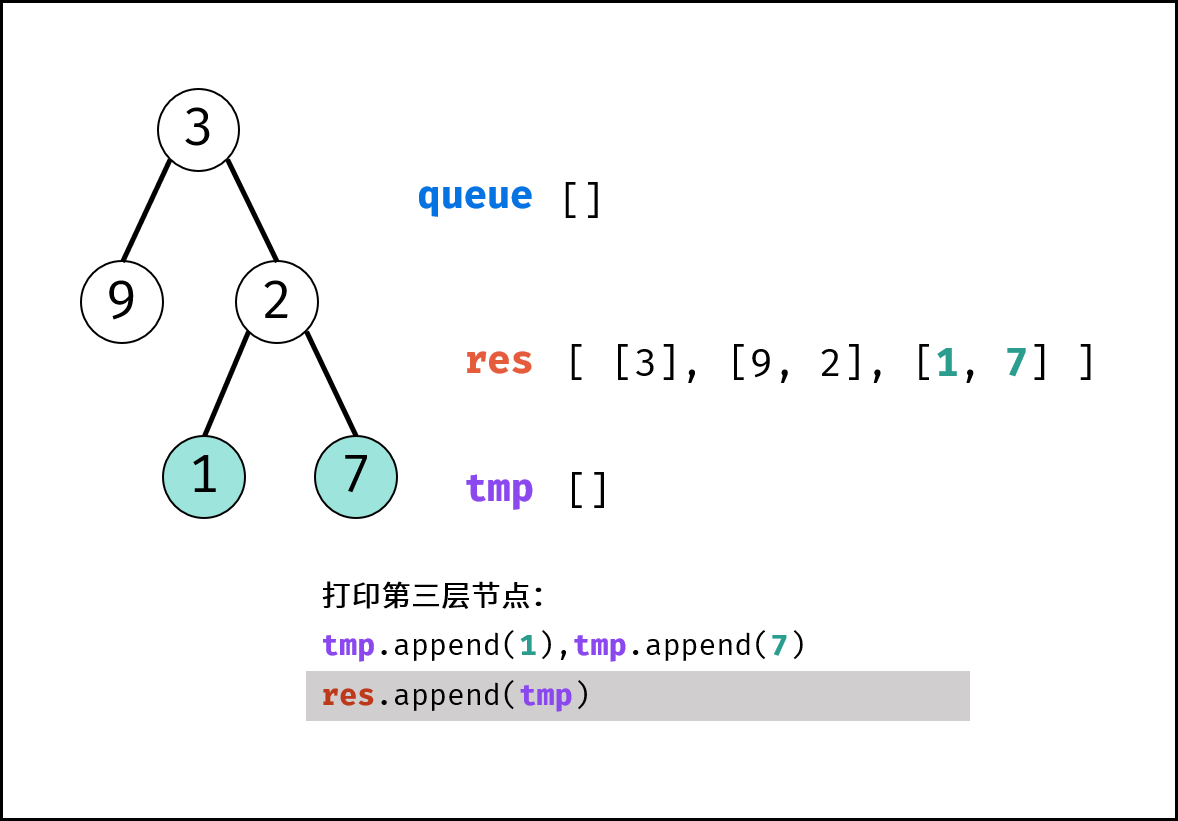
   3. 将当前层结果 tmp 添加入 res 。
4. 返回值： 返回打印结果列表 res 即可。

<,,,,,,,,,>

代码： ​

Python 中使用 collections 中的双端队列 deque() ，其 popleft() 方法可达到 $O(1)$ 时间复杂度；列表 list 的 pop(0) 方法时间复杂度为 $O(N)$ 。

class Solution:
    def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
        if not root: return []
        res, queue = [], collections.deque()
        queue.append(root)
        while queue:
            tmp = []
            for _ in range(len(queue)):
                node = queue.popleft()
                tmp.append(node.val)
                if node.left: queue.append(node.left)
                if node.right: queue.append(node.right)
            res.append(tmp)
        return res

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        Queue<TreeNode> queue = new LinkedList<>();
        List<List<Integer>> res = new ArrayList<>();
        if (root != null) queue.add(root);
        while (!queue.isEmpty()) {
            List<Integer> tmp = new ArrayList<>();
            for(int i = queue.size(); i > 0; i--) {
                TreeNode node = queue.poll();
                tmp.add(node.val);
                if (node.left != null) queue.add(node.left);
                if (node.right != null) queue.add(node.right);
            }
            res.add(tmp);
        }
        return res;
    }
}

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        queue<TreeNode*> que;
        vector<vector<int>> res;
        if (root != nullptr) que.push(root);
        while (!que.empty()) {
            vector<int> tmp;
            for(int i = que.size(); i > 0; --i) {
                root = que.front();
                que.pop();
                tmp.push_back(root->val);
                if (root->left != nullptr) que.push(root->left);
                if (root->right != nullptr) que.push(root->right);
            }
            res.push_back(tmp);
        }
        return res;
    }
};

复杂度分析： ​

• 时间复杂度 $O(N)$ ： $N$ 为二叉树的节点数量，即 BFS 需循环 $N$ 次。
• 空间复杂度 $O(N)$ ： 最差情况下，即当树为平衡二叉树时，最多有 $N/2$ 个树节点同时在 queue 中，使用 $O(N)$ 大小的额外空间。