解题思路:
本文将
arrayA,arrayB简写为A,B。
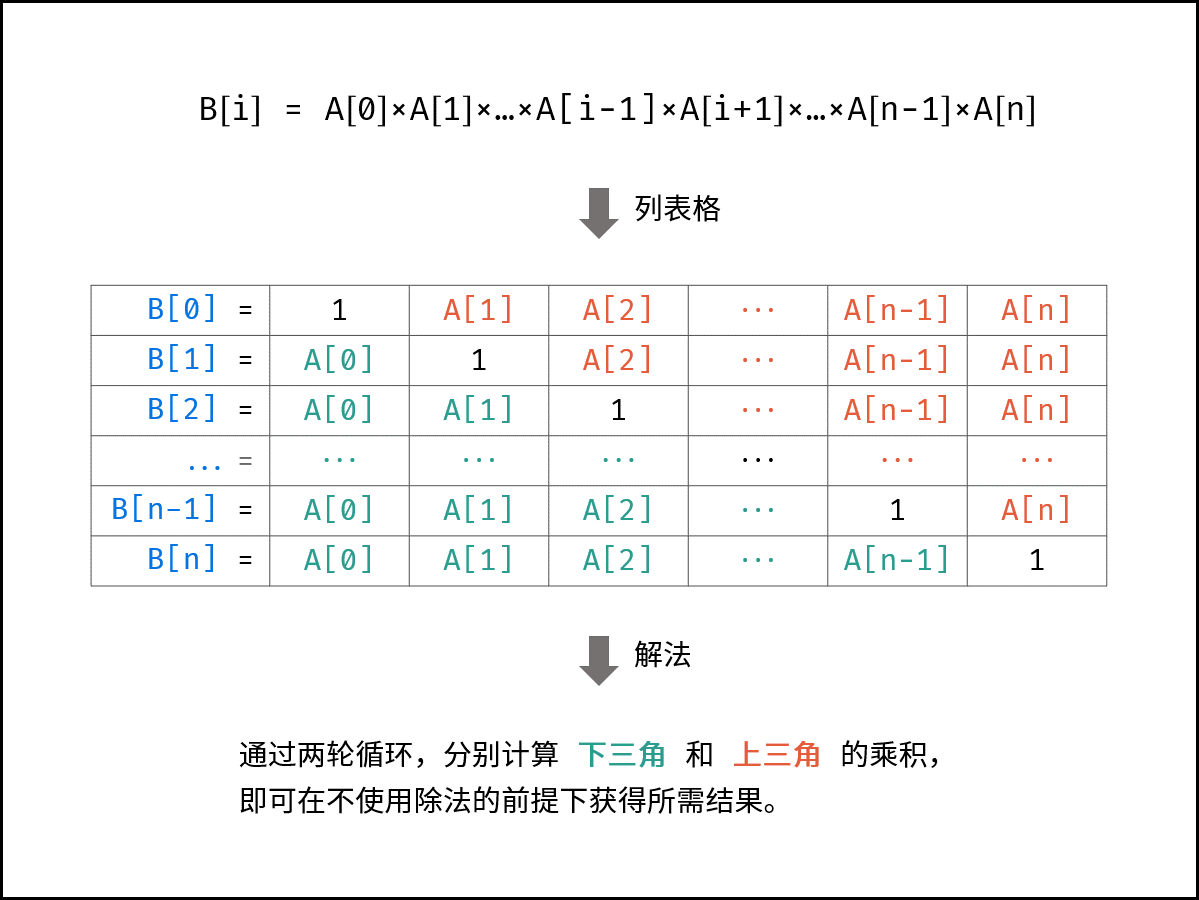
本题的难点在于 不能使用除法 ,即需要 只用乘法 生成数组 $B$ 。根据题目对 $B[i]$ 的定义,可列如下图所示的表格。
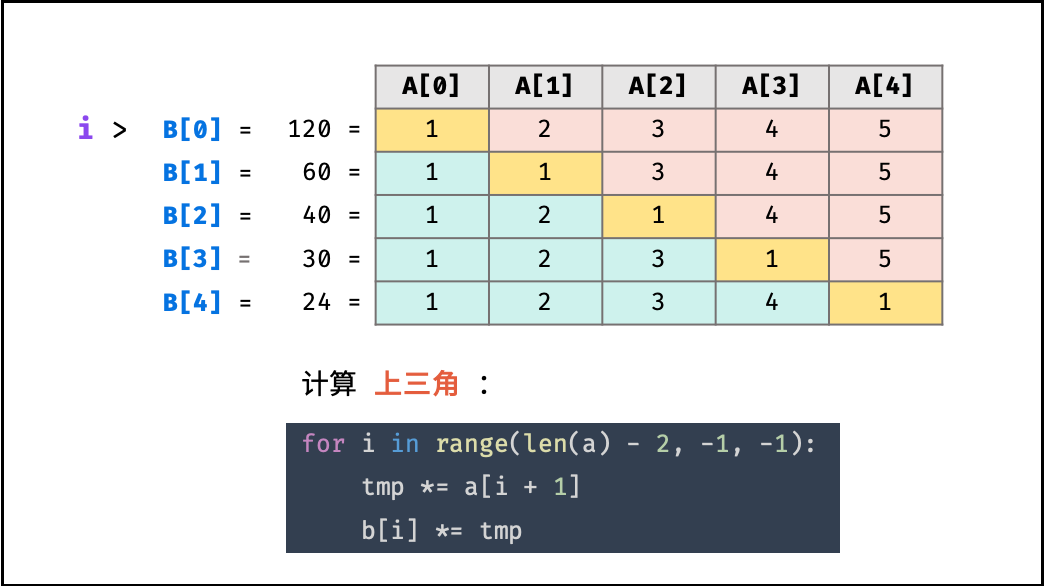
根据表格的主对角线(全为 $1$ ),可将表格分为 上三角 和 下三角 两部分。分别迭代计算下三角和上三角两部分的乘积,即可 不使用除法 就获得结果。
算法流程:
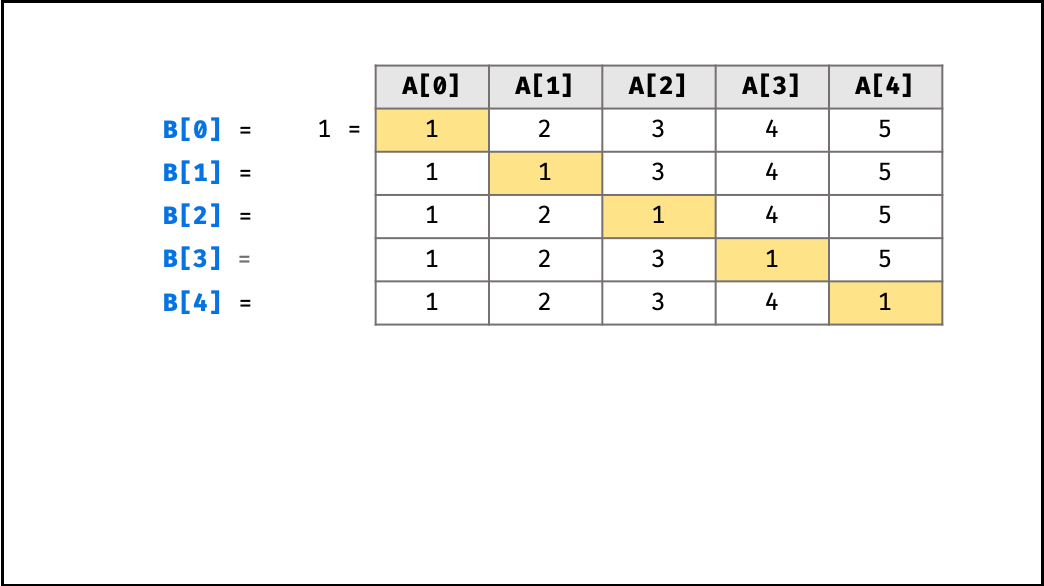
- 初始化:数组 $B$ ,其中 $B[0] = 1$ ;辅助变量 $tmp = 1$ ;
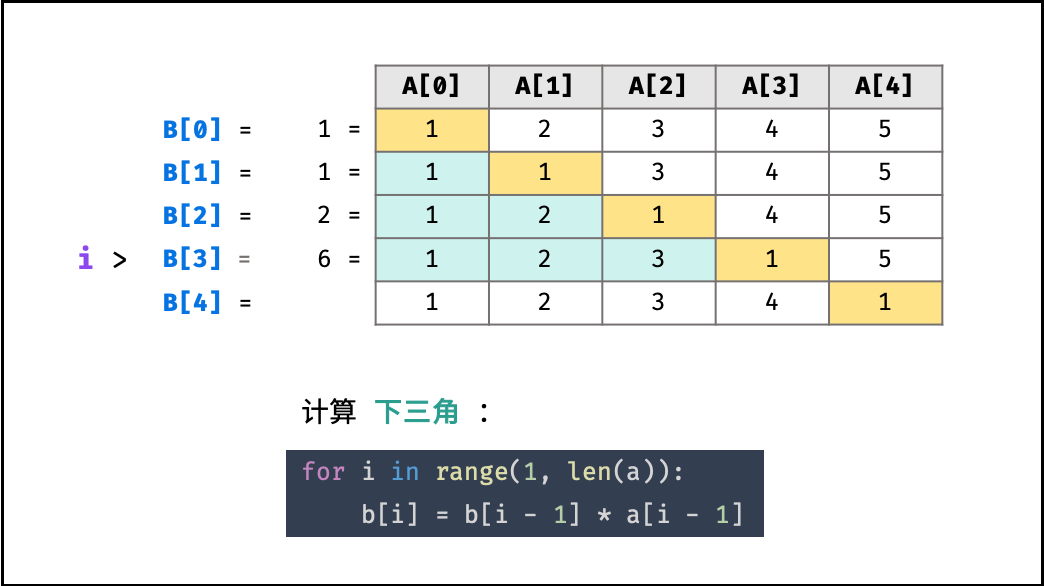
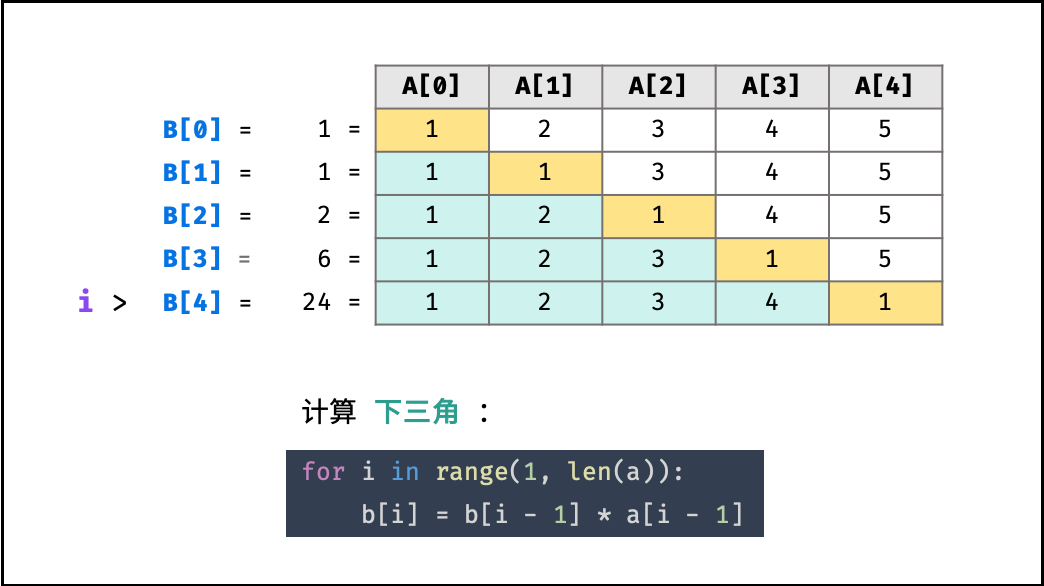
- 计算 $B[i]$ 的 下三角 各元素的乘积,直接乘入 $B[i]$ ;
- 计算 $B[i]$ 的 上三角 各元素的乘积,记为 $tmp$ ,并乘入 $B[i]$ ;
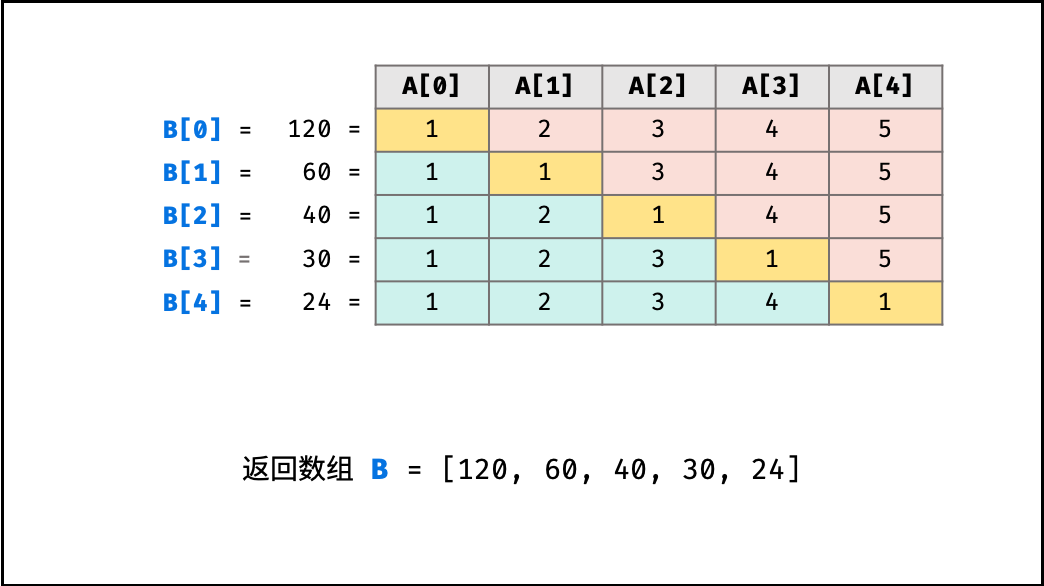
- 返回 $B$ 。
< ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, >
>
代码:
Python
class Solution:
def statisticalResult(self, arrayA: List[int]) -> List[int]:
arrayB, tmp = [1] * len(arrayA), 1
for i in range(1, len(arrayA)):
arrayB[i] = arrayB[i - 1] * arrayA[i - 1]
for i in range(len(arrayA) - 2, -1, -1):
tmp *= arrayA[i + 1]
arrayB[i] *= tmp
return arrayBJava
class Solution {
public int[] statisticalResult(int[] arrayA) {
int len = arrayA.length;
if(len == 0) return new int[0];
int[] arrayB = new int[len];
arrayB[0] = 1;
int tmp = 1;
for(int i = 1; i < len; i++) {
arrayB[i] = arrayB[i - 1] * arrayA[i - 1];
}
for(int i = len - 2; i >= 0; i--) {
tmp *= arrayA[i + 1];
arrayB[i] *= tmp;
}
return arrayB;
}
}C++
class Solution {
public:
vector<int> statisticalResult(vector<int>& arrayA) {
int len = arrayA.size();
if(len == 0) return {};
vector<int> arrayB(len, 1);
arrayB[0] = 1;
int tmp = 1;
for(int i = 1; i < len; i++) {
arrayB[i] = arrayB[i - 1] * arrayA[i - 1];
}
for(int i = len - 2; i >= 0; i--) {
tmp *= arrayA[i + 1];
arrayB[i] *= tmp;
}
return arrayB;
}
};复杂度分析:
- 时间复杂度 $O(N)$ : 其中 $N$ 为数组长度,两轮遍历数组 $A$ ,使用 $O(N)$ 时间。
- 空间复杂度 $O(1)$ : 变量 $tmp$ 使用常数大小额外空间(数组 $B$ 作为返回值,不计入复杂度考虑)。