解题思路： ​

利用 HashMap 可以通过遍历数组找到数字组合，时间和空间复杂度均为 $O(N)$ 。 注意本题的 $price$ 是 排序数组 ，因此可使用 双指针法 将空间优化至 $O(1)$ 。

算法流程： ​

1. 初始化： 双指针 $i$ , $j$ 分别指向数组 $price$ 的左右两端。
2. 循环搜索： 当双指针相遇时跳出；
   1. 计算和 $s = price[i] + price[j]$ ；
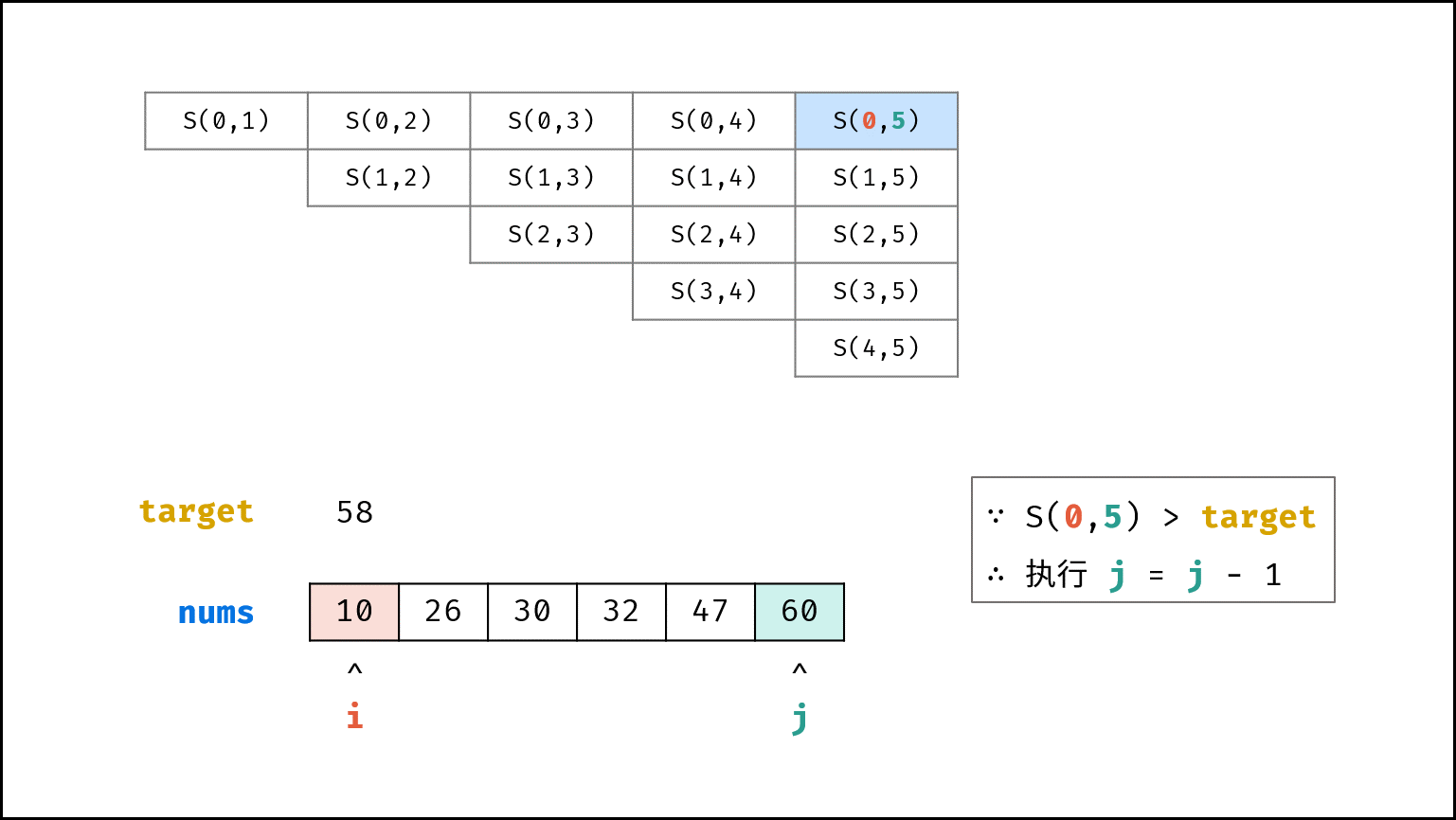
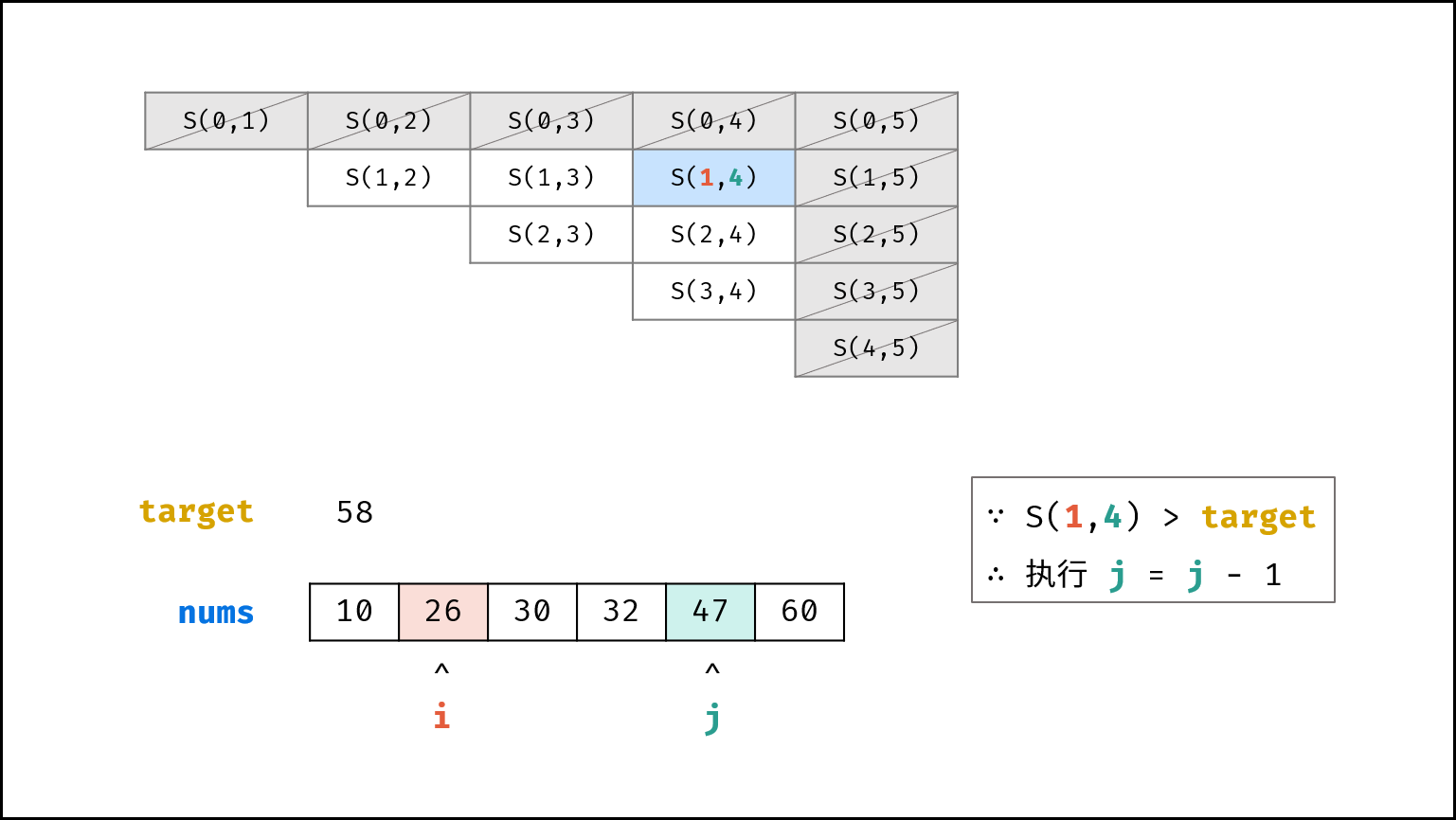
   2. 若 $s > target$ ，则指针 $j$ 向左移动，即执行 $j = j - 1$ ；
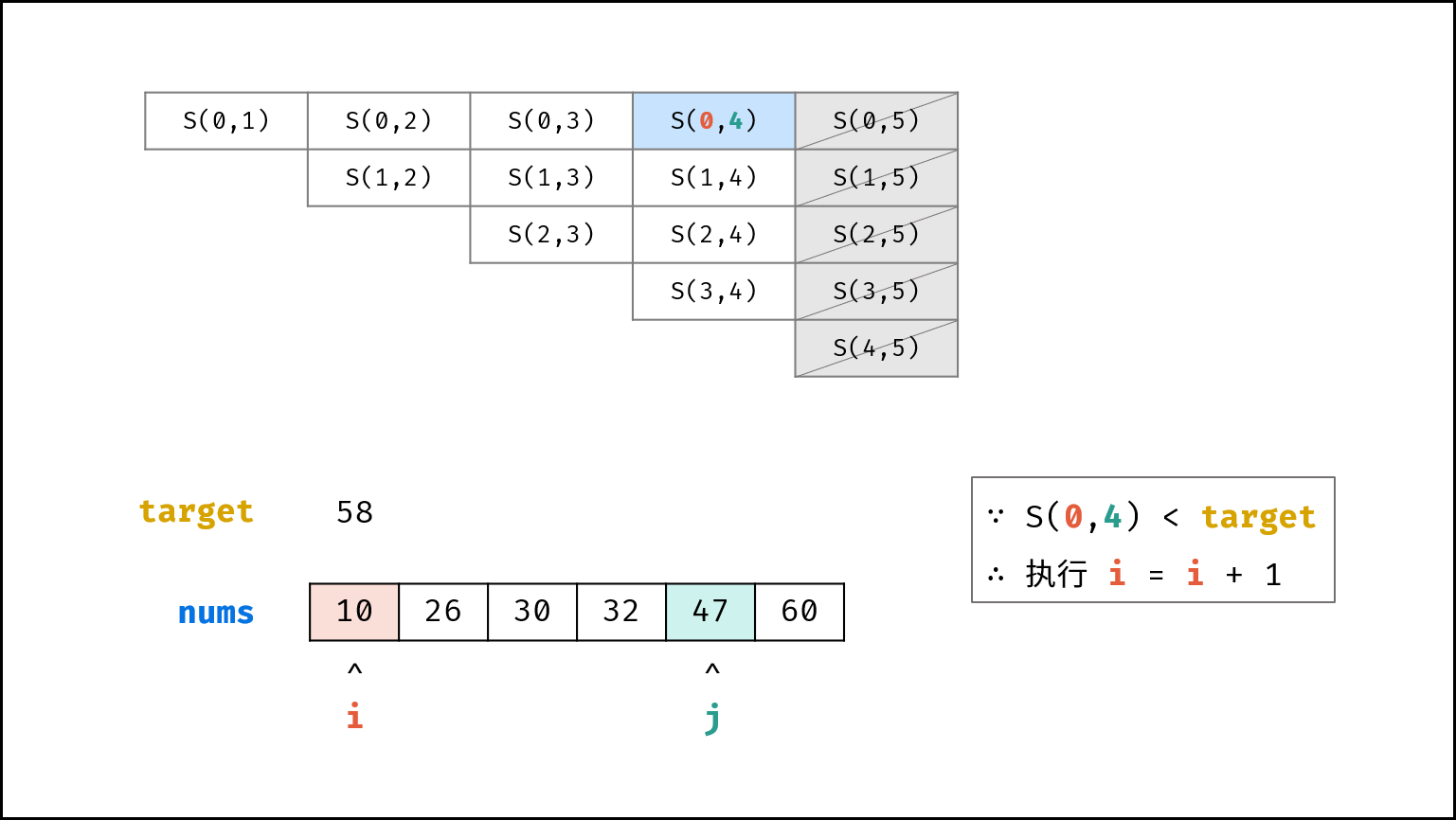
   3. 若 $s < target$ ，则指针 $i$ 向右移动，即执行 $i = i + 1$ ；
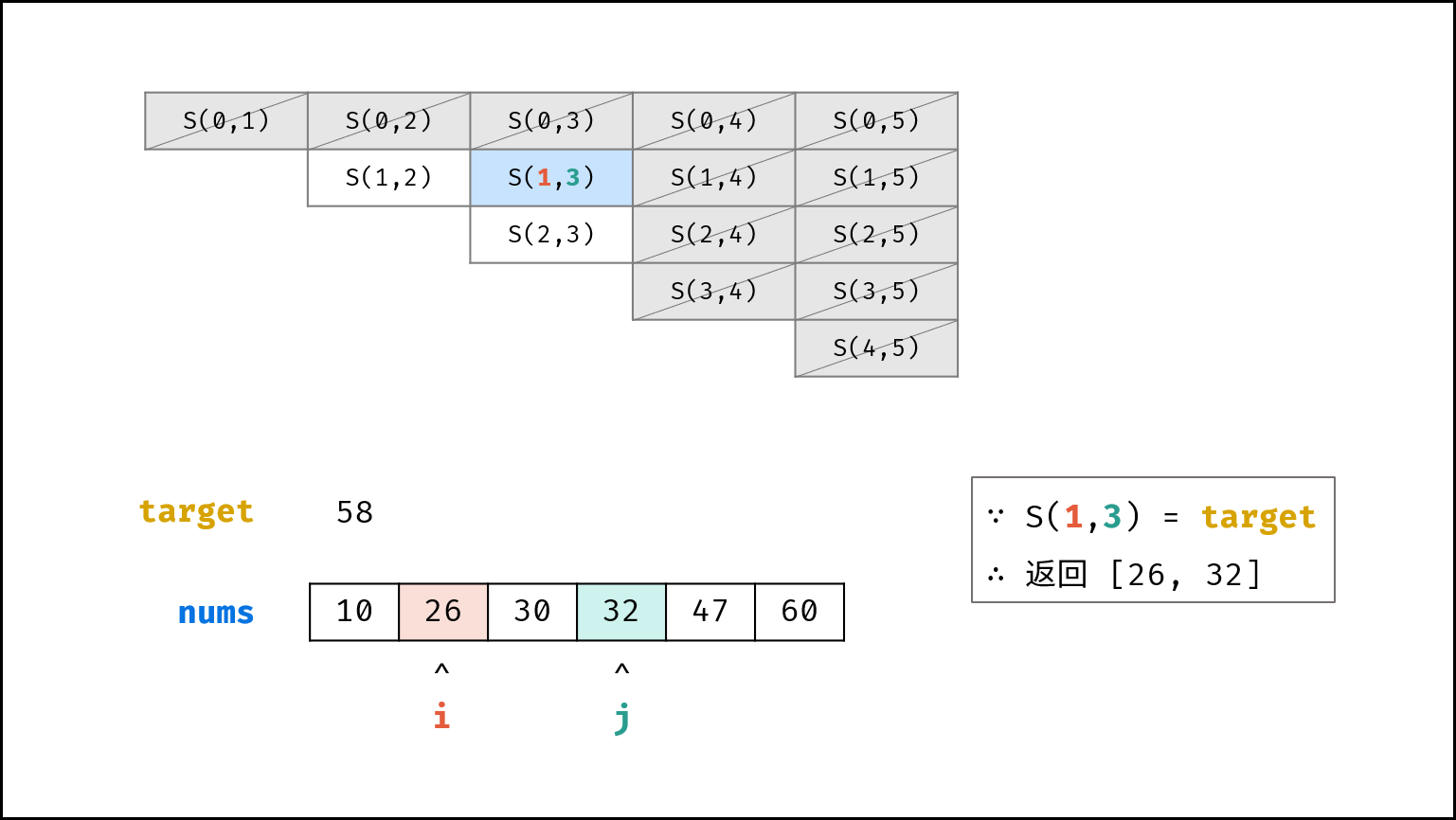
   4. 若 $s = target$ ，立即返回数组 $[price[i], price[j]]$ ；
3. 若循环结束，则返回空数组，代表无和为 $target$ 的数字组合。

下图中的 nums 对应本题的 price 。

<,,,>

正确性证明： ​

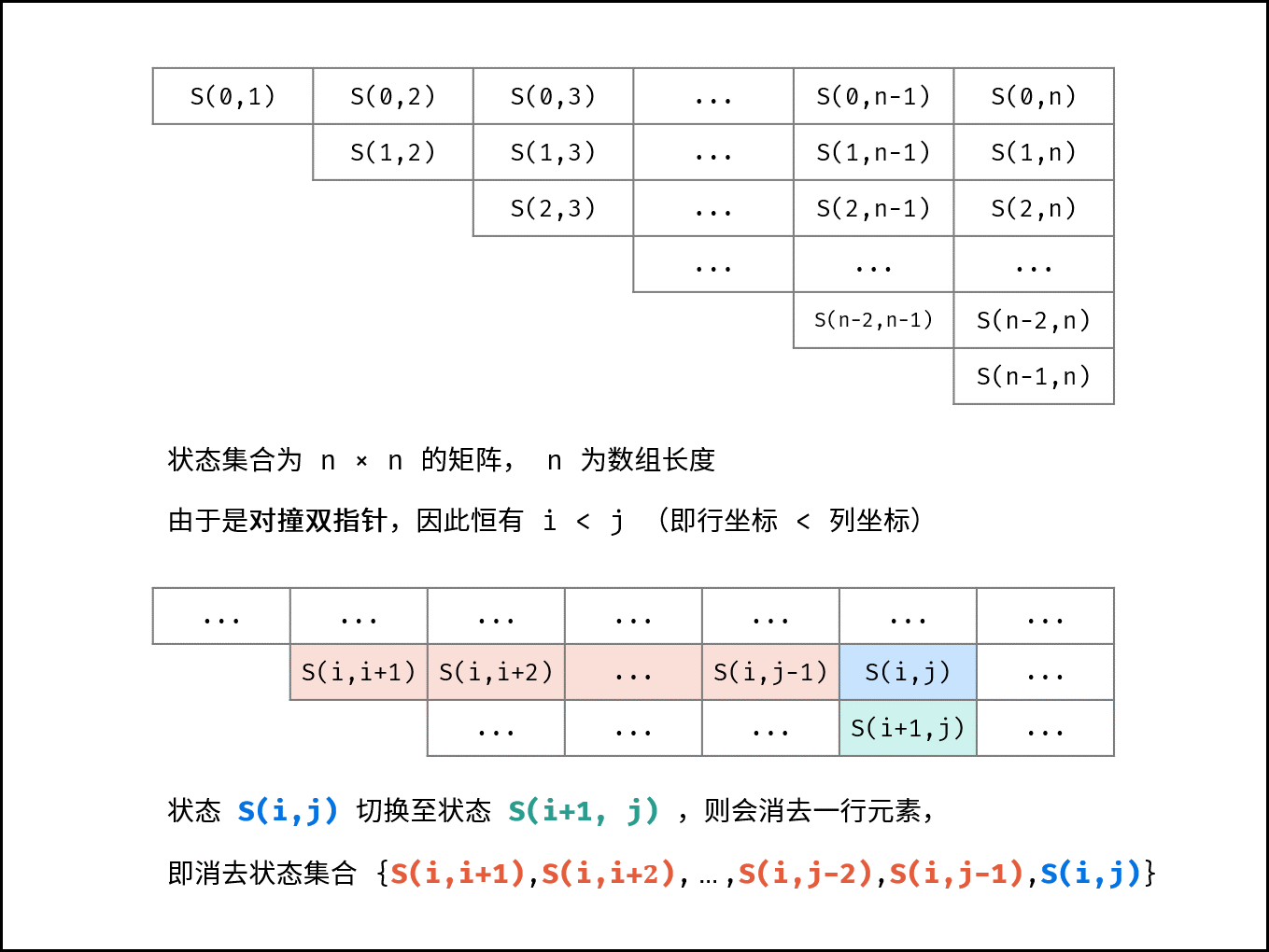
记每个状态为 $S(i, j)$ ，即 $S(i, j) = price[i] + price[j]$ 。假设 $S(i, j) < target$ ，则执行 $i = i + 1$ ，即状态切换至 $S(i + 1, j)$ 。

状态 $S(i, j)$ 切换至 $S(i + 1, j)$ ，则会消去一行元素，相当于 消去了状态集合 {$S(i, i + 1), S(i, i + 2), ..., S(i, j - 2), S(i, j - 1), S(i, j)$ } 。（由于双指针都是向中间收缩，因此这些状态之后不可能再遇到）。

由于 $price$ 是排序数组，因此这些 消去的状态 都一定满足 $S(i, j) < target$ ，即这些状态都 不是解 。

结论： 以上分析已证明 “每次指针 $i$ 的移动操作，都不会导致解的丢失” ，即指针 $i$ 的移动操作是安全的；同理，对于指针 $j$ 可得出同样推论；因此，此双指针法是正确的。

代码： ​

class Solution:
    def twoSum(self, price: List[int], target: int) -> List[int]:
        i, j = 0, len(price) - 1
        while i < j:
            s = price[i] + price[j]
            if s > target: j -= 1
            elif s < target: i += 1
            else: return price[i], price[j]
        return []

class Solution {
    public int[] twoSum(int[] price, int target) {
        int i = 0, j = price.length - 1;
        while(i < j) {
            int s = price[i] + price[j];
            if(s < target) i++;
            else if(s > target) j--;
            else return new int[] { price[i], price[j] };
        }
        return new int[0];
    }
}

class Solution {
public:
    vector<int> twoSum(vector<int>& price, int target) {
        int i = 0, j = price.size() - 1;
        while(i < j) {
            int s = price[i] + price[j];
            if(s < target) i++;
            else if(s > target) j--;
            else return { price[i], price[j] };
        }
        return {};
    }
};

复杂度分析： ​

• 时间复杂度 $O(N)$ ： $N$ 为数组 $price$ 的长度；双指针共同线性遍历整个数组。
• 空间复杂度 $O(1)$ ： 变量 $i$, $j$ 使用常数大小的额外空间。