解题思路:
题目说明:从棋盘的左上角开始拿格子里的珠宝,并每次 向右 或者 向下 移动一格、直到到达棋盘的右下角。 根据题目说明,易得某单元格只可能从上边单元格或左边单元格到达。
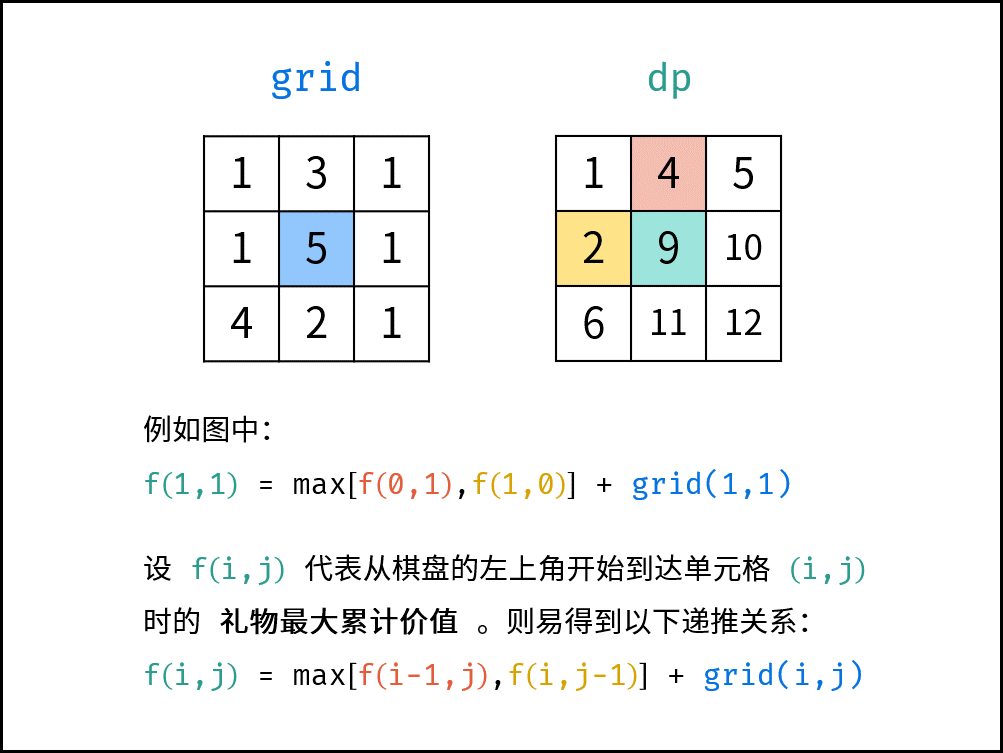
设 $f(i, j)$ 为从棋盘左上角走至单元格 $(i ,j)$ 的珠宝最大累计价值,易得到以下递推关系:$f(i,j)$ 等于 $f(i,j-1)$ 和 $f(i-1,j)$ 中的较大值加上当前单元格珠宝价值 $frame(i,j)$ 。
$$ f(i,j) = \max[f(i,j-1), f(i-1,j)] + frame(i,j) $$
因此,可用动态规划解决此问题,以上公式便为转移方程。
下图中的
grid对应本题的frame。
动态规划解析:
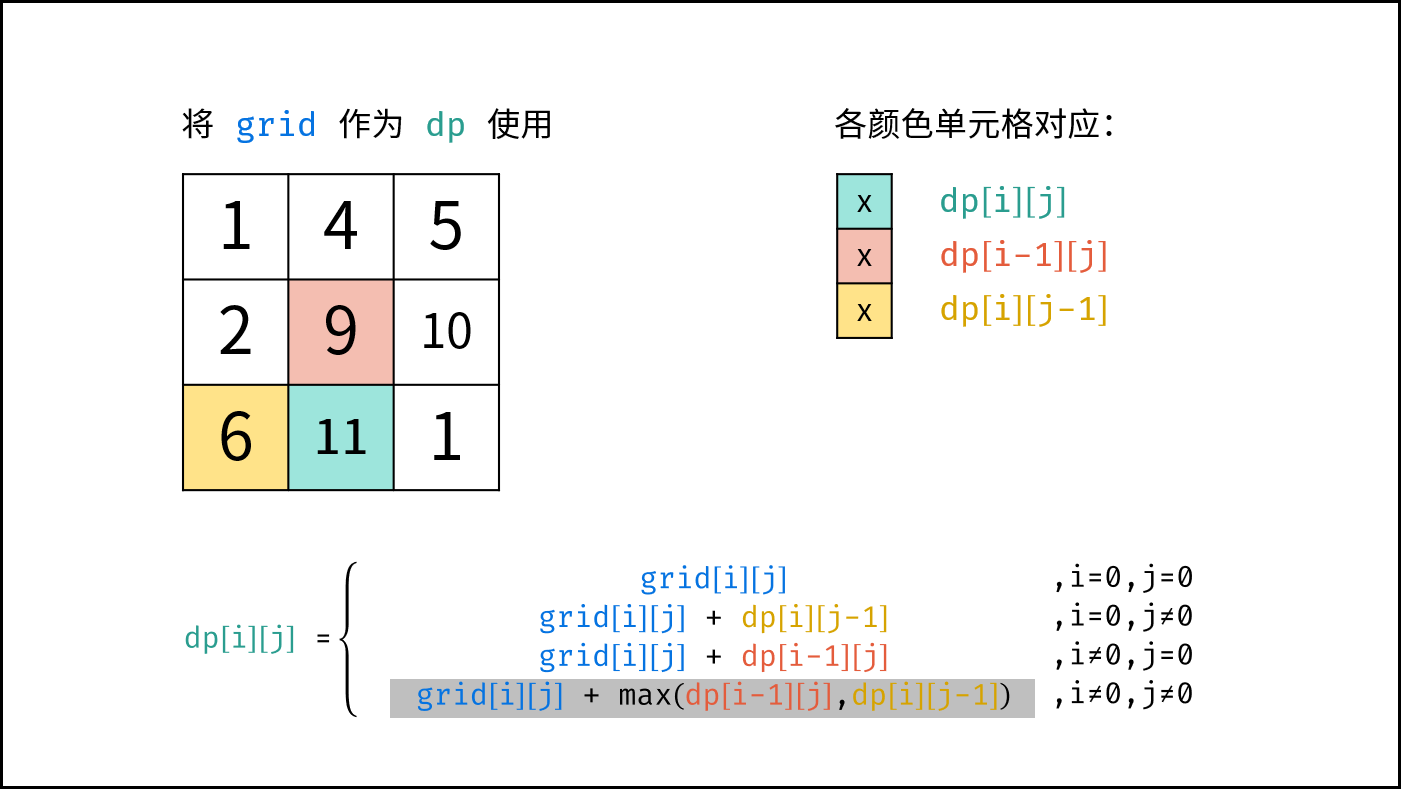
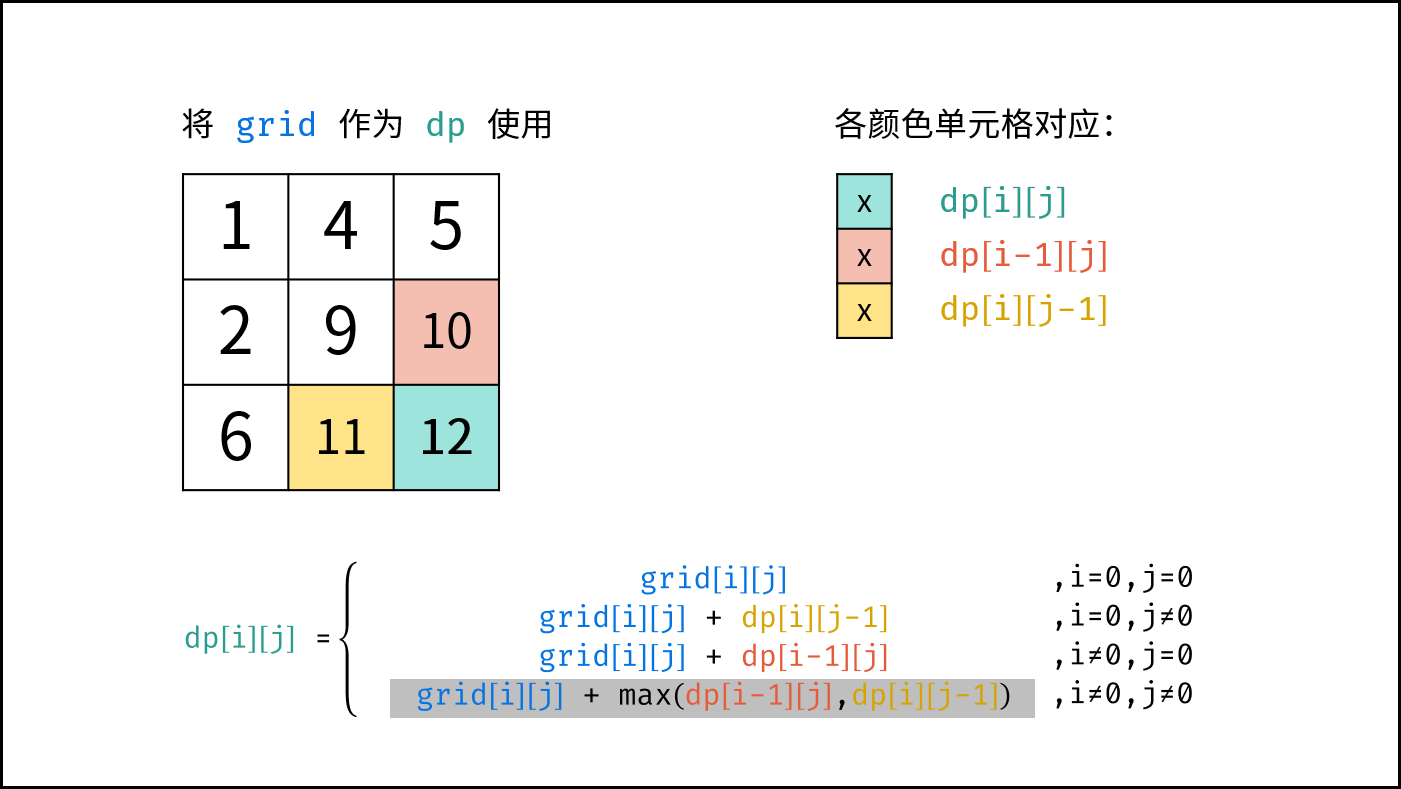
状态定义: 设动态规划矩阵 $dp$ ,$dp(i,j)$ 代表从棋盘的左上角开始,到达单元格 $(i,j)$ 时能拿到珠宝的最大累计价值。
转移方程:
- 当 $i = 0$ 且 $j = 0$ 时,为起始元素;
- 当 $i = 0$ 且 $j \ne 0$ 时,为矩阵第一行元素,只可从左边到达;
- 当 $i \ne 0$ 且 $j = 0$ 时,为矩阵第一列元素,只可从上边到达;
- 当 $i \ne 0$ 且 $j \ne 0$ 时,可从左边或上边到达;
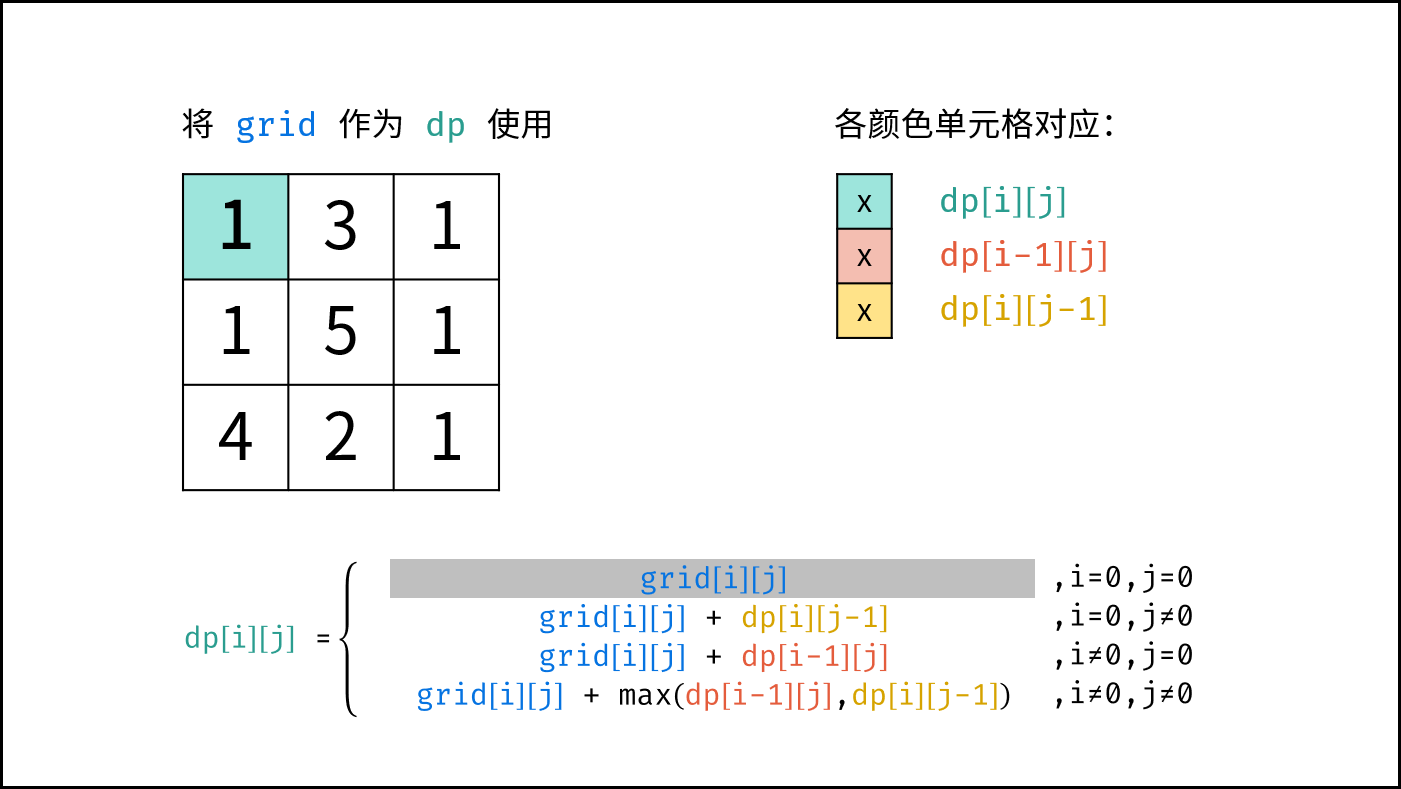
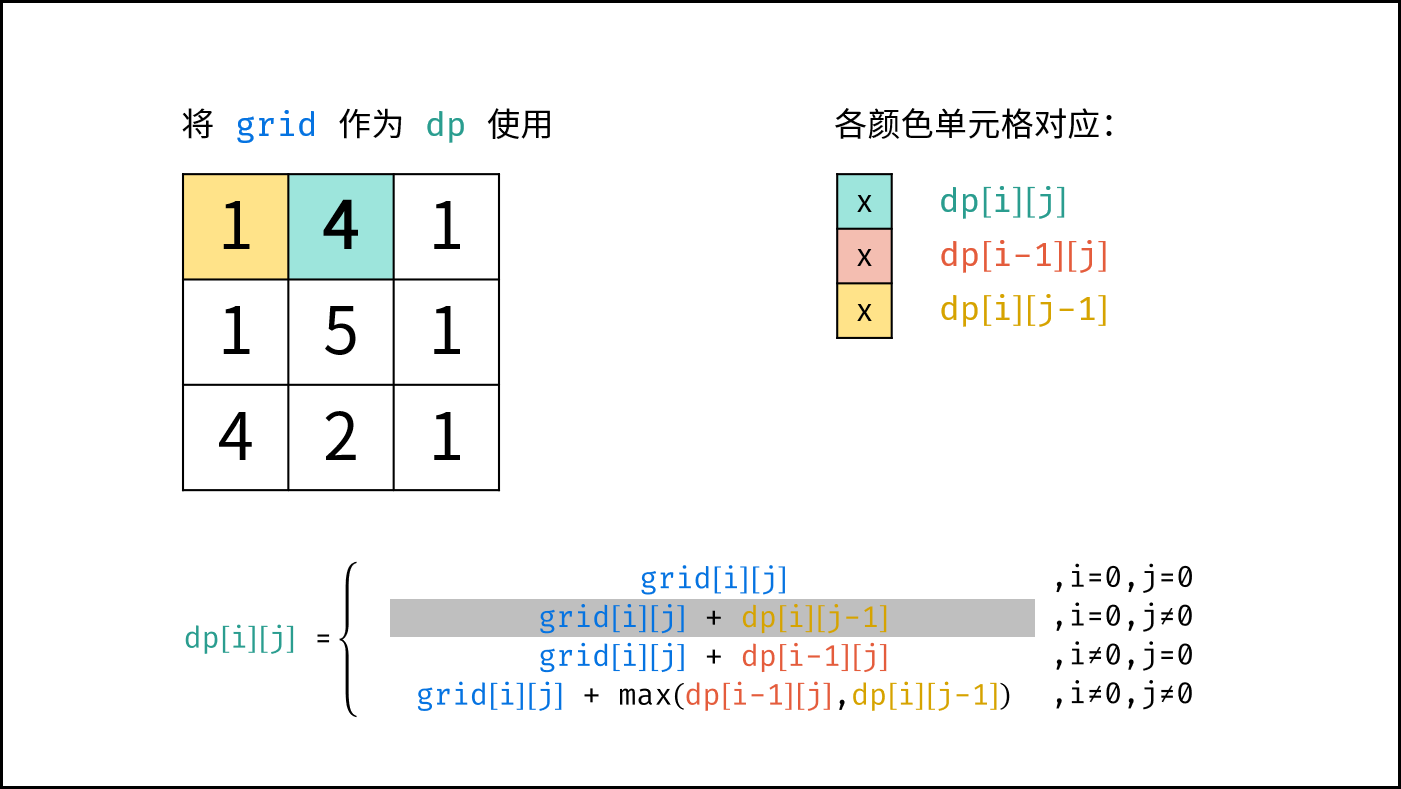
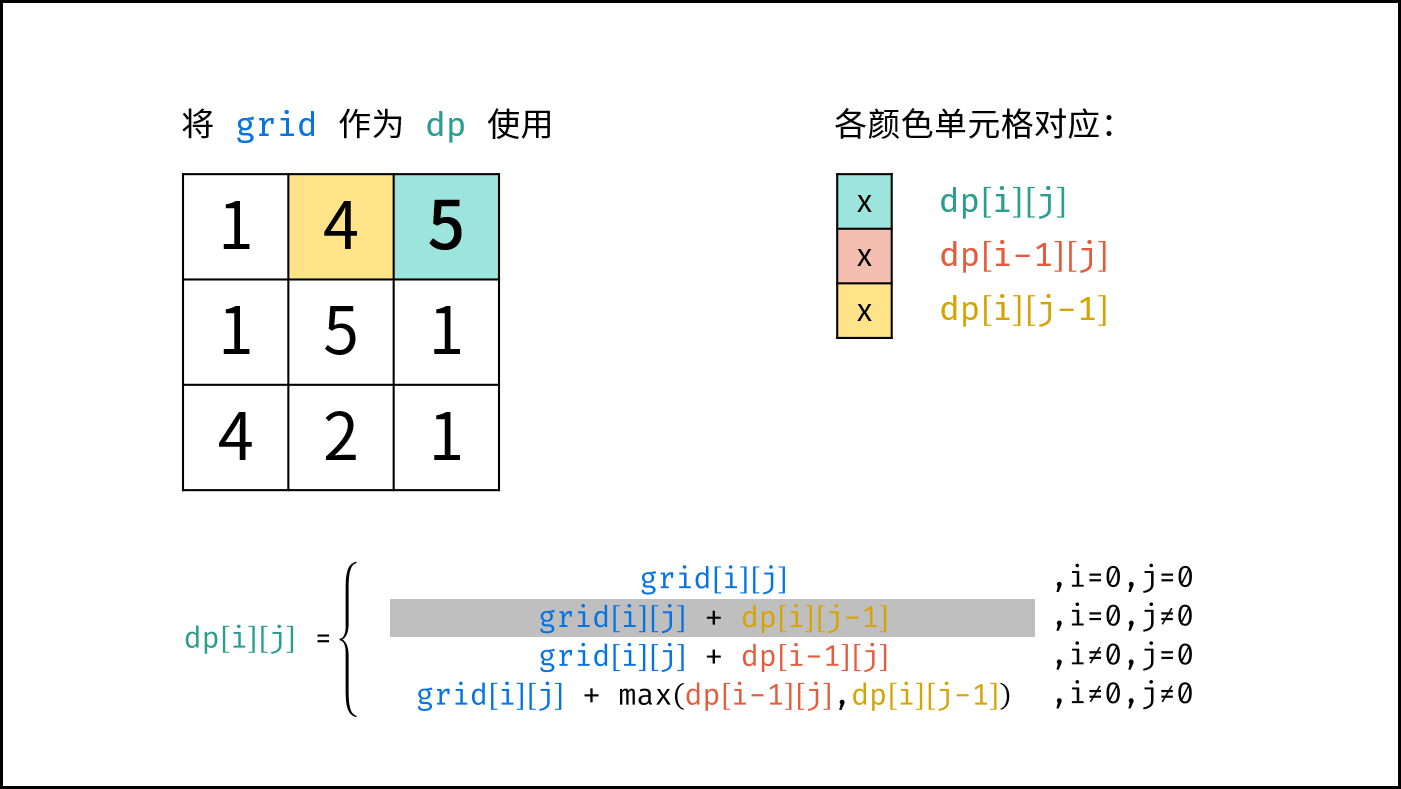
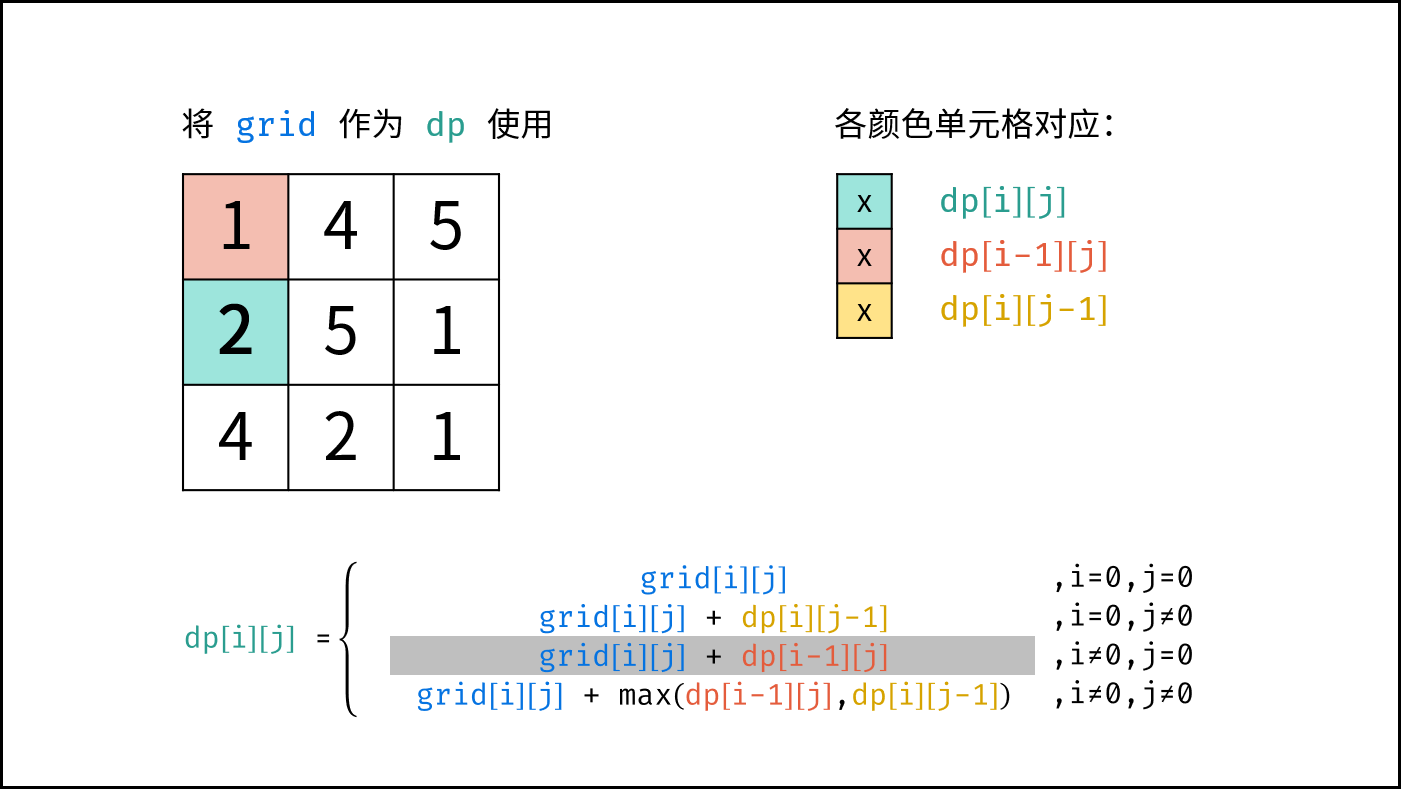
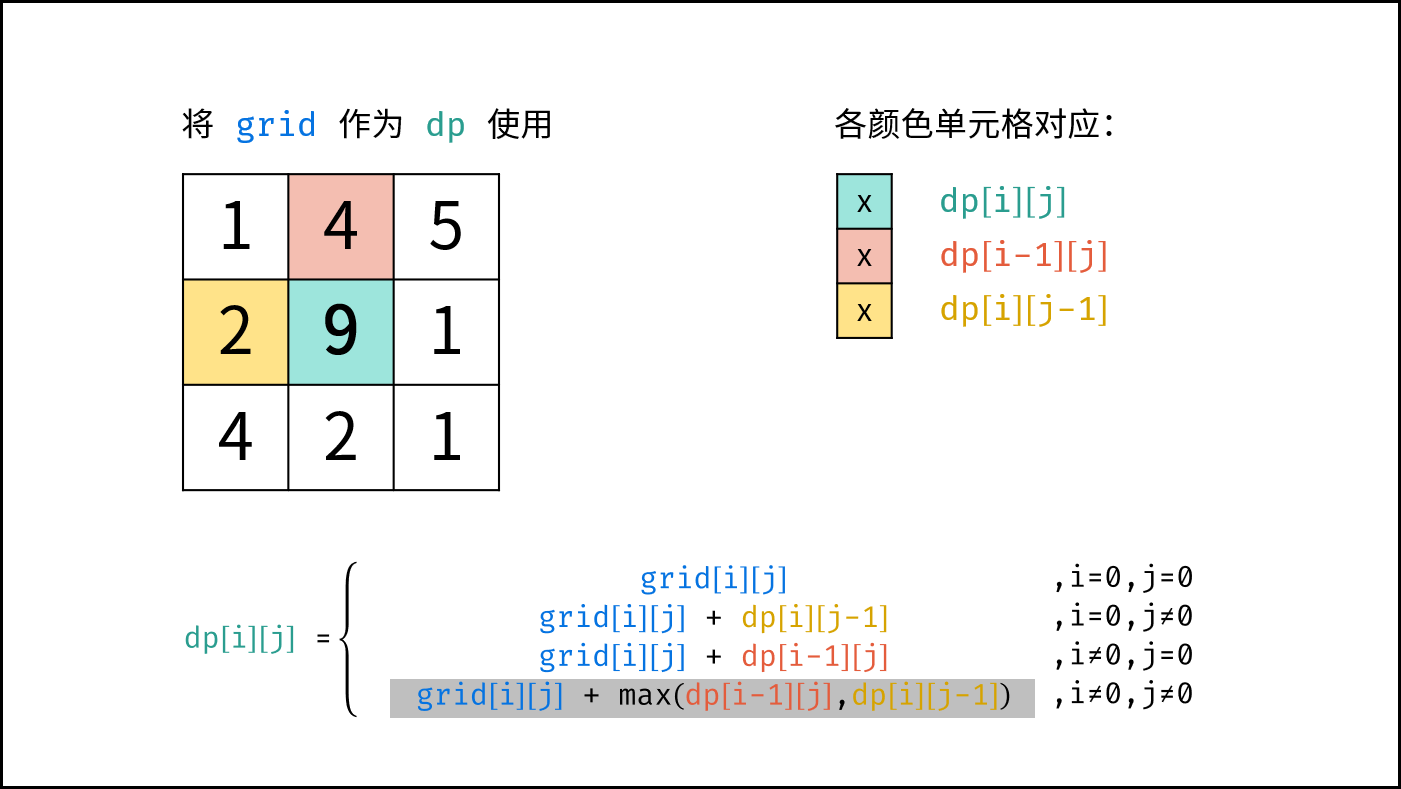
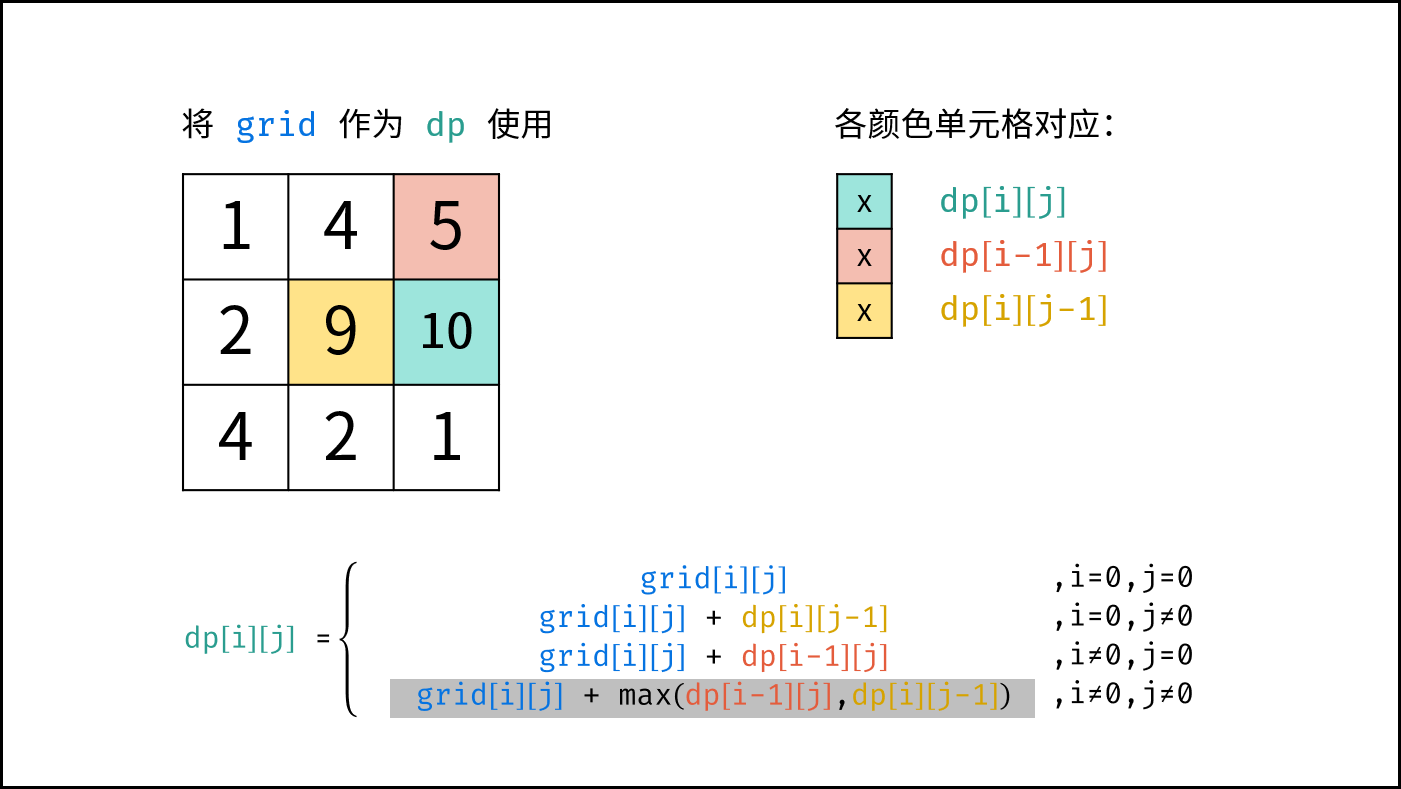
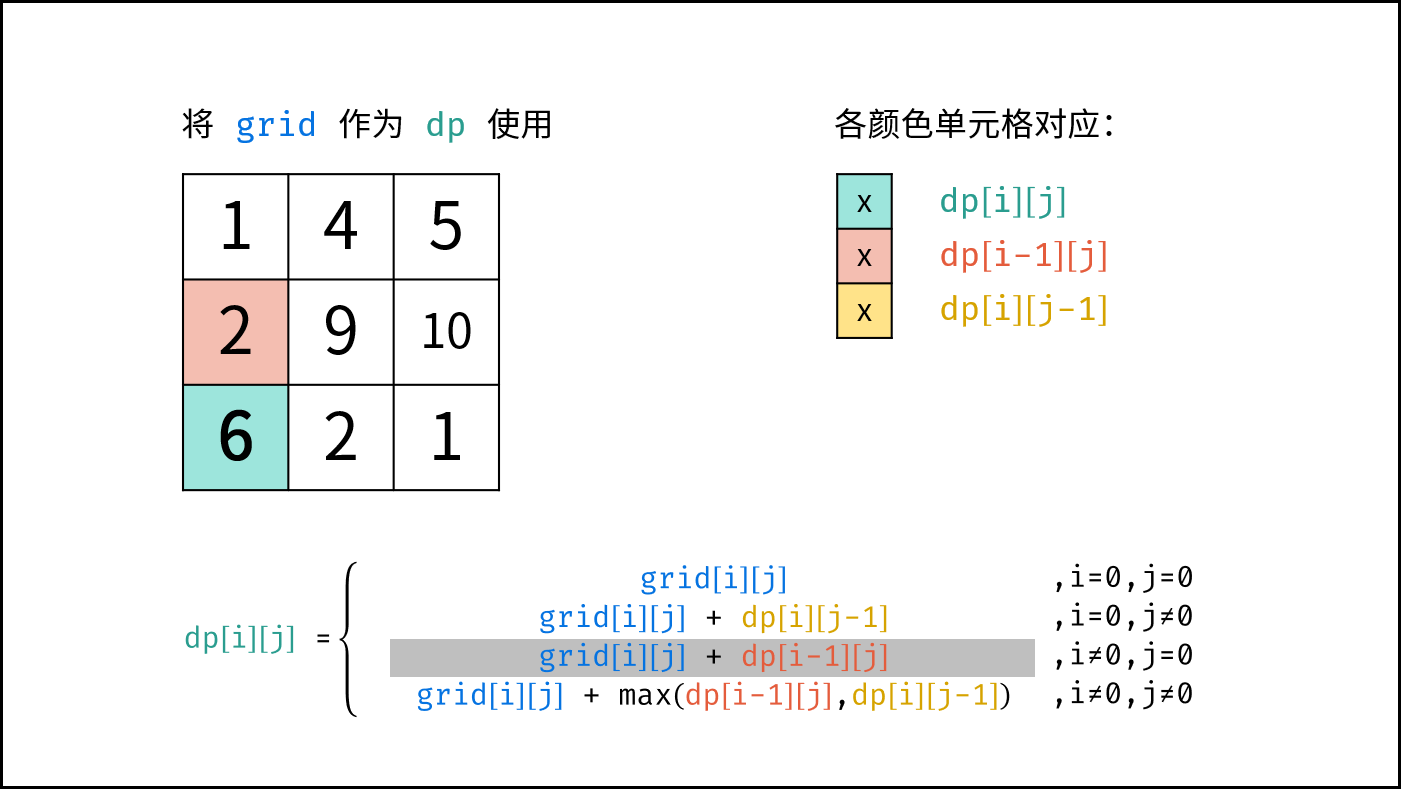
$$ dp(i,j)= \begin{cases} frame(i,j) & {,i=0, j=0}\ frame(i,j) + dp(i,j-1) & {,i=0, j \ne 0}\ frame(i,j) + dp(i-1,j) & {,i \ne 0, j=0}\ frame(i,j) + \max[dp(i-1,j),dp(i,j-1)]& ,{i \ne 0, j \ne 0} \end{cases} $$
初始状态: $dp[0][0] = frame[0][0]$ ,即到达单元格 $(0,0)$ 时能拿到珠宝的最大累计价值为 $frame[0][0]$ ;
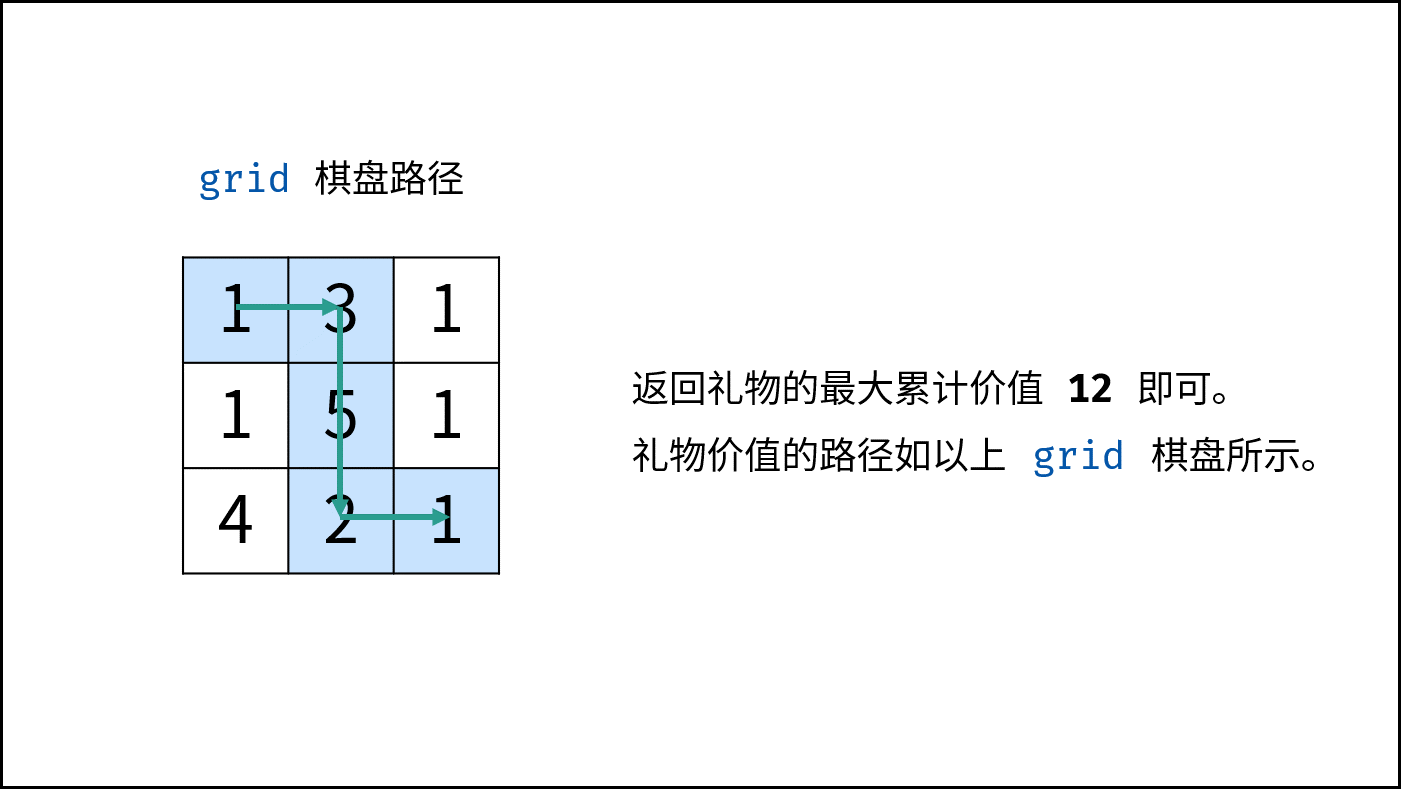
返回值: $dp[m-1][n-1]$ ,$m, n$ 分别为矩阵的行高和列宽,即返回 $dp$ 矩阵右下角元素。
空间优化:
由于 $dp[i][j]$ 只与 $dp[i-1][j]$ , $dp[i][j-1]$ , $frame[i][j]$ 有关系,因此可以将原矩阵 $frame$ 用作 $dp$ 矩阵,即直接在 $frame$ 上修改即可。
应用此方法可省去 $dp$ 矩阵使用的额外空间,因此空间复杂度从 $O(MN)$ 降至 $O(1)$ 。
< ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, >
>
代码:
class Solution:
def jewelleryValue(self, frame: List[List[int]]) -> int:
for i in range(len(frame)):
for j in range(len(frame[0])):
if i == 0 and j == 0: continue
if i == 0: frame[i][j] += frame[i][j - 1]
elif j == 0: frame[i][j] += frame[i - 1][j]
else: frame[i][j] += max(frame[i][j - 1], frame[i - 1][j])
return frame[-1][-1]class Solution {
public int jewelleryValue(int[][] frame) {
int m = frame.length, n = frame[0].length;
for(int i = 0; i < m; i++) {
for(int j = 0; j < n; j++) {
if(i == 0 && j == 0) continue;
if(i == 0) frame[i][j] += frame[i][j - 1] ;
else if(j == 0) frame[i][j] += frame[i - 1][j];
else frame[i][j] += Math.max(frame[i][j - 1], frame[i - 1][j]);
}
}
return frame[m - 1][n - 1];
}
}class Solution {
public:
int jewelleryValue(vector<vector<int>>& frame) {
int m = frame.size(), n = frame[0].size();
for(int i = 0; i < m; i++) {
for(int j = 0; j < n; j++) {
if(i == 0 && j == 0) continue;
if(i == 0) frame[i][j] += frame[i][j - 1] ;
else if(j == 0) frame[i][j] += frame[i - 1][j];
else frame[i][j] += max(frame[i][j - 1], frame[i - 1][j]);
}
}
return frame[m - 1][n - 1];
}
};以上代码逻辑清晰,和转移方程直接对应,但仍可提升效率,这是因为:当 $frame$ 矩阵很大时,$i = 0$ 或 $j = 0$ 的情况仅占极少数,相当循环每轮都冗余了一次判断。因此,可先初始化矩阵第一行和第一列,再开始遍历递推。
class Solution:
def jewelleryValue(self, frame: List[List[int]]) -> int:
m, n = len(frame), len(frame[0])
for j in range(1, n): # 初始化第一行
frame[0][j] += frame[0][j - 1]
for i in range(1, m): # 初始化第一列
frame[i][0] += frame[i - 1][0]
for i in range(1, m):
for j in range(1, n):
frame[i][j] += max(frame[i][j - 1], frame[i - 1][j])
return frame[-1][-1]class Solution {
public int jewelleryValue(int[][] frame) {
int m = frame.length, n = frame[0].length;
for(int j = 1; j < n; j++) // 初始化第一行
frame[0][j] += frame[0][j - 1];
for(int i = 1; i < m; i++) // 初始化第一列
frame[i][0] += frame[i - 1][0];
for(int i = 1; i < m; i++)
for(int j = 1; j < n; j++)
frame[i][j] += Math.max(frame[i][j - 1], frame[i - 1][j]);
return frame[m - 1][n - 1];
}
}class Solution {
public:
int jewelleryValue(vector<vector<int>>& frame) {
int m = frame.size(), n = frame[0].size();
for(int j = 1; j < n; j++) // 初始化第一行
frame[0][j] += frame[0][j - 1];
for(int i = 1; i < m; i++) // 初始化第一列
frame[i][0] += frame[i - 1][0];
for(int i = 1; i < m; i++)
for(int j = 1; j < n; j++)
frame[i][j] += max(frame[i][j - 1], frame[i - 1][j]);
return frame[m - 1][n - 1];
}
};复杂度分析:
- 时间复杂度 $O(MN)$ : $M, N$ 分别为矩阵行高、列宽;动态规划需遍历整个 $frame$ 矩阵,使用 $O(MN)$ 时间。
- 空间复杂度 $O(1)$ : 原地修改使用常数大小的额外空间。