自律小屋

Appearance

当前页大纲

解题思路： ​

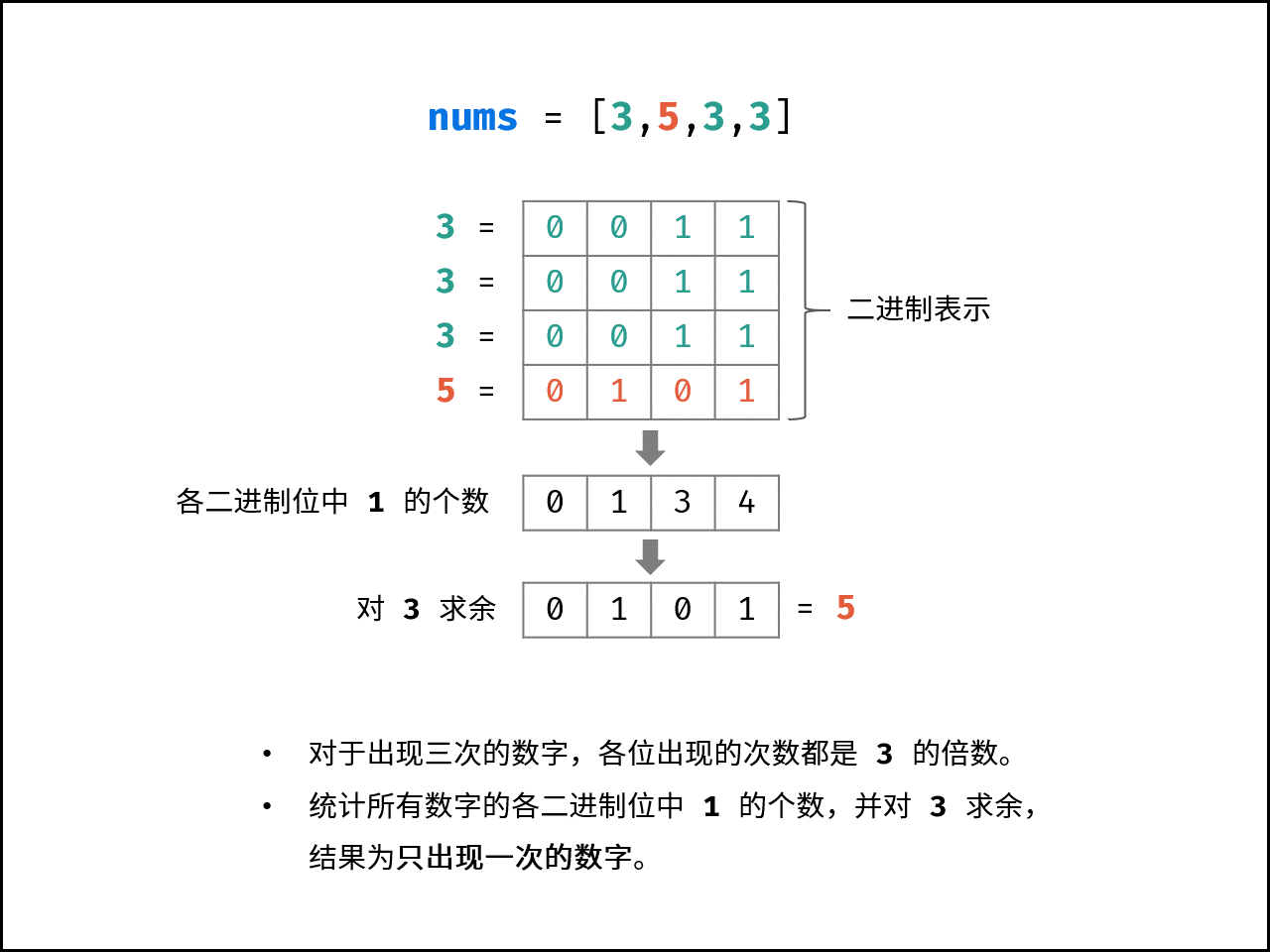
如下图所示，考虑数字的二进制形式，对于出现三次的数字，各 二进制位 出现的次数都是 $3$ 的倍数。 因此，统计所有数字的各二进制位中 $1$ 的出现次数，并对 $3$ 求余，结果则为只出现一次的数字。

下图中的 nums 对应本题的 actions 。

Picture1.png

方法一：有限状态自动机 ​

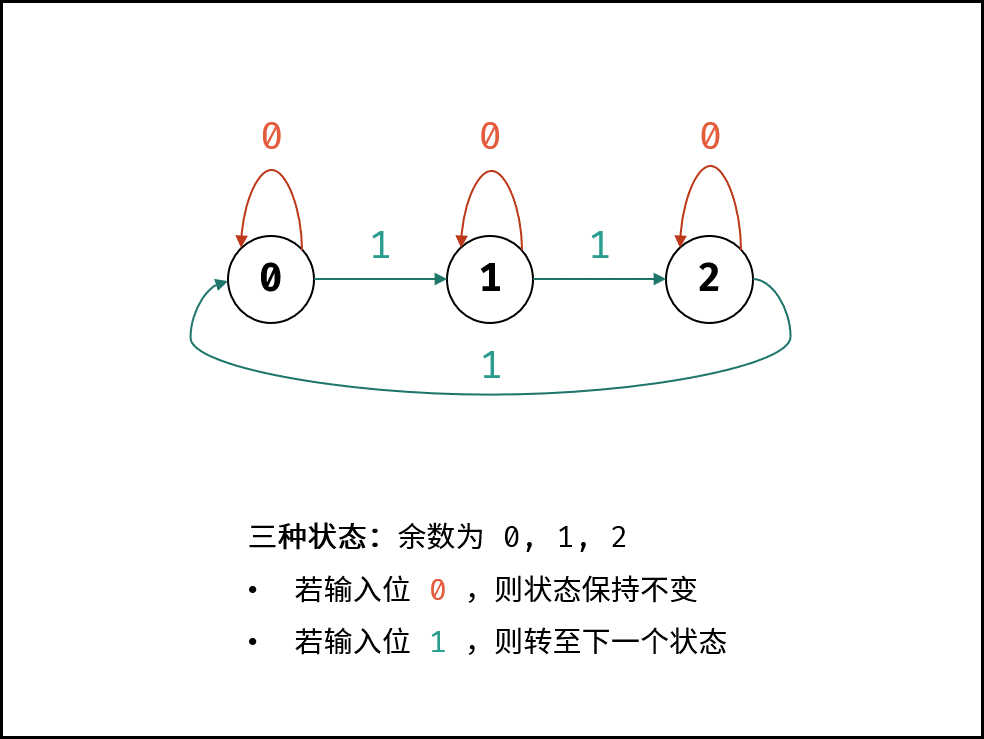
各二进制位的 位运算规则相同 ，因此只需考虑一位即可。如下图所示，对于所有数字中的某二进制位 $1$ 的个数，存在 3 种状态，即对 3 余数为 $0, 1, 2$ 。

  • 若输入二进制位 $1$ ，则状态按照以下顺序转换；
  • 若输入二进制位 $0$ ，则状态不变。

$$ 0 \rightarrow 1 \rightarrow 2 \rightarrow 0 \rightarrow \cdots $$

Picture2.png

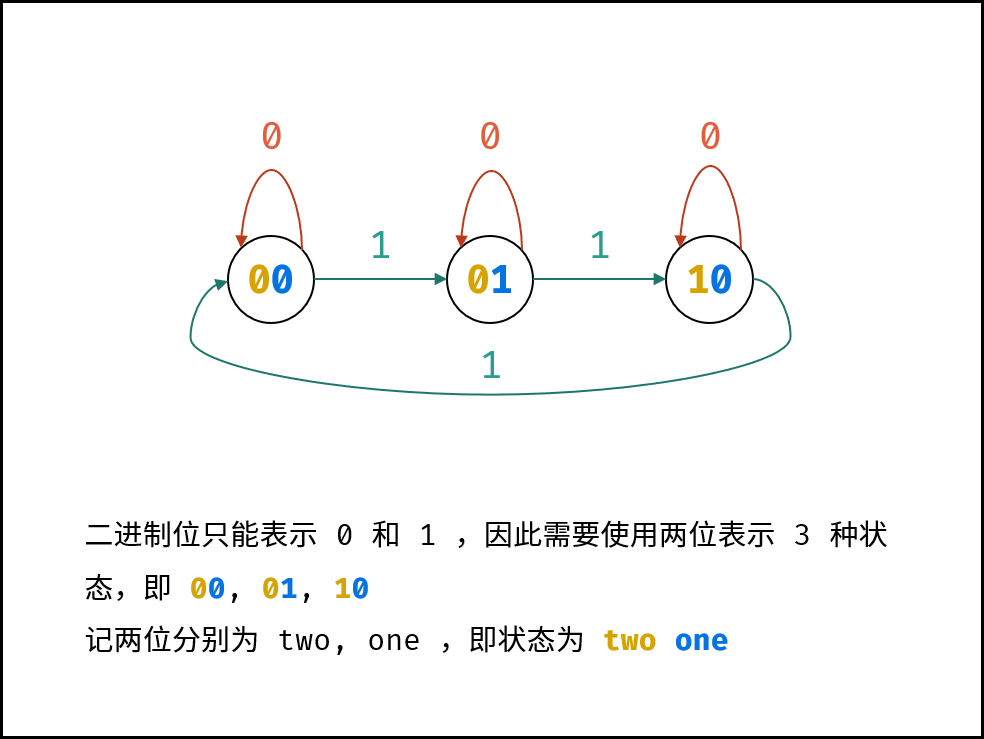
如下图所示，由于二进制只能表示 $0, 1$ ，因此需要使用两个二进制位来表示 $3$ 个状态。设此两位分别为 $two$ , $one$ ，则状态转换变为：

$$ 00 \rightarrow 01 \rightarrow 10 \rightarrow 00 \rightarrow \cdots $$

Picture3.png

接下来，需要通过 状态转换表 导出 状态转换的计算公式 。首先回忆一下位运算特点，对于任意二进制位 $x$ ，有：

  • 异或运算：x ^ 0 = x​ ，x ^ 1 = ~x
  • 与运算：x & 0 = 0 ，x & 1 = x

计算 $one$ 方法：

设当前状态为 $two$ $one$ ，此时输入二进制位 $n$ 。如下图所示，通过对状态表的情况拆分，可推出 $one$ 的计算方法为：

Python
if two == 0:
  if n == 0:
    one = one
  if n == 1:
    one = ~one
if two == 1:
    one = 0

引入 异或运算 ，可将以上拆分简化为：

Python
if two == 0:
    one = one ^ n
if two == 1:
    one = 0

引入 与运算 ，可继续简化为：

Python
one = one ^ n & ~two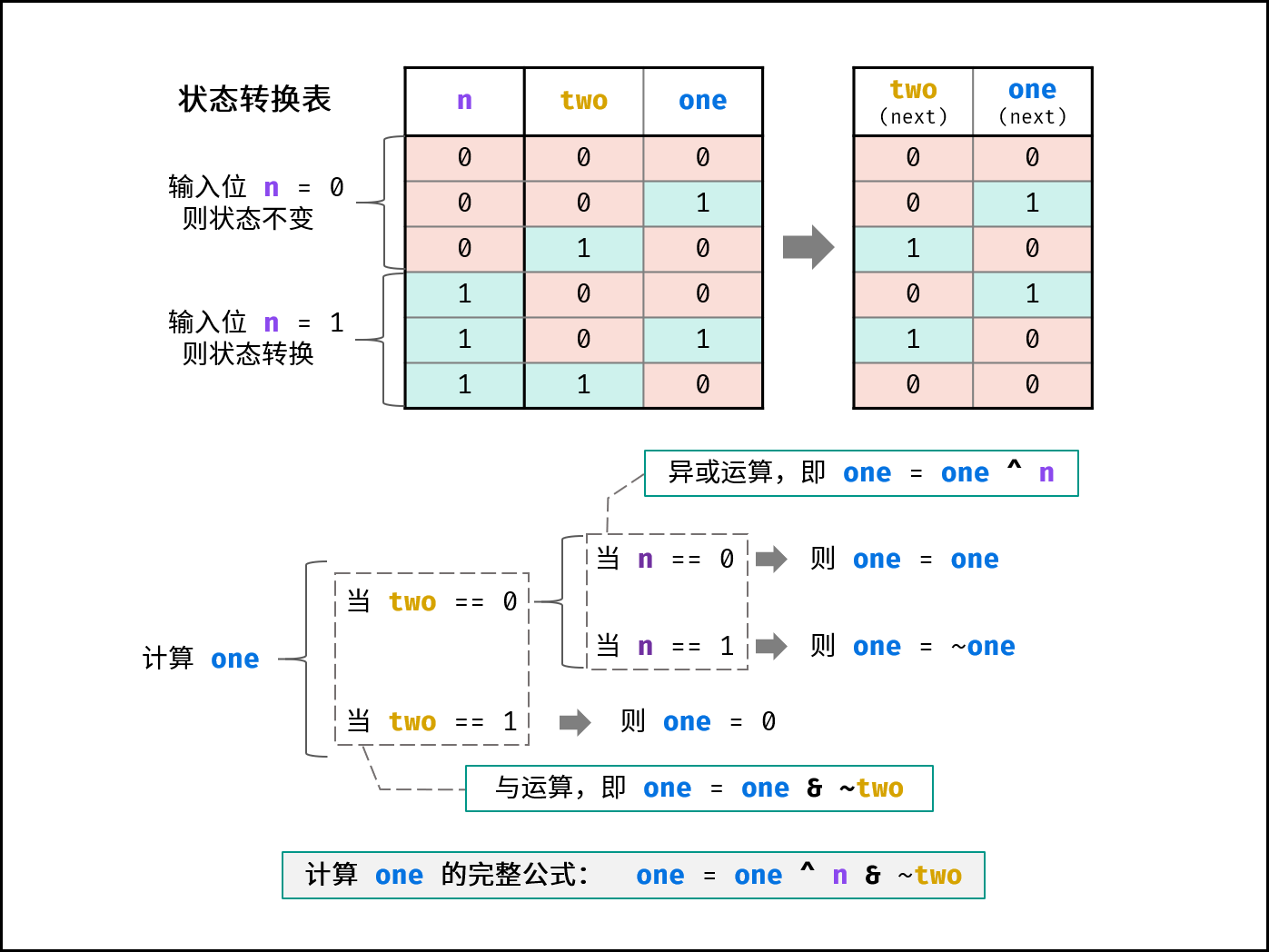

Picture4.png

计算 $two$ 方法：

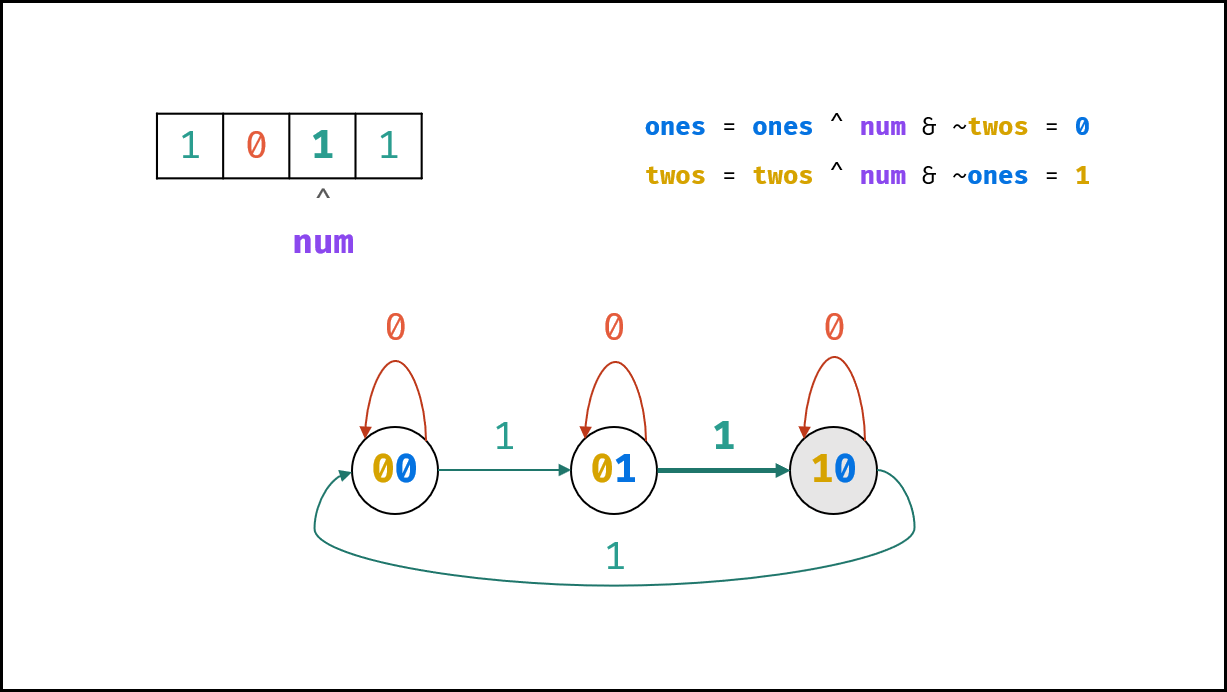
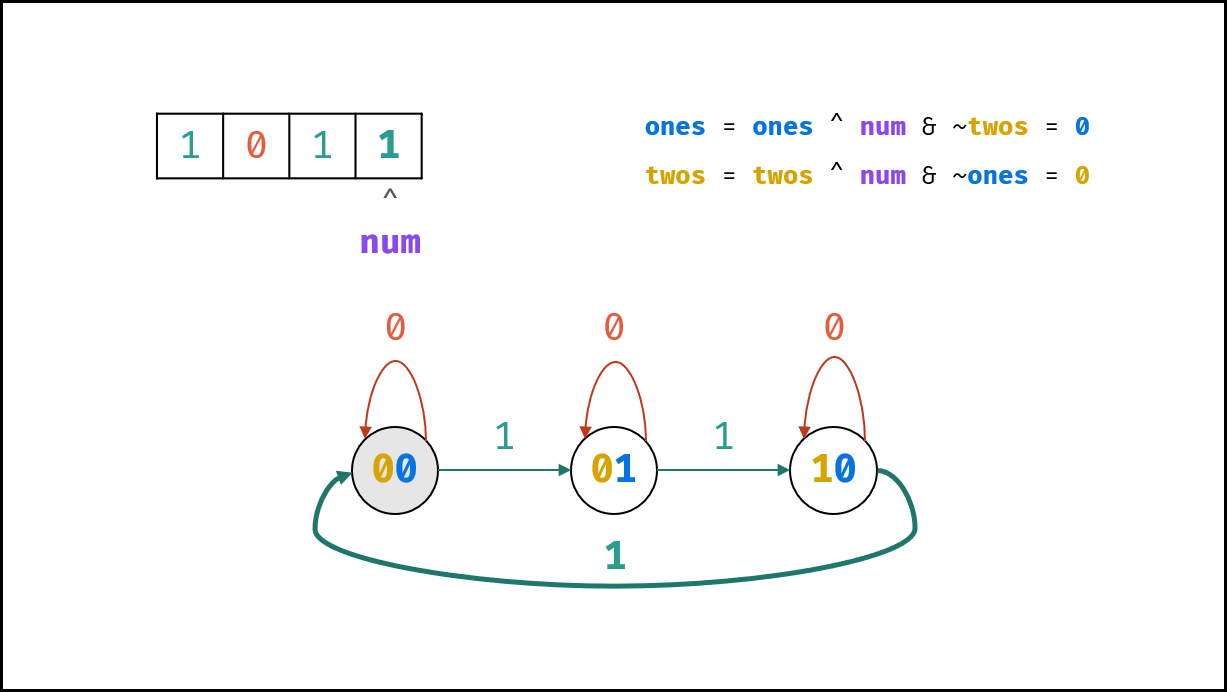
由于是先计算 $one$ ，因此应在新 $one$ 的基础上计算 $two$ 。 如下图所示，修改为新 $one$ 后，得到了新的状态图。观察发现，可以使用同样的方法计算 $two$ ，即：

Python
two = two ^ n & ~one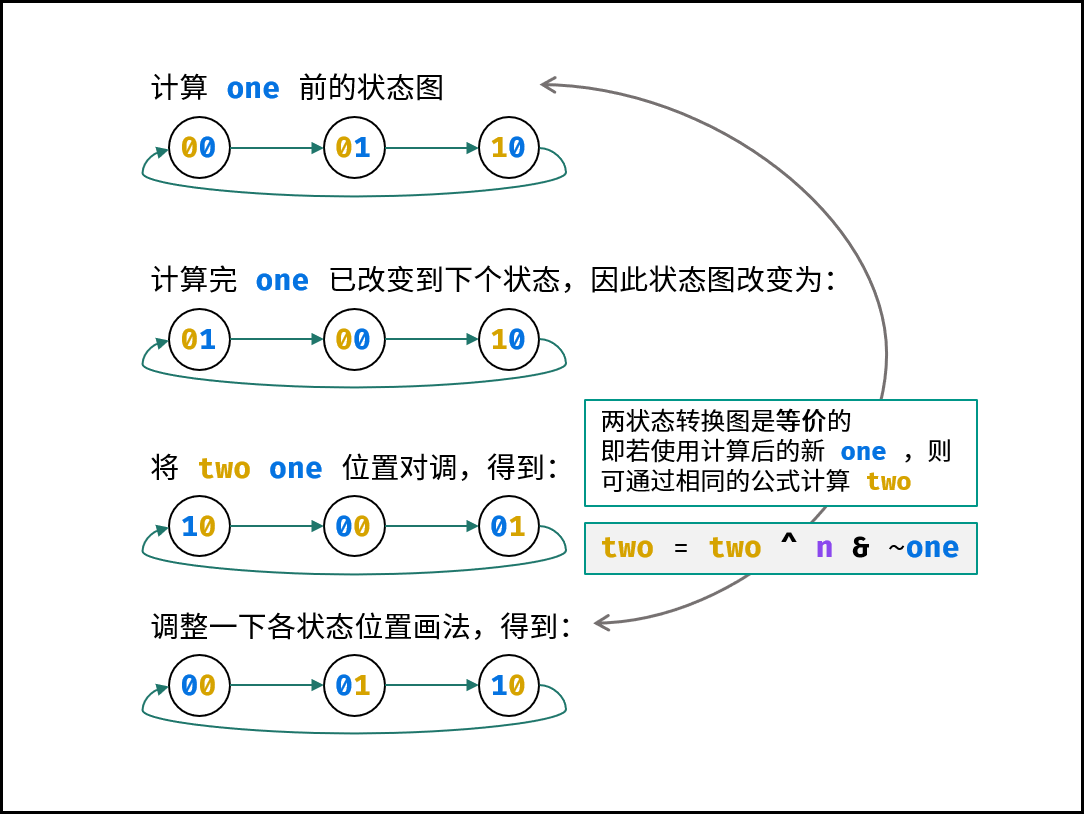

Picture5.png

返回值：

以上是对数字的二进制中 “一位” 的分析，而 int 类型的其他 31 位具有相同的运算规则，因此可将以上公式直接套用在 32 位数上。

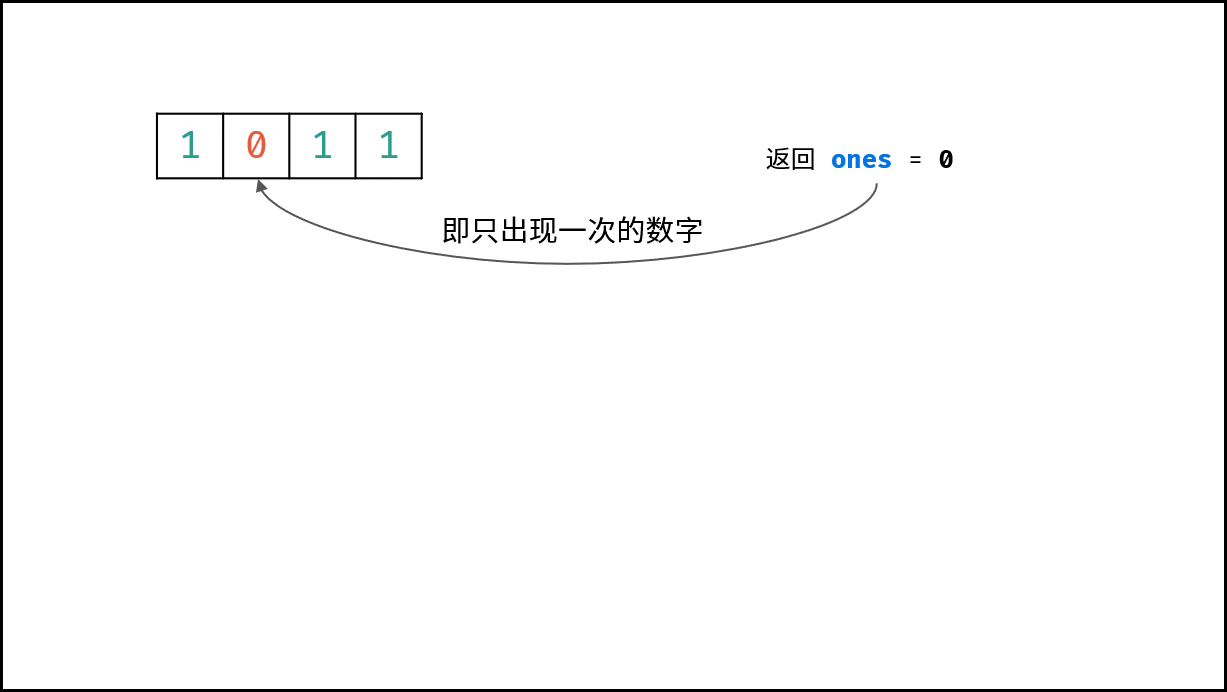
遍历完所有数字后，各二进制位都处于状态 $00$ 和状态 $01$ （取决于 “只出现一次的数字” 的各二进制位是 $1$ 还是 $0$ ），而此两状态是由 $one$ 来记录的（此两状态下 $twos$ 恒为 $0$ ），因此返回 $ones$ 即可。

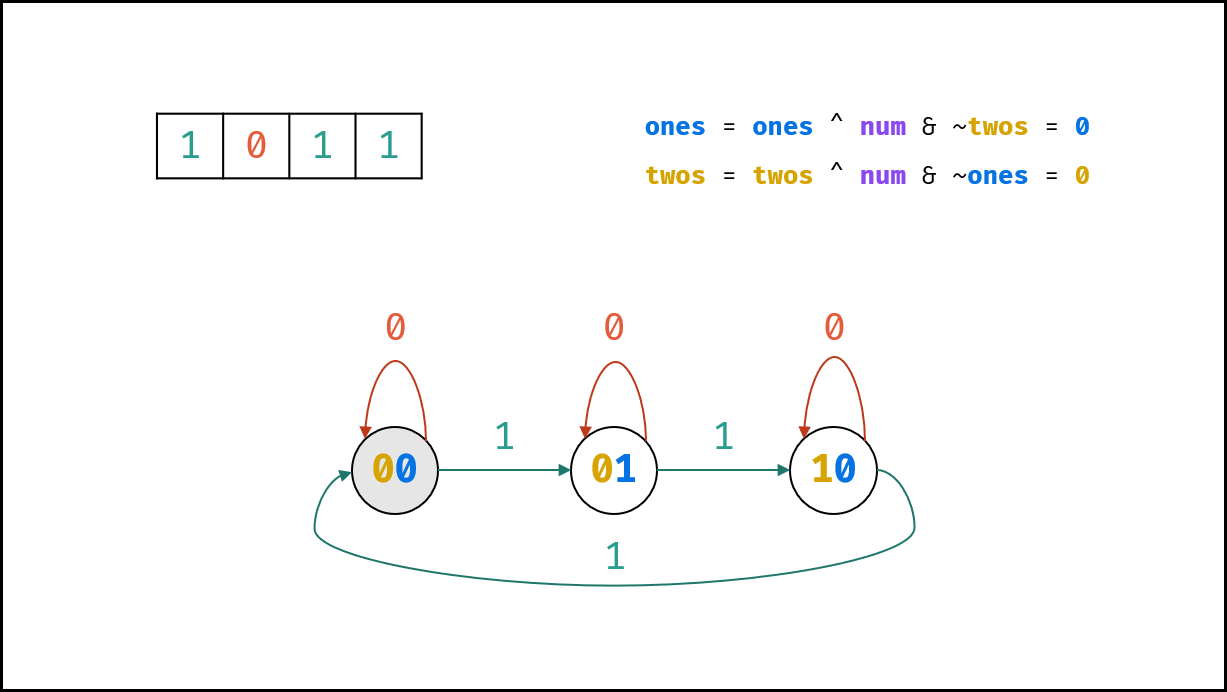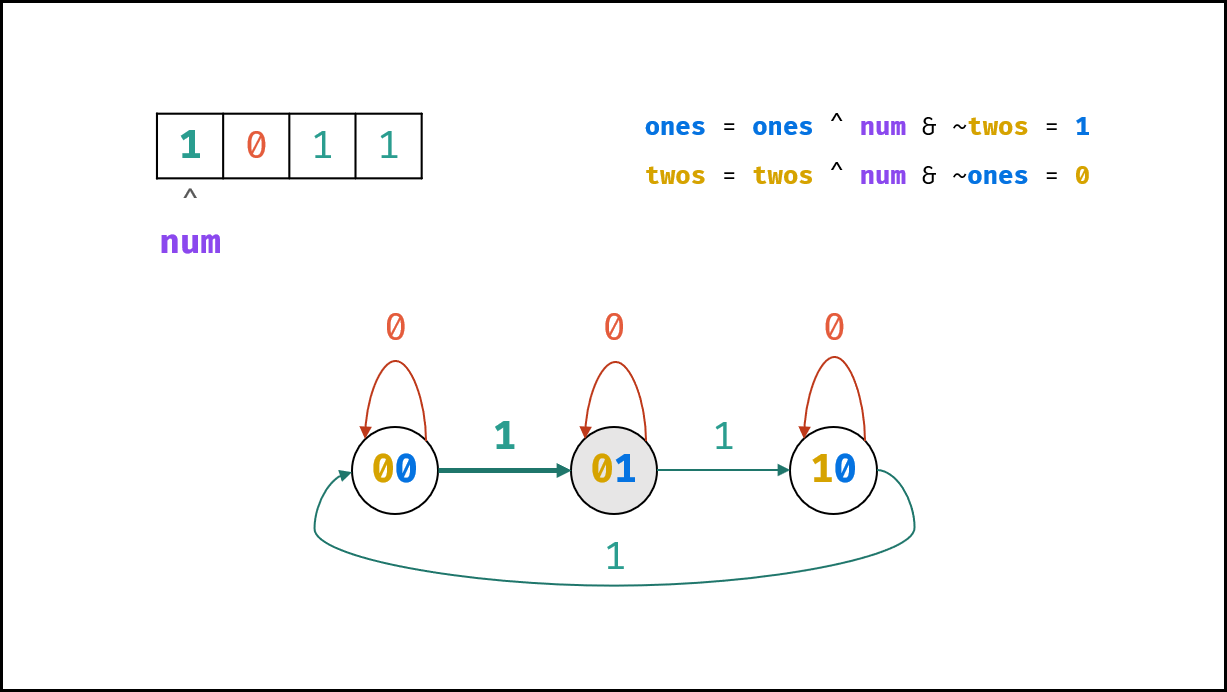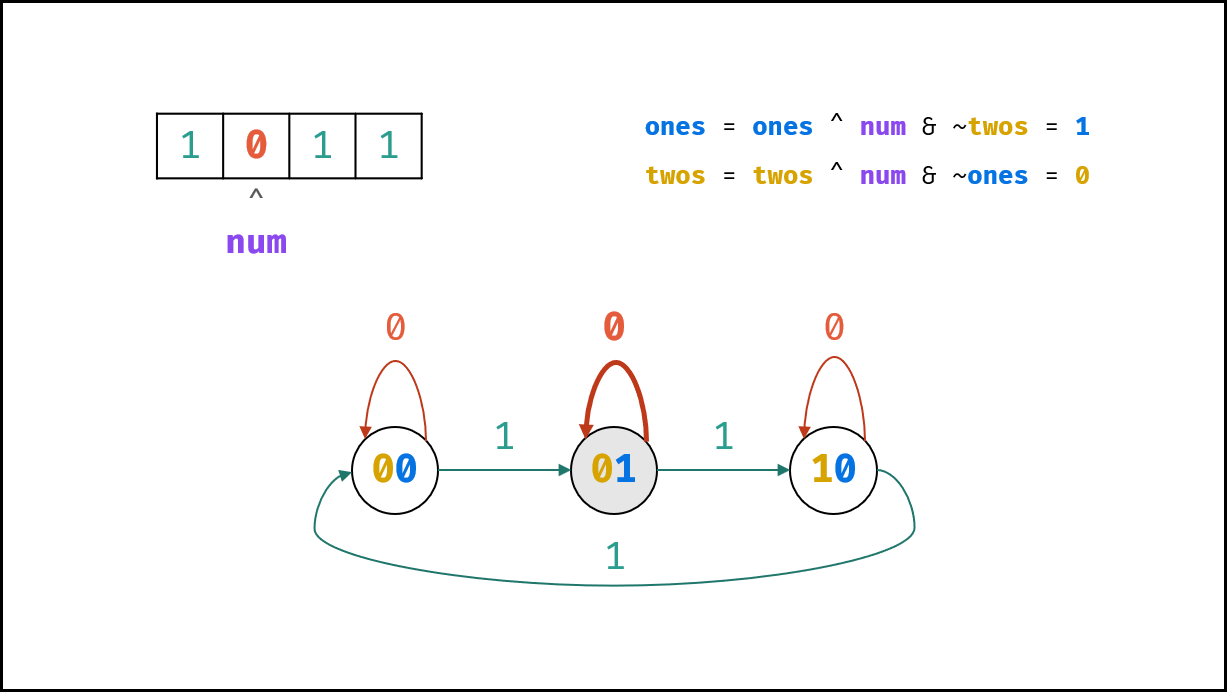<Picture6.png,Picture7.png,Picture8.png,Picture9.png,Picture10.png,Picture11.png>

代码： ​

Python
class Solution:
    def trainingPlan(self, actions: List[int]) -> int:
        ones, twos = 0, 0
        for action in actions:
            ones = ones ^ action & ~twos
            twos = twos ^ action & ~ones
        return ones
Java
class Solution {
    public int trainingPlan(int[] actions) {
        int ones = 0, twos = 0;
        for(int action : actions){
            ones = ones ^ action & ~twos;
            twos = twos ^ action & ~ones;
        }
        return ones;
    }
}
C++
class Solution {
public:
    int trainingPlan(vector<int>& actions) {
        int ones = 0, twos = 0;
        for(int action : actions){
            ones = ones ^ action & ~twos;
            twos = twos ^ action & ~ones;
        }
        return ones;
    }
};

复杂度分析： ​

  • 时间复杂度 $O(N)$ ： 其中 $N$ 位数组 $actions$ 的长度；遍历数组占用 $O(N)$ ，每轮中的常数个位运算操作占用 $O(32 \times3 \times 2) = O(1)$ 。
  • 空间复杂度 $O(1)$ ： 变量 $ones$ , $twos$ 使用常数大小的额外空间。

方法二：遍历统计 ​

此方法相对容易理解，但效率较低，总体推荐方法一。

使用 与运算 ，可获取二进制数字 $action$ 的最右一位 $n_1$ ：

$$ n_1 = action & i $$

配合 右移操作 ，可从低位至高位，获取 $action$ 所有位的值（设 int 类型从低至高的位数为第 0 位 至第 31 位，即 $n_0$ ~ $n_{31}$ ）：

$$ action = action >> 1 $$

建立一个长度为 32 的数组 $counts$ ，通过以上方法可记录所有数字的各二进制位的 $1$ 的出现次数之和。

Python
counts = [0] * 32
for action in actions:
    for i in range(32):
        counts[i] += action & 1 # 更新第 i 位 1 的个数之和
        action >>= 1            # 第 i 位 --> 第 i + 1 位
Java
int[] counts = new int[32];
for(int action : actions) {
    for(int i = 0; i < 32; i++) {
        counts[i] += action & 1; // 更新第 i 位 1 的个数之和
        action >>= 1;            // 第 i 位 --> 第 i + 1 位
    }
}
C++
int counts[32] = {0};         // C++ 初始化数组需要写明初始值 0
for(int action : actions) {
    for(int i = 0; i < 32; i++) {
        counts[i] += action & 1; // 更新第 i 位 1 的个数之和
        action >>= 1;            // 第 i 位 --> 第 i + 1 位
    }
}

将 $counts$ 各元素对 $3$ 求余，则结果为 “只出现一次的数字” 的各二进制位。

Python
for i in range(31, -1, -1):
    x = counts[i] %= 3 # 得到 “只出现一次的数字” 的第 i 位
Java
for(int i = 31; i >= 0; i--) {
    int x = counts[i] %= 3; // 得到 “只出现一次的数字” 的第 i 位
}
C++
for(int i = 31; i >= 0; i--) {
    int x = counts[i] % 3;  // 得到 “只出现一次的数字” 的第 i 位
}

利用 左移操作 和 或运算 ，可将 $counts$ 数组中各二进位的值恢复到数字 $res$ 上。

Python
for i in range(31, -1, -1):
    res <<= 1
    res |= counts[i] % 3 # 恢复第 i 位
Java
for(int i = 31; i >= 0; i--) {
    res <<= 1;
    res |= counts[i] % 3; // 恢复第 i 位
}
C++
for(int i = 31; i >= 0; i--) {
    res <<= 1;
    res |= counts[i] % 3; // 恢复第 i 位
}

最终返回 $res$ 即可。

由于 Python 的存储负数的特殊性，需要先将 $0$ - $31$ 位取反（即 res ^ 0xffffffff ），再将所有位取反（即 ~ ）。 此组合操作含义： 将数字 $31$ 以上位取反，$0$ - $31$ 位不变。

代码： ​

实际上，只需要修改求余数值 $m$ ，即可实现解决 除了一个数字以外，其余数字都出现 $m$ 次 的通用问题。

设 int 类型从低至高的位数为第 0 位 至第 31 位。

Python
class Solution:
    def trainingPlan(self, actions: List[int]) -> int:
        counts = [0] * 32
        for action in actions:
            for i in range(32):
                counts[i] += action & 1 # 更新第 i 位 1 的个数之和
                action >>= 1            # 第 i 位 --> 第 i 位
        res, m = 0, 3
        for i in range(31, -1, -1):
            res <<= 1
            res |= counts[i] % m        # 恢复第 i 位
        return res if counts[31] % m == 0 else ~(res ^ 0xffffffff)
Java
class Solution {
    public int trainingPlan(int[] actions) {
        int[] counts = new int[32];
        for(int action : actions) {
            for(int i = 0; i < 32; i++) {
                counts[i] += action & 1; // 更新第 i 位 1 的个数之和
                action >>= 1;            // 第 i 位 --> 第 i 位
            }
        }
        int res = 0, m = 3;
        for(int i = 31; i >= 0; i--) {
            res <<= 1;
            res |= counts[i] % m;        // 恢复第 i 位
        }
        return res;
    }
}
C++
class Solution {
public:
    int trainingPlan(vector<int>& actions) {
        int counts[32] = {0};            // C++ 初始化数组需要写明初始值 0
        for(int action : actions) {
            for(int i = 0; i < 32; i++) {
                counts[i] += action & 1; // 更新第 i 位 1 的个数之和
                action >>= 1;            // 第 i 位 --> 第 i 位
            }
        }
        int res = 0, m = 3;
        for(int i = 31; i >= 0; i--) {
            res <<= 1;
            res |= counts[i] % m;        // 恢复第 i 位
        }
        return res;
    }
};

复杂度分析： ​

  • 时间复杂度 $O(N)$ ： 其中 $N$ 位数组 $actions$ 的长度；遍历数组占用 $O(N)$ ，每轮中的常数个位运算操作占用 $O(1)$ 。
  • 空间复杂度 $O(1)$ ： 数组 $counts$ 长度恒为 $32$ ，占用常数大小的额外空间。

MIT License.

Copyright © 2024 自律小屋