自律小屋

Appearance

当前页大纲

空间复杂度 ​

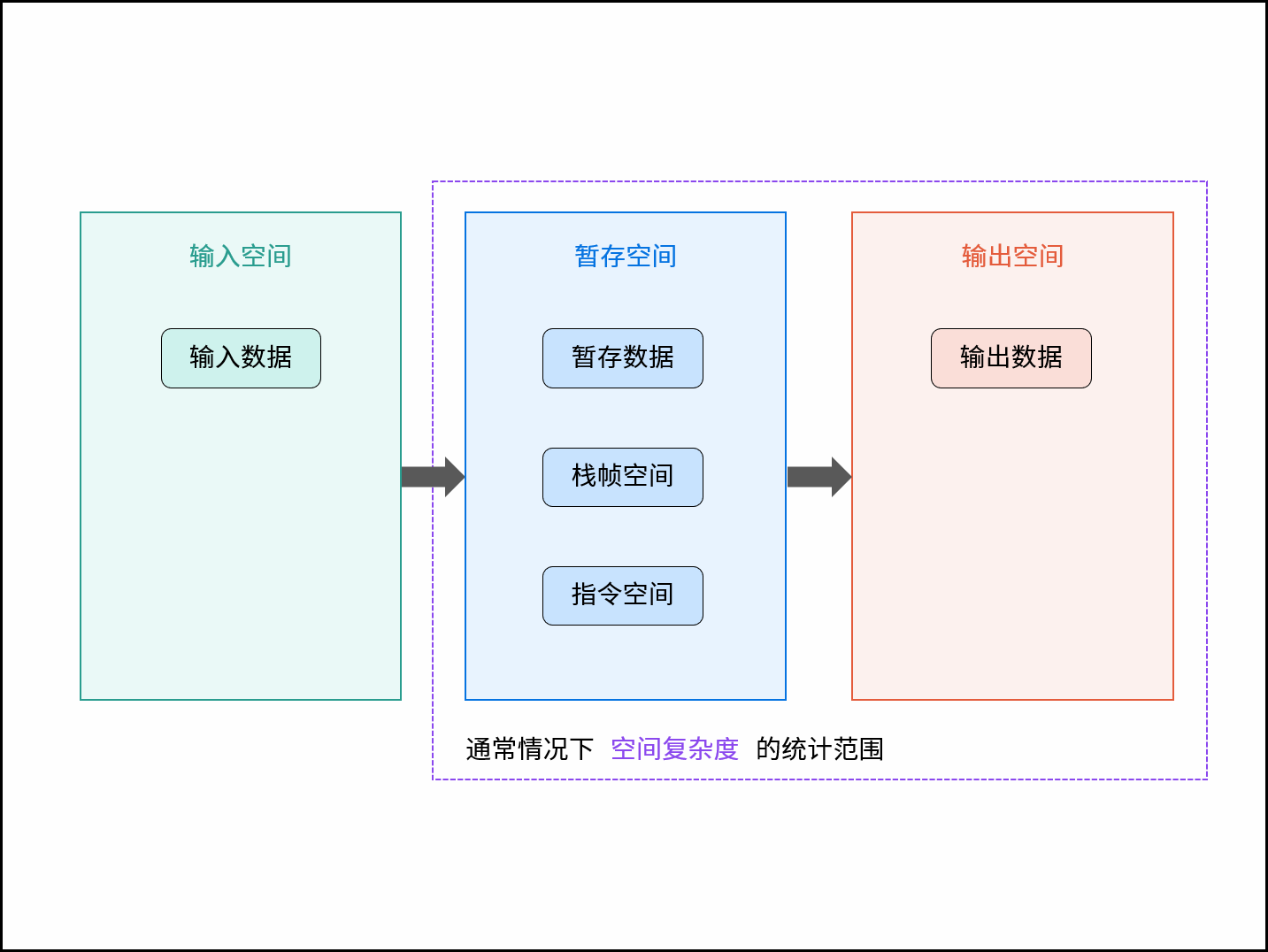
空间复杂度涉及的空间类型有：

  • 输入空间： 存储输入数据所需的空间大小；
  • 暂存空间： 算法运行过程中，存储所有中间变量和对象等数据所需的空间大小；
  • 输出空间： 算法运行返回时，存储输出数据所需的空间大小；

通常情况下，空间复杂度指在输入数据大小为 $N$ 时，算法运行所使用的「暂存空间」+「输出空间」的总体大小。

Picture1.png

而根据不同来源，算法使用的内存空间分为三类：

指令空间：

编译后，程序指令所使用的内存空间。

数据空间：

算法中的各项变量使用的空间，包括：声明的常量、变量、动态数组、动态对象等使用的内存空间。

Python
class Node:
    def __init__(self, val):
        self.val = val
        self.next = None

def algorithm(N):
    num = N         # 变量
    nums = [0] * N  # 动态数组
    node = Node(N)  # 动态对象
Java
class Node {
    int val;
    Node next;
    Node(int x) { val = x; }
}

void algorithm(int N) {
    int num = N;             // 变量
    int[] nums = new int[N]; // 动态数组
    Node node = new Node(N); // 动态对象
}
C++
struct Node {
    int val;
    Node *next;
    Node(int x) : val(x), next(NULL) {}
};

void algorithm(int N) {
    int num = N;              // 变量
    int nums[N];              // 动态数组
    Node* node = new Node(N); // 动态对象
}

栈帧空间：

程序调用函数是基于栈实现的，函数在调用期间，占用常量大小的栈帧空间，直至返回后释放。如以下代码所示，在循环中调用函数，每轮调用 test() 返回后，栈帧空间已被释放，因此空间复杂度仍为 $O(1)$ 。

Python
def test():
    return 0

def algorithm(N):
    for _ in range(N):
        test()
Java
int test() {
    return 0;
}

void algorithm(int N) {
    for (int i = 0; i < N; i++) {
        test();
    }
}
C++
int test() {
    return 0;
}

void algorithm(int N) {
    for (int i = 0; i < N; i++) {
        test();
    }
}

算法中，栈帧空间的累计常出现于递归调用。如以下代码所示，通过递归调用，会同时存在 $N$ 个未返回的函数 algorithm() ，此时累计使用 $O(N)$ 大小的栈帧空间。

Python
def algorithm(N):
    if N <= 1: return 1
    return algorithm(N - 1) + 1
Java
int algorithm(int N) {
    if (N <= 1) return 1;
    return algorithm(N - 1) + 1;
}
C++
int algorithm(int N) {
    if (N <= 1) return 1;
    return algorithm(N - 1) + 1;
}

符号表示 ​

通常情况下，空间复杂度统计算法在 “最差情况” 下使用的空间大小，以体现算法运行所需预留的空间量，使用符号 $O$ 表示。

最差情况有两层含义，分别为「最差输入数据」、算法运行中的「最差运行点」。例如以下代码：

输入整数 $N$ ，取值范围 $N \geq 1$ ；

  • 最差输入数据： 当 $N \leq 10$ 时，数组 nums 的长度恒定为 10 ，空间复杂度为 $O(10) = O(1)$ ；当 $N > 10$ 时，数组 $nums$ 长度为 $N$ ，空间复杂度为 $O(N)$ ；因此，空间复杂度应为最差输入数据情况下的 $O(N)$ 。
  • 最差运行点： 在执行 nums = [0] * 10 时，算法仅使用 $O(1)$ 大小的空间；而当执行 nums = [0] * N 时，算法使用 $O(N)$ 的空间；因此，空间复杂度应为最差运行点的 $O(N)$ 。
Python
def algorithm(N):
    num = 5             # O(1)
    nums = [0] * 10     # O(1)
    if N > 10:
        nums = [0] * N  # O(N)
Java
void algorithm(int N) {
    int num = 5;              // O(1)
    int[] nums = new int[10]; // O(1)
    if (N > 10) {
        nums = new int[N];    // O(N)
    }
}
C++
void algorithm(int N) {
    int num = 5;           // O(1)
    vector<int> nums(10);  // O(1)
    if (N > 10) {
        nums.resize(N);    // O(N)
    }
}

常见种类 ​

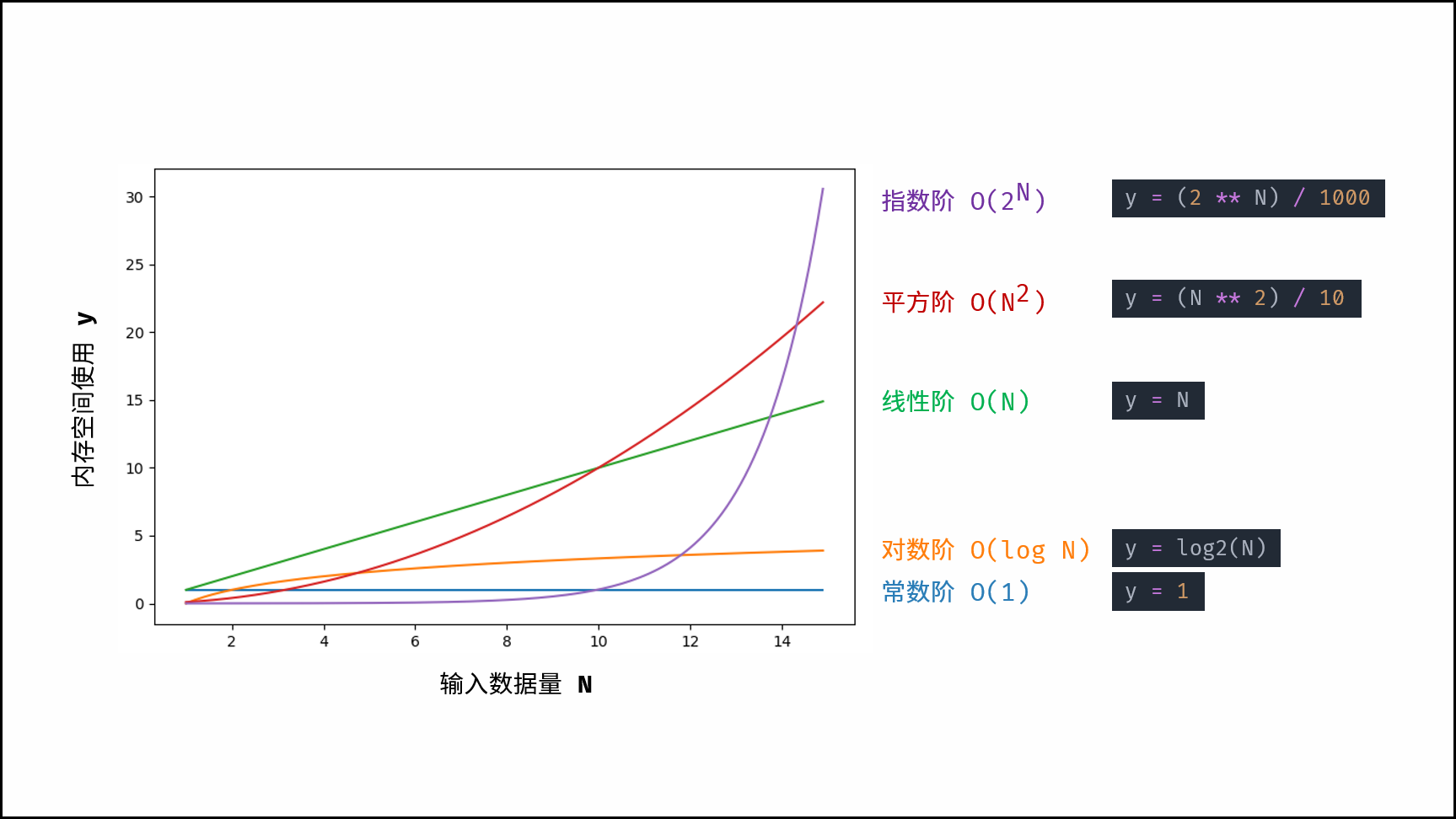
根据从小到大排列，常见的算法空间复杂度有：

$$ O(1) < O(\log N) < O(N) < O(N^2) < O(2^N) $$

Picture2.png

对于以下所有示例，设输入数据大小为正整数 $N$ ，节点类 Node 、函数 test() 如以下代码所示。

Python
# 节点类 Node
class Node:
    def __init__(self, val):
        self.val = val
        self.next = None

# 函数 test()
def test():
    return 0
Java
// 节点类 Node
class Node {
    int val;                 // 变量
    Node next;               // 动态数组
    Node(int x) { val = x; } // 动态对象
}

// 函数 test()
int test() {
    return 0;
}
C++
// 节点类 Node
struct Node {
    int val;
    Node *next;
    Node(int x) : val(x), next(NULL) {}
};

// 函数 test()
int test() {
    return 0;
}

常数 $O(1)$ ： ​

普通常量、变量、对象、元素数量与输入数据大小 $N$ 无关的集合，皆使用常数大小的空间。

Python
def algorithm(N):
    num = 0
    nums = [0] * 10000
    node = Node(0)
    dic = { 0: '0' }
Java
void algorithm(int N) {
    int num = 0;
    int[] nums = new int[10000];
    Node node = new Node(0);
    Map<Integer, String> dic = new HashMap<>() {{ put(0, "0"); }};
}
C++
void algorithm(int N) {
    int num = 0;
    int nums[10000];
    Node* node = new Node(0);
    unordered_map<int, string> dic;
    dic.emplace(0, "0");
}

如以下代码所示，虽然函数 test() 调用了 $N$ 次，但每轮调用后 test() 已返回，无累计栈帧空间使用，因此空间复杂度仍为 $O(1)$ 。

Python
def algorithm(N):
    for _ in range(N):
        test()
Java
void algorithm(int N) {
    for (int i = 0; i < N; i++) {
        test();
    }
}
C++
void algorithm(int N) {
    for (int i = 0; i < N; i++) {
        test();
    }
}

线性 $O(N)$ ： ​

元素数量与 $N$ 呈线性关系的任意类型集合（常见于一维数组、链表、哈希表等），皆使用线性大小的空间。

Python
def algorithm(N):
    nums_1 = [0] * N
    nums_2 = [0] * (N // 2)

    nodes = [Node(i) for i in range(N)]
    
    dic = {}
    for i in range(N):
        dic[i] = str(i)
Java
void algorithm(int N) {
    int[] nums_1 = new int[N];
    int[] nums_2 = new int[N / 2];

    List<Node> nodes = new ArrayList<>();
    for (int i = 0; i < N; i++) {
        nodes.add(new Node(i));
    }

    Map<Integer, String> dic = new HashMap<>();
    for (int i = 0; i < N; i++) {
        dic.put(i, String.valueOf(i));
    }
}
C++
void algorithm(int N) {
    int nums_1[N];
    int nums_2[N / 2 + 1];

    vector<Node*> nodes;
    for (int i = 0; i < N; i++) {
        nodes.push_back(new Node(i));
    }

    unordered_map<int, string> dic;
    for (int i = 0; i < N; i++) {
        dic.emplace(i, to_string(i));
    }
}

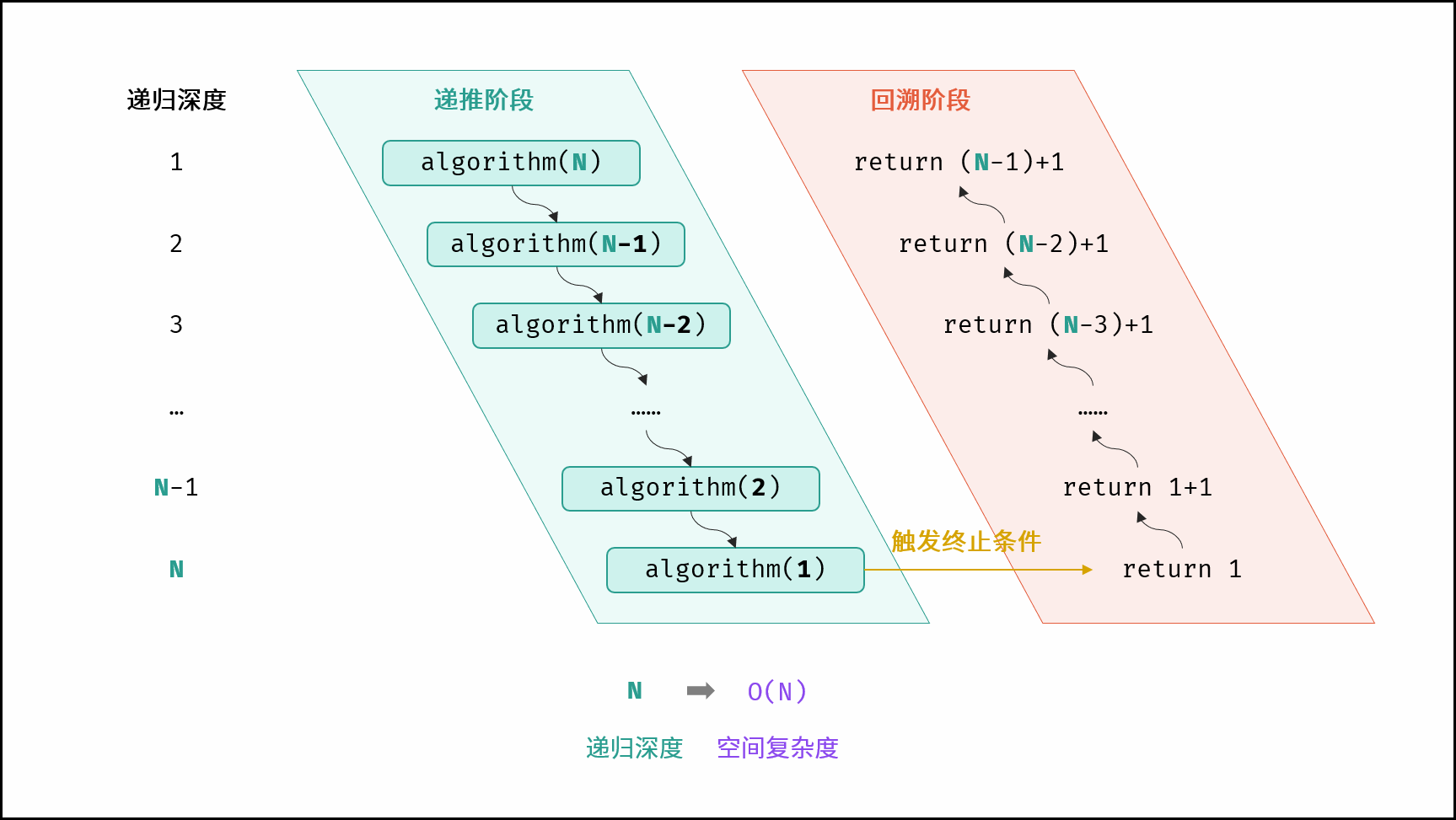
如下图与代码所示，此递归调用期间，会同时存在 $N$ 个未返回的 algorithm() 函数，因此使用 $O(N)$ 大小的栈帧空间。

Python
def algorithm(N):
    if N <= 1: return 1
    return algorithm(N - 1) + 1
Java
int algorithm(int N) {
    if (N <= 1) return 1;
    return algorithm(N - 1) + 1;
}
C++
int algorithm(int N) {
    if (N <= 1) return 1;
    return algorithm(N - 1) + 1;
}

Picture3.png

平方 $O(N^2)$ ： ​

元素数量与 $N$ 呈平方关系的任意类型集合（常见于矩阵），皆使用平方大小的空间。

Python
def algorithm(N):
    num_matrix = [[0 for j in range(N)] for i in range(N)]
    node_matrix = [[Node(j) for j in range(N)] for i in range(N)]
Java
void algorithm(int N) {
    int num_matrix[][] = new int[N][N];

    List<List<Node>> node_matrix = new ArrayList<>();
    for (int i = 0; i < N; i++) {
        List<Node> nodes = new ArrayList<>();
        for (int j = 0; j < N; j++) {
            nodes.add(new Node(j));
        }
        node_matrix.add(nodes);
    }
}
C++
void algorithm(int N) {
    vector<vector<int>> num_matrix;
    for (int i = 0; i < N; i++) {
        vector<int> nums;
        for (int j = 0; j < N; j++) {
            nums.push_back(0);
        }
        num_matrix.push_back(nums);
    }

    vector<vector<Node*>> node_matrix;
    for (int i = 0; i < N; i++) {
        vector<Node*> nodes;
        for (int j = 0; j < N; j++) {
            nodes.push_back(new Node(j));
        }
        node_matrix.push_back(nodes);
    }
}

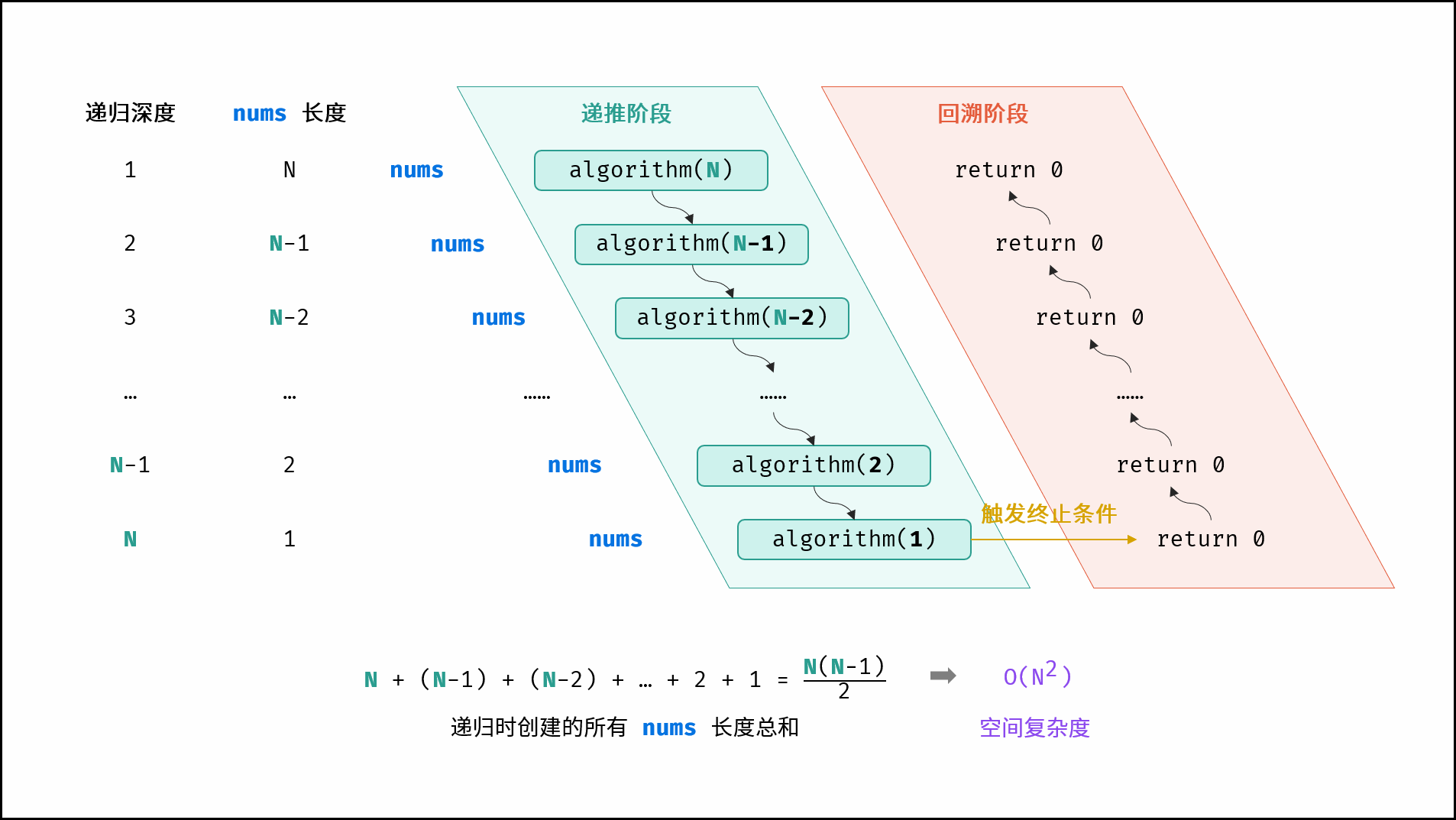
如下图与代码所示，递归调用时同时存在 $N$ 个未返回的 algorithm() 函数，使用 $O(N)$ 栈帧空间；每层递归函数中声明了数组，平均长度为 $\frac{N}{2}$ ，使用 $O(N)$ 空间；因此总体空间复杂度为 $O(N^2)$ 。

Python
def algorithm(N):
    if N <= 0: return 0
    nums = [0] * N
    return algorithm(N - 1)
Java
int algorithm(int N) {
    if (N <= 0) return 0;
    int[] nums = new int[N];
    return algorithm(N - 1);
}
C++
int algorithm(int N) {
    if (N <= 0) return 0;
    int nums[N];
    return algorithm(N - 1);
}

Picture4.png

指数 $O(2^N)$ ： ​

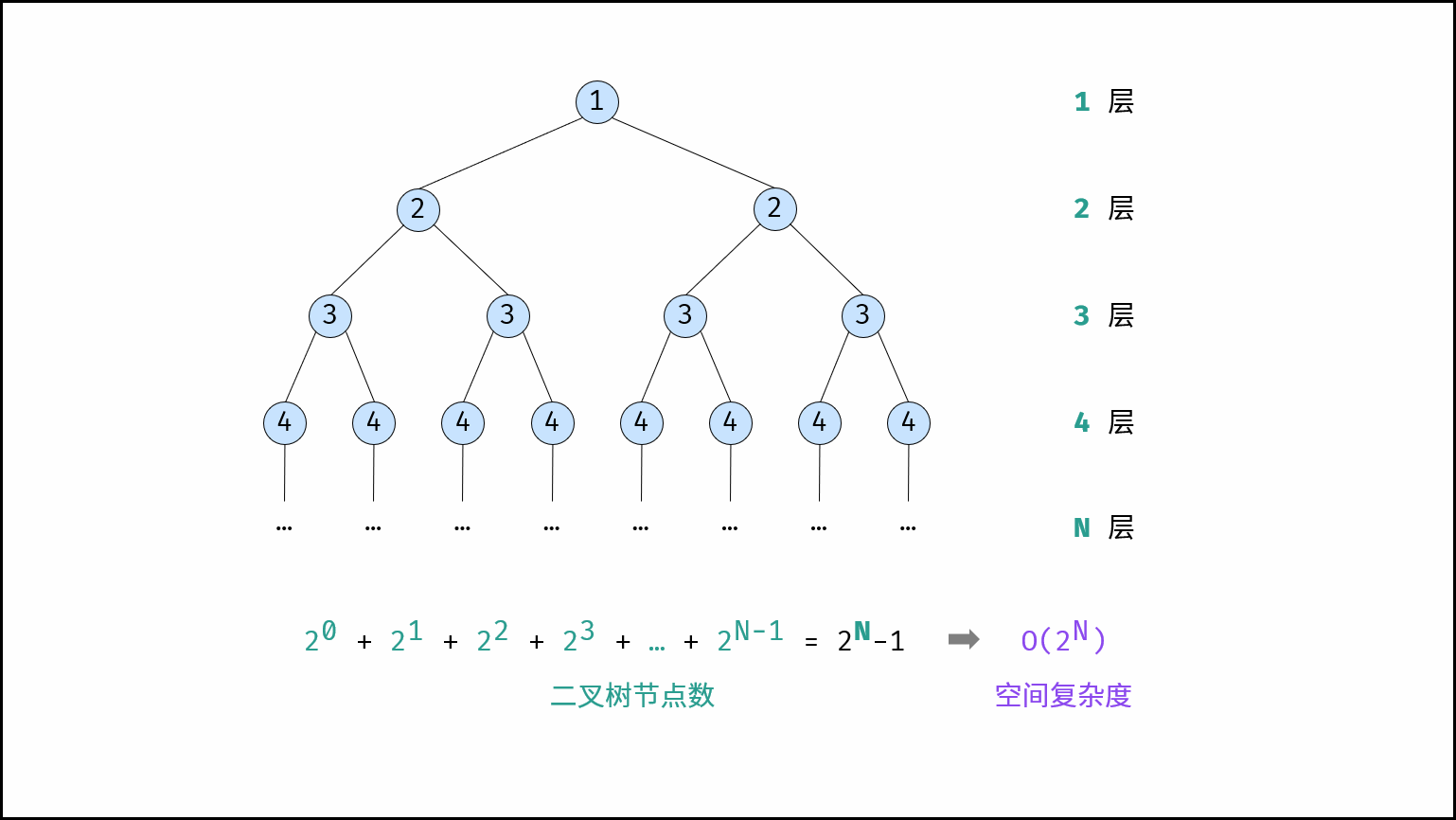
指数阶常见于二叉树、多叉树。例如，高度为 $N$ 的「满二叉树」的节点数量为 $2^N$ ，占用 $O(2^N)$ 大小的空间；同理，高度为 $N$ 的「满 $m$ 叉树」的节点数量为 $m^N$ ，占用 $O(m^N) = O(2^N)$ 大小的空间。

Picture5.png

对数 $O(\log N)$ ： ​

对数阶常出现于分治算法的栈帧空间累计、数据类型转换等，例如：

  • 快速排序 ，平均空间复杂度为 $\Theta(\log N)$ ，最差空间复杂度为 $O(N)$ 。拓展知识：通过应用 尾递归优化 ，可以将快速排序的最差空间复杂度限定至 $O(N)$ 。
  • 数字转化为字符串 ，设某正整数为 $N$ ，则字符串的空间复杂度为 $O(\log N)$ 。推导如下：正整数 $N$ 的位数为 $log_{10} N$ ，即转化的字符串长度为 $\log_{10} N$ ，因此空间复杂度为 $O(\log N)$ 。

时空权衡 ​

对于算法的性能，需要从时间和空间的使用情况来综合评价。优良的算法应具备两个特性，即时间和空间复杂度皆较低。而实际上，对于某个算法问题，同时优化时间复杂度和空间复杂度是非常困难的。降低时间复杂度，往往是以提升空间复杂度为代价的，反之亦然。

由于当代计算机的内存充足，通常情况下，算法设计中一般会采取「空间换时间」的做法，即牺牲部分计算机存储空间，来提升算法的运行速度。

以 LeetCode 全站第一题 两数之和 为例，「暴力枚举」和「辅助哈希表」分别为「空间最优」和「时间最优」的两种算法。

方法一：暴力枚举 ​

时间复杂度 $O(N^2)$ ，空间复杂度 $O(1)$ ；属于「时间换空间」，虽然仅使用常数大小的额外空间，但运行速度过慢。

Python
class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        for i in range(len(nums) - 1):
            for j in range(i + 1, len(nums)):
                if nums[i] + nums[j] == target:
                    return i, j
        return
Java
class Solution {
    public int[] twoSum(int[] nums, int target) {
        int size = nums.length;
        for (int i = 0; i < size - 1; i++) {
            for (int j = i + 1; j < size; j++) {
                if (nums[i] + nums[j] == target)
                    return new int[] { i, j };
            }
        }
        return new int[0];
    }
}
C++
class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        int size = nums.size();
        for (int i = 0; i < size - 1; i++) {
            for (int j = i + 1; j < size; j++) {
                if (nums[i] + nums[j] == target)
                    return { i, j };
            }
        }
        return {};
    }
};

方法二：辅助哈希表 ​

时间复杂度 $O(N)$ ，空间复杂度 $O(N)$ ；属于「空间换时间」，借助辅助哈希表 dic ，通过保存数组元素值与索引的映射来提升算法运行效率，是本题的最佳解法。

Python
class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        dic = {}
        for i in range(len(nums)):
            if target - nums[i] in dic:
                return dic[target - nums[i]], i
            dic[nums[i]] = i
        return []
Java
class Solution {
    public int[] twoSum(int[] nums, int target) {
        int size = nums.length;
        Map<Integer, Integer> dic = new HashMap<>();
        for (int i = 0; i < size; i++) {
            if (dic.containsKey(target - nums[i])) {
                return new int[] { dic.get(target - nums[i]), i };
            }
            dic.put(nums[i], i);
        }
        return new int[0];
    }
}
C++
class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        int size = nums.size();
        unordered_map<int, int> dic;
        for (int i = 0; i < size; i++) {
            if (dic.find(target - nums[i]) != dic.end()) {
                return { dic[target - nums[i]], i };
            }
            dic.emplace(nums[i], i);
        }
        return {};
    }
};

示例题目 ​

在 LeetCode 题目中，「输入空间」和「输出空间」往往是固定的，是必须使用的内存空间。因希望专注于算法性能对比，本 LeetBook 的题目解析的空间复杂度仅统计「暂存空间」大小。

空间复杂度示例题解
$O(1)$斐波那契数、训练计划 III
$O(\log N)$库存管理 III、找到第 k 位数字
$O(N)$图书整理 I、动态口令
$O(N^2)$衣橱整理、套餐内商品的排列顺序

MIT License.

Copyright © 2024 自律小屋