方法一：哈希表 ​

利用数据结构特点，容易想到使用哈希表（Set）记录数组的各个数字，当查找到重复数字则直接返回。

算法流程： ​

1. 初始化： 新建 HashSet ，记为 $hmap$ ；
2. 遍历数组 $documents$ 中的每个数字 $doc$ ：
   1. 当 $doc$ 在 $hmap$ 中，说明重复，直接返回 $doc$ ；
   2. 将 $doc$ 添加至 $hmap$ 中；
3. 返回 $-1$ 。本题中一定有重复数字，因此这里返回多少都可以。

下图中的 nums 对应本题的 documents 。

<,,,,,>

代码： ​

class Solution:
    def findRepeatDocument(self, documents: List[int]) -> int:
        hmap = set()
        for doc in documents:
            if doc in hmap: return doc
            hmap.add(doc)
        return -1

class Solution {
    public int findRepeatDocument(int[] documents) {
        Set<Integer> hmap = new HashSet<>();
        for(int doc : documents) {
            if(hmap.contains(doc)) return doc;
            hmap.add(doc);
        }
        return -1;
    }
}

class Solution {
public:
    int findRepeatDocument(vector<int>& documents) {
        unordered_map<int, bool> map;
        for(int doc : documents) {
            if(map[doc]) return doc;
            map[doc] = true;
        }
        return -1;
    }
};

复杂度分析： ​

• 时间复杂度 $O(N)$ ： 遍历数组使用 $O(N)$ ，HashSet 添加与查找元素皆为 $O(1)$ 。
• 空间复杂度 $O(N)$ ： HashSet 占用 $O(N)$ 大小的额外空间。

方法二：原地交换 ​

题目说明尚未被充分使用，即 在一个长度为 n 的数组 documents 里的所有数字都在 0 ~ n-1 的范围内 。 此说明含义：数组元素的 索引 和 值 是 一对多 的关系。 因此，可遍历数组并通过交换操作，使元素的 索引 与 值 一一对应（即 $documents[i] = i$ ）。因而，就能通过索引映射对应的值，起到与字典等价的作用。

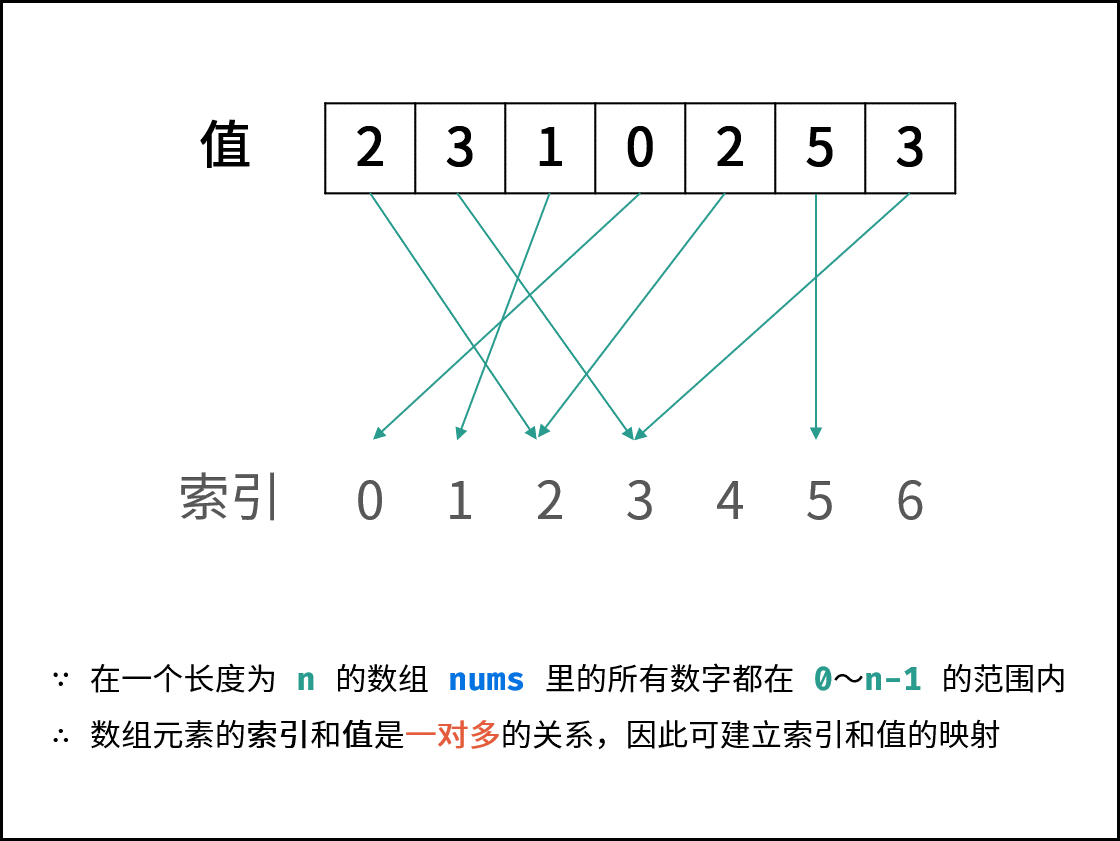
遍历中，第一次遇到数字 $x$ 时，将其交换至索引 $x$ 处；而当第二次遇到数字 $x$ 时，一定有 $documents[x] = x$ ，此时即可得到一组重复数字。

算法流程： ​

1. 遍历数组 $documents$ ，设索引初始值为 $i = 0$ :

   1. 若 $documents[i] = i$ ： 说明此数字已在对应索引位置，无需交换，因此跳过；
   2. 若 $documents[documents[i]] = documents[i]$ ： 代表索引 $documents[i]$ 处和索引 $i$ 处的元素值都为 $documents[i]$ ，即找到一组重复值，返回此值 $documents[i]$ ；
   3. 否则： 交换索引为 $i$ 和 $documents[i]$ 的元素值，将此数字交换至对应索引位置。

2. 若遍历完毕尚未返回，则返回 $-1$ 。

<,,,,,,,,>

代码： ​

Python 中，$a, b = c, d$ 操作的原理是先暂存元组 $(c, d)$ ，然后 “按左右顺序” 赋值给 a 和 b 。 因此，若写为 $documents[i], documents[documents[i]] = documents[documents[i]], documents[i]$ ，则 $documents[i]$ 会先被赋值，之后 $documents[documents[i]]$ 指向的元素则会出错。

class Solution:
    def findRepeatDocument(self, documents: List[int]) -> int:
        i = 0
        while i < len(documents):
            if documents[i] == i:
                i += 1
                continue
            if documents[documents[i]] == documents[i]: return documents[i]
            documents[documents[i]], documents[i] = documents[i], documents[documents[i]]
        return -1

class Solution {
    public int findRepeatDocument(int[] documents) {
        int i = 0;
        while(i < documents.length) {
            if(documents[i] == i) {
                i++;
                continue;
            }
            if(documents[documents[i]] == documents[i]) return documents[i];
            int tmp = documents[i];
            documents[i] = documents[tmp];
            documents[tmp] = tmp;
        }
        return -1;
    }
}

class Solution {
public:
    int findRepeatDocument(vector<int>& documents) {
        int i = 0;
        while(i < documents.size()) {
            if(documents[i] == i) {
                i++;
                continue;
            }
            if(documents[documents[i]] == documents[i])
                return documents[i];
            swap(documents[i],documents[documents[i]]);
        }
        return -1;
    }
};

复杂度分析： ​

• 时间复杂度 $O(N)$ ： 遍历数组使用 $O(N)$ ，每轮遍历的判断和交换操作使用 $O(1)$ 。
• 空间复杂度 $O(1)$ ： 使用常数复杂度的额外空间。