解题思路:
给定一长度为 $N$ 的无序数组,其中位数的计算方法:首先对数组执行排序(使用 $O(N \log N)$ 时间),然后返回中间元素即可(使用 $O(1)$ 时间)。
针对本题,根据以上思路,可以将数据流保存在一个列表中,并在添加元素时 保持数组有序 。此方法的时间复杂度为 $O(N)$ ,其中包括: 查找元素插入位置 $O(\log N)$ (二分查找)、向数组某位置插入元素 $O(N)$ (插入位置之后的元素都需要向后移动一位)。
借助 堆 可进一步优化时间复杂度。
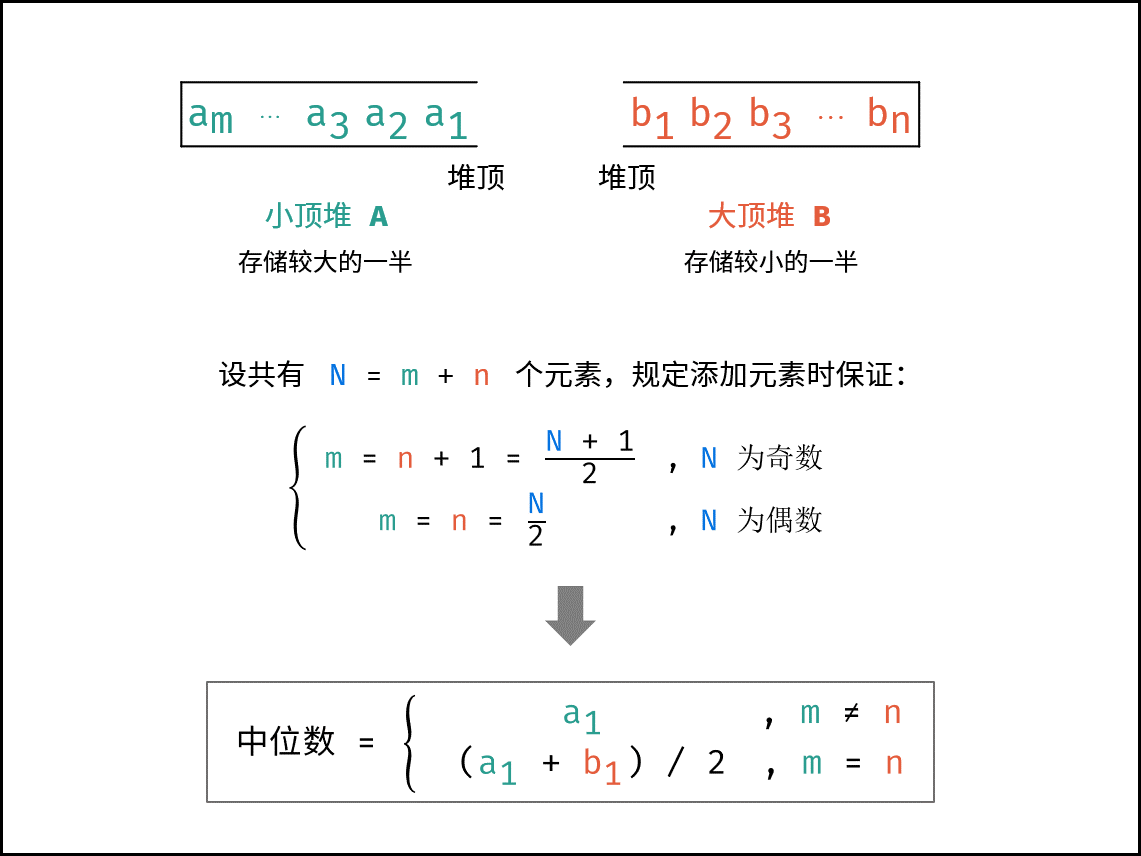
建立一个 小顶堆 $A$ 和 大顶堆 $B$ ,各保存列表的一半元素,且规定:
- $A$ 保存 较大 的一半,长度为 $\frac{N}{2}$( $N$ 为偶数)或 $\frac{N+1}{2}$( $N$ 为奇数);
- $B$ 保存 较小 的一半,长度为 $\frac{N}{2}$( $N$ 为偶数)或 $\frac{N-1}{2}$( $N$ 为奇数);
随后,中位数可仅根据 $A, B$ 的堆顶元素计算得到。
算法流程:
设元素总数为 $N = m + n$ ,其中 $m$ 和 $n$ 分别为 $A$ 和 $B$ 中的元素个数。
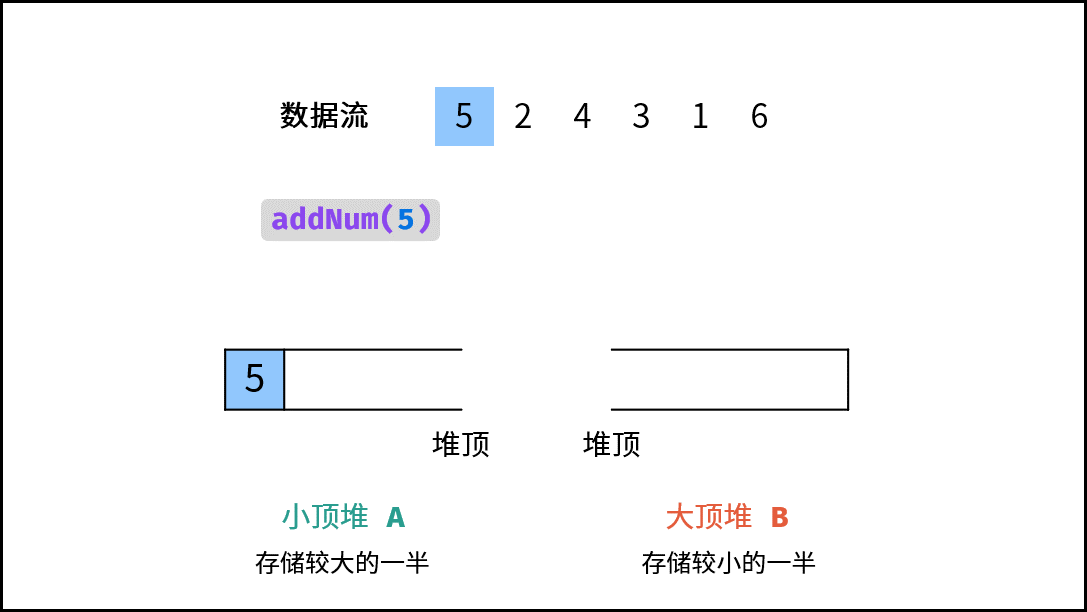
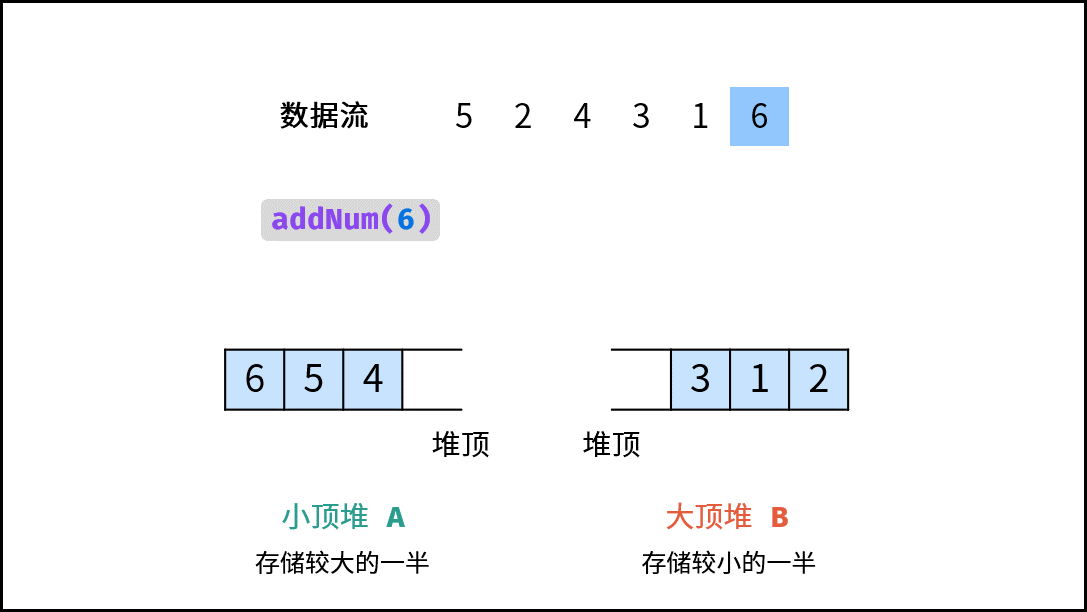
addNum(num) 函数:
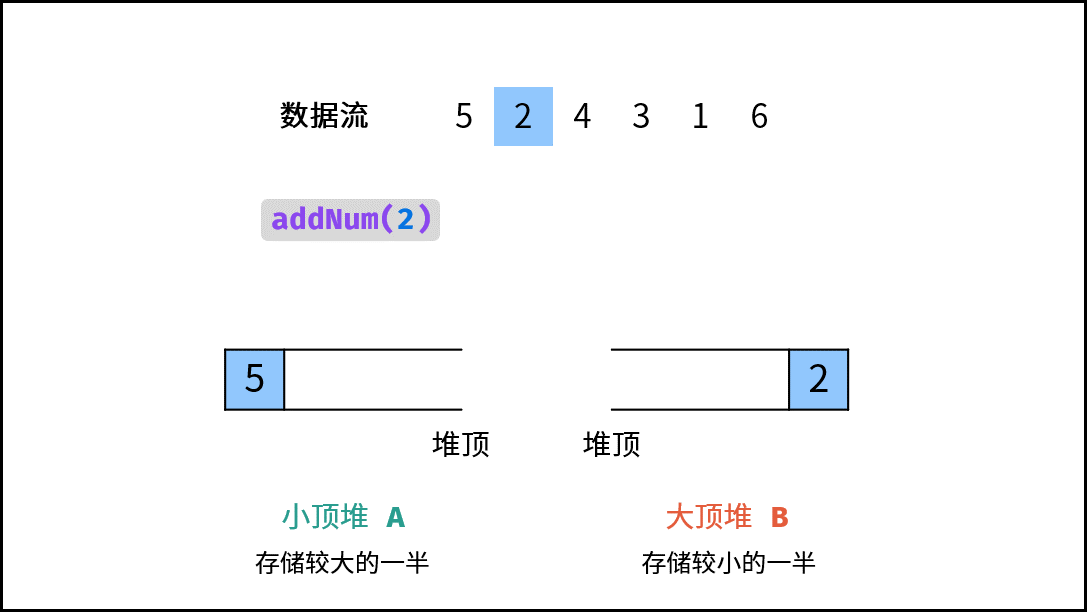
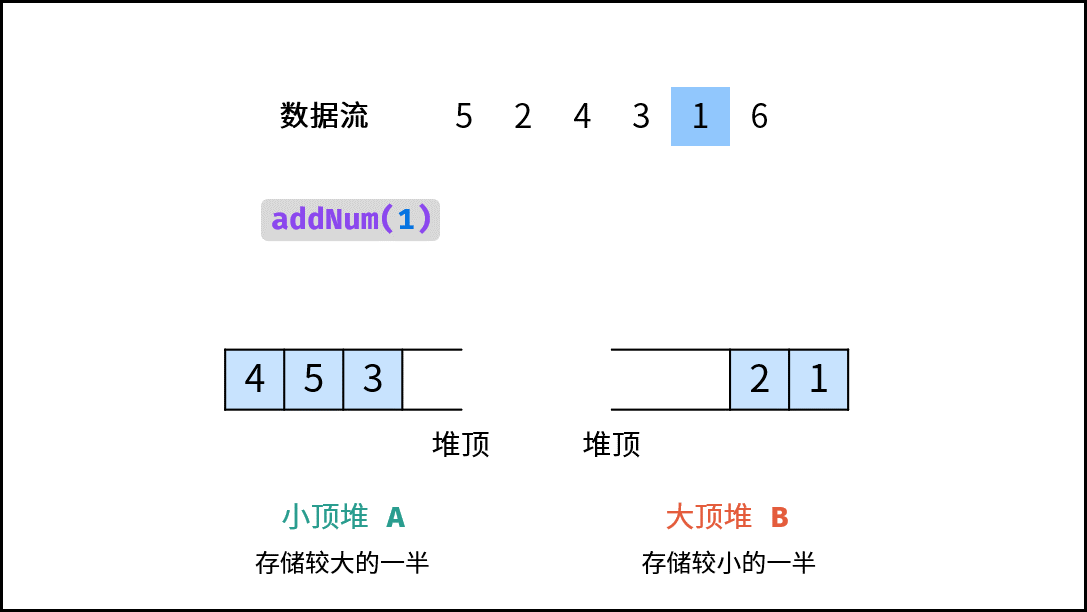
- 当 $m = n$(即 $N$ 为 偶数):需向 $A$ 添加一个元素。实现方法:将新元素 $num$ 插入至 $B$ ,再将 $B$ 堆顶元素插入至 $A$ ;
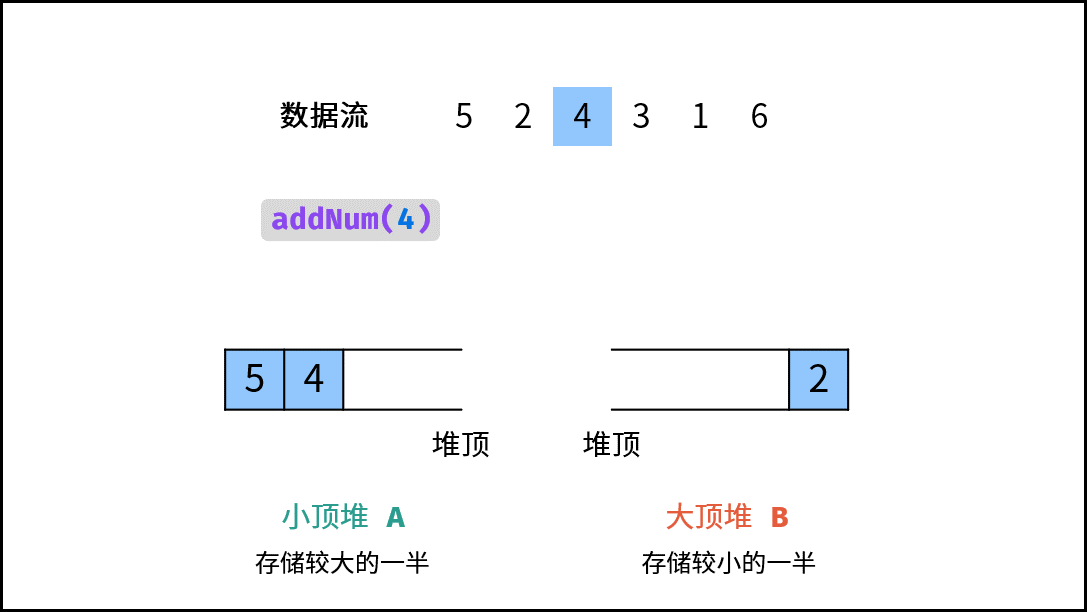
- 当 $m \ne n$(即 $N$ 为 奇数):需向 $B$ 添加一个元素。实现方法:将新元素 $num$ 插入至 $A$ ,再将 $A$ 堆顶元素插入至 $B$ ;
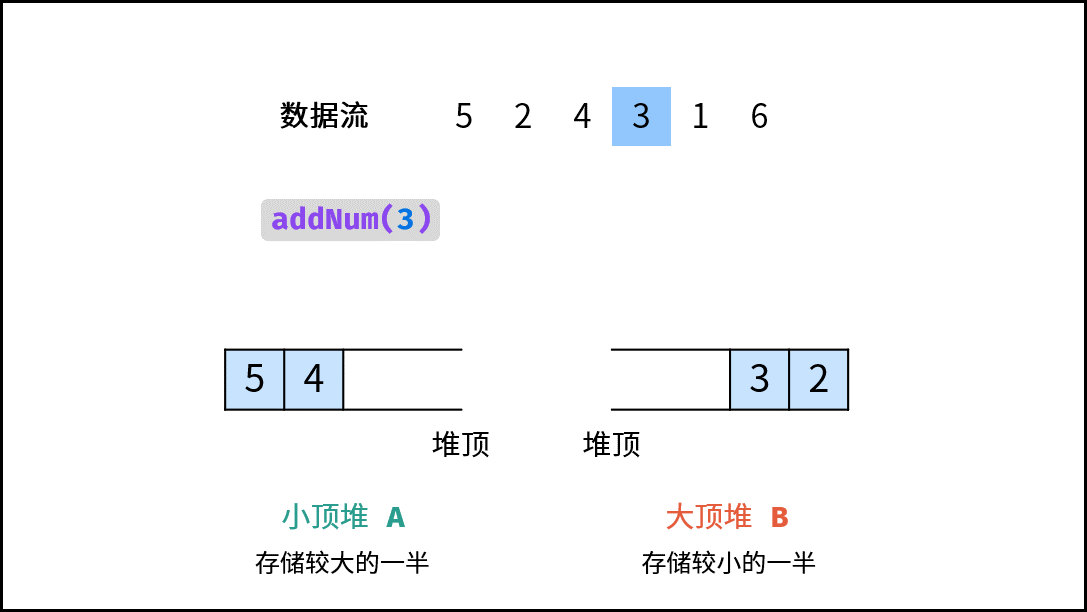
假设插入数字 $num$ 遇到情况
1.。由于 $num$ 可能属于 “较小的一半” (即属于 $B$ ),因此不能将 $nums$ 直接插入至 $A$ 。而应先将 $num$ 插入至 $B$ ,再将 $B$ 堆顶元素插入至 $A$ 。这样就可以始终保持 $A$ 保存较大一半、 $B$ 保存较小一半。
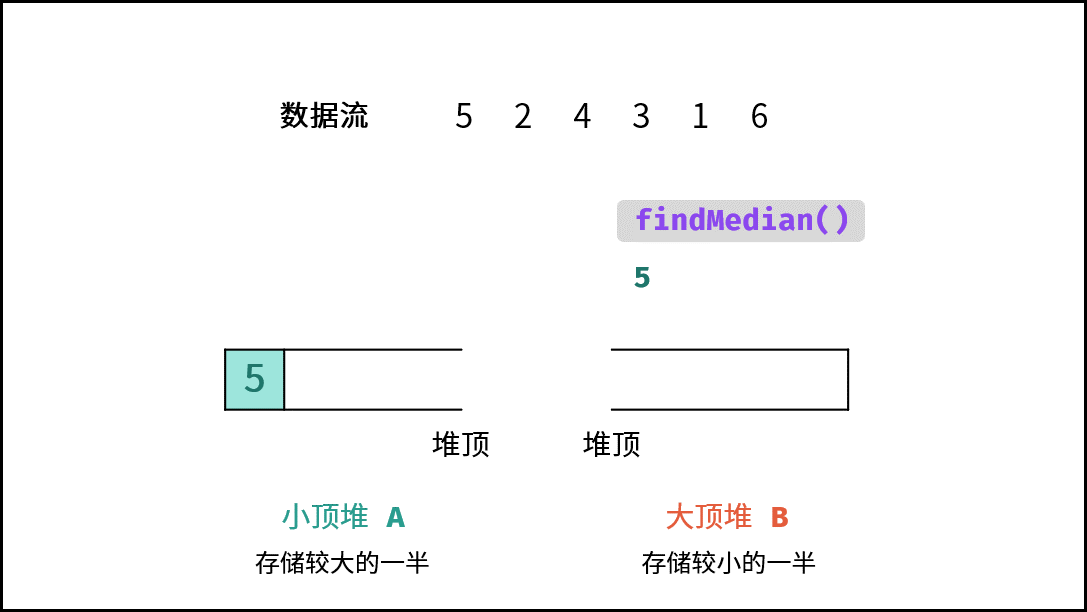
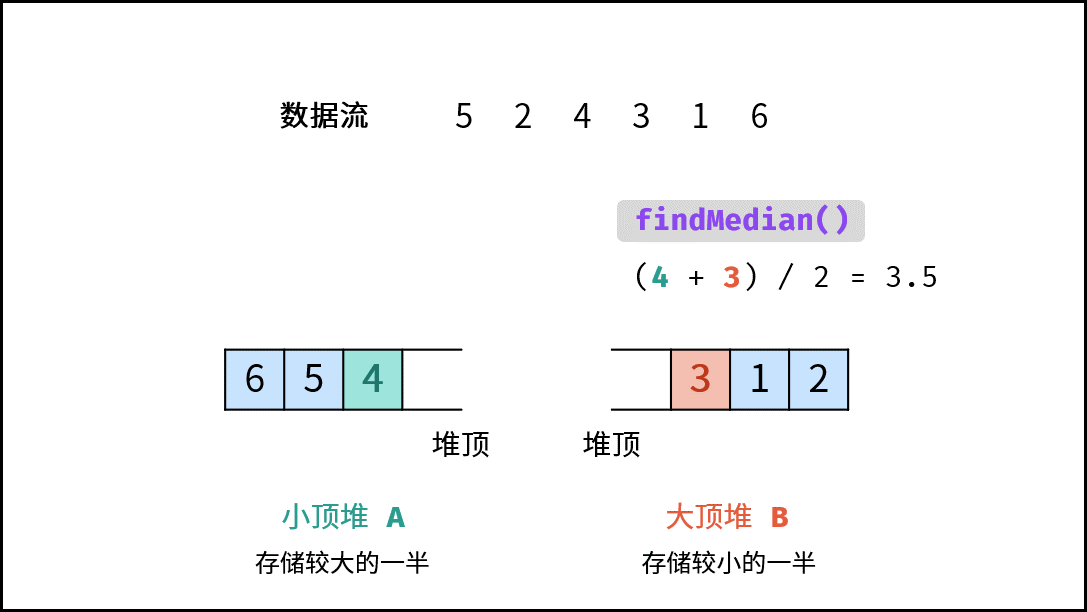
findMedian() 函数:
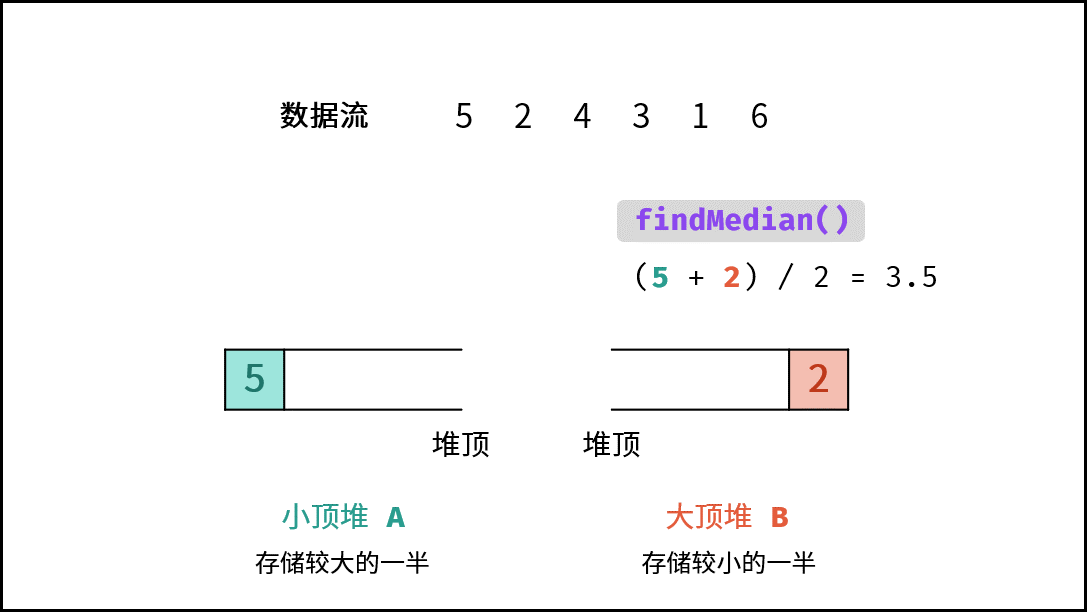
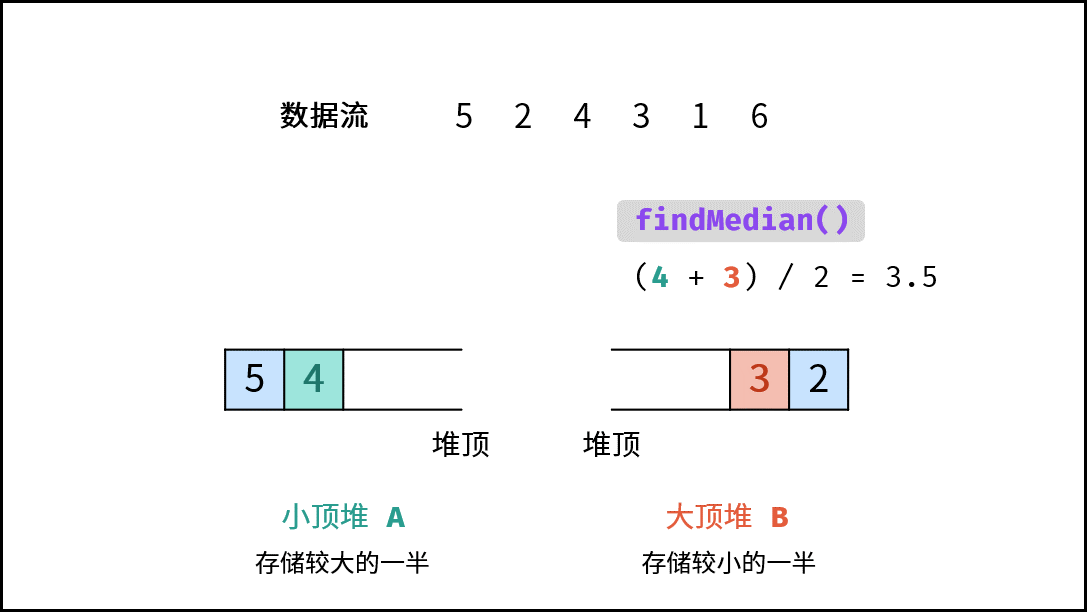
- 当 $m = n$( $N$ 为 偶数):则中位数为 $($ $A$ 的堆顶元素 + $B$ 的堆顶元素 $)/2$。
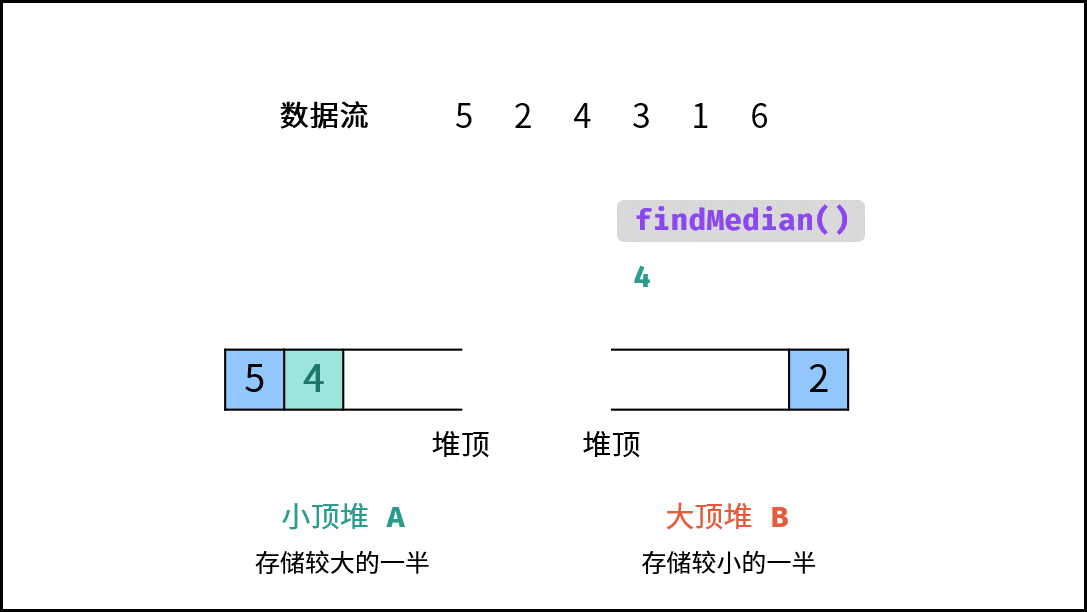
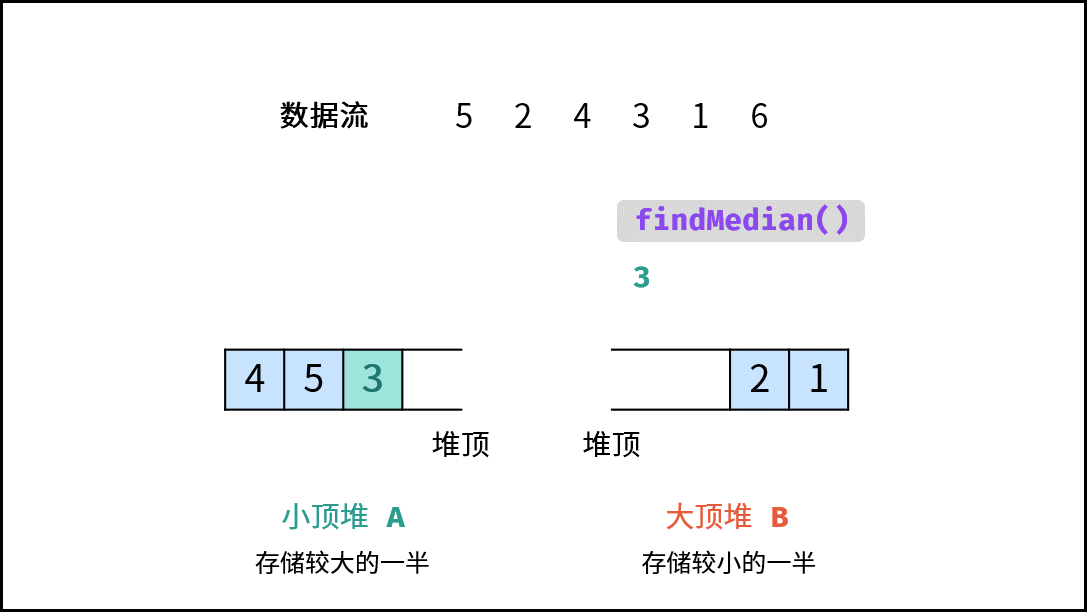
- 当 $m \ne n$( $N$ 为 奇数):则中位数为 $A$ 的堆顶元素。
< ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, >
>
代码:
Python 中 heapq 模块是小顶堆。实现 大顶堆 方法: 小顶堆的插入和弹出操作均将元素 取反 即可。 Java 使用 PriorityQueue<>((x, y) -> (y - x)) 可方便实现大顶堆。 C++ 中 greater 为小顶堆,less 为大顶堆。
from heapq import *
class MedianFinder:
def __init__(self):
self.A = [] # 小顶堆,保存较大的一半
self.B = [] # 大顶堆,保存较小的一半
def addNum(self, num: int) -> None:
if len(self.A) != len(self.B):
heappush(self.A, num)
heappush(self.B, -heappop(self.A))
else:
heappush(self.B, -num)
heappush(self.A, -heappop(self.B))
def findMedian(self) -> float:
return self.A[0] if len(self.A) != len(self.B) else (self.A[0] - self.B[0]) / 2.0class MedianFinder {
Queue<Integer> A, B;
public MedianFinder() {
A = new PriorityQueue<>(); // 小顶堆,保存较大的一半
B = new PriorityQueue<>((x, y) -> (y - x)); // 大顶堆,保存较小的一半
}
public void addNum(int num) {
if(A.size() != B.size()) {
A.add(num);
B.add(A.poll());
} else {
B.add(num);
A.add(B.poll());
}
}
public double findMedian() {
return A.size() != B.size() ? A.peek() : (A.peek() + B.peek()) / 2.0;
}
}class MedianFinder {
public:
priority_queue<int, vector<int>, greater<int>> A; // 小顶堆,保存较大的一半
priority_queue<int, vector<int>, less<int>> B; // 大顶堆,保存较小的一半
MedianFinder() { }
void addNum(int num) {
if(A.size() != B.size()) {
A.push(num);
B.push(A.top());
A.pop();
} else {
B.push(num);
A.push(B.top());
B.pop();
}
}
double findMedian() {
return A.size() != B.size() ? A.top() : (A.top() + B.top()) / 2.0;
}
};Push item on the heap, then pop and return the smallest item from the heap. The combined action runs more efficiently than heappush() followed by a separate call to heappop().
根据以上文档说明,可将 Python 代码优化为:
from heapq import *
class MedianFinder:
def __init__(self):
self.A = [] # 小顶堆,保存较大的一半
self.B = [] # 大顶堆,保存较小的一半
def addNum(self, num: int) -> None:
if len(self.A) != len(self.B):
heappush(self.B, -heappushpop(self.A, num))
else:
heappush(self.A, -heappushpop(self.B, -num))
def findMedian(self) -> float:
return self.A[0] if len(self.A) != len(self.B) else (self.A[0] - self.B[0]) / 2.0复杂度分析:
- 时间复杂度:
- 查找中位数 $O(1)$ : 获取堆顶元素使用 $O(1)$ 时间;
- 添加数字 $O(\log N)$ : 堆的插入和弹出操作使用 $O(\log N)$ 时间。
- 空间复杂度 $O(N)$ : 其中 $N$ 为数据流中的元素数量,小顶堆 $A$ 和大顶堆 $B$ 最多同时保存 $N$ 个元素。