自律小屋 | 自律小屋

解题思路：

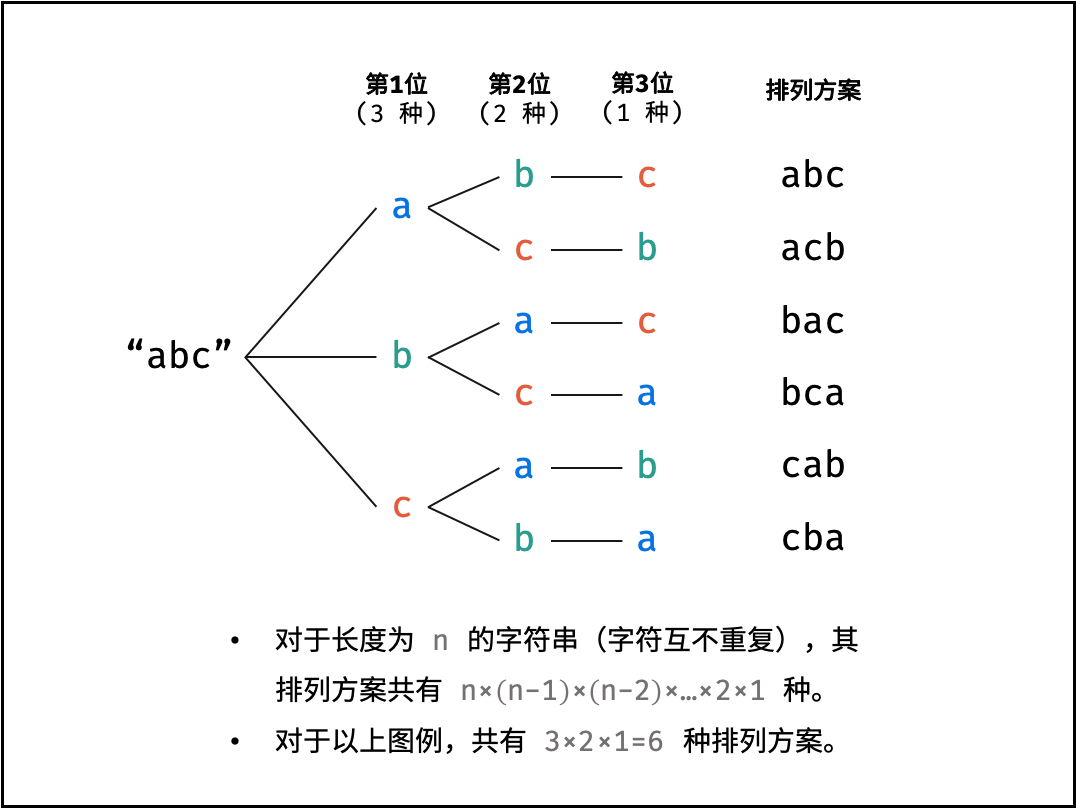
对于一个长度为 $n$ 的字符串（假设字符互不重复），其排列方案数共有：

$$ n \times (n-1) \times (n-2) … \times 2 \times 1 $$

排列方案的生成：

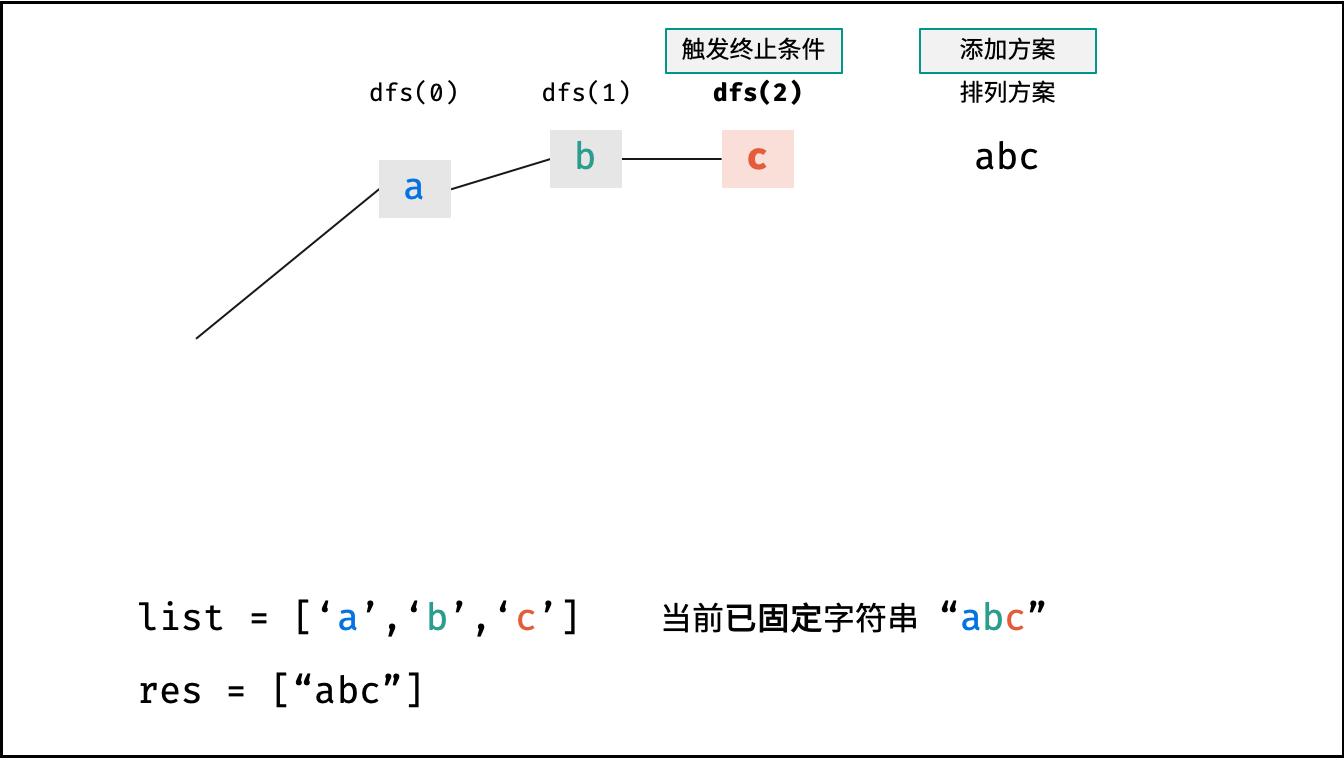
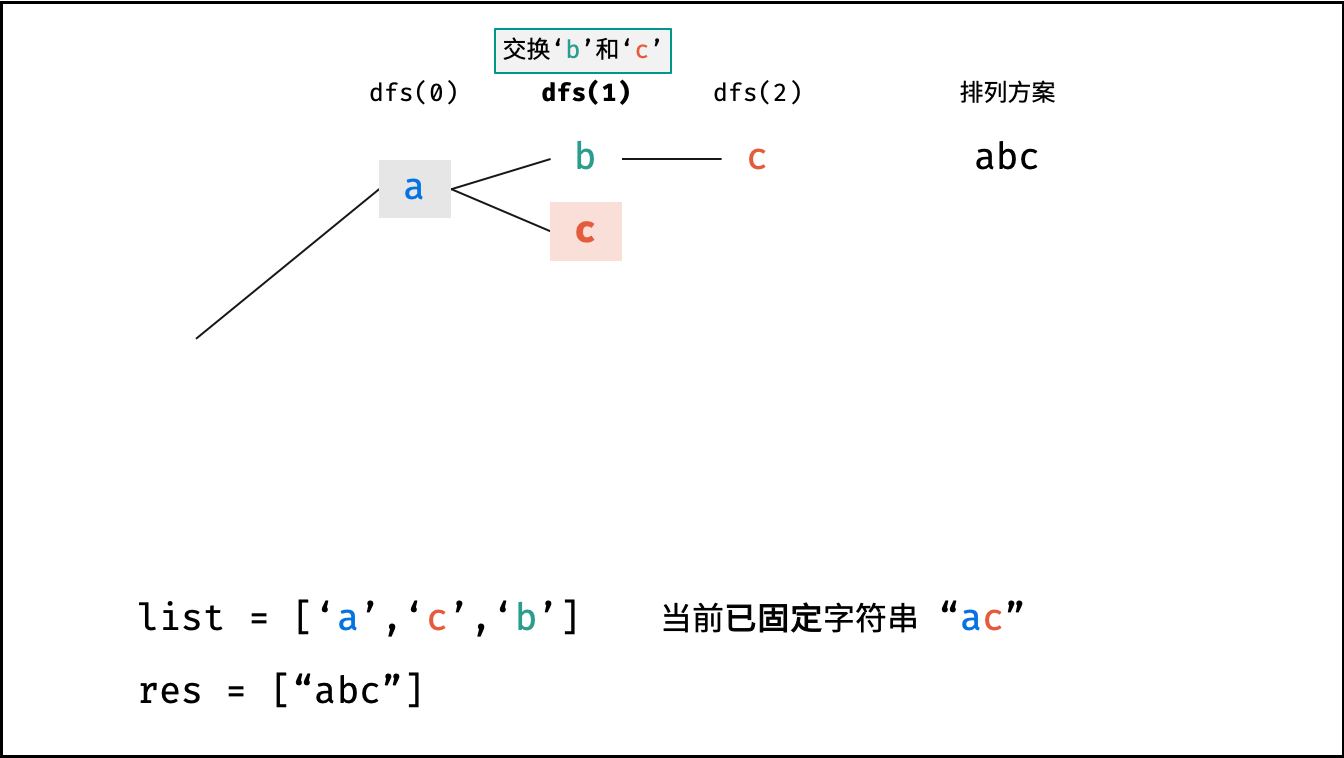
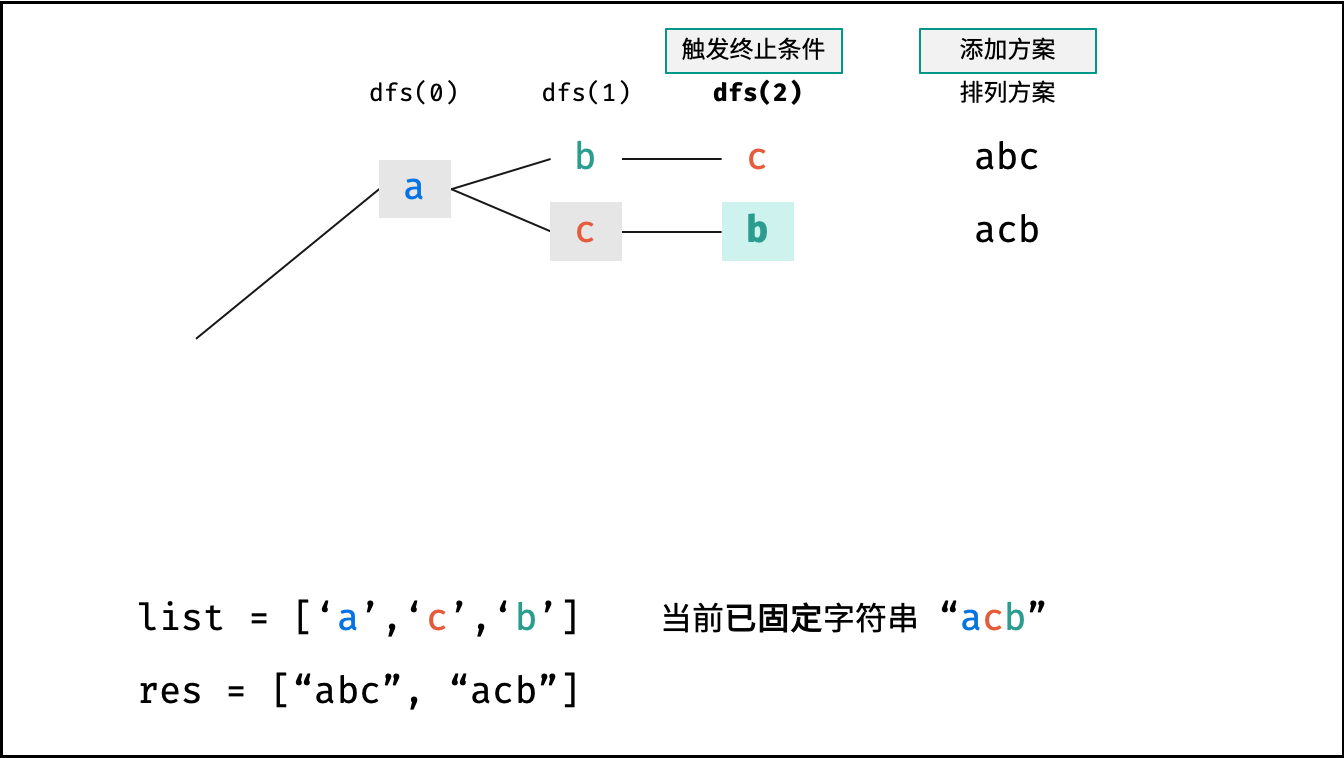
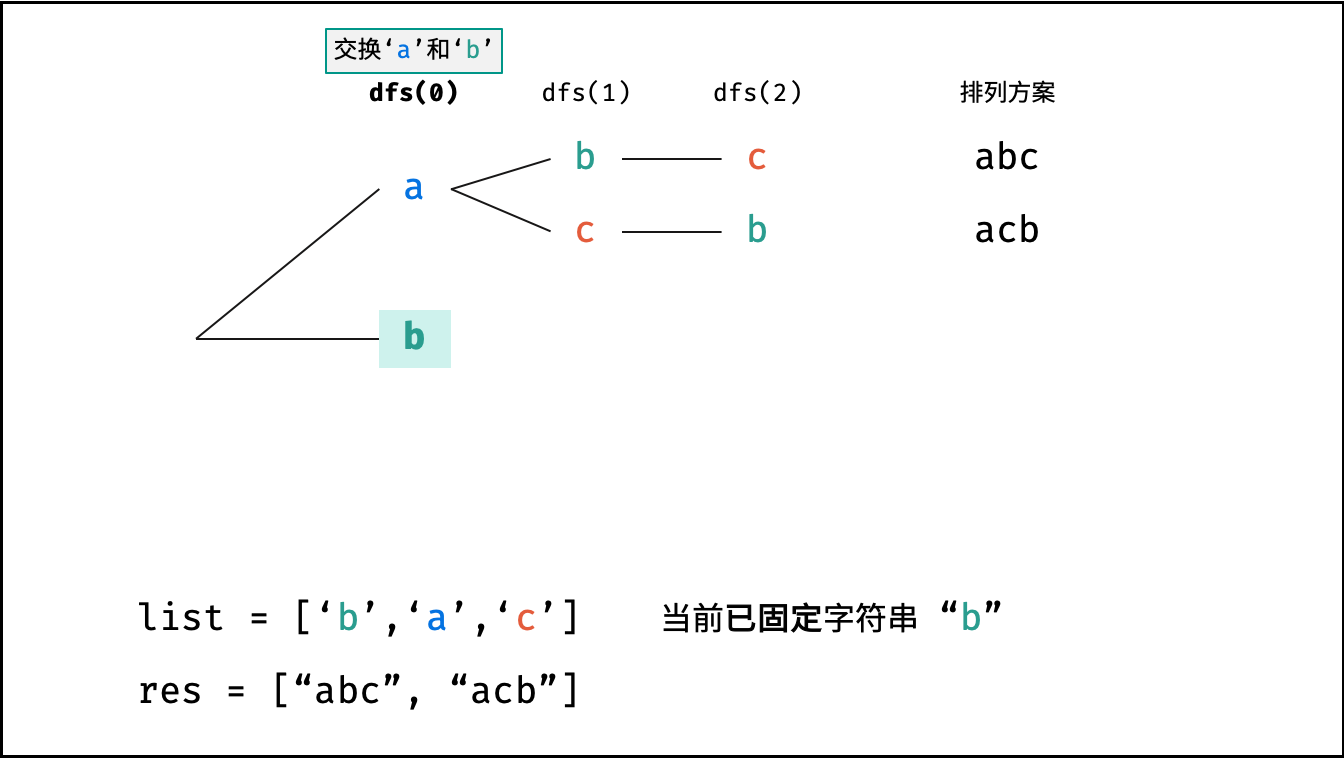
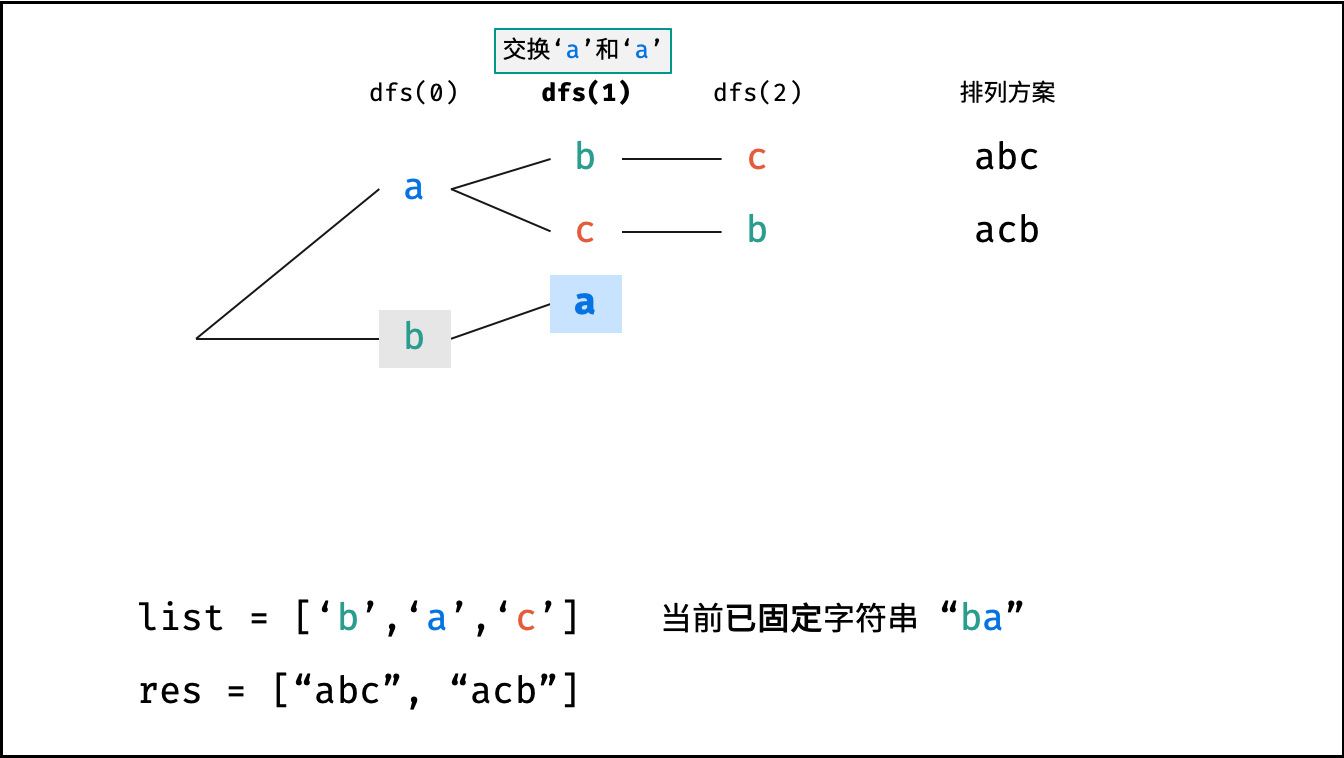
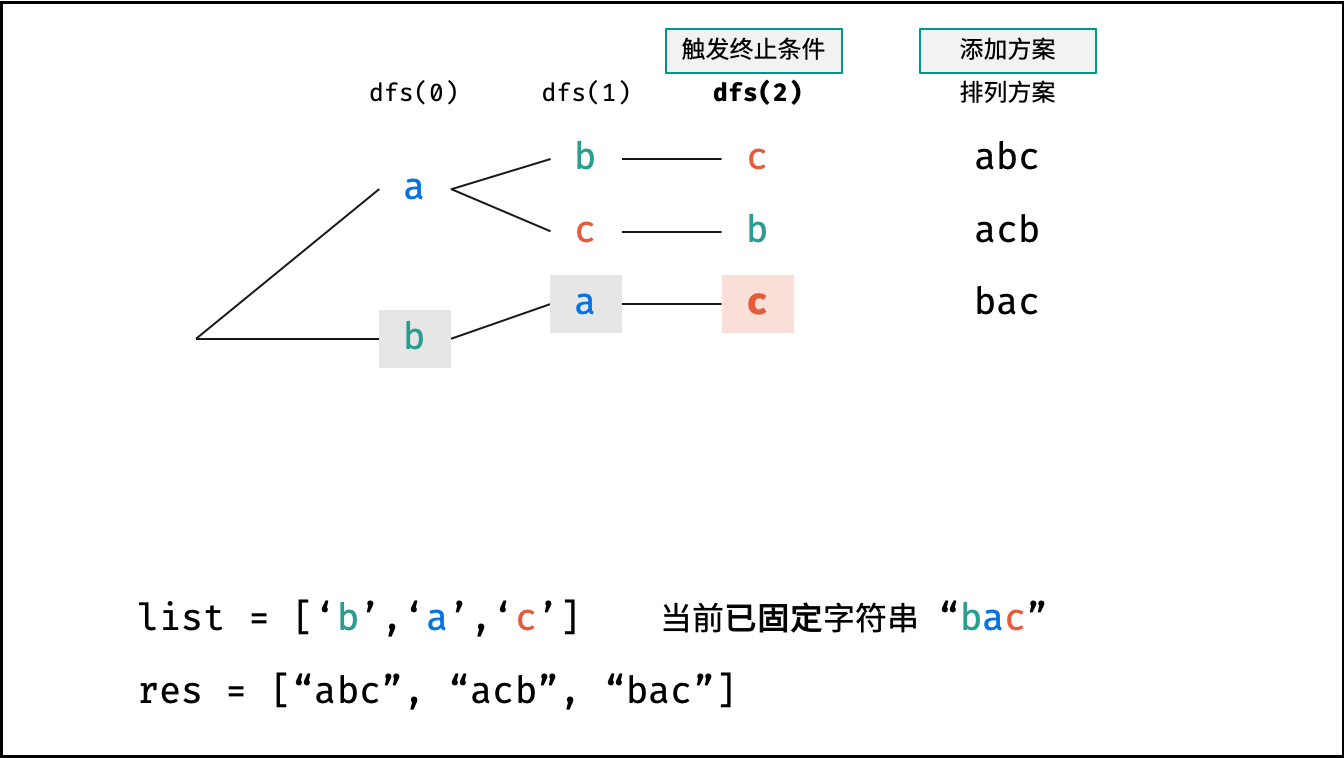
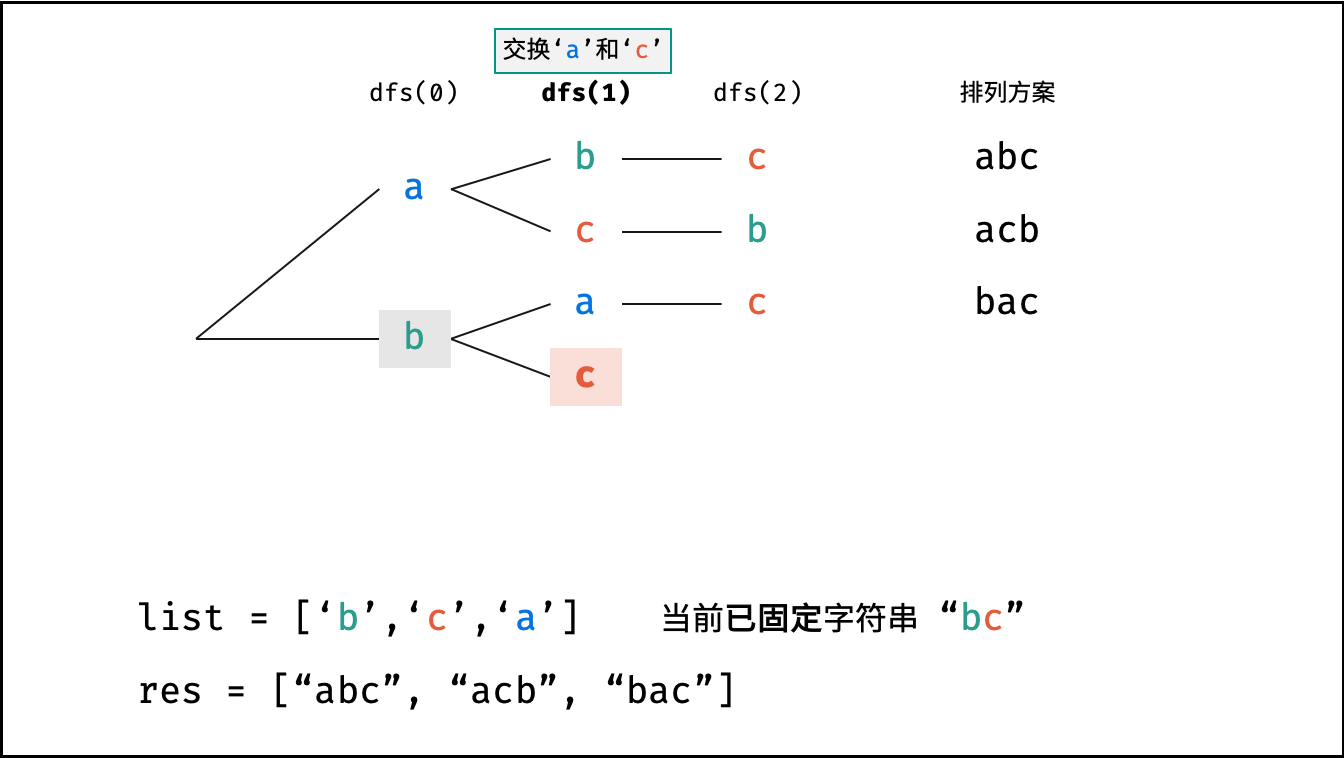
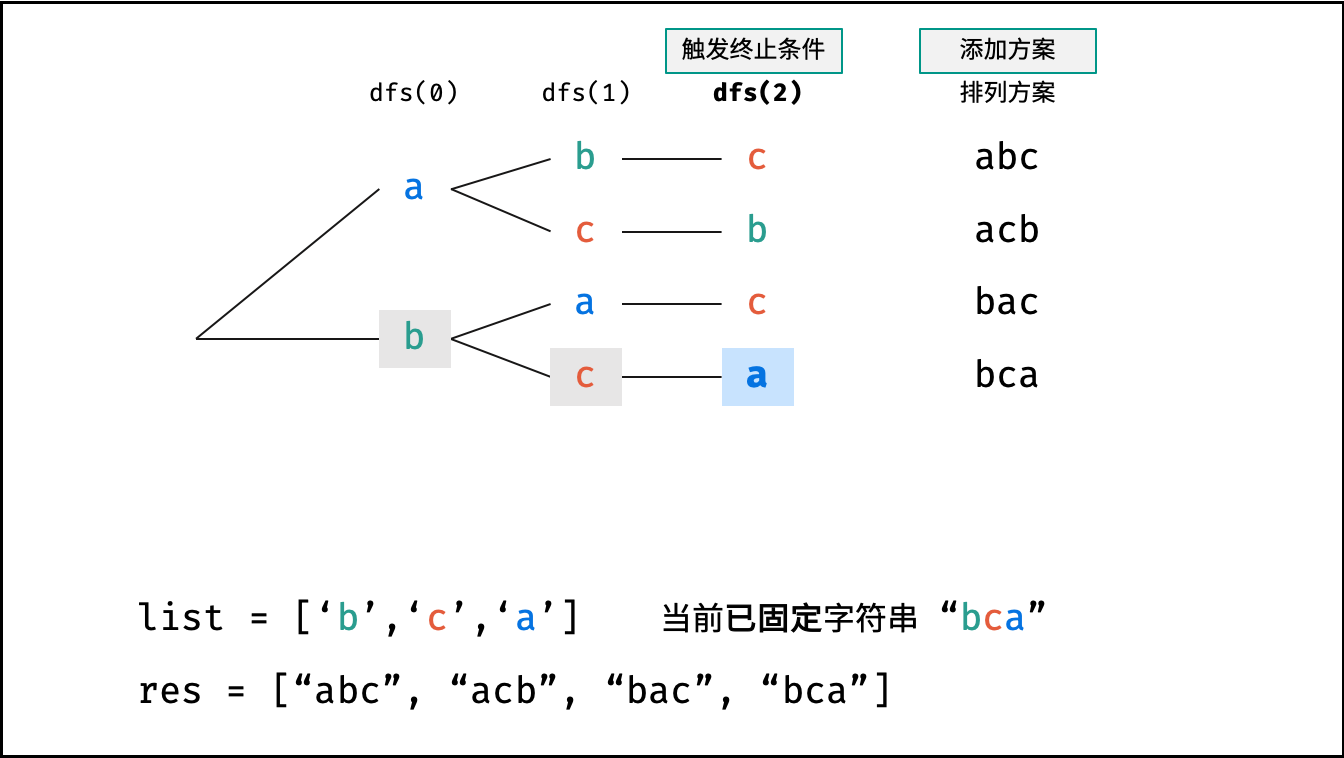
根据字符串排列的特点，考虑深度优先搜索所有排列方案。即通过字符交换，先固定第 $1$ 位字符（ $n$ 种情况）、再固定第 $2$ 位字符（ $n-1$ 种情况）、... 、最后固定第 $n$ 位字符（ $1$ 种情况）。

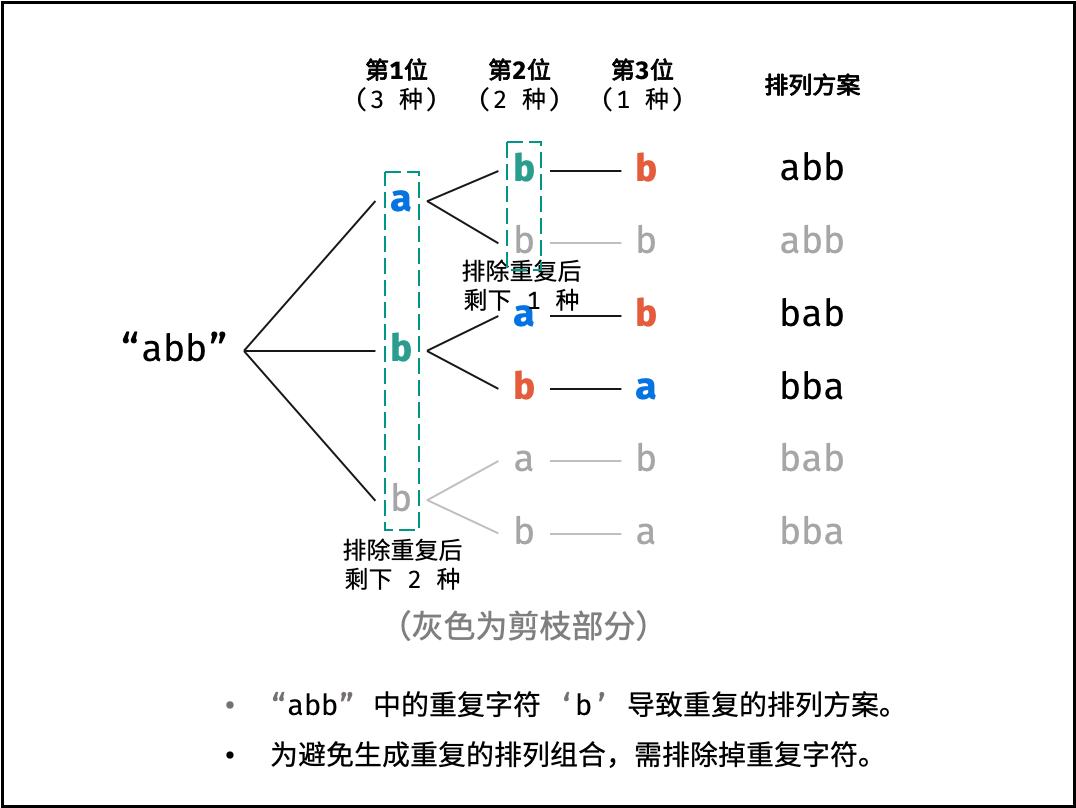
重复排列方案与剪枝：

当字符串存在重复字符时，排列方案中也存在重复的排列方案。为排除重复方案，需在固定某位字符时，保证 “每种字符只在此位固定一次” ，即遇到重复字符时不交换，直接跳过。从 DFS 角度看，此操作称为 “剪枝” 。

递归解析：

终止条件： 当 x = len(arr) - 1 时，代表所有位已固定（最后一位只有 $1$ 种情况），则将当前组合 arr 转化为字符串并加入 res ，并返回；
递推参数： 当前固定位 x ；
递推工作： 初始化一个 Set ，用于排除重复的字符；将第 x 位字符与 i $\in$ [x, len(arr)] 字符分别交换，并进入下层递归；
1. 剪枝： 若 arr[i] 在 Set 中，代表其是重复字符，因此 “剪枝” ；
2. 将 arr[i] 加入 Set ，以便之后遇到重复字符时剪枝；
3. 固定字符： 将字符 arr[i] 和 arr[x] 交换，即固定 arr[i] 为当前位字符；
4. 开启下层递归： 调用 dfs(x + 1) ，即开始固定第 x + 1 个字符；
5. 还原交换： 将字符 arr[i] 和 arr[x] 交换（还原之前的交换）；

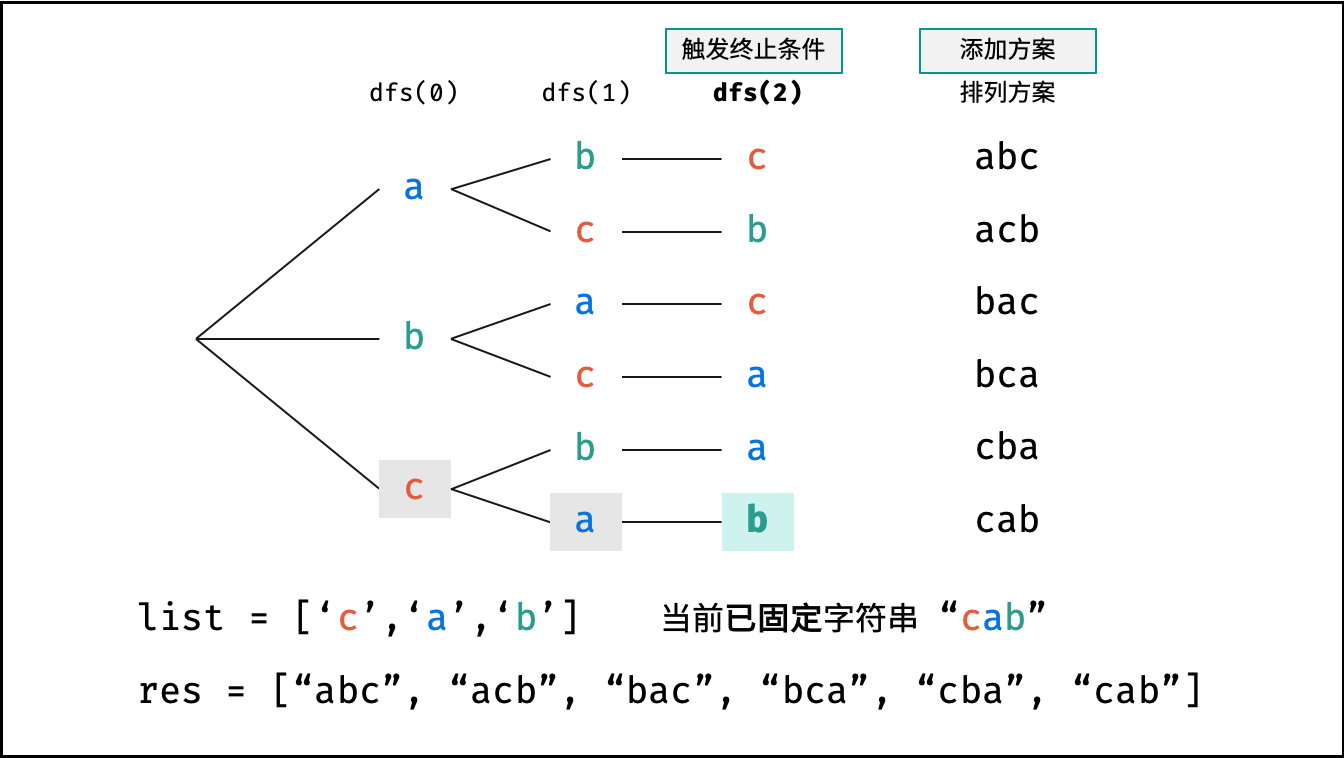
下图的测试样例为 goods = "abc" 。

<,,,,,,,,,,,,,,,>

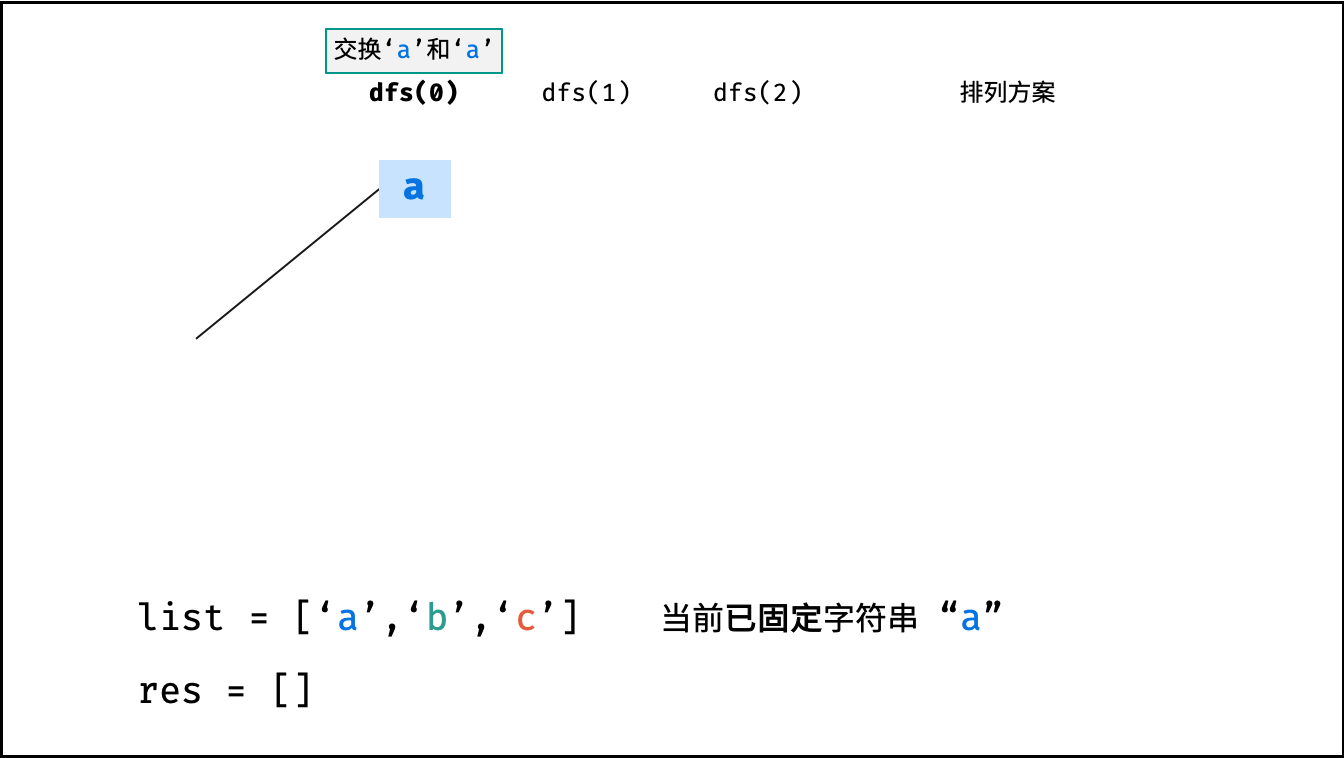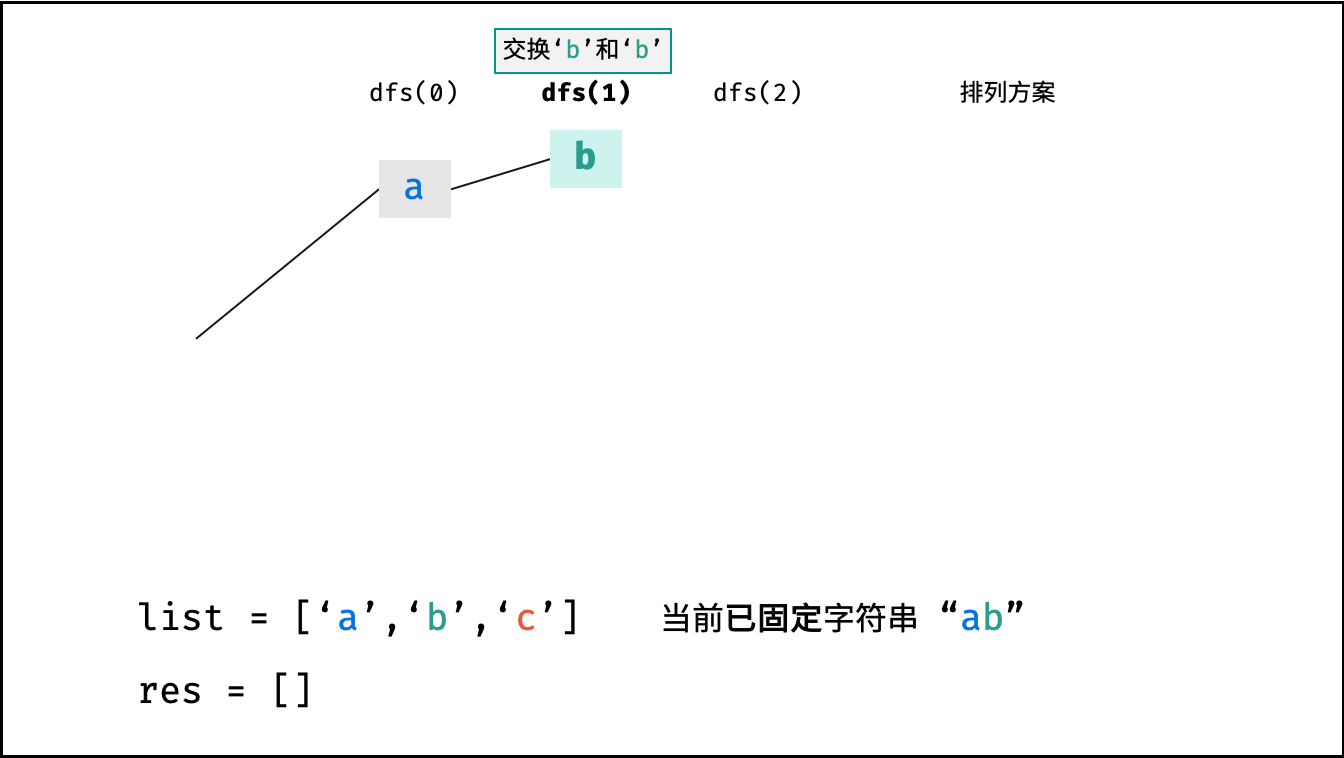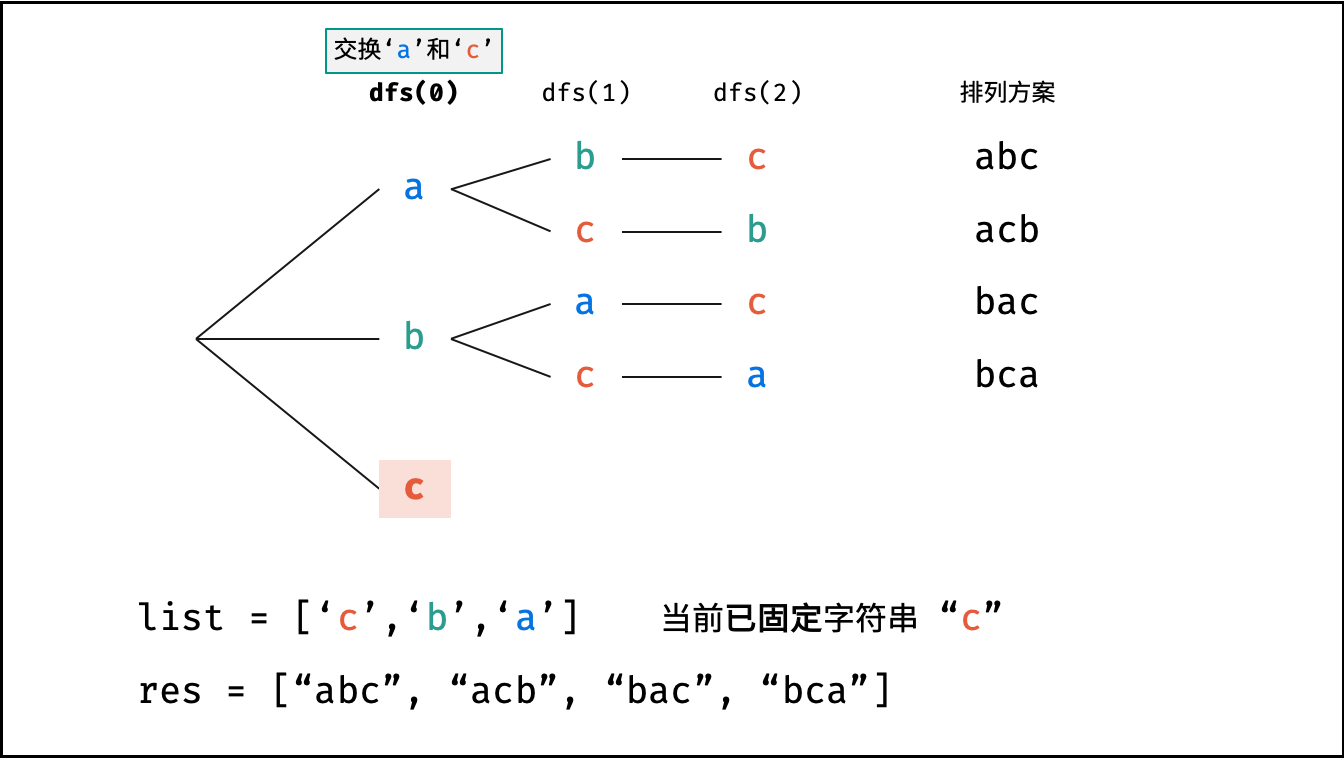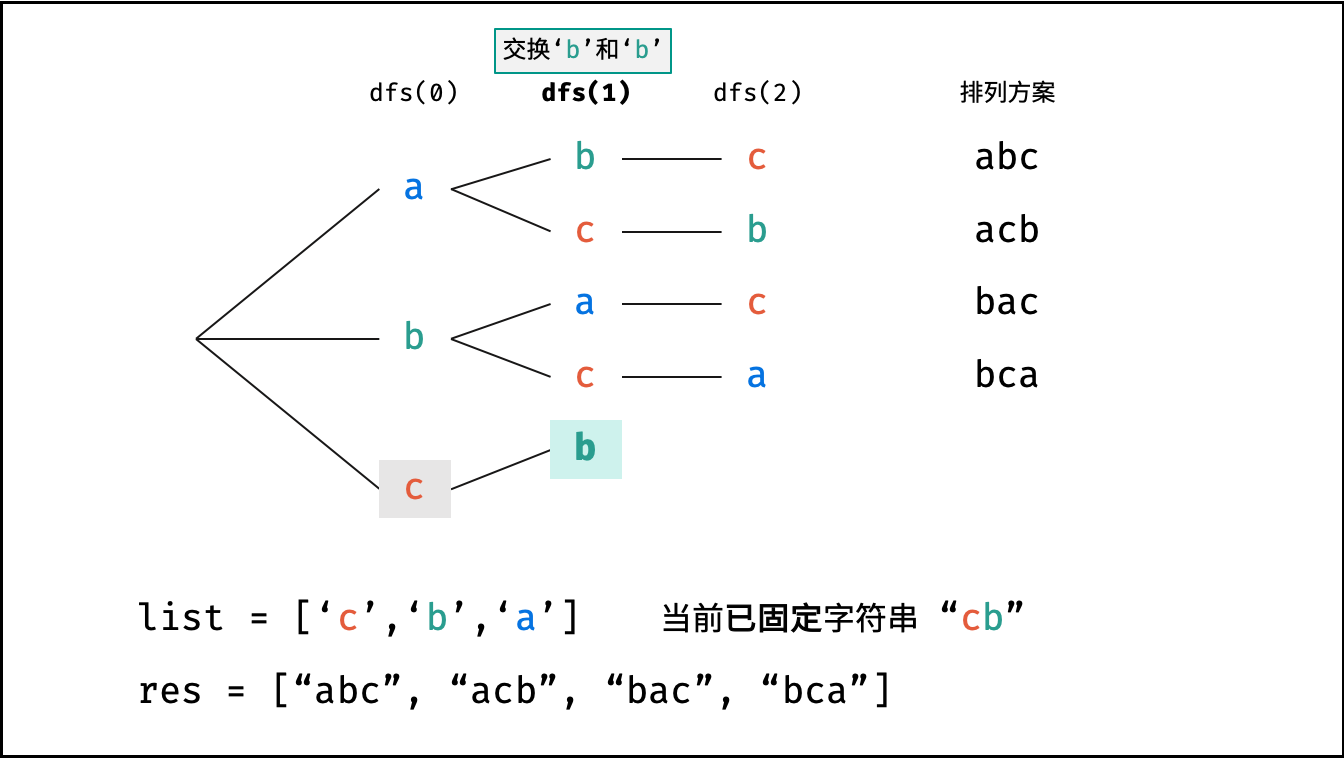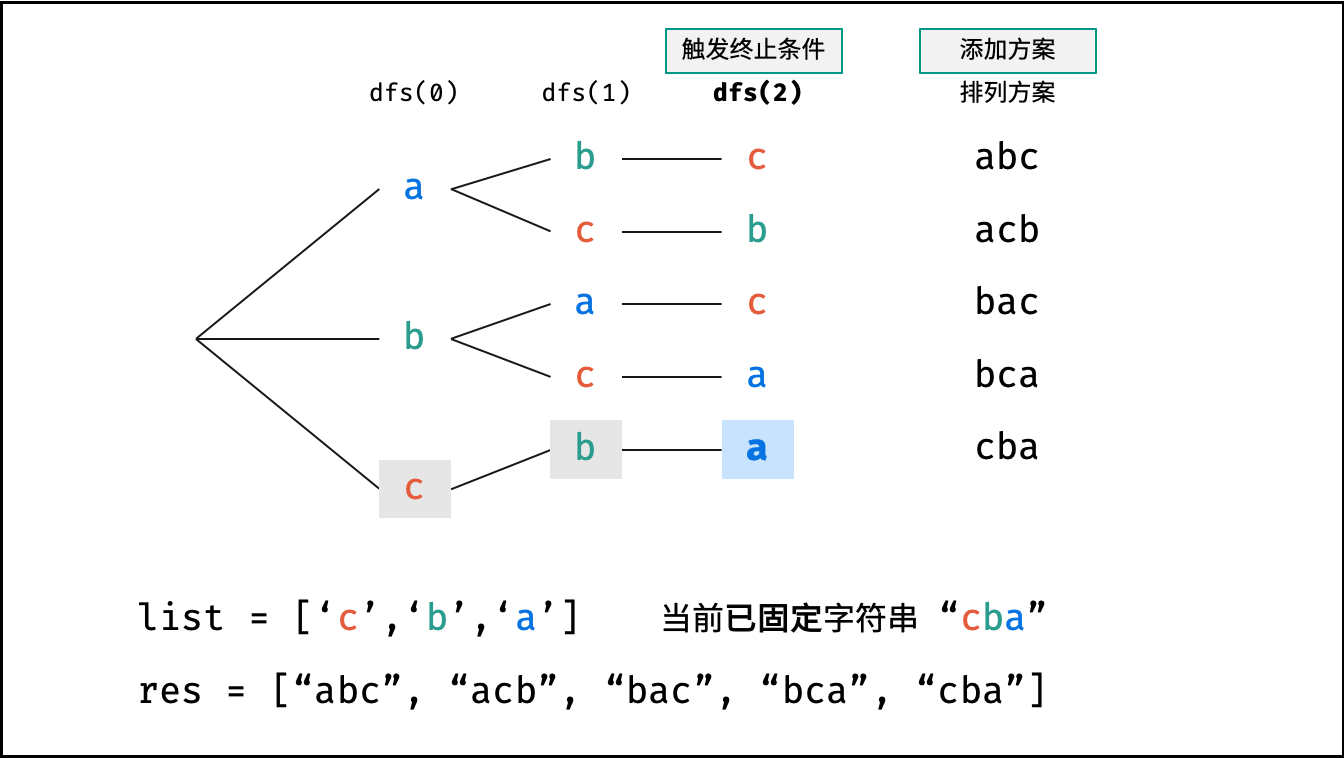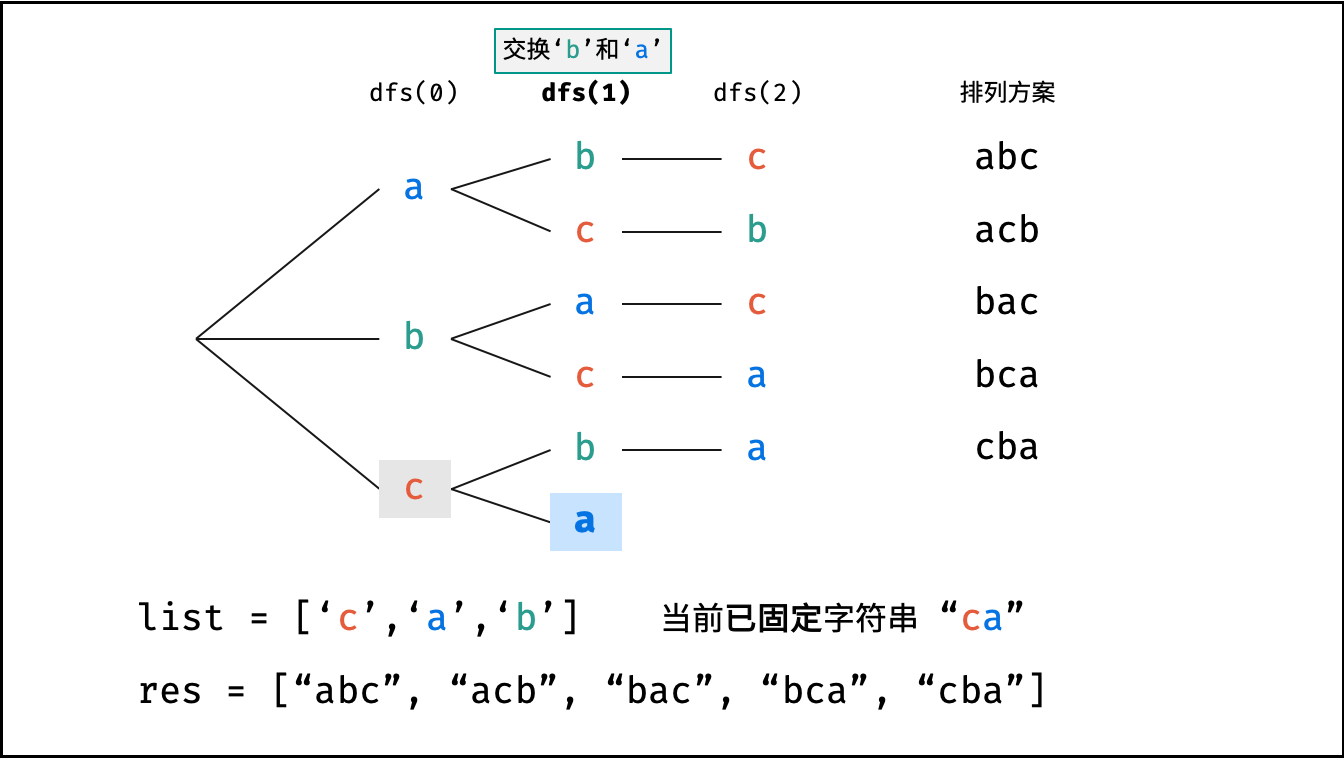代码：

Python

class Solution:
    def goodsOrder(self, goods: str) -> List[str]:
        arr, res = list(goods), []
        def dfs(x):
            if x == len(arr) - 1:
                res.append(''.join(arr))   # 添加排列方案
                return
            hmap = set()
            for i in range(x, len(arr)):
                if arr[i] in hmap: continue # 重复，因此剪枝
                hmap.add(arr[i])
                arr[i], arr[x] = arr[x], arr[i]  # 交换，将 arr[i] 固定在第 x 位
                dfs(x + 1)               # 开启固定第 x + 1 位字符
                arr[i], arr[x] = arr[x], arr[i]  # 恢复交换
        dfs(0)
        return res

Java

class Solution {
    List<String> res = new LinkedList<>();
    char[] arr;
    public String[] goodsOrder(String goods) {
        arr = goods.toCharArray();
        dfs(0);
        return res.toArray(new String[res.size()]);
    }
    void dfs(int x) {
        if(x == arr.length - 1) {
            res.add(String.valueOf(arr));      // 添加排列方案
            return;
        }
        HashSet<Character> set = new HashSet<>();
        for(int i = x; i < arr.length; i++) {
            if(set.contains(arr[i])) continue; // 重复，因此剪枝
            set.add(arr[i]);
            swap(i, x);                      // 交换，将 arr[i] 固定在第 x 位
            dfs(x + 1);                      // 开启固定第 x + 1 位字符
            swap(i, x);                      // 恢复交换
        }
    }
    void swap(int a, int b) {
        char tmp = arr[a];
        arr[a] = arr[b];
        arr[b] = tmp;
    }
}

C++

class Solution {
public:
    vector<string> goodsOrder(string goods) {
        dfs(goods, 0);
        return res;
    }
private:
    vector<string> res;
    void dfs(string goods, int x) {
        if(x == goods.size() - 1) {
            res.push_back(goods);                       // 添加排列方案
            return;
        }
        set<int> st;
        for(int i = x; i < goods.size(); i++) {
            if(st.find(goods[i]) != st.end()) continue; // 重复，因此剪枝
            st.insert(goods[i]);
            swap(goods[i], goods[x]);                       // 交换，将 goods[i] 固定在第 x 位
            dfs(goods, x + 1);                          // 开启固定第 x + 1 位字符
            swap(goods[i], goods[x]);                       // 恢复交换
        }
    }
};

复杂度分析：

时间复杂度 $O(N!N)$ ： $N$ 为字符串 goods 的长度；时间复杂度和字符串排列的方案数成线性关系，方案数为 $N \times (N-1) \times (N-2) … \times 2 \times 1$ ，即复杂度为 $O(N!)$ ；字符串拼接操作 join() 使用 $O(N)$ ；因此总体时间复杂度为 $O(N!N)$ 。
空间复杂度 $O(N^2)$ ： 全排列的递归深度为 $N$ ，系统累计使用栈空间大小为 $O(N)$ ；递归中辅助 Set 累计存储的字符数量最多为 $N + (N-1) + ... + 2 + 1 = (N+1)N/2$ ，即占用 $O(N^2)$ 的额外空间。

解题思路： ​

递归解析： ​

代码： ​

复杂度分析： ​

解题思路：

递归解析：

代码：

复杂度分析：