解题思路： ​

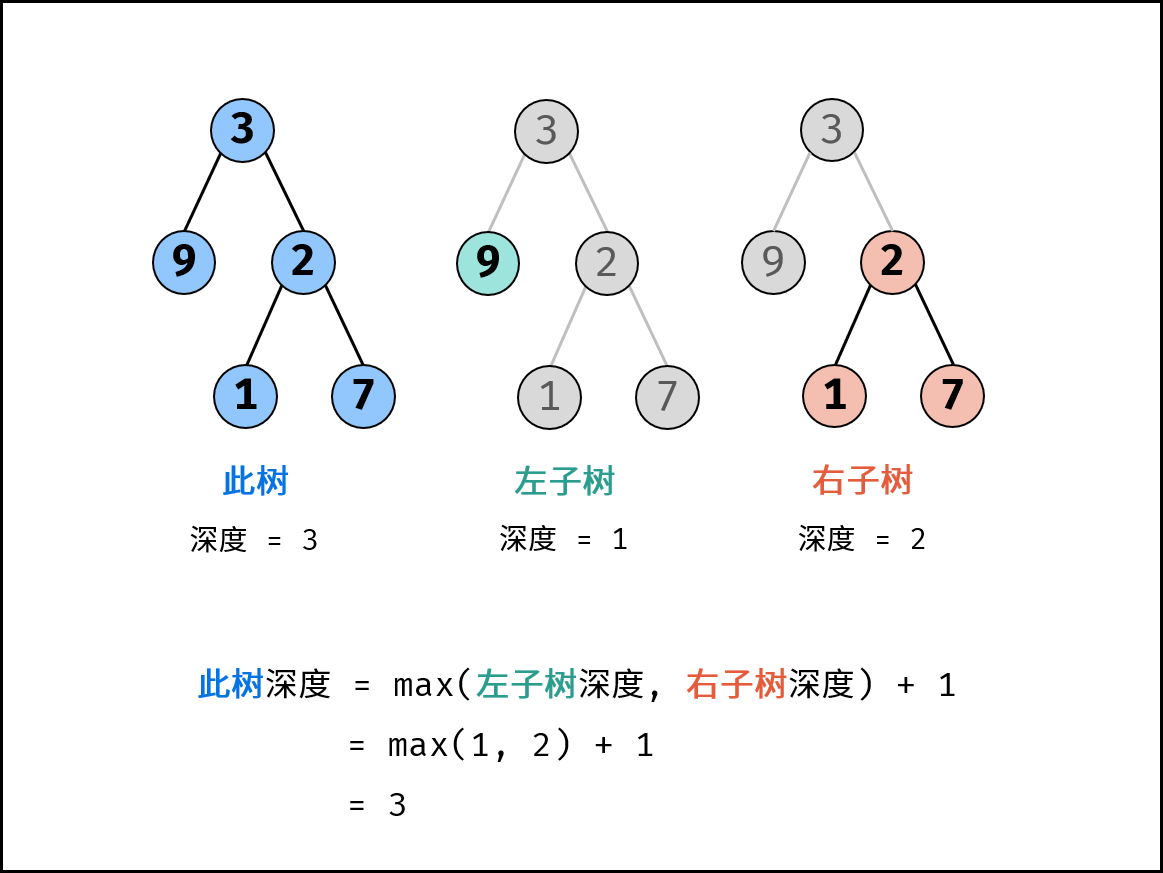
以下两种方法均基于以下性质推出： 此树的深度 等于 左子树的深度 与 右子树的深度 中的 最大值 $+1$ 。

方法一：后序遍历 + 剪枝 （从底至顶） ​

此方法为本题的最优解法，但剪枝的方法不易第一时间想到。

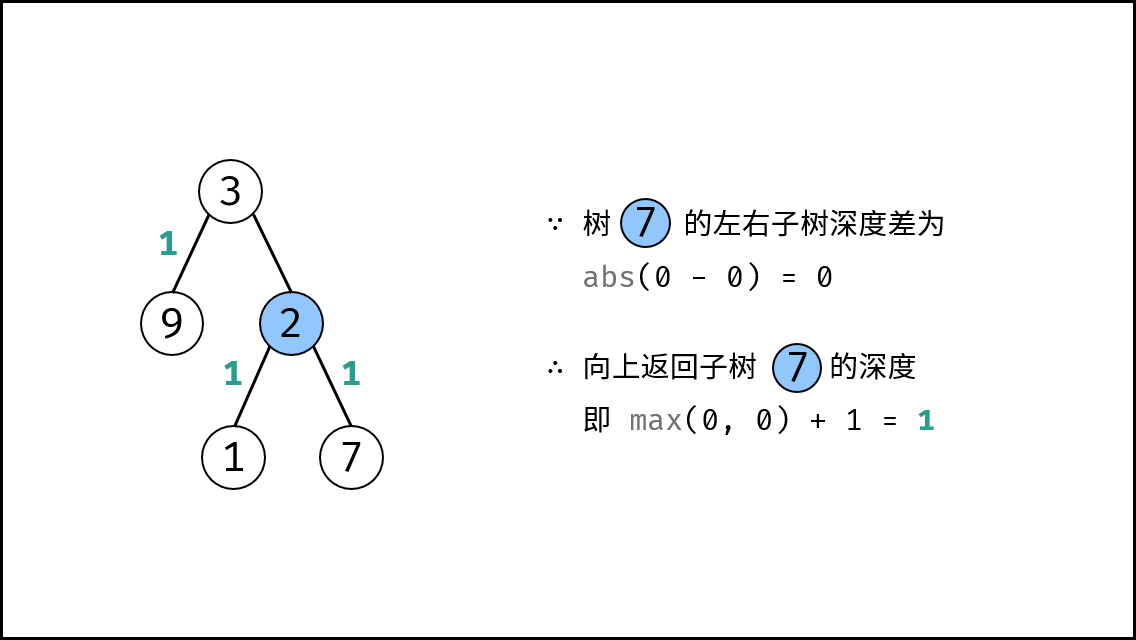
思路是对二叉树做后序遍历，从底至顶返回子树深度，若判定某子树不是平衡树则 “剪枝” ，直接向上返回。

算法流程： ​

recur(root) 函数：

• 返回值：
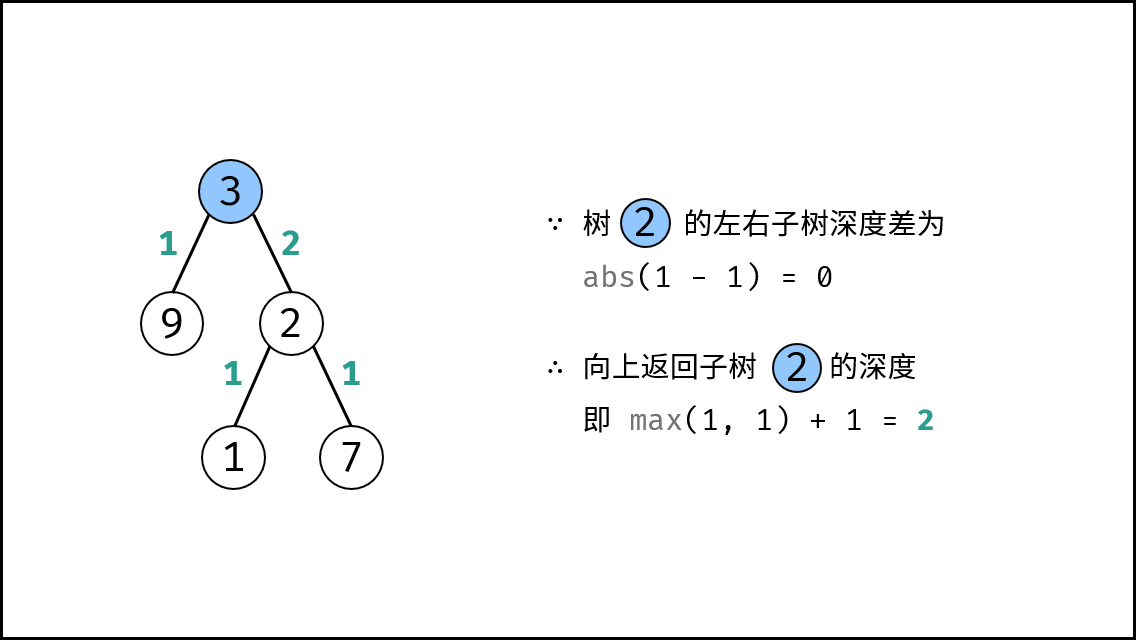
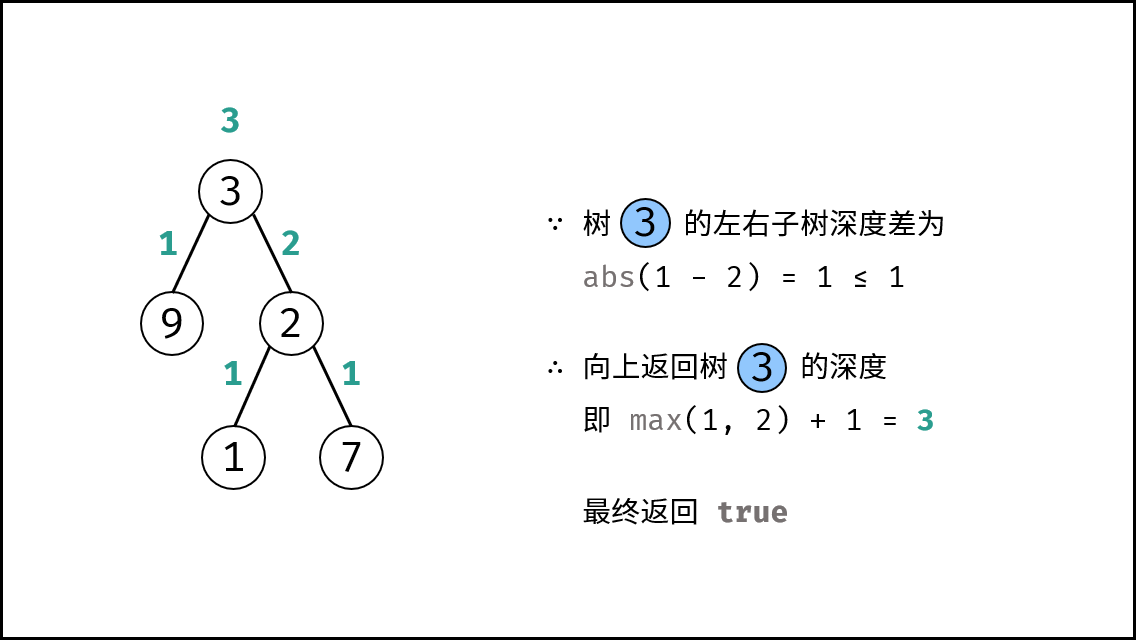
  1. 当节点root 左 / 右子树的深度差 $\leq 1$ ：则返回当前子树的深度，即节点 root 的左 / 右子树的深度最大值 $+1$ （ max(left, right) + 1 ）；
  2. 当节点root 左 / 右子树的深度差 $> 1$ ：则返回 $-1$ ，代表 此子树不是平衡树 。
• 终止条件：
  1. 当 root 为空：说明越过叶节点，因此返回高度 $0$ ；
  2. 当左（右）子树深度为 $-1$ ：代表此树的 左（右）子树 不是平衡树，因此剪枝，直接返回 $-1$ ；

isBalanced(root) 函数：

• 返回值： 若 recur(root) != -1 ，则说明此树平衡，返回 $\text{true}$ ； 否则返回 $\text{false}$ 。

<,,,,,,,,,>

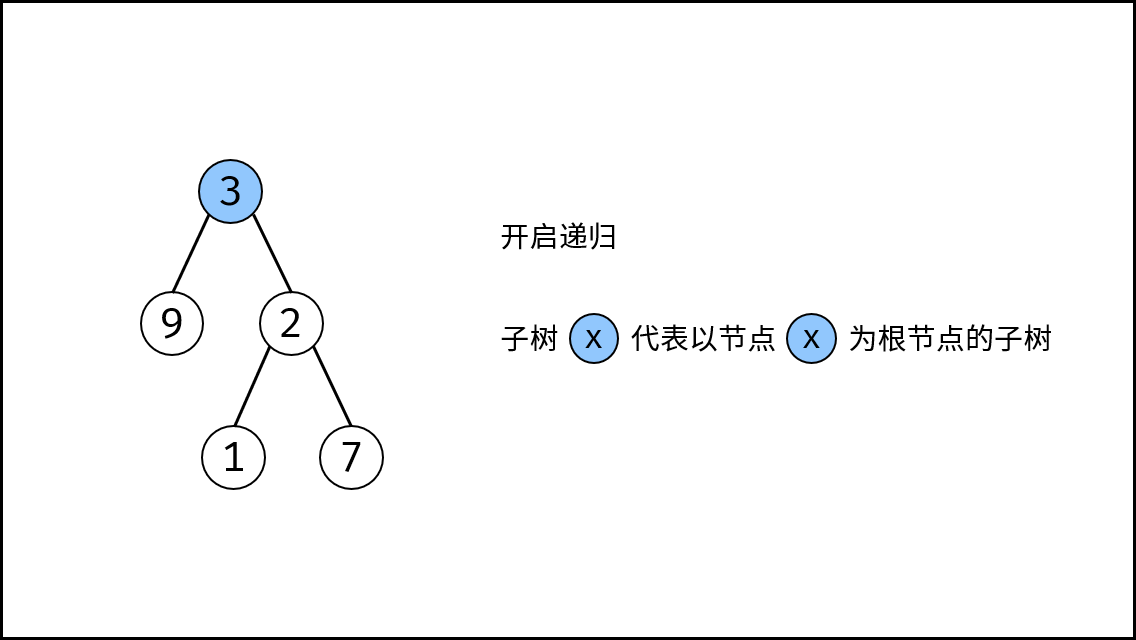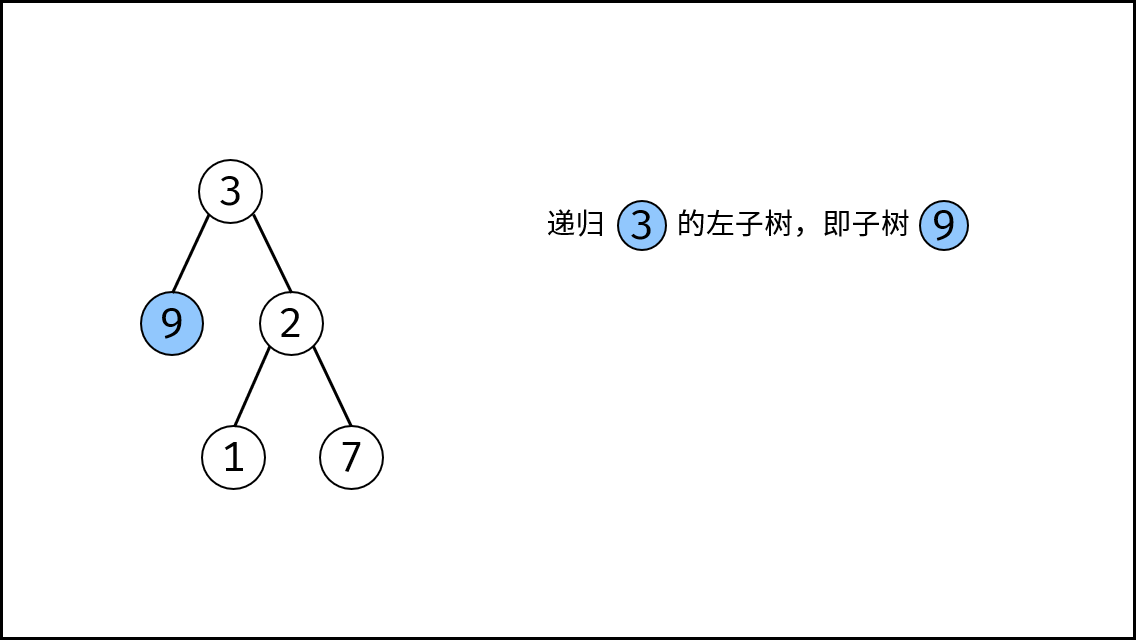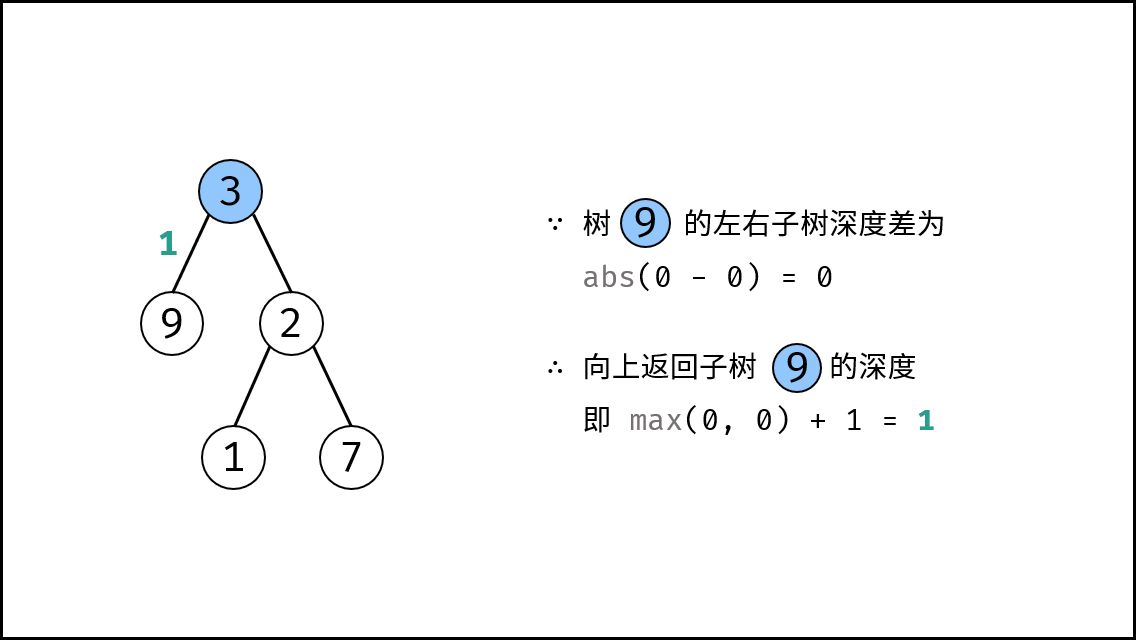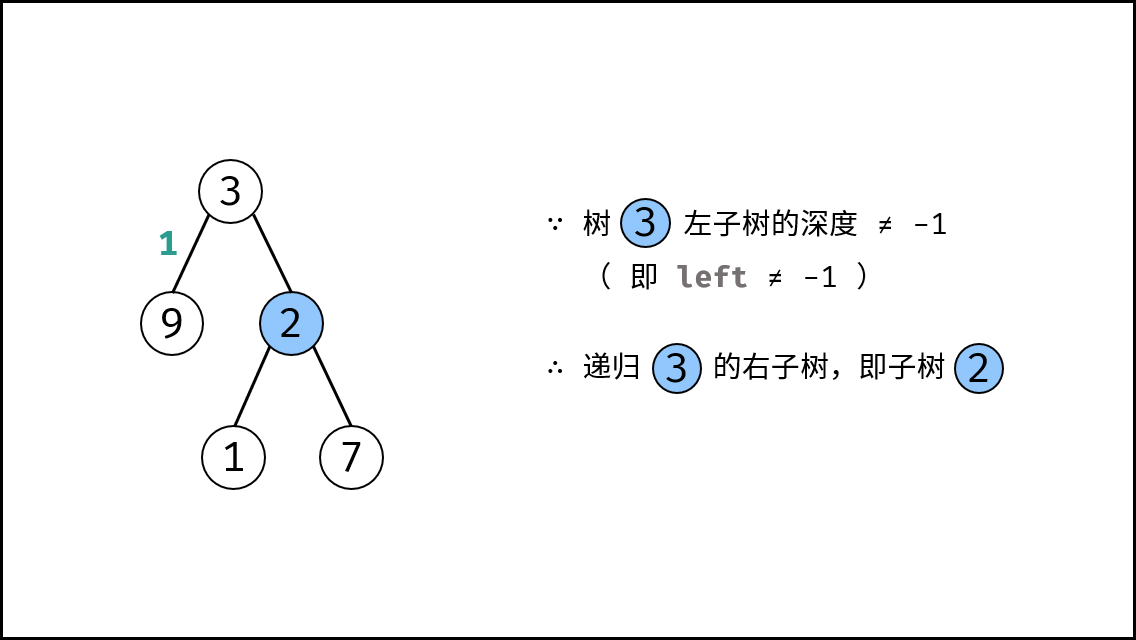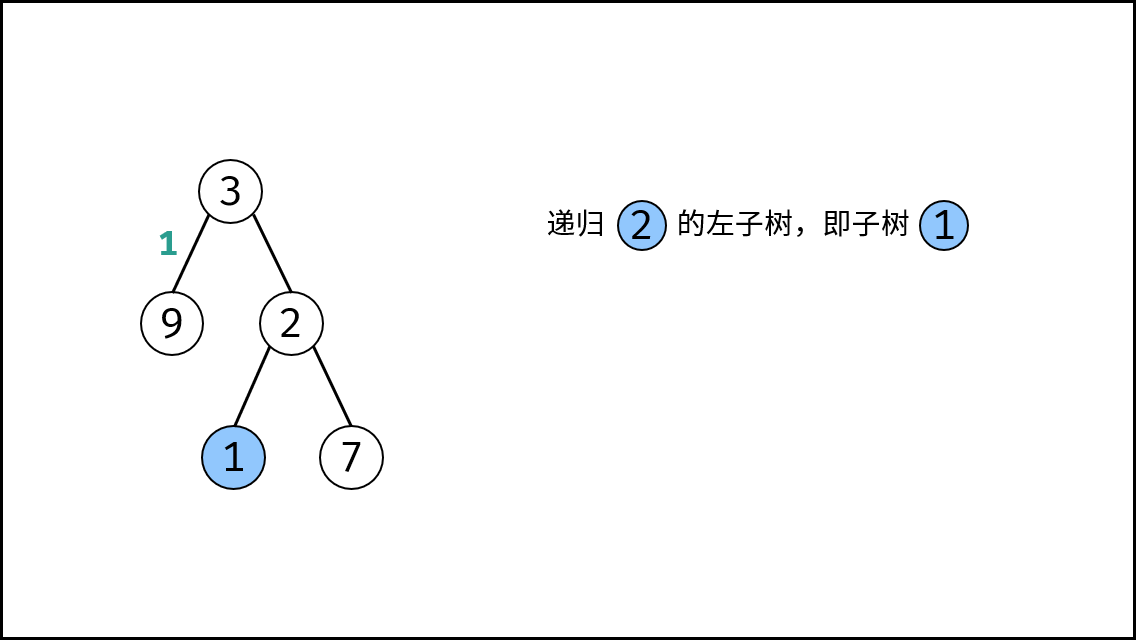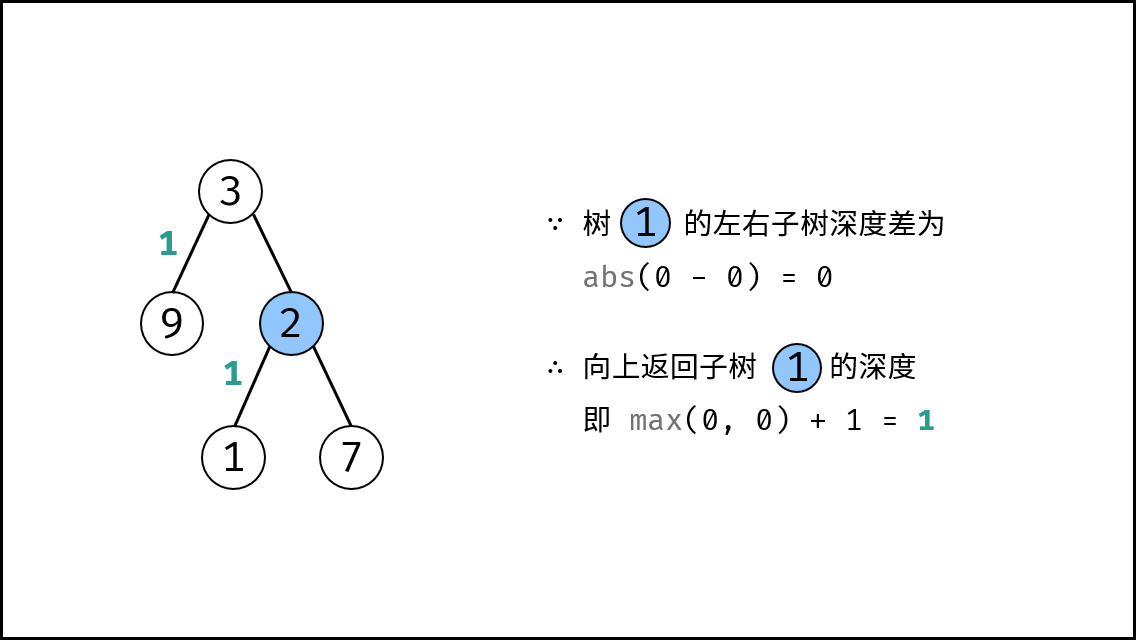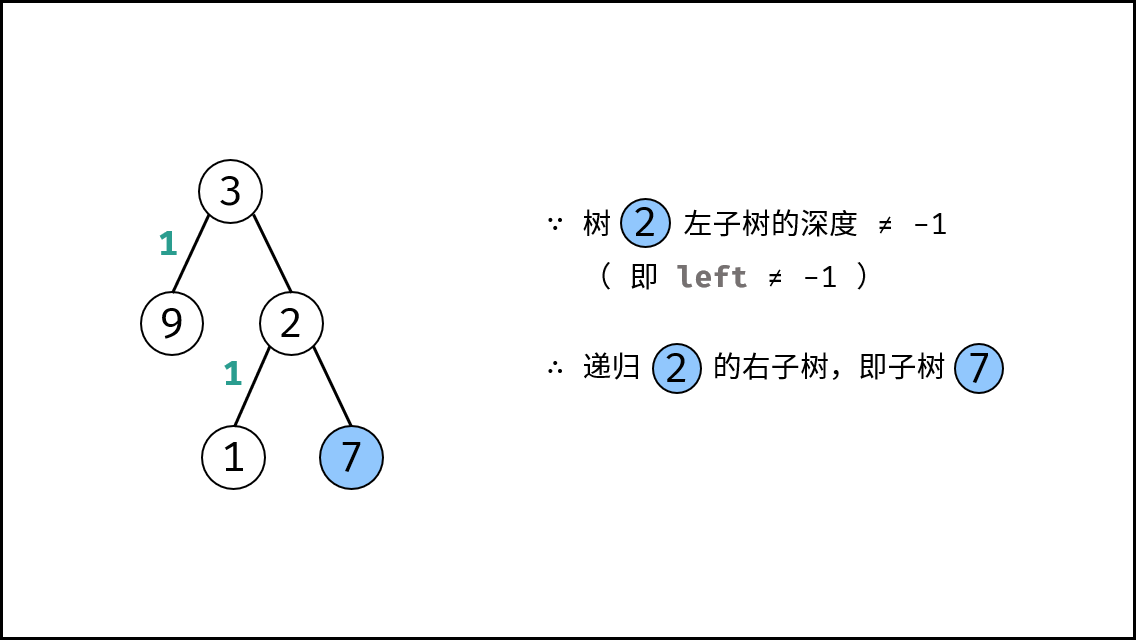代码： ​

class Solution:
    def isBalanced(self, root: Optional[TreeNode]) -> bool:
        def recur(root):
            if not root: return 0
            left = recur(root.left)
            if left == -1: return -1
            right = recur(root.right)
            if right == -1: return -1
            return max(left, right) + 1 if abs(left - right) <= 1 else -1

        return recur(root) != -1

class Solution {
    public boolean isBalanced(TreeNode root) {
        return recur(root) != -1;
    }

    private int recur(TreeNode root) {
        if (root == null) return 0;
        int left = recur(root.left);
        if(left == -1) return -1;
        int right = recur(root.right);
        if(right == -1) return -1;
        return Math.abs(left - right) < 2 ? Math.max(left, right) + 1 : -1;
    }
}

class Solution {
public:
    bool isBalanced(TreeNode* root) {
        return recur(root) != -1;
    }
private:
    int recur(TreeNode* root) {
        if (root == nullptr) return 0;
        int left = recur(root->left);
        if(left == -1) return -1;
        int right = recur(root->right);
        if(right == -1) return -1;
        return abs(left - right) < 2 ? max(left, right) + 1 : -1;
    }
};

复杂度分析： ​

• 时间复杂度 $O(N)$： $N$ 为树的节点数；最差情况下，需要递归遍历树的所有节点。
• 空间复杂度 $O(N)$： 最差情况下（树退化为链表时），系统递归需要使用 $O(N)$ 的栈空间。

方法二：先序遍历 + 判断深度 （从顶至底） ​

此方法容易想到，但会产生大量重复计算，时间复杂度较高。

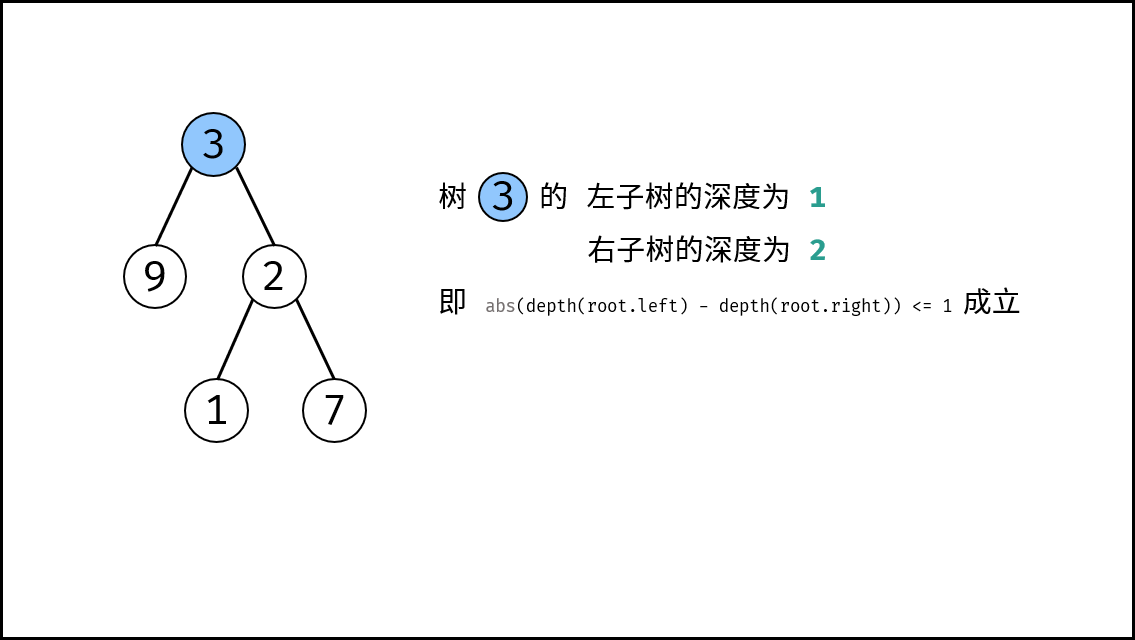
思路是构造一个获取当前子树的深度的函数 depth(root) （即 面试题55 - I. 二叉树的深度 ），通过比较某子树的左右子树的深度差 abs(depth(root.left) - depth(root.right)) <= 1 是否成立，来判断某子树是否是二叉平衡树。若所有子树都平衡，则此树平衡。

算法流程： ​

isBalanced(root) 函数： 判断树 root 是否平衡

• 特例处理： 若树根节点 root 为空，则直接返回 $\text{true}$ ；
• 返回值： 所有子树都需要满足平衡树性质，因此以下三者使用与逻辑 $&&$ 连接；
  1. abs(self.depth(root.left) - self.depth(root.right)) <= 1 ：判断 当前子树 是否是平衡树；
  2. self.isBalanced(root.left) ： 先序遍历递归，判断 当前子树的左子树 是否是平衡树；
  3. self.isBalanced(root.right) ： 先序遍历递归，判断 当前子树的右子树 是否是平衡树；

depth(root) 函数： 计算树 root 的深度

• 终止条件： 当 root 为空，即越过叶子节点，则返回高度 $0$ ；
• 返回值： 返回左 / 右子树的深度的最大值 $+1$ 。

<,,,,,>

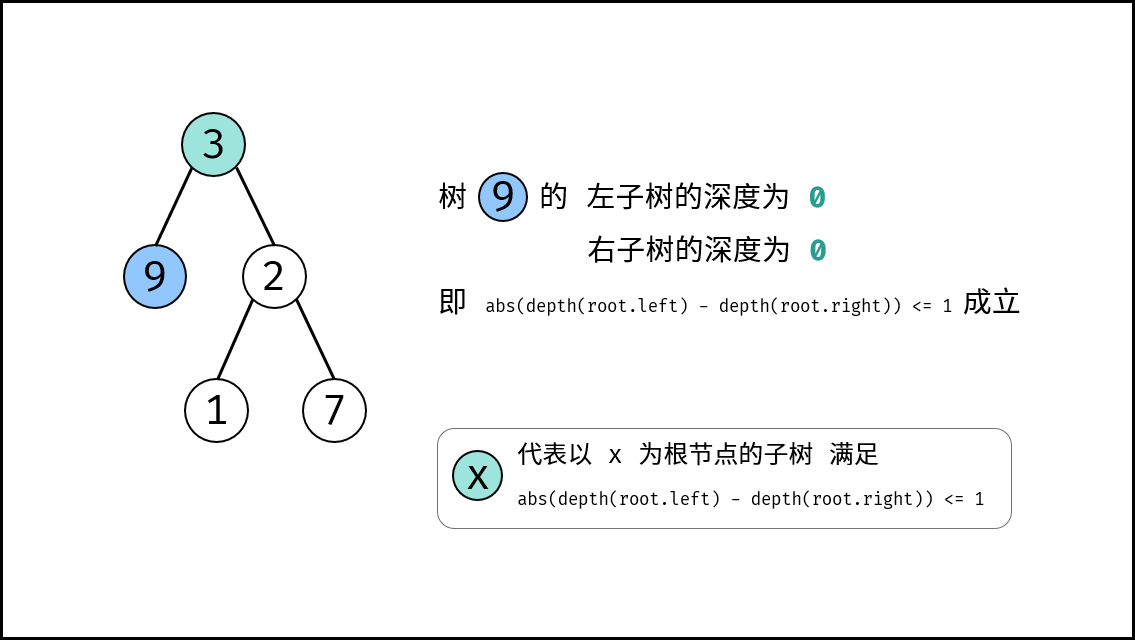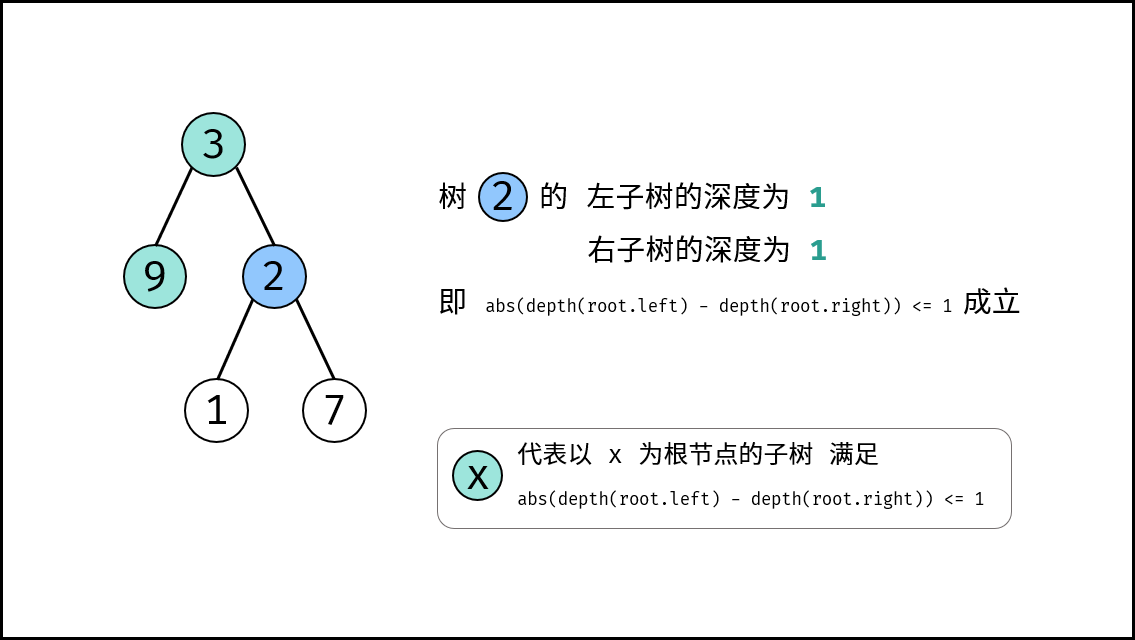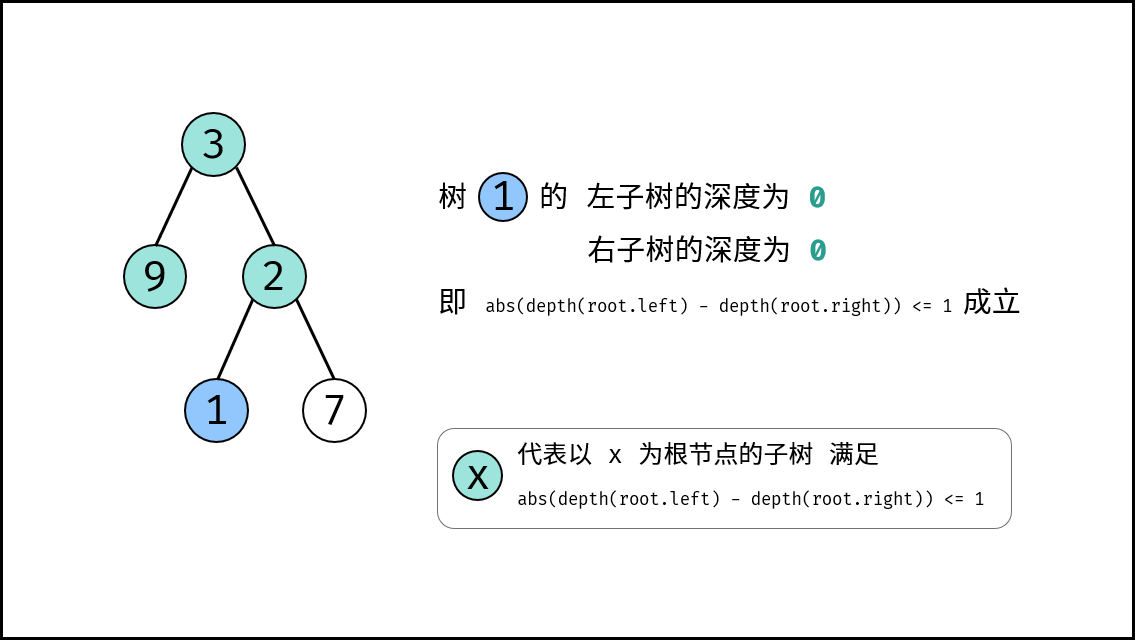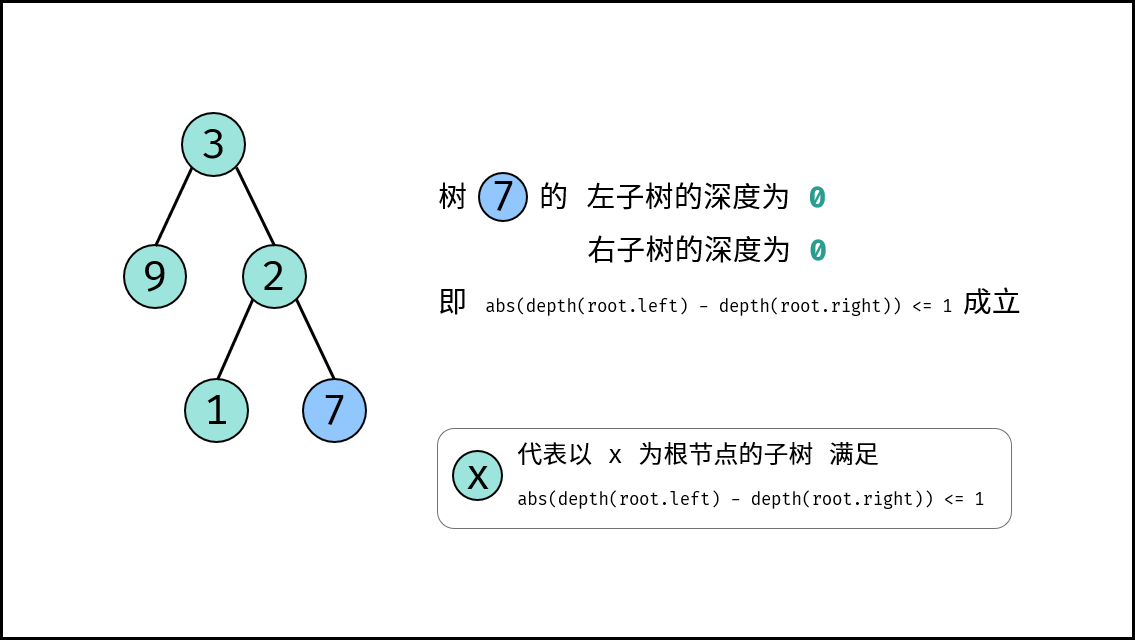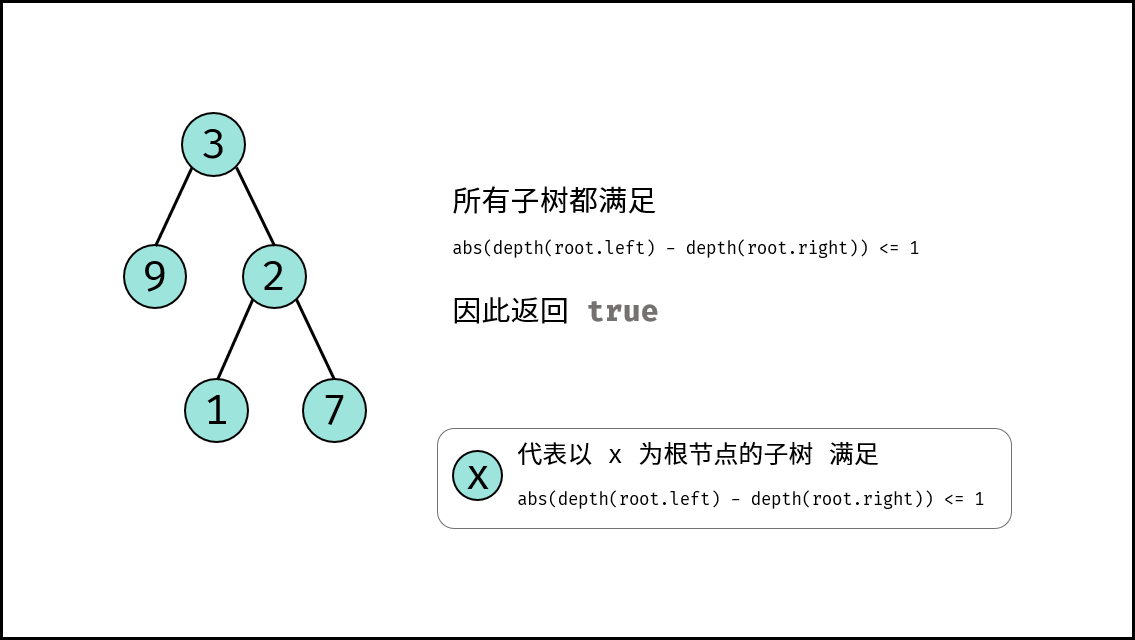代码： ​

class Solution:
    def isBalanced(self, root: Optional[TreeNode]) -> bool:
        if not root: return True
        return abs(self.depth(root.left) - self.depth(root.right)) <= 1 and \
            self.isBalanced(root.left) and self.isBalanced(root.right)

    def depth(self, root):
        if not root: return 0
        return max(self.depth(root.left), self.depth(root.right)) + 1

class Solution {
    public boolean isBalanced(TreeNode root) {
        if (root == null) return true;
        return Math.abs(depth(root.left) - depth(root.right)) <= 1 && isBalanced(root.left) && isBalanced(root.right);
    }

    private int depth(TreeNode root) {
        if (root == null) return 0;
        return Math.max(depth(root.left), depth(root.right)) + 1;
    }
}

class Solution {
public:
    bool isBalanced(TreeNode* root) {
        if (root == nullptr) return true;
        return abs(depth(root->left) - depth(root->right)) <= 1 && isBalanced(root->left) && isBalanced(root->right);
    }
private:
    int depth(TreeNode* root) {
        if (root == nullptr) return 0;
        return max(depth(root->left), depth(root->right)) + 1;
    }
};

复杂度分析： ​

• 时间复杂度 $O(N \log N)$： 最差情况下（为 “满二叉树” 时），isBalanced(root) 遍历树所有节点，判断每个节点的深度 depth(root) 需要遍历 各子树的所有节点 。
  • 满二叉树高度的复杂度 $O(log N)$ ，将满二叉树按层分为 $log (N+1)$ 层；
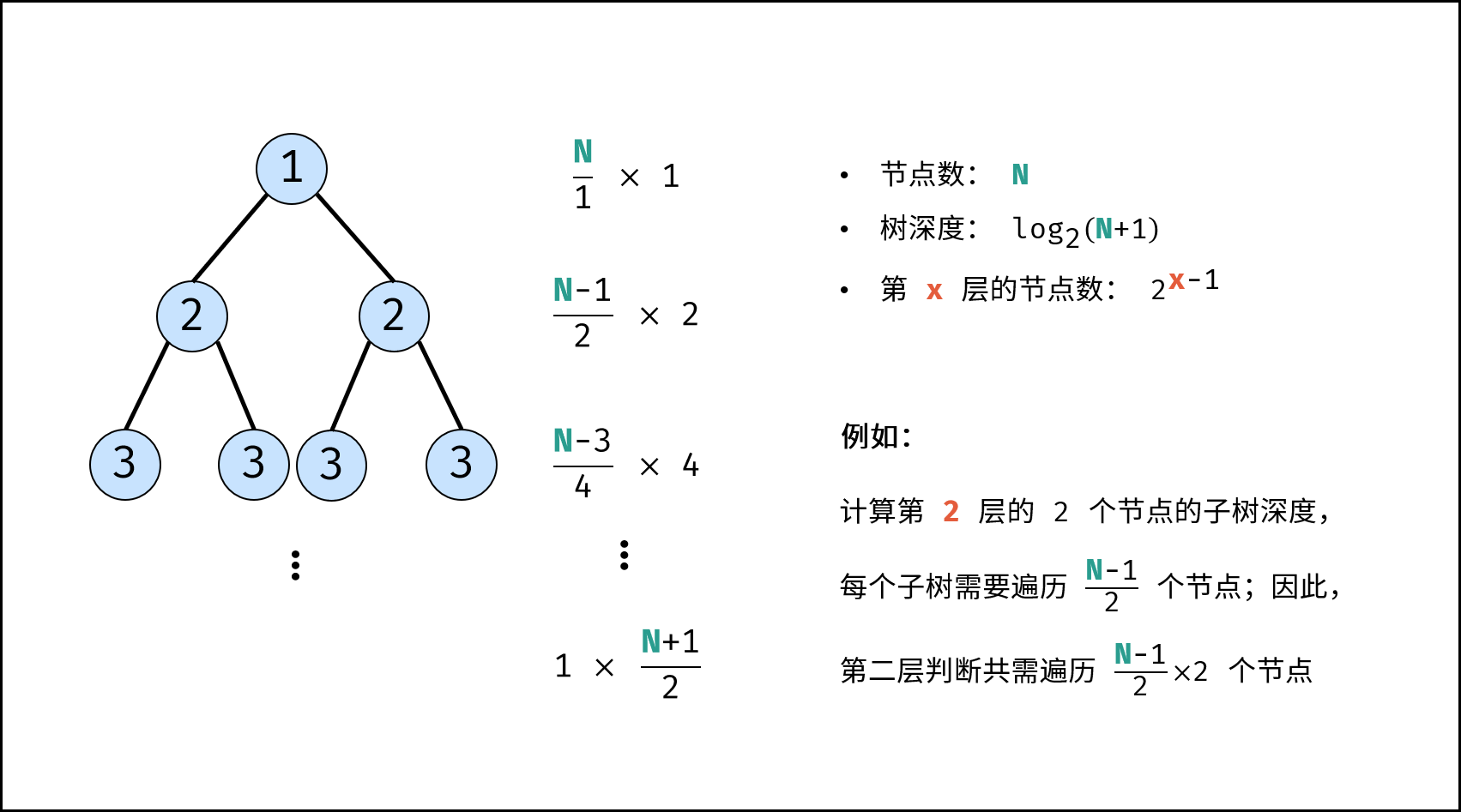
  • 通过调用 depth(root) ，判断二叉树各层的节点的对应子树的深度，需遍历节点数量为 $N \times 1, \frac{N-1}{2} \times 2, \frac{N-3}{4} \times 4, \frac{N-7}{8} \times 8, ..., 1 \times \frac{N+1}{2}$ 。因此各层执行 depth(root) 的时间复杂度为 $O(N)$ （每层开始，最多遍历 $N$ 个节点，最少遍历 $\frac{N+1}{2}$ 个节点）。

  其中，$\frac{N-3}{4} \times 4$ 代表从此层开始总共需遍历 $N-3$ 个节点，此层共有 $4$ 个节点，因此每个子树需遍历 $\frac{N-3}{4}$ 个节点。

  • 因此，总体时间复杂度 $=$ 每层执行复杂度 $\times$ 层数复杂度 = $O(N \times \log N)$ 。

• 空间复杂度 $O(N)$： 最差情况下（树退化为链表时），系统递归需要使用 $O(N)$ 的栈空间。