解题思路:
前序遍历性质: 节点按照 [ 根节点 | 左子树 | 右子树 ] 排序。 中序遍历性质: 节点按照 [ 左子树 | 根节点 | 右子树 ] 排序。
以题目示例为例:
- 前序遍历划分
[ 3 | 9 | 20 15 7 ]- 中序遍历划分
[ 9 | 3 | 15 20 7 ]
根据以上性质,可得出以下推论:
- 前序遍历的首元素 为 树的根节点
node的值。 - 在中序遍历中搜索根节点
node的索引 ,可将 中序遍历 划分为[ 左子树 | 根节点 | 右子树 ]。 - 根据中序遍历中的左(右)子树的节点数量,可将 前序遍历 划分为
[ 根节点 | 左子树 | 右子树 ]。
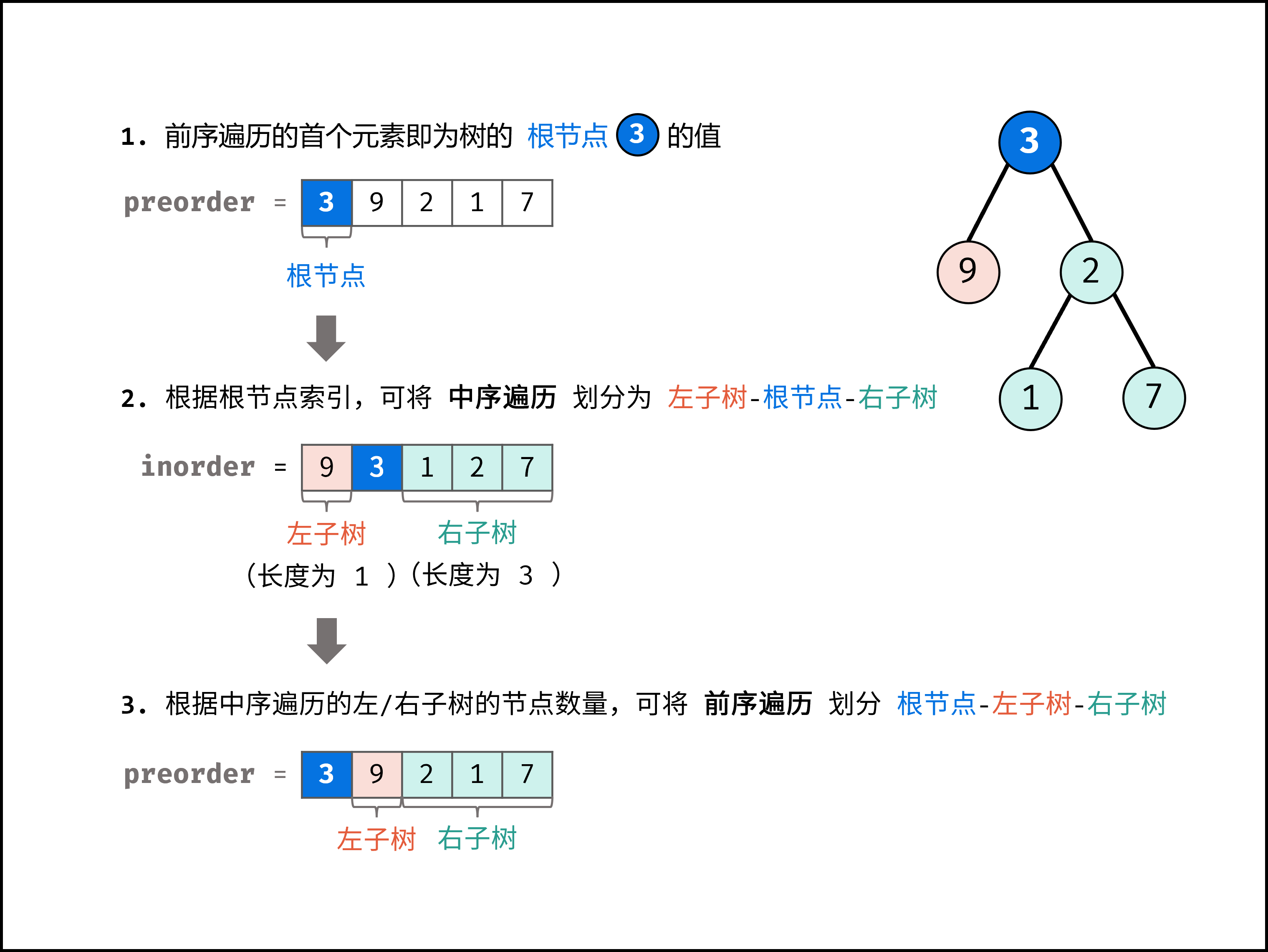
通过以上三步,可确定 三个节点 :1.树的根节点、2.左子树根节点、3.右子树根节点。
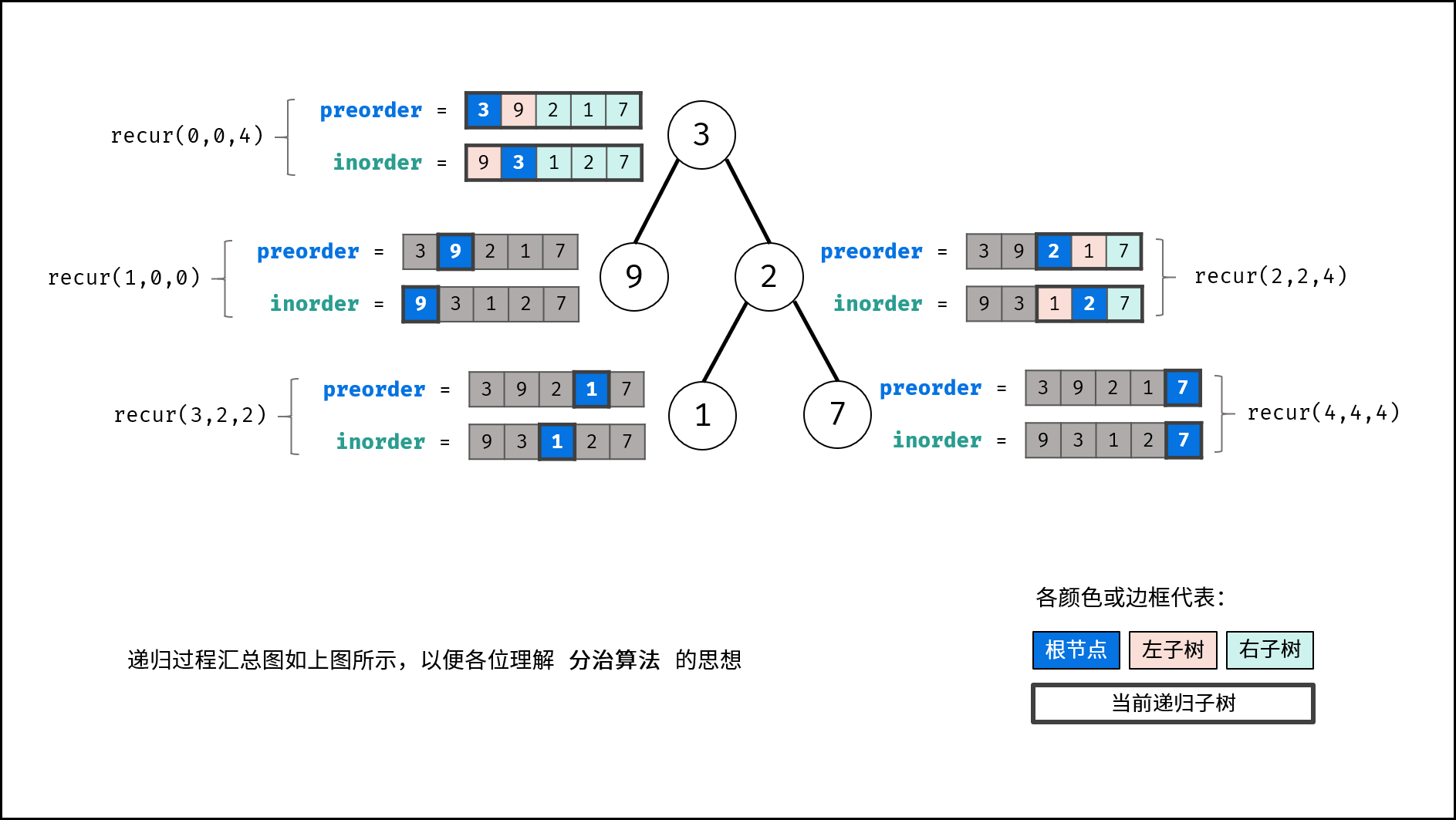
根据「分治算法」思想,对于树的左、右子树,仍可复用以上方法划分子树的左右子树。
分治解析:
递推参数: 根节点在前序遍历的索引 root 、子树在中序遍历的左边界 left 、子树在中序遍历的右边界 right ;
终止条件: 当 left > right ,代表已经越过叶节点,此时返回 $\text{null}$ ;
递推工作:
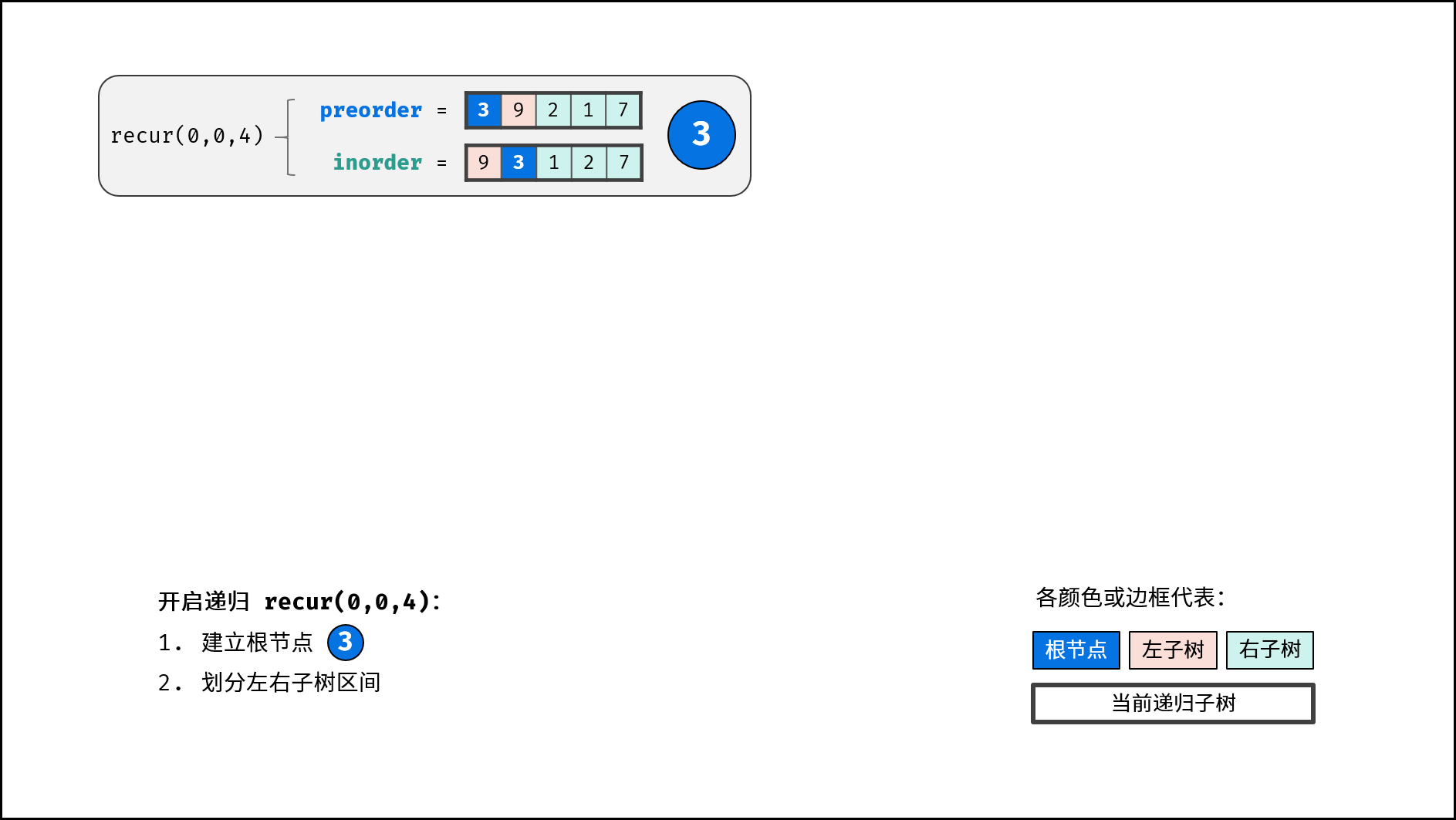
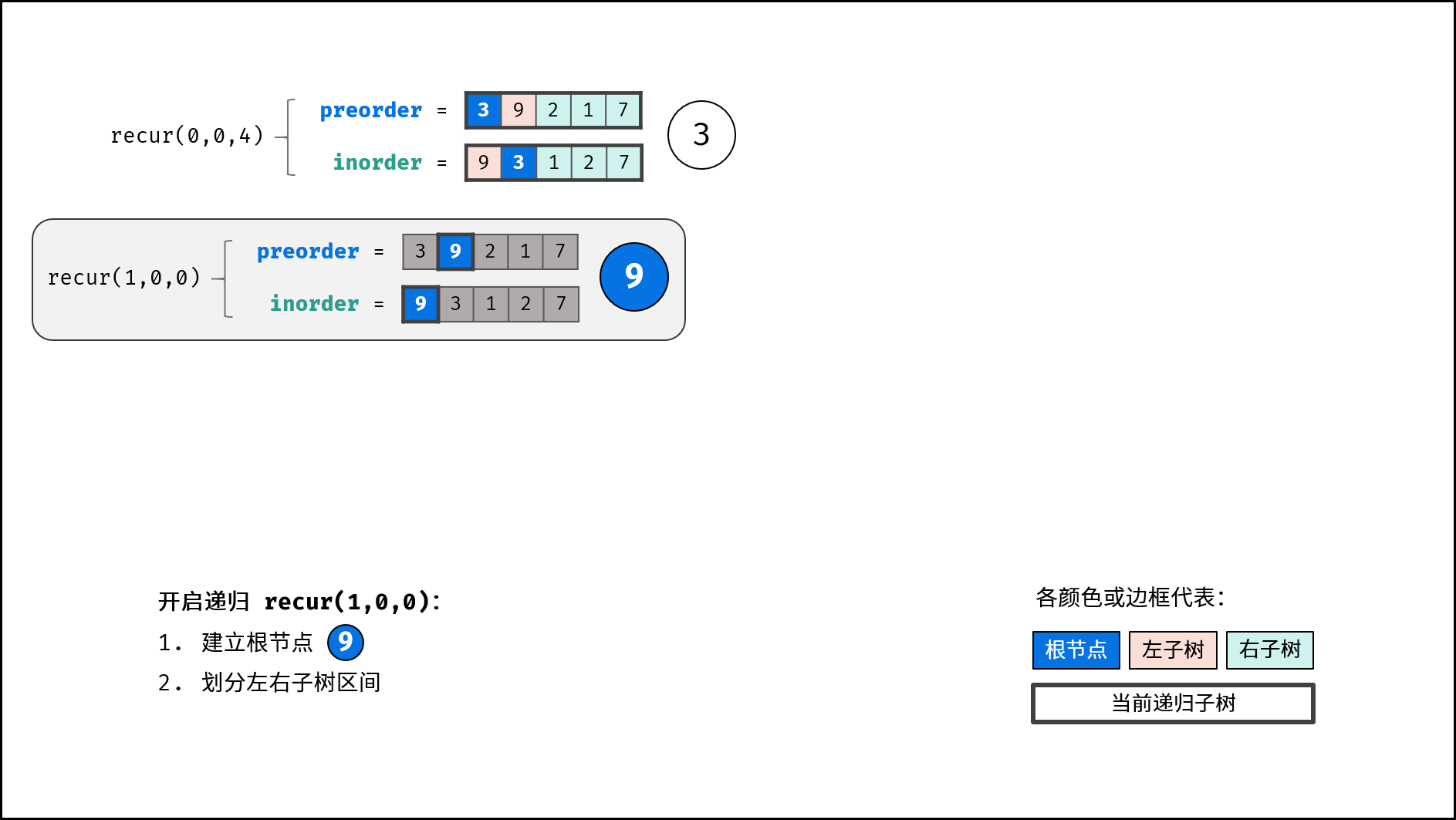
- 建立根节点
node: 节点值为preorder[root]; - 划分左右子树: 查找根节点在中序遍历
inorder中的索引i;
为了提升效率,本文使用哈希表
hmap存储中序遍历的值与索引的映射,查找操作的时间复杂度为 $O(1)$ ;
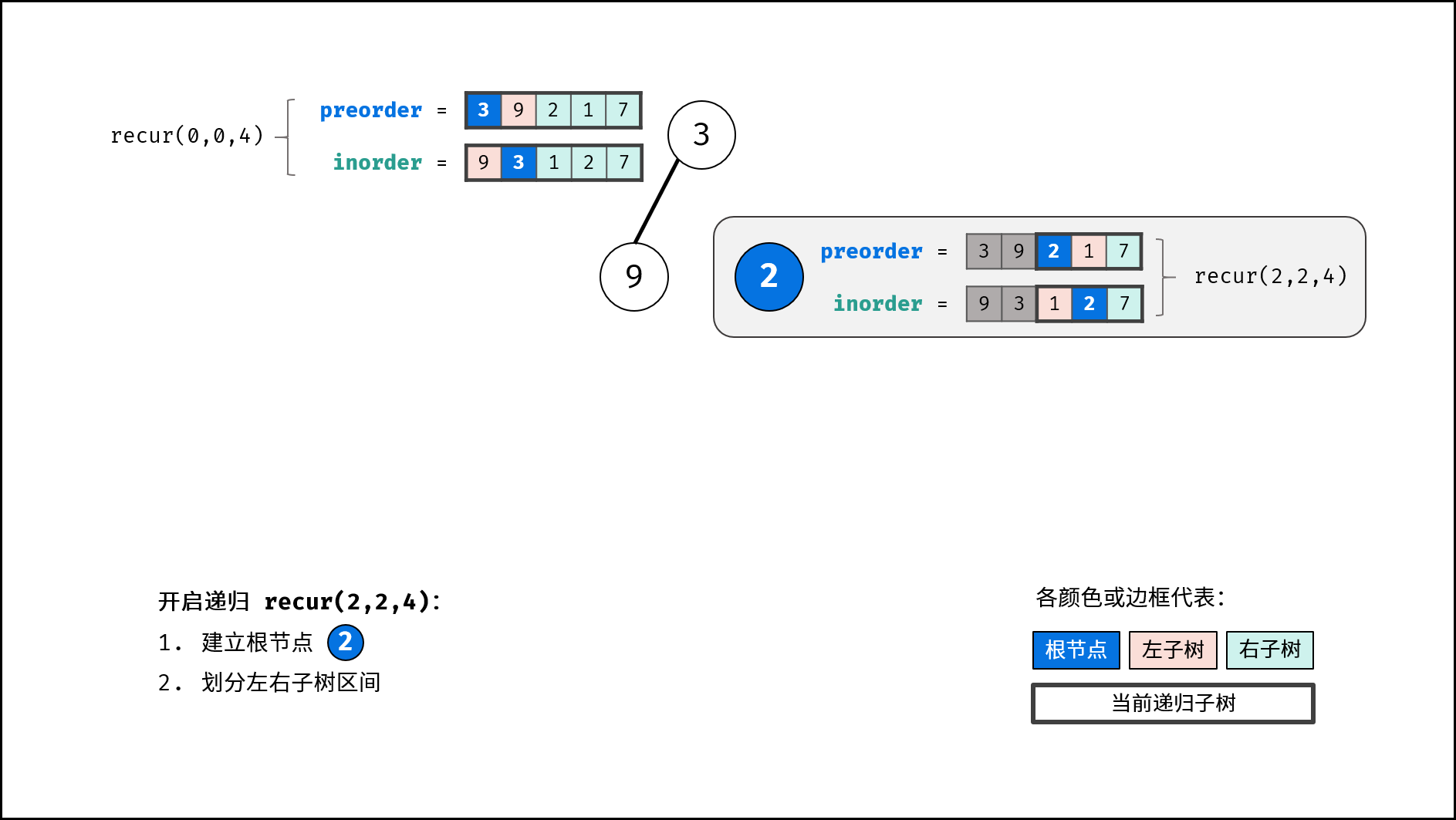
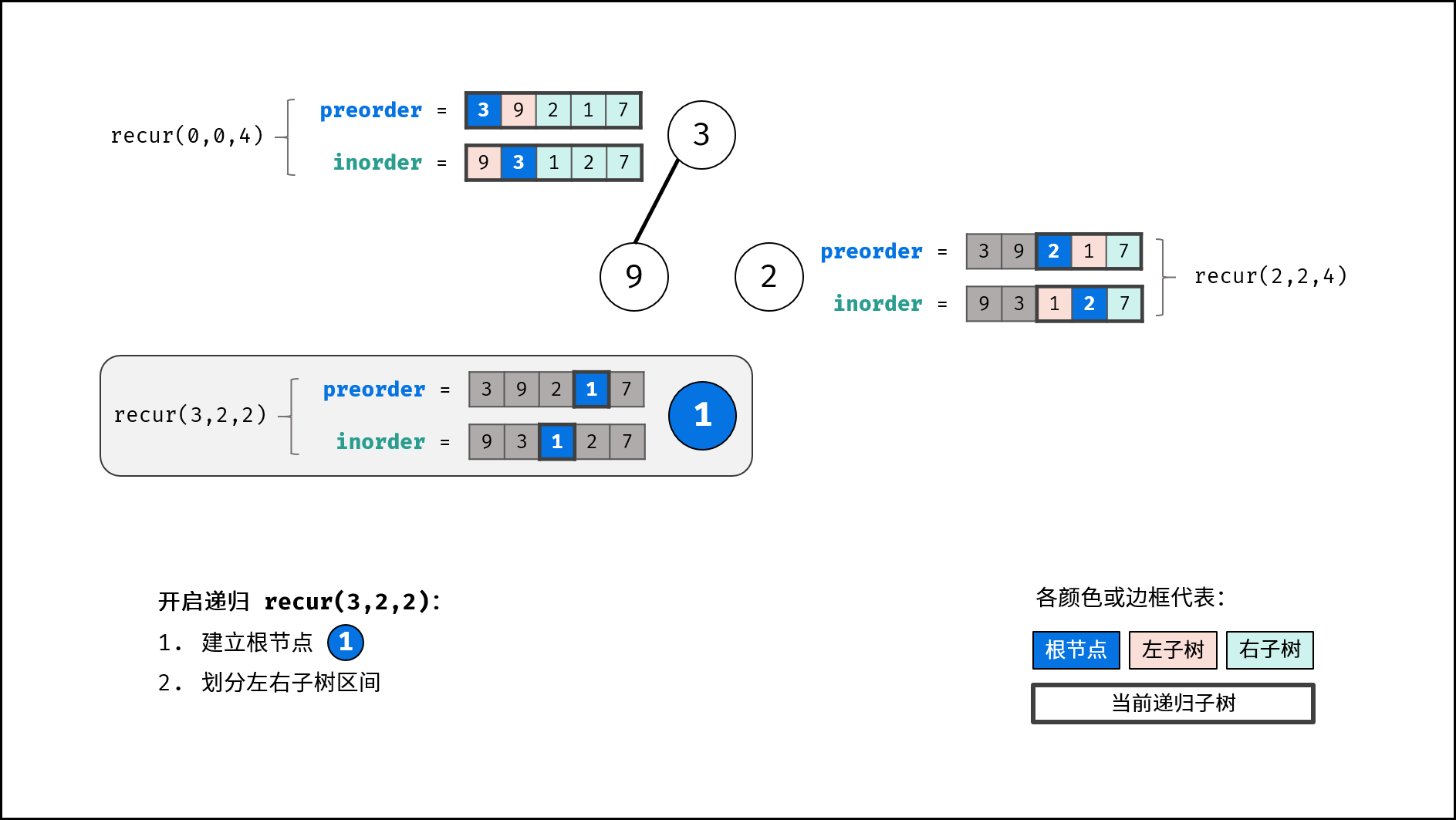
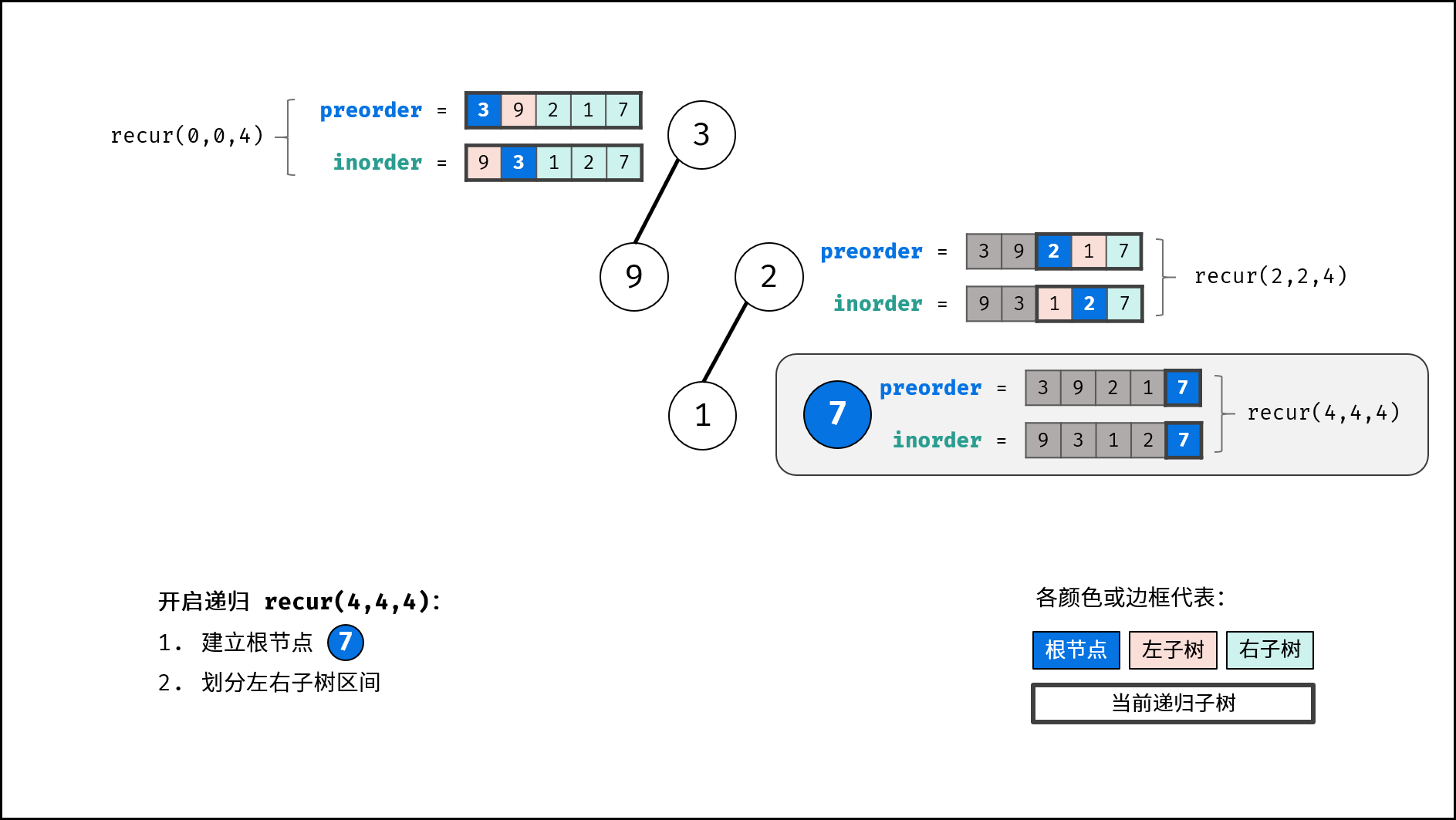
- 构建左右子树: 开启左右子树递归;
| 根节点索引 | 中序遍历左边界 | 中序遍历右边界 | |
|---|---|---|---|
| 左子树 | root + 1 | left | i - 1 |
| 右子树 | i - left + root + 1 | i + 1 | right |
TIPS:
i - left + root + 1含义为根节点索引 + 左子树长度 + 1
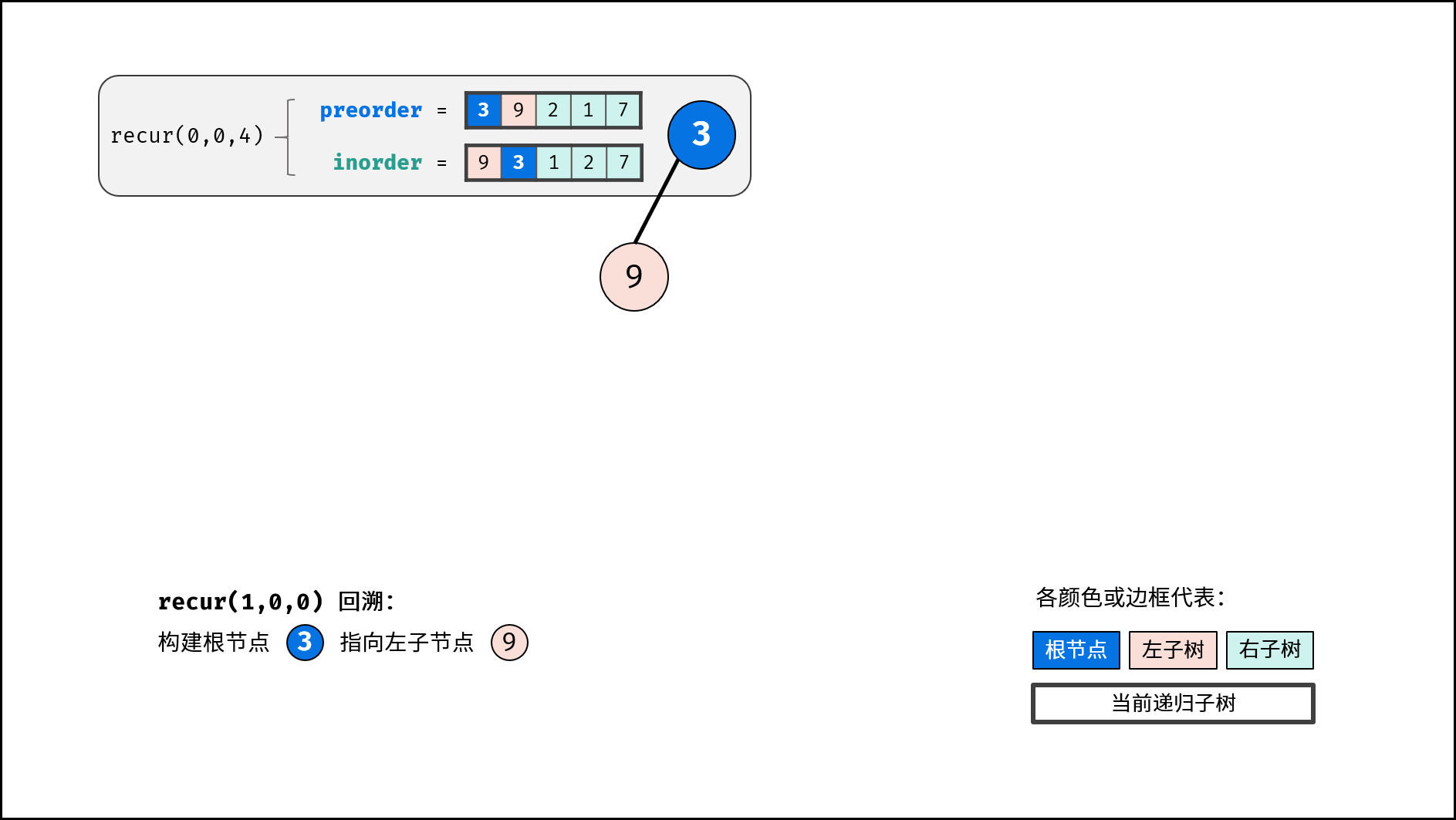
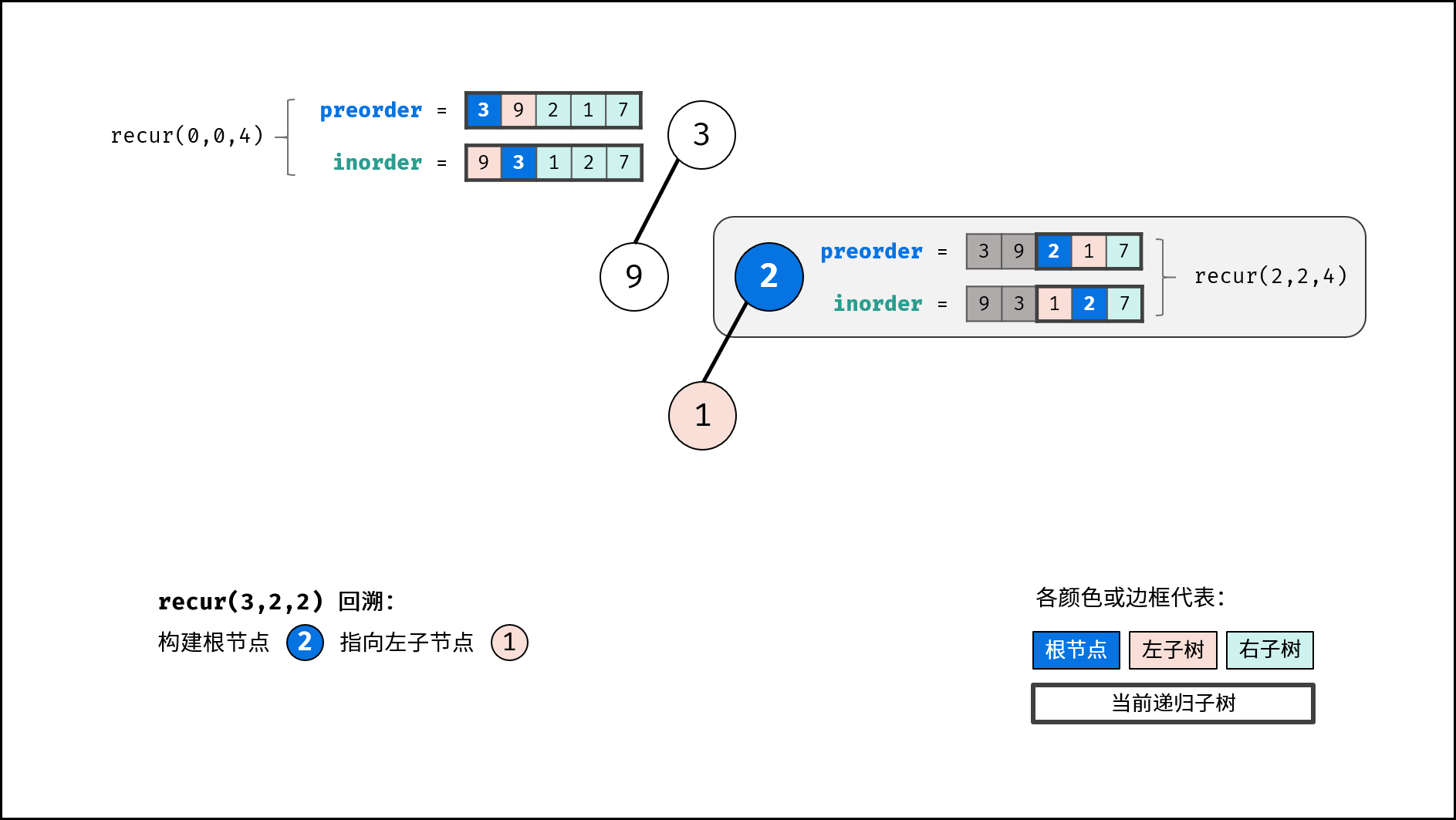
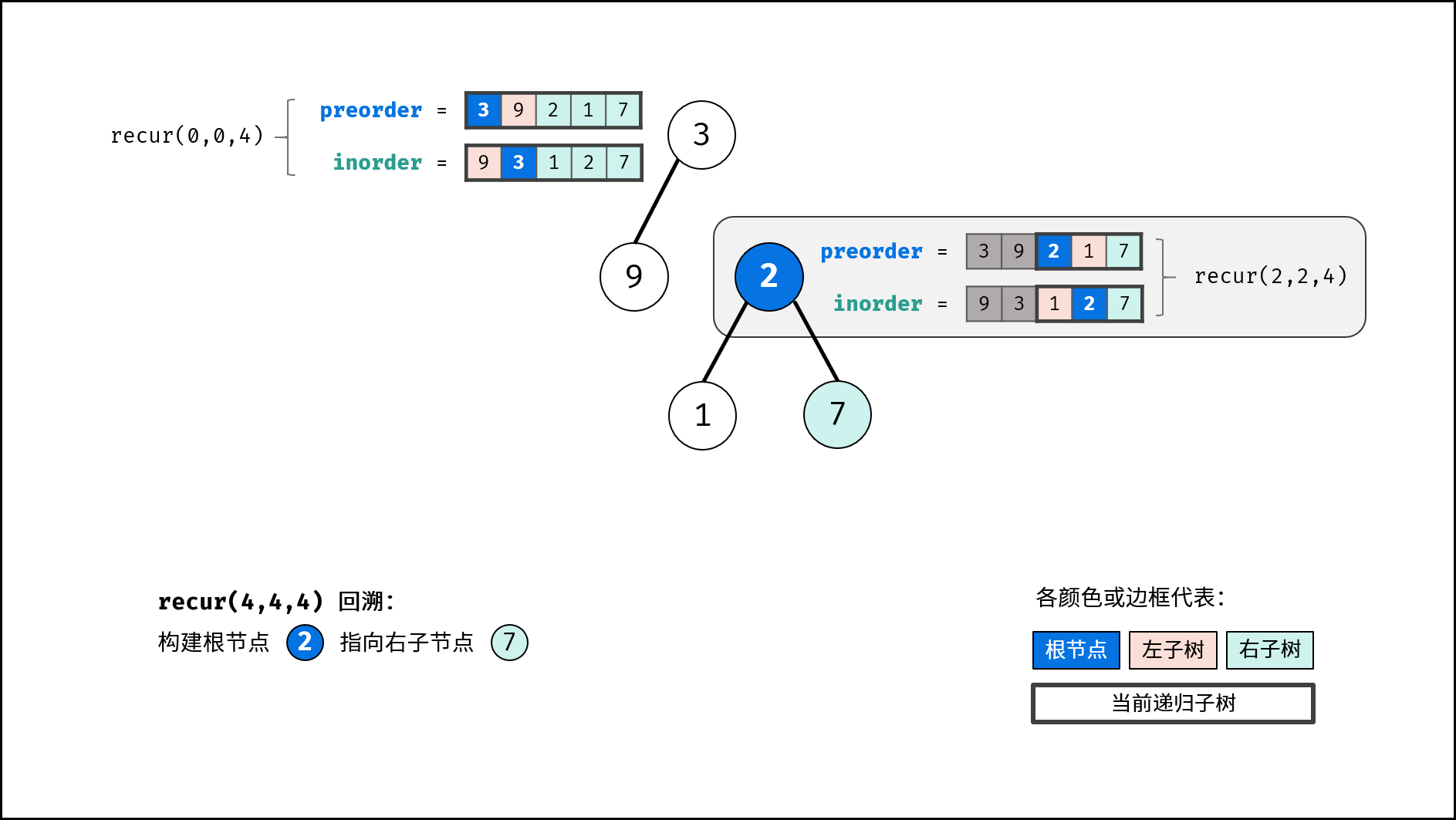
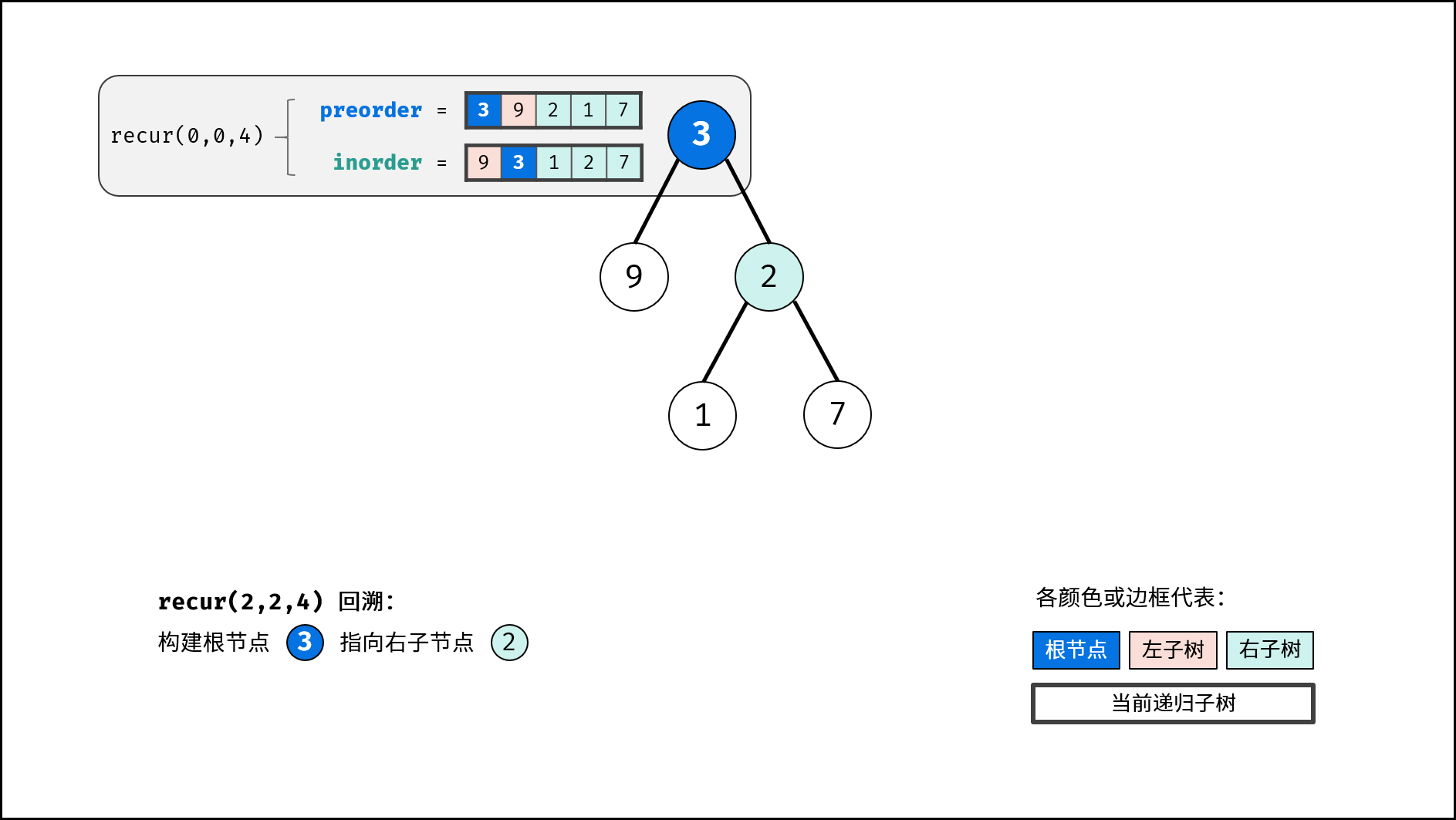
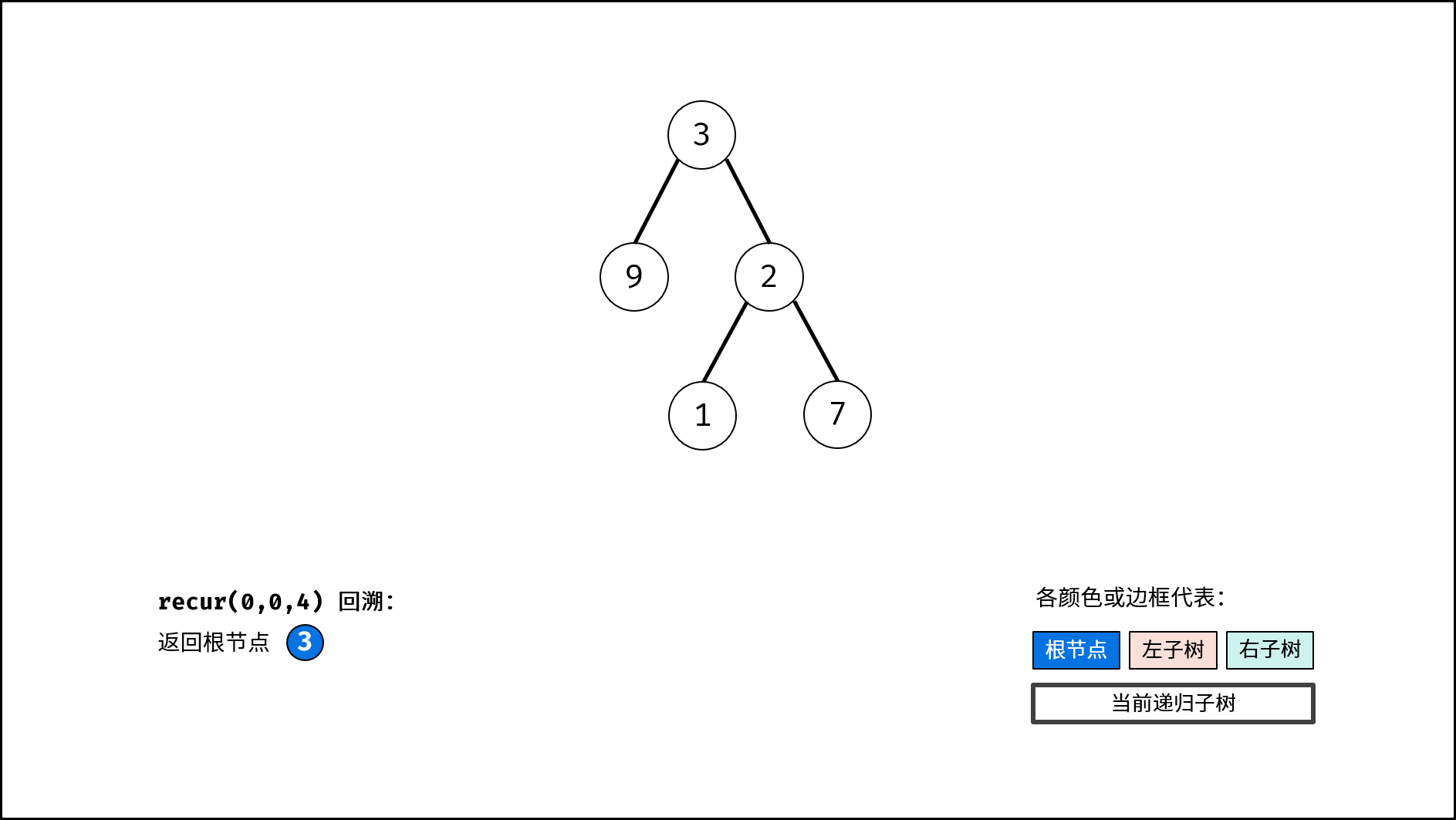
返回值: 回溯返回 node ,作为上一层递归中根节点的左 / 右子节点;
< ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, >
>
代码:
注意:本文方法只适用于 “无重复节点值” 的二叉树。
Python
class Solution:
def deduceTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
def recur(root, left, right):
if left > right: return # 递归终止
node = TreeNode(preorder[root]) # 建立根节点
i = hmap[preorder[root]] # 划分根节点、左子树、右子树
node.left = recur(root + 1, left, i - 1) # 开启左子树递归
node.right = recur(i - left + root + 1, i + 1, right) # 开启右子树递归
return node # 回溯返回根节点
hmap, preorder = {}, preorder
for i in range(len(inorder)):
hmap[inorder[i]] = i
return recur(0, 0, len(inorder) - 1)Java
class Solution {
int[] preorder;
HashMap<Integer, Integer> hmap = new HashMap<>();
public TreeNode deduceTree(int[] preorder, int[] inorder) {
this.preorder = preorder;
for(int i = 0; i < inorder.length; i++)
hmap.put(inorder[i], i);
return recur(0, 0, inorder.length - 1);
}
TreeNode recur(int root, int left, int right) {
if(left > right) return null; // 递归终止
TreeNode node = new TreeNode(preorder[root]); // 建立根节点
int i = hmap.get(preorder[root]); // 划分根节点、左子树、右子树
node.left = recur(root + 1, left, i - 1); // 开启左子树递归
node.right = recur(root + i - left + 1, i + 1, right); // 开启右子树递归
return node; // 回溯返回根节点
}
}C++
class Solution {
public:
TreeNode* deduceTree(vector<int>& preorder, vector<int>& inorder) {
this->preorder = preorder;
for(int i = 0; i < inorder.size(); i++)
hmap[inorder[i]] = i;
return recur(0, 0, inorder.size() - 1);
}
private:
vector<int> preorder;
unordered_map<int, int> hmap;
TreeNode* recur(int root, int left, int right) {
if(left > right) return nullptr; // 递归终止
TreeNode* node = new TreeNode(preorder[root]); // 建立根节点
int i = hmap[preorder[root]]; // 划分根节点、左子树、右子树
node->left = recur(root + 1, left, i - 1); // 开启左子树递归
node->right = recur(root + i - left + 1, i + 1, right); // 开启右子树递归
return node; // 回溯返回根节点
}
};复杂度分析:
- 时间复杂度 $O(N)$ : 其中 $N$ 为树的节点数量。初始化 HashMap 需遍历
inorder,占用 $O(N)$ 。递归共建立 $N$ 个节点,每层递归中的节点建立、搜索操作占用 $O(1)$ ,因此使用 $O(N)$ 时间。 - 空间复杂度 $O(N)$ : HashMap 使用 $O(N)$ 额外空间;最差情况下(输入二叉树为链表时),递归深度达到 $N$ ,占用 $O(N)$ 的栈帧空间;因此总共使用 $O(N)$ 空间。