自律小屋

Appearance

当前页大纲

方法一：快速排序 ​

本题使用排序算法解决最直观，对数组 stock 执行排序，再返回前 $cnt$ 个元素即可。使用任意排序算法皆可，本文采用并介绍 快速排序 ，为下文 方法二 做铺垫。

快速排序原理： ​

快速排序算法有两个核心点，分别为 “哨兵划分” 和 “递归” 。

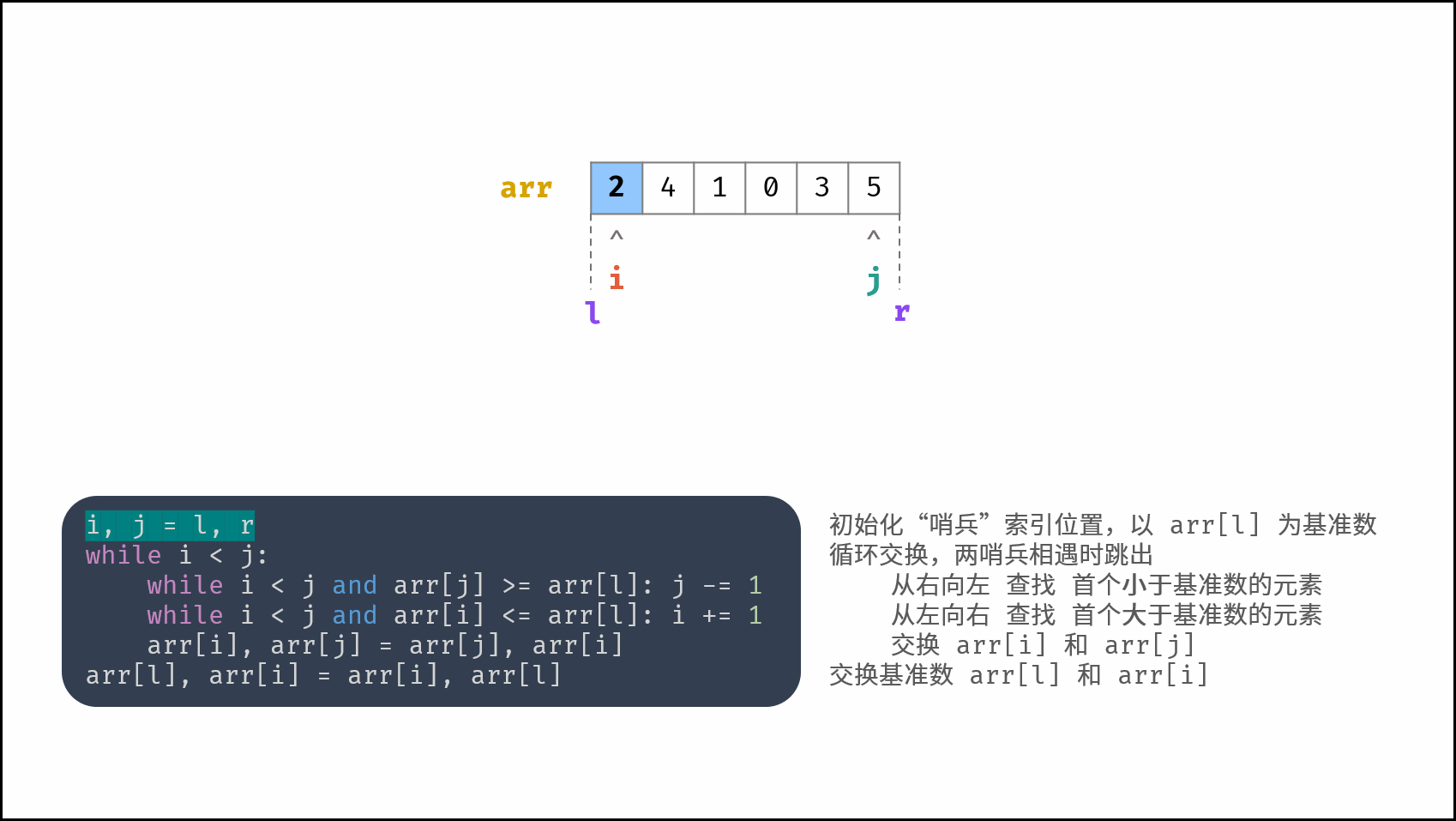
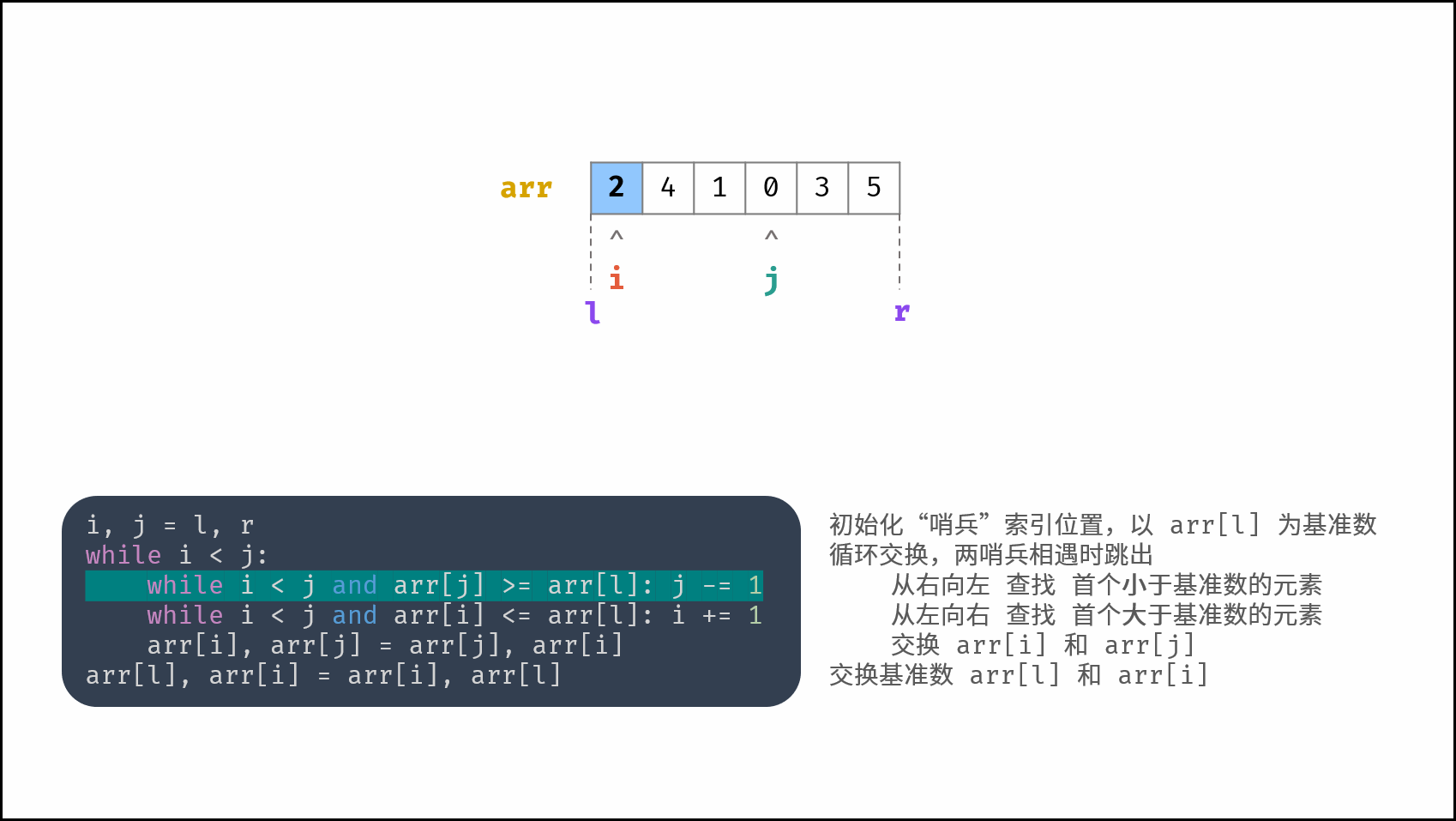
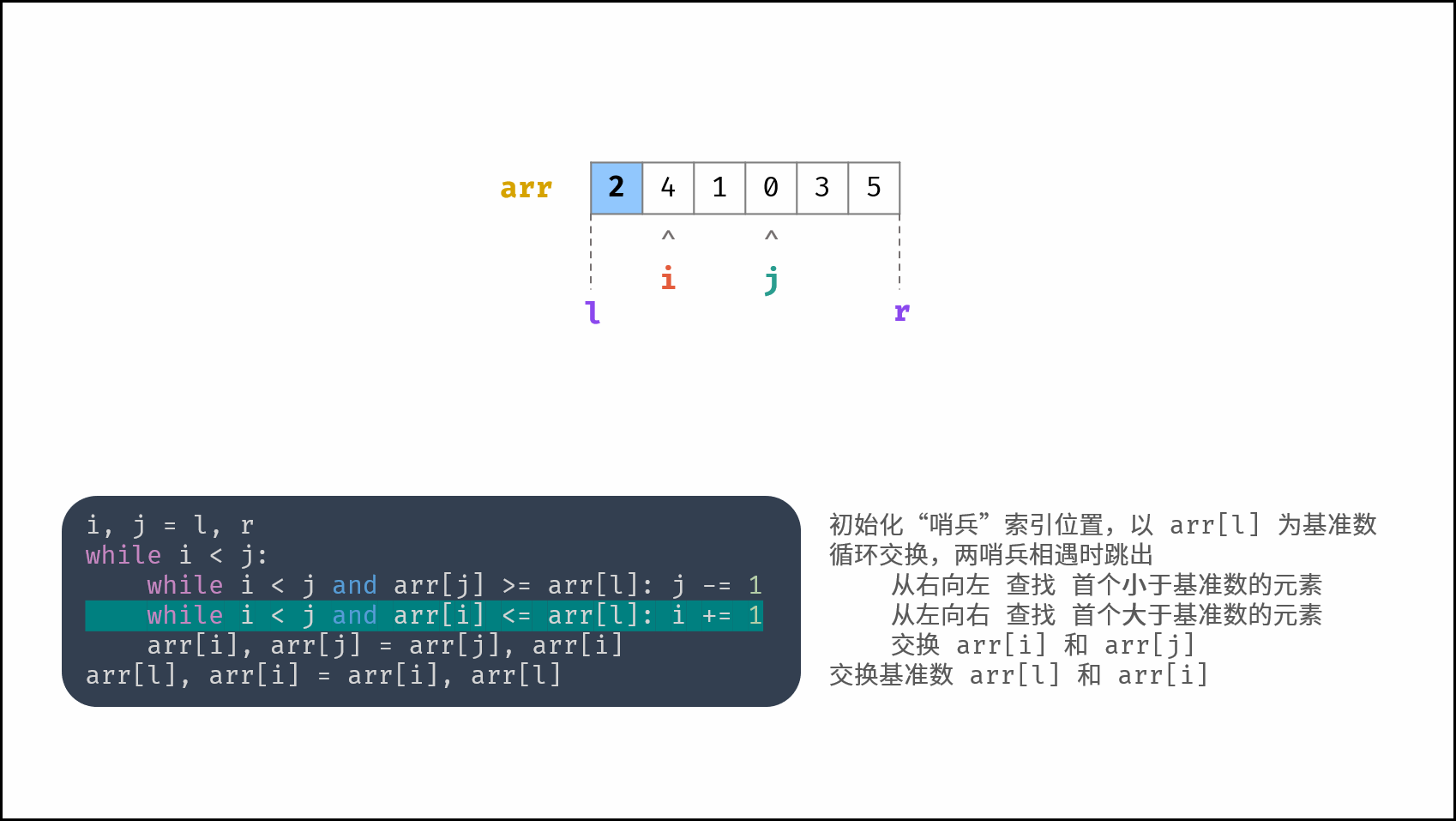
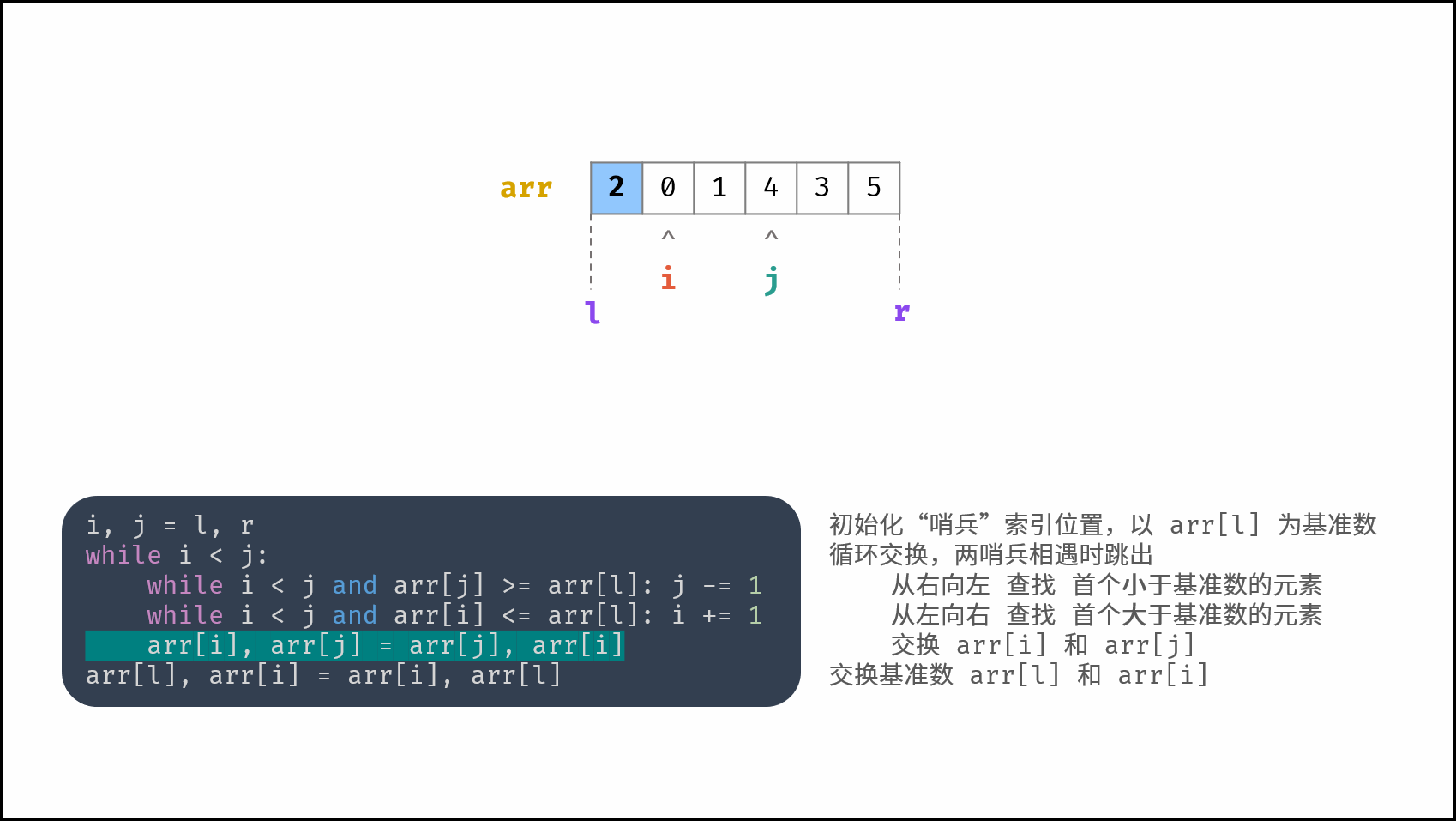
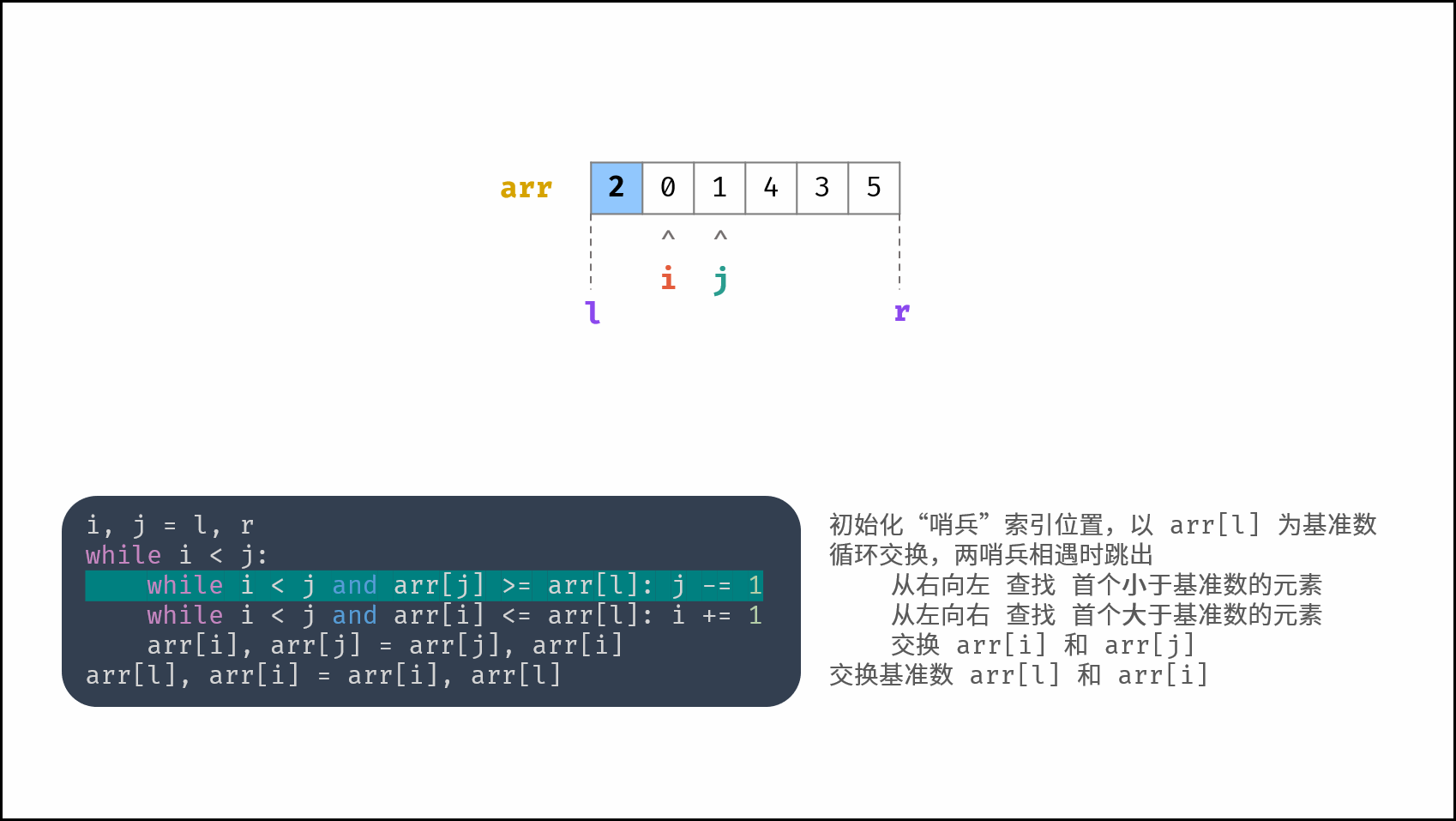
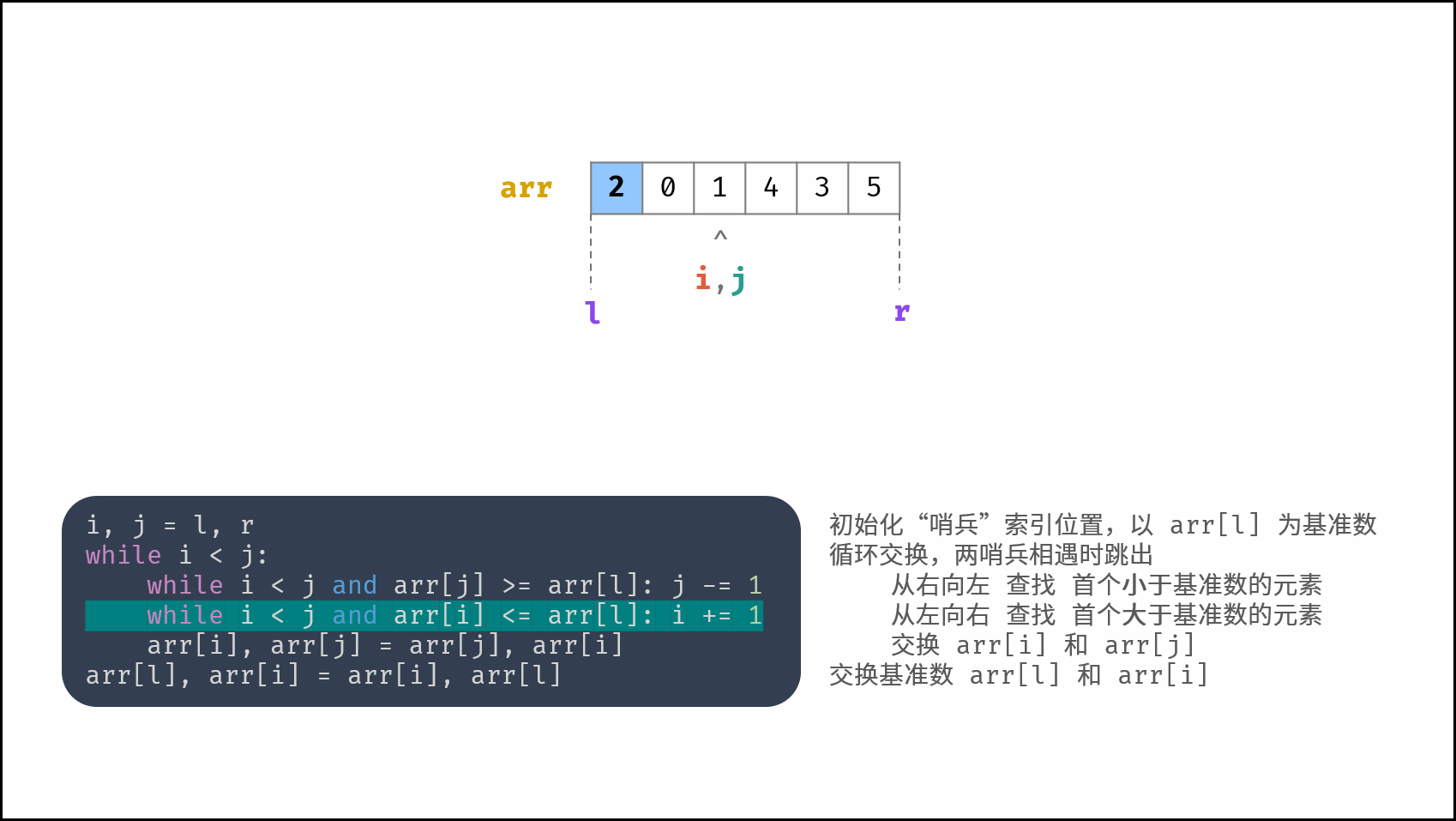
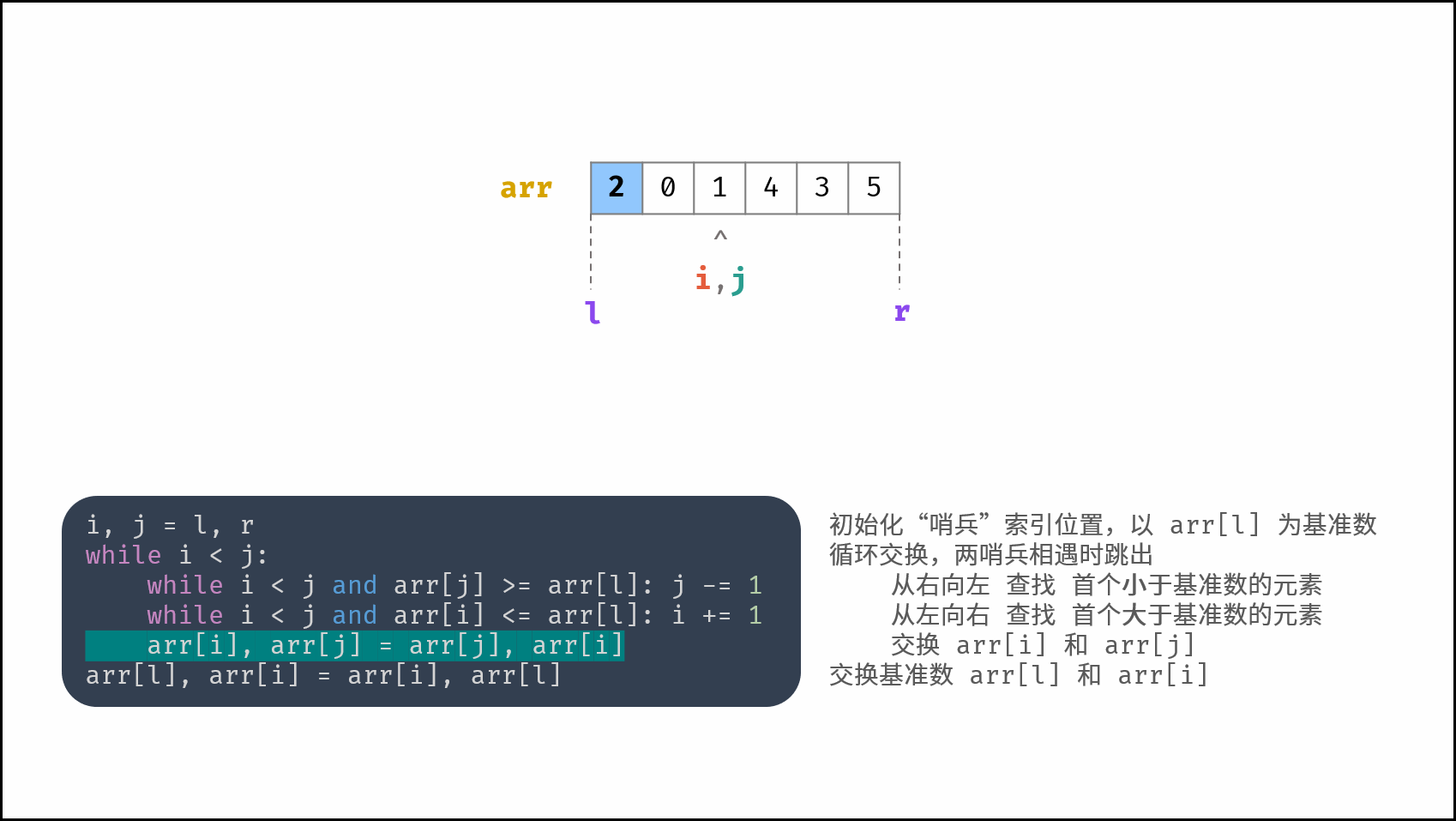
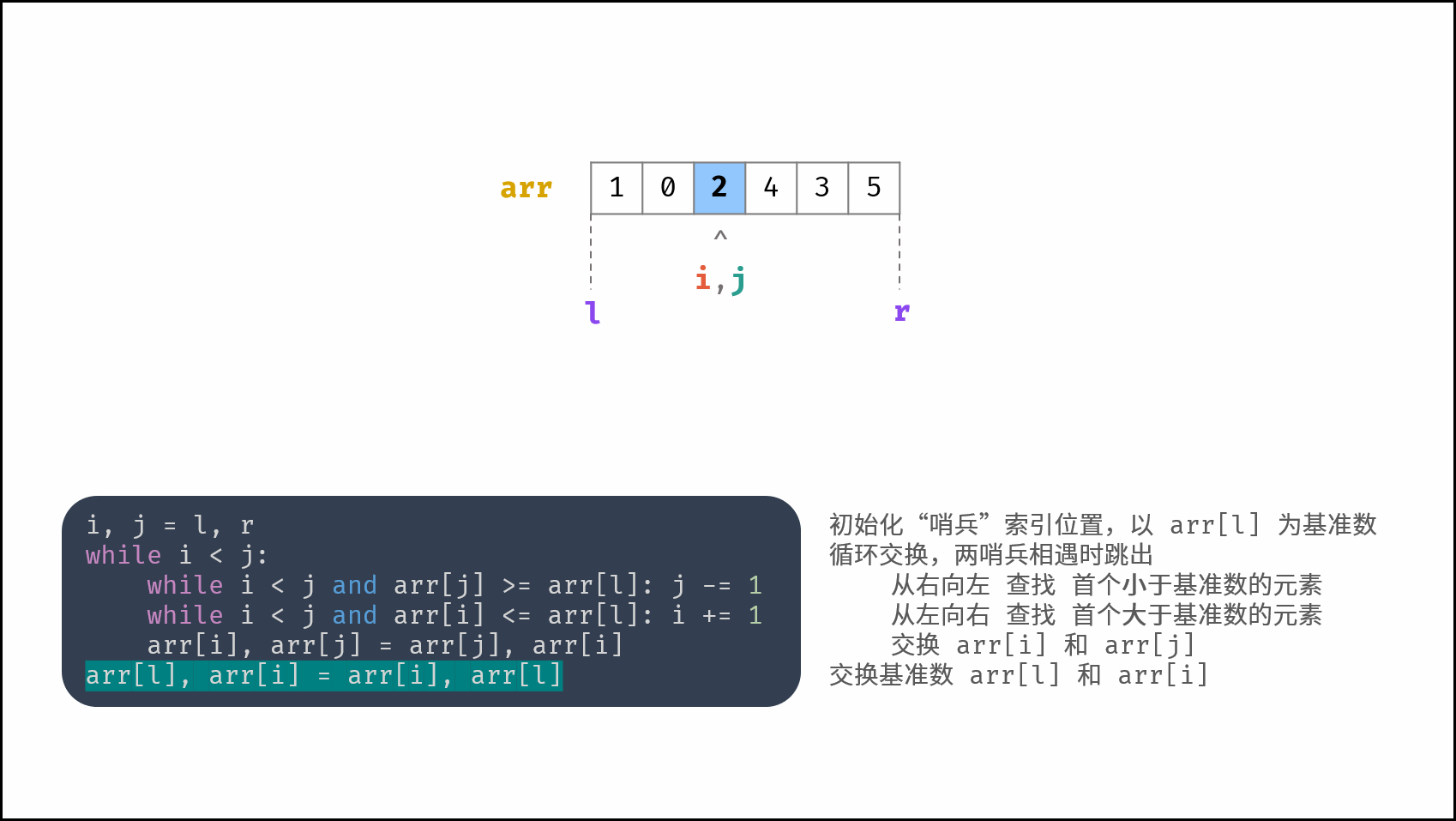
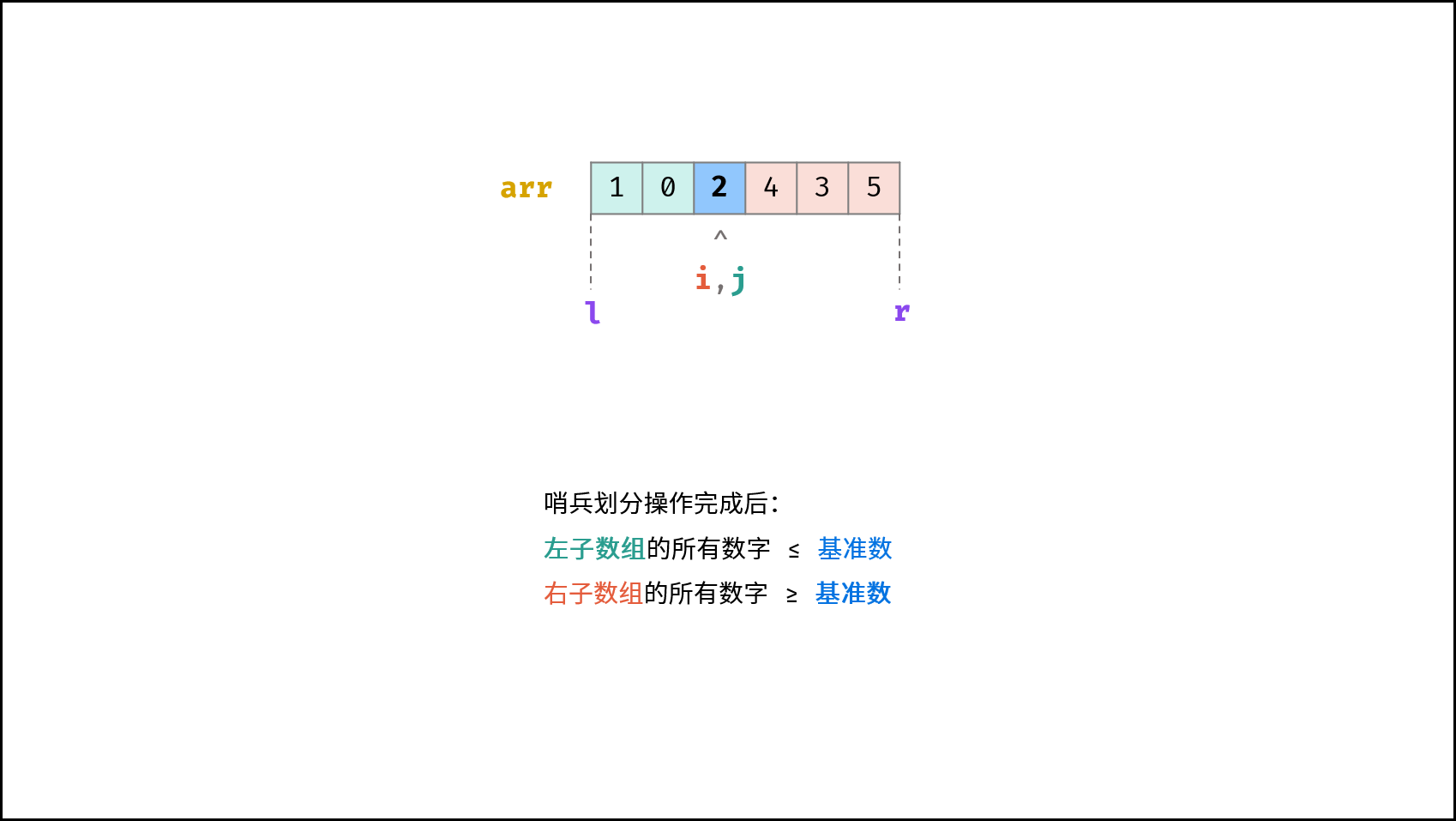
哨兵划分操作： 以数组某个元素（一般选取首元素）为 基准数 ，将所有小于基准数的元素移动至其左边，大于基准数的元素移动至其右边。

如下图所示，为哨兵划分操作流程。通过一轮 哨兵划分 ，可将数组排序问题拆分为 两个较短数组的排序问题 （本文称之为左（右）子数组）。

<Picture2.png,Picture3.png,Picture4.png,Picture5.png,Picture6.png,Picture7.png,Picture8.png,Picture9.png,Picture10.png>

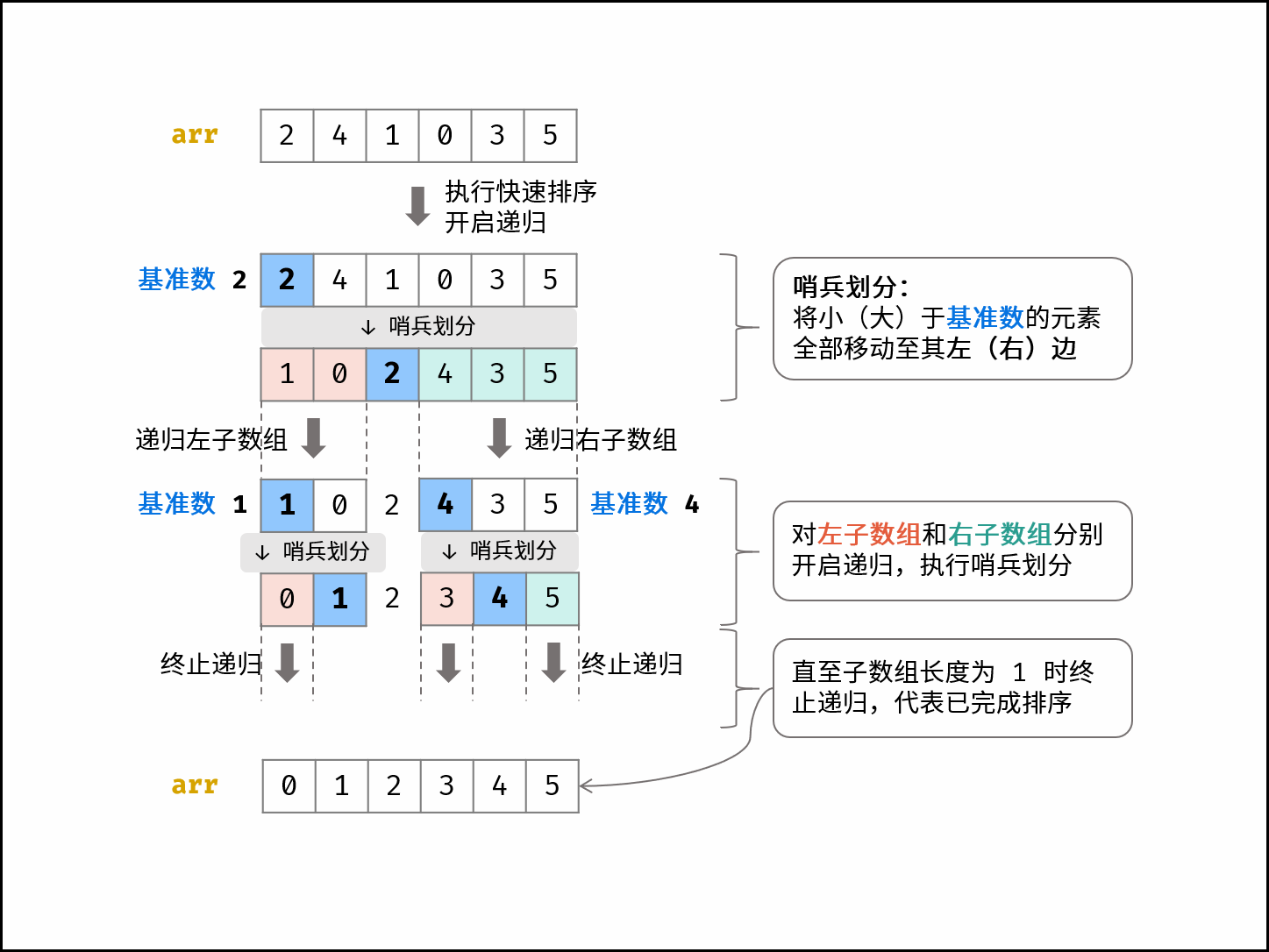
递归： 对 左子数组 和 右子数组 递归执行 哨兵划分，直至子数组长度为 1 时终止递归，即可完成对整个数组的排序。

如下图所示，为示例数组 [2,4,1,0,3,5] 的快速排序流程。观察发现，快速排序和 二分法 的原理类似，都是以 $\log$ 时间复杂度实现搜索区间缩小。

Picture1.png

代码： ​

Python
class Solution:
    def inventoryManagement(self, stock: List[int], cnt: int) -> List[int]:
        def quick_sort(stock, l, r):
            # 子数组长度为 1 时终止递归
            if l >= r: return
            # 哨兵划分操作（以 stock[l] 作为基准数）
            i, j = l, r
            while i < j:
                while i < j and stock[j] >= stock[l]: j -= 1
                while i < j and stock[i] <= stock[l]: i += 1
                stock[i], stock[j] = stock[j], stock[i]
            stock[l], stock[i] = stock[i], stock[l]
            # 递归左（右）子数组执行哨兵划分
            quick_sort(stock, l, i - 1)
            quick_sort(stock, i + 1, r)
        
        quick_sort(stock, 0, len(stock) - 1)
        return stock[:cnt]
Java
class Solution {
    public int[] inventoryManagement(int[] stock, int cnt) {
        quickSort(stock, 0, stock.length - 1);
        return Arrays.copyOf(stock, cnt);
    }
    private void quickSort(int[] stock, int l, int r) {
        // 子数组长度为 1 时终止递归
        if (l >= r) return;
        // 哨兵划分操作（以 stock[l] 作为基准数）
        int i = l, j = r;
        while (i < j) {
            while (i < j && stock[j] >= stock[l]) j--;
            while (i < j && stock[i] <= stock[l]) i++;
            swap(stock, i, j);
        }
        swap(stock, i, l);
        // 递归左（右）子数组执行哨兵划分
        quickSort(stock, l, i - 1);
        quickSort(stock, i + 1, r);
    }
    private void swap(int[] stock, int i, int j) {
        int tmp = stock[i];
        stock[i] = stock[j];
        stock[j] = tmp;
    }
}
C++
class Solution {
public:
    vector<int> inventoryManagement(vector<int>& stock, int cnt) {
        quickSort(stock, 0, stock.size() - 1);
        vector<int> res;
        res.assign(stock.begin(), stock.begin() + cnt);
        return res;
    }
private:
    void quickSort(vector<int>& stock, int l, int r) {
        // 子数组长度为 1 时终止递归
        if (l >= r) return;
        // 哨兵划分操作（以 stock[l] 作为基准数）
        int i = l, j = r;
        while (i < j) {
            while (i < j && stock[j] >= stock[l]) j--;
            while (i < j && stock[i] <= stock[l]) i++;
            swap(stock[i], stock[j]);
        }
        swap(stock[i], stock[l]);
        // 递归左（右）子数组执行哨兵划分
        quickSort(stock, l, i - 1);
        quickSort(stock, i + 1, r);
    }
};

复杂度分析： ​

  • 时间复杂度 $O(N \log N)$ ： 库函数、快排等排序算法的平均时间复杂度为 $O(N \log N)$ 。
  • 空间复杂度 $O(N)$ ： 快速排序的递归深度最好（平均）为 $O(\log N)$ ，最差情况（即输入数组完全倒序）为 $O(N)$。

方法二：快速选择 ​

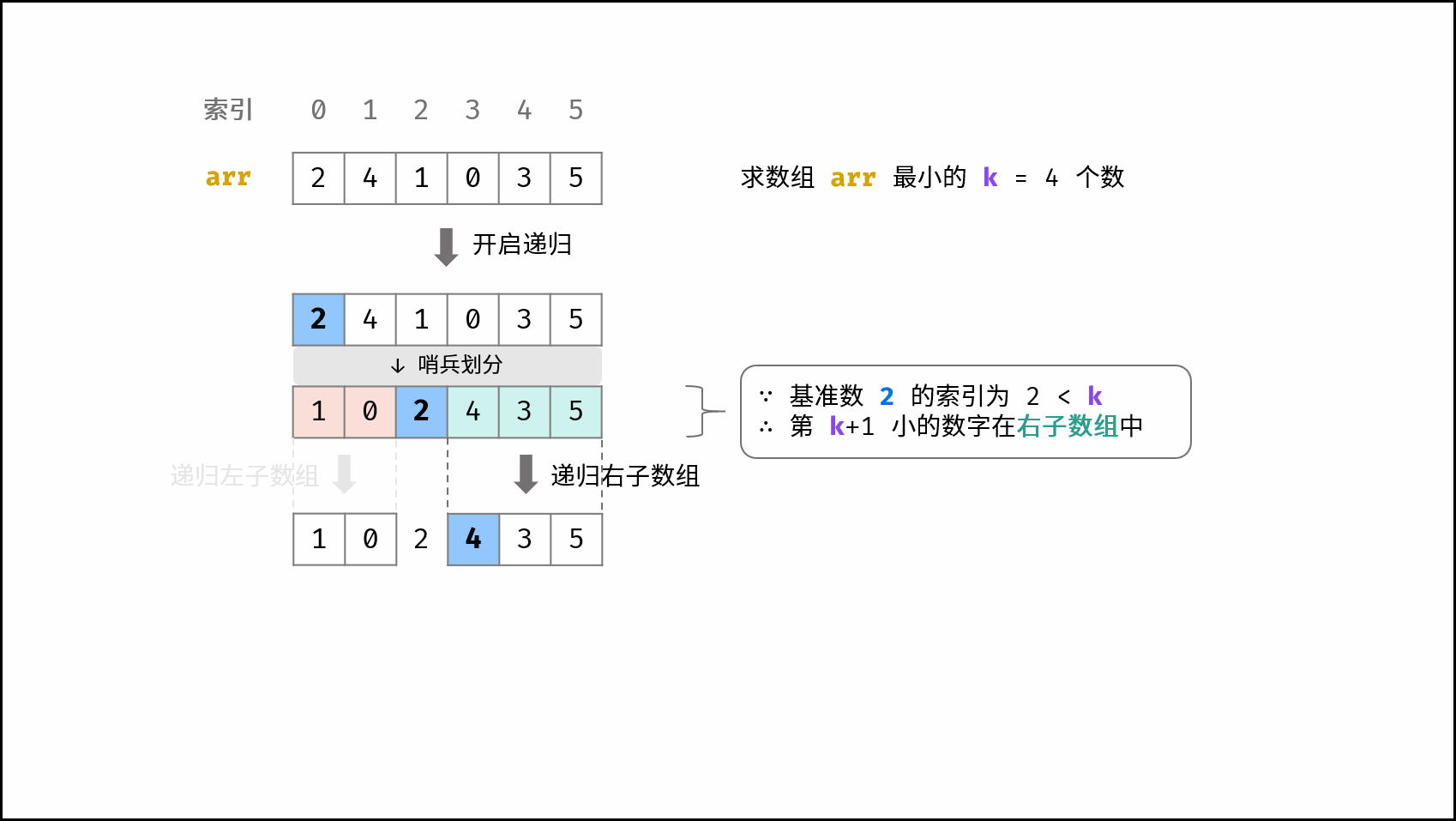
题目只要求返回最小的 cnt 个数，对这 cnt 个数的顺序并没有要求。因此，只需要将数组划分为 最小的 $cnt$ 个数 和 其他数字 两部分即可，而快速排序的哨兵划分可完成此目标。

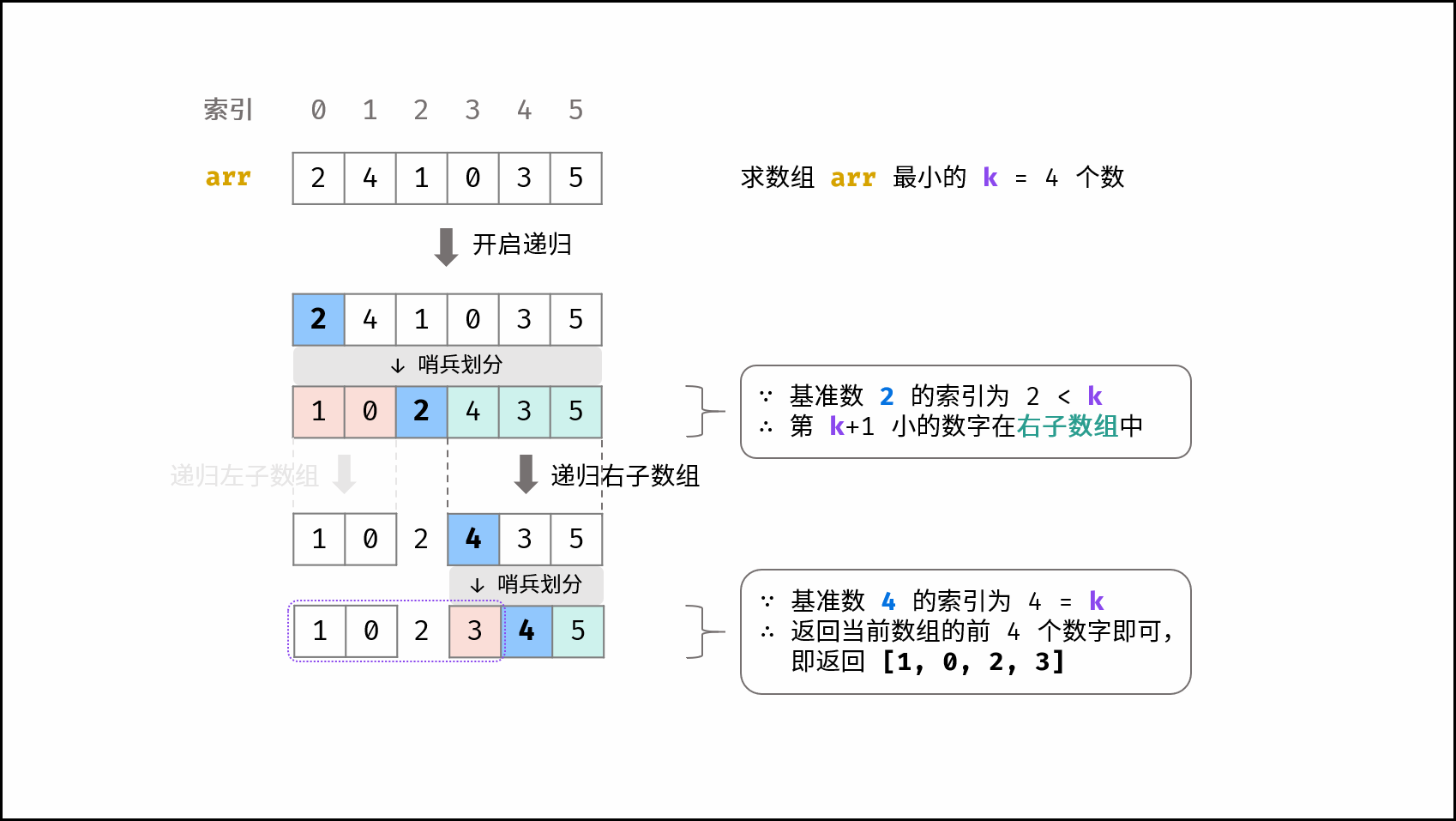
根据快速排序原理，如果某次哨兵划分后 基准数正好是第 $cnt+1$ 小的数字 ，那么此时基准数左边的所有数字便是题目所求的 最小的 cnt 个数 。

根据此思路，考虑在每次哨兵划分后，判断基准数在数组中的索引是否等于 $cnt$ ，若 $\text{true}$ 则直接返回此时数组的前 $cnt$ 个数字即可。

算法流程： ​

inventoryManagement() 函数：

  1. 若 $cnt$ 大于数组长度，则直接返回整个数组；
  2. 执行并返回 quick_sort() 即可；

quick_sort() 函数：

注意，此时 quick_sort() 的功能不是排序整个数组，而是搜索并返回最小的 $cnt$ 个数。

  1. 哨兵划分：
  • 划分完毕后，基准数为 stock[i] ，左 / 右子数组区间分别为 $[l, i - 1]$ , $[i + 1, r]$ ；
  1. 递归或返回：
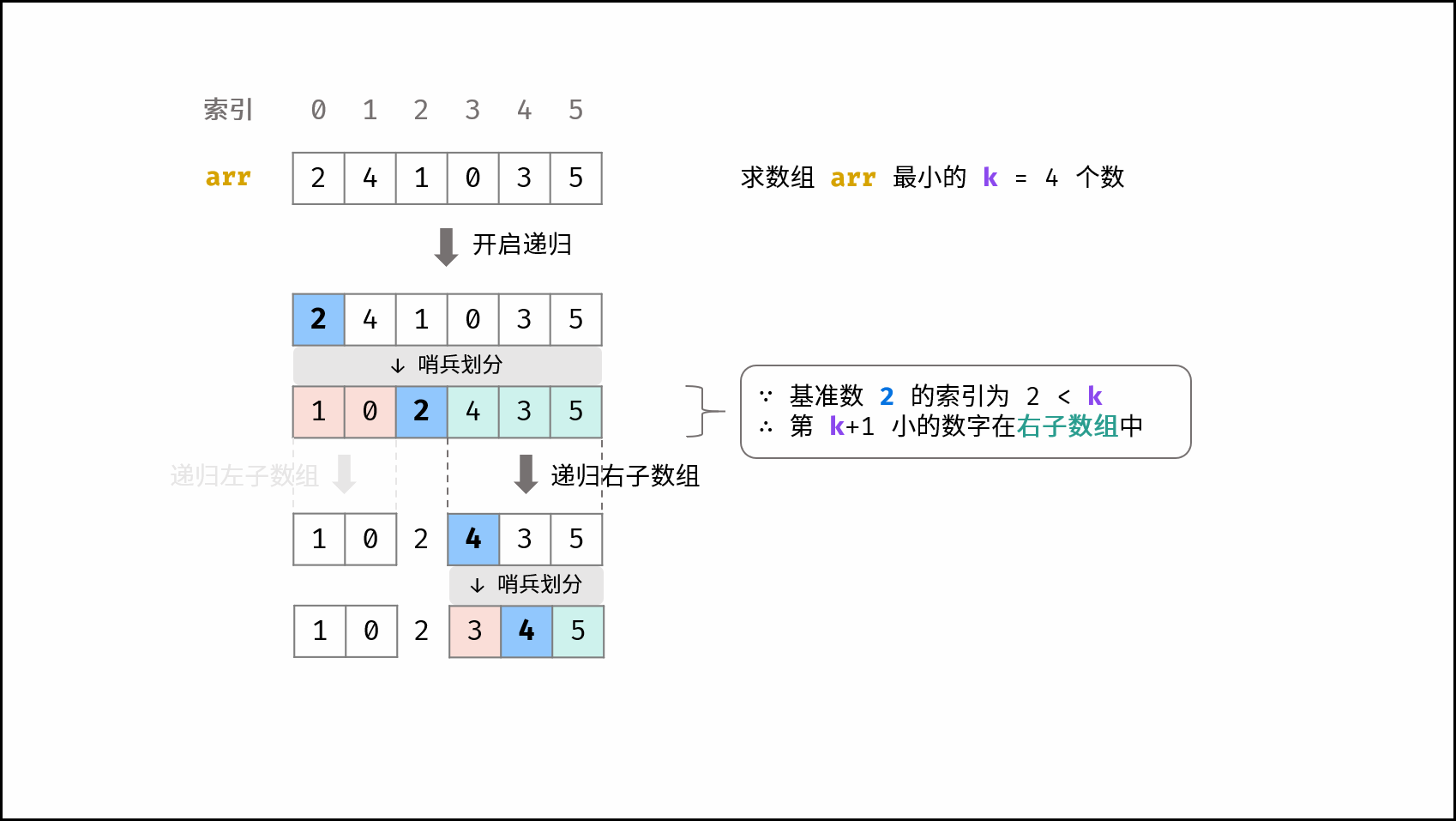
  • 若 $cnt < i$ ，代表第 $cnt + 1$ 小的数字在 左子数组 中，则递归左子数组；
  • 若 $cnt > i$ ，代表第 $cnt + 1$ 小的数字在 右子数组 中，则递归右子数组；
  • 若 $cnt = i$ ，代表此时 stock[cnt] 即为第 $cnt + 1$ 小的数字，则直接返回数组前 $cnt$ 个数字即可；

<Picture12.png,Picture13.png,Picture14.png,Picture15.png,Picture16.png,Picture17.png>

代码： ​

Python
class Solution:
    def inventoryManagement(self, stock: List[int], cnt: int) -> List[int]:
        if cnt >= len(stock): return stock
        def quick_sort(l, r):
            i, j = l, r
            while i < j:
                while i < j and stock[j] >= stock[l]: j -= 1
                while i < j and stock[i] <= stock[l]: i += 1
                stock[i], stock[j] = stock[j], stock[i]
            stock[l], stock[i] = stock[i], stock[l]
            if cnt < i: return quick_sort(l, i - 1) 
            if cnt > i: return quick_sort(i + 1, r)
            return stock[:cnt]
            
        return quick_sort(0, len(stock) - 1)
Java
class Solution {
    public int[] inventoryManagement(int[] stock, int cnt) {
        if (cnt >= stock.length) return stock;
        return quickSort(stock, cnt, 0, stock.length - 1);
    }
    private int[] quickSort(int[] stock, int cnt, int l, int r) {
        int i = l, j = r;
        while (i < j) {
            while (i < j && stock[j] >= stock[l]) j--;
            while (i < j && stock[i] <= stock[l]) i++;
            swap(stock, i, j);
        }
        swap(stock, i, l);
        if (i > cnt) return quickSort(stock, cnt, l, i - 1);
        if (i < cnt) return quickSort(stock, cnt, i + 1, r);
        return Arrays.copyOf(stock, cnt);
    }
    private void swap(int[] stock, int i, int j) {
        int tmp = stock[i];
        stock[i] = stock[j];
        stock[j] = tmp;
    }
}
C++
class Solution {
public:
    vector<int> inventoryManagement(vector<int>& stock, int cnt) {
        if (cnt >= stock.size()) return stock;
        return quickSort(stock, cnt, 0, stock.size() - 1);
    }
private:
    vector<int> quickSort(vector<int>& stock, int cnt, int l, int r) {
        int i = l, j = r;
        while (i < j) {
            while (i < j && stock[j] >= stock[l]) j--;
            while (i < j && stock[i] <= stock[l]) i++;
            swap(stock[i], stock[j]);
        }
        swap(stock[i], stock[l]);
        if (i > cnt) return quickSort(stock, cnt, l, i - 1);
        if (i < cnt) return quickSort(stock, cnt, i + 1, r);
        vector<int> res;
        res.assign(stock.begin(), stock.begin() + cnt);
        return res;
    }
};

复杂度分析： ​

本方法优化时间复杂度的本质是通过判断舍去了不必要的递归（哨兵划分）。

  • 时间复杂度 $O(N)$ ： 其中 $N$ 为数组元素数量；对于长度为 $N$ 的数组执行哨兵划分操作的时间复杂度为 $O(N)$ ；每轮哨兵划分后根据 $cnt$ 和 $i$ 的大小关系选择递归，由于 $i$ 分布的随机性，则向下递归子数组的平均长度为 $\frac{N}{2}$ ；因此平均情况下，哨兵划分操作一共有 $N + \frac{N}{2} + \frac{N}{4} + ... + \frac{N}{N} = \frac{N - \frac{1}{2}}{1 - \frac{1}{2}} = 2N - 1$ （等比数列求和），即总体时间复杂度为 $O(N)$ 。
  • 空间复杂度 $O(\log N)$ ： 划分函数的平均递归深度为 $O(\log N)$ 。

MIT License.

Copyright © 2024 自律小屋