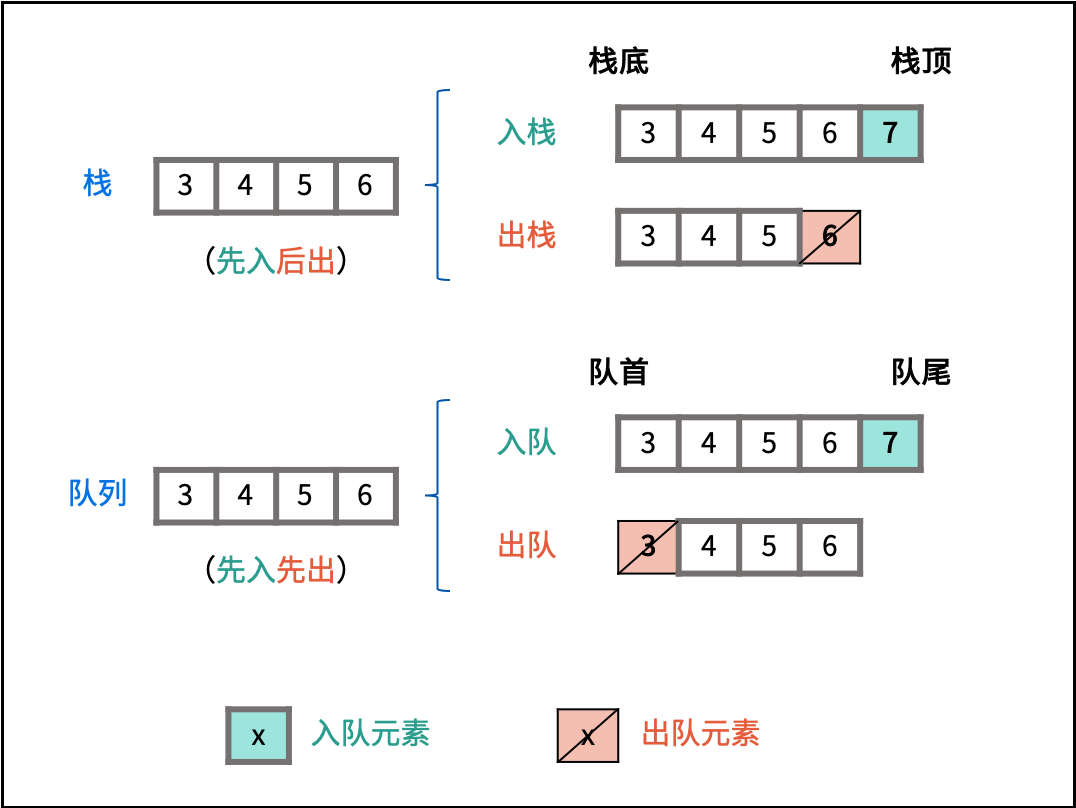
解题思路： ​

我们可将两个书车看作两个“栈”，本题可被转化为“用两个栈实现一个队列”。

栈实现队列的出队操作效率低下：栈底元素（对应队首元素）无法直接删除，需要将上方所有元素出栈。

列表倒序操作可使用双栈实现：设有含三个元素的栈 A = [1,2,3] 和空栈 B = [] 。若循环执行 A 元素出栈并添加入栈 B ，直到栈 A 为空，则 A = [] , B = [3,2,1] ，即栈 B 元素为栈 A 元素倒序。

利用栈 B 删除队首元素：倒序后，B 执行出栈则相当于删除了 A 的栈底元素，即对应队首元素。

题目要求实现 加入队尾appendTail() 和 删除队首deleteHead() 两个函数的正常工作。因此，可以设计栈 A 用于加入队尾操作，栈 B 用于将元素倒序，从而实现删除队首元素。

函数设计： ​

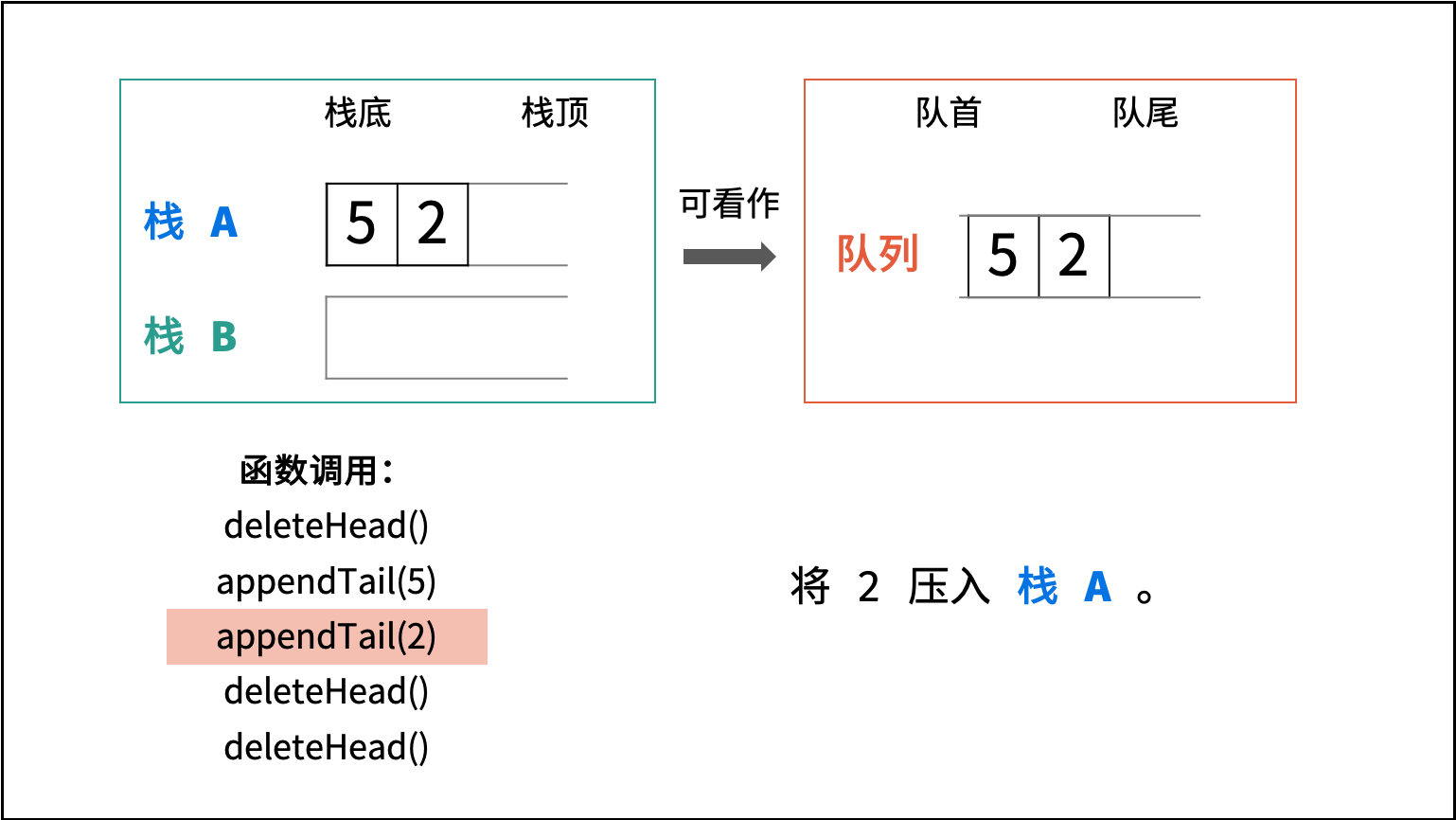
1. 加入队尾 appendTail() ： 将数字 val 加入栈 A 即可。
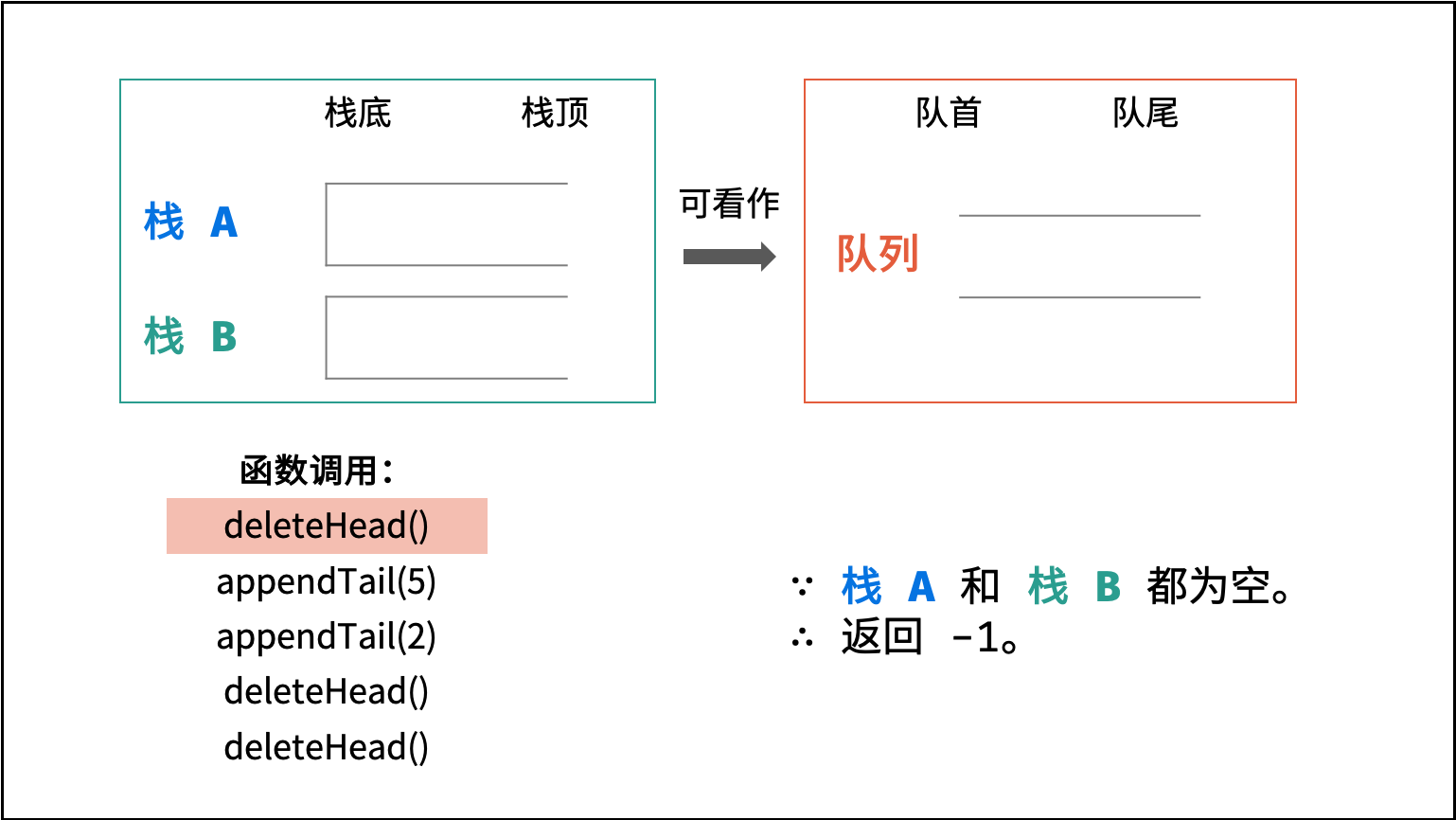
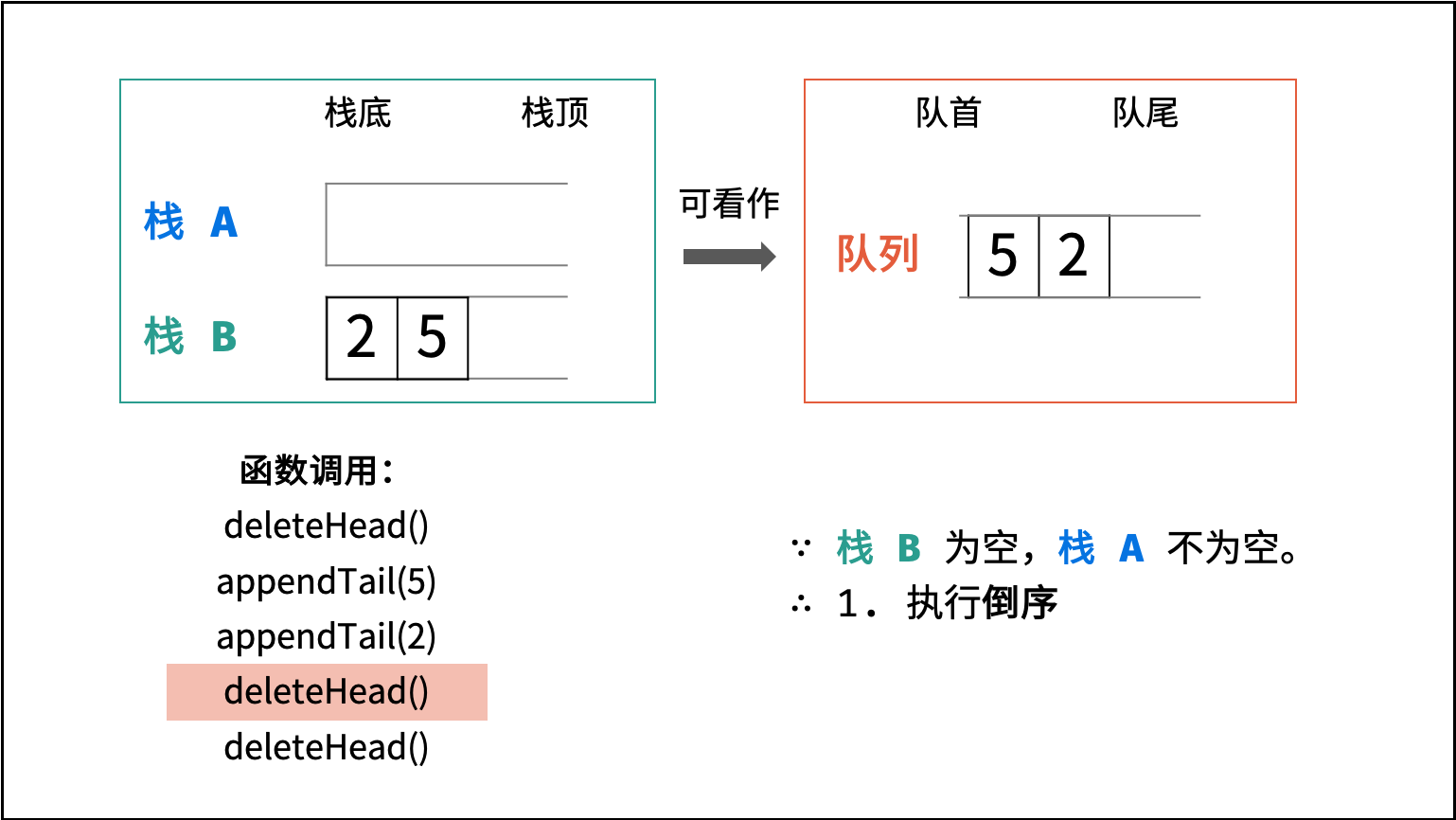
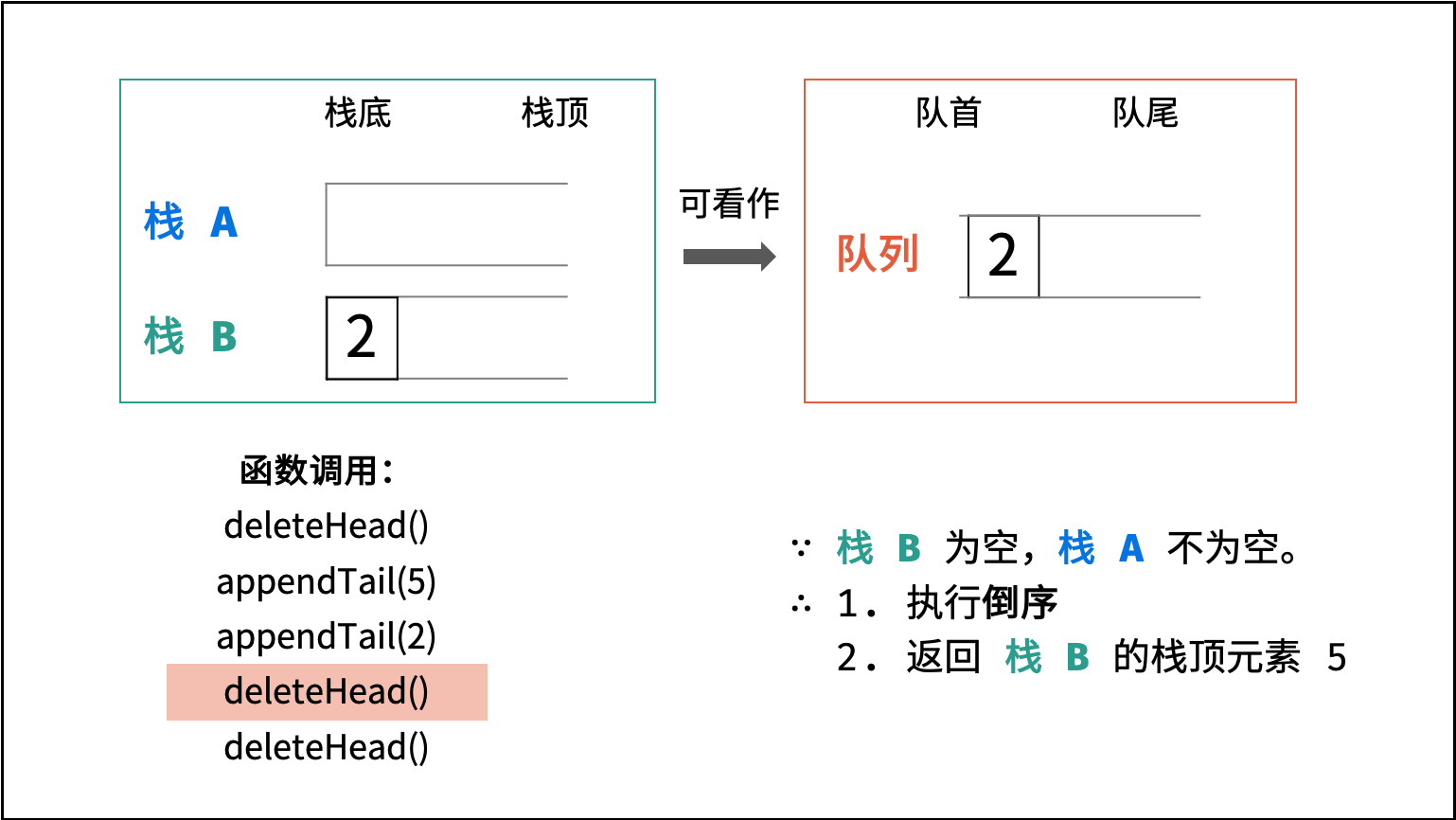
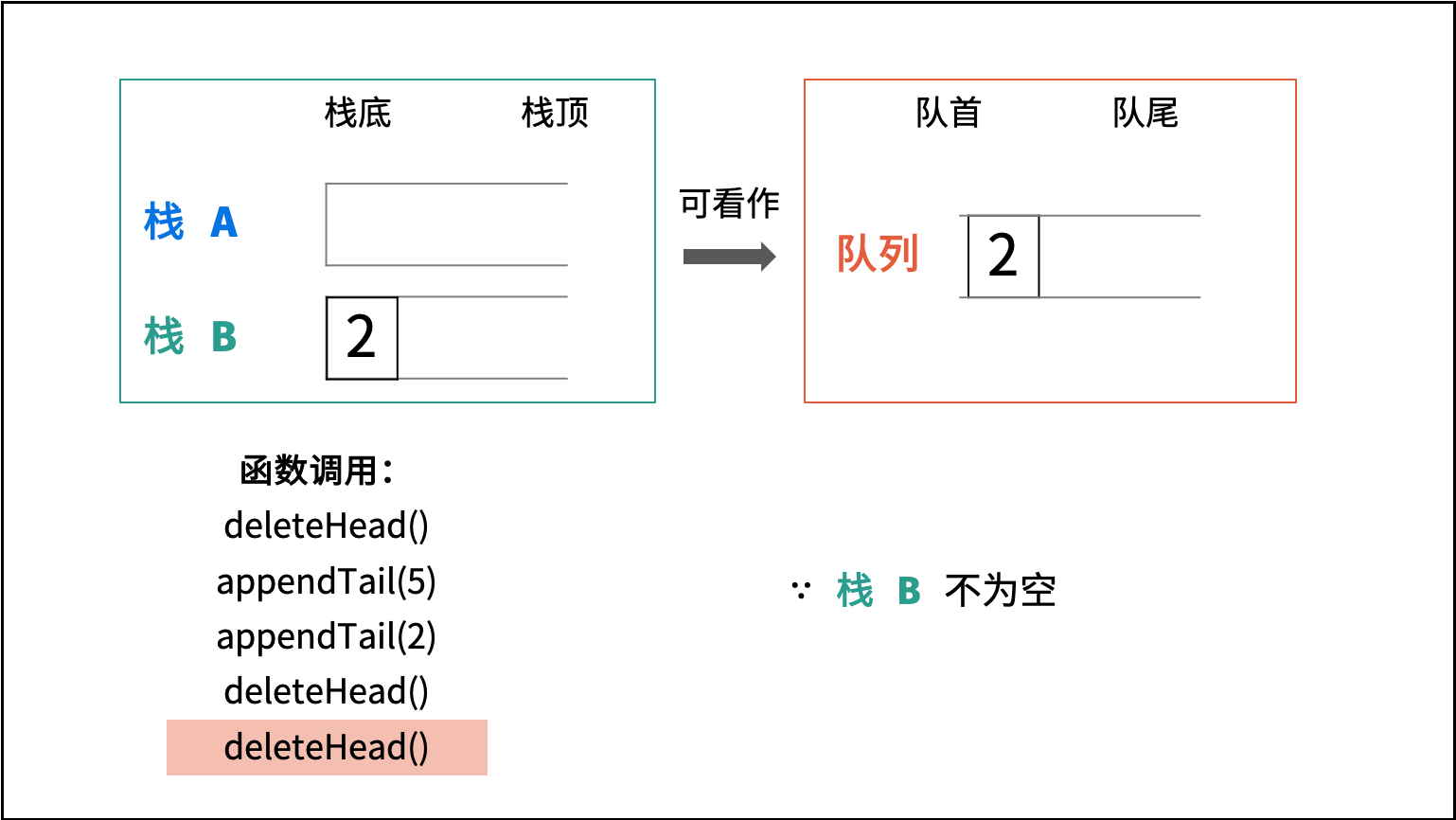
2. 删除队首deleteHead() ： 有以下三种情况。
   1. 当栈 B 不为空： B中仍有已完成倒序的元素，因此直接返回 B 的栈顶元素。
   2. 否则，当 A 为空： 即两个栈都为空，无元素，因此返回 -1 。
   3. 否则： 将栈 A 元素全部转移至栈 B 中，实现元素倒序，并返回栈 B 的栈顶元素。

<,,,,,,,>

代码： ​

Python 和 Java 的栈的 pop() 函数返回栈顶元素，而 C++ 不返回；因此对于 C++ ，需要先使用 top() 方法暂存栈顶元素，再执行 pop() 出栈操作。

class CQueue:
    def __init__(self):
        self.A, self.B = [], []

    def appendTail(self, value: int) -> None:
        self.A.append(value)

    def deleteHead(self) -> int:
        if self.B: return self.B.pop()
        if not self.A: return -1
        while self.A:
            self.B.append(self.A.pop())
        return self.B.pop()

class CQueue {
    LinkedList<Integer> A, B;
    public CQueue() {
        A = new LinkedList<Integer>();
        B = new LinkedList<Integer>();
    }
    public void appendTail(int value) {
        A.addLast(value);
    }
    public int deleteHead() {
        if(!B.isEmpty()) return B.removeLast();
        if(A.isEmpty()) return -1;
        while(!A.isEmpty())
            B.addLast(A.removeLast());
        return B.removeLast();
    }
}

class CQueue {
public:
    stack<int> A, B;
    CQueue() {}
    void appendTail(int value) {
        A.push(value);
    }
    int deleteHead() {
        if(!B.empty()) {
            int tmp = B.top();
            B.pop();
            return tmp;
        }
        if(A.empty()) return -1;
        while(!A.empty()) {
            int tmp = A.top();
            A.pop();
            B.push(tmp);
        }
        int tmp = B.top();
        B.pop();
        return tmp;
    }
};

复杂度分析： ​

以下分析仅满足添加 $N$ 个元素并删除 $N$ 个元素，即栈初始和结束状态下都为空的情况。

• 时间复杂度： appendTail()函数为 $O(1)$ ；deleteHead() 函数在 $N$ 次队首元素删除操作中总共需完成 $N$ 个元素的倒序。
• 空间复杂度 $O(N)$ ： 最差情况下，栈 A 和 B 共保存 $N$ 个元素。