时间复杂度

根据定义，时间复杂度指输入数据大小为 $N$ 时，算法运行所需花费的时间。需要注意：

统计的是算法的「计算操作数量」，而不是「运行的绝对时间」。计算操作数量和运行绝对时间呈正相关关系，并不相等。算法运行时间受到「编程语言、计算机处理器速度、运行环境」等多种因素影响。例如，同样的算法使用 Python 或 C++ 实现、使用 CPU 或 GPU 、使用本地 IDE 或力扣平台提交，运行时间都不同。
体现的是计算操作随数据大小 $N$ 变化时的变化情况。假设算法运行总共需要「 $1$ 次操作」、「 $100$ 次操作」，此两情况的时间复杂度都为常数级 $O(1)$ ；需要「 $N$ 次操作」、「 $100N$ 次操作」的时间复杂度都为 $O(N)$ 。

符号表示

根据输入数据的特点，时间复杂度具有「最差」、「平均」、「最佳」三种情况，分别使用 $O$ , $\Theta$ , $\Omega$ 三种符号表示。以下借助一个查找算法的示例题目帮助理解。

题目： 输入长度为 $N$ 的整数数组 nums ，判断此数组中是否有数字 $7$ ，若有则返回 true ，否则返回 $\text{false}$ 。

解题算法： 线性查找，即遍历整个数组，遇到 $7$ 则返回 true 。

代码：

Python

def find_seven(nums):
    for num in nums:
        if num == 7:
            return True
    return False

Java

boolean findSeven(int[] nums) {
    for (int num : nums) {
        if (num == 7)
            return true;
    }
    return false;
}

C++

bool findSeven(vector<int>& nums) {
    for (int num : nums) {
        if (num == 7)
            return true;
    }
    return false;
}

最佳情况 $\Omega(1)$ ： nums = [7, a, b, c, ...] ，即当数组首个数字为 $7$ 时，无论 nums 有多少元素，线性查找的循环次数都为 $1$ 次；
最差情况 $O(N)$ ： nums = [a, b, c, ...] 且 nums 中所有数字都不为 $7$ ，此时线性查找会遍历整个数组，循环 $N$ 次；
平均情况 $\Theta$ ： 需要考虑输入数据的分布情况，计算所有数据情况下的平均时间复杂度；例如本题目，需要考虑数组长度、数组元素的取值范围等；

大 $O$ 是最常使用的时间复杂度评价渐进符号，下文示例与本 LeetBook 题目解析皆使用 $O$ 。

常见种类

根据从小到大排列，常见的算法时间复杂度主要有：

$$ O(1) < O(\log N) < O(N) < O(N\log N) < O(N^2) < O(2^N) < O(N!) $$

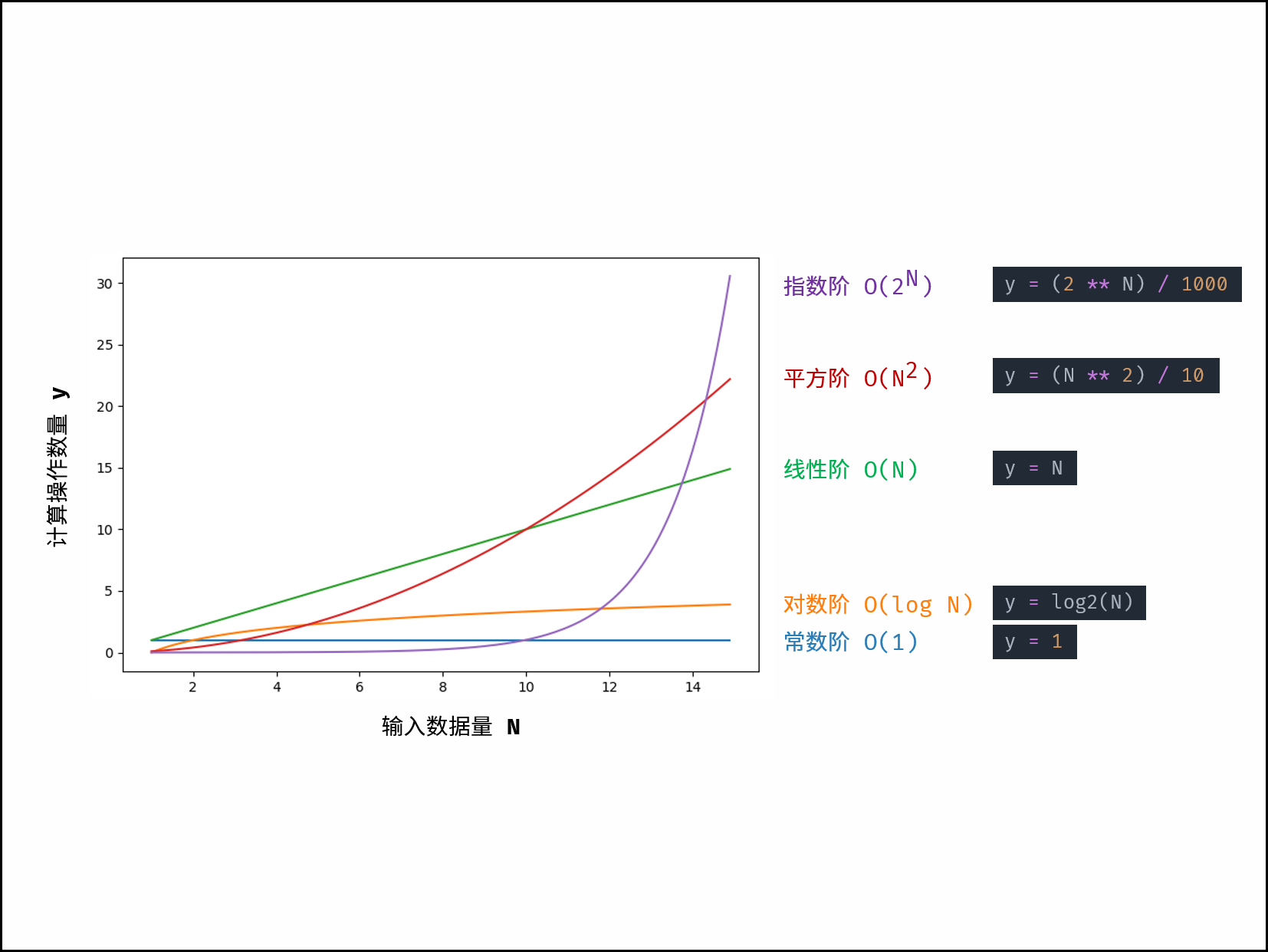
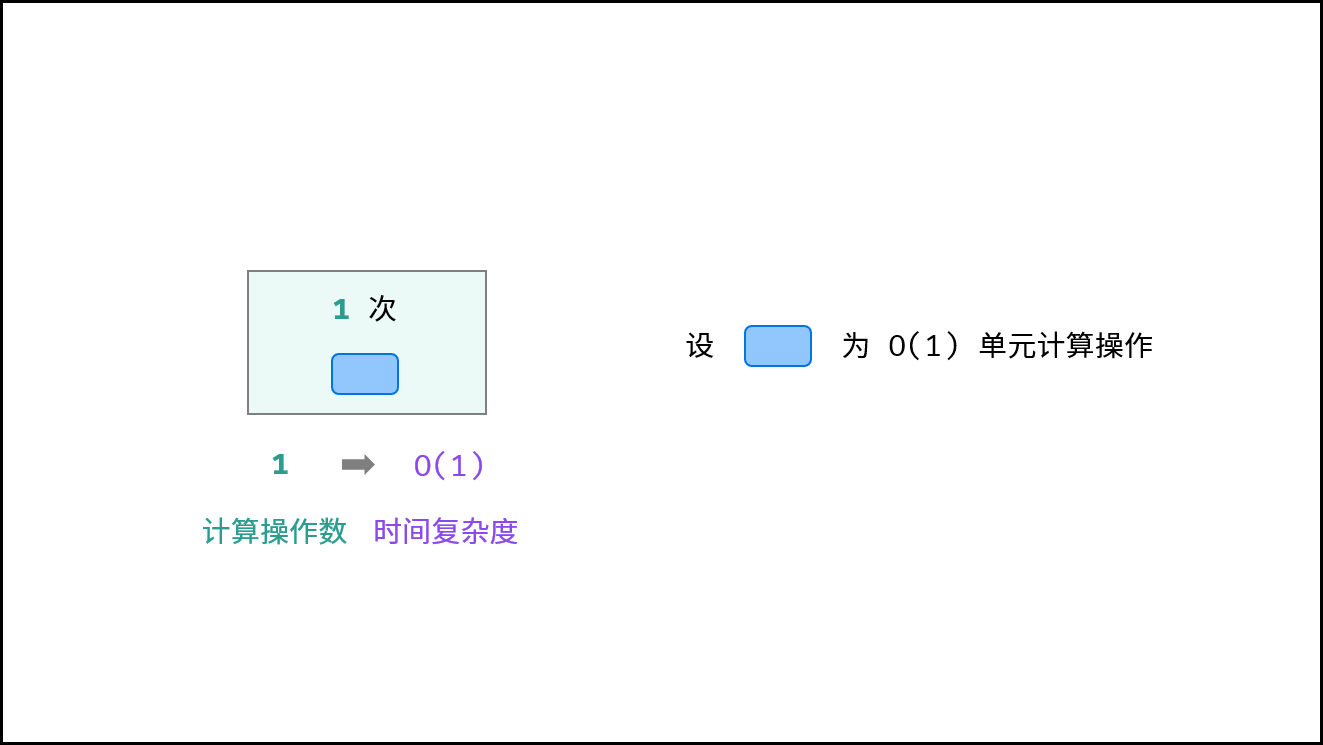
对于以下所有示例，设输入数据大小为 $N$ ，计算操作数量为 $count$ 。图中每个「蓝色方块」代表一个单元计算操作。

常数 $O(1)$ ：

运行次数与 $N$ 大小呈常数关系，即不随输入数据大小 $N$ 的变化而变化。

Python

def algorithm(N):
    a = 1
    b = 2
    x = a * b + N
    return 1

Java

int algorithm(int N) {
    int a = 1;
    int b = 2;
    int x = a * b + N;
    return 1;
}

C++

int algorithm(int N) {
    int a = 1;
    int b = 2;
    int x = a * b + N;
    return 1;
}

对于以下代码，无论 $a$ 取多大，都与输入数据大小 $N$ 无关，因此时间复杂度仍为 $O(1)$ 。

Python

def algorithm(N):
    count = 0
    a = 10000
    for i in range(a):
        count += 1
    return count

Java

int algorithm(int N) {
    int count = 0;
    int a = 10000;
    for (int i = 0; i < a; i++) {
        count++;
    }
    return count;
}

C++

int algorithm(int N) {
    int count = 0;
    int a = 10000;
    for (int i = 0; i < a; i++) {
        count++;
    }
    return count;
}

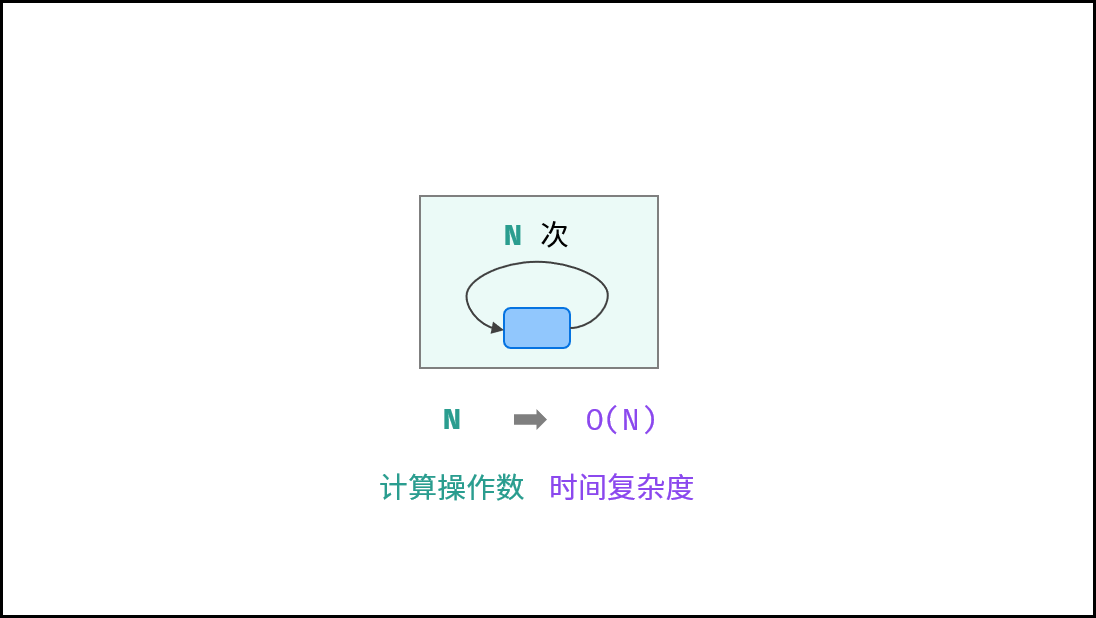
线性 $O(N)$ ：

循环运行次数与 $N$ 大小呈线性关系，时间复杂度为 $O(N)$ 。

Python

def algorithm(N):
    count = 0
    for i in range(N):
        count += 1
    return count

Java

int algorithm(int N) {
    int count = 0;
    for (int i = 0; i < N; i++)
        count++;
    return count;
}

C++

int algorithm(int N) {
    int count = 0;
    for (int i = 0; i < N; i++)
        count++;
    return count;
}

对于以下代码，虽然是两层循环，但第二层与 $N$ 大小无关，因此整体仍与 $N$ 呈线性关系。

Python

def algorithm(N):
    count = 0
    a = 10000
    for i in range(N):
        for j in range(a):
            count += 1
    return count

Java

int algorithm(int N) {
    int count = 0;
    int a = 10000;
    for (int i = 0; i < N; i++) {
        for (int j = 0; j < a; j++) {
            count++;
        }
    }
    return count;
}

C++

int algorithm(int N) {
    int count = 0;
    int a = 10000;
    for (int i = 0; i < N; i++) {
        for (int j = 0; j < a; j++) {
            count++;
        }
    }
    return count;
}

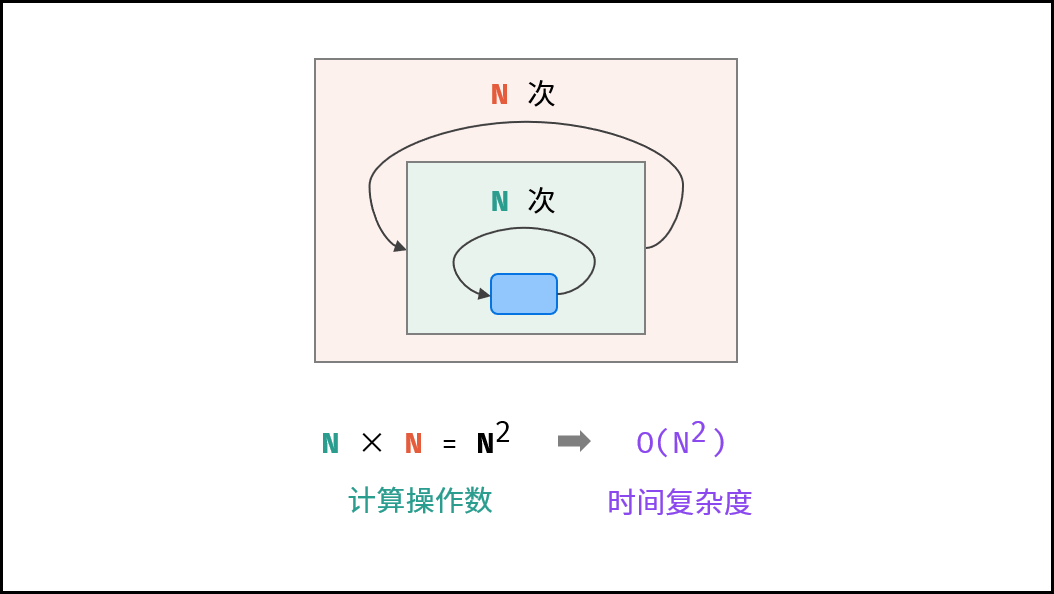
平方 $O(N^2)$ ：

两层循环相互独立，都与 $N$ 呈线性关系，因此总体与 $N$ 呈平方关系，时间复杂度为 $O(N^2)$ 。

Python

def algorithm(N):
    count = 0
    for i in range(N):
        for j in range(N):
            count += 1
    return count

Java

int algorithm(int N) {
    int count = 0;
    for (int i = 0; i < N; i++) {
        for (int j = 0; j < N; j++) {
            count++;
        }
    }
    return count;
}

C++

int algorithm(int N) {
    int count = 0;
    for (int i = 0; i < N; i++) {
        for (int j = 0; j < N; j++) {
            count++;
        }
    }
    return count;
}

以「冒泡排序」为例，其包含两层独立循环：

第一层复杂度为 $O(N)$ ；
第二层平均循环次数为 $\frac{N}{2}$ ，复杂度为 $O(N)$ ，推导过程如下：

$$ O(\frac{N}{2}) = O(\frac{1}{2})O(N) = O(1)O(N) = O(N) $$

因此，冒泡排序的总体时间复杂度为 $O(N^2)$ ，代码如下所示。

Python

def bubble_sort(nums):
    N = len(nums)
    for i in range(N - 1):
        for j in range(N - 1 - i):
            if nums[j] > nums[j + 1]:
                nums[j], nums[j + 1] = nums[j + 1], nums[j]
    return nums

Java

int[] bubbleSort(int[] nums) {
    int N = nums.length;
    for (int i = 0; i < N - 1; i++) {
        for (int j = 0; j < N - 1 - i; j++) {
            if (nums[j] > nums[j + 1]) {
                int tmp = nums[j];
                nums[j] = nums[j + 1];
                nums[j + 1] = tmp;
            }
        }
    }
    return nums;
}

C++

vector<int> bubbleSort(vector<int>& nums) {
    int N = nums.size();
    for (int i = 0; i < N - 1; i++) {
        for (int j = 0; j < N - 1 - i; j++) {
            if (nums[j] > nums[j + 1]) {
                swap(nums[j], nums[j + 1]);
            }
        }
    }
    return nums;
}

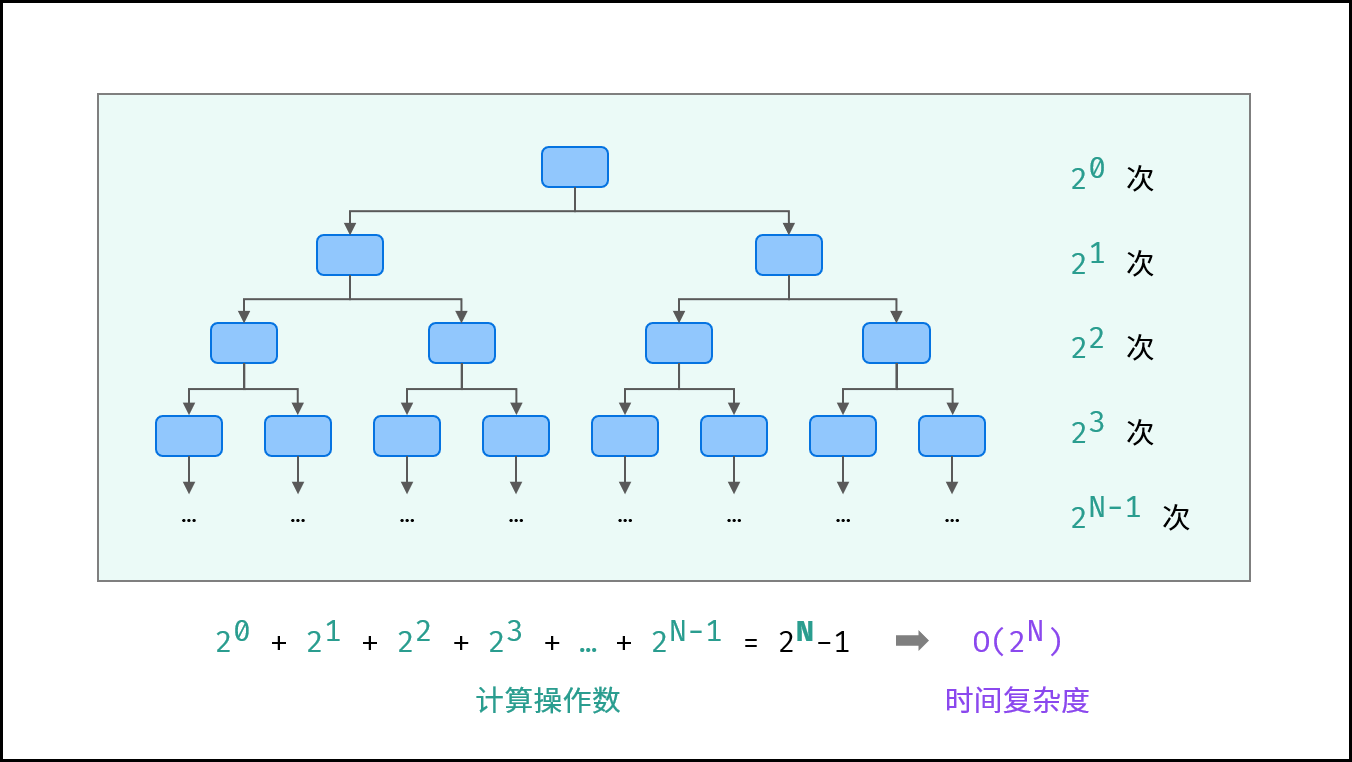
指数 $O(2^N)$ ：

生物学科中的 “细胞分裂” 即是指数级增长。初始状态为 $1$ 个细胞，分裂一轮后为 $2$ 个，分裂两轮后为 $4$ 个，……，分裂 $N$ 轮后有 $2^N$ 个细胞。

算法中，指数阶常出现于递归，算法原理图与代码如下所示。

Python

def algorithm(N):
    if N <= 0: return 1
    count_1 = algorithm(N - 1)
    count_2 = algorithm(N - 1)
    return count_1 + count_2

Java

int algorithm(int N) {
    if (N <= 0) return 1;
    int count_1 = algorithm(N - 1);
    int count_2 = algorithm(N - 1);
    return count_1 + count_2;
}

C++

int algorithm(int N) {
    if (N <= 0) return 1;
    int count_1 = algorithm(N - 1);
    int count_2 = algorithm(N - 1);
    return count_1 + count_2;
}

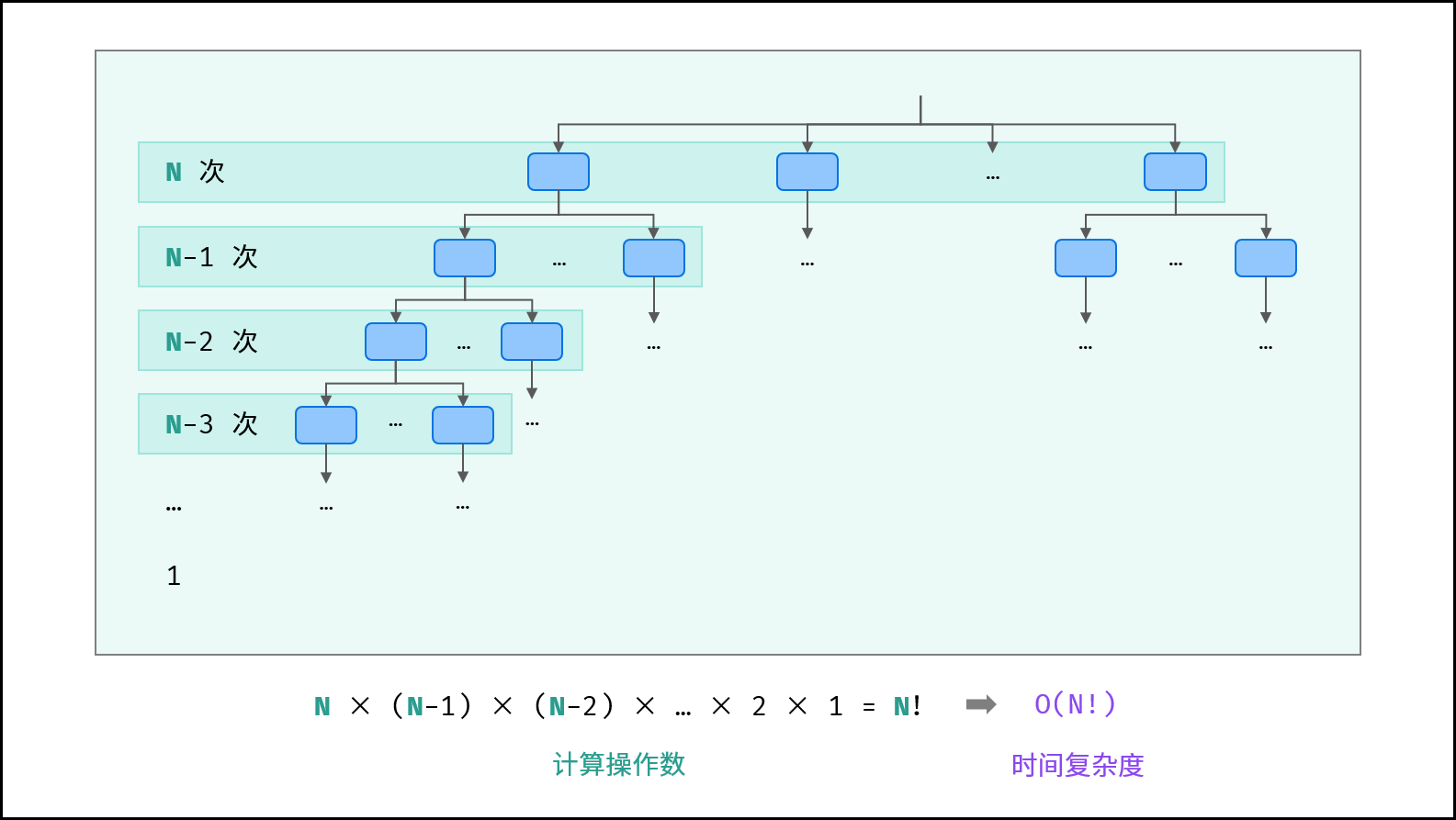
阶乘 $O(N!)$ ：

阶乘阶对应数学上常见的 “全排列” 。即给定 $N$ 个互不重复的元素，求其所有可能的排列方案，则方案数量为：

$$ N \times (N - 1) \times (N - 2) \times \cdots \times 2 \times 1 = N! $$

如下图与代码所示，阶乘常使用递归实现，算法原理：第一层分裂出 $N$ 个，第二层分裂出 $N - 1$ 个，…… ，直至到第 $N$ 层时终止并回溯。

Python

def algorithm(N):
    if N <= 0: return 1
    count = 0
    for _ in range(N):
        count += algorithm(N - 1)
    return count

Java

int algorithm(int N) {
    if (N <= 0) return 1;
    int count = 0;
    for (int i = 0; i < N; i++) {
        count += algorithm(N - 1);
    }
    return count;
}

C++

int algorithm(int N) {
    if (N <= 0) return 1;
    int count = 0;
    for (int i = 0; i < N; i++) {
        count += algorithm(N - 1);
    }
    return count;
}

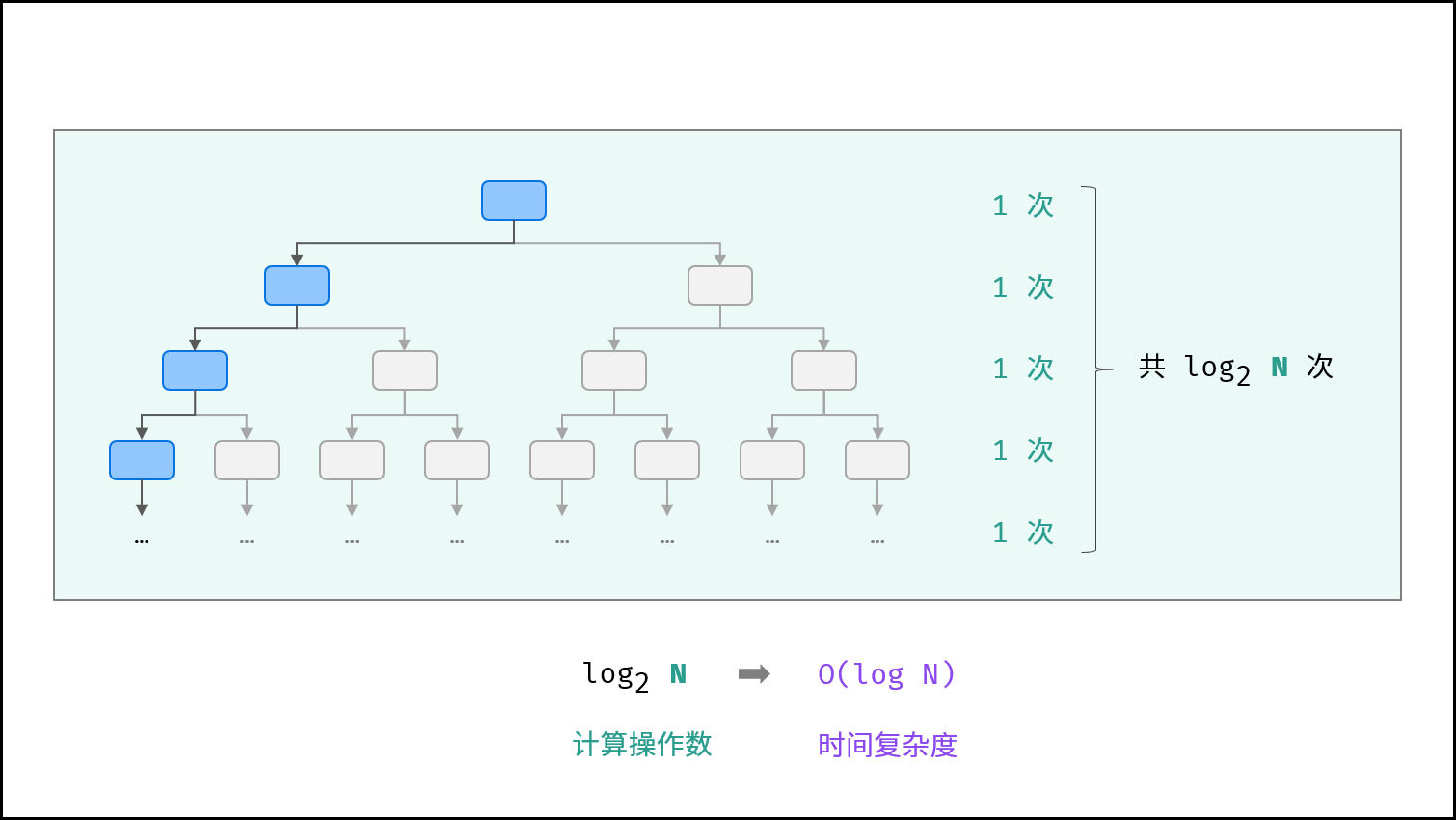
对数 $O(\log N)$ ：

对数阶与指数阶相反，指数阶为 “每轮分裂出两倍的情况” ，而对数阶是 “每轮排除一半的情况” 。对数阶常出现于「二分法」、「分治」等算法中，体现着 “一分为二” 或 “一分为多” 的算法思想。

设循环次数为 $m$ ，则输入数据大小 $N$ 与 $2 ^ m$ 呈线性关系，两边同时取 $log_2$ 对数，则得到循环次数 $m$ 与 $\log_2 N$ 呈线性关系，即时间复杂度为 $O(\log N)$ 。

Python

def algorithm(N):
    count = 0
    i = N
    while i > 1:
        i = i / 2
        count += 1
    return count

Java

int algorithm(int N) {
    int count = 0;
    float i = N;
    while (i > 1) {
        i = i / 2;
        count++;
    }
    return count;
}

C++

int algorithm(int N) {
    int count = 0;
    float i = N;
    while (i > 1) {
        i = i / 2;
        count++;
    }
    return count;
}

如以下代码所示，对于不同 $a$ 的取值，循环次数 $m$ 与 $\log_a N$ 呈线性关系，时间复杂度为 $O(\log_a N)$ 。而无论底数 $a$ 取值，时间复杂度都可记作 $O(\log N)$ ，根据对数换底公式的推导如下：

$$ O(\log_a N) = \frac{O(\log_2 N)}{O(\log_2 a)} = O(\log N) $$

Python

def algorithm(N):
    count = 0
    i = N
    a = 3
    while i > 1:
        i = i / a
        count += 1
    return count

Java

int algorithm(int N) {
    int count = 0;
    float i = N;
    int a = 3;
    while (i > 1) {
        i = i / a;
        count++;
    }
    return count;
}

C++

int algorithm(int N) {
    int count = 0;
    float i = N;
    int a = 3;
    while (i > 1) {
        i = i / a;
        count++;
    }
    return count;
}

如下图所示，为二分查找的时间复杂度示意图，每次二分将搜索区间缩小一半。

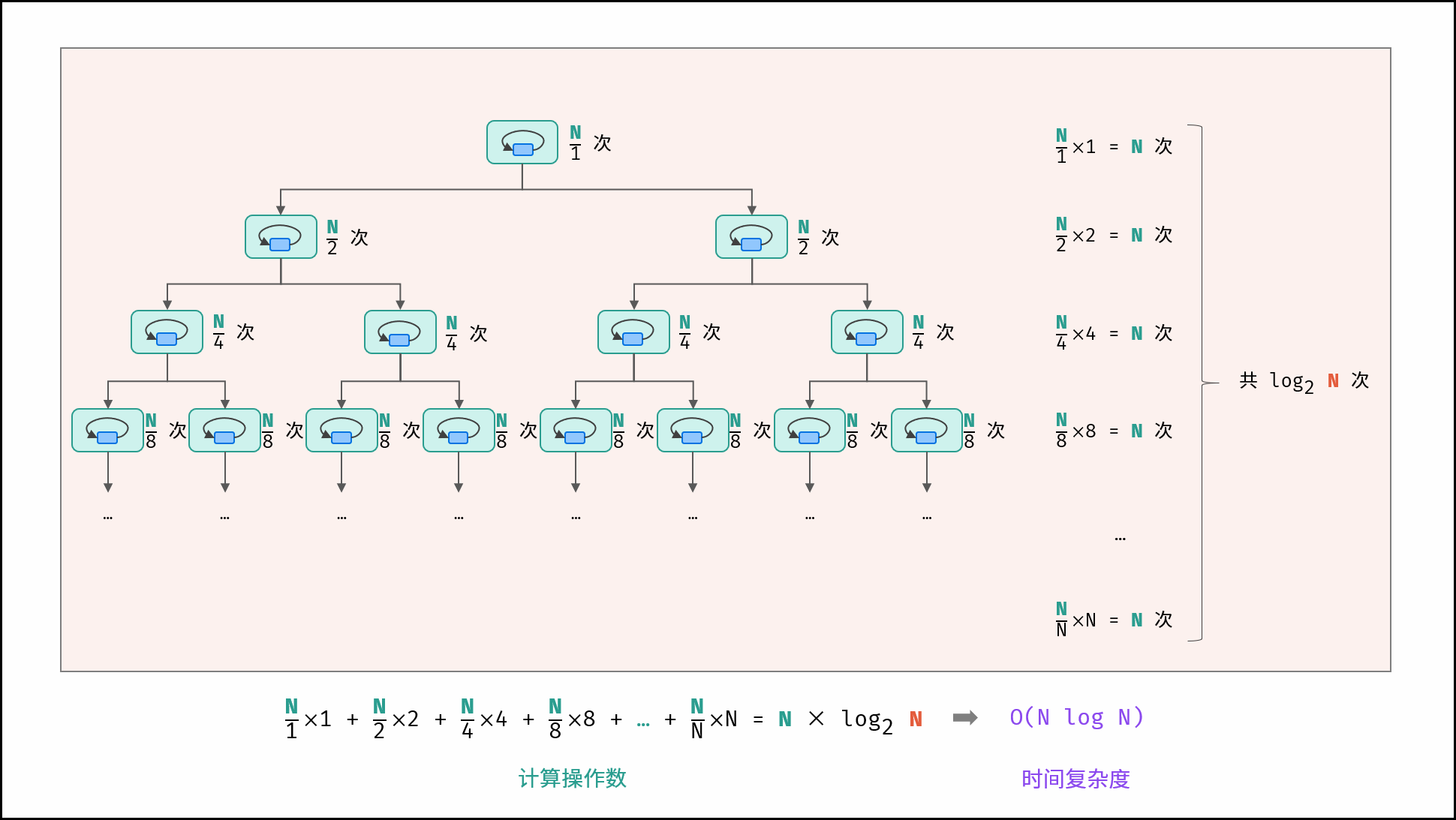
线性对数 $O(N \log N)$ ：

两层循环相互独立，第一层和第二层时间复杂度分别为 $O(\log N)$ 和 $O(N)$ ，则总体时间复杂度为 $O(N \log N)$ ；

Python

def algorithm(N):
    count = 0
    i = N
    while i > 1:
        i = i / 2
        for j in range(N):
            count += 1

Java

int algorithm(int N) {
    int count = 0;
    float i = N;
    while (i > 1) {
        i = i / 2;
        for (int j = 0; j < N; j++)
            count++;
    }
    return count;
}

C++

int algorithm(int N) {
    int count = 0;
    float i = N;
    while (i > 1) {
        i = i / 2;
        for (int j = 0; j < N; j++)
            count++;
    }
    return count;
}

线性对数阶常出现于排序算法，例如「快速排序」、「归并排序」、「堆排序」等，其时间复杂度原理如下图所示。

示例题目

以下列举本 LeetBook 中各时间复杂度的对应示例题解，以帮助加深理解。

时间复杂度	示例题解
$O(1)$	砍竹子 I、文物朝代判断
$O(\log N)$	Pow(x, n)、统计目标成绩的出现次数
$O(N)$	训练计划 III、斐波那契数
$O(N \log N)$	破解闯关密码、交易逆序对的总数
$O(N^2)$	验证二叉搜索树的后序遍历序列、招式拆解 I
$O(N!)$	套餐内商品的排列顺序

时间复杂度 ​

符号表示 ​

常见种类 ​

常数 $O(1)$ ： ​

线性 $O(N)$ ： ​

平方 $O(N^2)$ ： ​

指数 $O(2^N)$ ： ​

阶乘 $O(N!)$ ： ​

对数 $O(\log N)$ ： ​

线性对数 $O(N \log N)$ ： ​

示例题目 ​

时间复杂度

符号表示

常见种类

常数 $O(1)$ ：

线性 $O(N)$ ：

平方 $O(N^2)$ ：

指数 $O(2^N)$ ：

阶乘 $O(N!)$ ：

对数 $O(\log N)$ ：

线性对数 $O(N \log N)$ ：

示例题目