自律小屋 | 自律小屋

方法一：递归

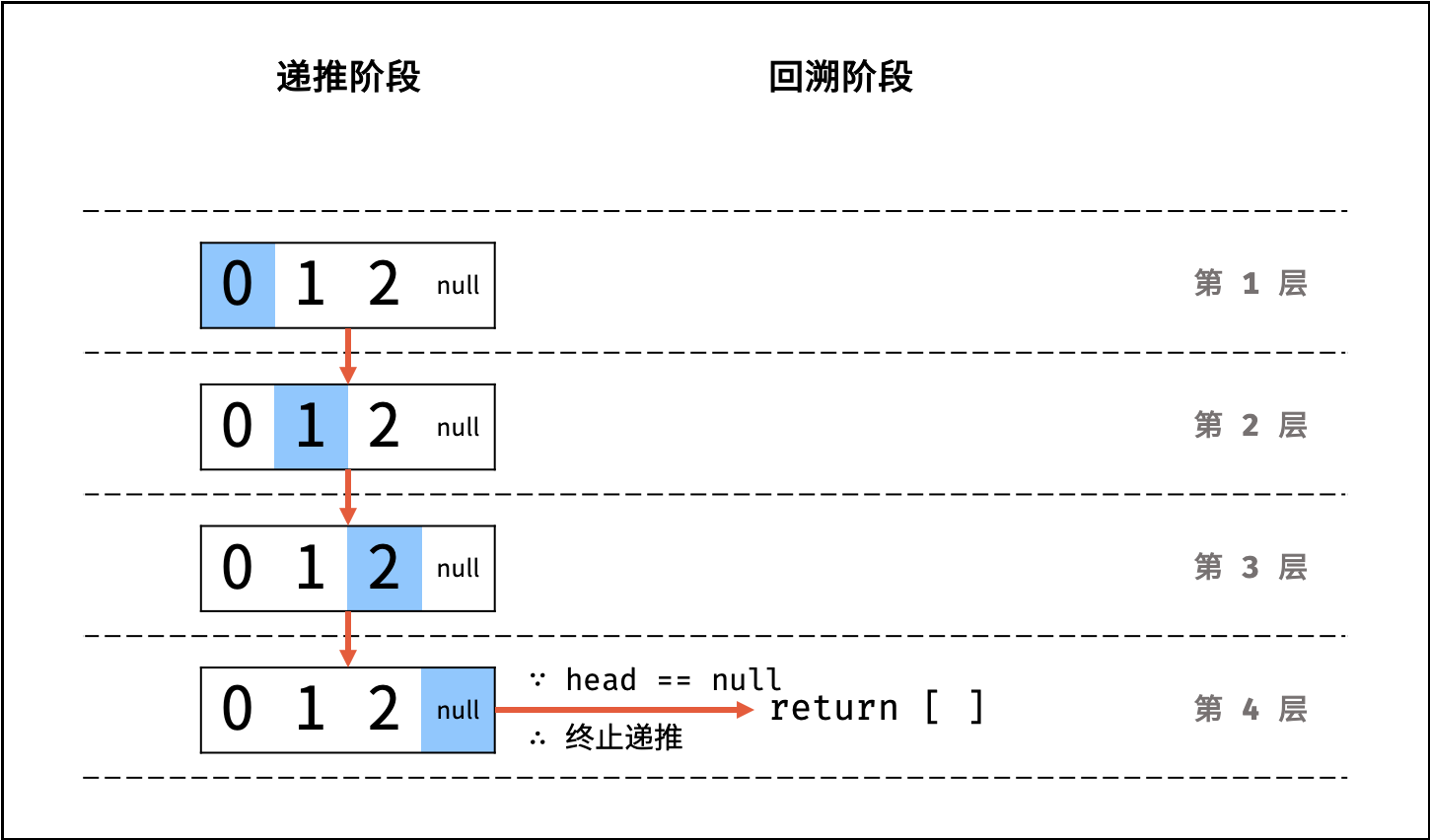
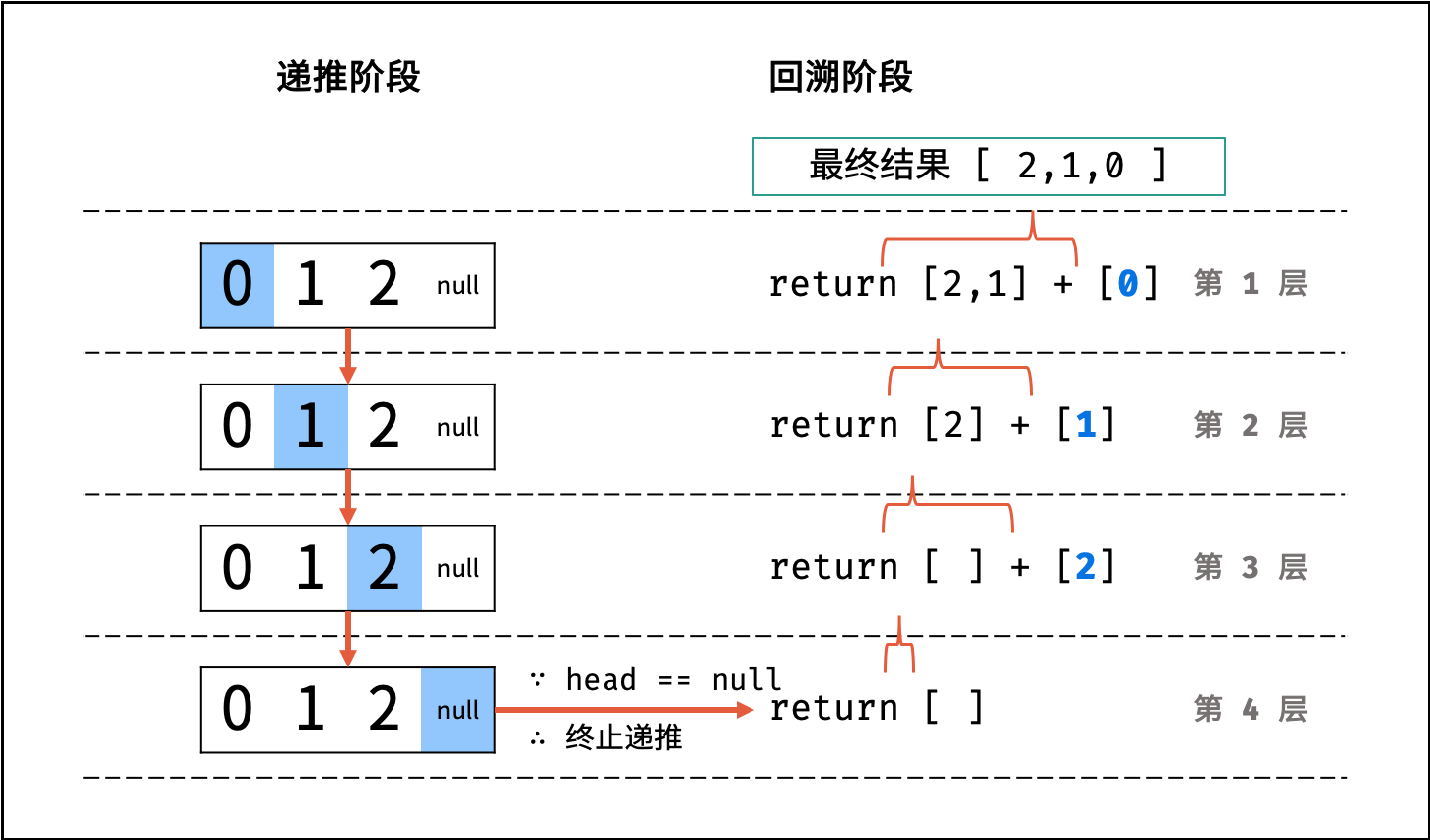
利用递归，先递推至链表末端；回溯时，依次将节点值加入列表，即可实现链表值的倒序输出。

终止条件： 当 head == None 时，代表越过了链表尾节点，则返回空列表；
递推工作： 访问下一节点 head.next ；
回溯阶段：
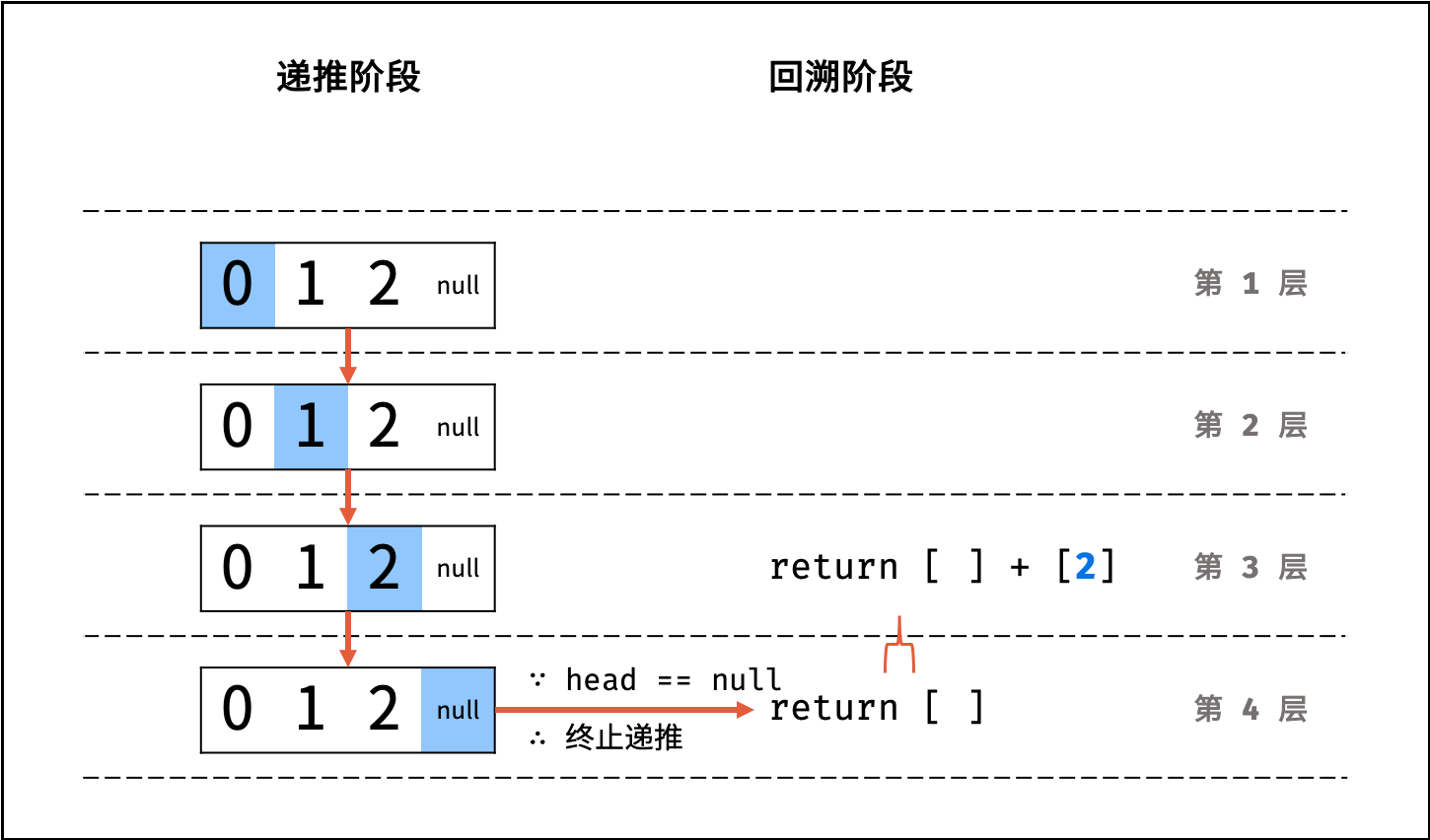
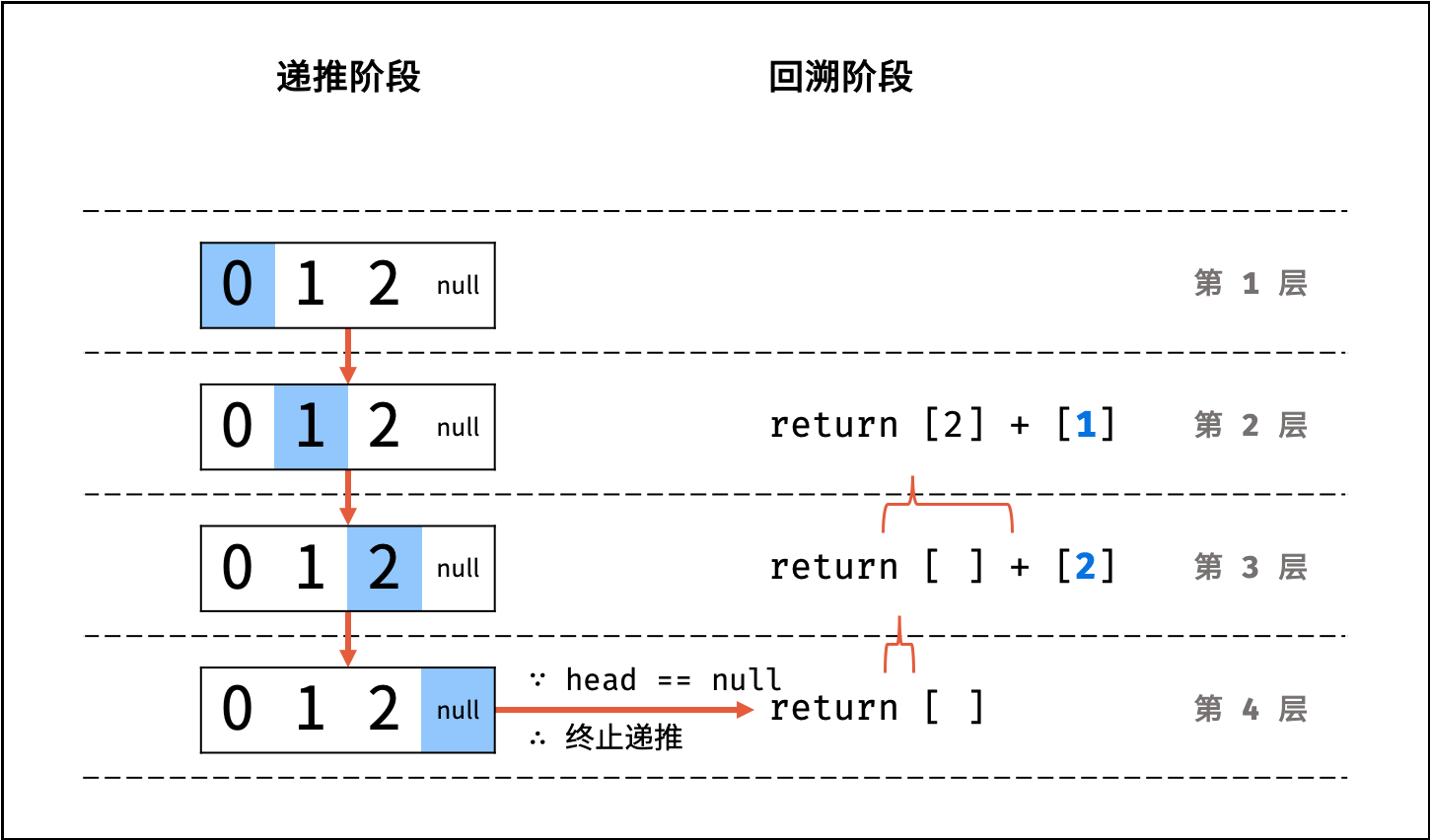
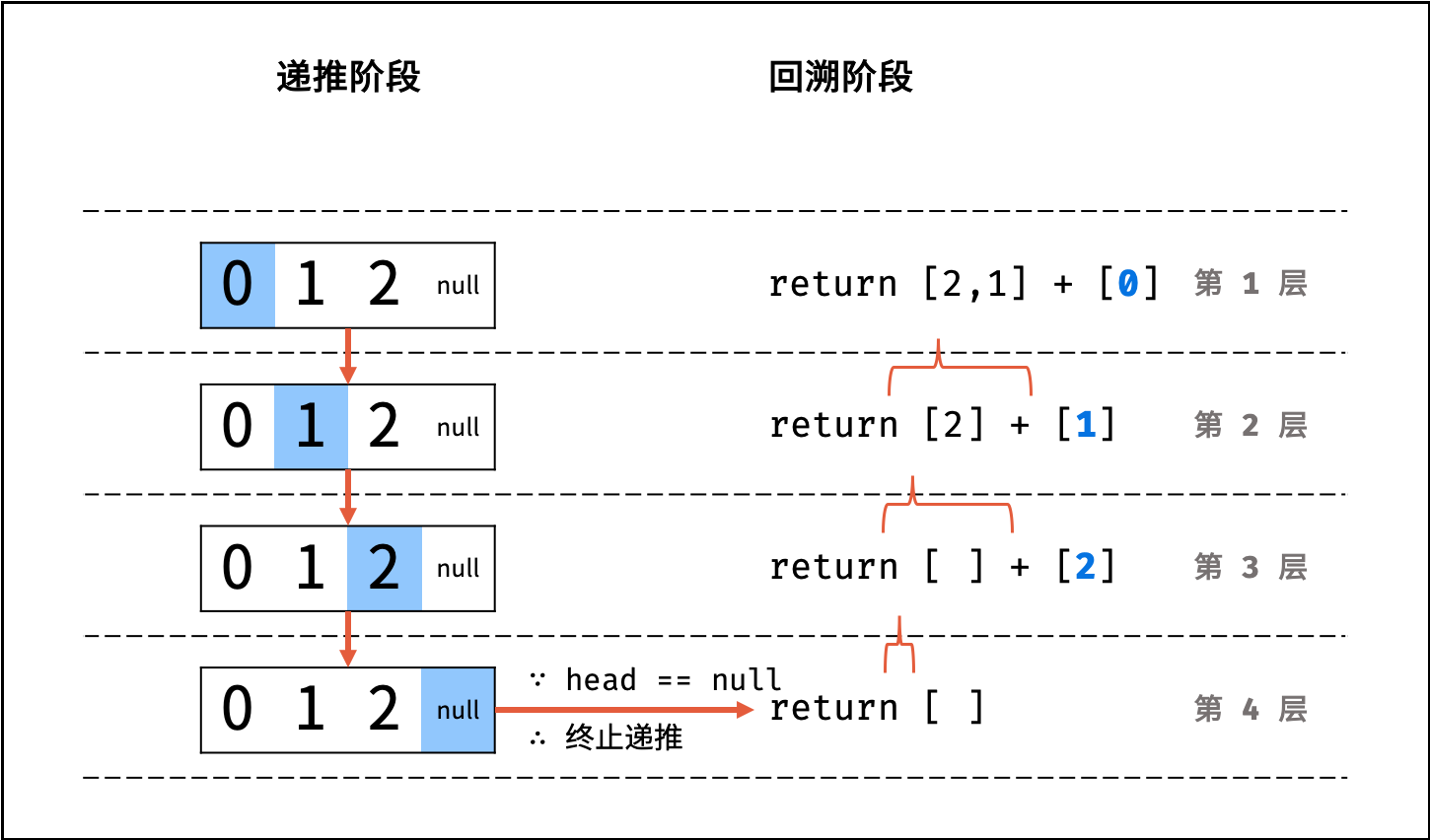
- Python： 返回 当前 list + 当前节点值 [head.val] ；
- Java / C++： 将当前节点值 head.val 加入列表 tmp ；

<,,,,,,,,>

代码：

Python

class Solution:
    def reverseBookList(self, head: Optional[ListNode]) -> List[int]:
        return self.reverseBookList(head.next) + [head.val] if head else []

Java

class Solution {
    ArrayList<Integer> tmp = new ArrayList<Integer>();
    public int[] reverseBookList(ListNode head) {
        recur(head);
        int[] res = new int[tmp.size()];
        for(int i = 0; i < res.length; i++)
            res[i] = tmp.get(i);
        return res;
    }
    void recur(ListNode head) {
        if(head == null) return;
        recur(head.next);
        tmp.add(head.val);
    }
}

C++

class Solution {
public:
    vector<int> reverseBookList(ListNode* head) {
        recur(head);
        return res;
    }
private:
    vector<int> res;
    void recur(ListNode* head) {
        if(head == nullptr) return;
        recur(head->next);
        res.push_back(head->val);
    }
};

复杂度分析：

时间复杂度 $O(N)$： 遍历链表，递归 $N$ 次。
空间复杂度 $O(N)$： 系统递归需要使用 $O(N)$ 的栈空间。

方法二：辅助栈法

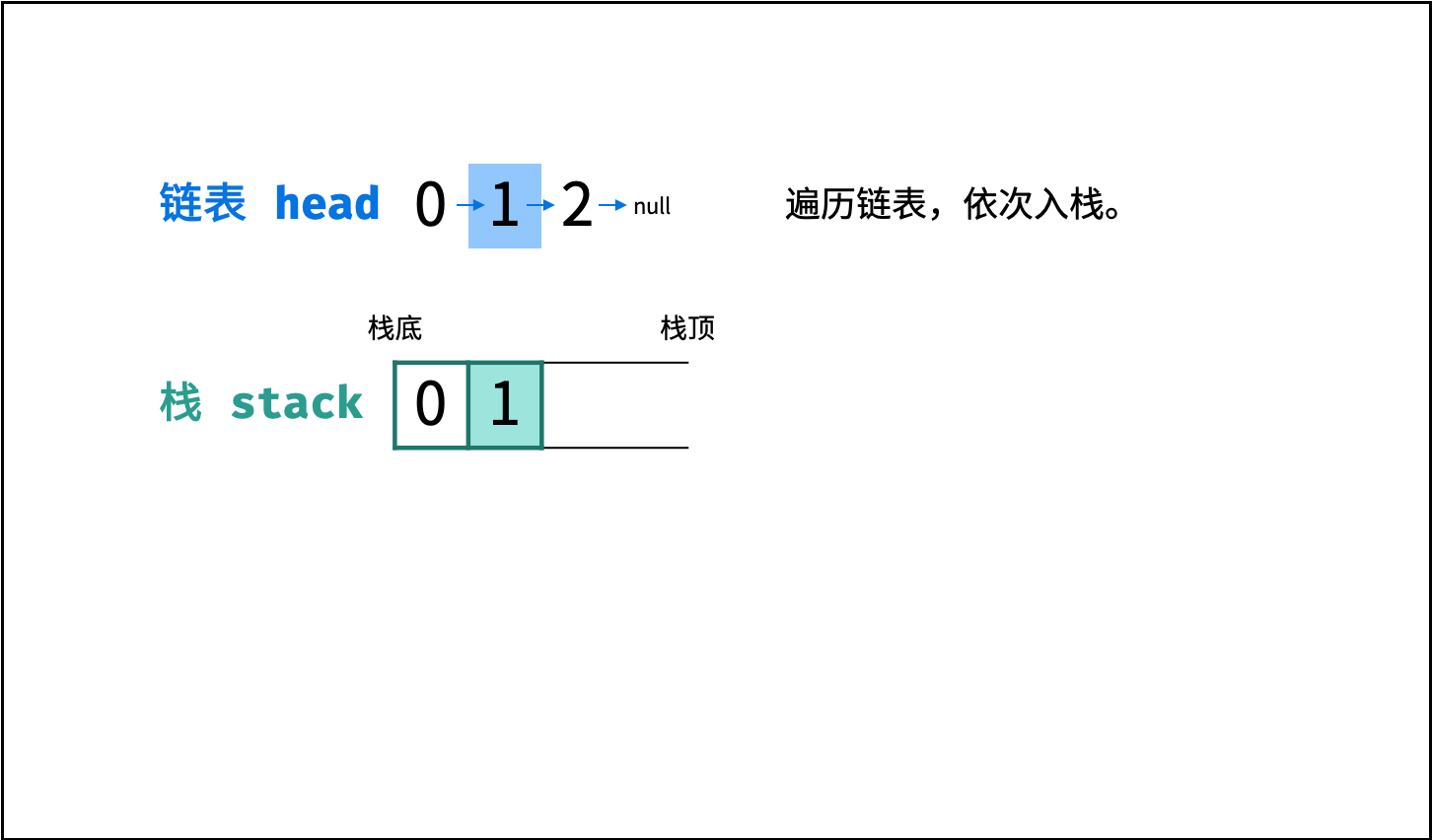
链表只能 从前至后 访问每个节点，而题目要求 倒序输出 各节点值，这种 先入后出 的需求可以借助栈来实现。

算法流程：

入栈： 遍历链表，将各节点值 push 入栈。
出栈： 将各节点值 pop 出栈，存储于数组并返回。

图解以 Java 代码为例，Python 无需将 stack 转移至 res，而是直接返回倒序数组。

<,,,,,,,>

代码：

Java 数组长度不可变，因此使用 List 先存储，再转为数组并返回。

Python

class Solution:
    def reverseBookList(self, head: ListNode) -> List[int]:
        stack = []
        while head:
            stack.append(head.val)
            head = head.next
        return stack[::-1]

Java

class Solution {
    public int[] reverseBookList(ListNode head) {
        LinkedList<Integer> stack = new LinkedList<Integer>();
        while(head != null) {
            stack.addLast(head.val);
            head = head.next;
        }
        int[] res = new int[stack.size()];
        for(int i = 0; i < res.length; i++)
            res[i] = stack.removeLast();
    return res;
    }
}

C++

class Solution {
public:
    vector<int> reverseBookList(ListNode* head) {
        stack<int> stk;
        while(head != nullptr) {
            stk.push(head->val);
            head = head->next;
        }
        vector<int> res;
        while(!stk.empty()) {
            res.push_back(stk.top());
            stk.pop();
        }
        return res;
    }
};

复杂度分析：

时间复杂度 $O(N)$： 入栈和出栈共使用 $O(N)$ 时间。
空间复杂度 $O(N)$： 辅助栈 stack 和数组 res 共使用 $O(N)$ 的额外空间。

方法一：递归 ​

代码： ​

复杂度分析： ​

方法二：辅助栈法 ​

算法流程： ​

代码： ​

复杂度分析： ​

方法一：递归

代码：

复杂度分析：

方法二：辅助栈法

算法流程：

代码：

复杂度分析：