解题思路:
如下图所示,题目要求将链表反转。本文介绍迭代(双指针)、递归两种实现方法。
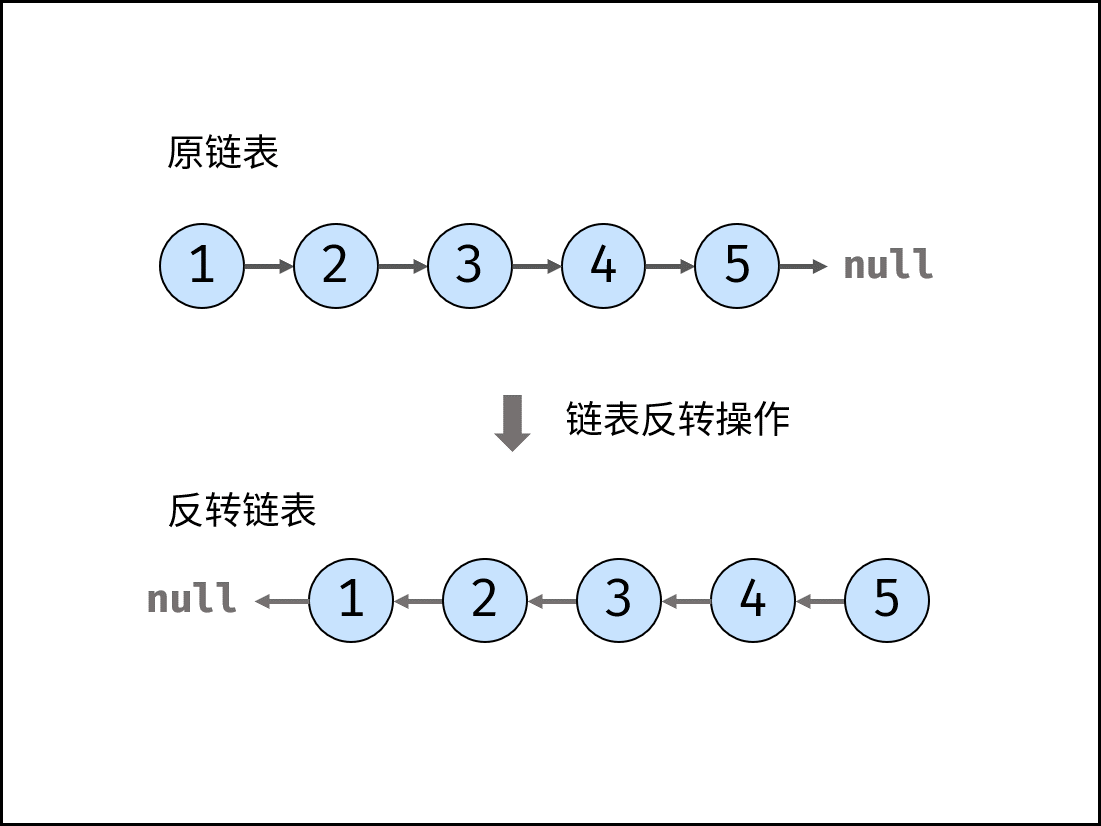
方法一:迭代(双指针)
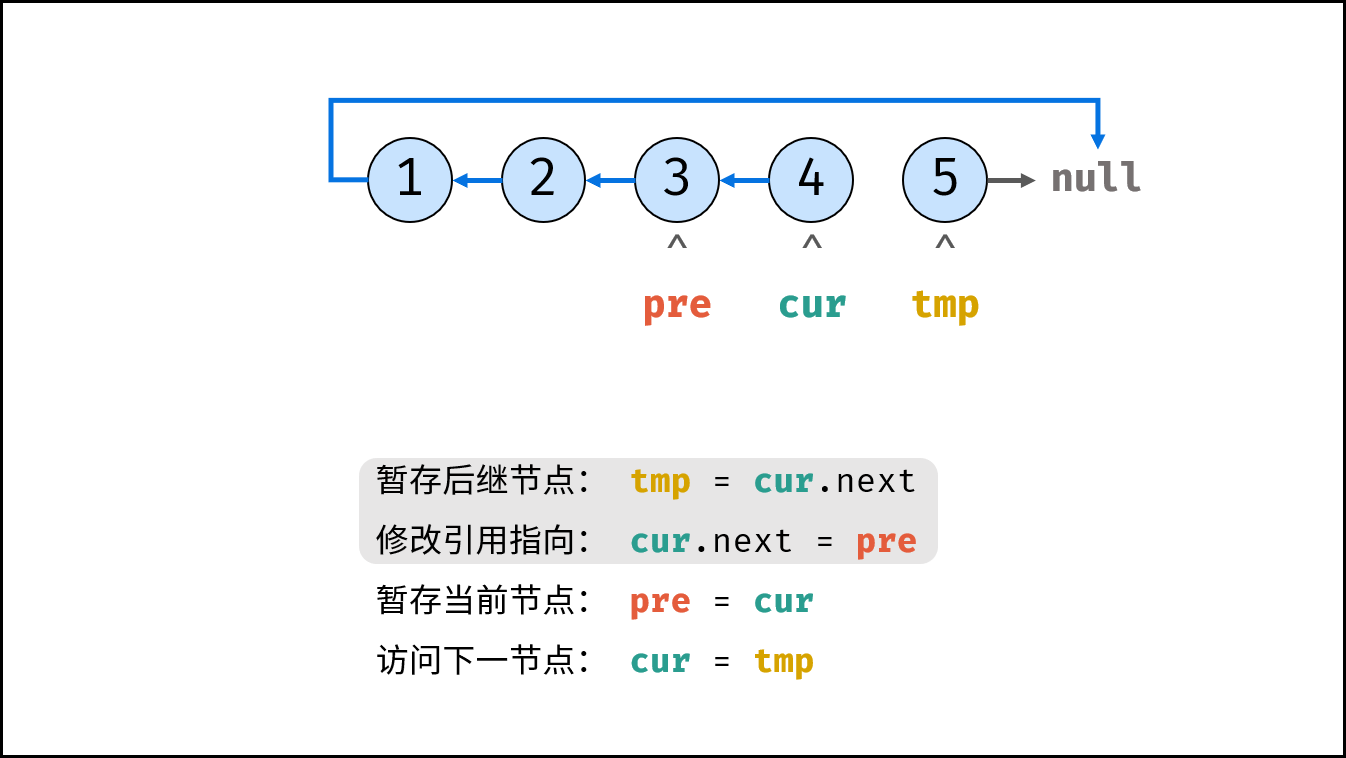
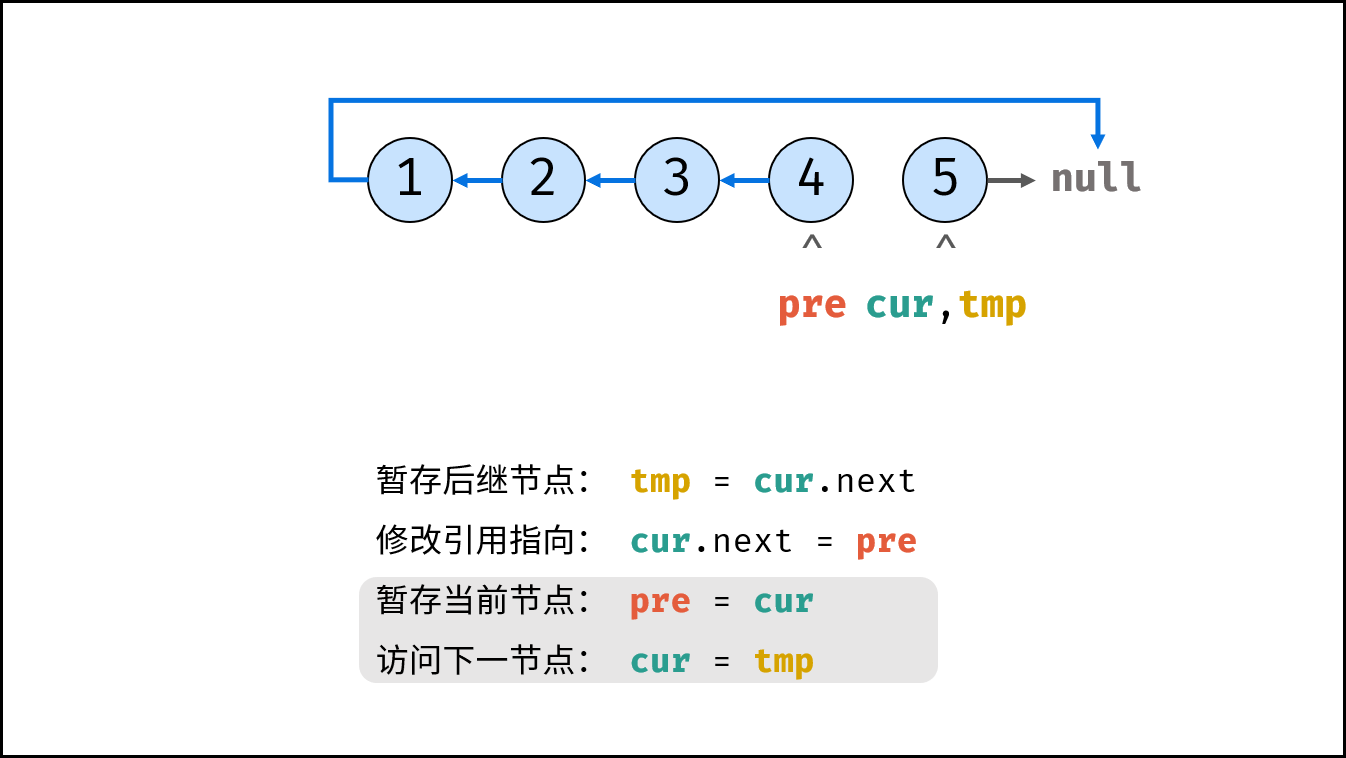
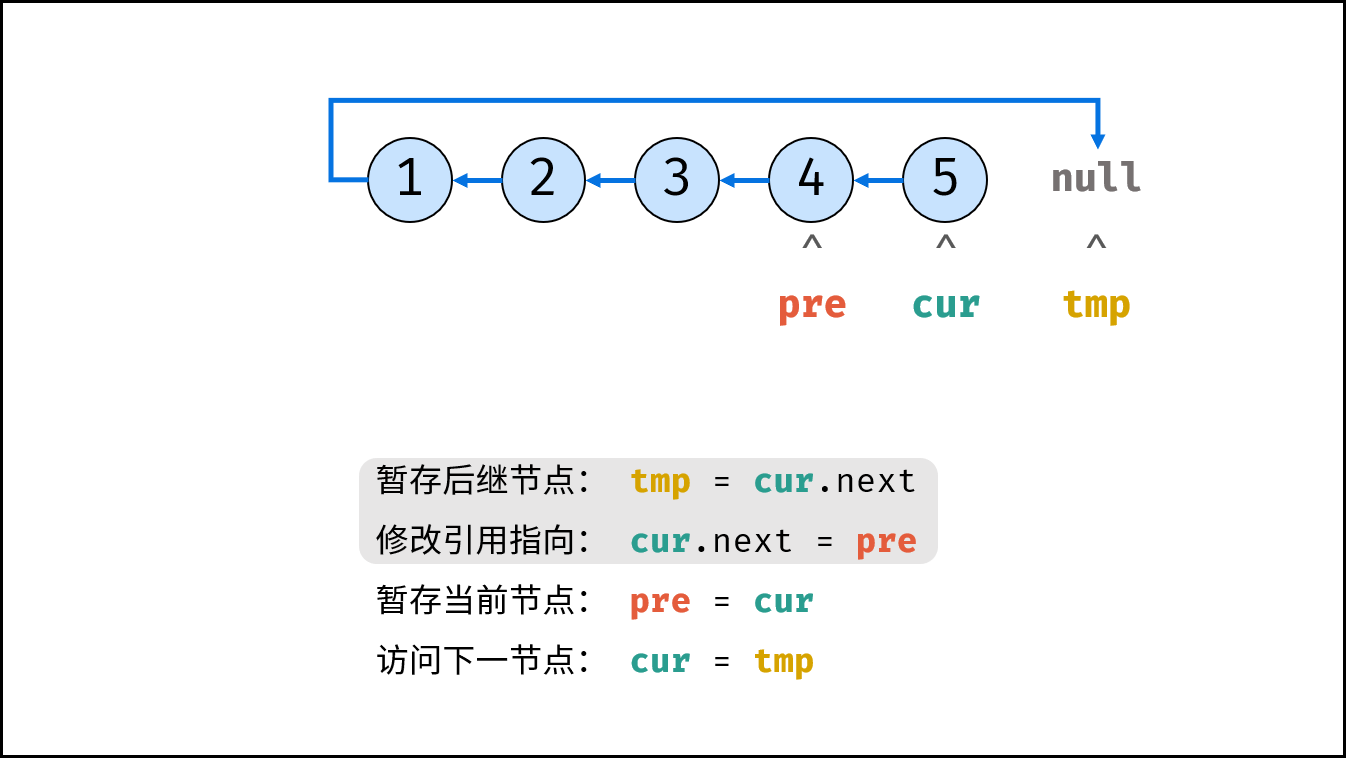
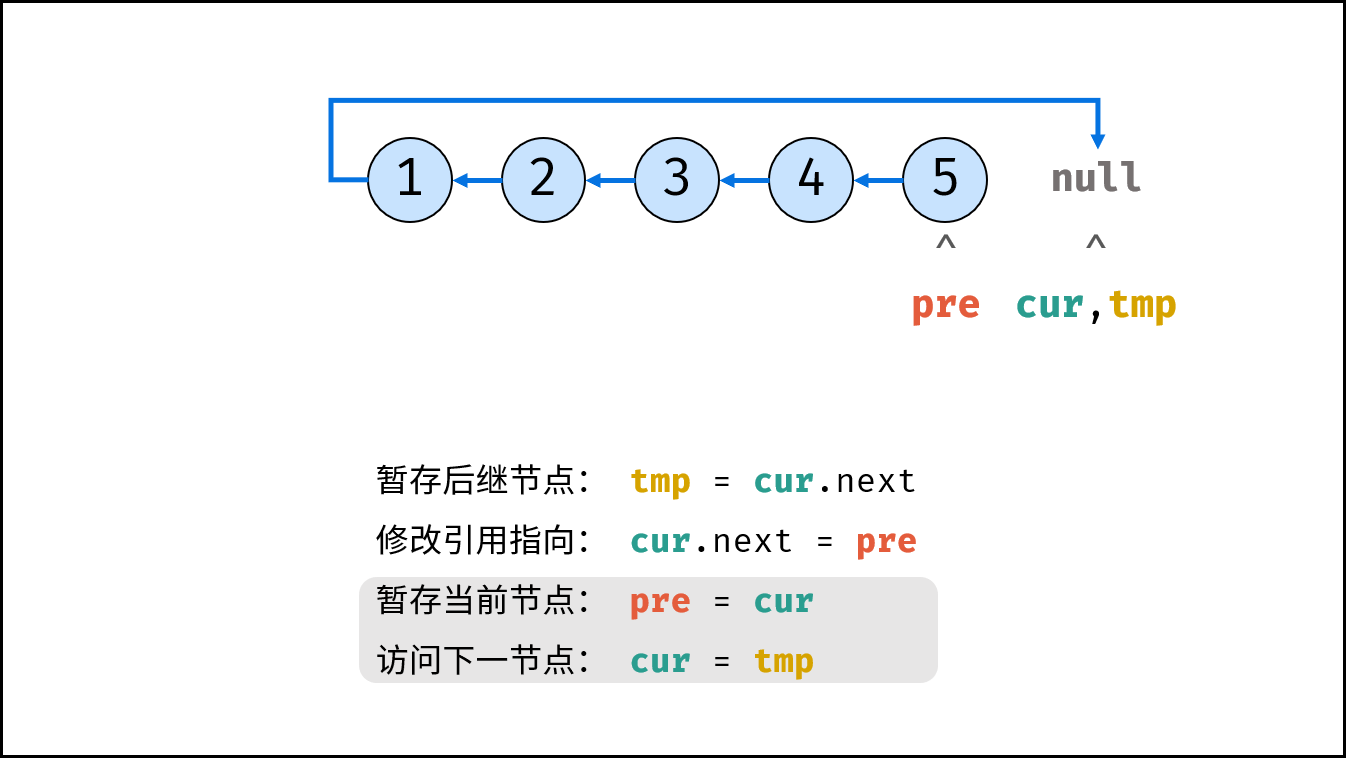
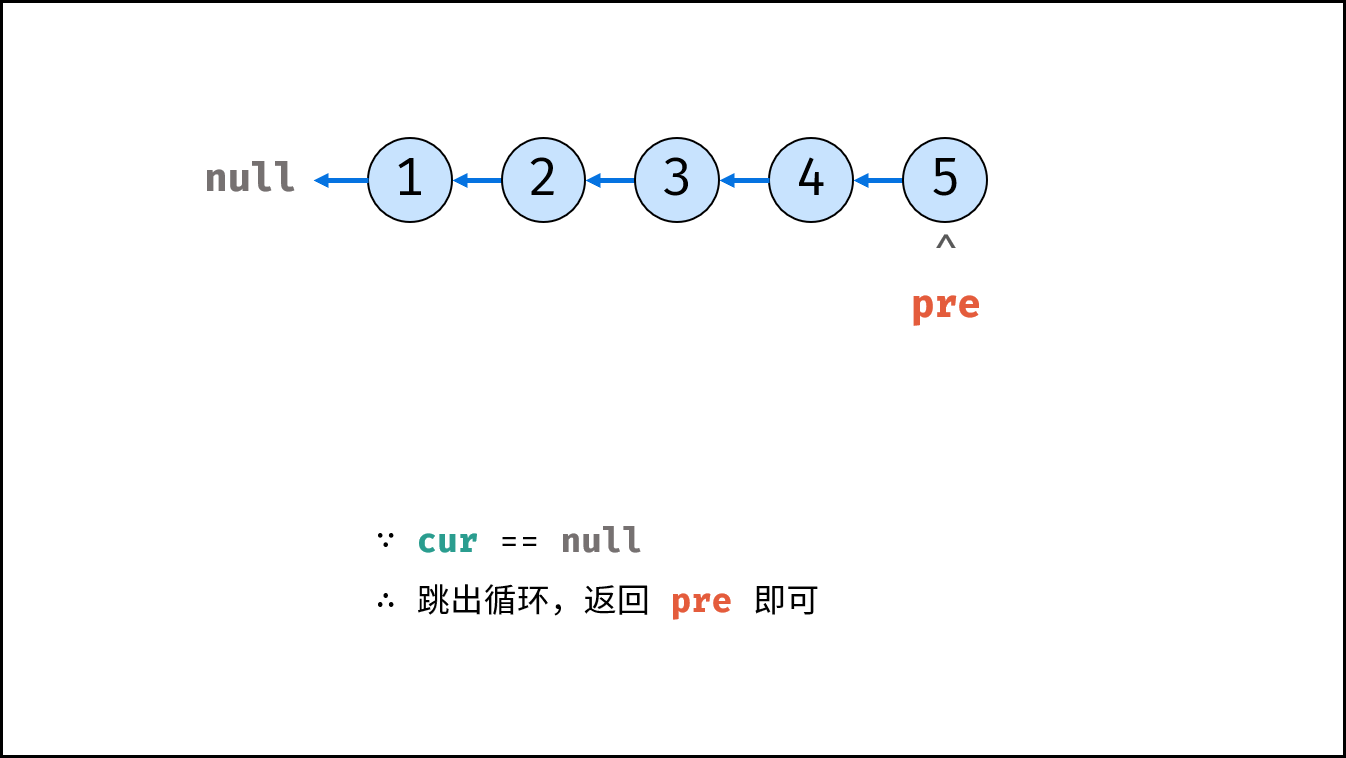
考虑遍历链表,并在访问各节点时修改 next 引用指向,算法流程见注释。
<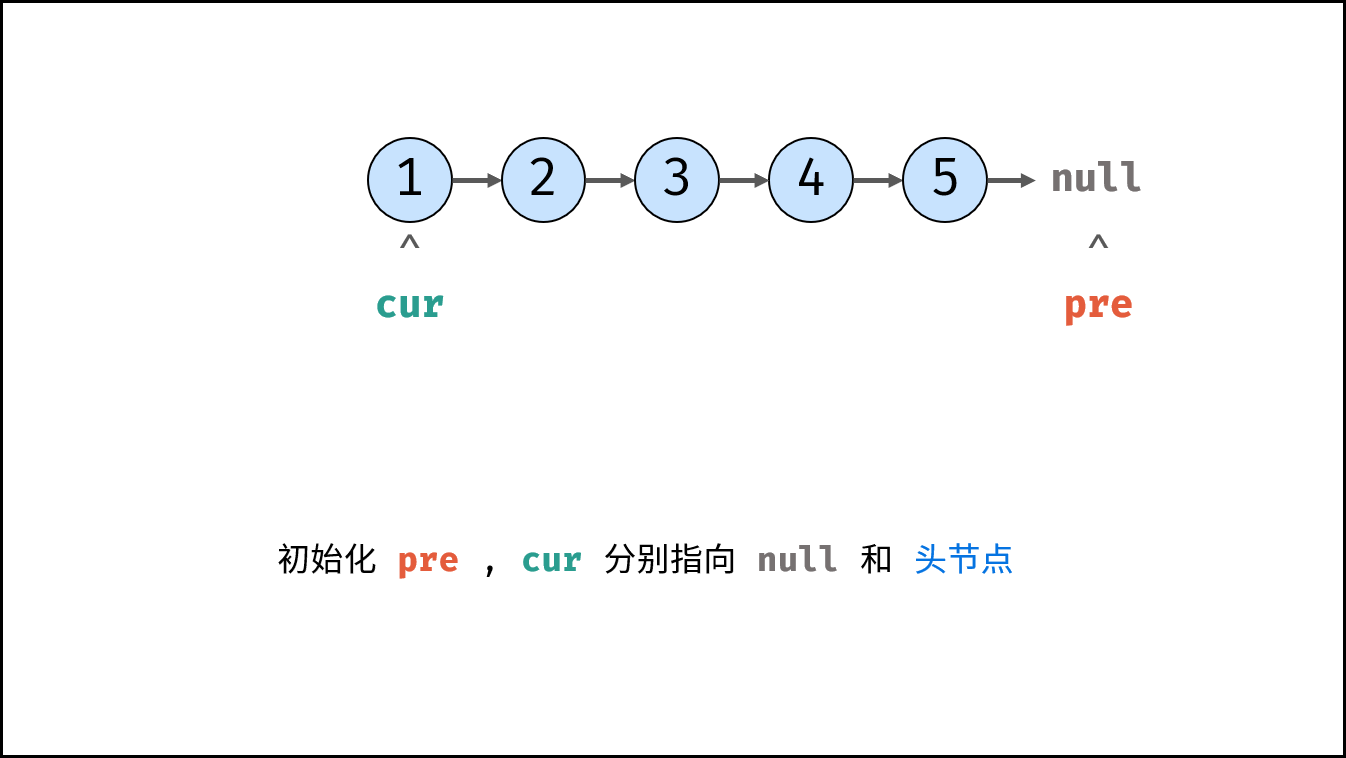 ,
,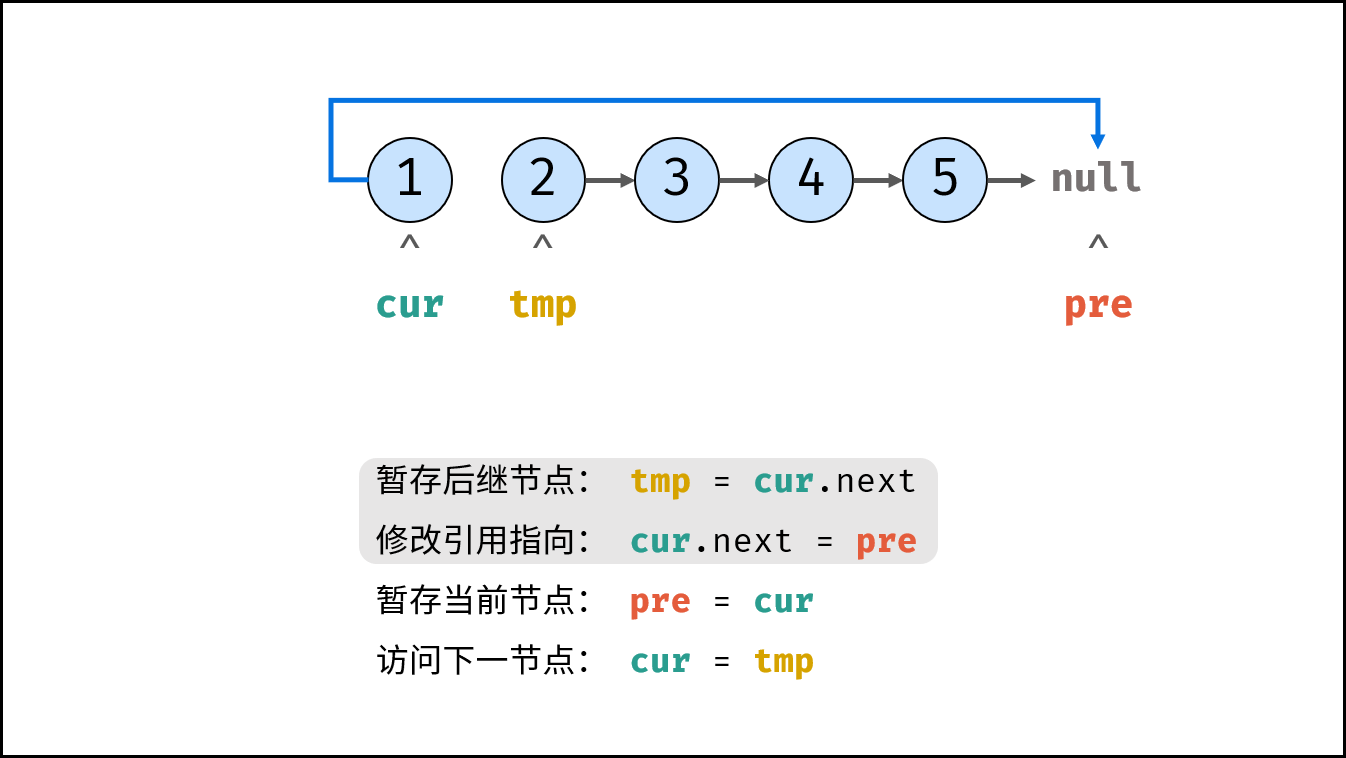 ,
,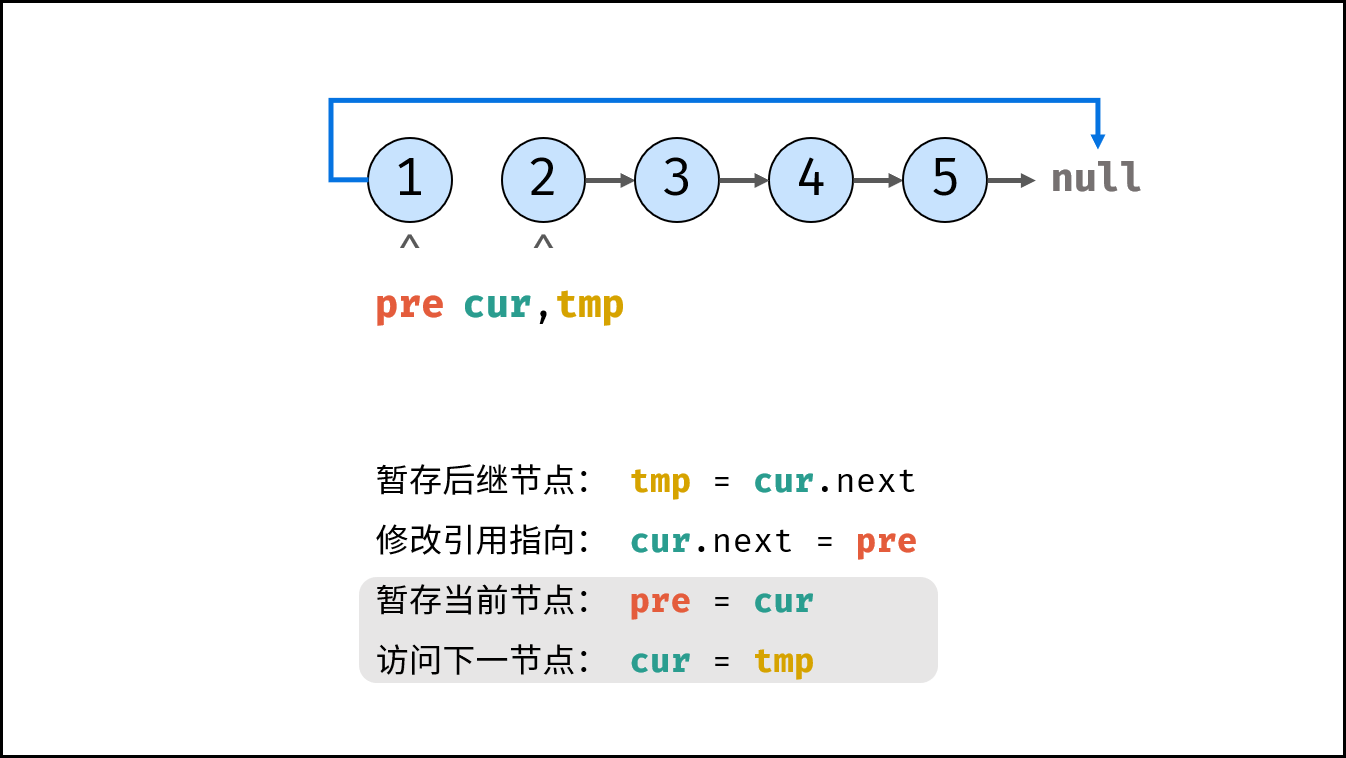 ,
,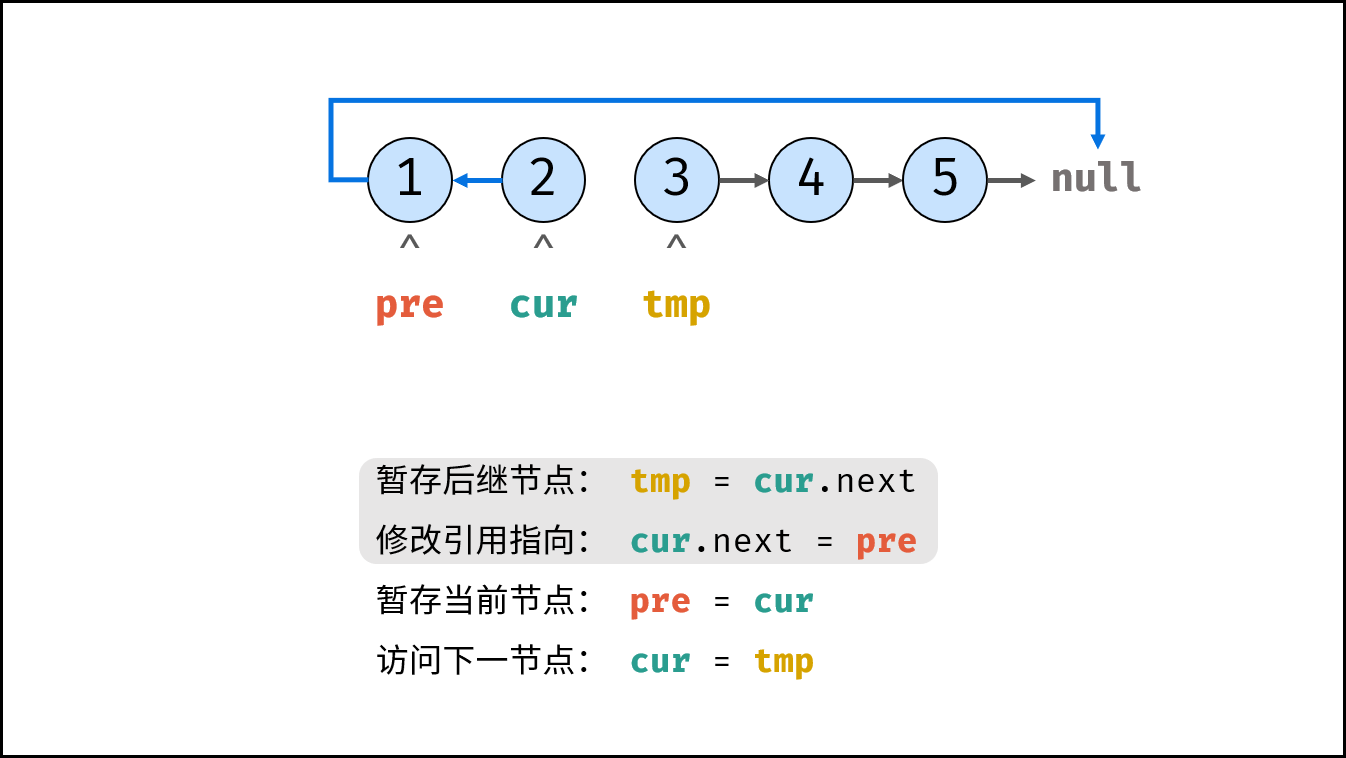 ,
,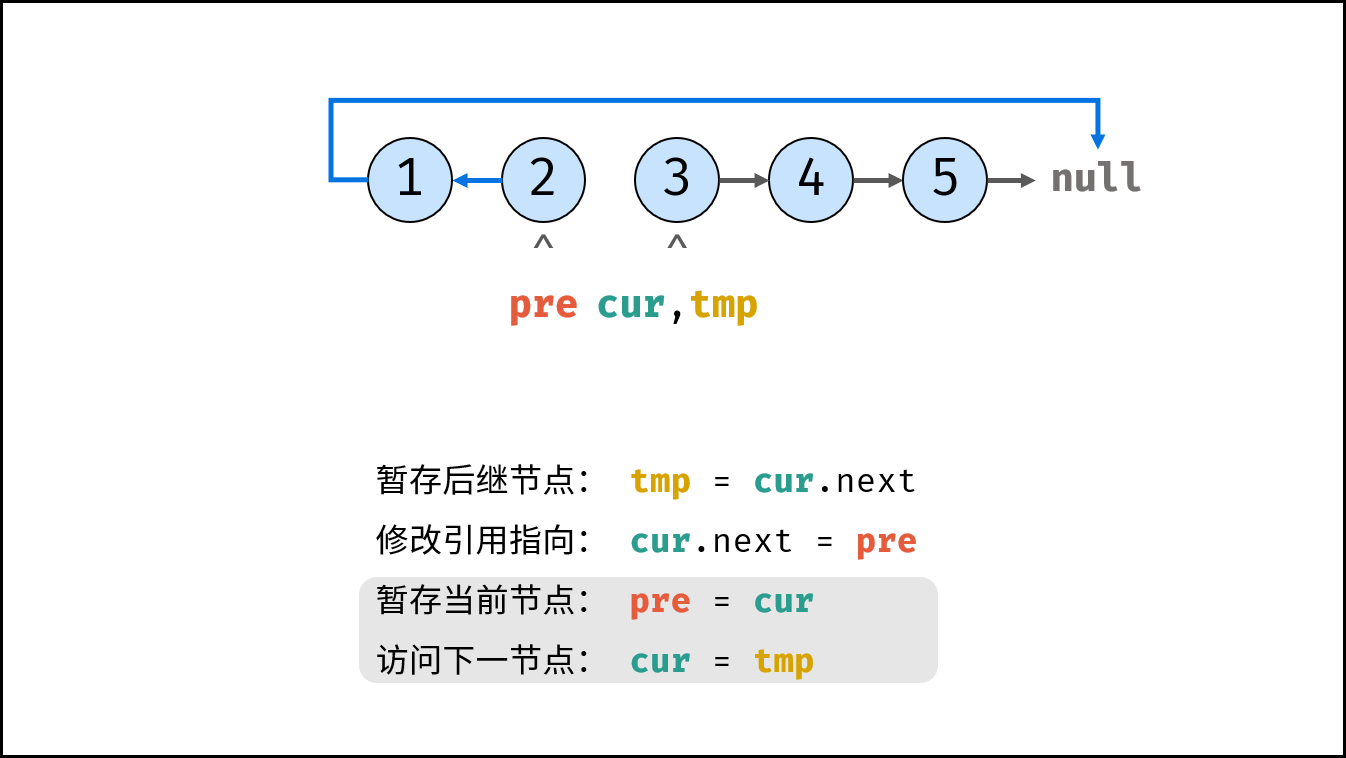 ,
,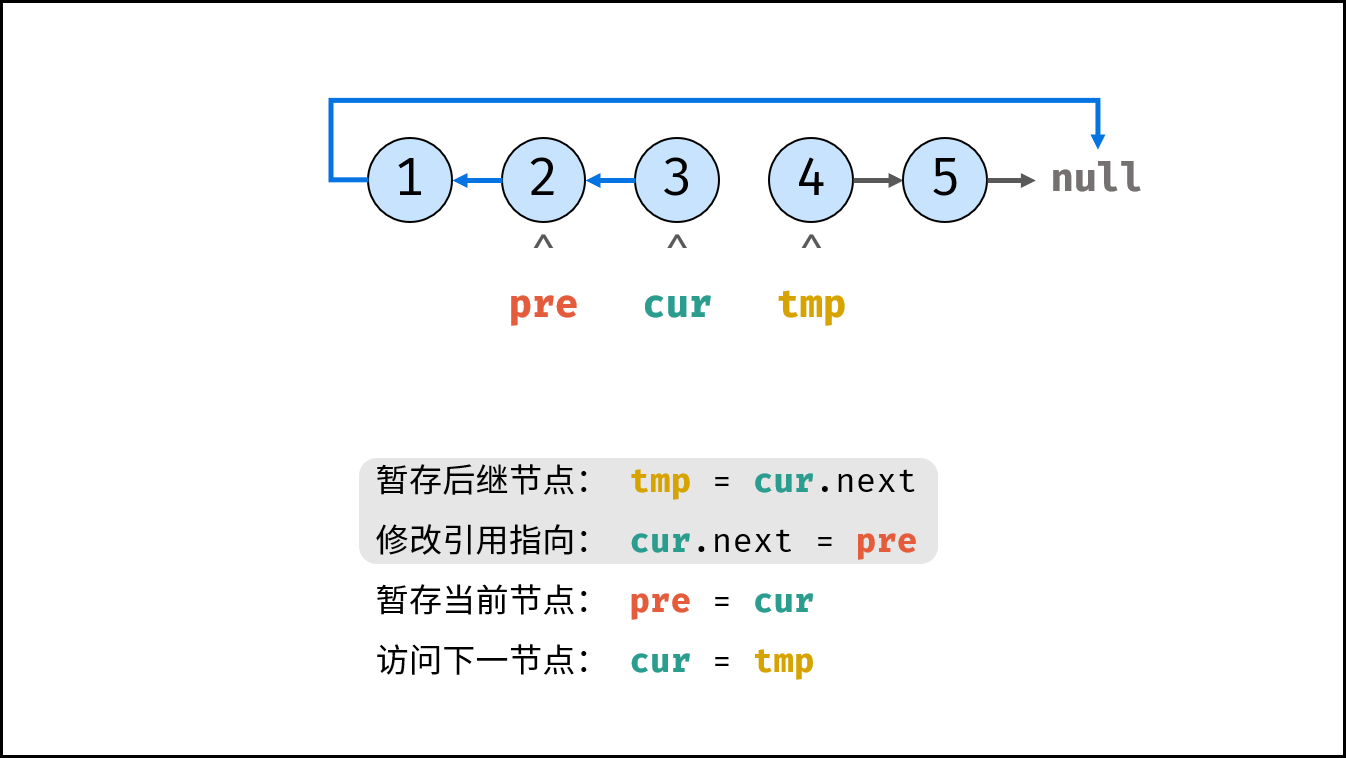 ,
,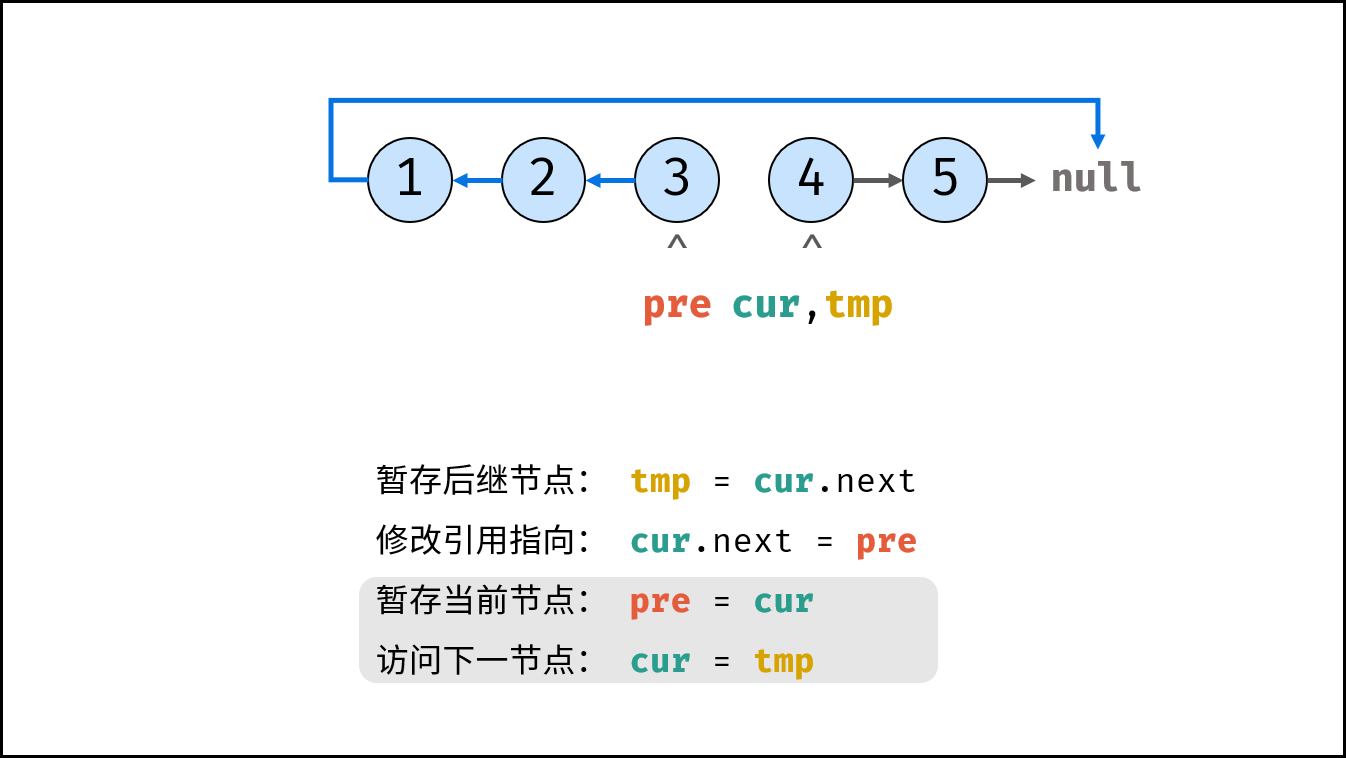 ,
, ,
, ,
, ,
, ,
, >
>
代码:
Python
class Solution:
def trainningPlan(self, head: ListNode) -> ListNode:
cur, pre = head, None
while cur:
tmp = cur.next # 暂存后继节点 cur.next
cur.next = pre # 修改 next 引用指向
pre = cur # pre 暂存 cur
cur = tmp # cur 访问下一节点
return preJava
class Solution {
public ListNode trainningPlan(ListNode head) {
ListNode cur = head, pre = null;
while(cur != null) {
ListNode tmp = cur.next; // 暂存后继节点 cur.next
cur.next = pre; // 修改 next 引用指向
pre = cur; // pre 暂存 cur
cur = tmp; // cur 访问下一节点
}
return pre;
}
}C++
class Solution {
public:
ListNode* trainningPlan(ListNode* head) {
ListNode *cur = head, *pre = nullptr;
while(cur != nullptr) {
ListNode* tmp = cur->next; // 暂存后继节点 cur.next
cur->next = pre; // 修改 next 引用指向
pre = cur; // pre 暂存 cur
cur = tmp; // cur 访问下一节点
}
return pre;
}
};复杂度分析:
- 时间复杂度 $O(N)$ : 遍历链表使用线性大小时间。
- 空间复杂度 $O(1)$ : 变量
pre和cur使用常数大小额外空间。
方法二:递归
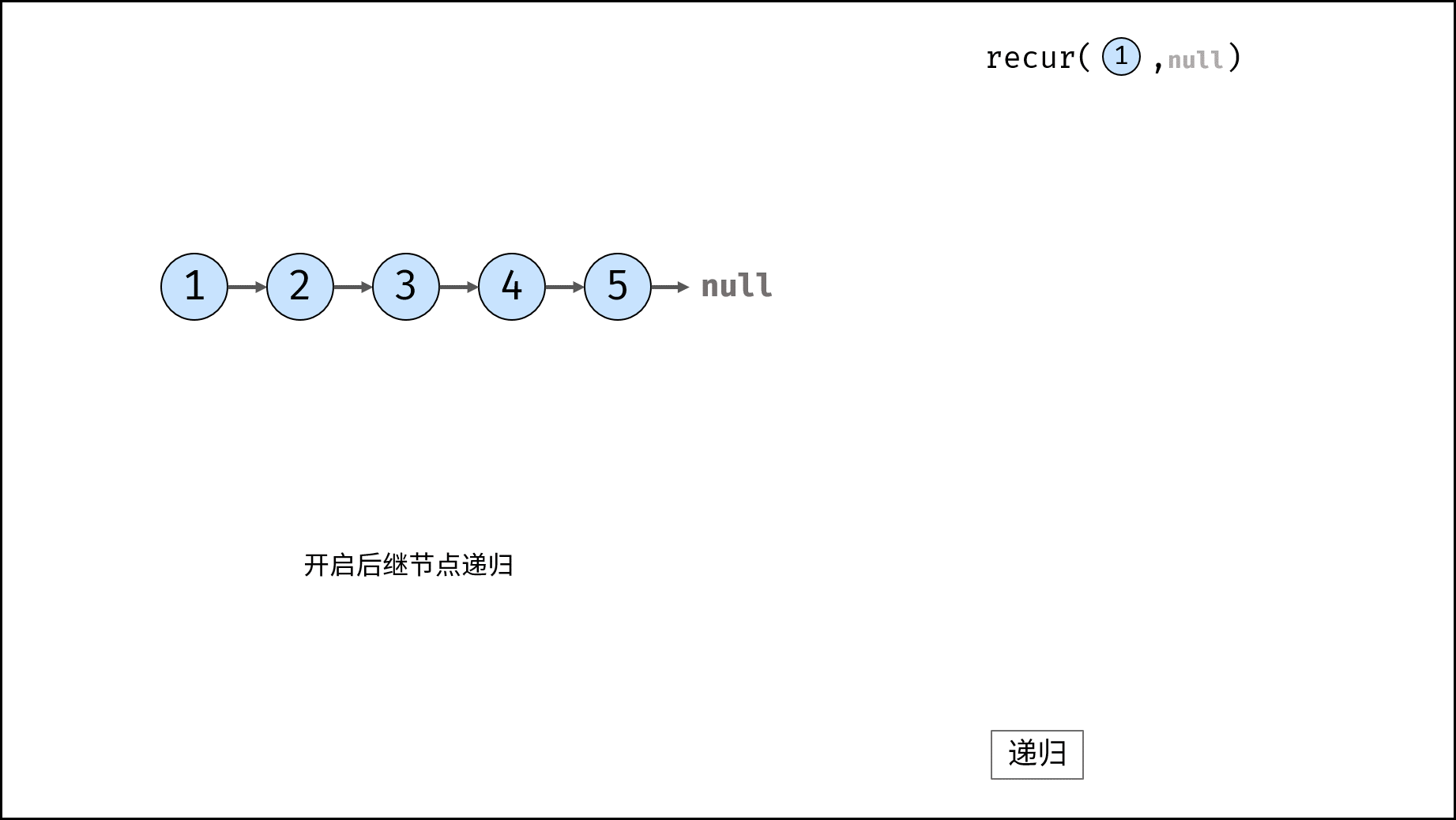
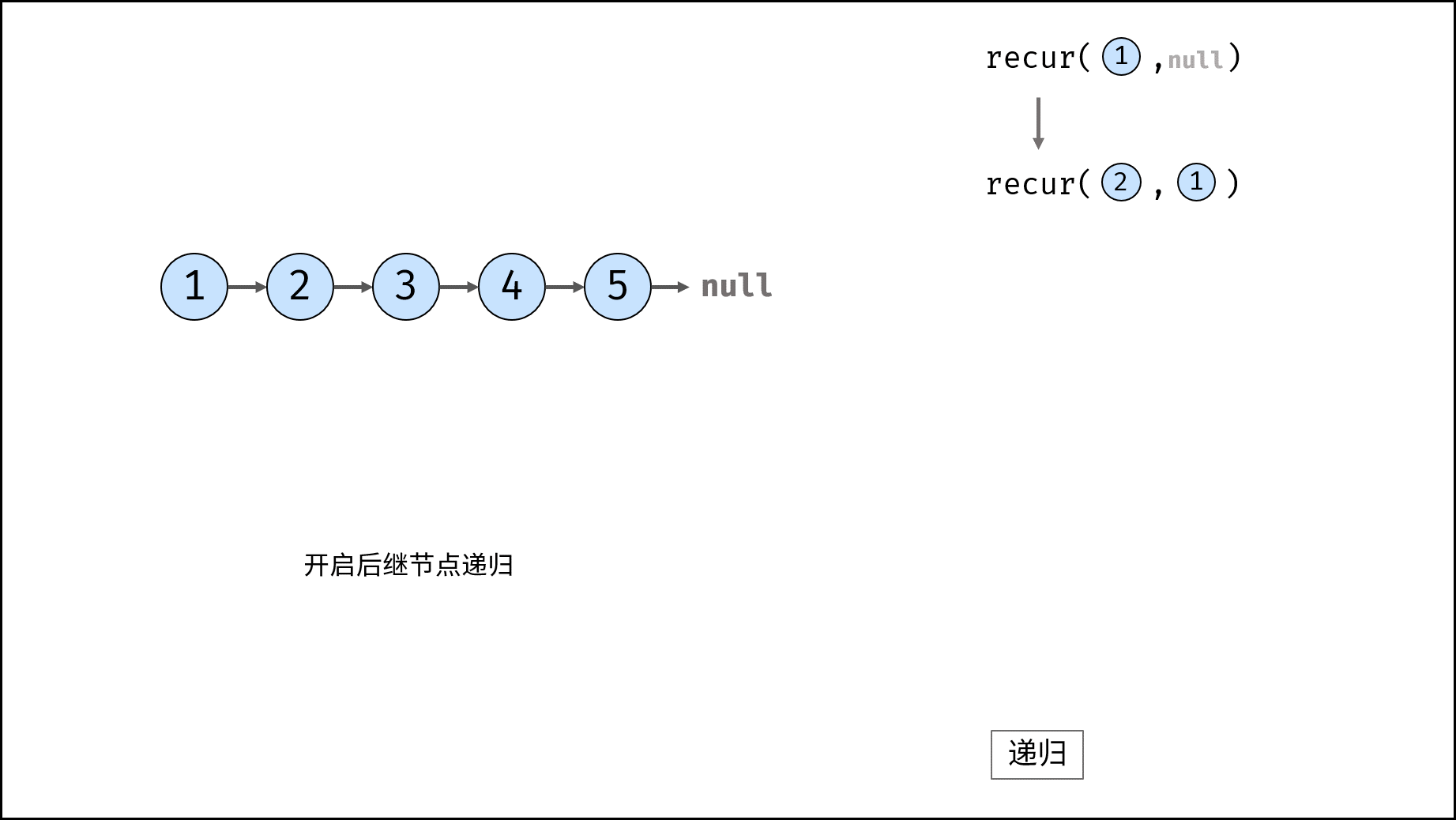
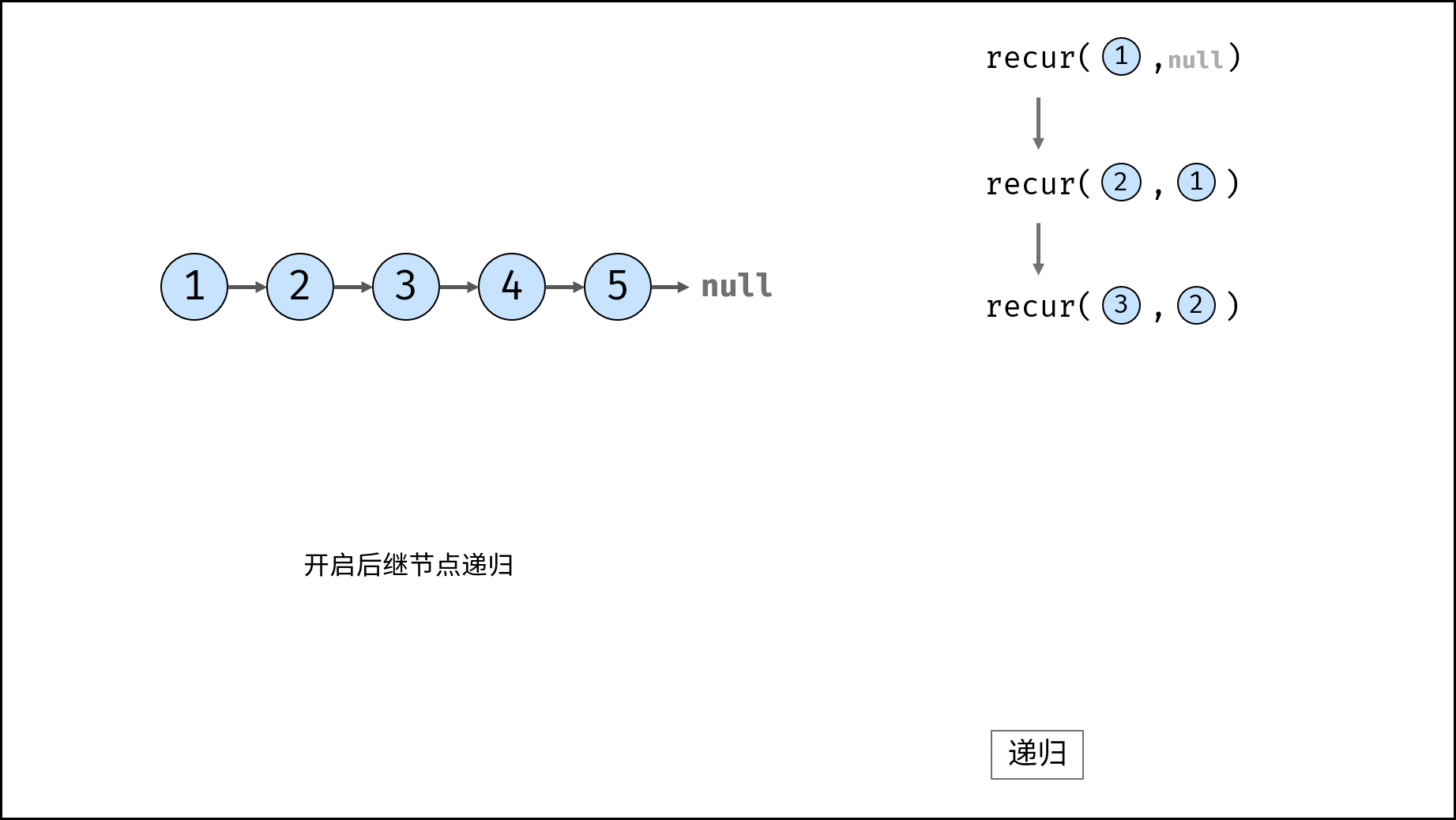
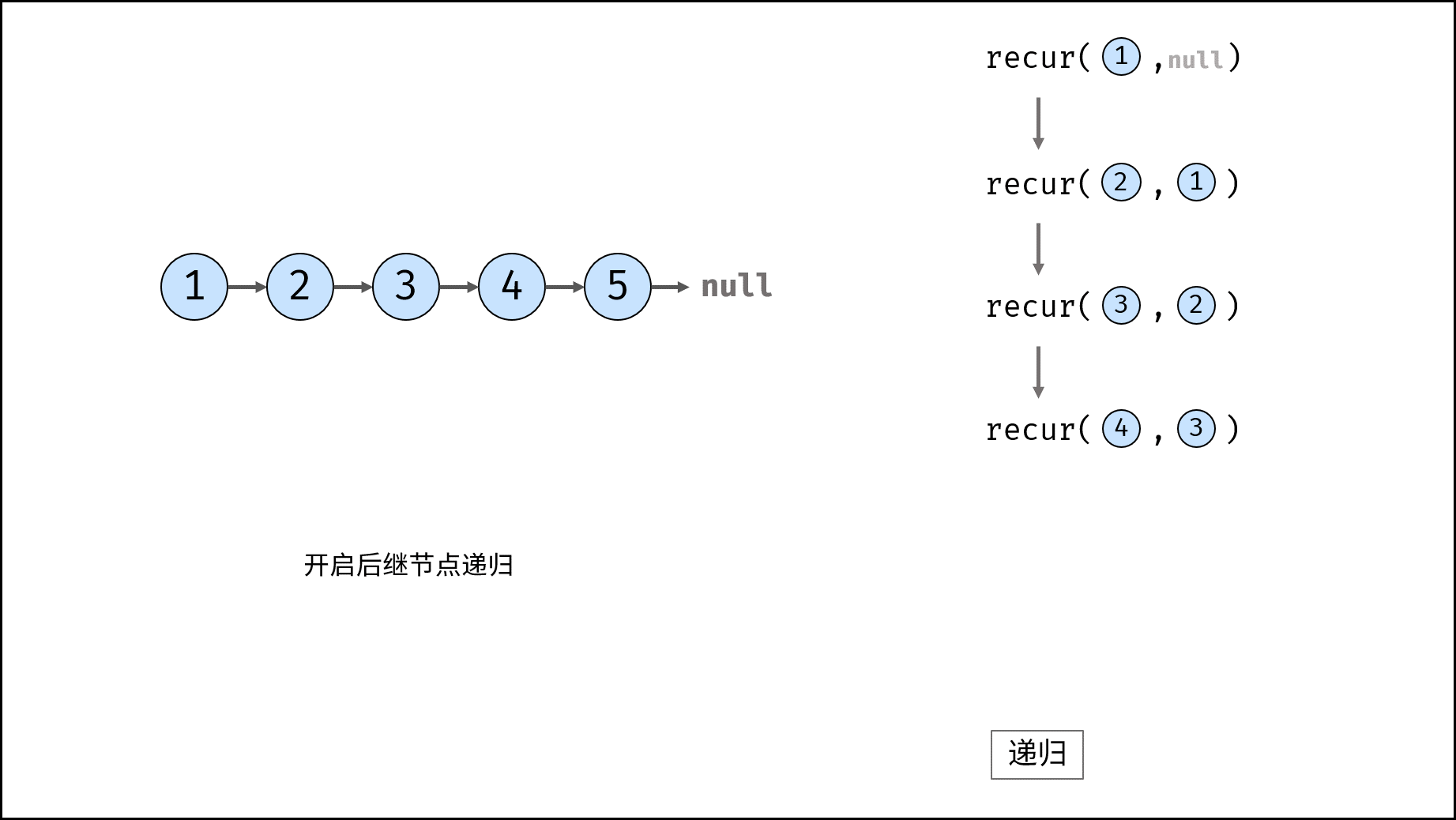
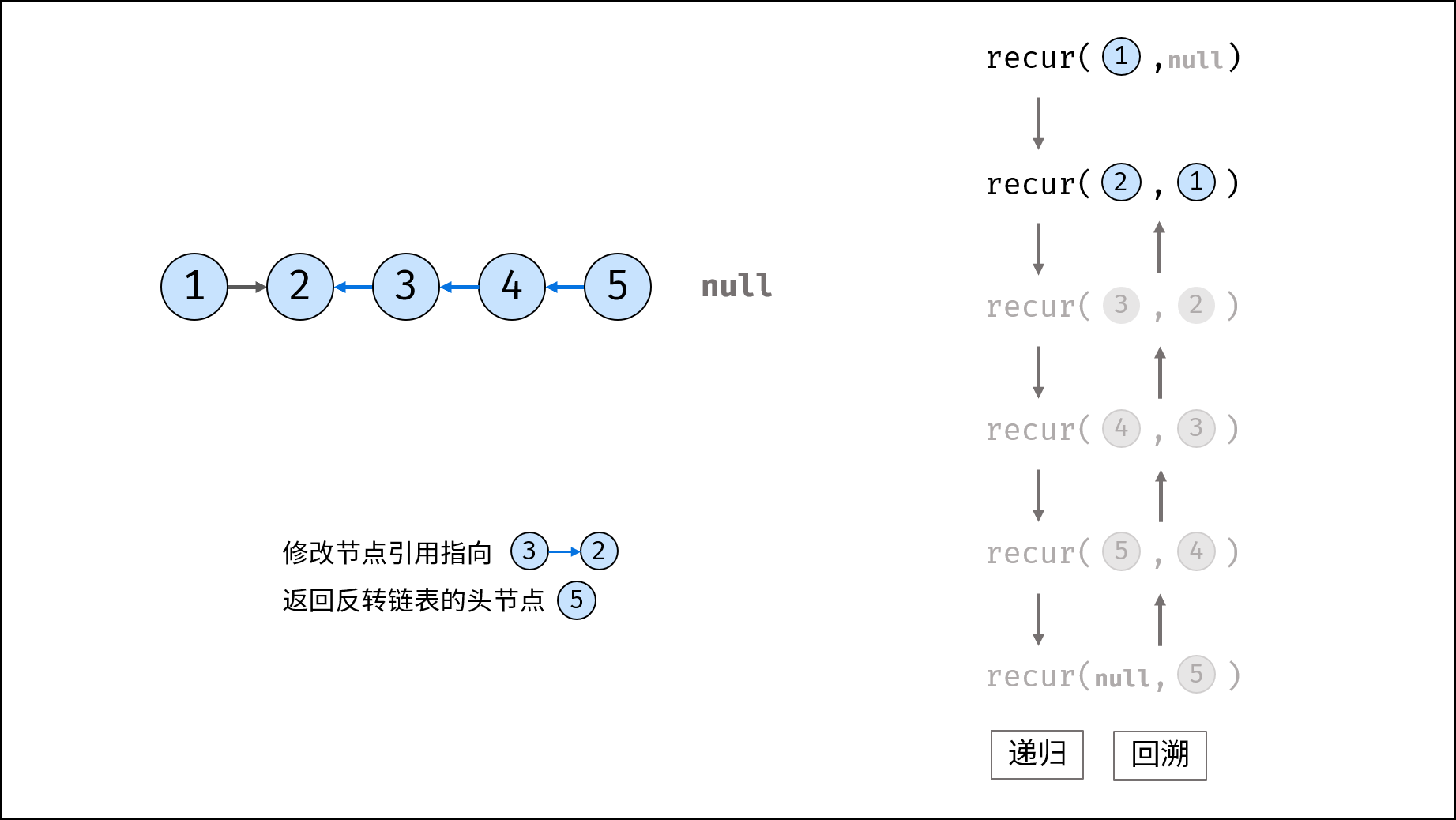
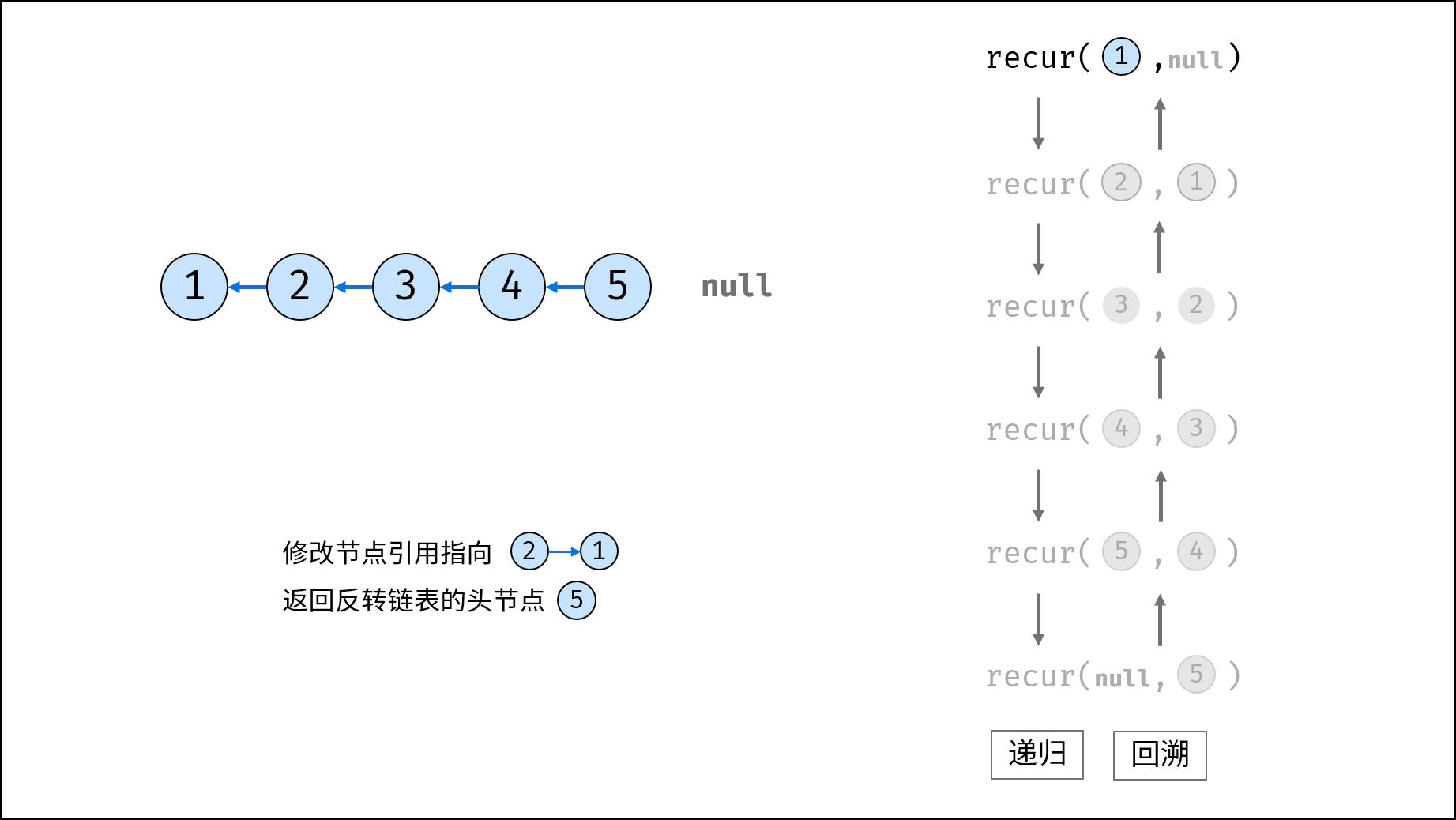
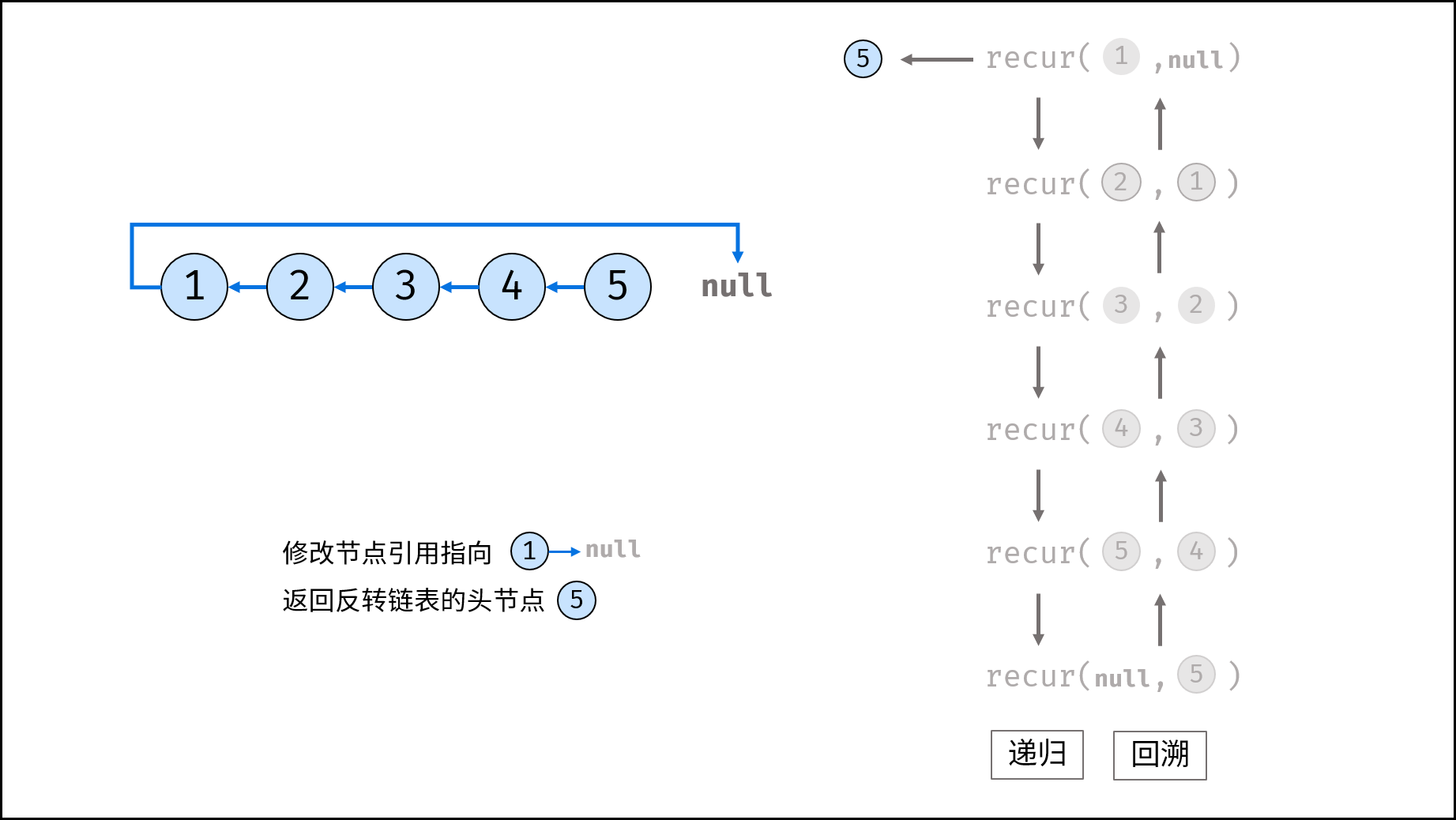
考虑使用递归遍历链表,当越过尾节点后终止递归,在回溯时修改各节点的 next 引用指向。
recur(cur, pre) 递归函数:
- 终止条件:当
cur为空,则返回尾节点pre(即反转链表的头节点); - 递归后继节点,记录返回值(即反转链表的头节点)为
res; - 修改当前节点
cur引用指向前驱节点pre; - 返回反转链表的头节点
res;
trainningPlan(head) 函数:
调用并返回 recur(head, null) 。传入 null 是因为反转链表后,head 节点指向 null ;
< ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, >
>
代码:
Python
class Solution:
def trainningPlan(self, head: ListNode) -> ListNode:
def recur(cur, pre):
if not cur: return pre # 终止条件
res = recur(cur.next, cur) # 递归后继节点
cur.next = pre # 修改节点引用指向
return res # 返回反转链表的头节点
return recur(head, None) # 调用递归并返回Java
class Solution {
public ListNode trainningPlan(ListNode head) {
return recur(head, null); // 调用递归并返回
}
private ListNode recur(ListNode cur, ListNode pre) {
if (cur == null) return pre; // 终止条件
ListNode res = recur(cur.next, cur); // 递归后继节点
cur.next = pre; // 修改节点引用指向
return res; // 返回反转链表的头节点
}
}C++
class Solution {
public:
ListNode* trainningPlan(ListNode* head) {
return recur(head, nullptr); // 调用递归并返回
}
private:
ListNode* recur(ListNode* cur, ListNode* pre) {
if (cur == nullptr) return pre; // 终止条件
ListNode* res = recur(cur->next, cur); // 递归后继节点
cur->next = pre; // 修改节点引用指向
return res; // 返回反转链表的头节点
}
};复杂度分析:
- 时间复杂度 $O(N)$ : 遍历链表使用线性大小时间。
- 空间复杂度 $O(N)$ : 遍历链表的递归深度达到 $N$ ,系统使用 $O(N)$ 大小额外空间。