排序算法简介

排序算法用作实现列表的排序，列表元素可以是整数，也可以是浮点数、字符串等其他数据类型。生活中有许多需要排序算法的场景，例如：

整数排序： 对于一个整数数组，我们希望将所有数字从小到大排序；
字符串排序： 对于一个姓名列表，我们希望将所有单词按照字符先后排序；
自定义排序： 对于任意一个 已定义比较规则 的集合，我们希望将其按规则排序；

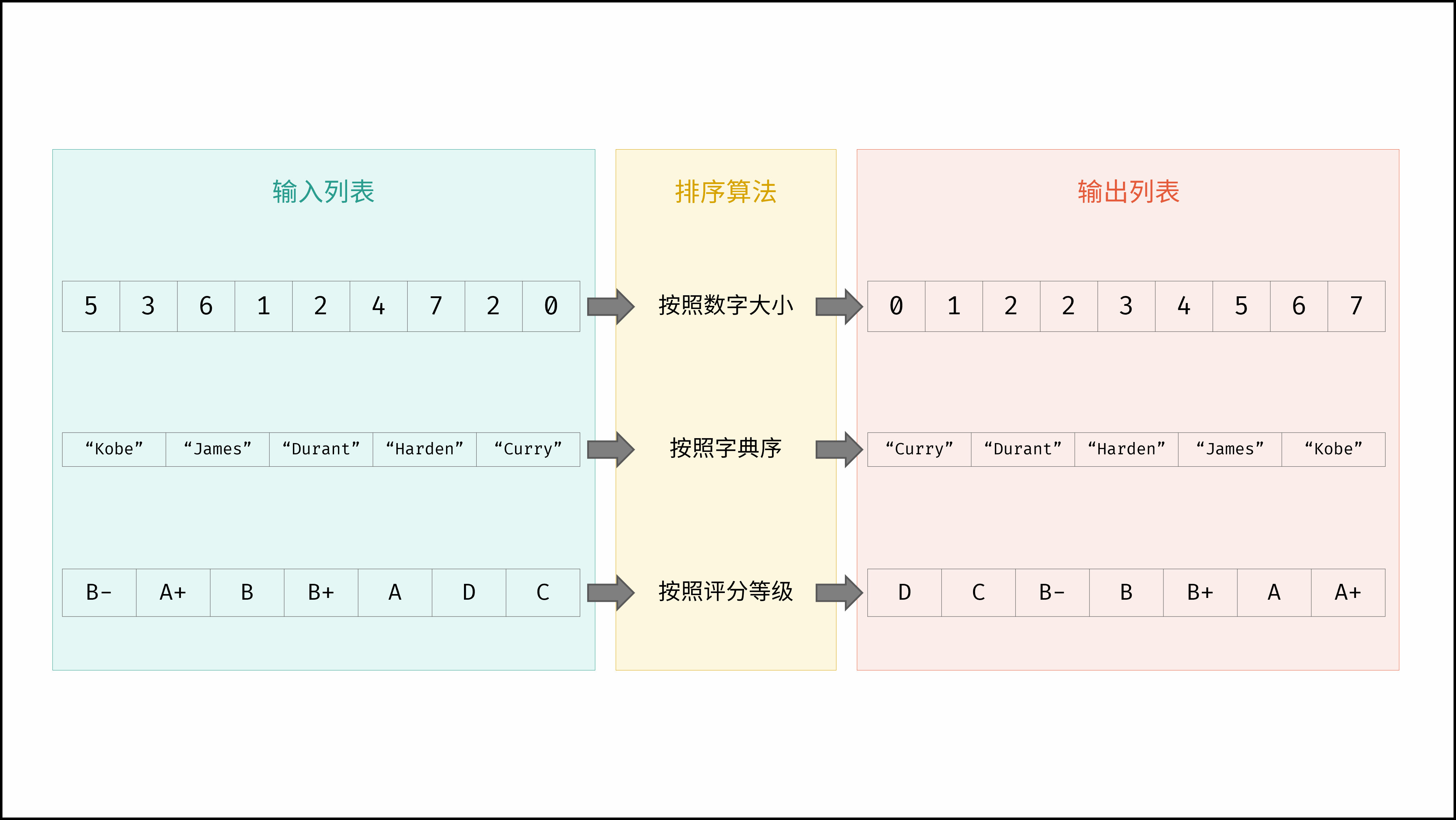
同时，某些算法需要在排序算法的基础上使用（即在排序数组上运行），例如：

二分查找： 根据数组已排序的特性，才能每轮确定排除两部分中的哪一部分；
双指针： 例如合并两个排序链表，根据已排序特性，才能通过双指针移动在线性时间内将其合并为一个排序链表。

接下来，本文将从「常见排序算法」、「分类方法」、「时间与空间复杂度」三方面入手，简要介绍排序算法。「各排序算法详细介绍」请见后续专栏文章。

常见算法

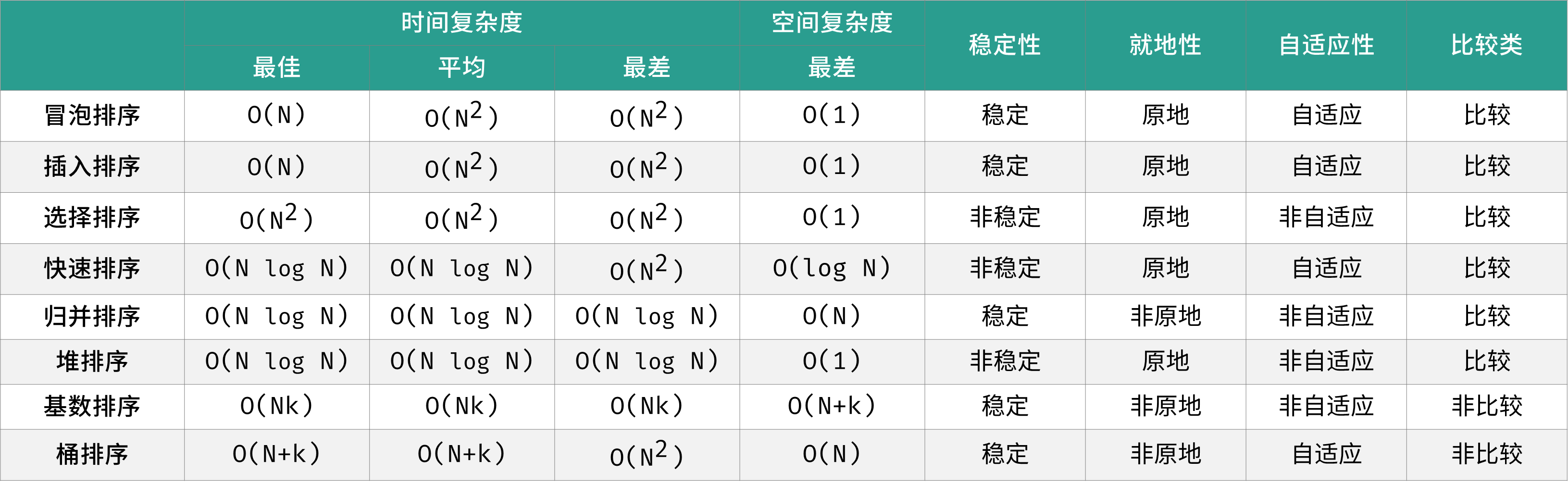
常见排序算法包括「冒泡排序」、「插入排序」、「选择排序」、「快速排序」、「归并排序」、「堆排序」、「基数排序」、「桶排ss序」。如下图所示，为各排序算法的核心特性与时空复杂度总结。

如下图所示，为在「随机乱序」、「接近有序」、「完全倒序」、「少数独特」四类输入数据下，各常见排序算法的排序过程。

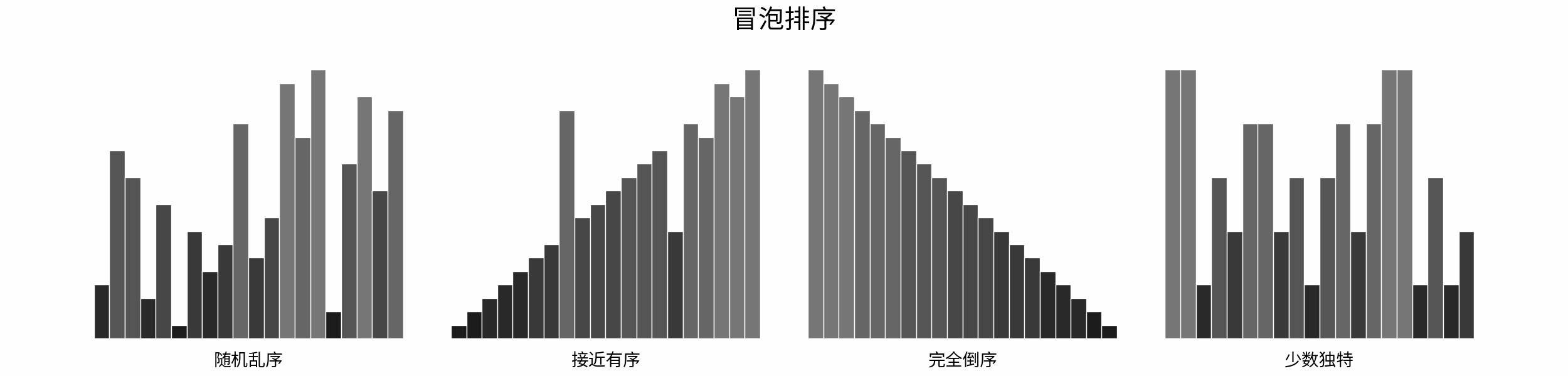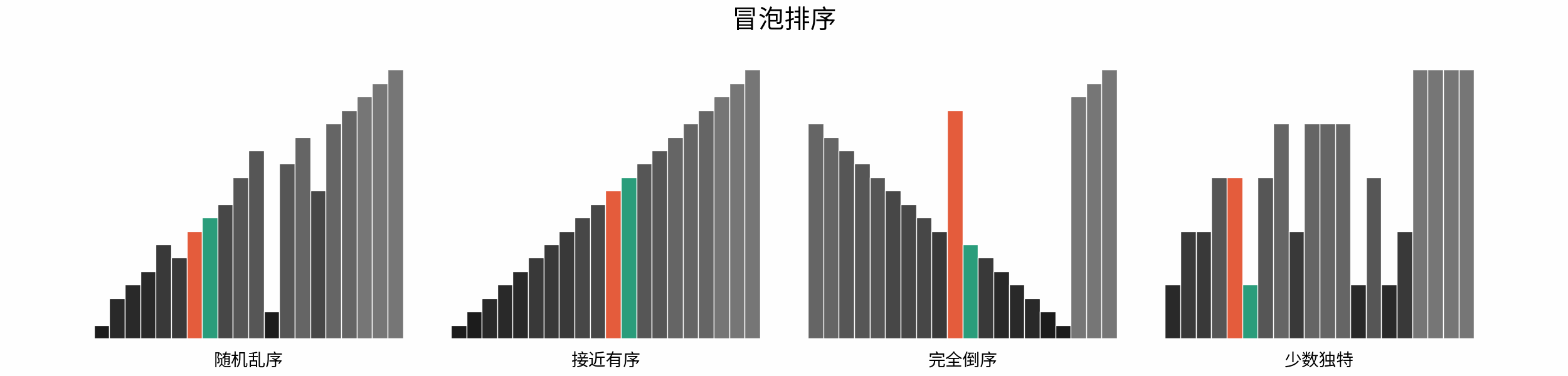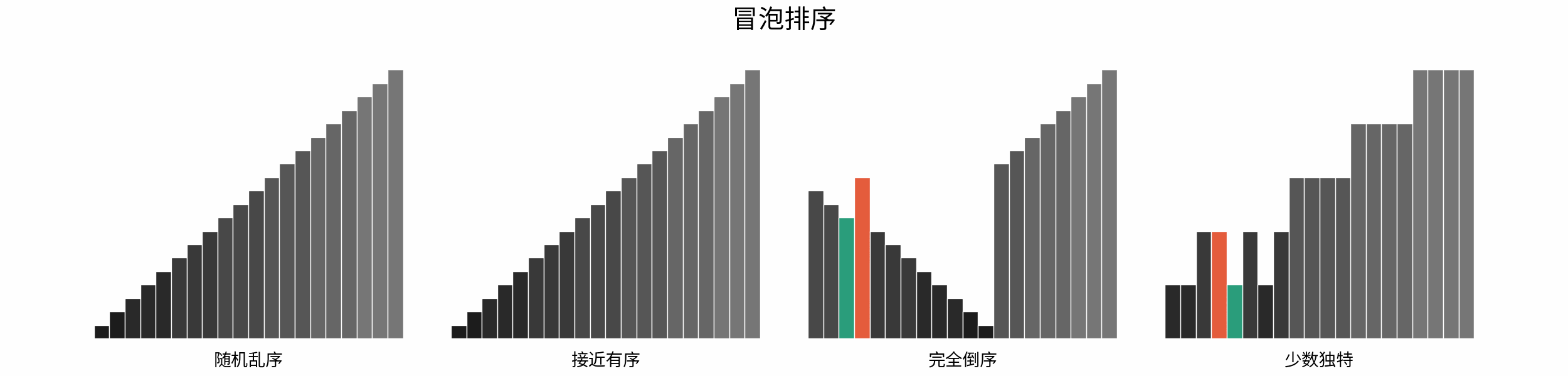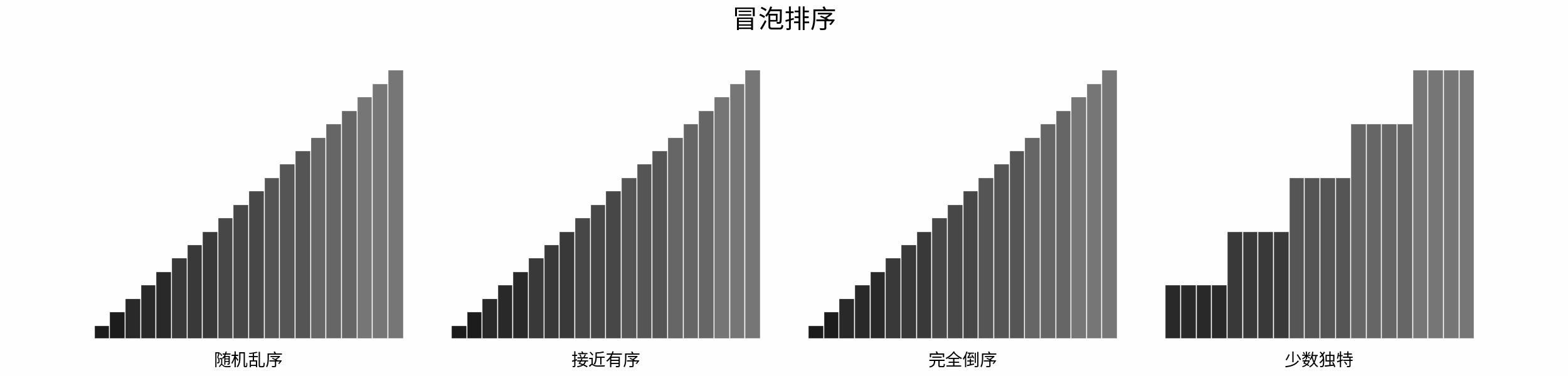
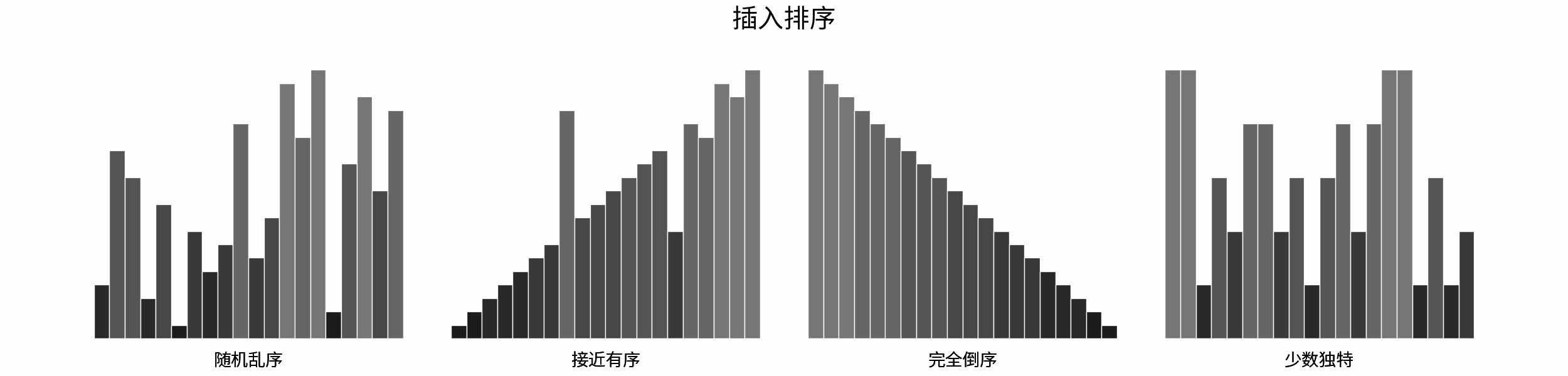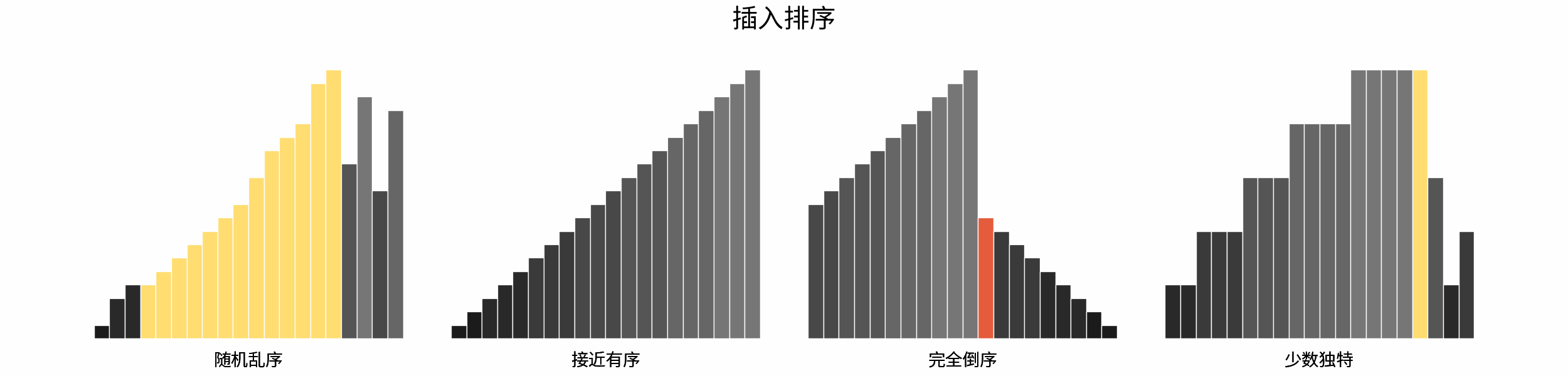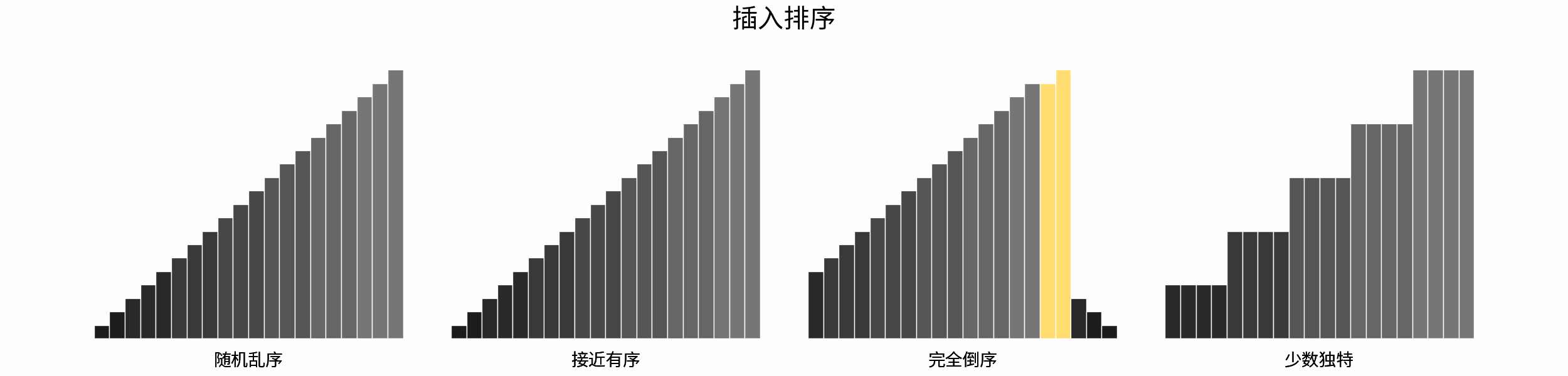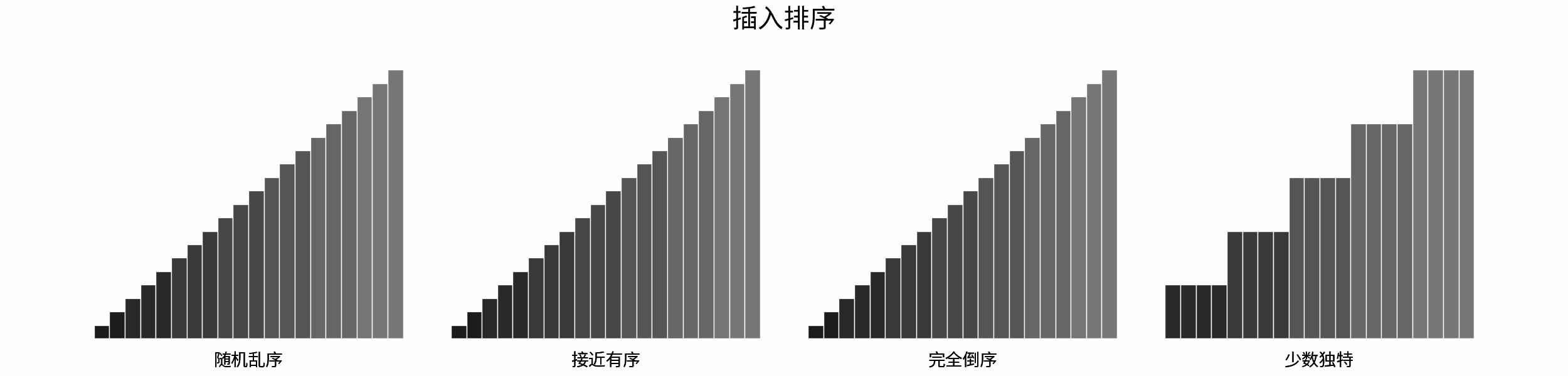
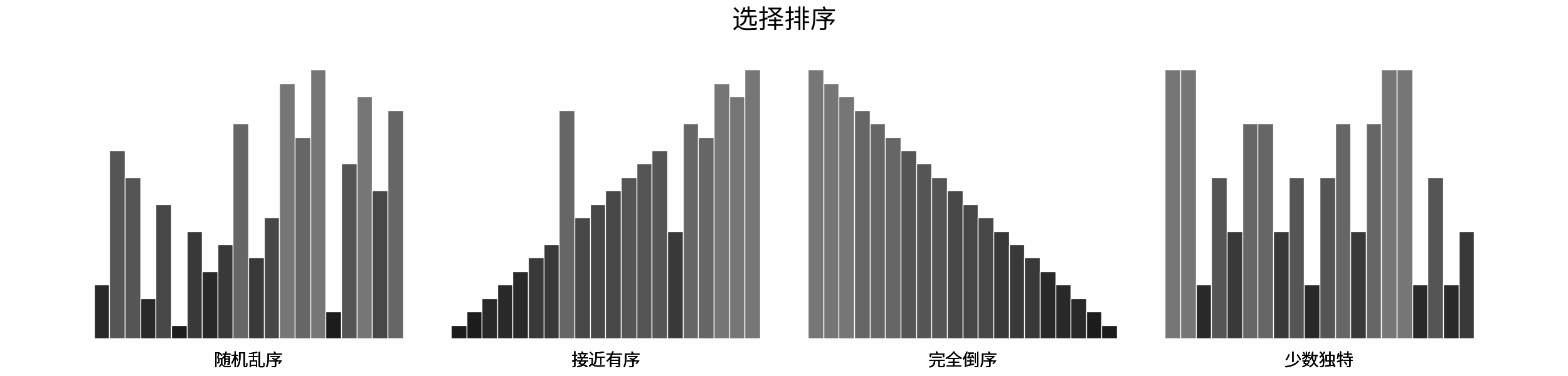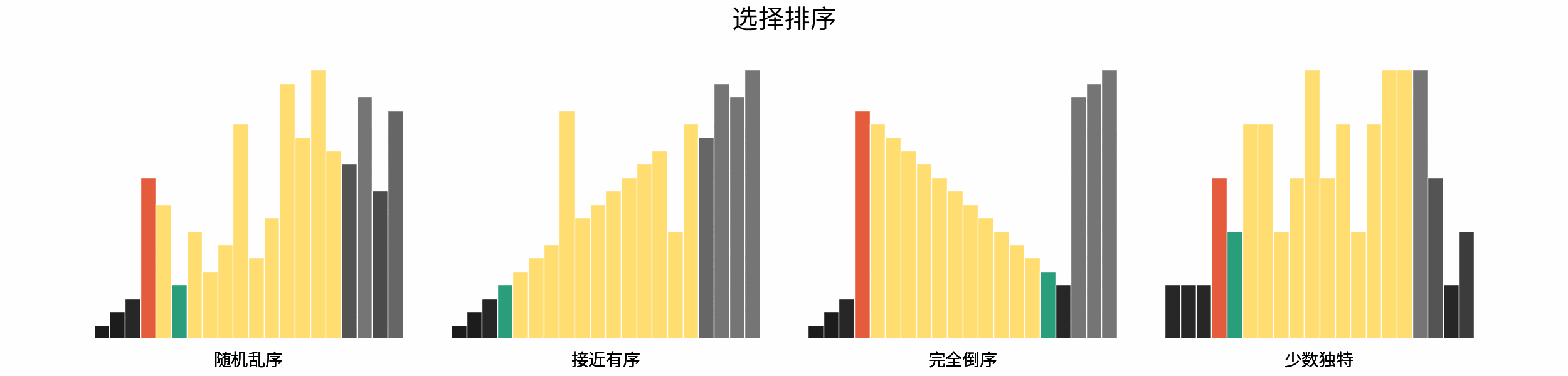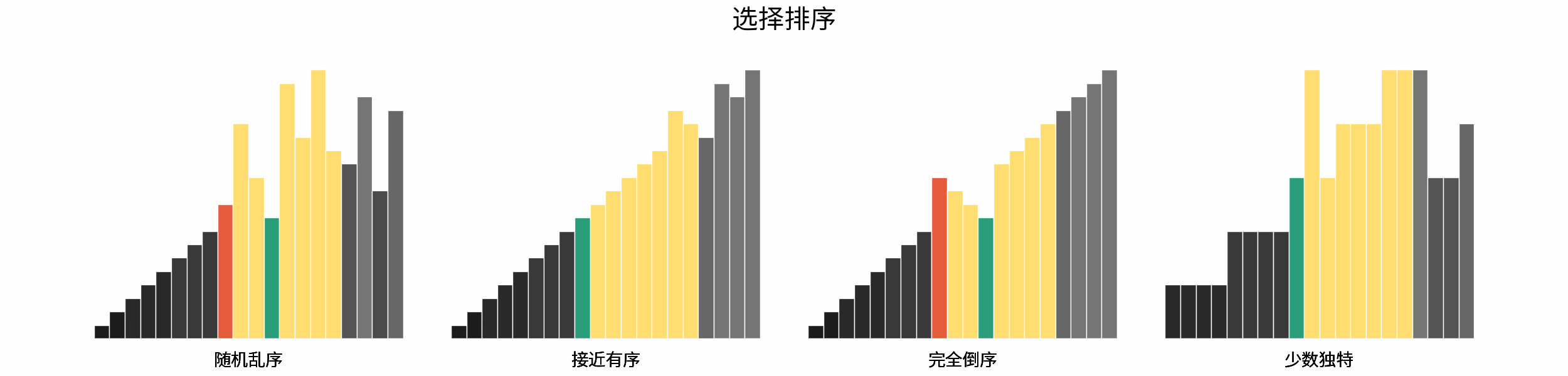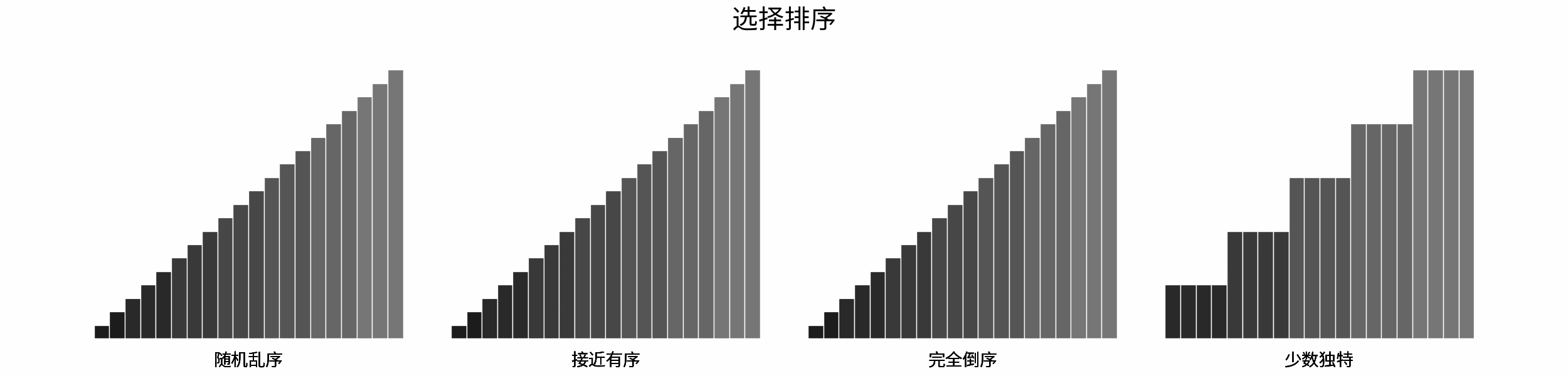
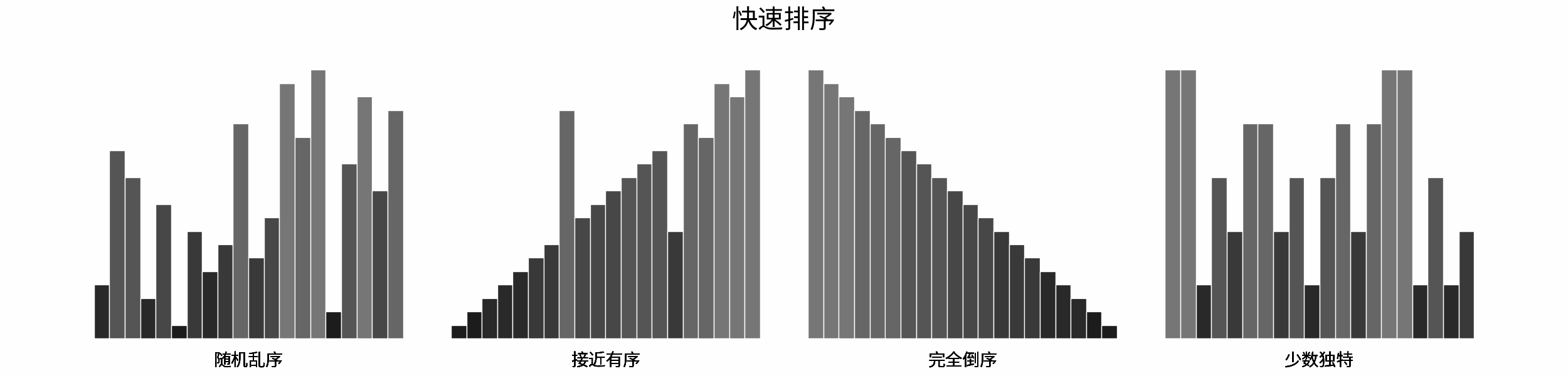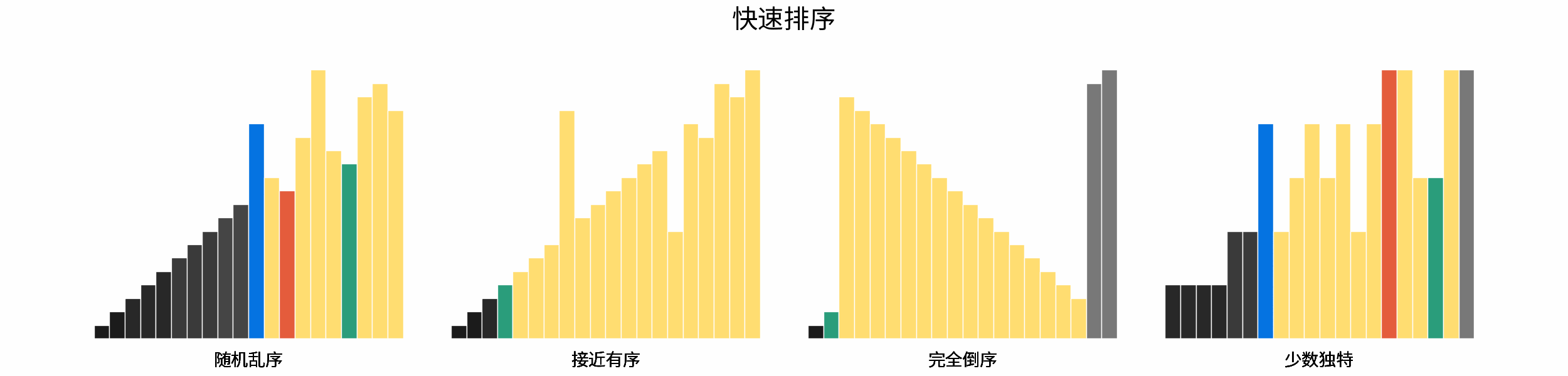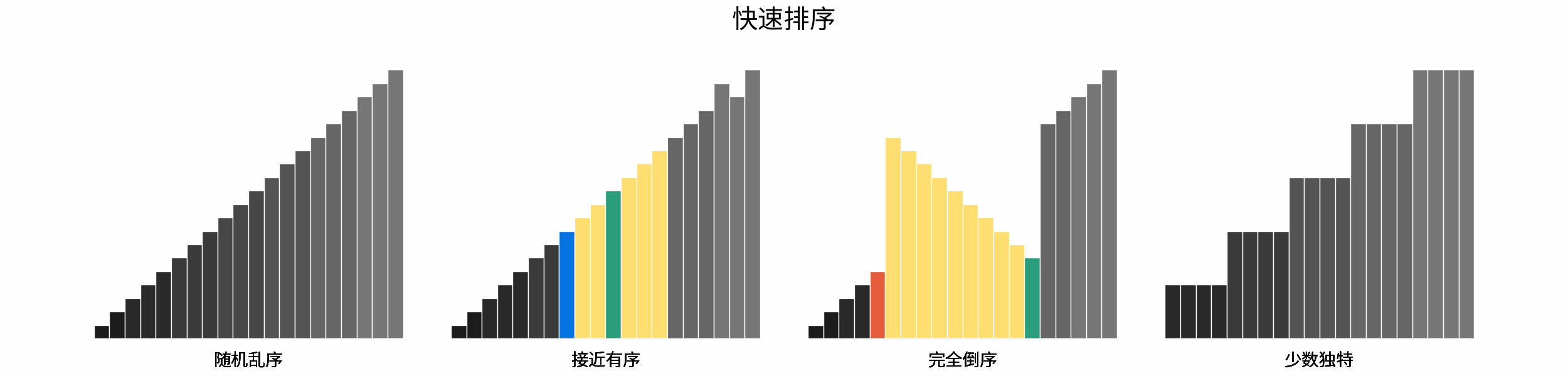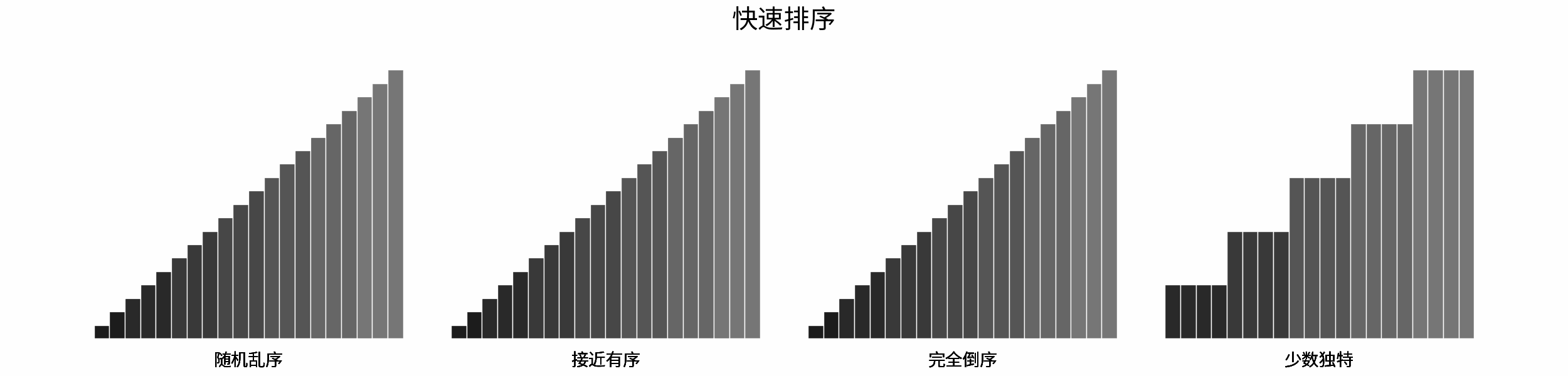
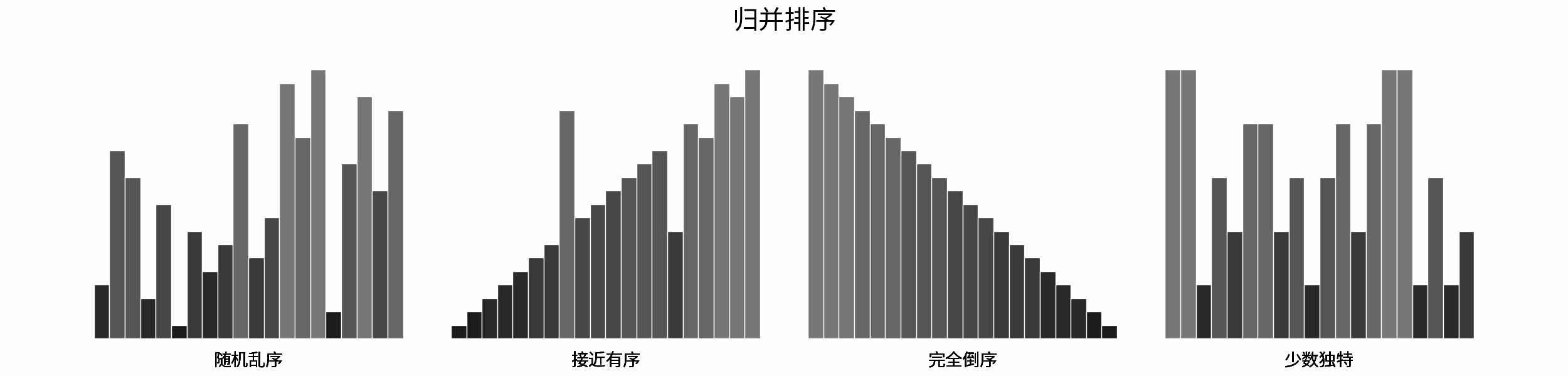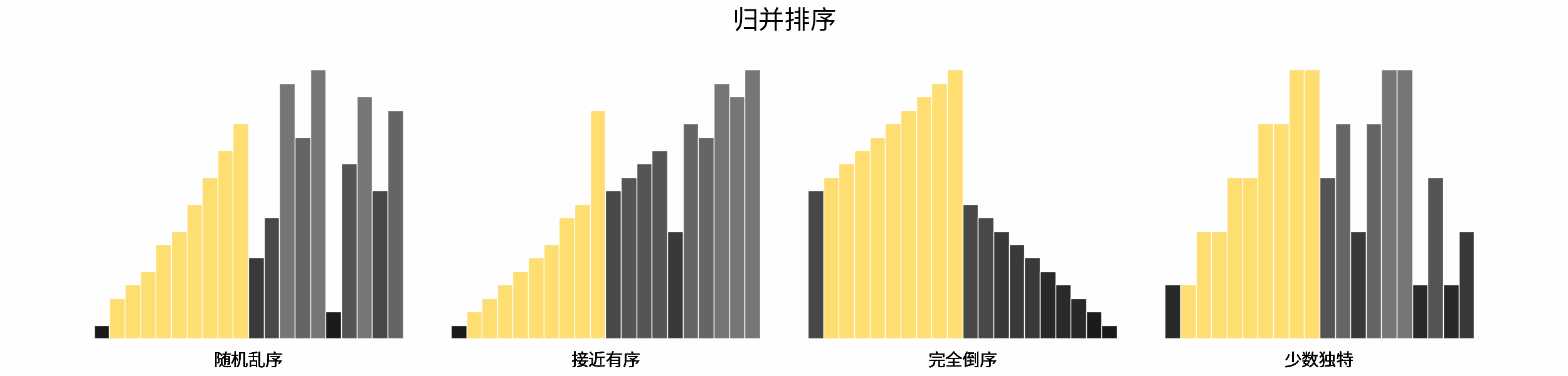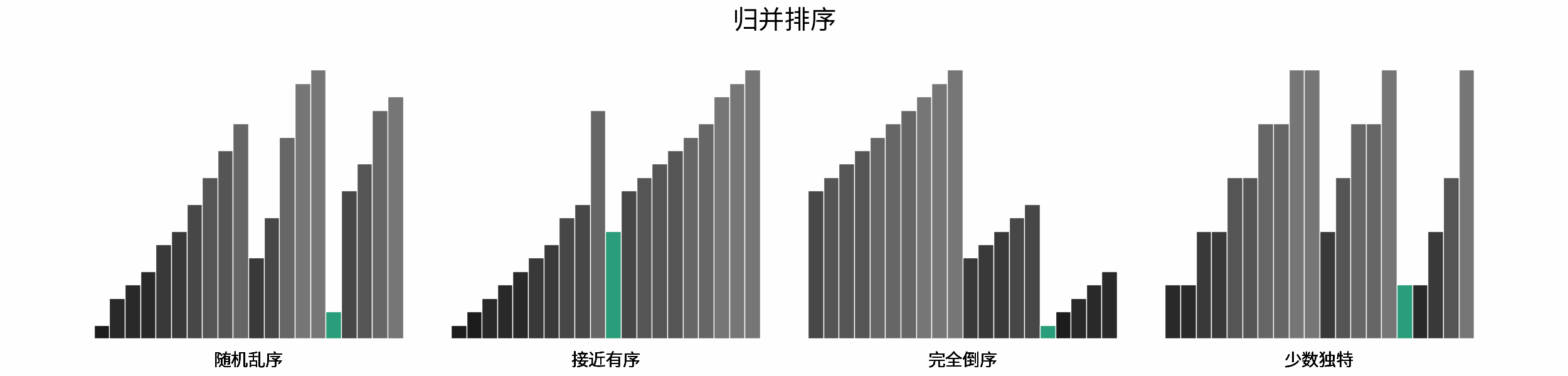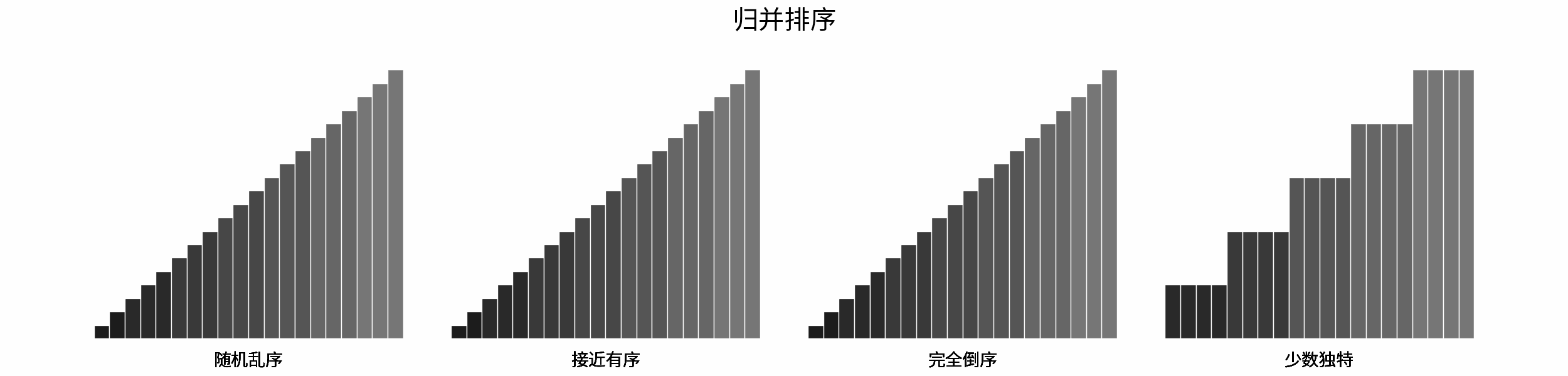
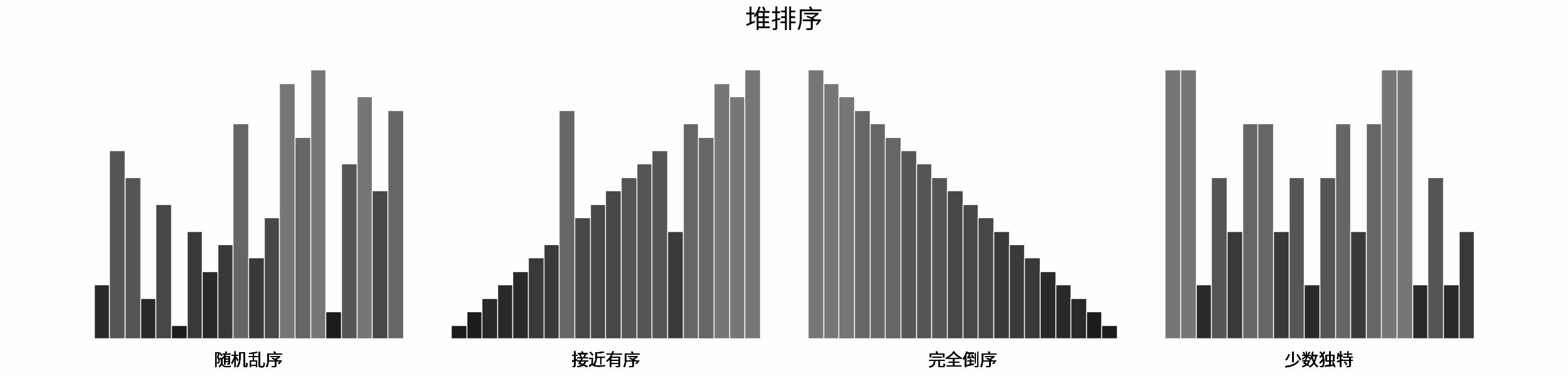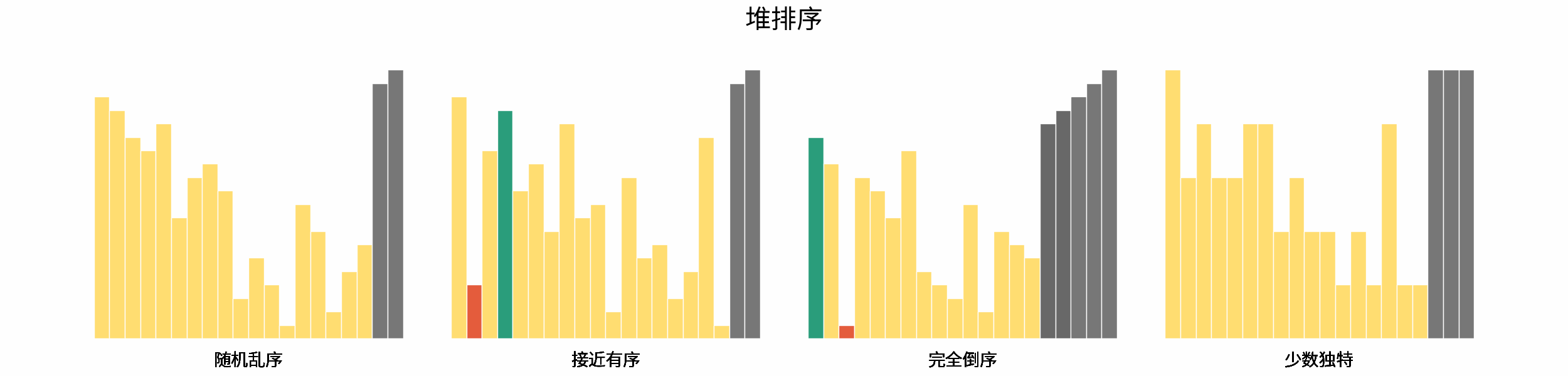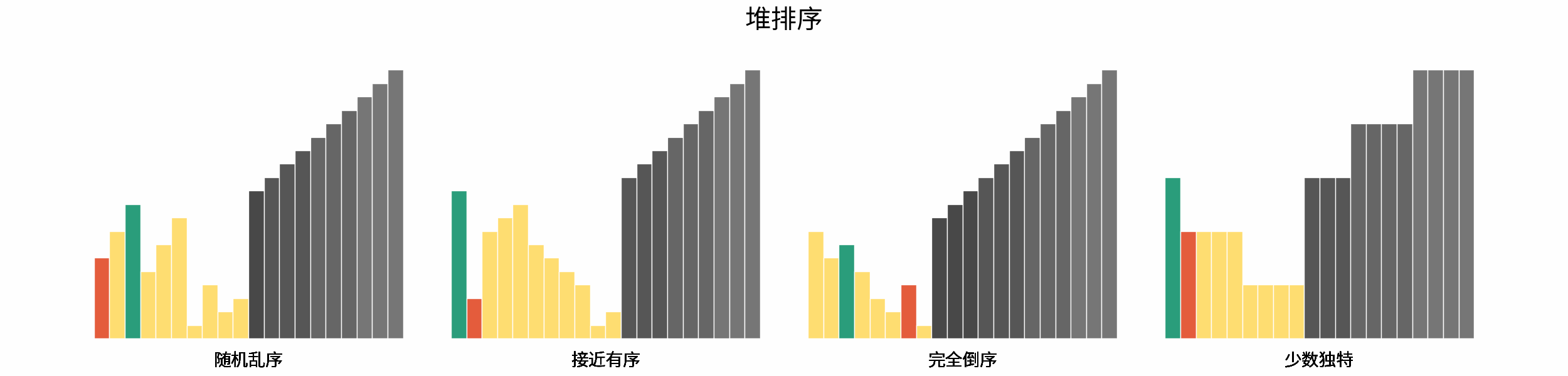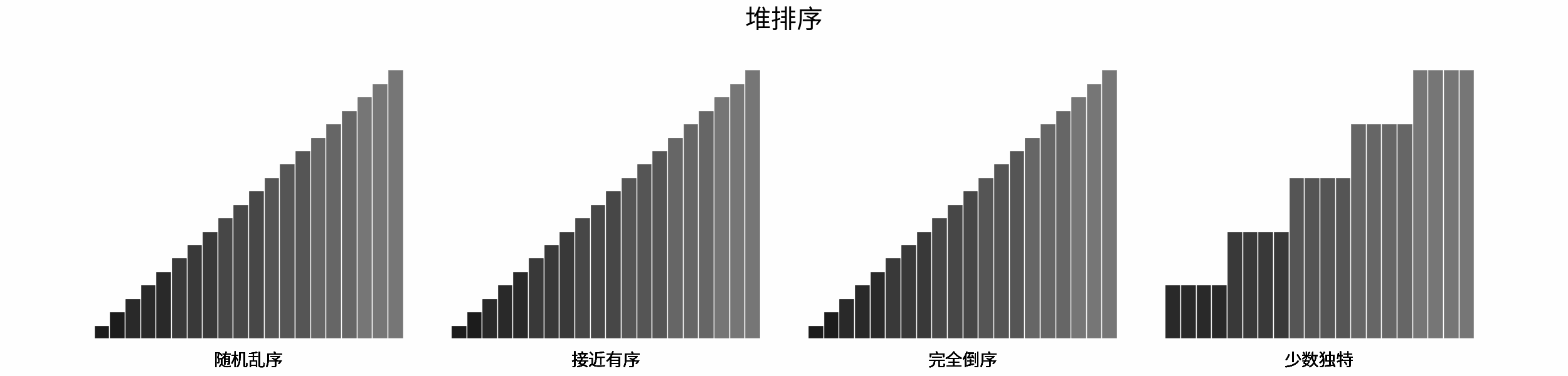
分类方法

排序算法主要可根据 稳定性 、就地性 、自适应性 分类。理想的排序算法具有以下特性：

具有稳定性，即相等元素的相对位置不变化；
具有就地性，即不使用额外的辅助空间；
具有自适应性，即时间复杂度受元素分布影响；

特别地，任意排序算法都 不同时具有以上所有特性 。因此，排序算法的选型使用取决于具体的列表类型、元素数量、元素分布情况等应用场景特点。

稳定性：

根据 相等元素 在数组中的 相对顺序 是否被改变，排序算法可分为「稳定排序」和「非稳定排序」两类。

「稳定排序」在完成排序后，不改变 相等元素在数组中的相对顺序。例如：冒泡排序、插入排序、归并排序、基数排序、桶排序。
「非稳定排序」在完成排序后，相等素在数组中的相对位置 可能被改变。例如：选择排序、快速排序、堆排序。

何时需考虑排序算法的稳定性？
数组排序中，由于元素皆为数字，因此稳定和非稳定排序皆可输出相同结果，此时无需考虑排序算法的稳定性。
非稳定排序会改变相等元素的相对次序，这在实际应用场景中可能是不能接受的。如以下代码所示，非稳定排序破坏了输入列表 people 按姓名排序的性质。
Python
# 人 = (姓名, 年龄) ，按姓名排序
people = [
    ('A', 19),
    ('B', 18),
    ('C', 21),
    ('D', 19),
    ('E', 23)
]

# 非稳定排序（按年龄）
sort_by_age(people)

# 人 = (姓名, 年龄) ，按年龄排序
people = [
    ('B', 18),
    ('D', 19), # ('D', 19) 和 ('A', 19) 的相对位置改变，输入时按姓名排序的性质丢失
    ('A', 19),
    ('C', 21),
    ('E', 23)
]

就地性：

根据排序过程中 是否使用额外内存（辅助数组），排序算法可分为「原地排序」和「异地排序」两类。一般地，由于不使用外部内存，原地排序相比非原地排序的执行效率更高。

「原地排序」不使用额外辅助数组，例如：冒泡排序、插入排序、选择排序、快速排序、堆排序。
「非原地排序」使用额外辅助数组，例如：归并排序、基数排序、桶排序。

自适应性：

根据算法 时间复杂度 是否 受待排序数组的元素分布影响 ，排序算法可分为「自适应排序」和「非自适应排序」两类。

「自适应排序」的时间复杂度受元素分布影响；例如：冒泡排序、插入排序、快速排序、桶排序。
「非自适应排序」的时间复杂度恒定；例如：选择排序、归并排序、堆排序、基数排序。

是否基于比较：

比较类排序基于元素之间的 比较算子（小于、相等、大于）来决定元素的相对顺序；相对的，非比较排序则不基于比较算子实现。

「基于比较排序」基于元素之间的比较完成排序，例如：冒泡排序、插入排序、选择排序、快速排序、归并排序、堆排序。
「非基于比较排序」不基于元素之间的比较完成排序，例如：基数排序、桶排序。

基于比较的排序算法的平均时间复杂度最优为 $O(N \log N)$ ，而非比较排序算法可以达到线性级别的时间复杂度。

时空复杂度

总体上看，排序算法追求时间与空间复杂度最低。而即使某些排序算法的时间复杂度相等，但实际性能还受 输入列表性质、元素数量、元素分布等 等因素影响。

设输入列表元素数量为 $N$ ，常见排序算法的「时间复杂度」和「空间复杂度」如下图所示。

算法	最佳时间	平均时间	最差时间	最差空间
冒泡排序	$\Omega(N)$	$\Theta(N^2)$	$O(N^2)$	$O(1)$
插入排序	$\Omega(N)$	$\Theta(N^2)$	$O(N^2)$	$O(1)$
选择排序	$\Omega(N^2)$	$\Theta(N^2)$	$O(N^2)$	$O(1)$
快速排序	$\Omega(N \log N )$	$\Theta(N \log N)$	$O(N^2)$	$O(\log N)$
归并排序	$\Omega(N \log N)$	$\Theta(N \log N)$	$O(N \log N)$	$O(N)$
堆排序	$\Omega(N \log N)$	$\Theta(N \log N)$	$O(N \log N)$	$O(1)$
基数排序	$\Omega(Nk)$	$\Theta(Nk)$	$O(Nk)$	$O(N + k)$
桶排序	$\Omega(N + k)$	$\Theta(N + k)$	$O(N^2)$	$O(N)$

对于上表，需要特别注意：

「基数排序」适用于正整数、字符串、特定格式的浮点数排序，$k$ 为最大数字的位数；「桶排序」中 $k$ 为桶的数量。
普通「冒泡排序」的最佳时间复杂度为 $O(N^2)$ ，通过增加标志位实现 提前返回 ，可以将最佳时间复杂度降低至 $O(N)$ 。
在输入列表完全倒序下，普通「快速排序」的空间复杂度劣化至 $O(N)$ ，通过代码优化 尾递归优化 保持算法递归较短子数组，可以将最差递归深度降低至 $\log N$ 。
普通「快速排序」总以最左或最右元素为基准数，因此在输入列表有序或倒序下，时间复杂度劣化至 $O(N^2)$ ；通过 随机选择基准数 ，可极大减少此类最差情况发生，尽可能地保持 $O(N \log N)$ 的时间复杂度。
若输入列表是数组，则归并排序的空间复杂度为 $O(N)$ ；而若排序链表，则「归并排序」不需要借助额外辅助空间，空间复杂度可以降低至 $O(1)$ 。

排序算法简介 ​

常见算法 ​

分类方法 ​

稳定性： ​

就地性： ​

自适应性： ​

是否基于比较： ​

时空复杂度 ​