解题思路:
观察不同解法的复杂度,可知动态规划是本题的最优解法。
| 常见解法 | 时间复杂度 | 空间复杂度 |
|---|---|---|
| 暴力搜索 | $O(N^2)$ | $O(1)$ |
| 分治思想 | $O(N \log N)$ | $O(\log N)$ |
| 动态规划 | $O(N)$ | $O(1)$ |
动态规划解析:
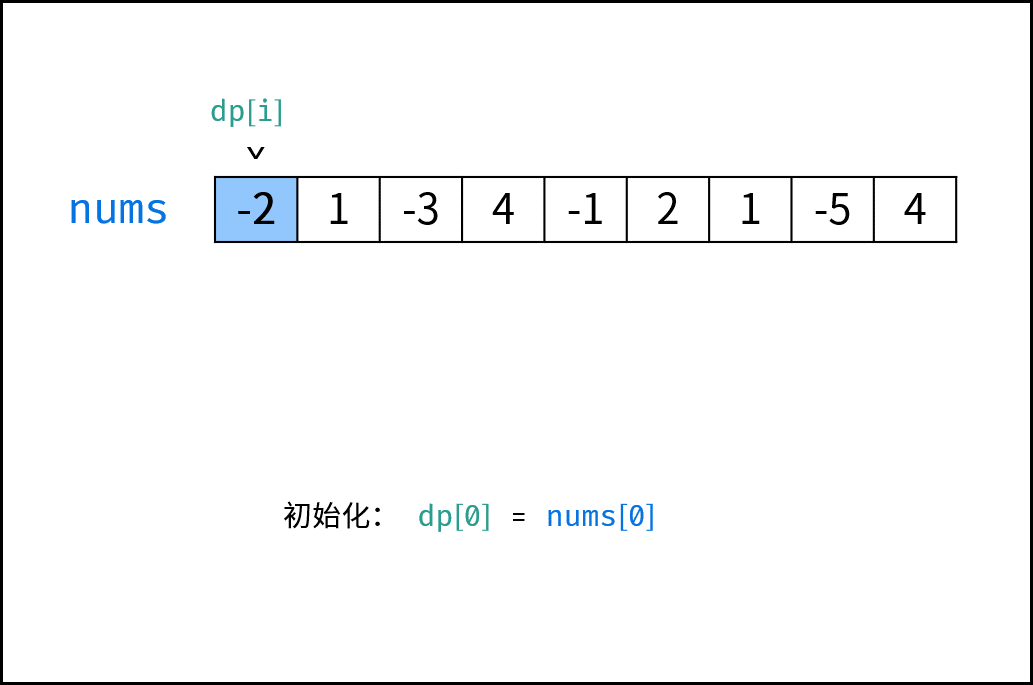
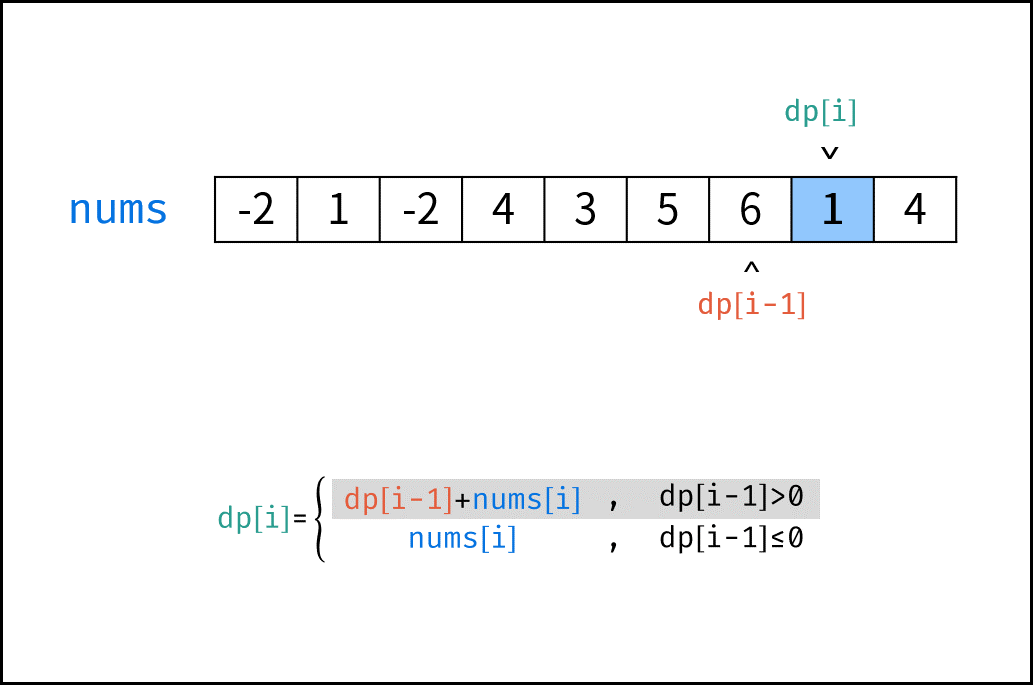
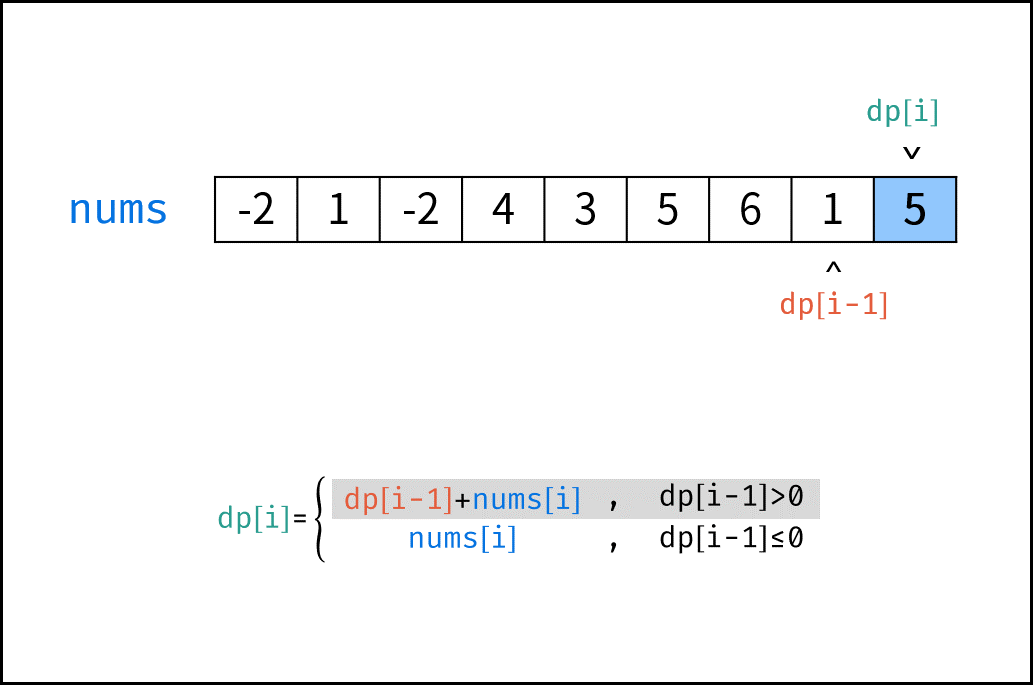
状态定义: 设动态规划列表 $dp$ ,$dp[i]$ 代表以元素 $sales[i]$ 为结尾的连续子数组最大和。
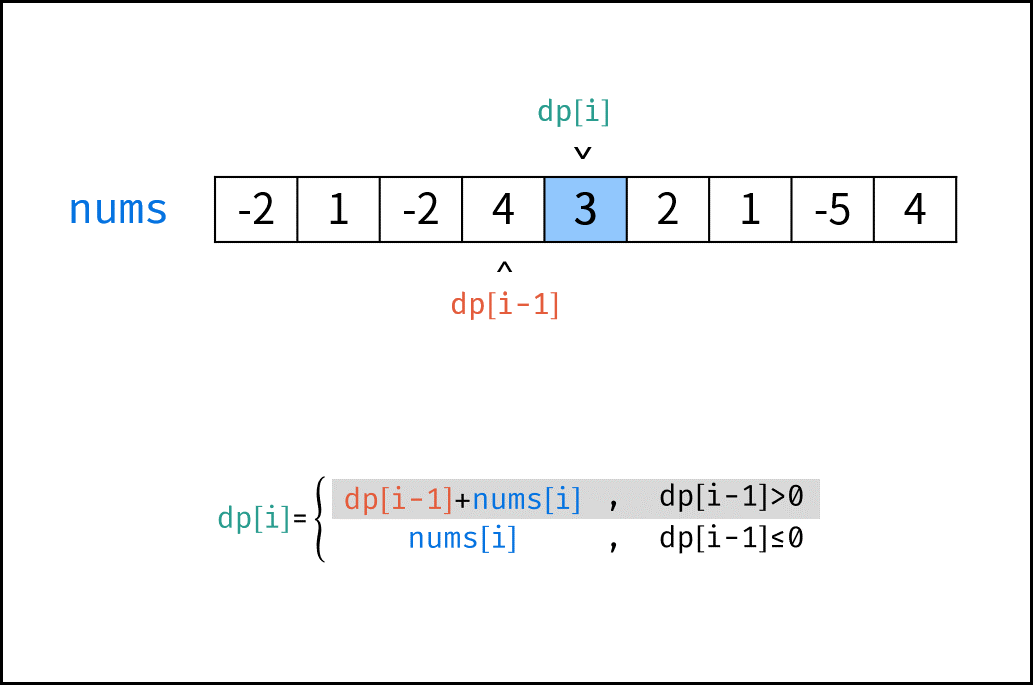
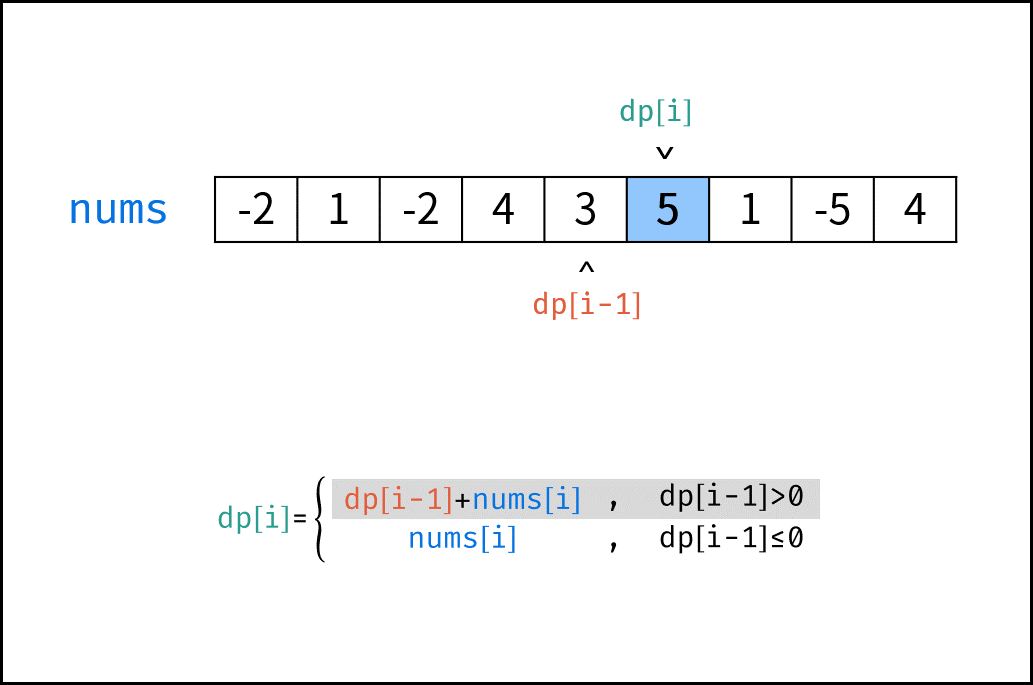
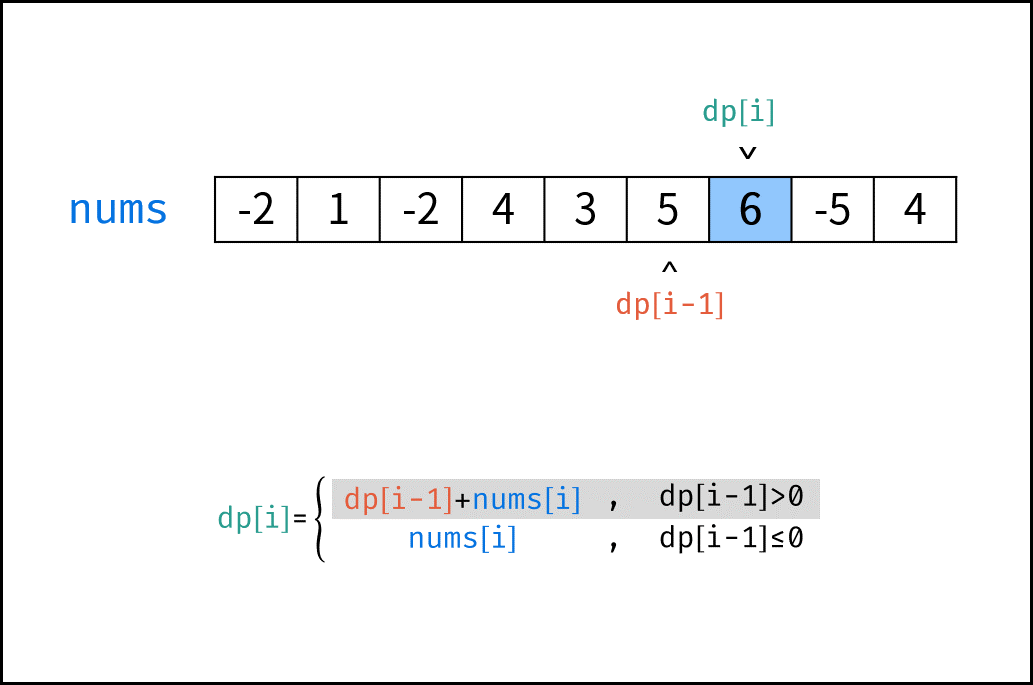
转移方程: 若 $dp[i-1] \leq 0$ ,说明 $dp[i - 1]$ 对 $dp[i]$ 产生负贡献,即 $dp[i-1] + sales[i]$ 还不如 $sales[i]$ 本身大。
$$ dp[i] = \begin{cases} dp[i-1] + sales[i] & , dp[i - 1] > 0 \ sales[i] & , dp[i - 1] \leq 0 \ \end{cases} $$
初始状态: $dp[0] = sales[0]$,即以 $sales[0]$ 结尾的连续子数组最大和为 $sales[0]$ 。
返回值: 返回 $dp$ 列表中的最大值,代表全局最大值。
下图中的
nums对应本题的sales。

空间优化:
由于 $dp[i]$ 只与 $dp[i-1]$ 和 $sales[i]$ 有关系,因此可以将原数组 $sales$ 用作 $dp$ 列表,即直接在 $sales$ 上修改即可。
由于省去 $dp$ 列表使用的额外空间,因此空间复杂度从 $O(N)$ 降至 $O(1)$ 。
< ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, >
>
代码:
Python
class Solution:
def maxSales(self, sales: List[int]) -> int:
for i in range(1, len(sales)):
sales[i] += max(sales[i - 1], 0)
return max(sales)Java
class Solution {
public int maxSales(int[] sales) {
int res = sales[0];
for(int i = 1; i < sales.length; i++) {
sales[i] += Math.max(sales[i - 1], 0);
res = Math.max(res, sales[i]);
}
return res;
}
}C++
class Solution {
public:
int maxSales(vector<int>& sales) {
int res = sales[0];
for(int i = 1; i < sales.size(); i++) {
if(sales[i - 1] > 0) sales[i] += sales[i - 1];
if(sales[i] > res) res = sales[i];
}
return res;
}
};复杂度分析:
- 时间复杂度 $O(N)$ : 线性遍历数组 $sales$ 即可获得结果,使用 $O(N)$ 时间。
- 空间复杂度 $O(1)$ : 使用常数大小的额外空间。