自律小屋 | 自律小屋

解题思路：

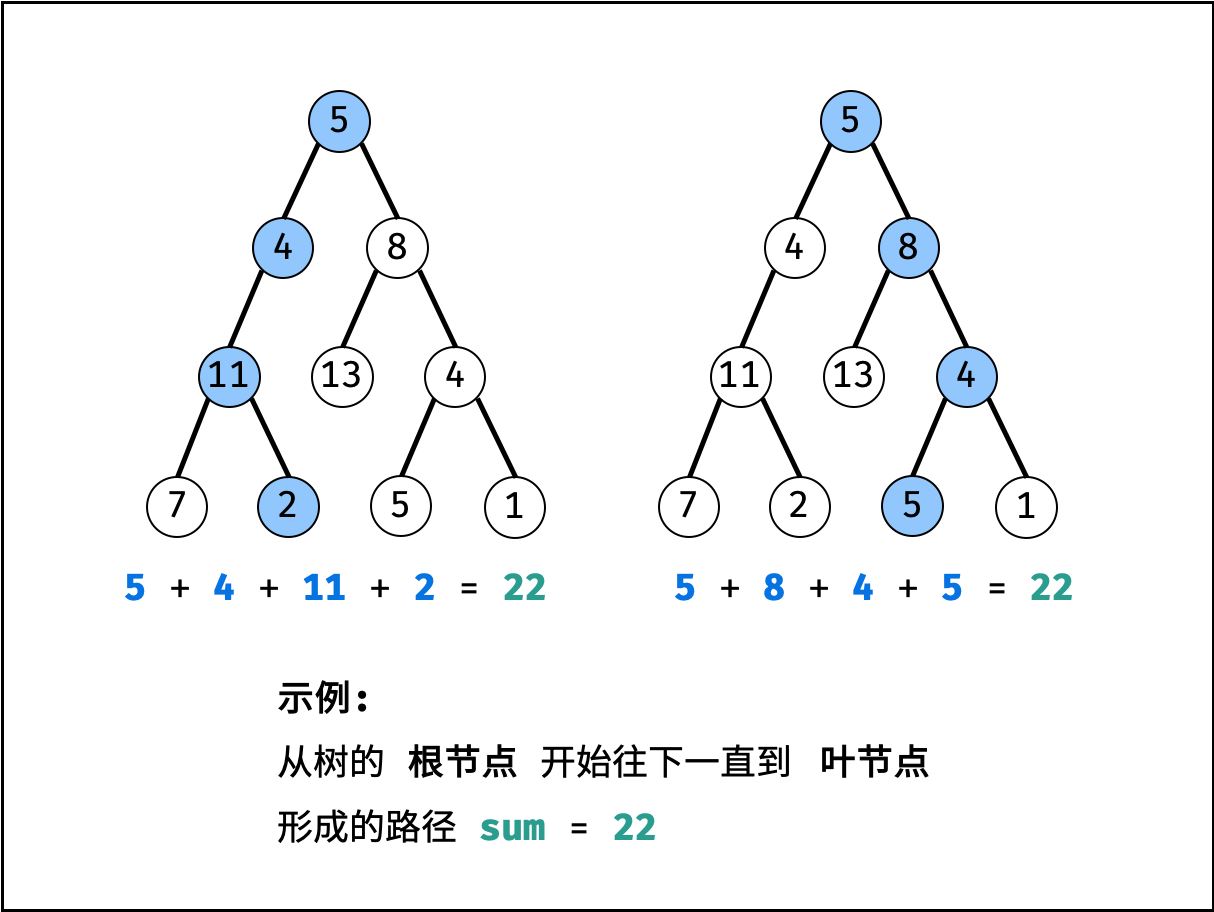
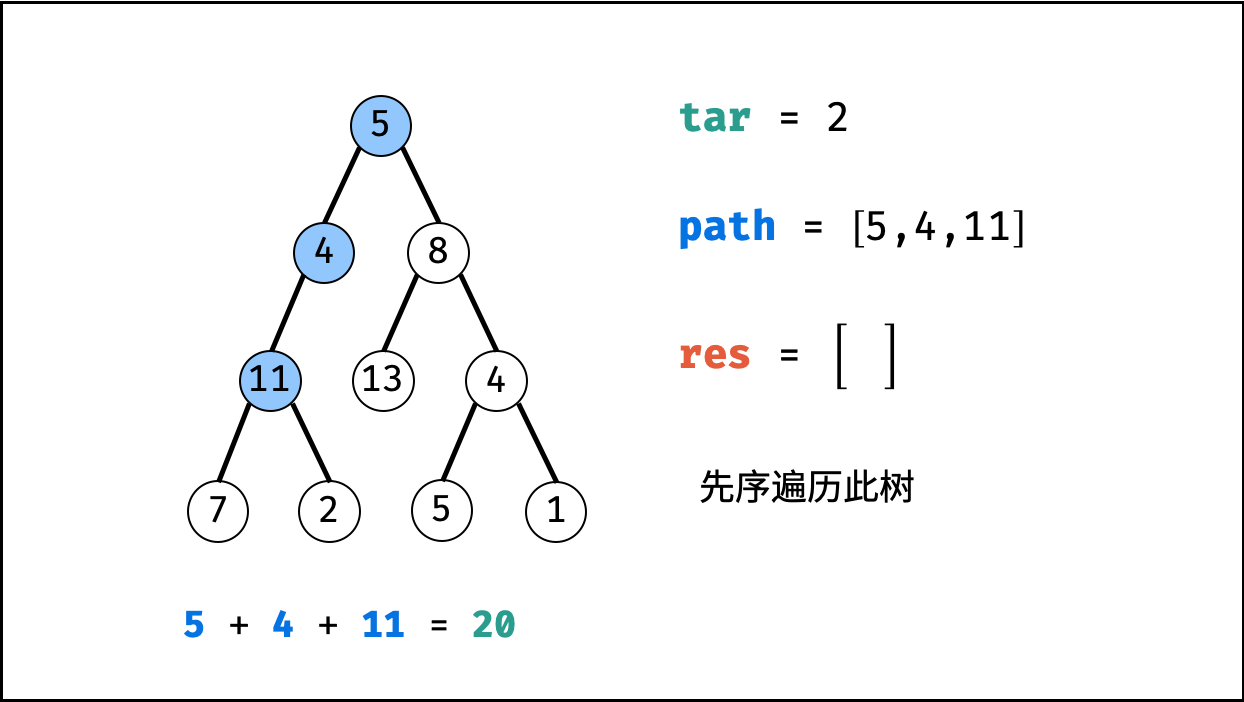
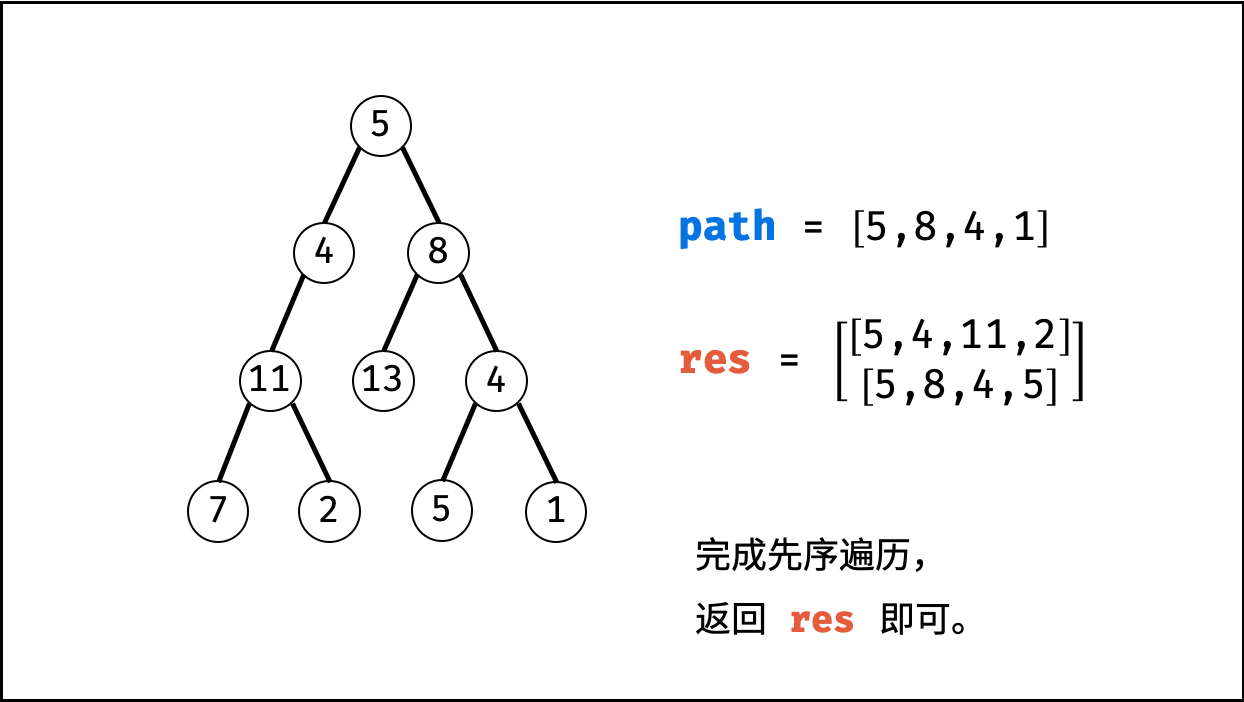
本题是典型的二叉树方案搜索问题，使用回溯法解决，其包含 先序遍历 + 路径记录 两部分。

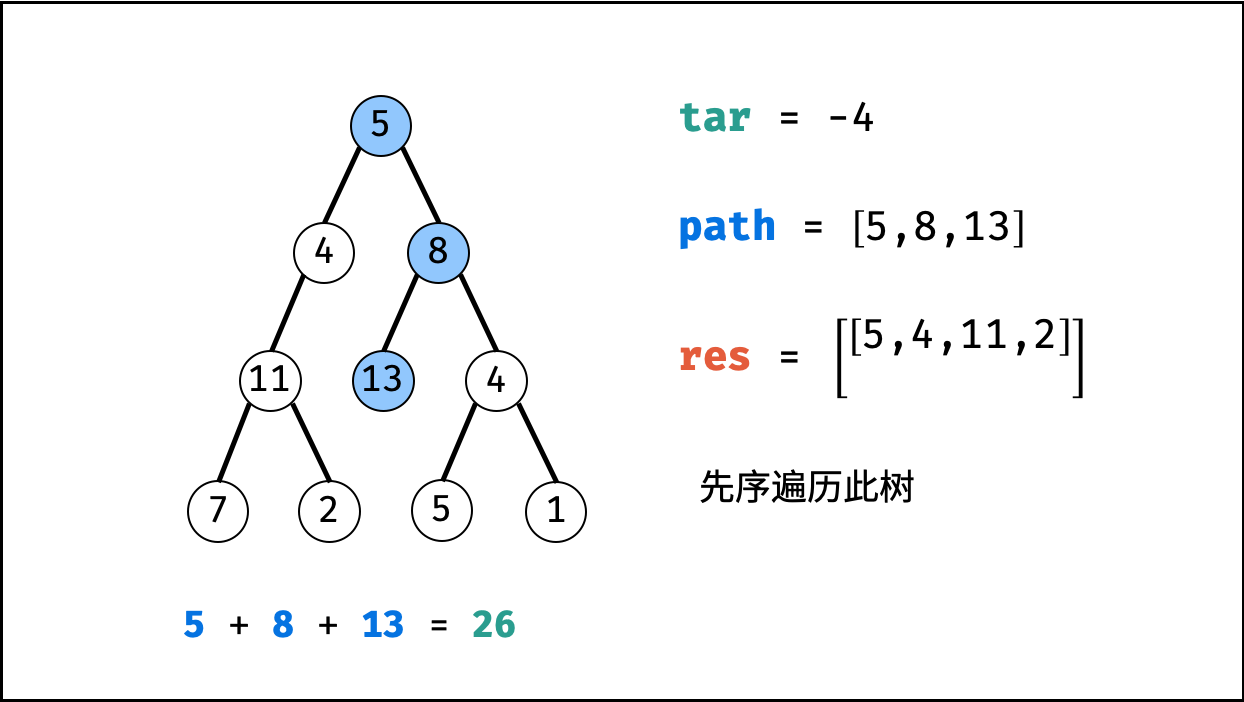
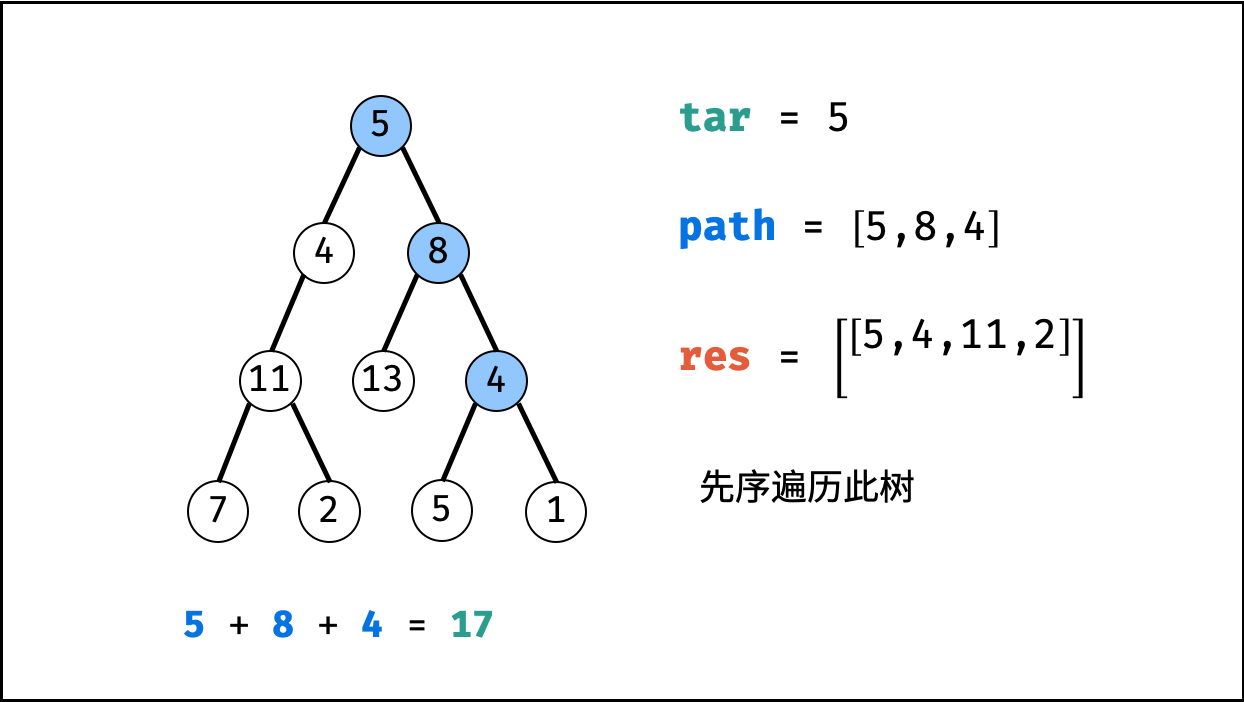
先序遍历： 按照 “根、左、右” 的顺序，遍历树的所有节点。
路径记录： 在先序遍历中，记录从根节点到当前节点的路径。当路径满足 (1) 根节点到叶节点形成的路径且 (2) 各节点值的和等于目标值 target 时，将此路径加入结果列表。

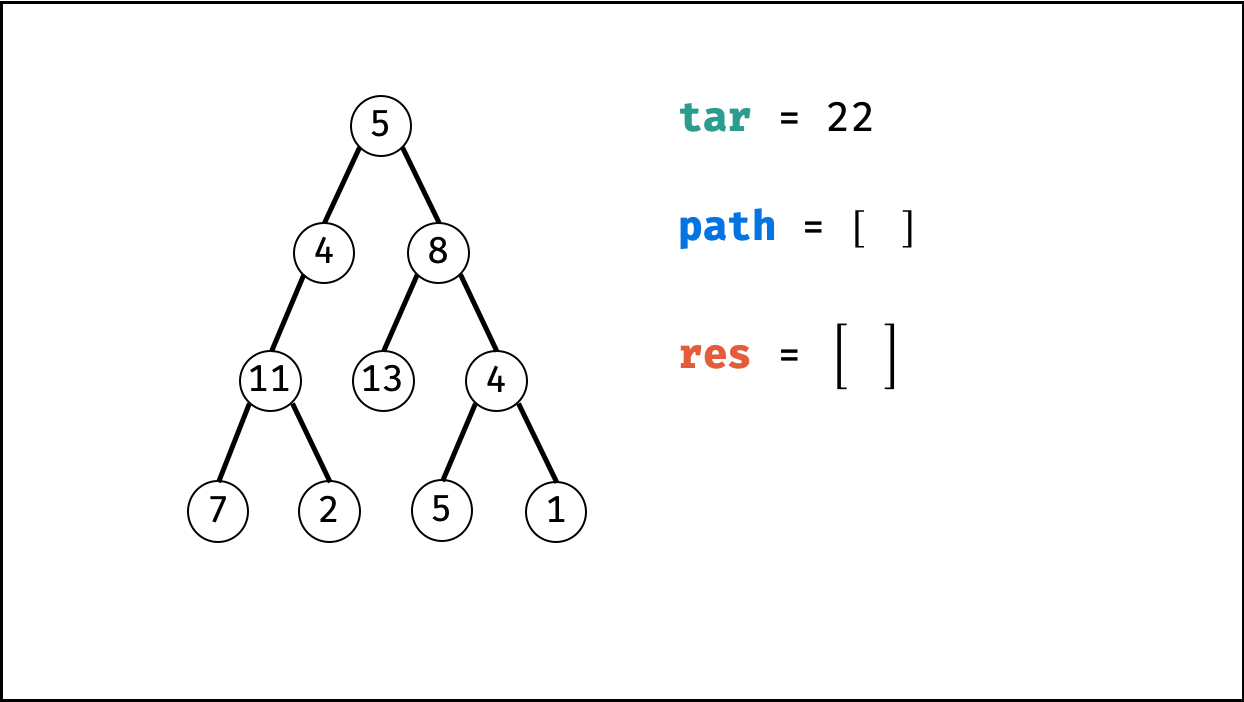
算法流程：

pathTarget(root, target) 函数：

初始化： 结果列表 res ，路径列表 path 。
返回值： 返回 res 即可。

recur(root, tar) 函数：

递推参数： 当前节点 root ，当前目标值 tar 。
终止条件： 若节点 root 为空，则直接返回。
递推工作：
1. 路径更新：将当前节点值 root.val 加入路径 path 。
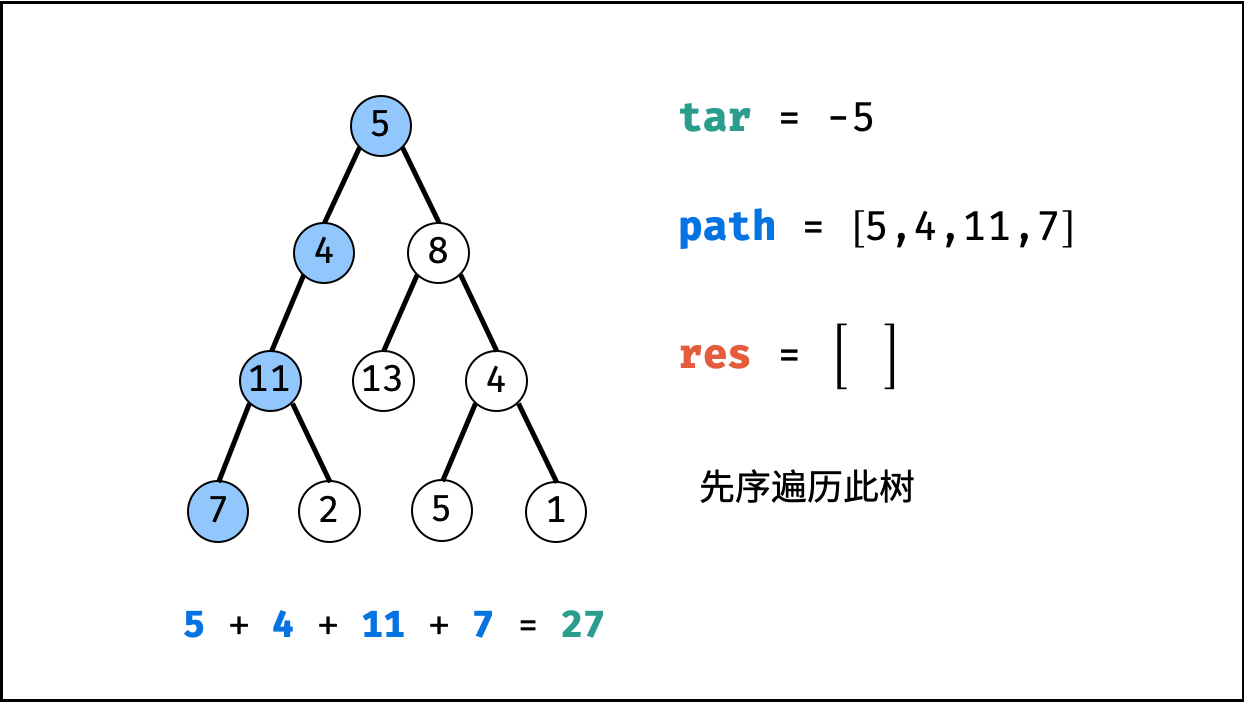
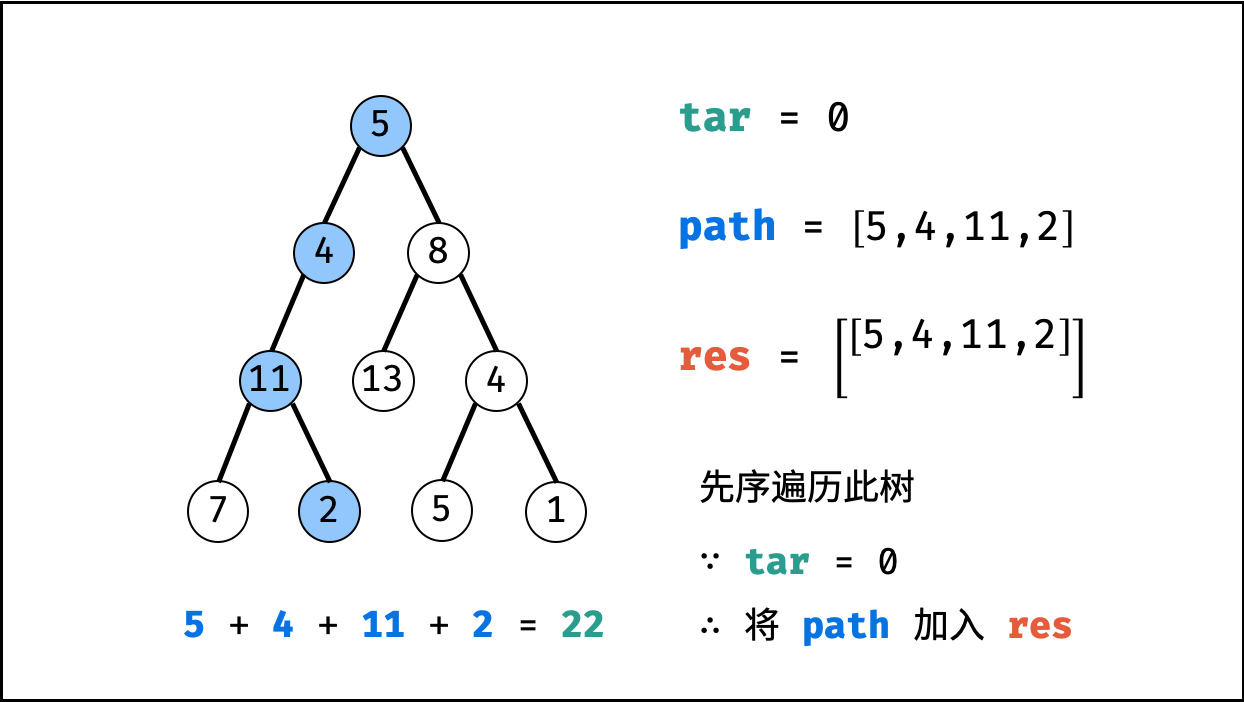
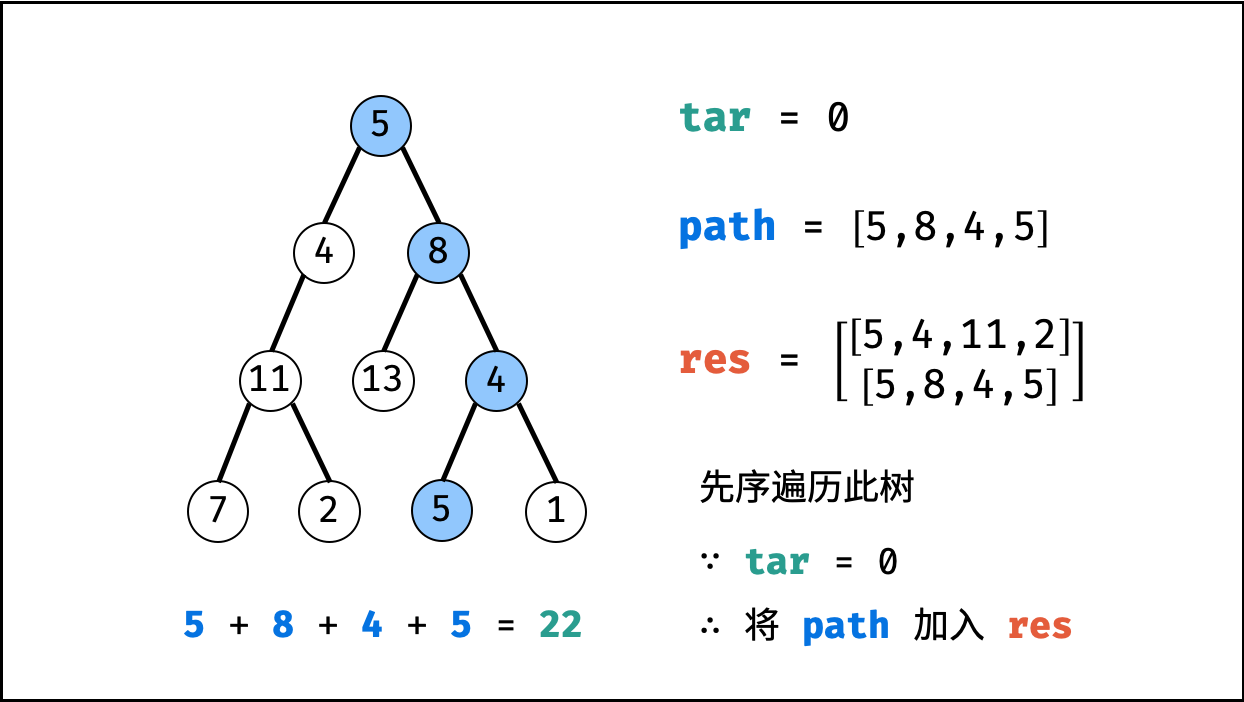
2. 目标值更新： tar = tar - root.val（即目标值 tar 从 target 减至 $0$ ）。
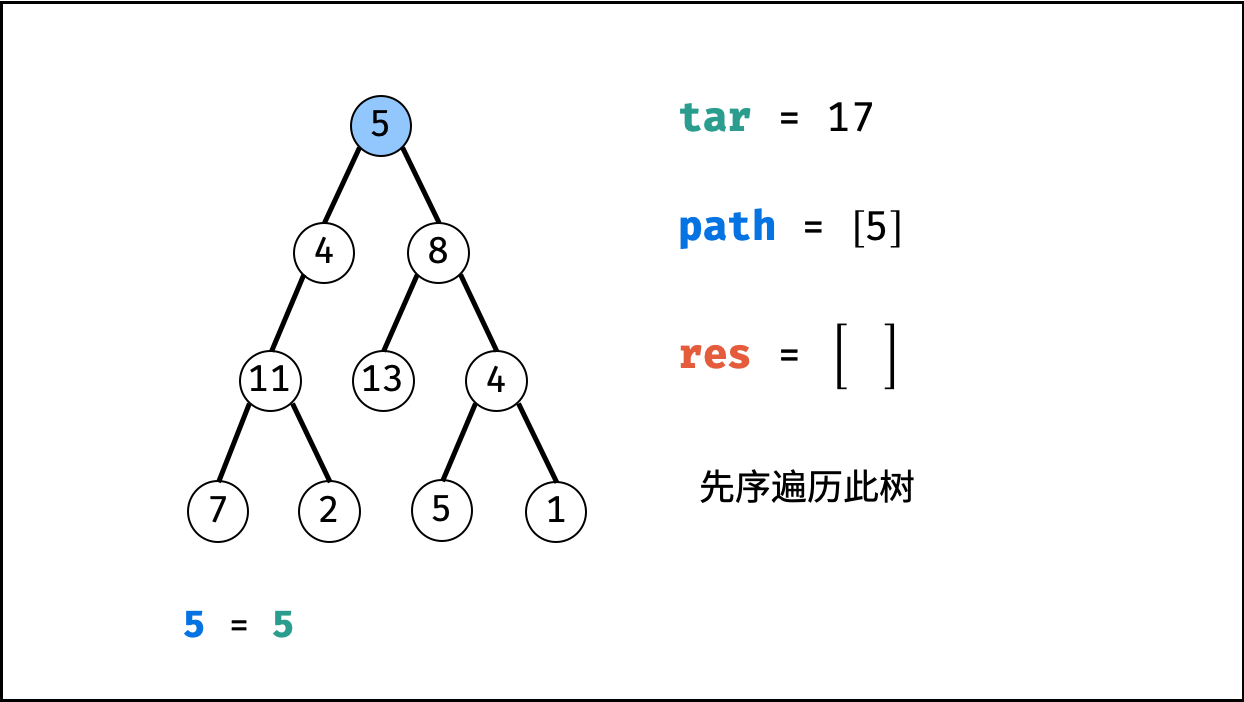
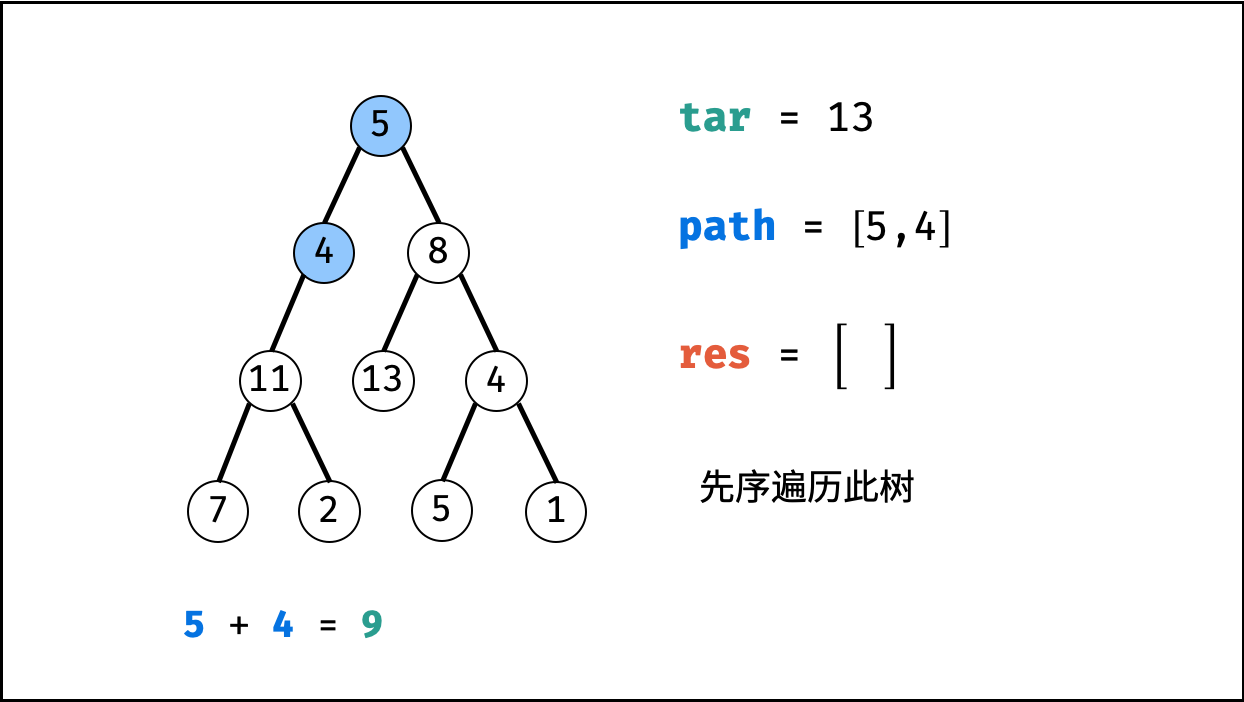
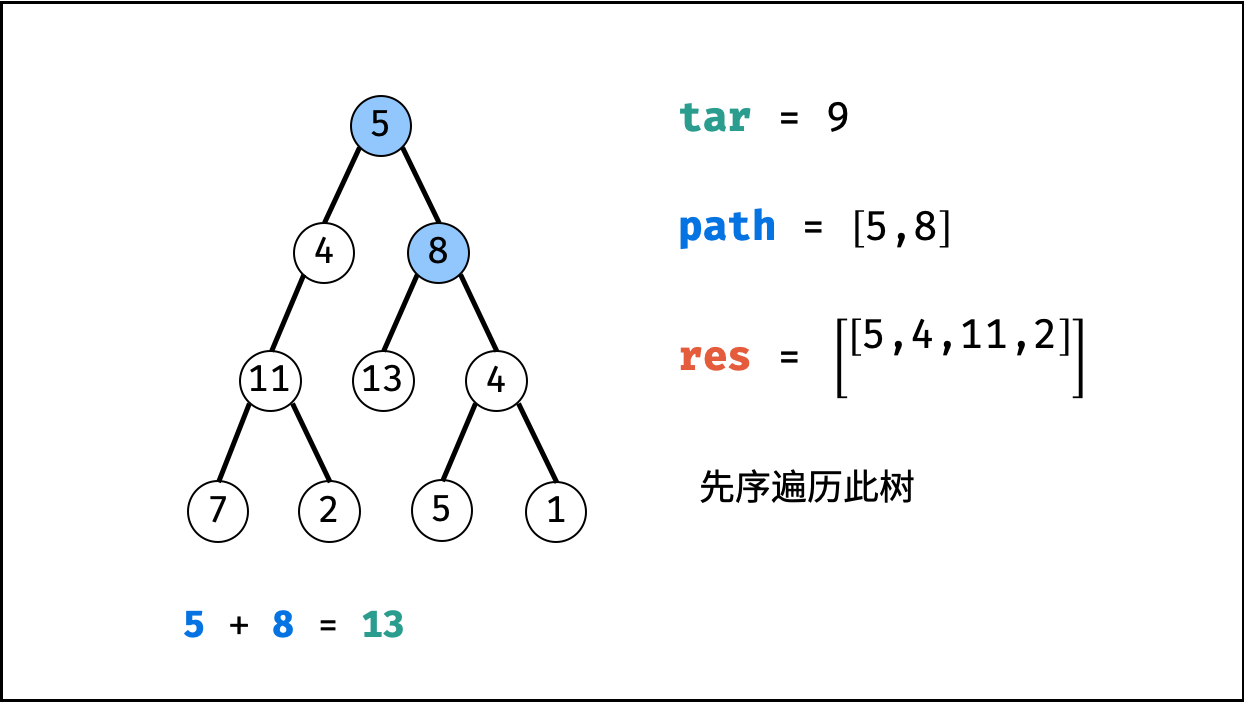
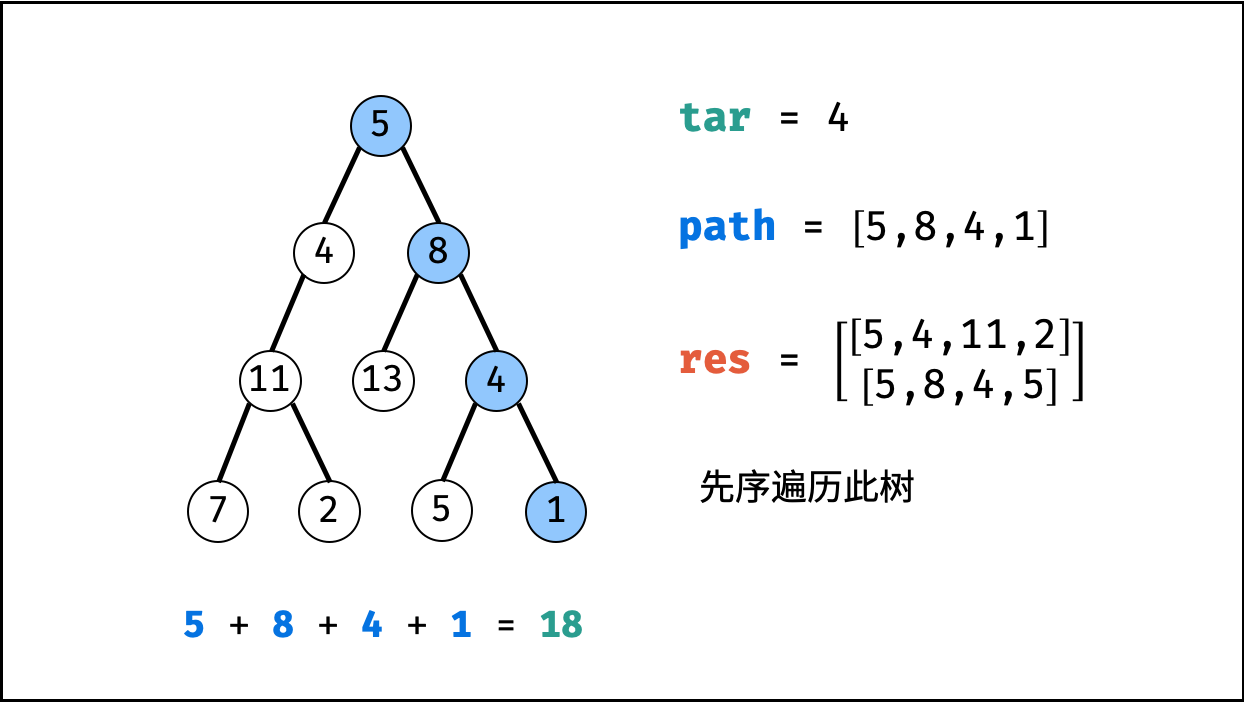
3. 路径记录：当 “root 为叶节点” 且 “路径和等于目标值” ，则将此路径 path 加入 res 。
4. 先序遍历：递归左 / 右子节点。
5. 路径恢复：向上回溯前，需要将当前节点从路径 path 中删除，即执行 path.pop() 。

<,,,,,,,,,,,>

代码：

以 Python 语言为例，记录路径时若直接执行 res.append(path) ，则是将此 path 对象加入了 res ；后续 path 改变时，res 中的 path 对象也会随之改变，因此无法实现结果记录。正确做法为：

Python: res.append(list(path)) ；
Java: res.add(new LinkedList(path)) ；
C++: res.push_back(path) ；

三者的原理都是避免直接添加 path 对象，而是拷贝了一个 path 对象并加入到 res 。

Python

class Solution:
    def pathTarget(self, root: TreeNode, target: int) -> List[List[int]]:
        res, path = [], []
        def recur(root, tar):
            if not root: return
            path.append(root.val)
            tar -= root.val
            if tar == 0 and not root.left and not root.right:
                res.append(list(path))
            recur(root.left, tar)
            recur(root.right, tar)
            path.pop()

        recur(root, target)
        return res

Java

class Solution {
    LinkedList<List<Integer>> res = new LinkedList<>();
    LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> pathTarget(TreeNode root, int target) {
        recur(root, target);
        return res;
    }
    void recur(TreeNode root, int tar) {
        if(root == null) return;
        path.add(root.val);
        tar -= root.val;
        if(tar == 0 && root.left == null && root.right == null)
            res.add(new LinkedList(path));
        recur(root.left, tar);
        recur(root.right, tar);
        path.removeLast();
    }
}

C++

class Solution {
public:
    vector<vector<int>> pathTarget(TreeNode* root, int target) {
        recur(root, target);
        return res;
    }
private:
    vector<vector<int>> res;
    vector<int> path;
    void recur(TreeNode* root, int tar) {
        if(root == nullptr) return;
        path.push_back(root->val);
        tar -= root->val;
        if(tar == 0 && root->left == nullptr && root->right == nullptr)
            res.push_back(path);
        recur(root->left, tar);
        recur(root->right, tar);
        path.pop_back();
    }
};

复杂度分析：

时间复杂度 $O(N)$ ： $N$ 为二叉树的节点数，先序遍历需要遍历所有节点。
空间复杂度 $O(N)$ ： 最差情况下，即树退化为链表时，path 存储所有树节点，使用 $O(N)$ 额外空间。

解题思路： ​

算法流程： ​

代码： ​

复杂度分析： ​

解题思路：

算法流程：

代码：

复杂度分析：