自律小屋 | 自律小屋

解题思路：

本题在简单问题上做了许多限制，需要使用排除法一步步导向答案。 $1+2+...+(target-1)+target$ 的计算方法主要有三种：平均计算、迭代、递归。

方法一： 平均计算 问题： 此计算必须使用 乘除法 ，因此本方法不可取，直接排除。

Java

public int mechanicalAccumulator(int target) {
    return (1 + target) * target / 2;
}

Python

def mechanicalAccumulator(target):
    return (1 + target) * target // 2

C++

int mechanicalAccumulator(int target) {
    return (1 + target) * target / 2;
}

方法二： 迭代 问题： 循环必须使用 $while$ 或 $for$ ，因此本方法不可取，直接排除。

Java

public int mechanicalAccumulator(int target) {
    int res = 0;
    for(int i = 1; i <= target; i++)
        res += i;
    return res;
}

Python

def mechanicalAccumulator(target):
    res = 0
    for i in range(1, target + 1):
        res += i
    return res

C++

int mechanicalAccumulator(int target) {
    int res = 0;
    for(int i = 1; i <= target; i++)
        res += i;
    return res;
}

方法三： 递归 问题： 终止条件需要使用 $if$ ，因此本方法不可取。 思考： 除了 $if$ 和 $switch$ 等判断语句外，是否有其他方法可用来终止递归？

Java

public int mechanicalAccumulator(int target) {
    if(target == 1) return 1;
    target += mechanicalAccumulator(target - 1);
    return target;
}

Python

def mechanicalAccumulator(target):
    if target == 1: return 1
    target += mechanicalAccumulator(target - 1)
    return target

C++

int mechanicalAccumulator(int target) {
    if(target == 1) return 1;
    target += mechanicalAccumulator(target - 1);
    return target;
}

下图中的 sumNums() 对应本题的 mechanicalAccumulator 。

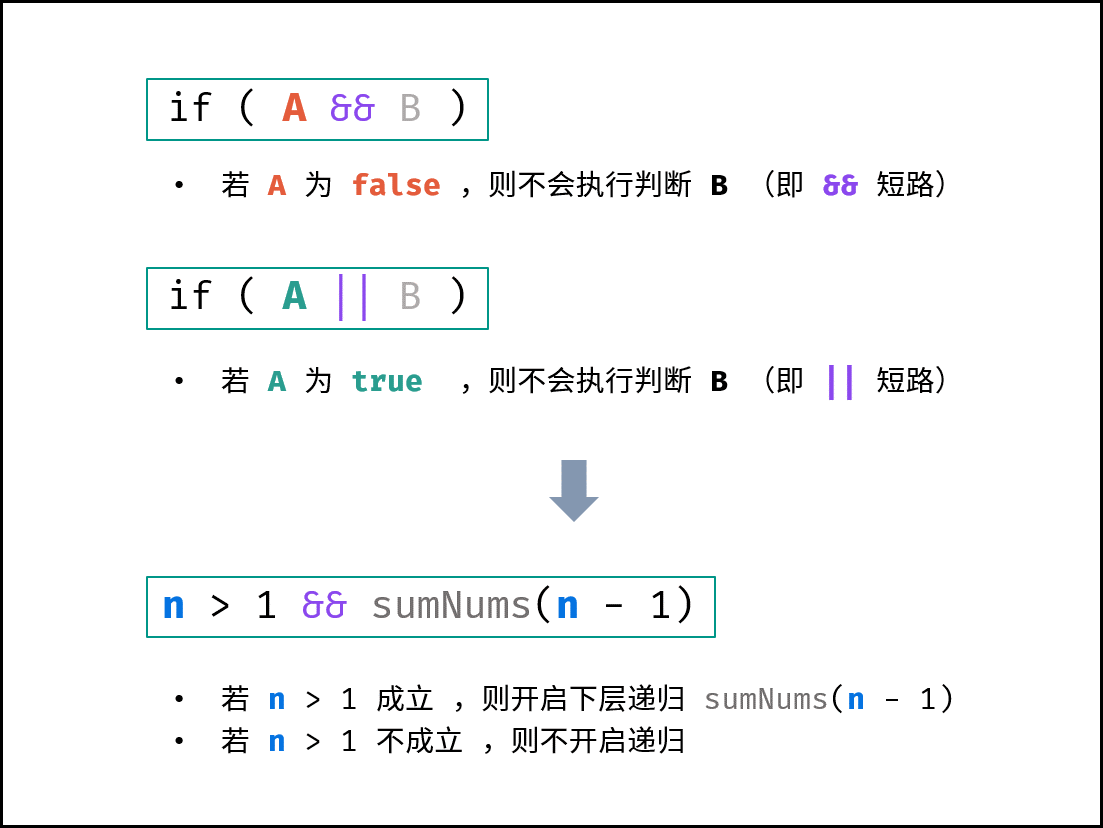
逻辑运算符的短路效应：

常见的逻辑运算符有三种，即 “与 $&&$ ”，“或 $||$ ”，“非 $!$ ” ；而其有重要的短路效应，如下所示：

Java

if(A && B)  // 若 A 为 false ，则 B 的判断不会执行（即短路），直接判定 A && B 为 false

if(A || B) // 若 A 为 true ，则 B 的判断不会执行（即短路），直接判定 A || B 为 true

本题需要实现 “当 $target = 1$ 时终止递归” 的需求，可通过短路效应实现。

Java

target > 1 && mechanicalAccumulator(target - 1) // 当 target = 1 时 target > 1 不成立 ，此时 “短路” ，终止后续递归

<,,,,,,,,>

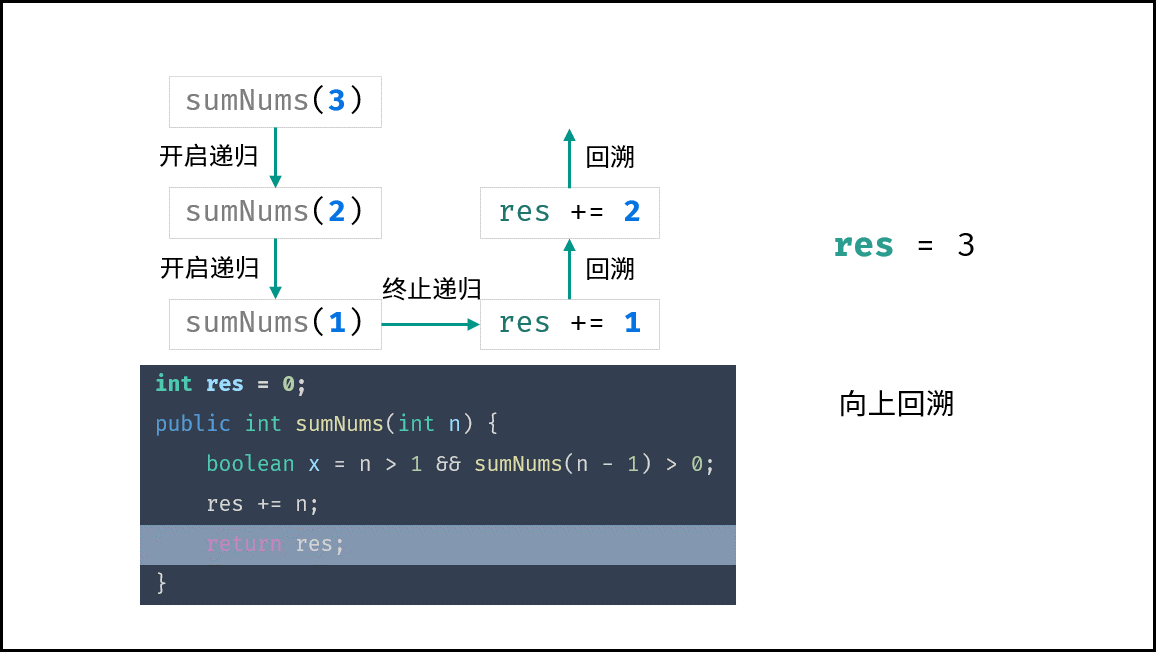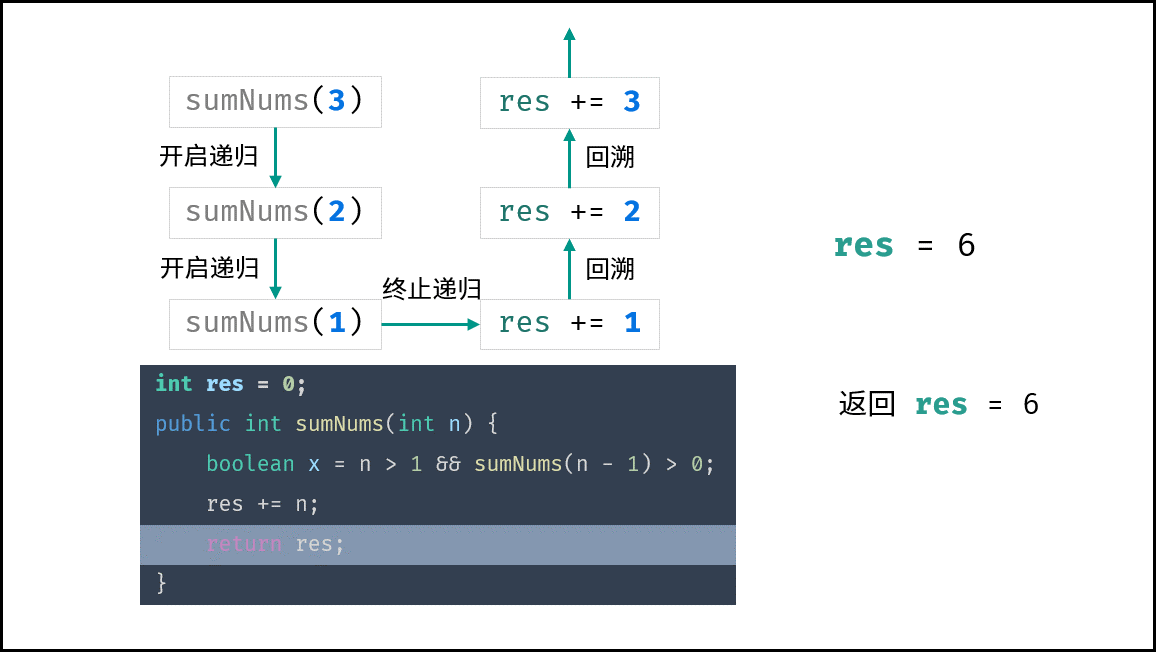代码：

Java 中，为构成语句，需加一个辅助布尔量 $x$ ，否则会报错；
Java 中，开启递归函数需改写为 mechanicalAccumulator(target - 1) > 0 ，此整体作为一个布尔量输出，否则会报错；
初始化变量 $res$ 记录结果。（ Java 可使用第二栏的简洁写法，不用借助变量 $res$ ）。

Java

class Solution {
    int res = 0;
    public int mechanicalAccumulator(int target) {
        boolean x = target > 1 && mechanicalAccumulator(target - 1) > 0;
        res += target;
        return res;
    }
}

Java

class Solution {
    public int mechanicalAccumulator(int target) {
        boolean x = target > 1 && (target += mechanicalAccumulator(target - 1)) > 0;
        return target;
    }
}

Python

class Solution:
    def __init__(self):
        self.res = 0
    def mechanicalAccumulator(self, target: int) -> int:
        target > 1 and self.mechanicalAccumulator(target - 1)
        self.res += target
        return self.res

C++

class Solution {
public:
    int mechanicalAccumulator(int target) {
        target > 1 && (target += mechanicalAccumulator(target - 1));
        return target;
    }
};

复杂度分析：

时间复杂度 $O(target)$ ： 计算 $target + (target-1) + ... + 2 + 1$ 需要开启 $target$ 个递归函数。
空间复杂度 $O(target)$ ： 递归深度达到 $target$ ，系统使用 $O(target)$ 大小的额外空间。

解题思路： ​

逻辑运算符的短路效应： ​

代码： ​

复杂度分析： ​

解题思路：

逻辑运算符的短路效应：

代码：

复杂度分析：