方法一：求和公式 ​

设连续正整数序列的左边界 $i$ 和右边界 $j$ ，则此序列的 元素和 $target$ 等于 元素平均值 $\frac{i + j}{2}$ 乘以 元素数量 $(j - i + 1)$ ，即：

$$ target = \frac{(i + j) \times (j - i + 1)}{2} $$

观察发现，当确定 元素和 $target$ 与 左边界 $i$ 时，可通过 解一元二次方程 ，直接计算出右边界 $j$ ，公式推导如下：

$$ \begin{aligned} target & = \frac{(i + j) \times (j - i + 1)}{2} \ & = \frac{j^2 + j - i^2 + i}{2} \ \end{aligned} $$

整理上式得：

$$ 0 = j^2 + j - (2 \times target + i^2 - i) $$

根据一元二次方程求根公式得：

$$ j = \frac{-1 \pm \sqrt{1 + 4(2 \times target + i^2 - i)}}{2} $$

由于 $j > i$ 恒成立，因此直接 舍去必为负数的解 ，即 $j$ 的唯一解求取公式为：

$$ \begin{aligned} j & = \frac{-1 + \sqrt{1 + 4(2 \times target + i^2 - i)}}{2} \end{aligned} $$

因此，通过从小到大遍历左边界 $i$ 来计算 以 $i$ 为起始数字的连续正整数序列 。每轮中，由以上公式计算得到右边界 $j$ ，当 $j$ 满足以下两个条件时记录结果：

1. $j$ 为 整数 ：符合题目所求「连续正整数序列」；
2. $i < j$ ：满足题目要求「至少含有两个数」；

当 $target = 9$ 时，以上求解流程如下图所示。

代码： ​

计算公式中 $i^2$ 项可能超过 int 类型取值范围，因此在 Java, C++ 中需要转化成 long 类型。

class Solution:
    def fileCombination(self, target: int):
        i, j, res = 1, 2, []
        while i < j:
            j = (-1 + (1 + 4 * (2 * target + i * i - i)) ** 0.5) / 2
            if i < j and j == int(j):
                res.append(list(range(i, int(j) + 1)))
            i += 1
        return res

class Solution {
    public int[][] fileCombination(int target) {
        int i = 1;
        double j = 2.0;
        List<int[]> res = new ArrayList<>();
        while(i < j) {
            j = (-1 + Math.sqrt(1 + 4 * (2 * target + (long) i * i - i))) / 2;
            if(i < j && j == (int)j) {
                int[] ans = new int[(int)j - i + 1];
                for(int k = i; k <= (int)j; k++)
                    ans[k - i] = k;
                res.add(ans);
            }
            i++;
        }
        return res.toArray(new int[0][]);
    }
}

class Solution {
public:
    vector<vector<int>> fileCombination(int target) {
        int i = 1;
        double j = 2.0;
        vector<vector<int>> res;
        while(i < j) {
            j = (-1 + sqrt(1 + 4 * (2 * target + (long) i * i - i))) / 2;
            if(i < j && j == (int)j) {
                vector<int> ans;
                for(int k = i; k <= (int)j; k++)
                    ans.push_back(k);
                res.push_back(ans);
            }
            i++;
        }
        return res;
    }
};

复杂度分析： ​

• 时间复杂度 $O(N)$ ： 其中 $N = target$ ；连续整数序列至少有两个数字，而 $i < j$ 恒成立，因此至多循环 $\frac{target}{2}$ 次，使用 $O(N)$ 时间；循环内，计算 $j$ 使用 $O(1)$ 时间；当 $i = 1$ 时，达到最大序列长度 $\frac{-1 + \sqrt{1 + 8s}}{2}$ ，考虑到解的稀疏性，将列表构建时间简化考虑为 $O(1)$ ；
• 空间复杂度 $O(1)$ ： 变量 $i$ , $j$ 使用常数大小的额外空间。

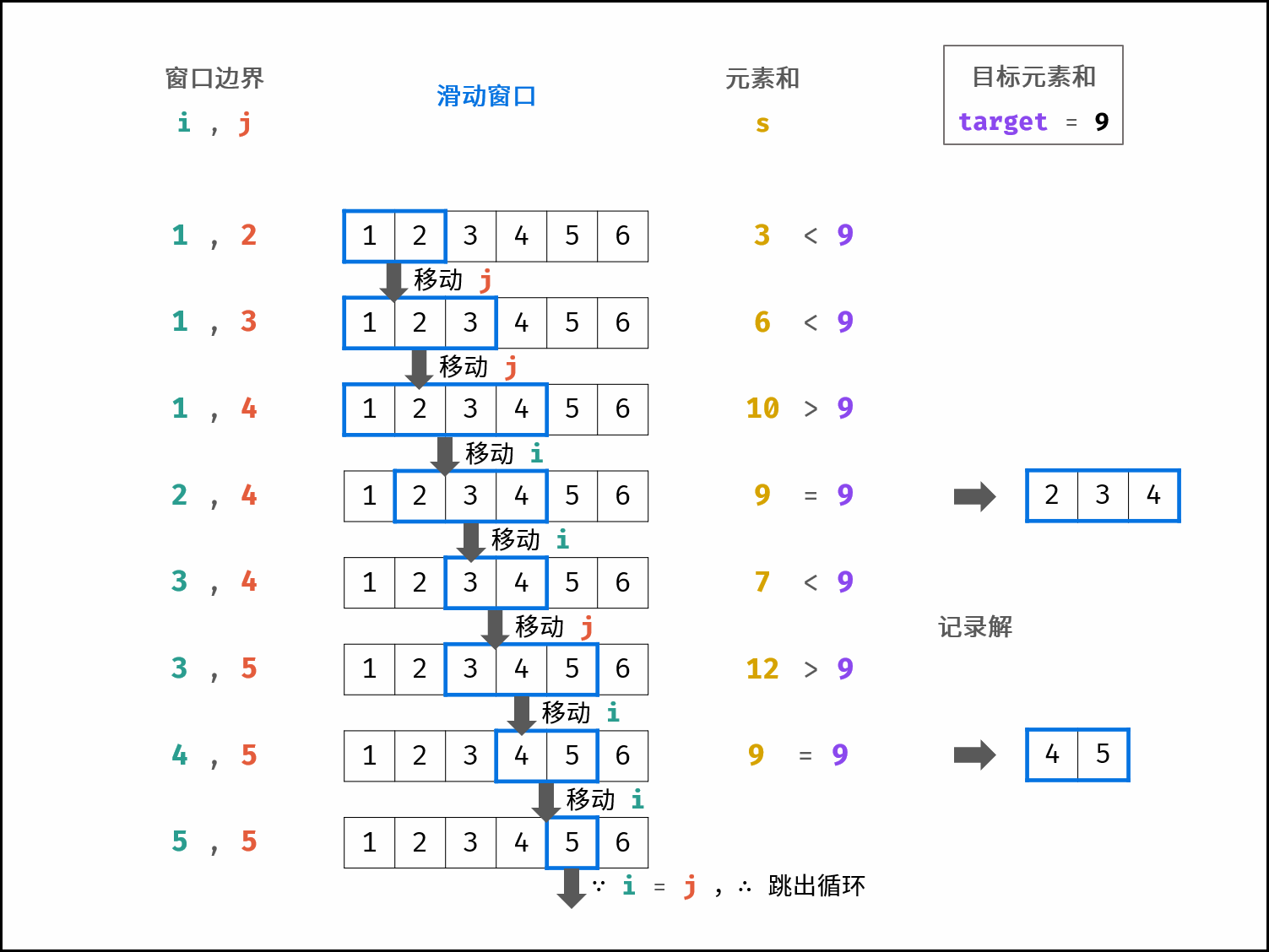
方法二：滑动窗口 ​

设连续正整数序列的左边界 $i$ 和右边界 $j$ ，则可构建滑动窗口从左向右滑动。循环中，每轮判断滑动窗口内元素和与目标值 $target$ 的大小关系，若相等则记录结果，若大于 $target$ 则移动左边界 $i$ （以减小窗口内的元素和），若小于 $target$ 则移动右边界 $j$ （以增大窗口内的元素和）。

算法流程： ​

1. 初始化： 左边界 $i = 1$ ，右边界 $j = 2$ ，元素和 $s = 3$ ，结果列表 $res$ ；

2. 循环： 当 $i \geq j$ 时跳出；

   • 当 $s > target$ 时： 向右移动左边界 $i = i + 1$ ，并更新元素和 $s$ ；
   • 当 $s < target$ 时： 向右移动右边界 $j = j + 1$ ，并更新元素和 $s$ ；
   • 当 $s = target$ 时： 记录连续整数序列，并向右移动左边界 $i = i + 1$ ；

3. 返回值： 返回结果列表 $res$ ；

当 $target = 9$ 时，以上求解流程如下图所示：

代码： ​

观察本文的算法流程发现，当 $s = target$ 和 $s > target$ 的移动边界操作相同，因此可以合并，代码如下所示。

class Solution:
    def fileCombination(self, target: int) -> List[List[int]]:
        i, j, s, res = 1, 2, 3, []
        while i < j:
            if s == target:
                res.append(list(range(i, j + 1)))
            if s >= target:
                s -= i
                i += 1
            else:
                j += 1
                s += j
        return res

class Solution {
    public int[][] fileCombination(int target) {
        int i = 1, j = 2, s = 3;
        List<int[]> res = new ArrayList<>();
        while(i < j) {
            if(s == target) {
                int[] ans = new int[j - i + 1];
                for(int k = i; k <= j; k++)
                    ans[k - i] = k;
                res.add(ans);
            }
            if(s >= target) {
                s -= i;
                i++;
            } else {
                j++;
                s += j;
            }
        }
        return res.toArray(new int[0][]);
    }
}

class Solution {
public:
    vector<vector<int>> fileCombination(int target) {
        int i = 1, j = 2, s = 3;
        vector<vector<int>> res;
        while(i < j) {
            if(s == target) {
                vector<int> ans;
                for(int k = i; k <= j; k++)
                    ans.push_back(k);
                res.push_back(ans);
            }
            if(s >= target) {
                s -= i;
                i++;
            } else {
                j++;
                s += j;
            }
        }
        return res;
    }
};

复杂度分析： ​

• 时间复杂度 $O(N)$ ： 其中 $N = target$ ；连续整数序列至少有两个数字，而 $i < j$ 恒成立，因此至多循环 $target$ 次（ $i$ , $j$ 都移动到 $\frac{target}{2}$ ），使用 $O(N)$ 时间；当 $i = 1$ 时，达到最大序列长度 $\frac{-1 + \sqrt{1 + 8s}}{2}$ ，考虑到解的稀疏性，将列表构建时间简化考虑为 $O(1)$ ；
• 空间复杂度 $O(1)$ ： 变量 $i$ , $j$ , $s$ 使用常数大小的额外空间。