解题思路： ​

如下图所示，给定一个放入序列 putIn 和拿取序列 takeOut ，则放入（压栈）和拿取（弹出）操作的顺序是 唯一确定 的。

下图中 pushed 和 popped 分别对应本题的 putIn 和 takeOut 。

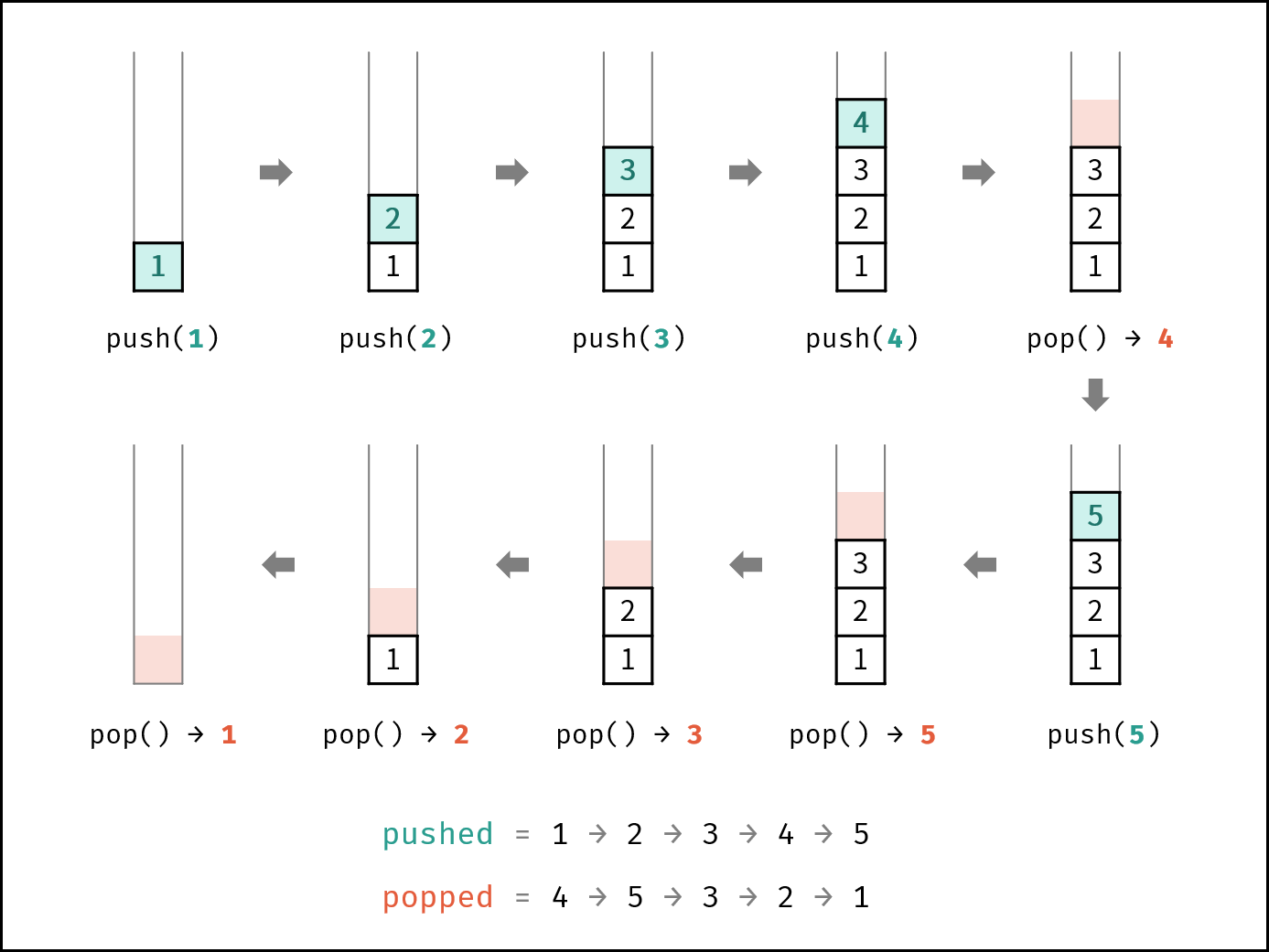
如下图所示，栈的数据操作具有 先入后出 的特性，因此某些拿取序列是无法实现的。

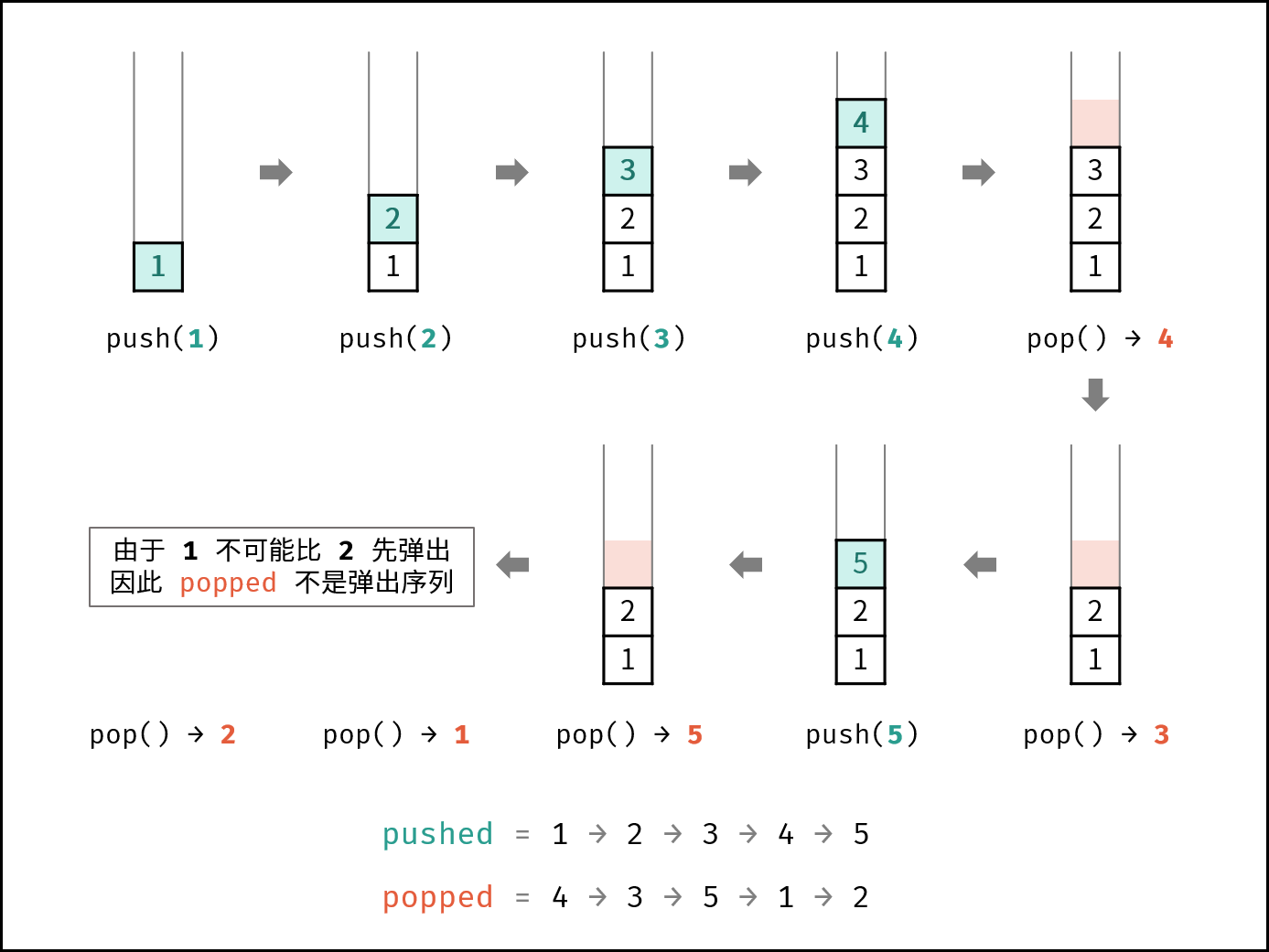
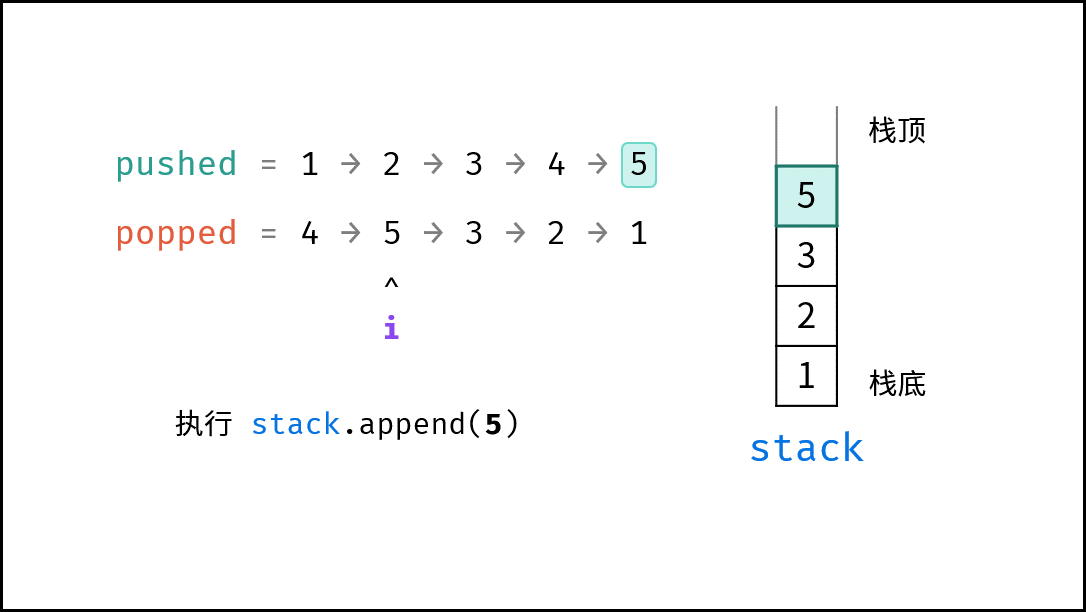
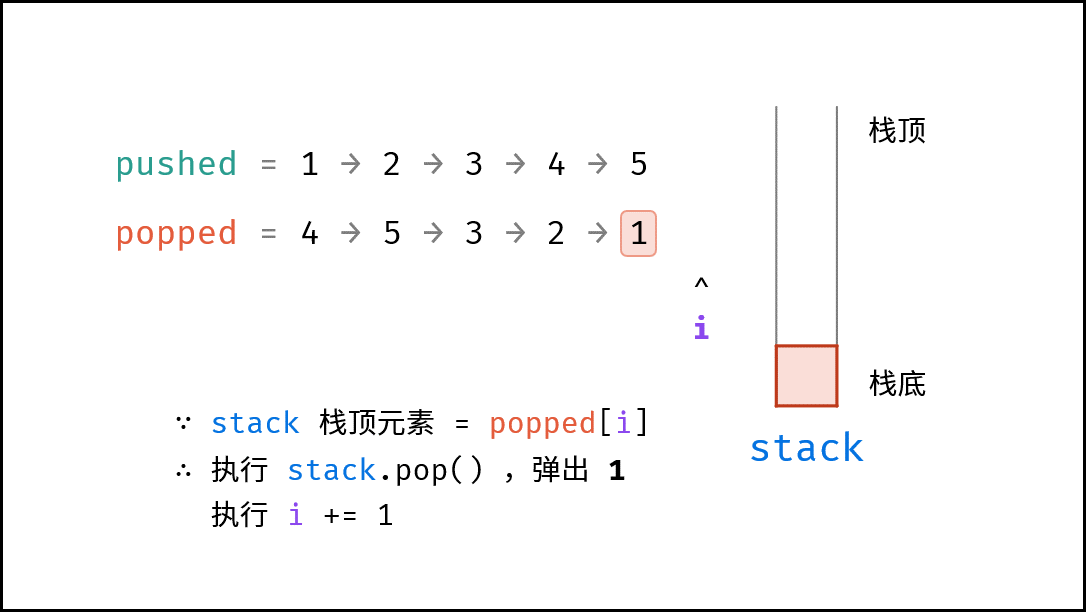
考虑借用一个辅助栈 stack ，模拟 放入 / 拿取操作的排列。根据是否模拟成功，即可得到结果。

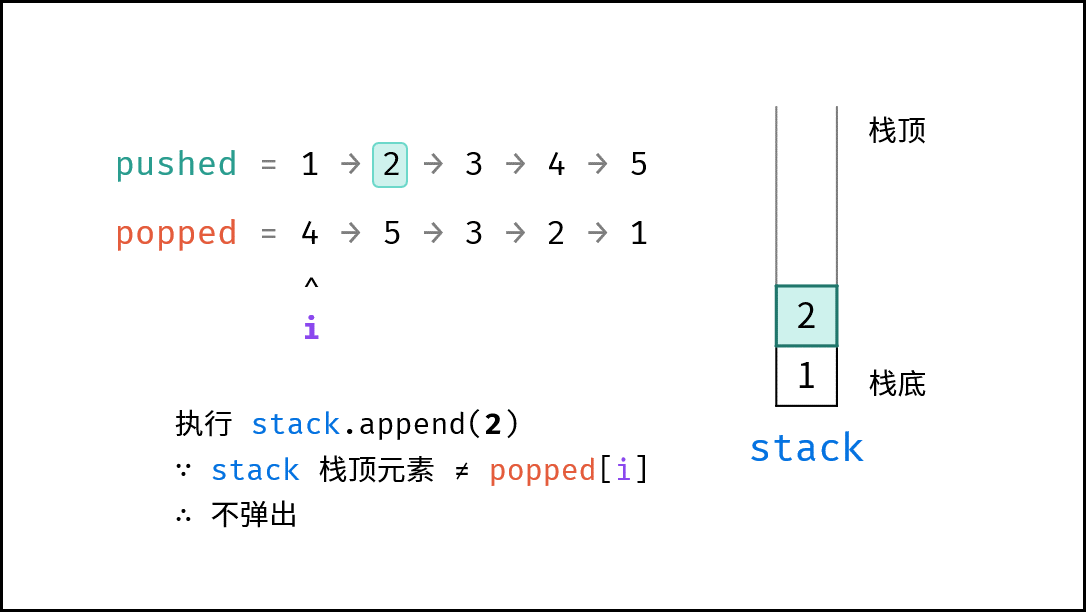
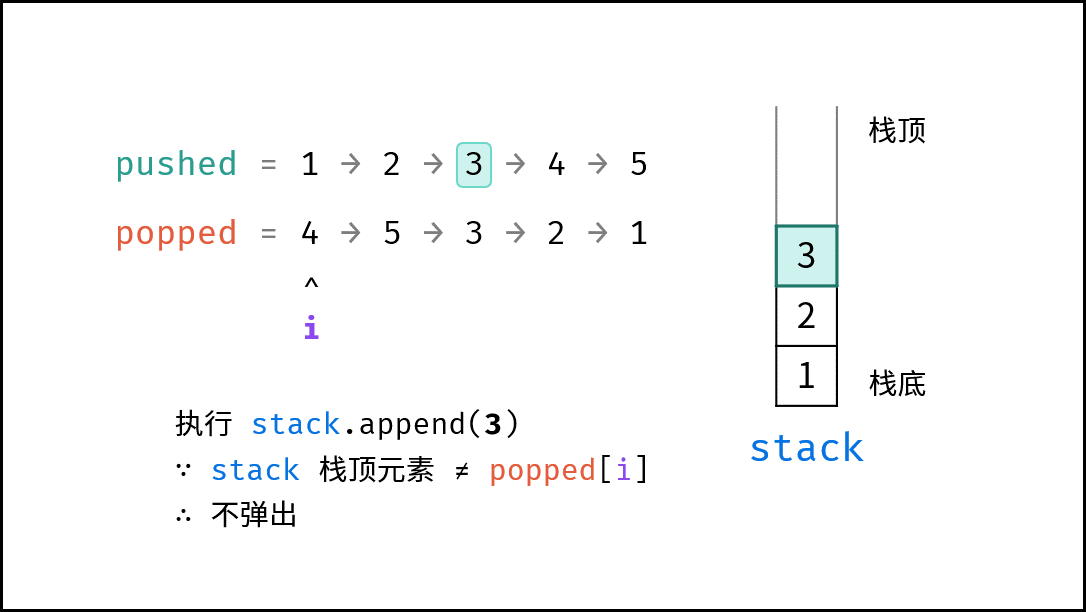
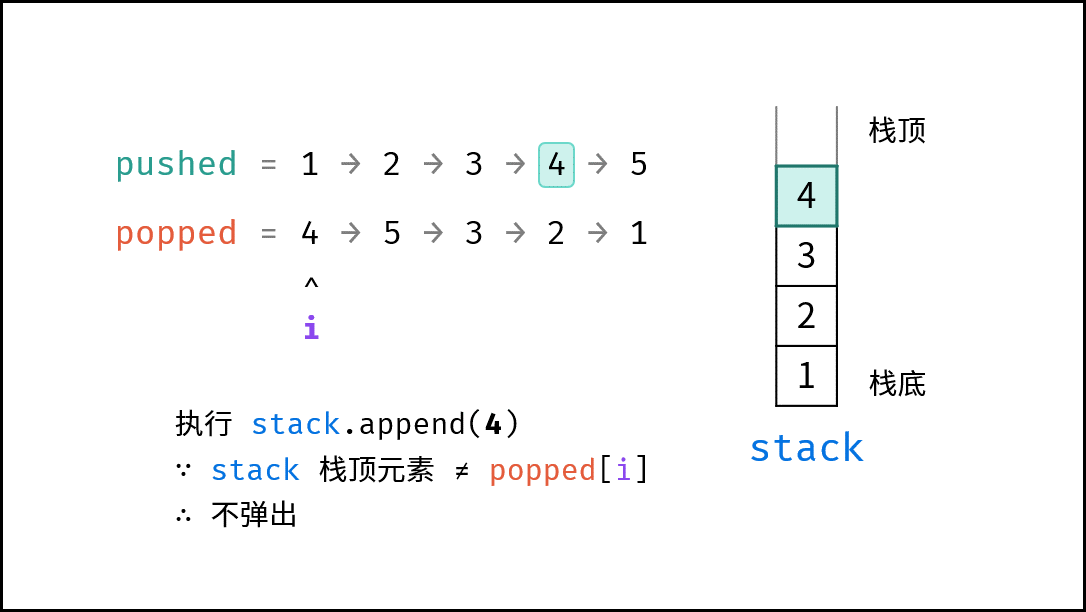
• 入栈操作： 按照压栈序列的顺序执行。
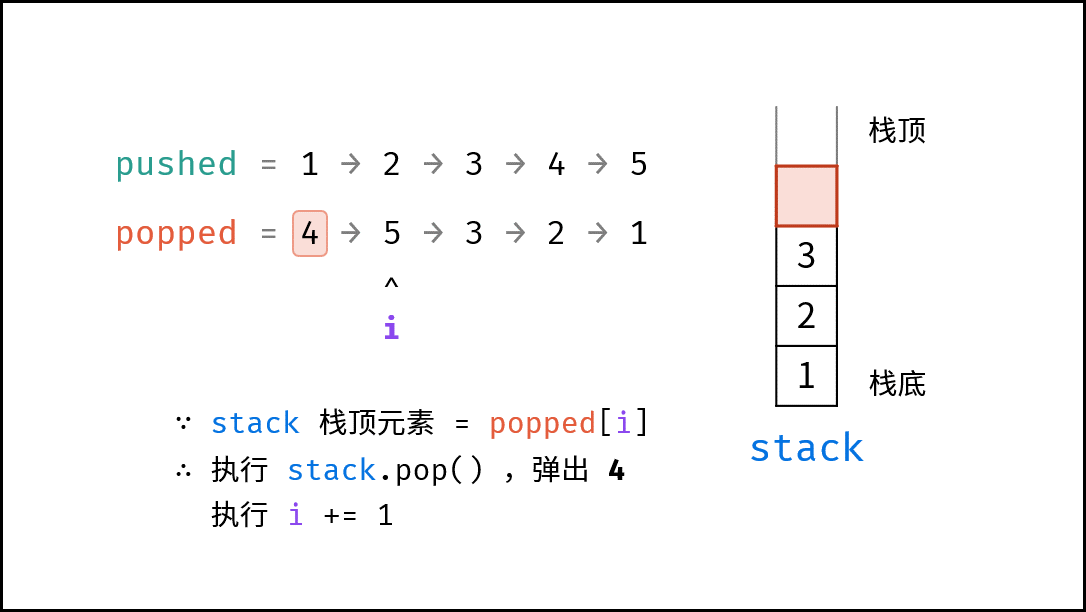
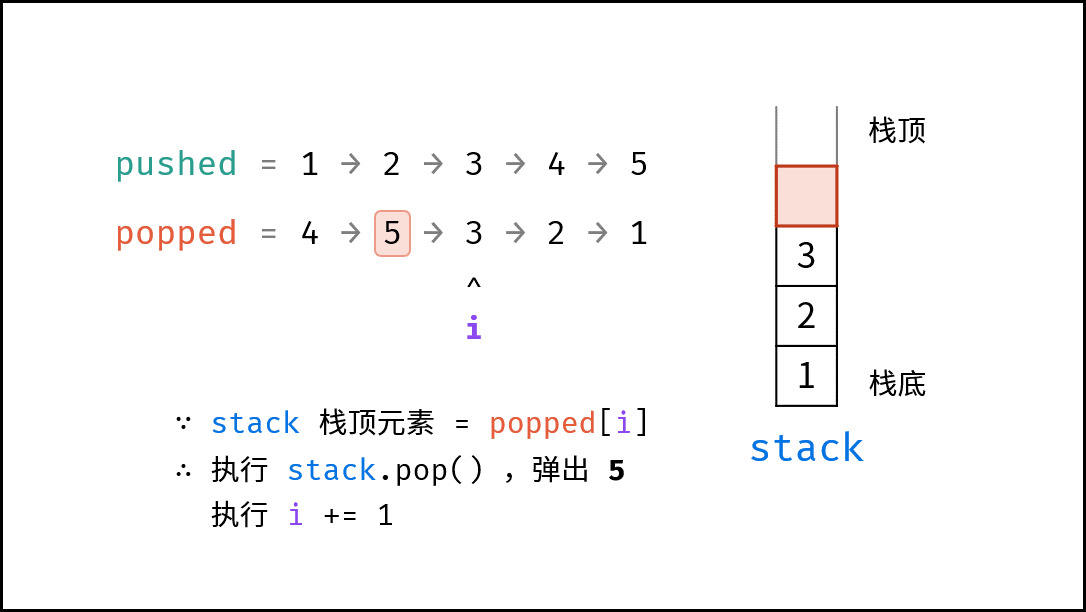
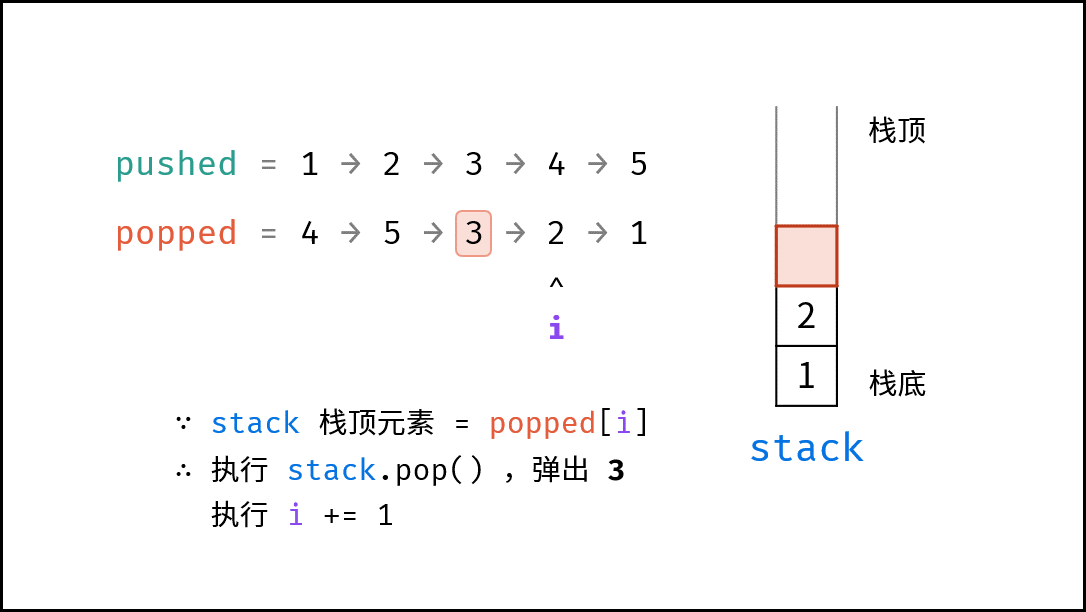
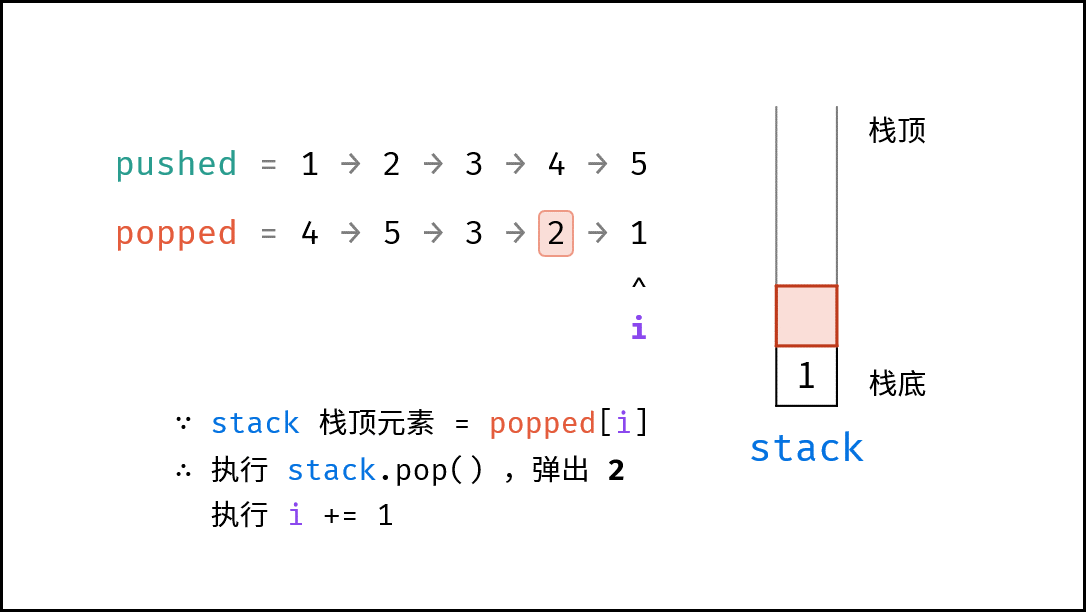
• 出栈操作： 每次入栈后，循环判断 “栈顶元素 $=$ 拿取序列的当前元素” 是否成立，将符合拿取序列顺序的栈顶元素全部拿取。

由于题目规定 “栈的所有数字均不相等” ，因此在循环入栈中，每个元素出栈的位置的可能性是唯一的（若有重复数字，则具有多个可出栈的位置）。因而，在遇到 “栈顶元素 $=$ 拿取序列的当前元素” 就应立即执行出栈。

算法流程： ​

1. 初始化： 辅助栈 stack ，拿取序列的索引 i ；
2. 遍历压栈序列： 各元素记为 num ；
   1. 元素 num 入栈；
   2. 循环出栈：若 stack 的栈顶元素 $=$ 拿取序列元素 takeOut[i] ，则执行出栈与 i++ ；
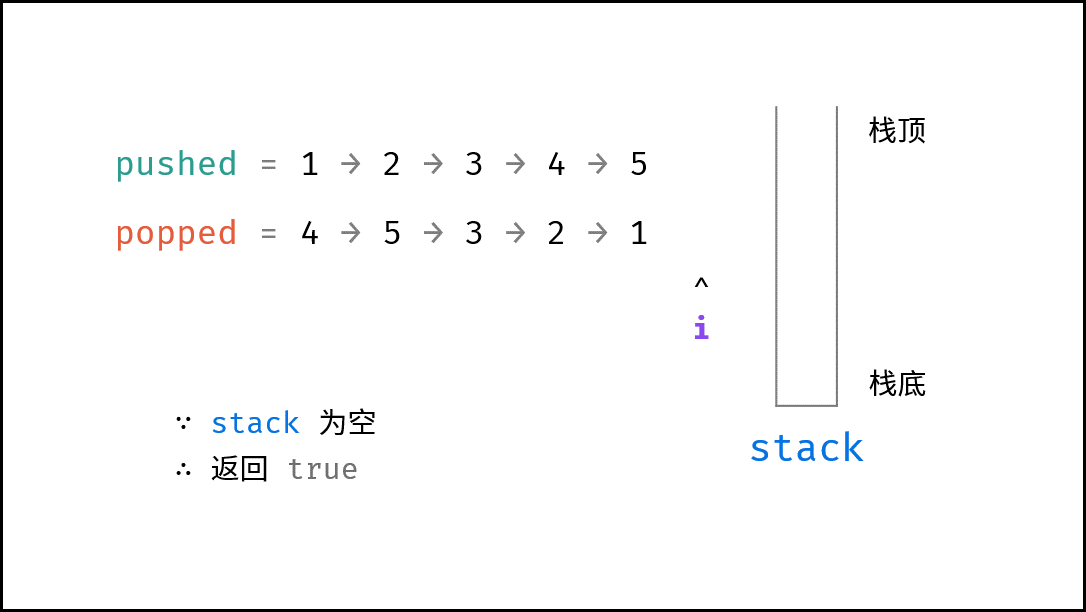
3. 返回值： 若 stack 为空，则此拿取序列合法。

<,,,,,,,,,,,>

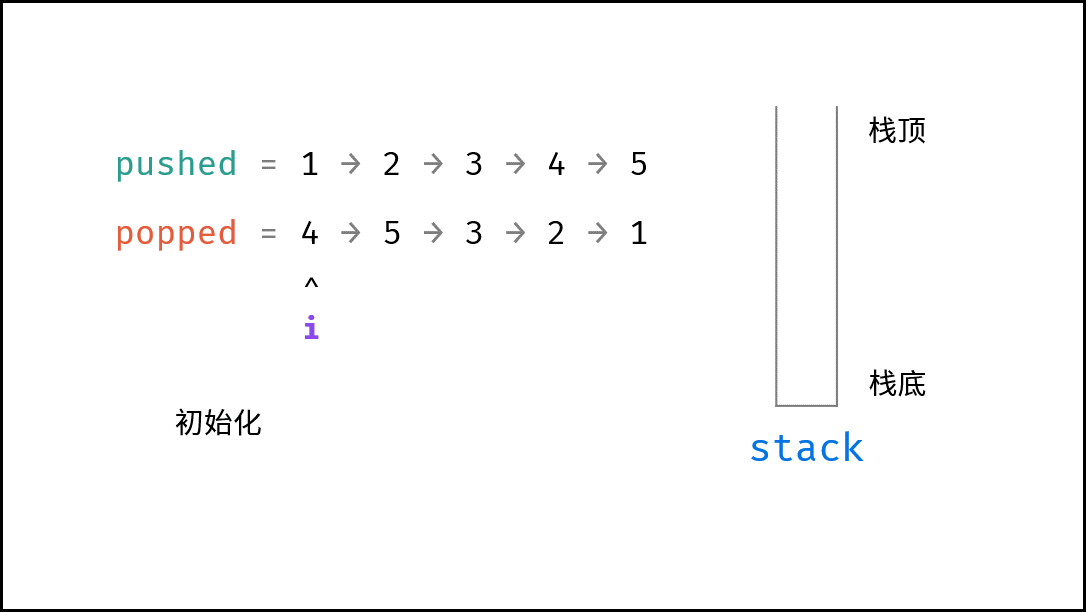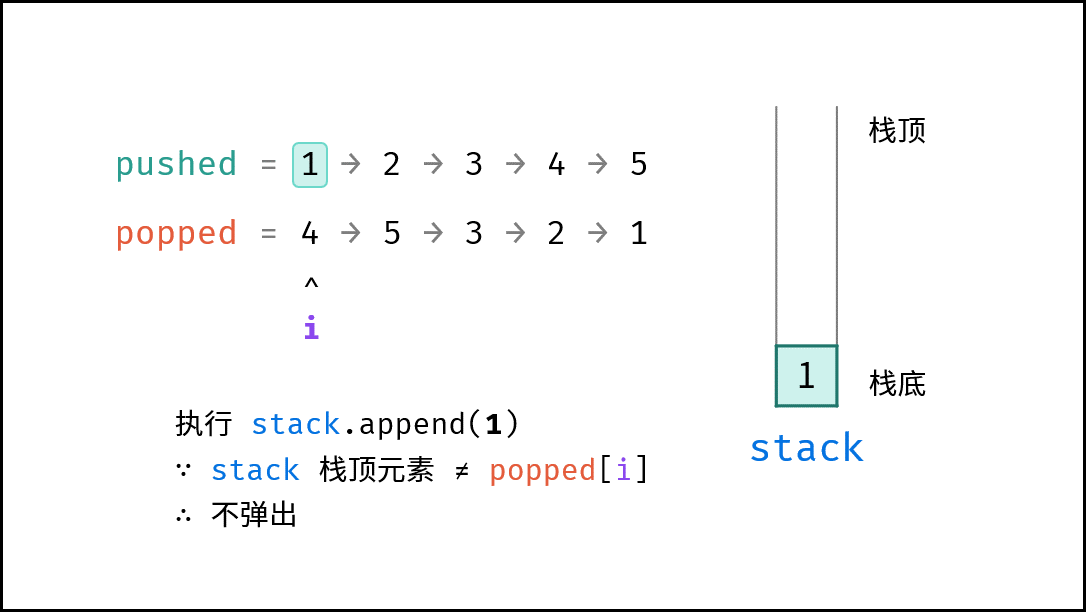代码： ​

题目指出 “putIn 是 takeOut 的排列” 。因此，无需考虑 putIn 和 takeOut 长度不同 或 包含元素不同 的情况。

class Solution:
    def validateBookSequences(self, putIn: List[int], takeOut: List[int]) -> bool:
        stack, i = [], 0
        for num in putIn:
            stack.append(num) # num 入栈
            while stack and stack[-1] == takeOut[i]: # 循环判断与出栈
                stack.pop()
                i += 1
        return not stack

class Solution {
    public boolean validateBookSequences(int[] putIn, int[] takeOut) {
        Stack<Integer> stack = new Stack<>();
        int i = 0;
        for(int num : putIn) {
            stack.push(num); // num 入栈
            while(!stack.isEmpty() && stack.peek() == takeOut[i]) { // 循环判断与出栈
                stack.pop();
                i++;
            }
        }
        return stack.isEmpty();
    }
}

class Solution {
public:
    bool validateBookSequences(vector<int>& putIn, vector<int>& takeOut) {
        stack<int> stk;
        int i = 0;
        for(int num : putIn) {
            stk.push(num); // num 入栈
            while(!stk.empty() && stk.top() == takeOut[i]) { // 循环判断与出栈
                stk.pop();
                i++;
            }
        }
        return stk.empty();
    }
};

复杂度分析： ​

• 时间复杂度 $O(N)$ ： 其中 $N$ 为列表 putIn 的长度；每个元素最多入栈与出栈一次，即最多共 $2N$ 次出入栈操作。
• 空间复杂度 $O(N)$ ： 辅助栈 stack 最多同时存储 $N$ 个元素。