解题思路： ​

直观来看，使用暴力统计法即可，即遍历数组的所有数字对并统计逆序对数量。此方法时间复杂度为 $O(N^2)$ ，观察题目给定的数组长度范围 $0 \leq N \leq 50000$ ，可知此复杂度是不能接受的。

「归并排序」与「逆序对」是息息相关的。归并排序体现了 “分而治之” 的算法思想，具体为：

• 分： 不断将数组从中点位置划分开（即二分法），将整个数组的排序问题转化为子数组的排序问题；
• 治： 划分到子数组长度为 1 时，开始向上合并，不断将 较短排序数组 合并为 较长排序数组，直至合并至原数组时完成排序；

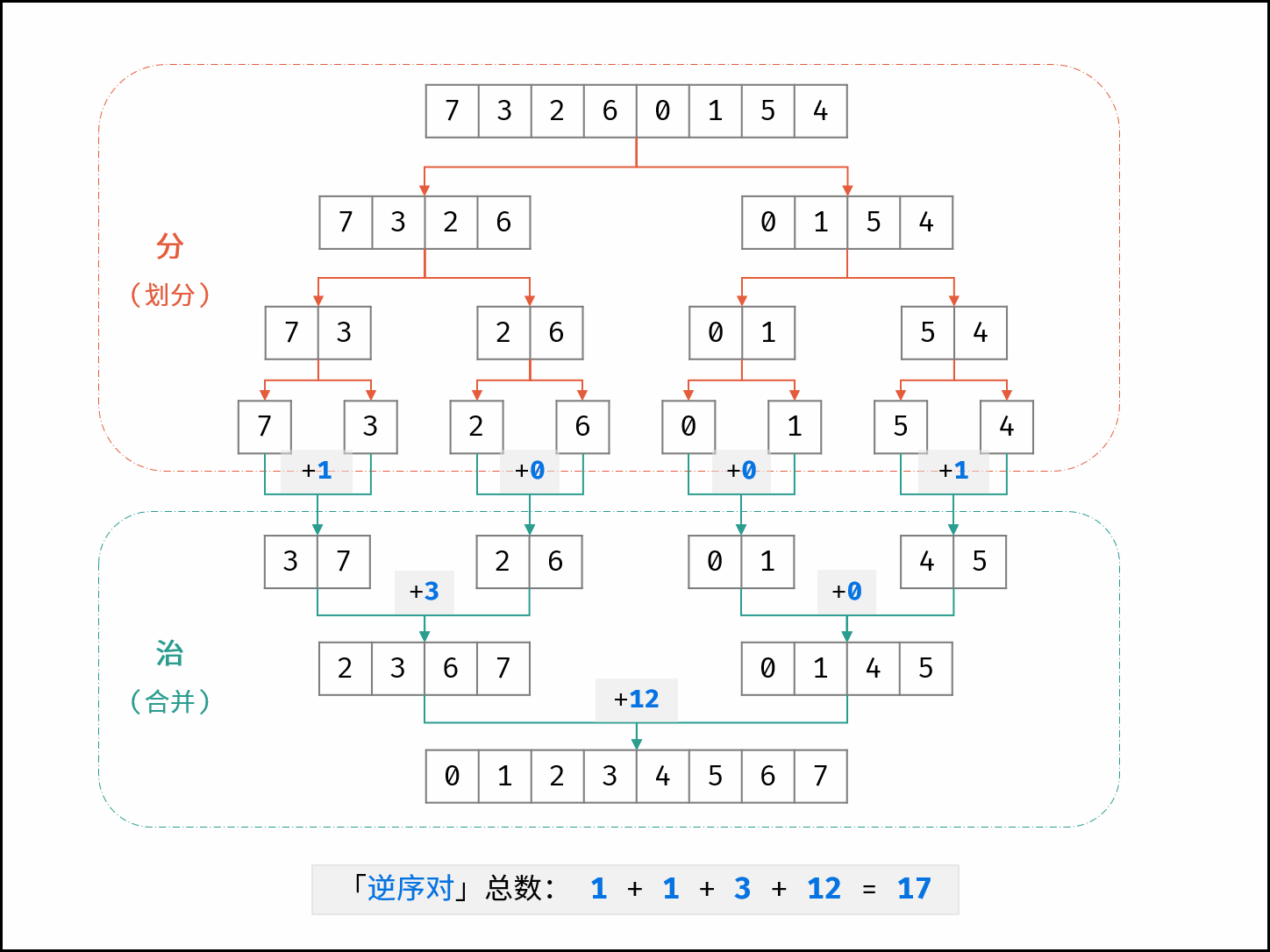
如下图所示，为数组 $[7, 3, 2, 6, 0, 1, 5, 4]$ 的归并排序过程。

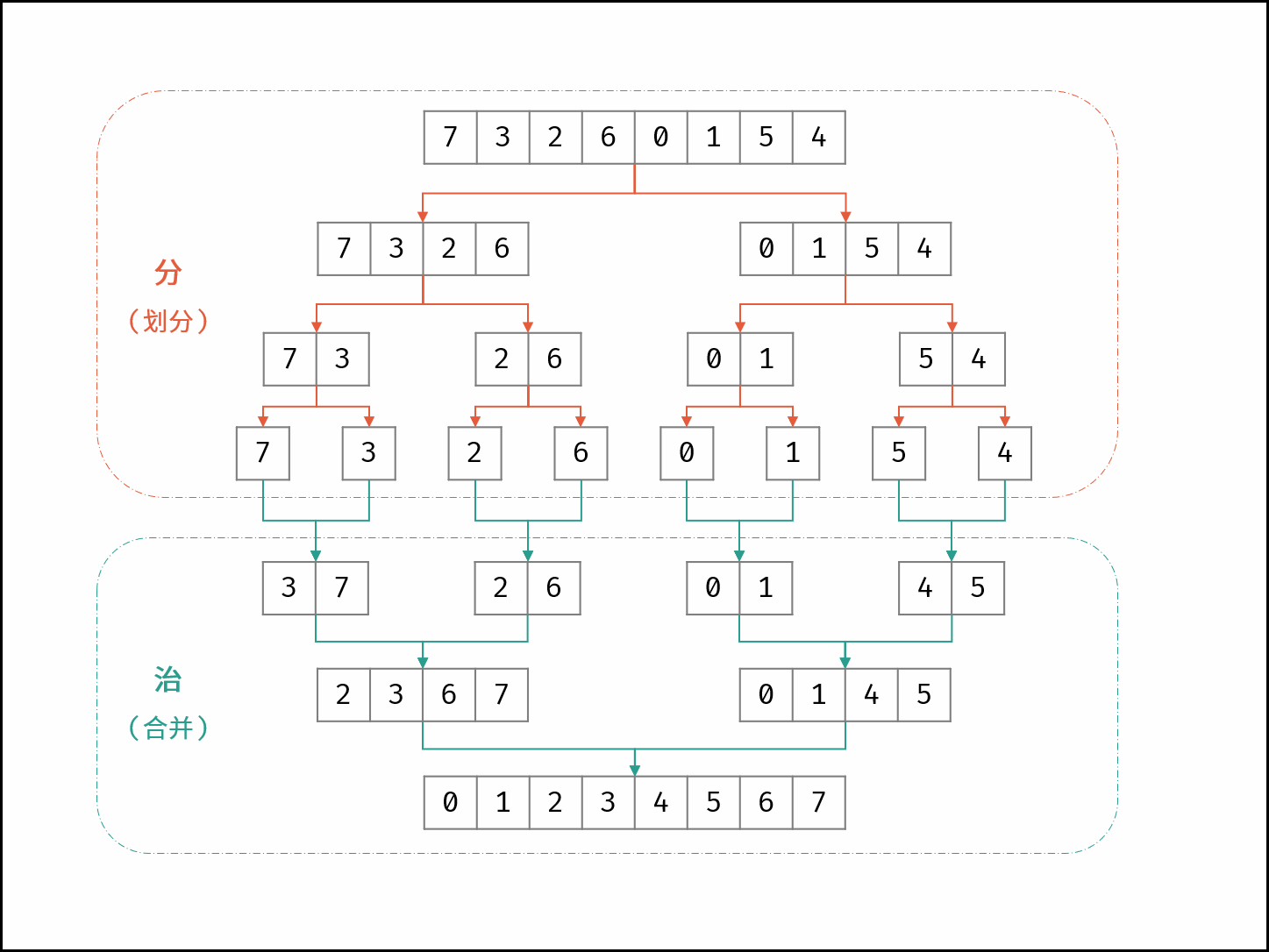
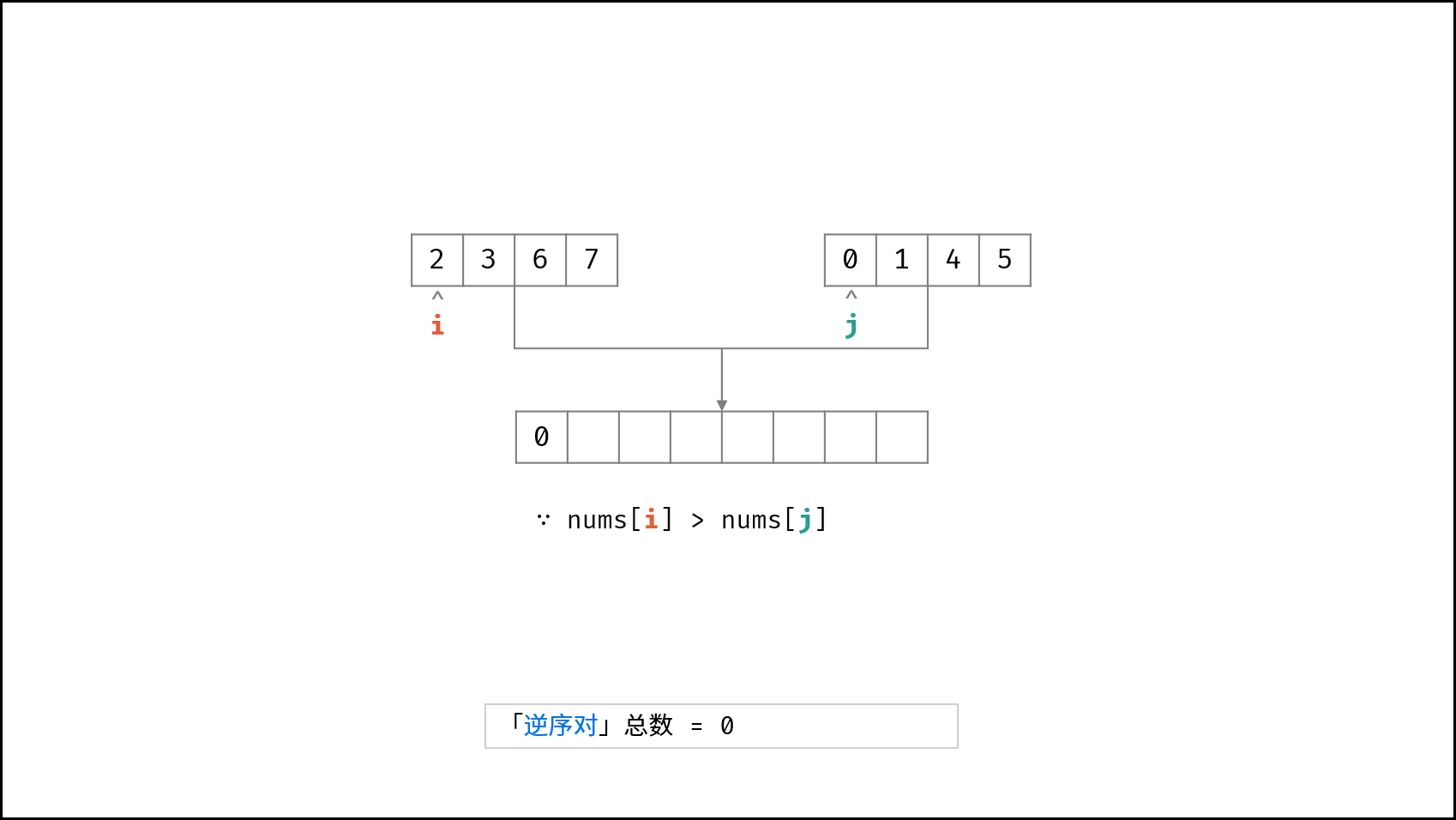
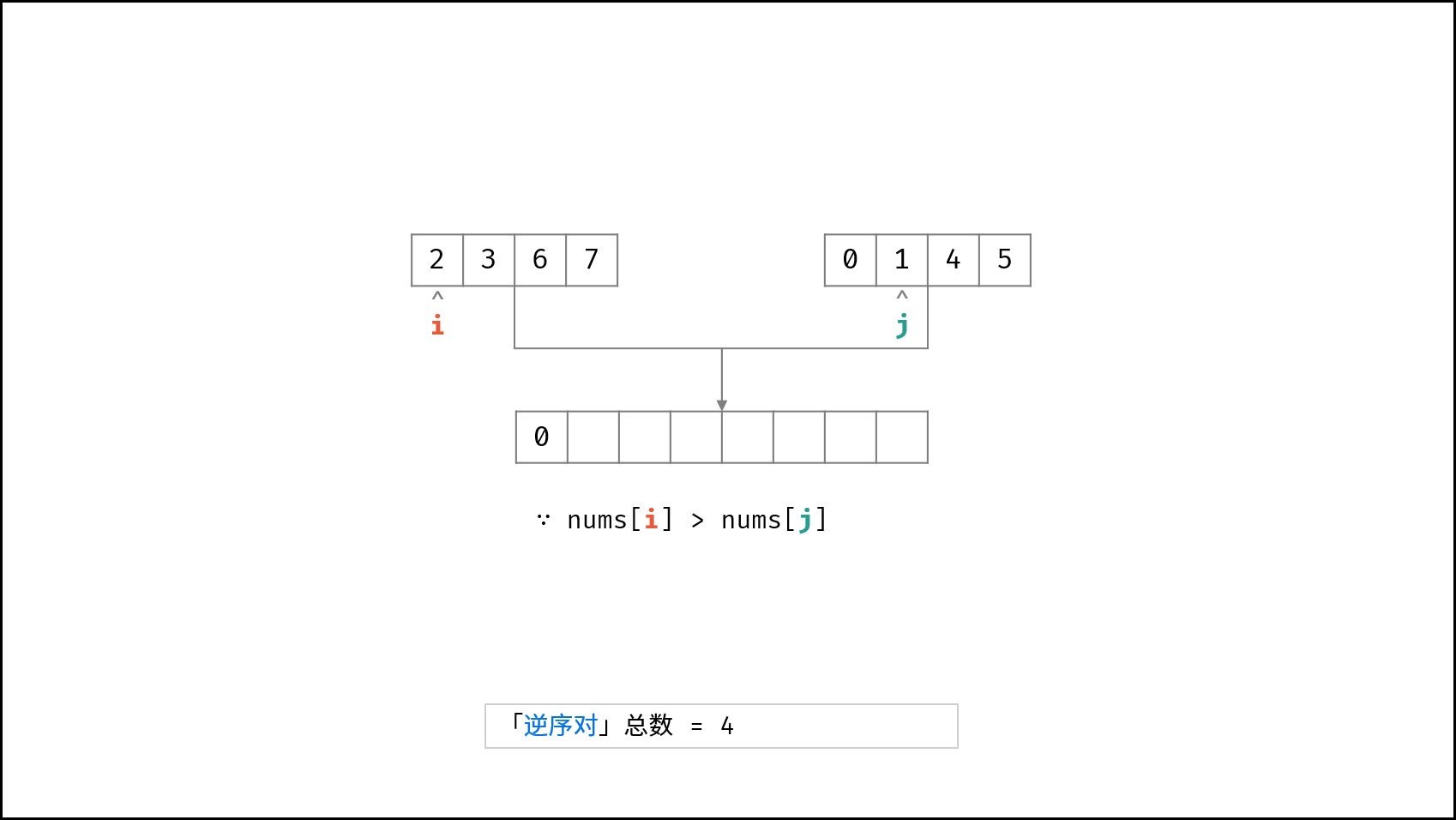
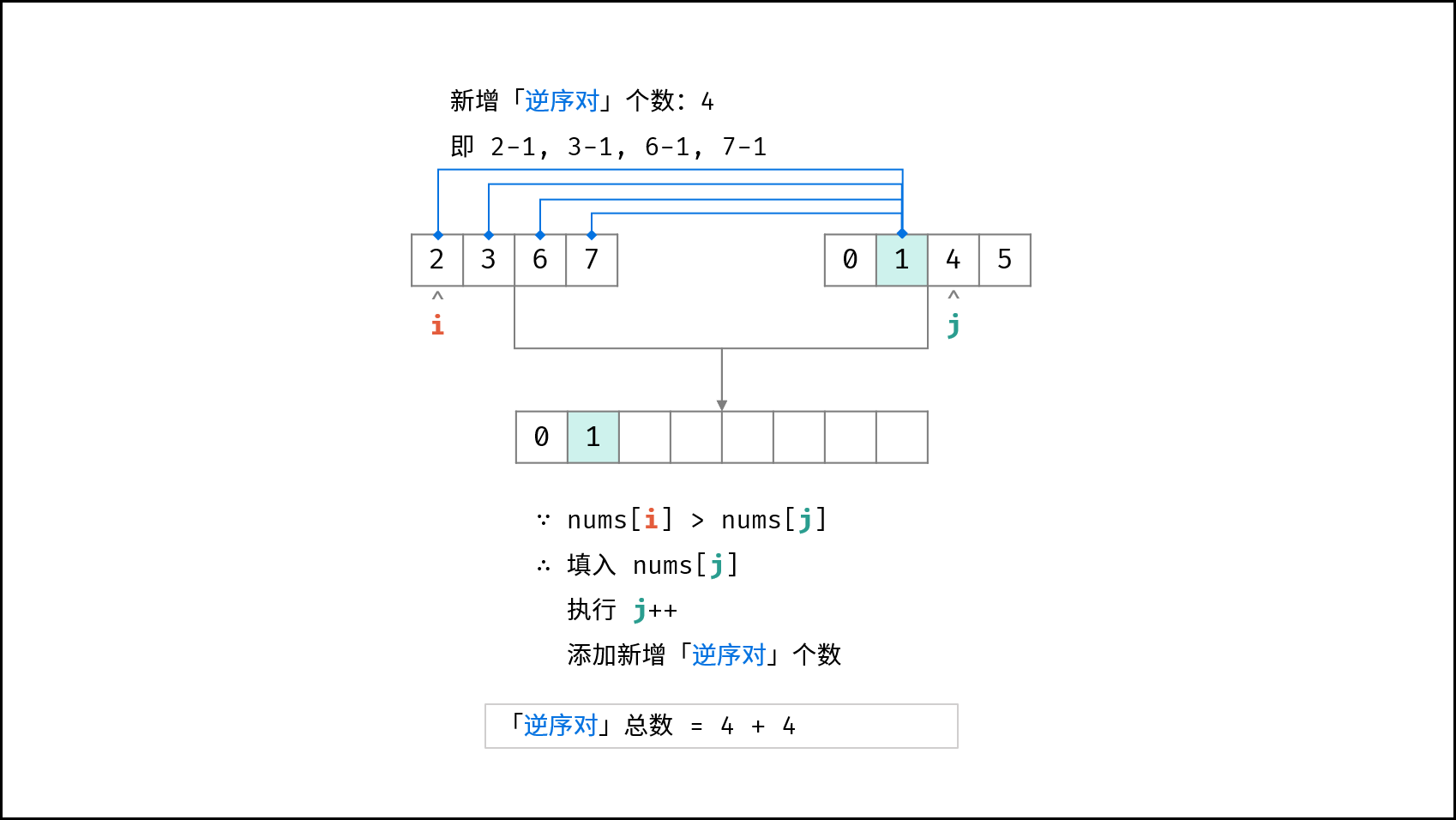
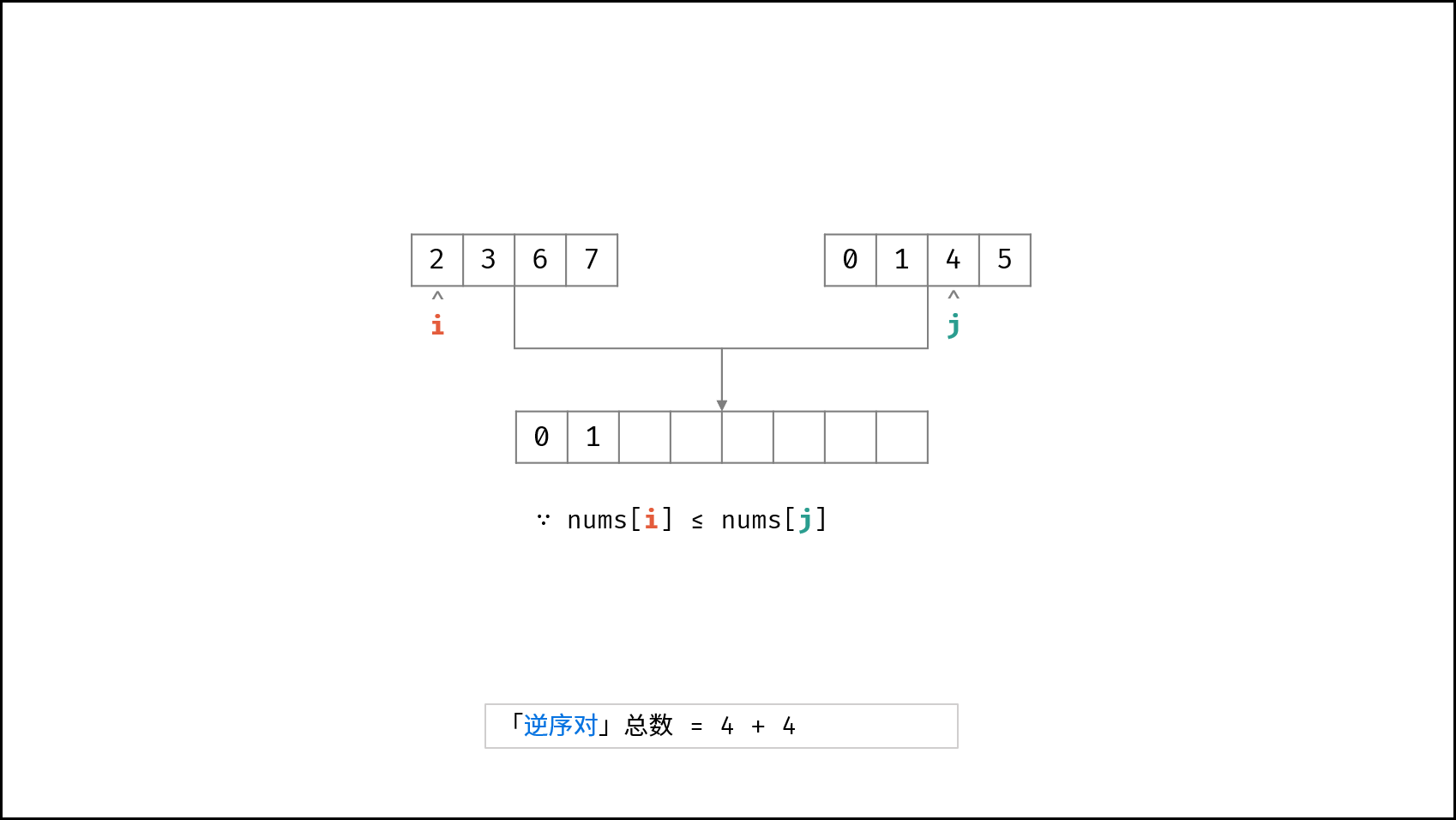
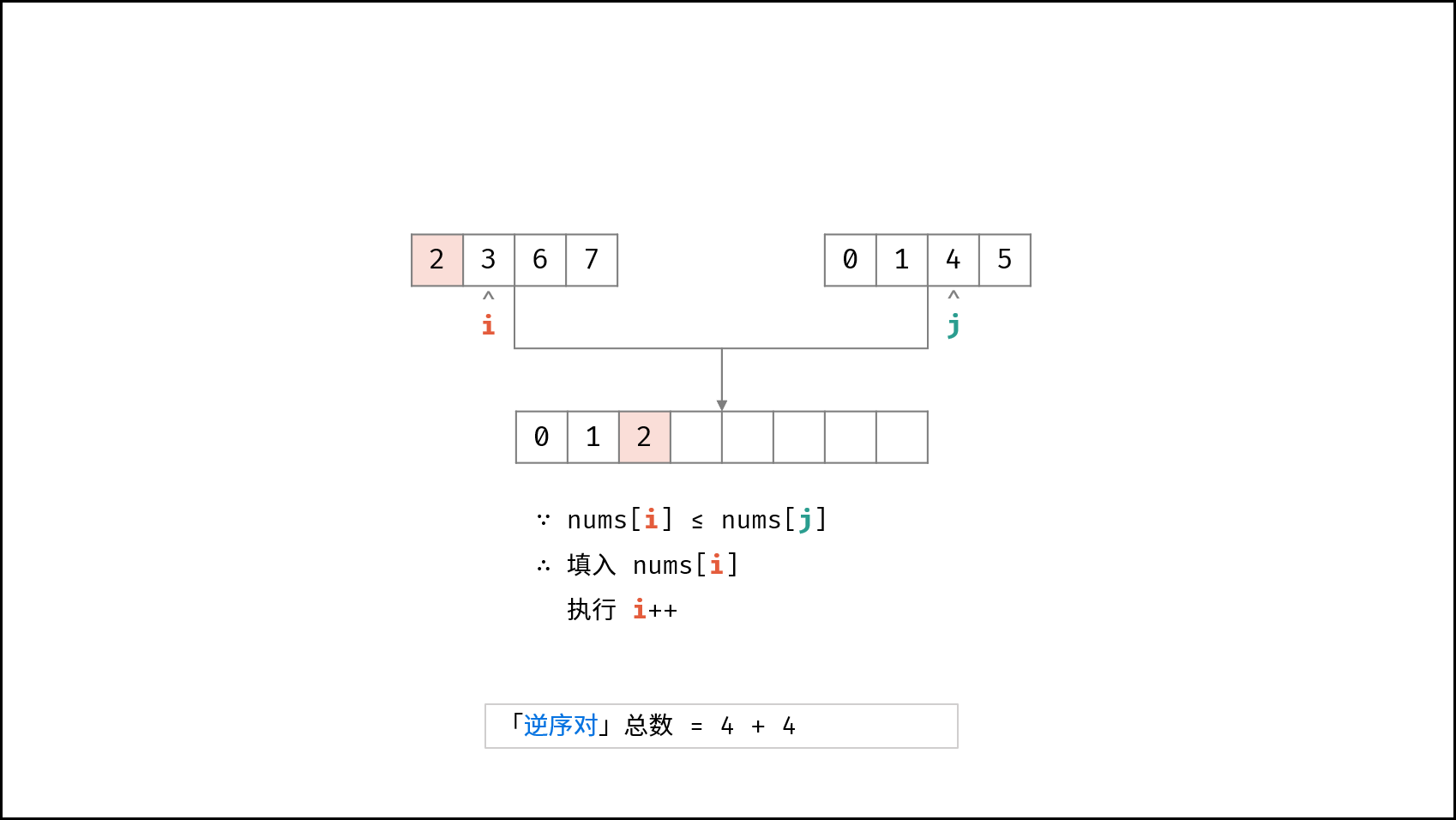
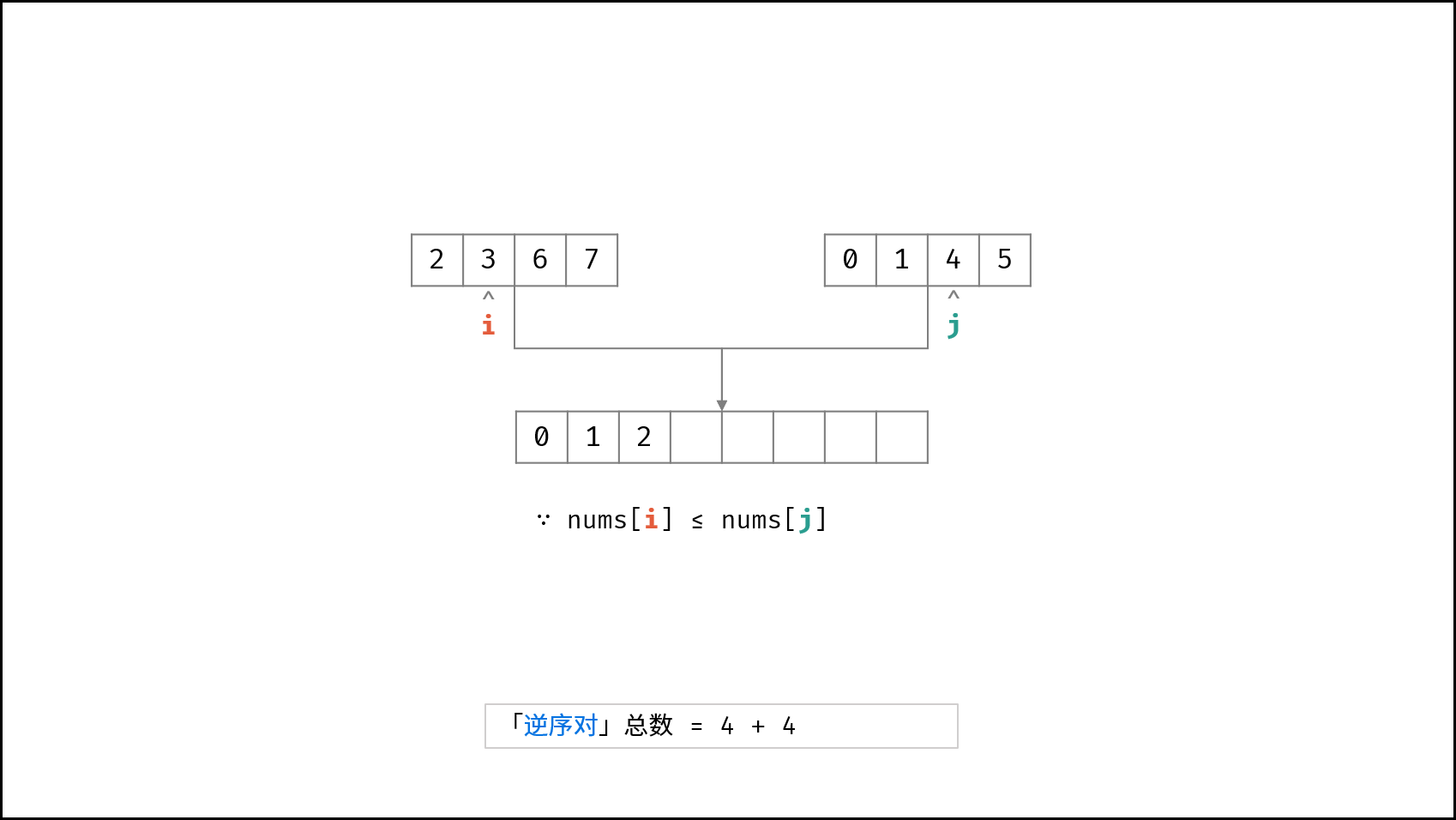
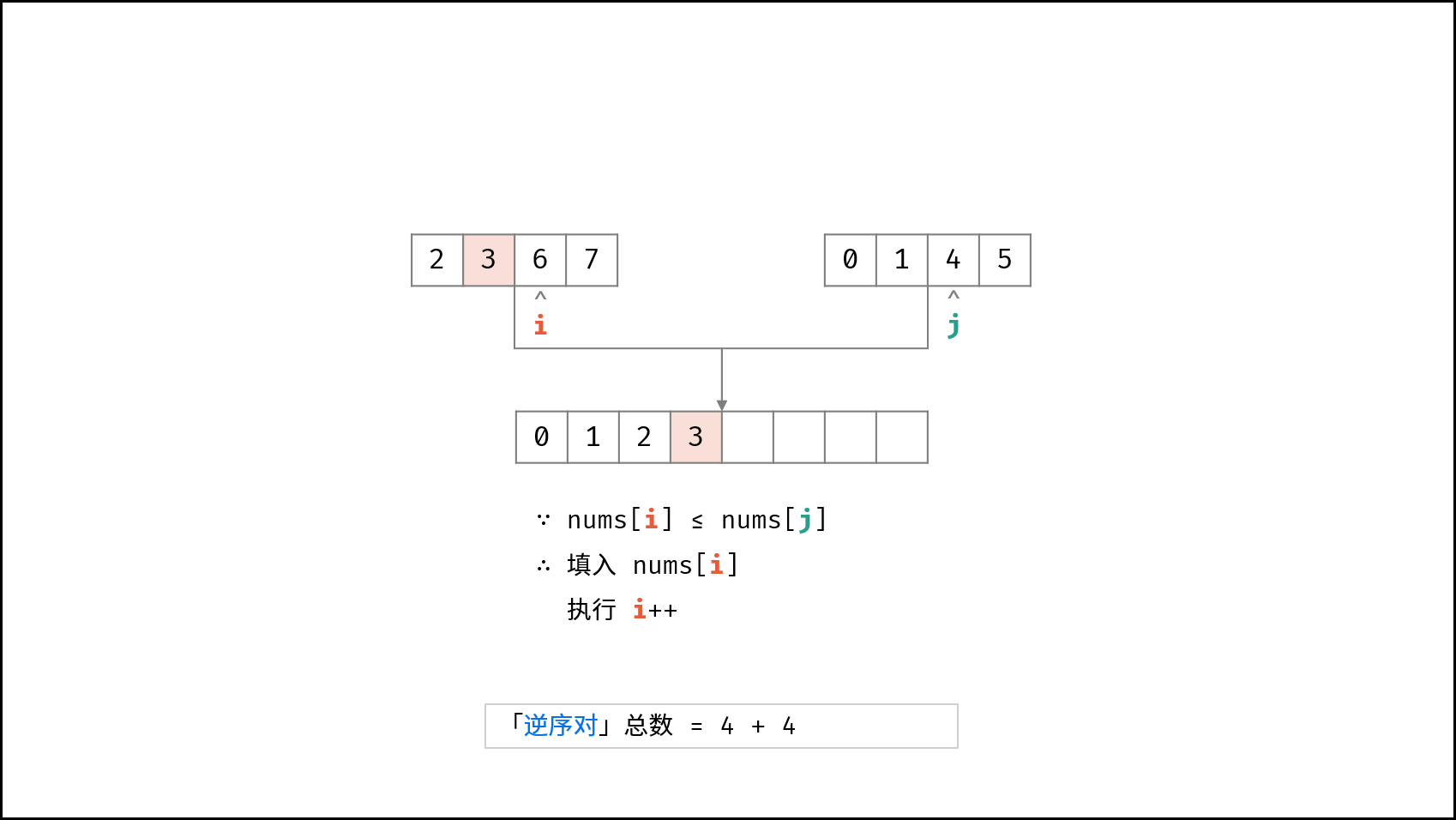
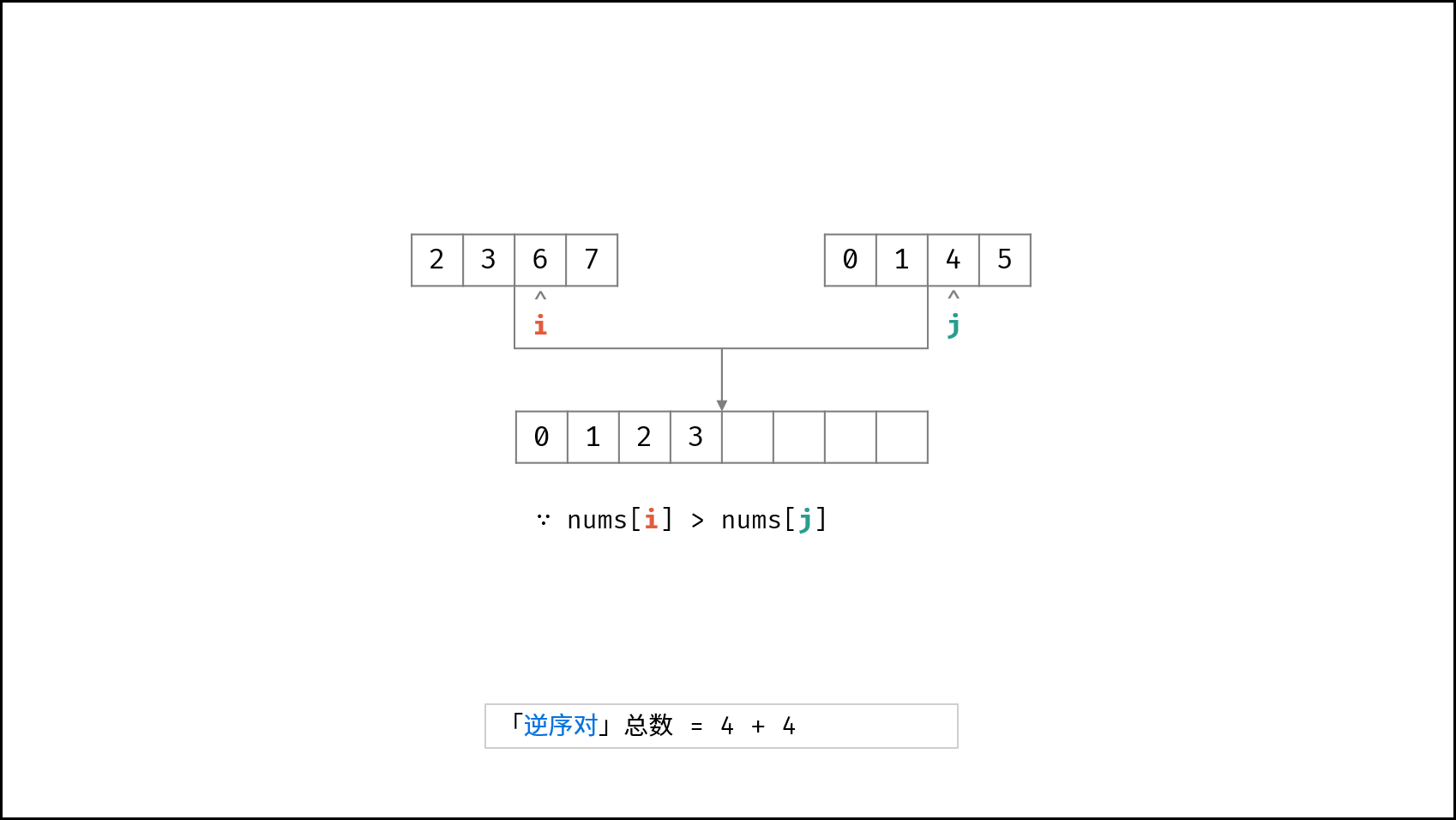
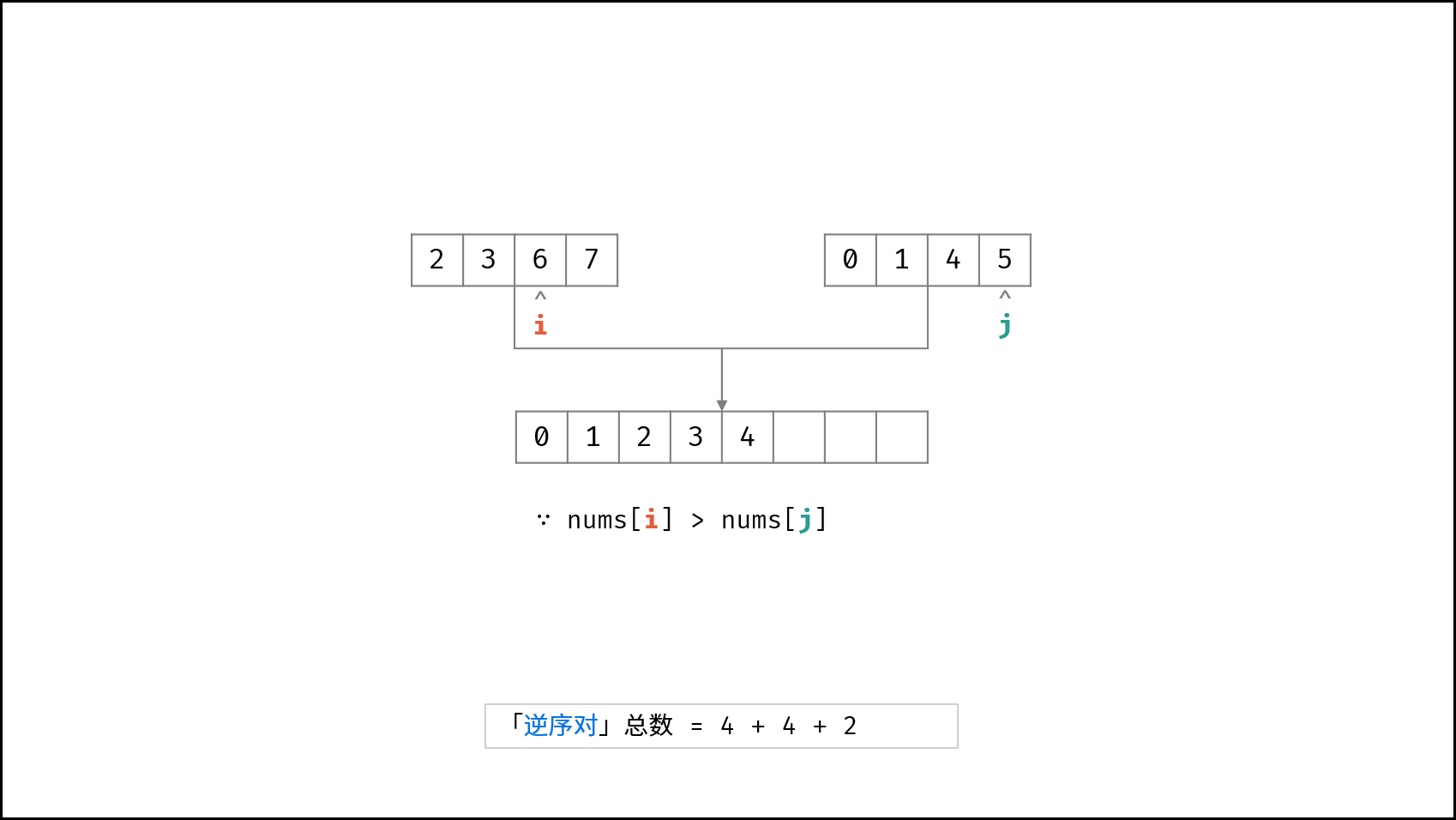
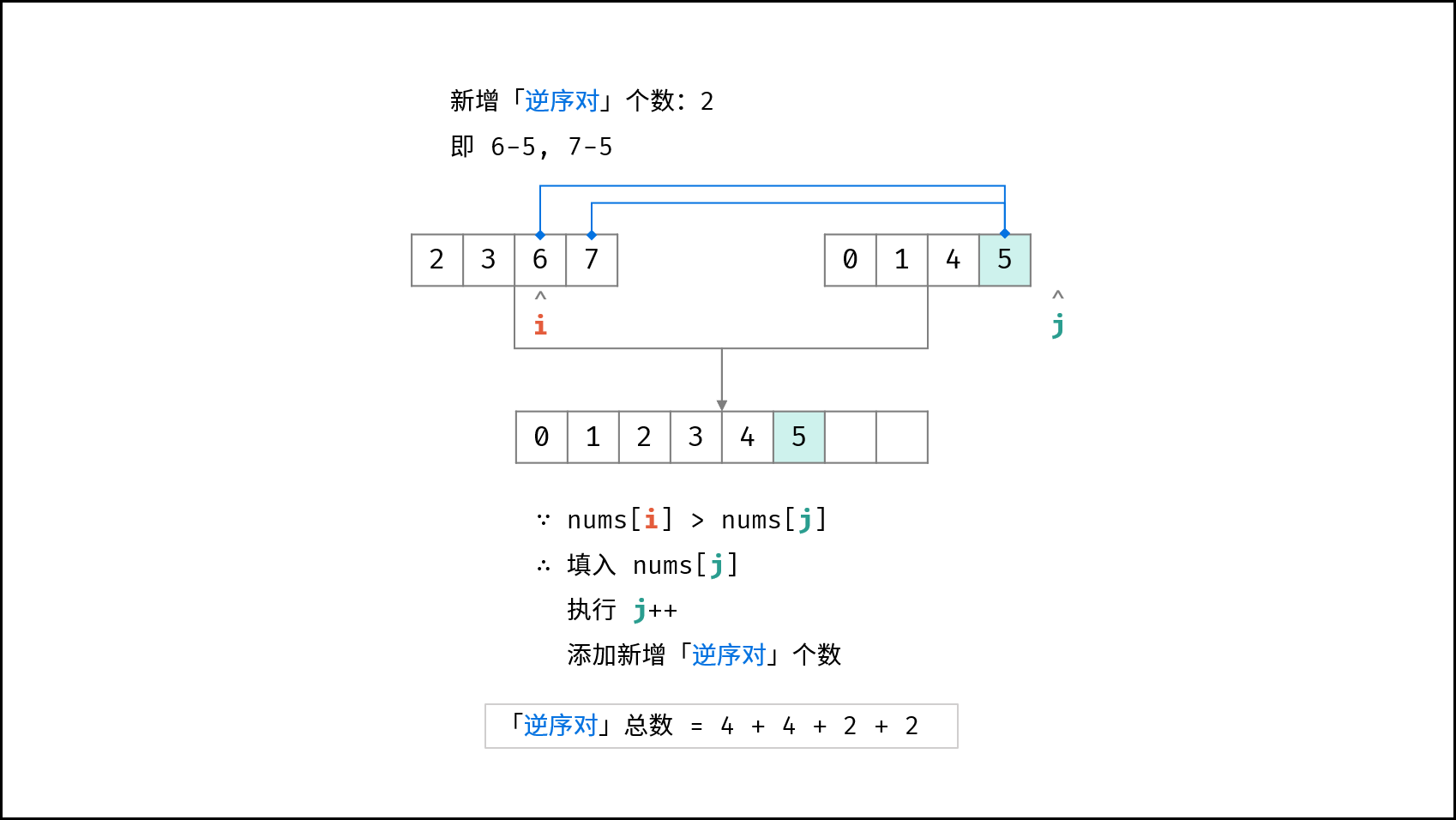
合并阶段 本质上是 合并两个排序数组 的过程，而每当遇到 左子数组当前元素 > 右子数组当前元素 时，意味着 「左子数组当前元素 至 末尾元素」 与 「右子数组当前元素」 构成了若干 「逆序对」 。

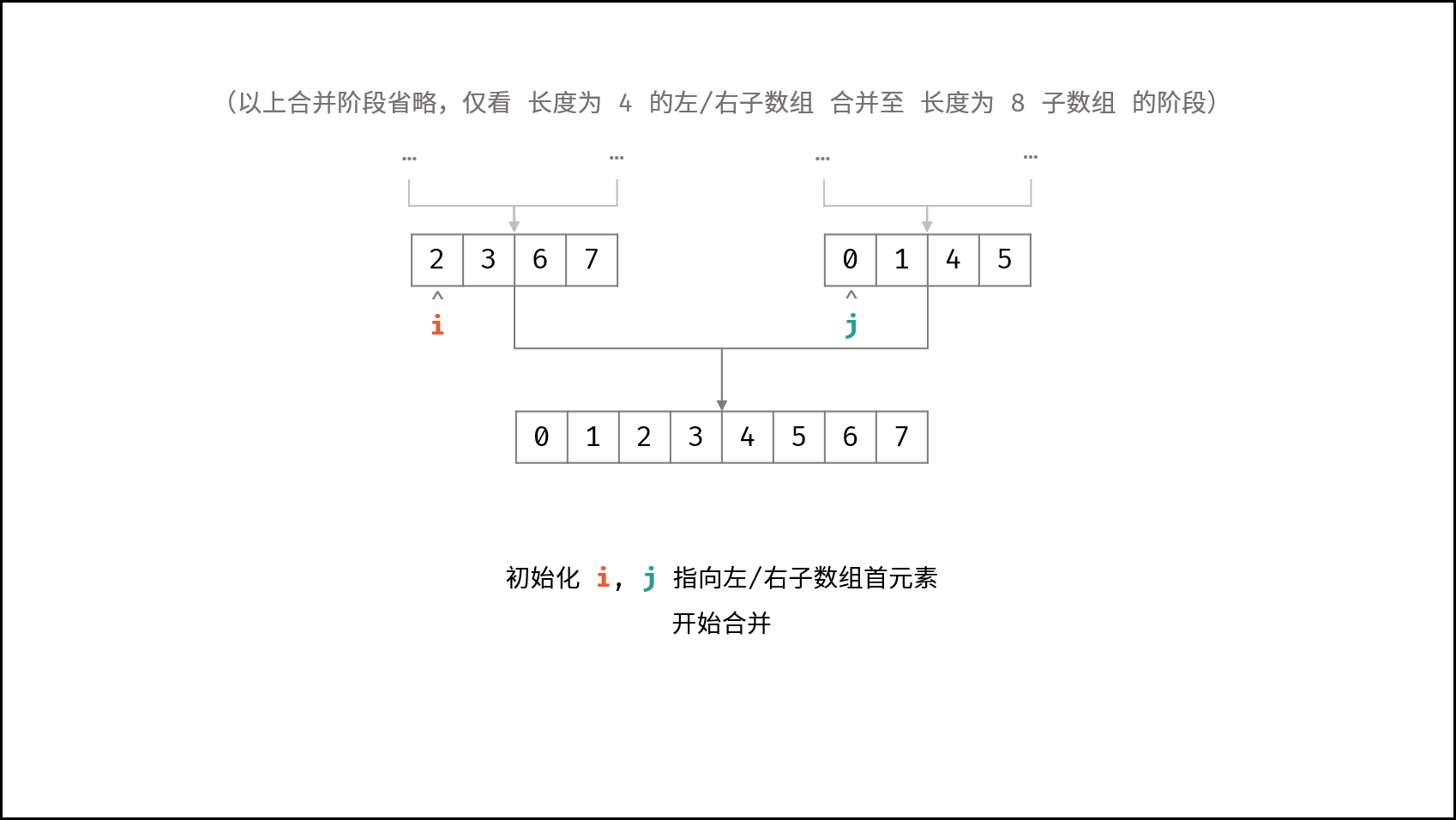
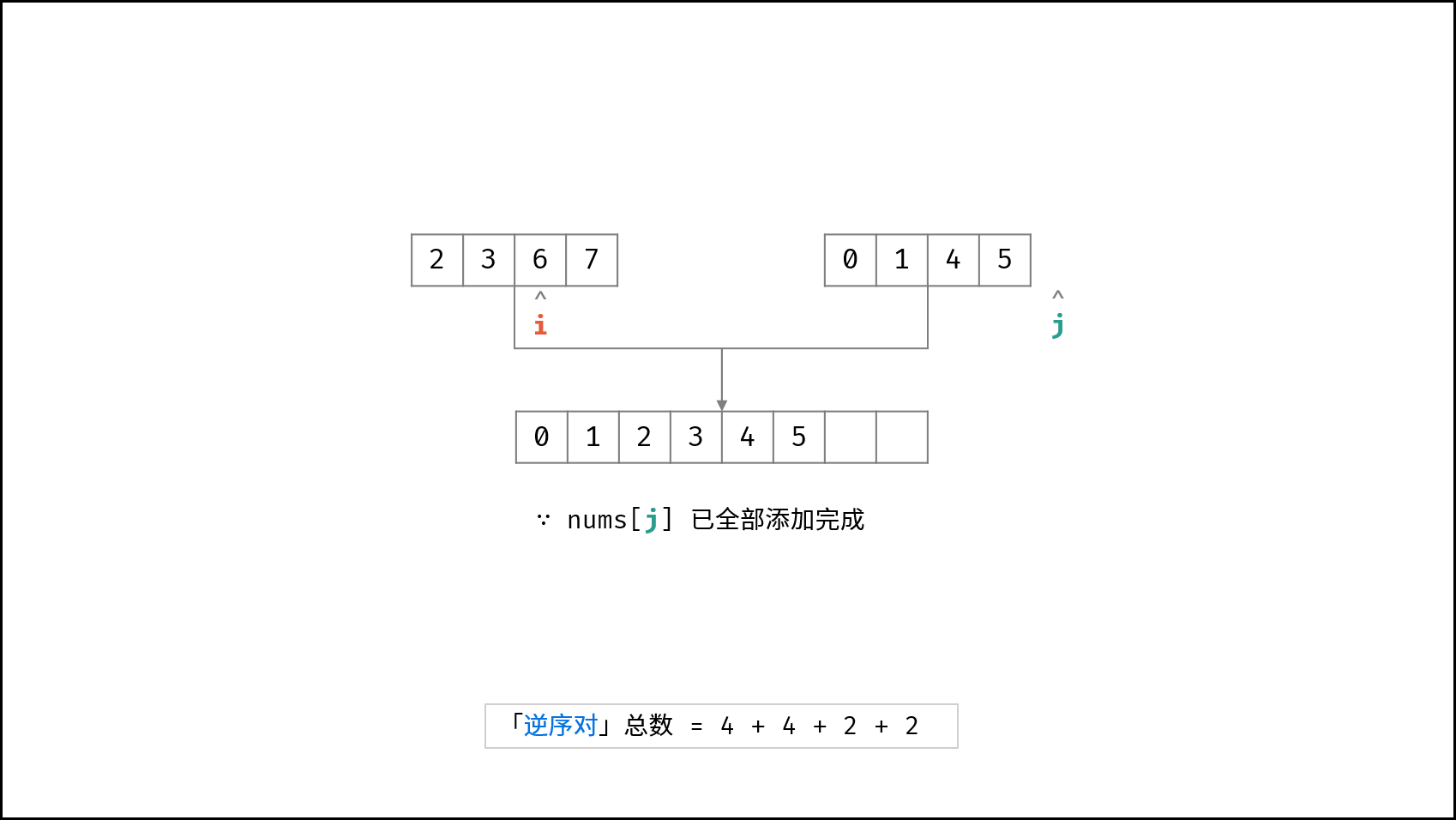
如下图所示，为左子数组 $[2, 3, 6, 7]$ 与 右子数组 $[0, 1, 4, 5]$ 的合并与逆序对统计过程。

<,,,,,,,,,,,,,,,,>

因此，考虑在归并排序的合并阶段统计「逆序对」数量，完成归并排序时，也随之完成所有逆序对的统计。

算法流程： ​

merge_sort() 归并排序与逆序对统计：

1. 终止条件： 当 $l \geq r$ 时，代表子数组长度为 1 ，此时终止划分；
2. 递归划分： 计算数组中点 $m$ ，递归划分左子数组 merge_sort(l, m) 和右子数组 merge_sort(m + 1, r) ；
3. 合并与逆序对统计：
   1. 暂存数组 $record$ 闭区间 $[l, r]$ 内的元素至辅助数组 $tmp$ ；
   2. 循环合并： 设置双指针 $i$ , $j$ 分别指向左 / 右子数组的首元素；
      • 当 $i = m + 1$ 时： 代表左子数组已合并完，因此添加右子数组当前元素 $tmp[j]$ ，并执行 $j = j + 1$ ；
      • 否则，当 $j = r + 1$ 时： 代表右子数组已合并完，因此添加左子数组当前元素 $tmp[i]$ ，并执行 $i = i + 1$ ；
      • 否则，当 $tmp[i] \leq tmp[j]$ 时： 添加左子数组当前元素 $tmp[i]$ ，并执行 $i = i + 1$；
      • 否则（即 $tmp[i] > tmp[j]$）时： 添加右子数组当前元素 $tmp[j]$ ，并执行 $j = j + 1$ ；此时构成 $m - i + 1$ 个「逆序对」，统计添加至 $res$ ；
4. 返回值： 返回直至目前的逆序对总数 $res$ ；

reversePairs() 主函数：

1. 初始化： 辅助数组 $tmp$ ，用于合并阶段暂存元素；
2. 返回值： 执行归并排序 merge_sort() ，并返回逆序对总数即可；

如下图所示，为数组 $[7, 3, 2, 6, 0, 1, 5, 4]$ 的归并排序与逆序对统计过程。

代码： ​

为简化代码，可将“当 $j = r + 1$ 时”与“当 $tmp[i] \leq tmp[j]$ 时”两判断项合并。

class Solution:
    def reversePairs(self, record: List[int]) -> int:
        def merge_sort(l, r):
            # 终止条件
            if l >= r: return 0
            # 递归划分
            m = (l + r) // 2
            res = merge_sort(l, m) + merge_sort(m + 1, r)
            # 合并阶段
            i, j = l, m + 1
            tmp[l:r + 1] = record[l:r + 1]
            for k in range(l, r + 1):
                if i == m + 1:
                    record[k] = tmp[j]
                    j += 1
                elif j == r + 1 or tmp[i] <= tmp[j]:
                    record[k] = tmp[i]
                    i += 1
                else:
                    record[k] = tmp[j]
                    j += 1
                    res += m - i + 1 # 统计逆序对
            return res
        
        tmp = [0] * len(record)
        return merge_sort(0, len(record) - 1)

class Solution {
    int[] record, tmp;
    public int reversePairs(int[] record) {
        this.record = record;
        tmp = new int[record.length];
        return mergeSort(0, record.length - 1);
    }
    private int mergeSort(int l, int r) {
        // 终止条件
        if (l >= r) return 0;
        // 递归划分
        int m = (l + r) / 2;
        int res = mergeSort(l, m) + mergeSort(m + 1, r);
        // 合并阶段
        int i = l, j = m + 1;
        for (int k = l; k <= r; k++)
            tmp[k] = record[k];
        for (int k = l; k <= r; k++) {
            if (i == m + 1)
                record[k] = tmp[j++];
            else if (j == r + 1 || tmp[i] <= tmp[j])
                record[k] = tmp[i++];
            else {
                record[k] = tmp[j++];
                res += m - i + 1; // 统计逆序对
            }
        }
        return res;
    }
}

class Solution {
public:
    int reversePairs(vector<int>& record) {
        vector<int> tmp(record.size());
        return mergeSort(0, record.size() - 1, record, tmp);
    }
private:
    int mergeSort(int l, int r, vector<int>& record, vector<int>& tmp) {
        // 终止条件
        if (l >= r) return 0;
        // 递归划分
        int m = (l + r) / 2;
        int res = mergeSort(l, m, record, tmp) + mergeSort(m + 1, r, record, tmp);
        // 合并阶段
        int i = l, j = m + 1;
        for (int k = l; k <= r; k++)
            tmp[k] = record[k];
        for (int k = l; k <= r; k++) {
            if (i == m + 1)
                record[k] = tmp[j++];
            else if (j == r + 1 || tmp[i] <= tmp[j])
                record[k] = tmp[i++];
            else {
                record[k] = tmp[j++];
                res += m - i + 1; // 统计逆序对
            }
        }
        return res;
    }
};

复杂度分析： ​

• 时间复杂度 $O(N \log N)$ ： 其中 $N$ 为数组长度；归并排序使用 $O(N \log N)$ 时间；
• 空间复杂度 $O(N)$ ： 辅助数组 $tmp$ 占用 $O(N)$ 大小的额外空间；