自律小屋 | 自律小屋

解题思路：

对于普通队列，入队 add() 和出队 remove() 的时间复杂度均为 $O(1)$ ；本题难点为实现查找最大值 get_max() 的 $O(1)$ 时间复杂度。假设队列中存储 $N$ 个元素，从中获取最大值需要遍历队列，时间复杂度为 $O(N)$ ，单从算法上无优化空间。

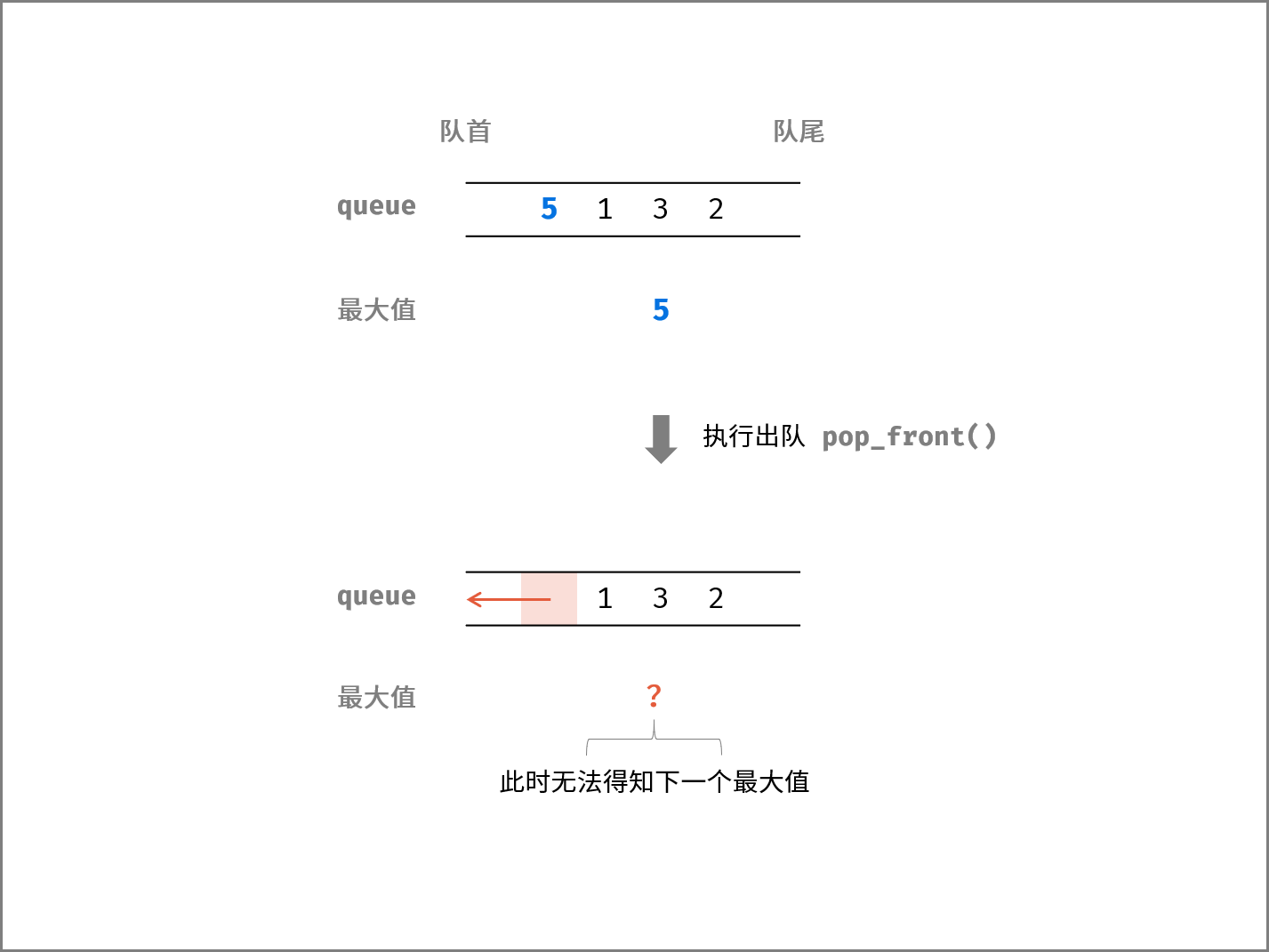
如下图所示，最直观的想法是 维护一个最大值变量 ，在元素入队时更新此变量即可；但当最大值出队后，并无法确定下一个 次最大值 ，因此不可行。

考虑利用 数据结构 来实现，即经常使用的 “空间换时间” 。如下图所示，考虑构建一个递减列表来保存队列 所有递减的元素 ，递减链表随着入队和出队操作实时更新，这样队列最大元素就始终对应递减列表的首元素，实现了获取最大值 $O(1)$ 时间复杂度。

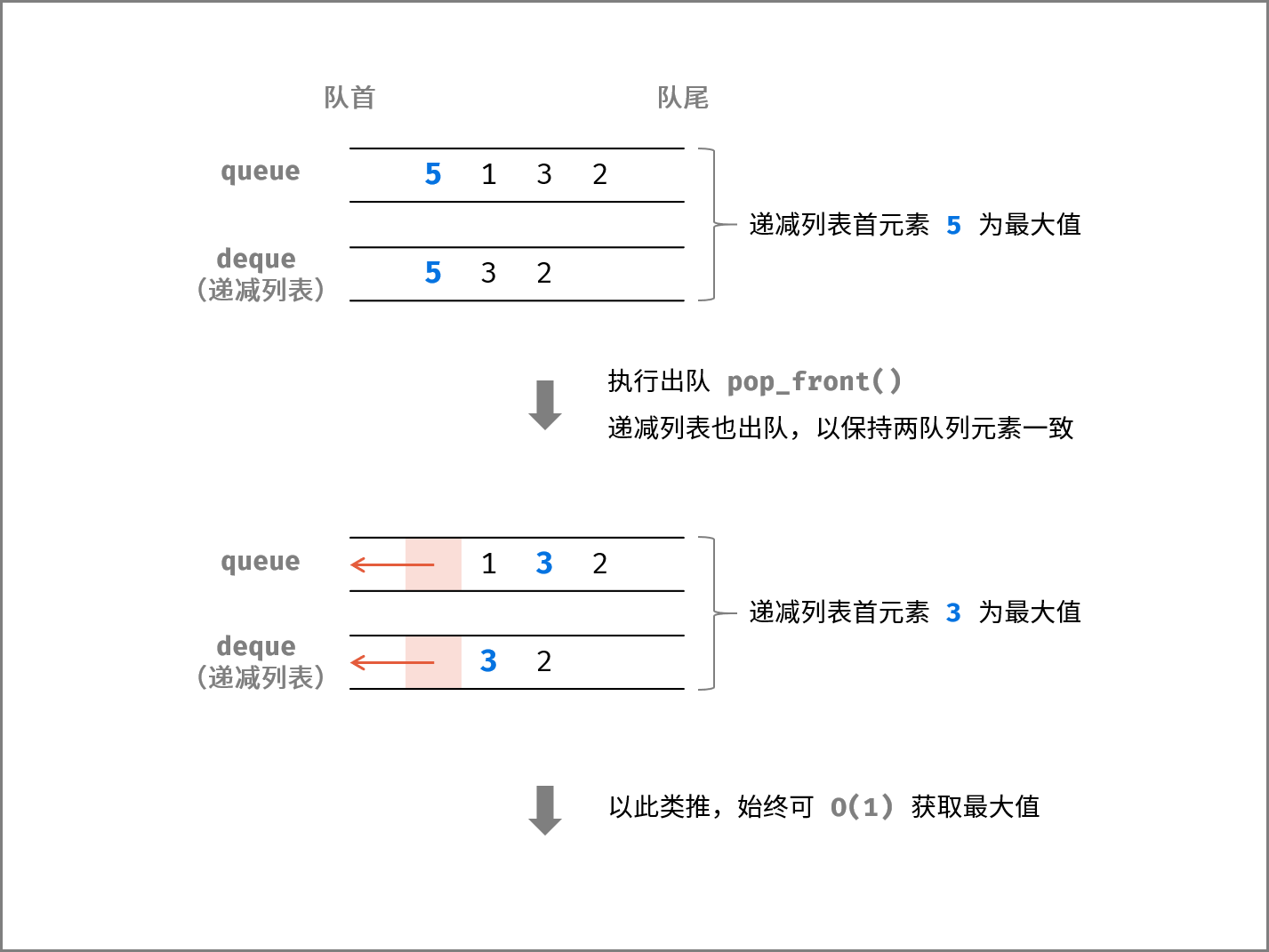
为了实现此递减列表，需要使用 双向队列 ，假设队列已经有若干元素：

当执行入队 add() 时：若入队一个比队列某些元素更大的数字 $x$ ，则为了保持此列表递减，需要将双向队列 尾部所有小于 $x$ 的元素 弹出。
当执行出队 remove() 时：若出队的元素是最大元素，则双向队列需要同时 将首元素出队 ，以保持队列和双向队列的元素一致性。

使用双向队列原因：维护递减列表需要元素队首弹出、队尾插入、队尾弹出操作皆为 $O(1)$ 时间复杂度。

函数设计：

初始化队列 queue ，双向队列 deque ；

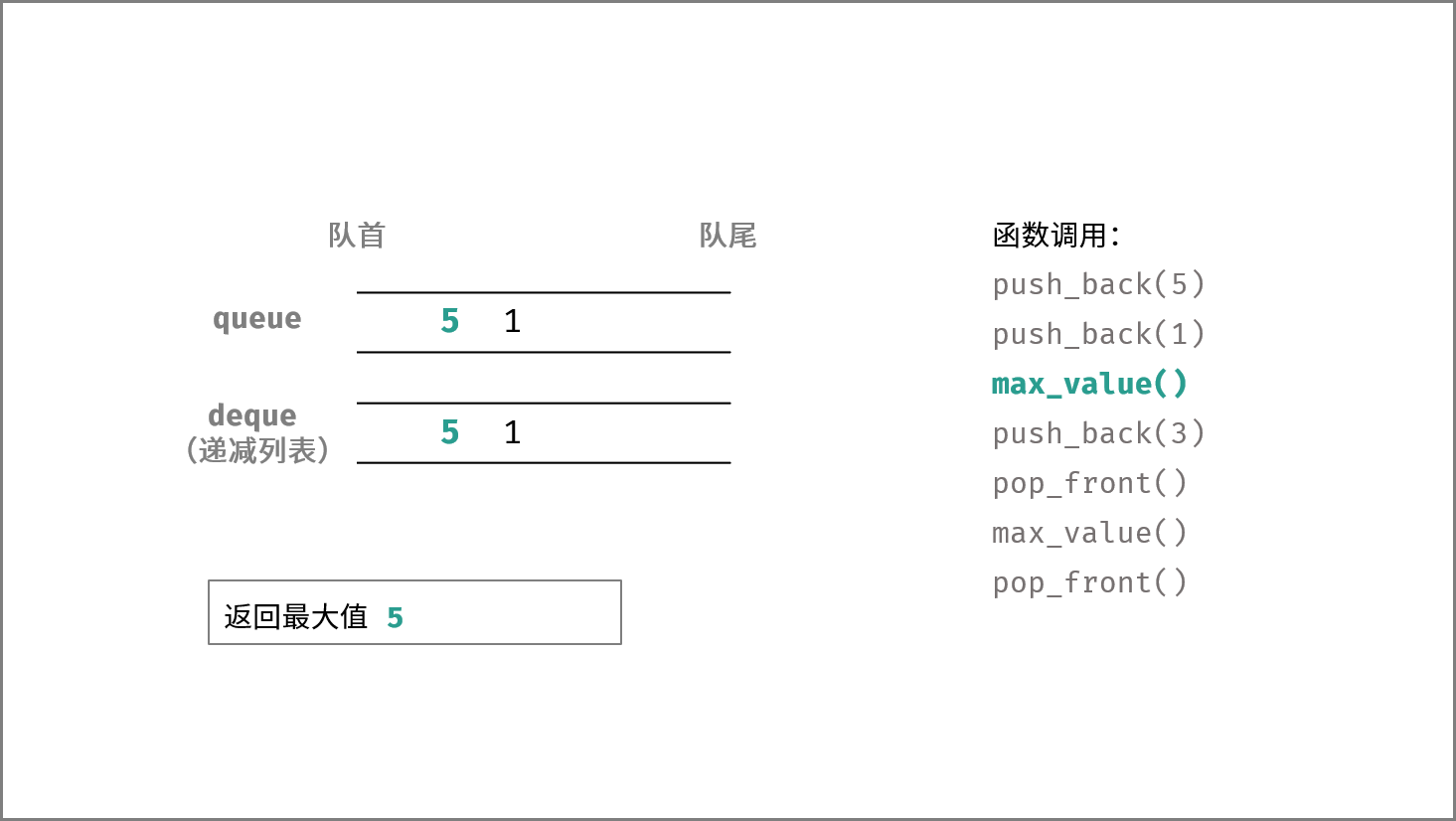
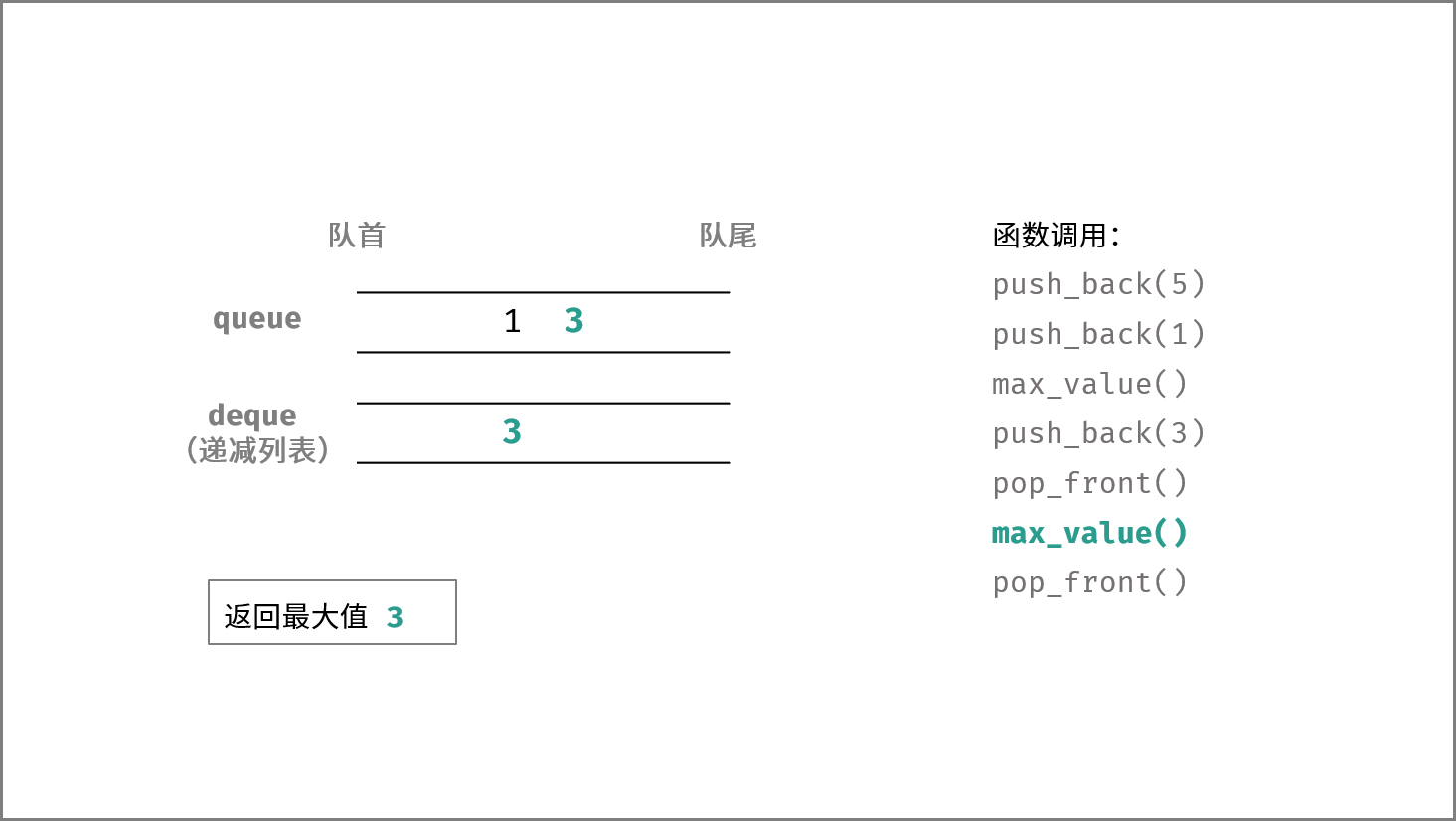
最大值 get_max() ：

当双向队列 deque 为空，则返回 $-1$ ；
否则，返回 deque 首元素；

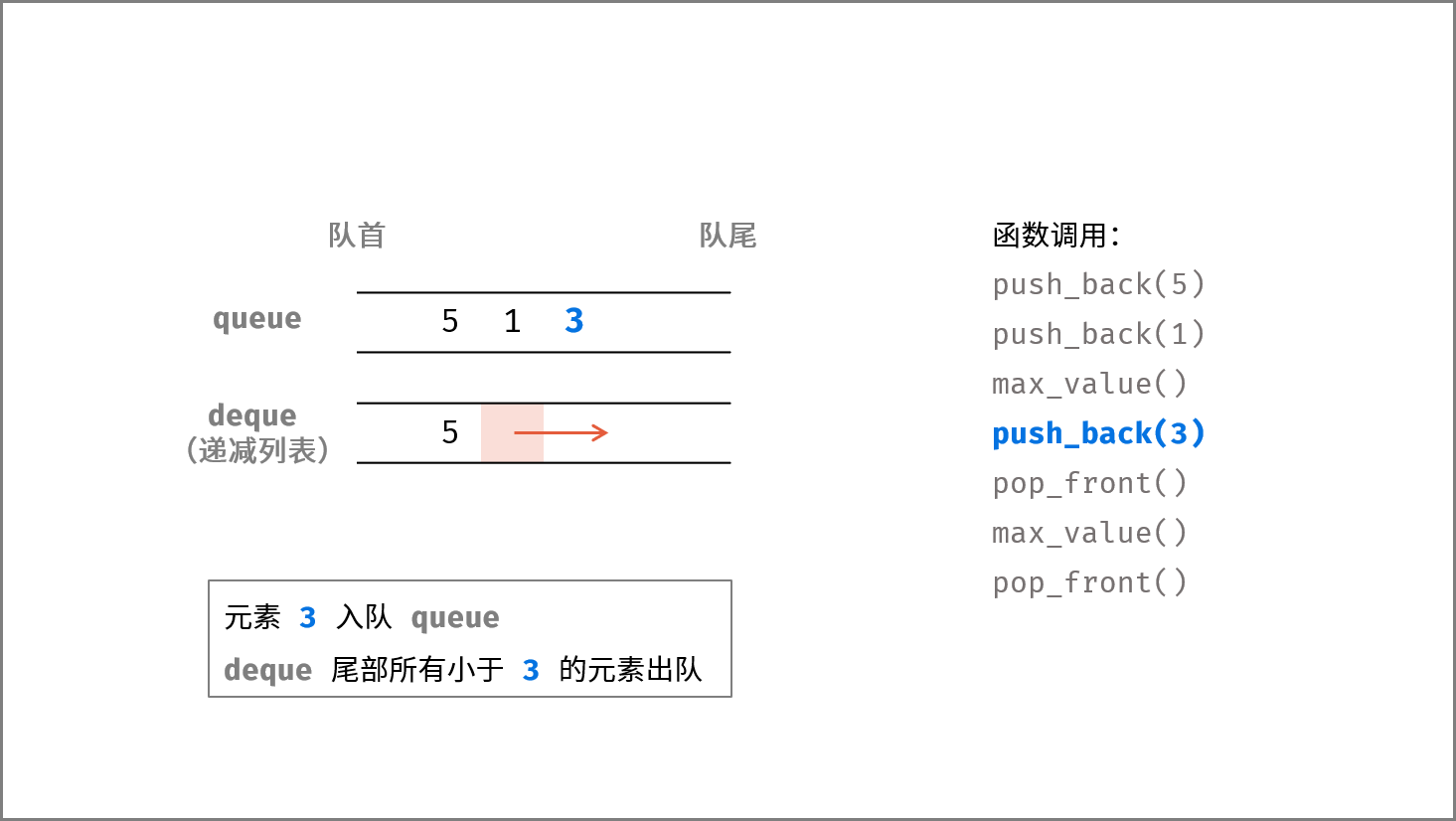
入队 add() ：

将元素 value 入队 queue ；
将双向队列中队尾所有小于 value 的元素弹出（以保持 deque 非单调递减），并将元素 value 入队 deque ；

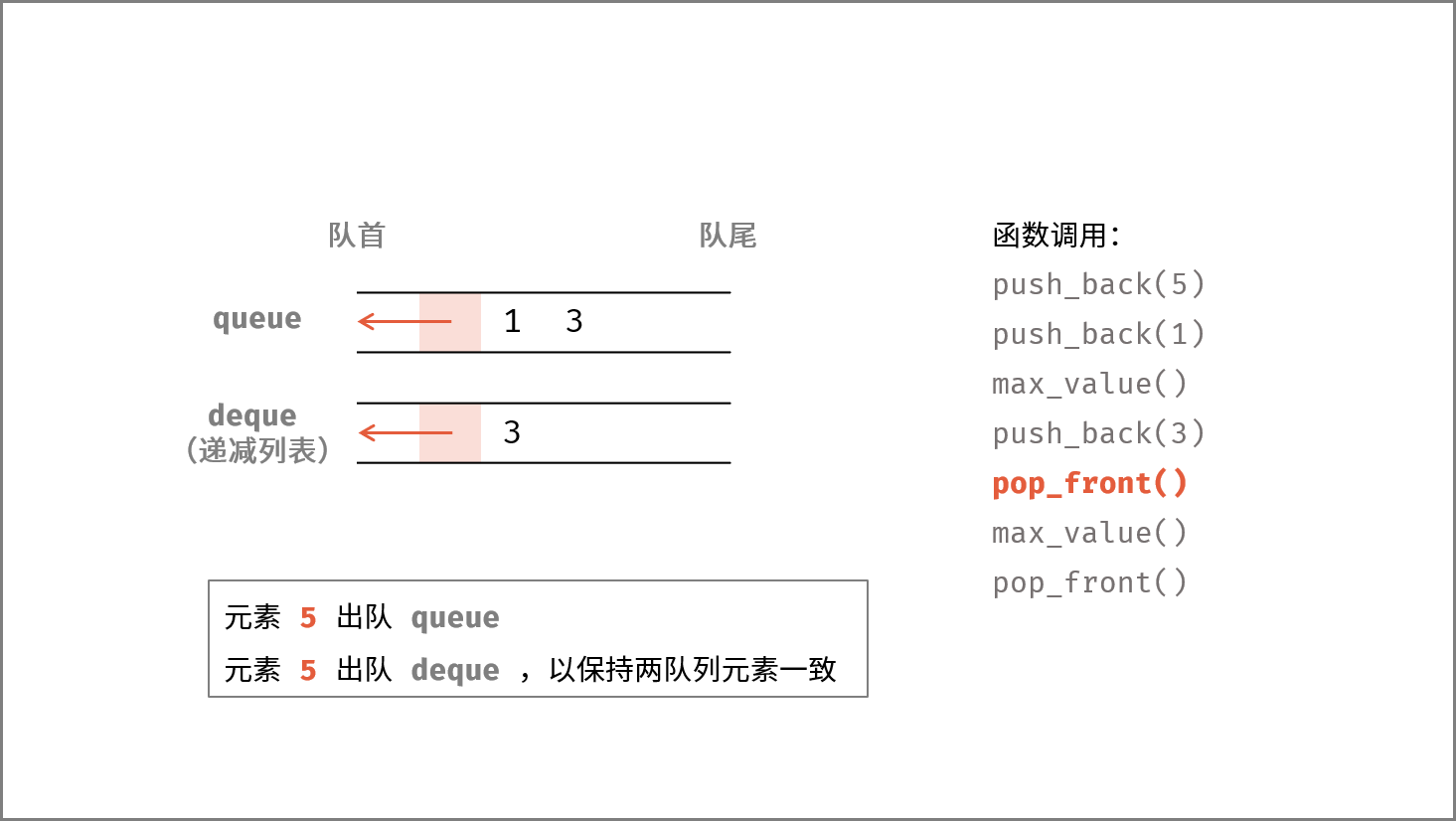
出队 remove() ：

若队列 queue 为空，则直接返回 $-1$ ；
否则，将 queue 首元素出队；
若 deque 首元素和 queue 首元素相等，则将 deque 首元素出队（以保持两队列 元素一致 ）；

设计双向队列为 单调不增 的原因：若队列 queue 中存在两个 值相同的最大元素 ，此时 queue 和 deque 同时弹出一个最大元素，而 queue 中还有一个此最大元素；即采用单调递减将导致两队列中的元素不一致。

下图中的 push_back() , pop_front() , max_value() 分别对应本题的 add() , remove() , get_max() 。

<,,,,,,,,>

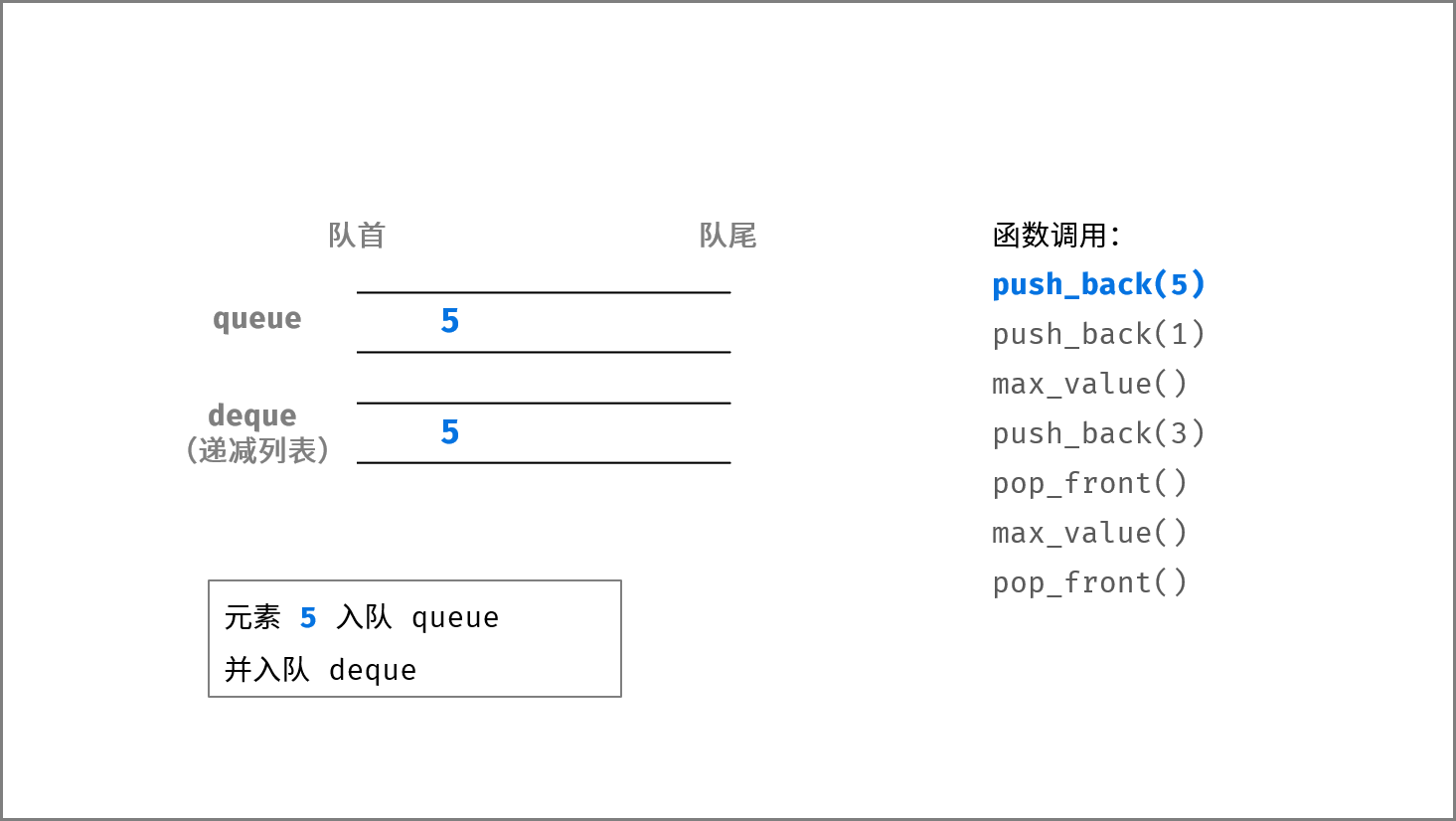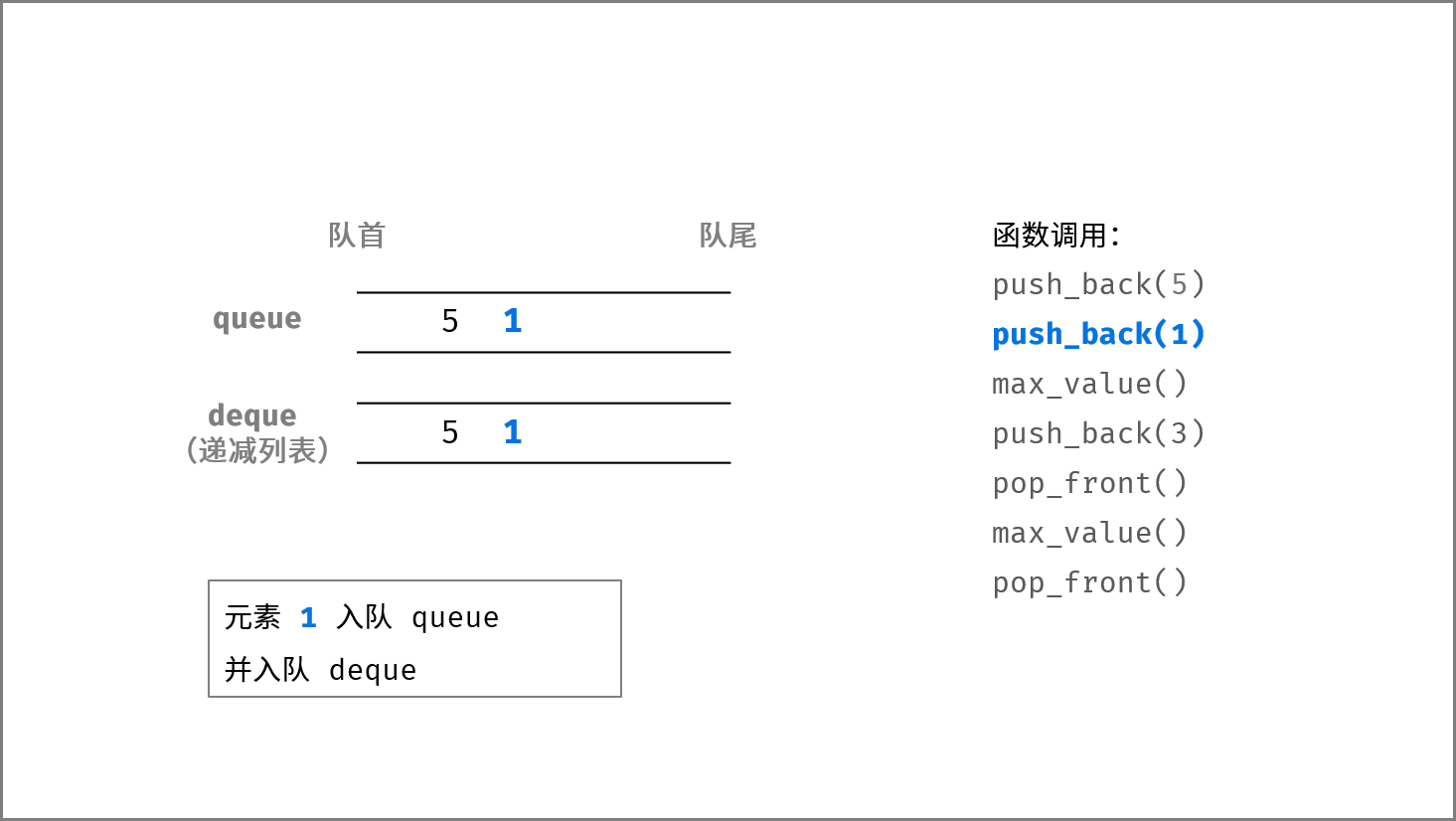代码：

Python

import queue

class Checkout:
    def __init__(self):
        self.queue = queue.Queue()
        self.deque = queue.deque()

    def get_max(self) -> int:
        return self.deque[0] if self.deque else -1

    def add(self, value: int) -> None:
        self.queue.put(value)
        while self.deque and self.deque[-1] < value:
            self.deque.pop()
        self.deque.append(value)

    def remove(self) -> int:
        if self.queue.empty(): return -1
        val = self.queue.get()
        if val == self.deque[0]:
            self.deque.popleft()
        return val

Java

class Checkout {
    Queue<Integer> queue;
    Deque<Integer> deque;
    public Checkout() {
        queue = new LinkedList<>();
        deque = new LinkedList<>();
    }
    public int get_max() {
        return deque.isEmpty() ? -1 : deque.peekFirst();
    }
    public void add(int value) {
        queue.offer(value);
        while(!deque.isEmpty() && deque.peekLast() < value)
            deque.pollLast();
        deque.offerLast(value);
    }
    public int remove() {
        if(queue.isEmpty()) return -1;
        if(queue.peek().equals(deque.peekFirst()))
            deque.pollFirst();
        return queue.poll();
    }
}

C++

class Checkout {
    queue<int> que;
    deque<int> deq;
public:
    Checkout() { }
    int get_max() {
        return deq.empty() ? -1 : deq.front();
    }
    void add(int value) {
        que.push(value);
        while(!deq.empty() && deq.back() < value)
            deq.pop_back();
        deq.push_back(value);
    }
    int remove() {
        if(que.empty()) return -1;
        int val = que.front();
        if(val == deq.front())
            deq.pop_front();
        que.pop();
        return val;
    }
};

复杂度分析：

时间复杂度 $O(1)$ ： get_max(), add(), remove() 方法的均摊时间复杂度均为 $O(1)$ ；
空间复杂度 $O(N)$ ： 当元素个数为 $N$ 时，最差情况下deque 中保存 $N$ 个元素，使用 $O(N)$ 的额外空间；

解题思路： ​

函数设计： ​

代码： ​

复杂度分析： ​

解题思路：

函数设计：

代码：

复杂度分析：