解题思路:
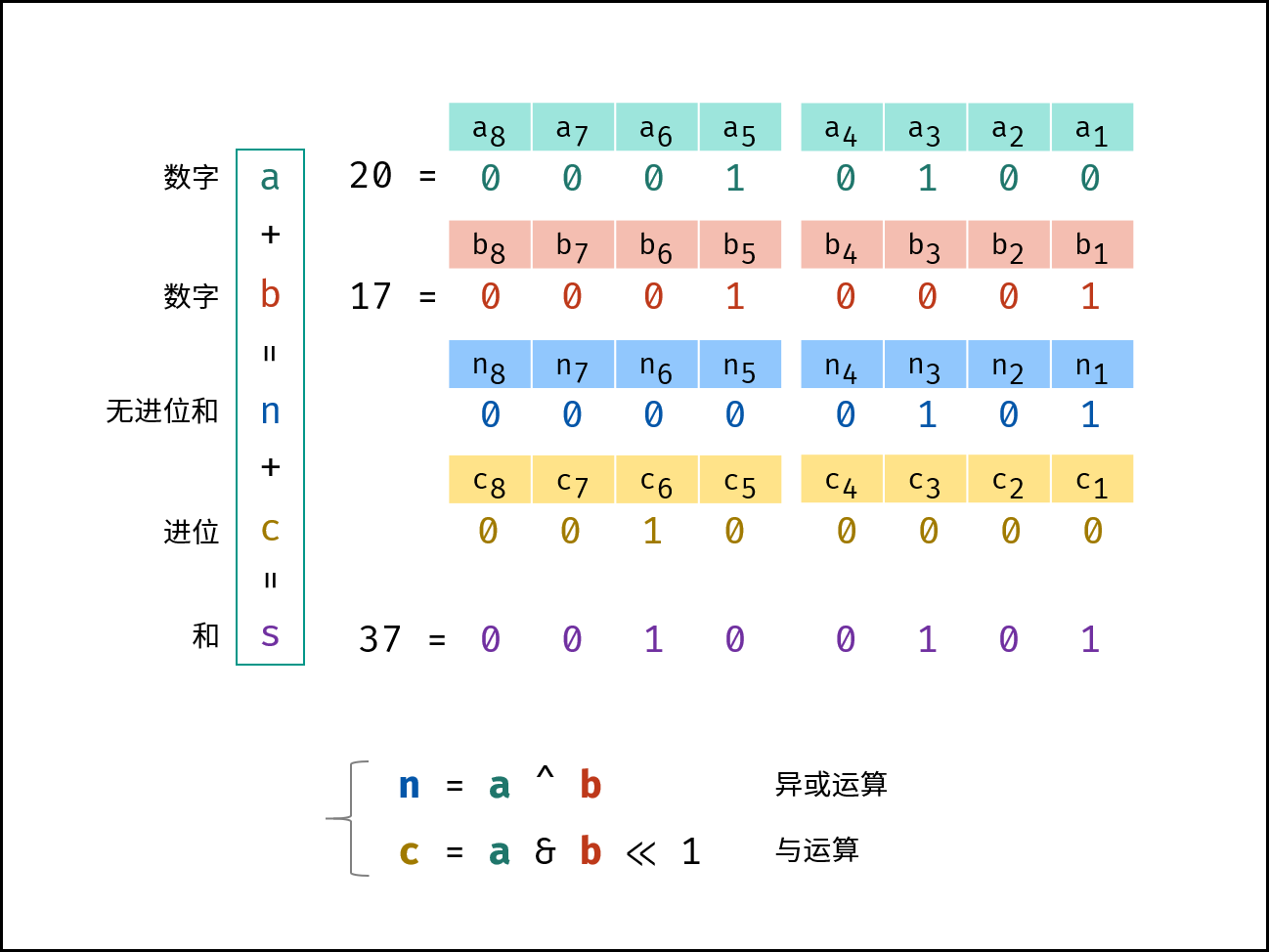
本题考察对位运算的灵活使用,即使用位运算实现加法。 设两数字的二进制形式 $a, b$ ,其求和 $s = a + b$ ,$a(i)$ 代表 $a$ 的二进制第 $i$ 位,则分为以下四种情况:
| $a(i)$ | $b(i)$ | 无进位和 $n(i)$ | 进位 $c(i+1)$ |
|---|---|---|---|
| $0$ | $0$ | $0$ | $0$ |
| $0$ | $1$ | $1$ | $0$ |
| $1$ | $0$ | $1$ | $0$ |
| $1$ | $1$ | $0$ | $1$ |
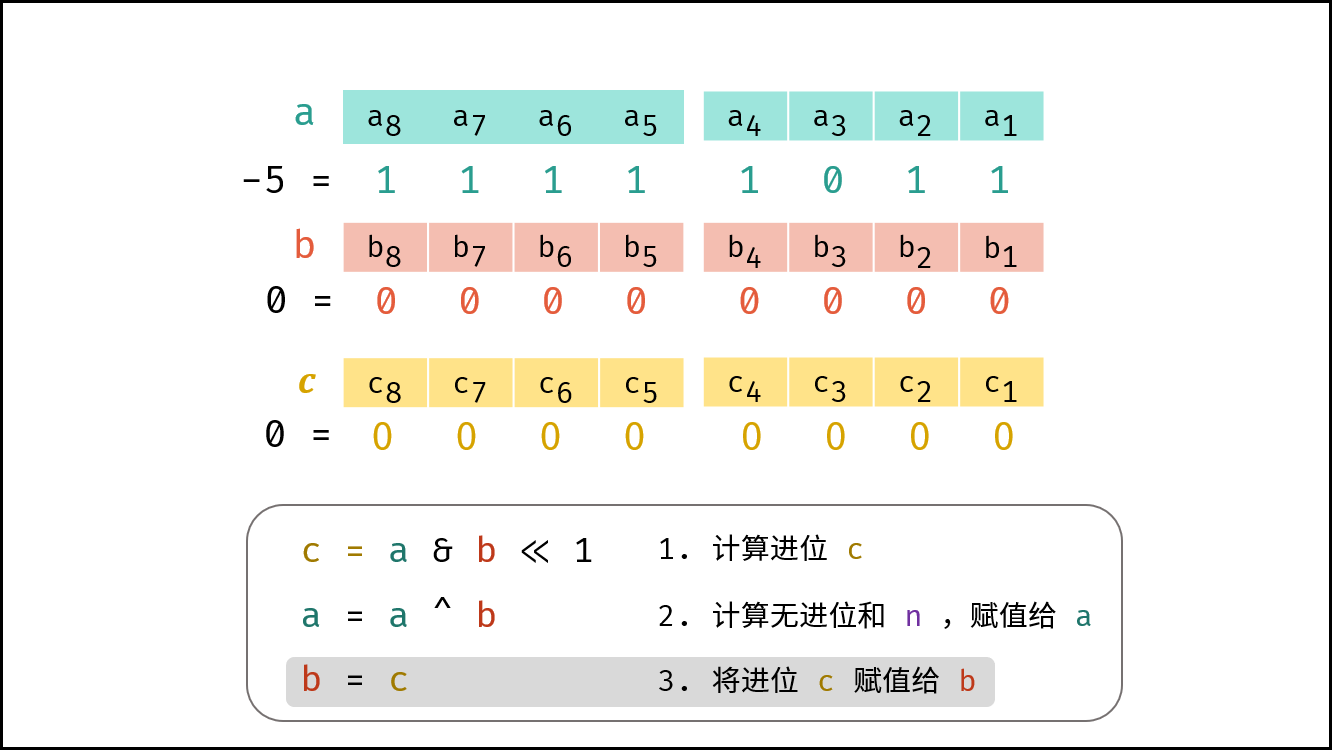
观察发现,无进位和 与 异或运算 规律相同,进位 和 与运算 规律相同(并需左移一位)。因此,无进位和 $n$ 与进位 $c$ 的计算公式如下;
$$ \begin{cases} n = a \oplus b & 非进位和:异或运算 \ c = a & b << 1 & 进位:与运算 + 左移一位 \end{cases} $$
(和 $s$ )$=$(非进位和 $n$ )$+$(进位 $c$ )。即可将 $s = a + b$ 转化为:
$$ s = a + b \Rightarrow s = n + c $$
循环求 $n$ 和 $c$ ,直至进位 $c = 0$ ;此时 $s = n$ ,返回 $n$ 即可。
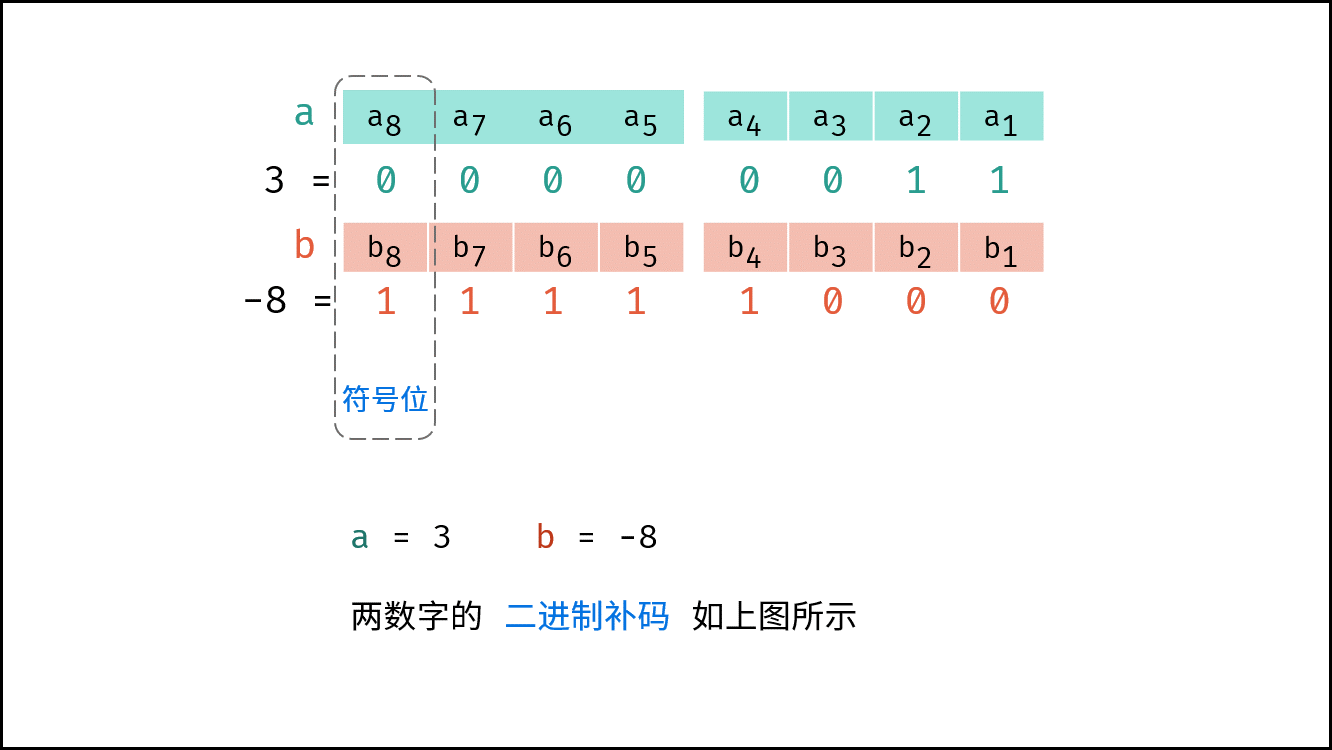
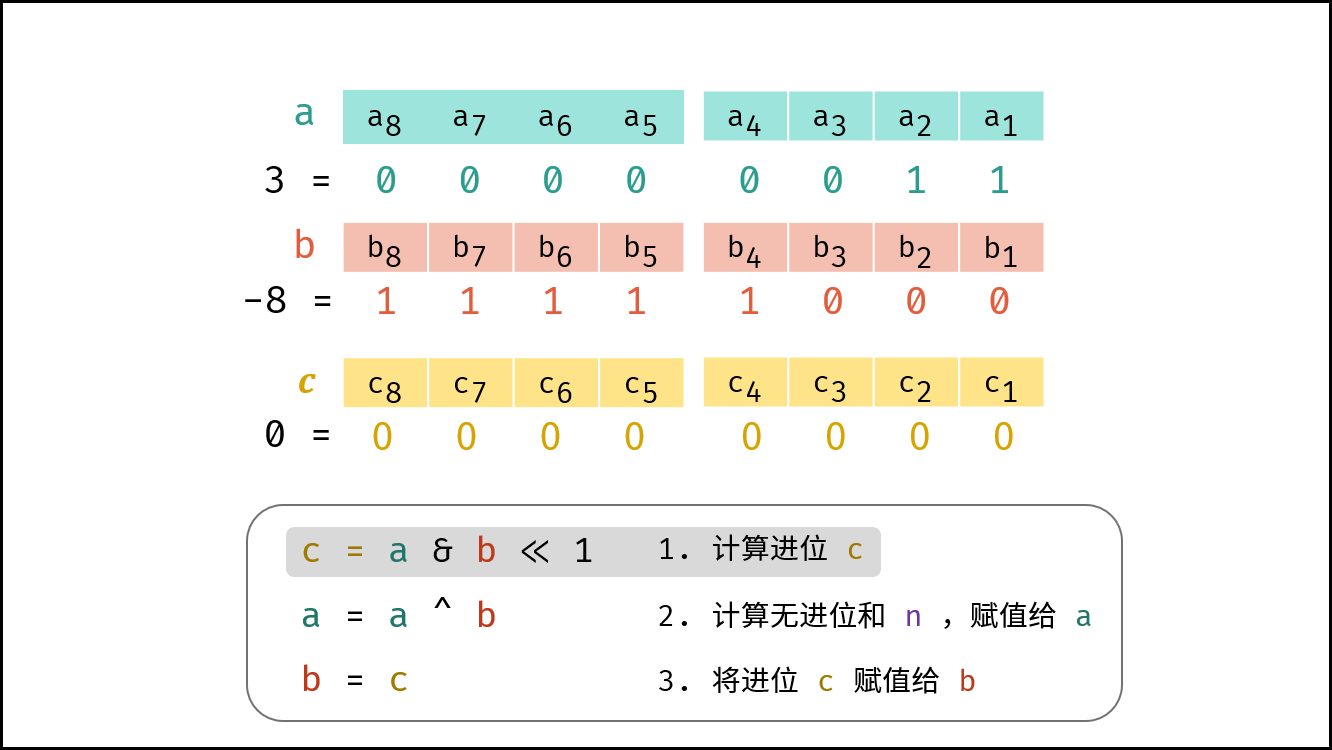
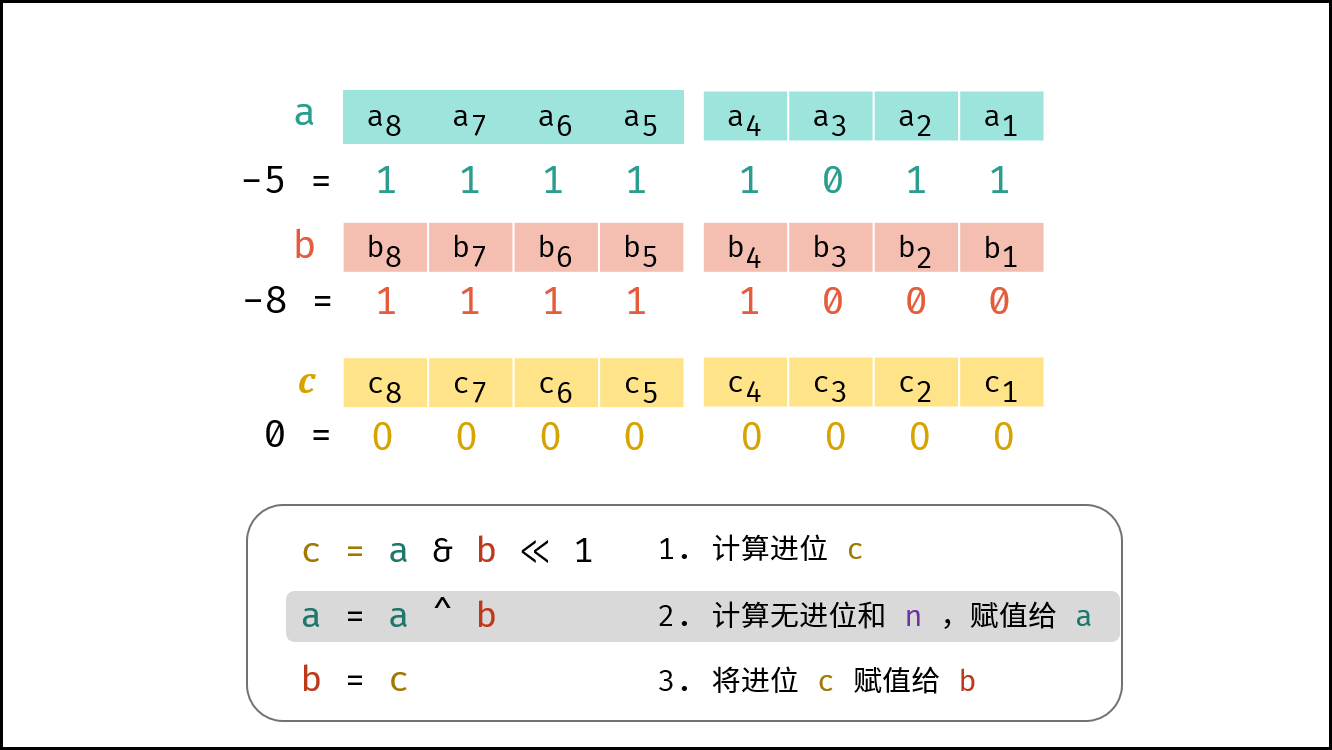
Q : 若数字 $a$ 和 $b$ 中有负数,则变成了减法,如何处理? A : 在计算机系统中,数值一律用 补码 来表示和存储。补码的优势: 加法、减法可以统一处理(CPU只有加法器)。因此,以上方法 同时适用于正数和负数的加法 。
复杂度分析:
- 时间复杂度 $O(1)$ : 最差情况下(例如 $a =$ 0x7fffffff , $b = 1$ 时),需循环 32 次,使用 $O(1)$ 时间;每轮中的常数次位操作使用 $O(1)$ 时间。
- 空间复杂度 $O(1)$ : 使用常数大小的额外空间。
< ,
, ,
, ,
, ,
, >
>
代码:
class Solution {
public int add(int a, int b) {
while(b != 0) { // 当进位为 0 时跳出
int c = (a & b) << 1; // c = 进位
a ^= b; // a = 非进位和
b = c; // b = 进位
}
return a;
}
}class Solution {
public:
int add(int a, int b) {
while(b != 0)
{
int c = (unsigned int)(a & b) << 1;
a ^= b;
b = c;
}
return a;
}
};class Solution:
def add(self, a: int, b: int) -> int:
x = 0xffffffff
a, b = a & x, b & x
while b != 0:
a, b = (a ^ b), (a & b) << 1 & x
return a if a <= 0x7fffffff else ~(a ^ x)由于 Python 的数字存储特点,需要做特殊考虑,以下详细介绍。
Python 负数的存储:
Python,Java, C++ 等语言中的数字都是以 补码 形式存储的。但 Python 没有 int , long 等不同长度变量,即在编程时无变量位数的概念。
获取负数的补码: 需要将数字与十六进制数 0xffffffff 相与。可理解为舍去此数字 32 位以上的数字(将 32 位以上都变为 $0$ ),从无限长度变为一个 32 位整数。
返回前数字还原: 若补码 $a$ 为负数( 0x7fffffff 是最大的正数的补码 ),需执行 ~(a ^ x) 操作,将补码还原至 Python 的存储格式。 a ^ x 运算将 1 至 32 位按位取反; ~ 运算是将整个数字取反;因此, ~(a ^ x) 是将 32 位以上的位取反,1 至 32 位不变。
print(hex(1)) # = 0x1 补码
print(hex(-1)) # = -0x1 负号 + 原码 ( Python 特色,Java 会直接输出补码)
print(hex(1 & 0xffffffff)) # = 0x1 正数补码
print(hex(-1 & 0xffffffff)) # = 0xffffffff 负数补码
print(-1 & 0xffffffff) # = 4294967295 ( Python 将其认为正数)