解题思路： ​

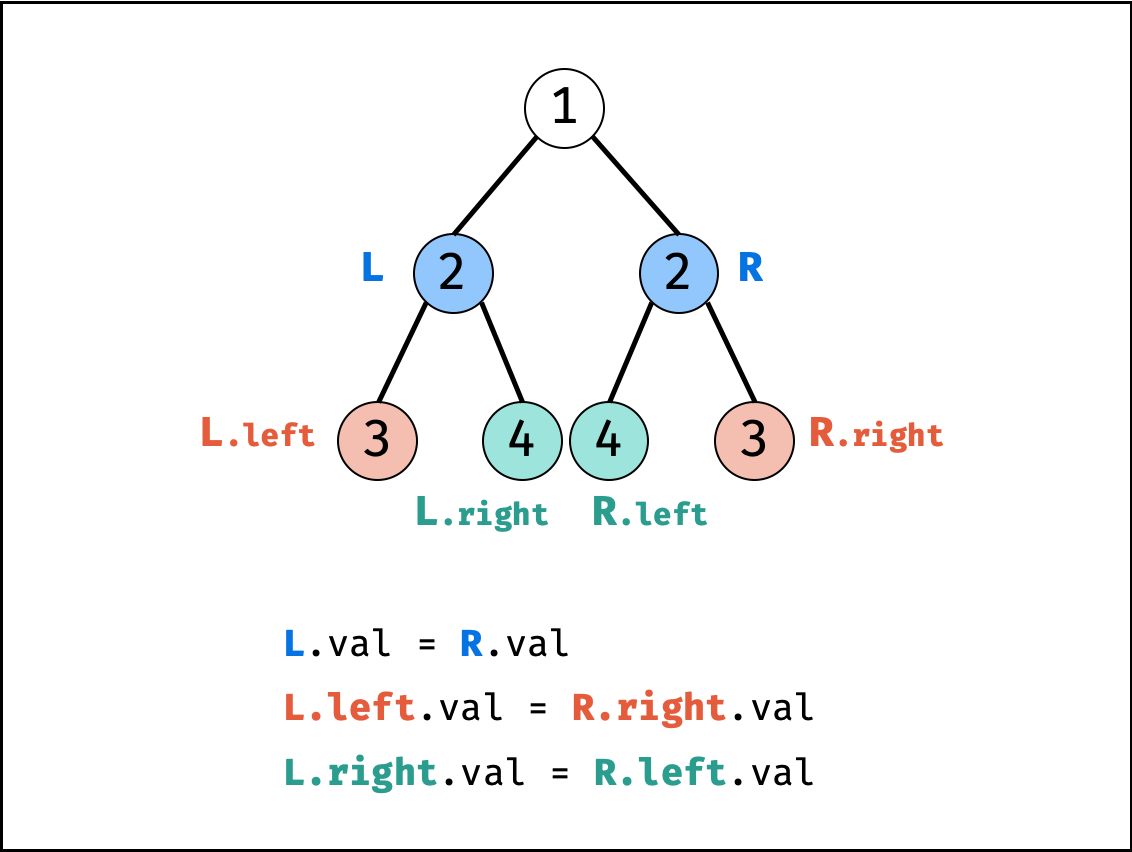
对称二叉树定义： 对于树中 任意两个对称节点 L 和 R ，一定有：

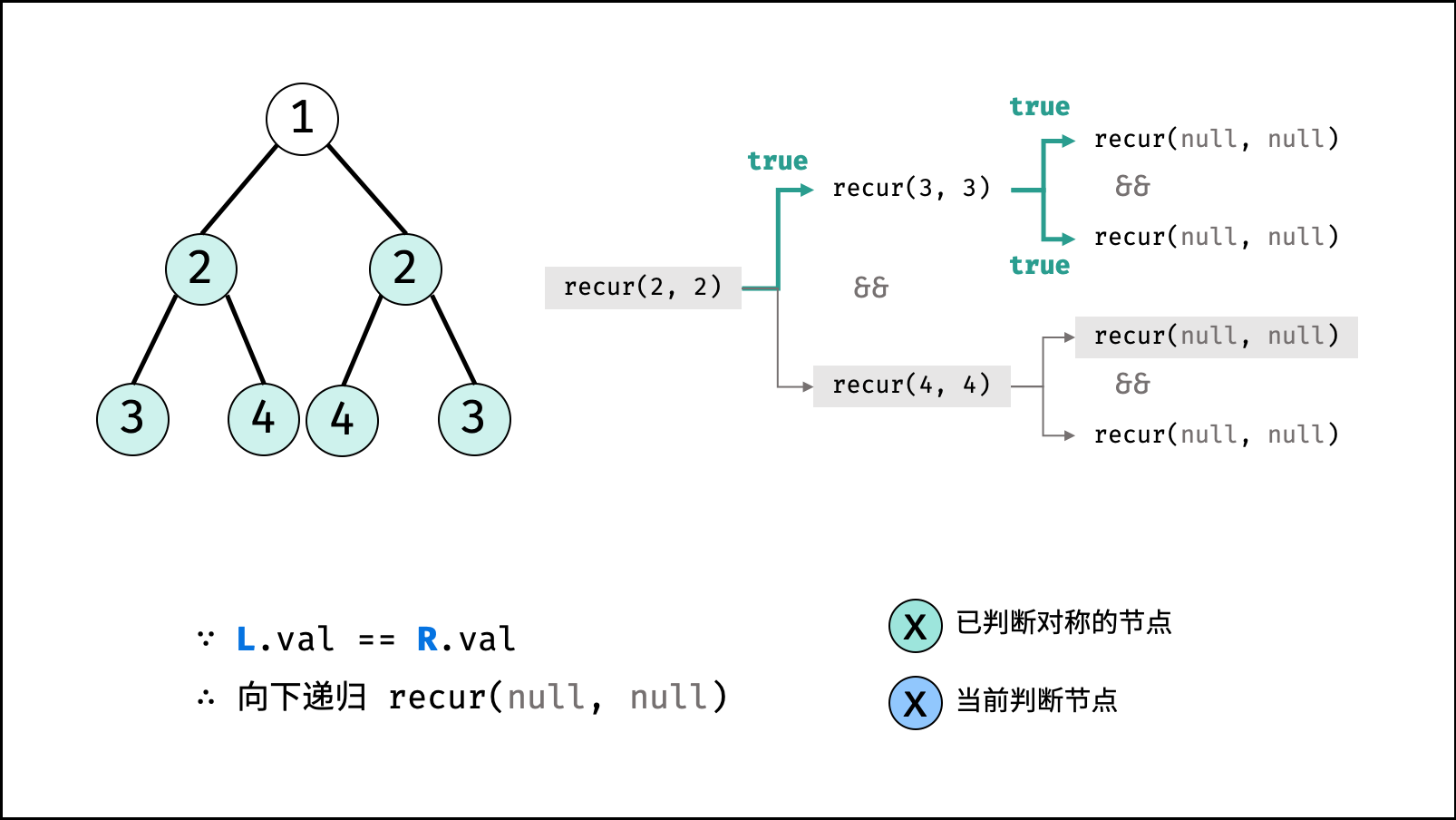
• L.val = R.val ：即此两对称节点值相等。
• L.left.val = R.right.val ：即 $L$ 的 左子节点 和 $R$ 的 右子节点 对称；
• L.right.val = R.left.val ：即 $L$ 的 右子节点 和 $R$ 的 左子节点 对称。

根据以上规律，考虑从顶至底递归，判断每对左右节点是否对称，从而判断树是否为对称二叉树。

算法流程： ​

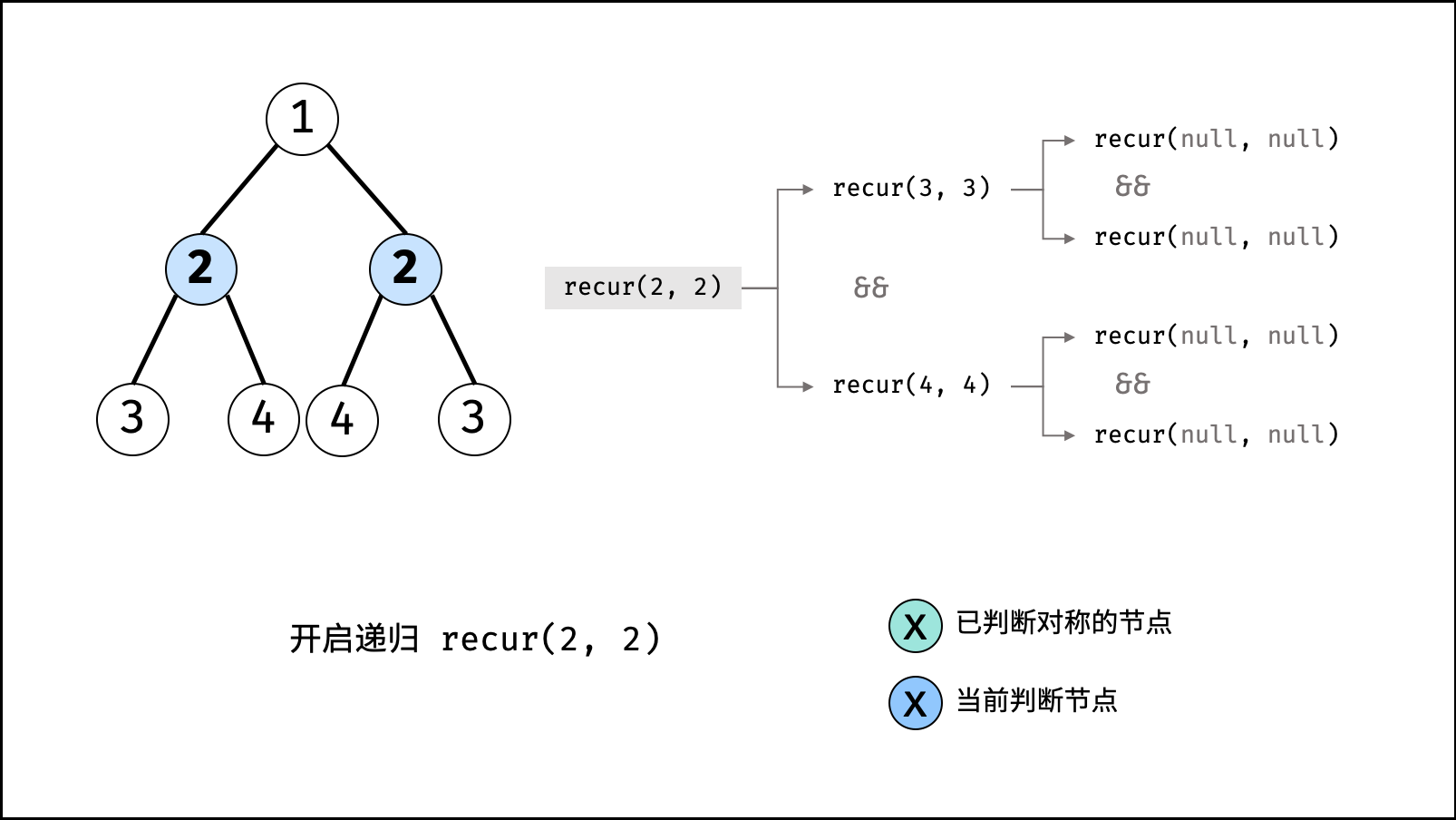
isSymmetric(root) ：

• 特例处理： 若根节点 root 为空，则直接返回 $true$ 。
• 返回值： 即 recur(root.left, root.right) ;

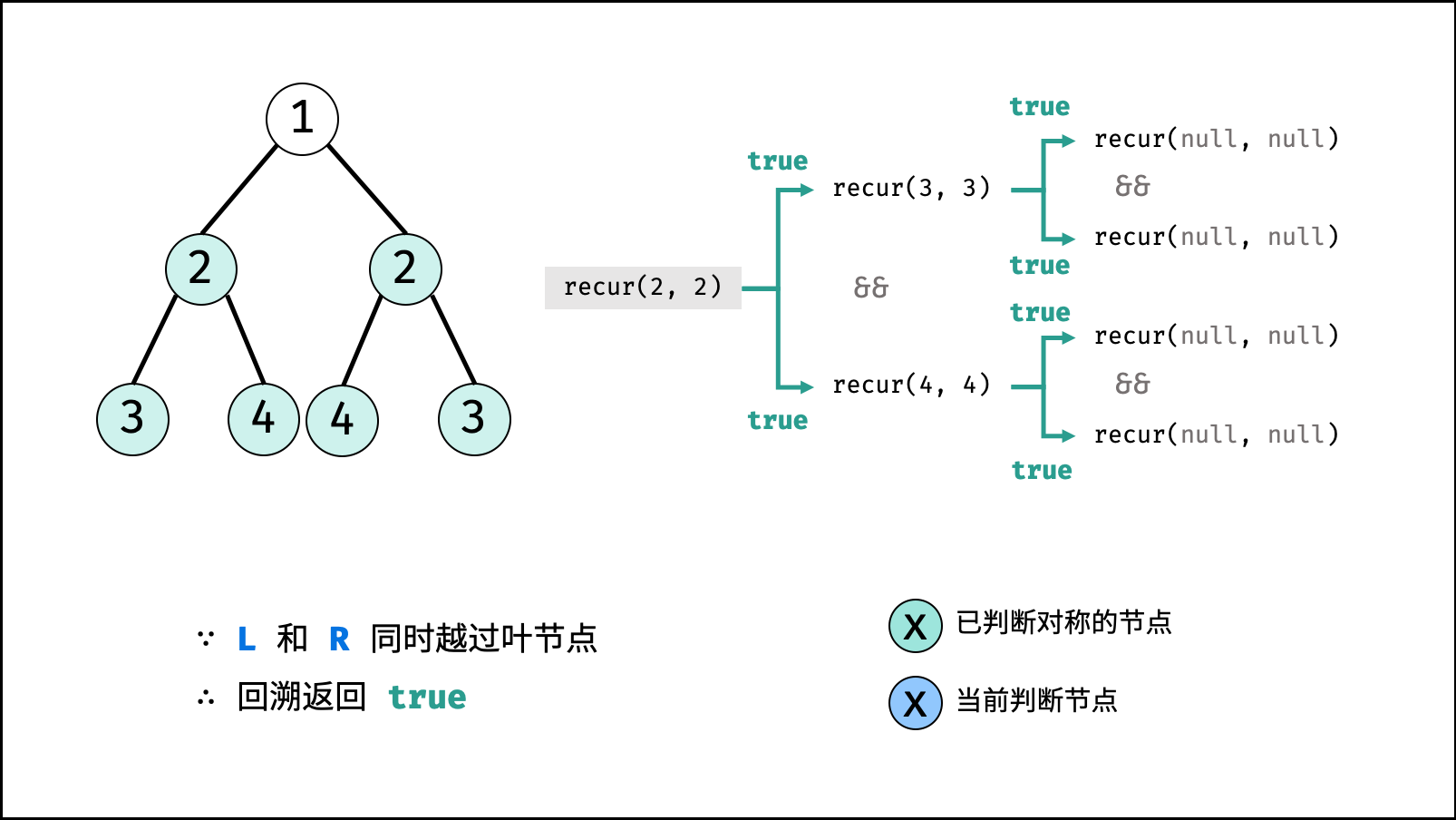
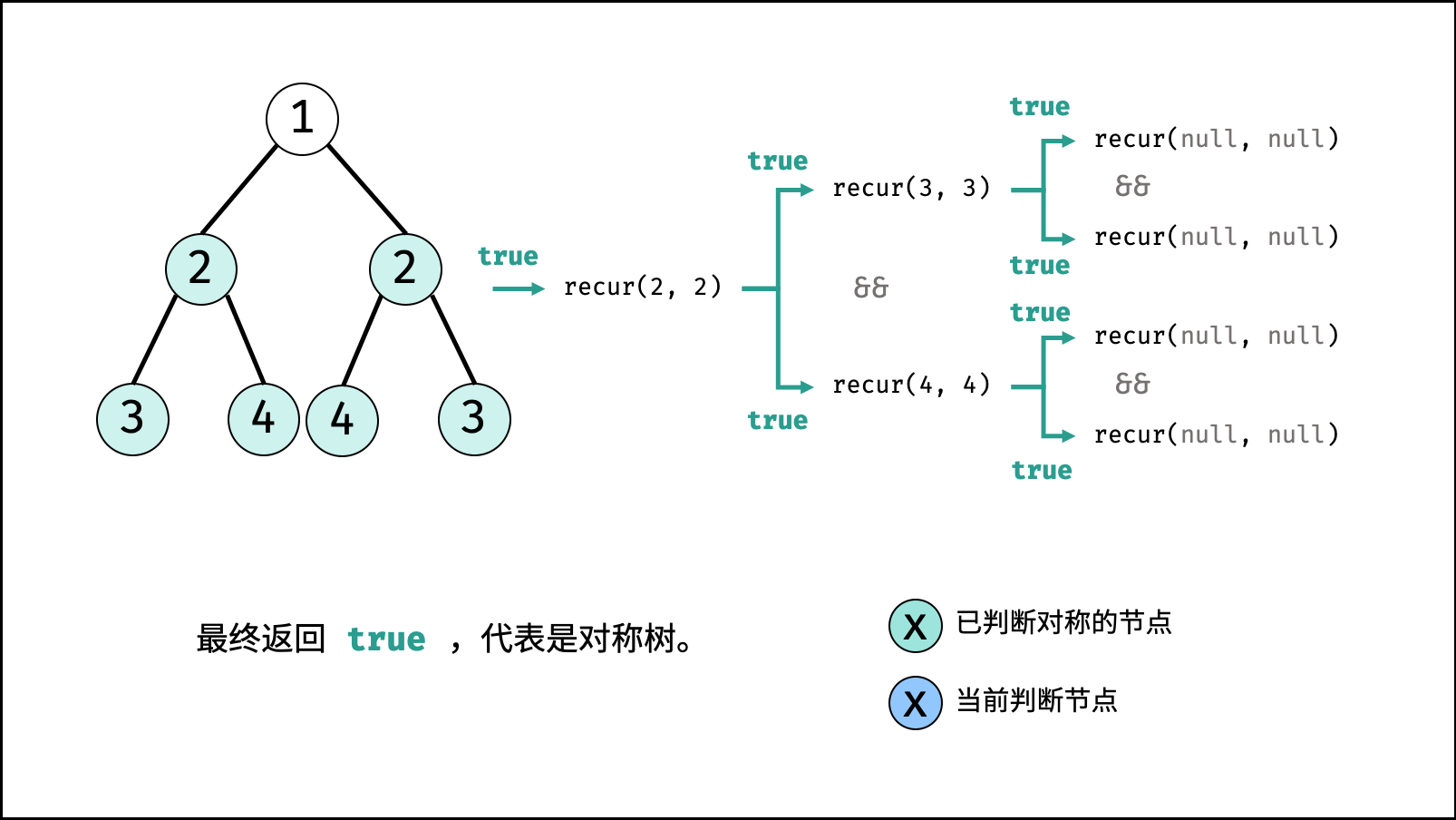
recur(L, R) ：

• 终止条件：
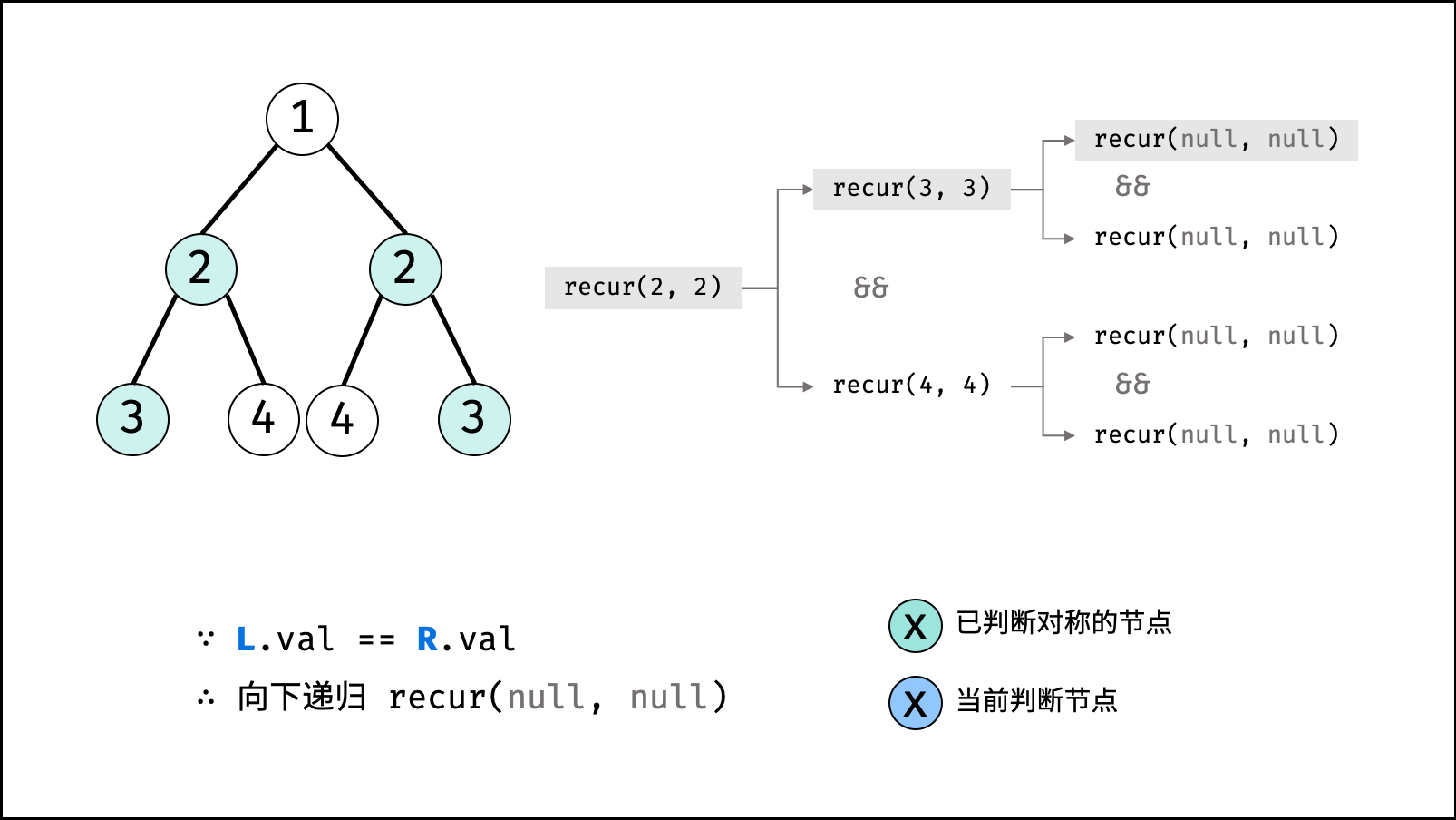
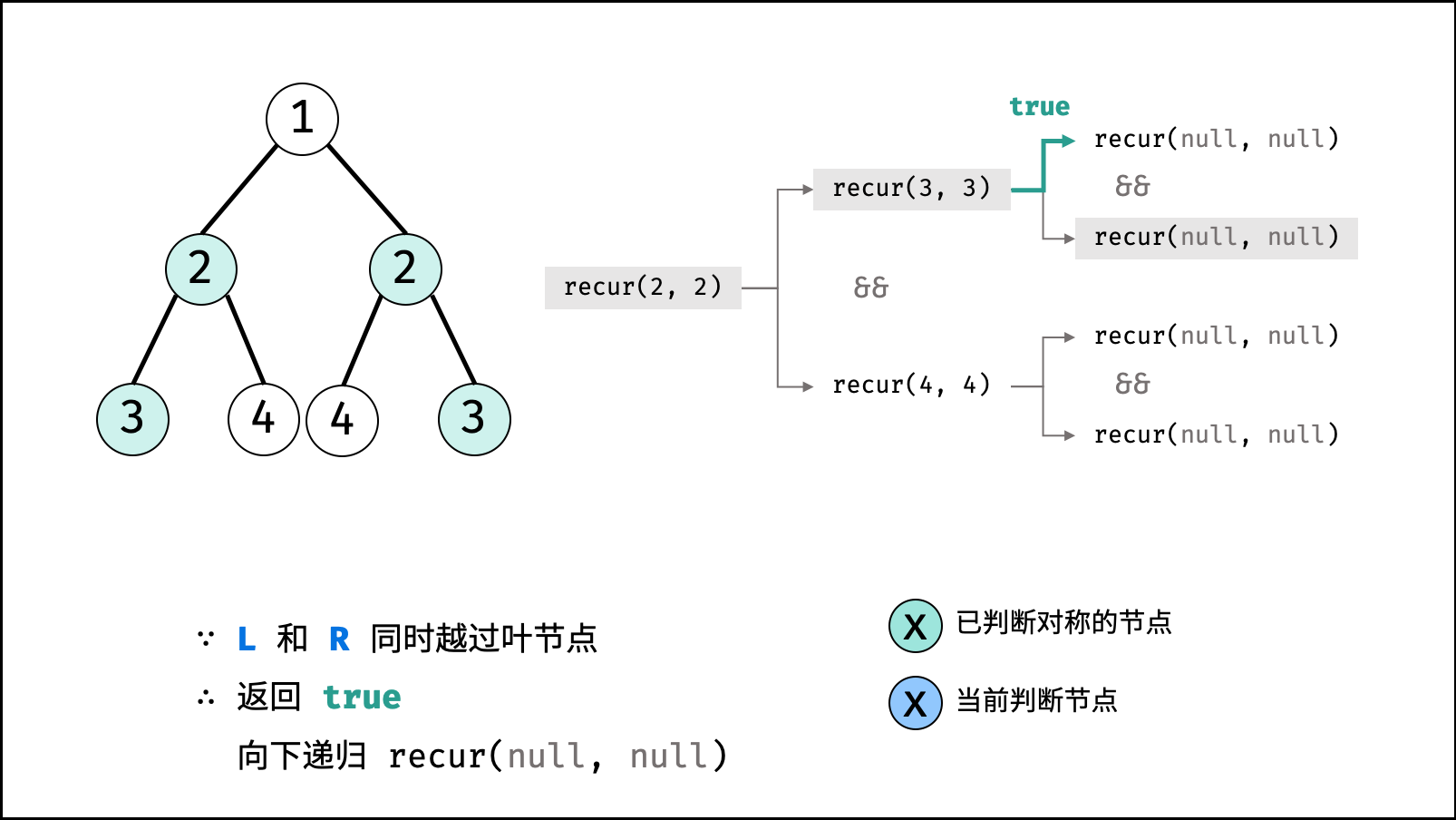
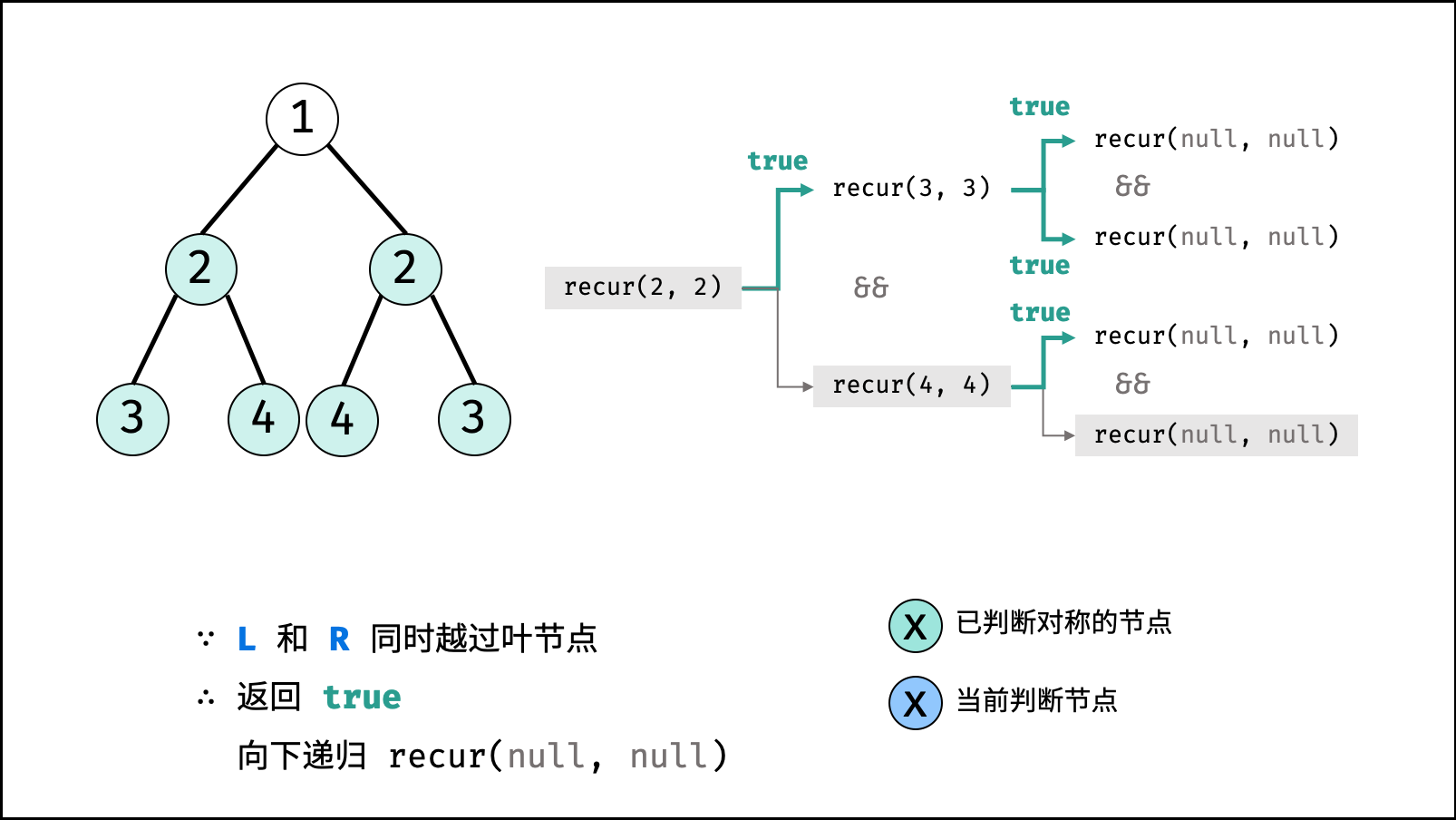
  • 当 L 和 R 同时越过叶节点： 此树从顶至底的节点都对称，因此返回 $true$ ；
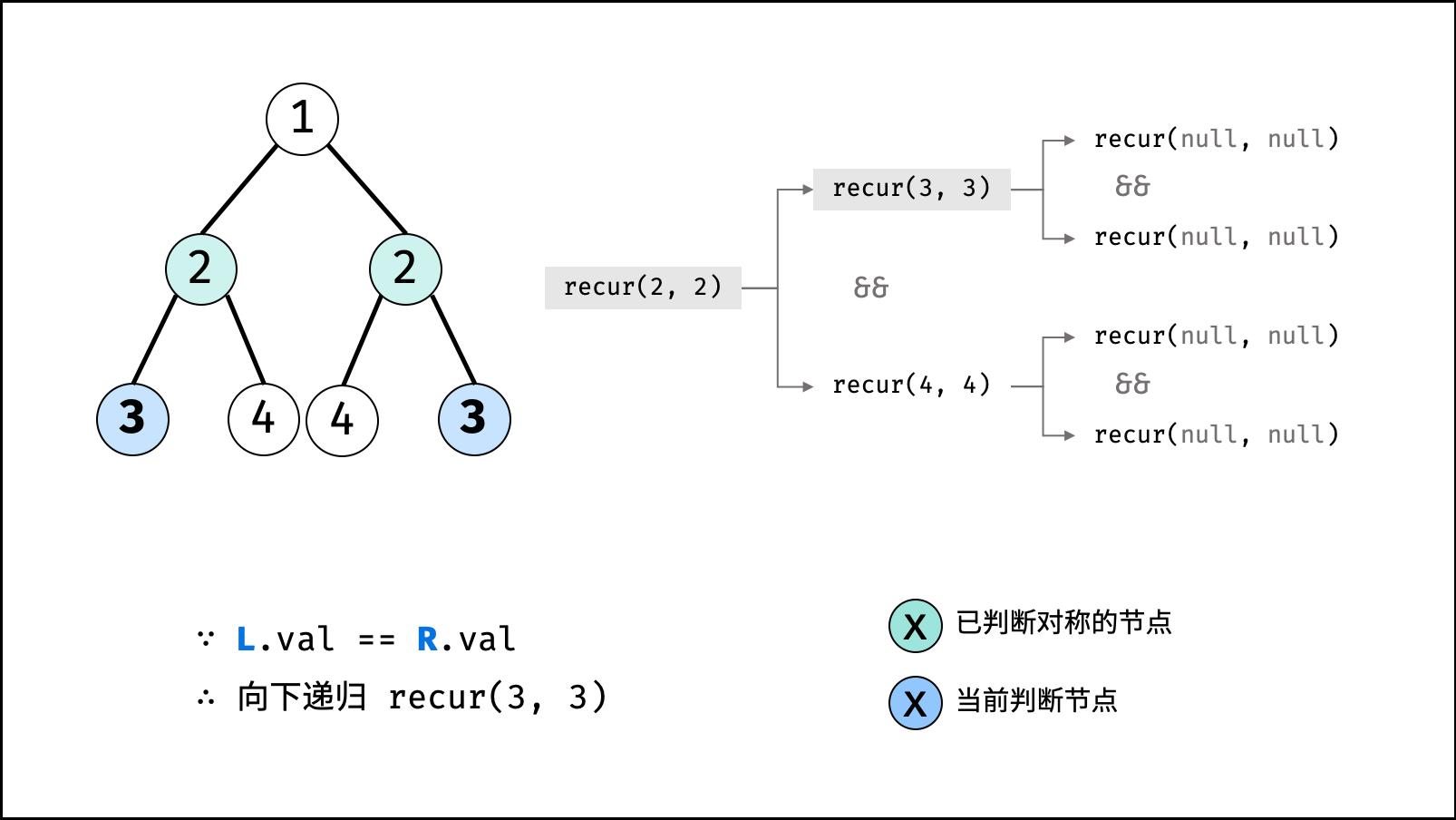
  • 当 L 或 R 中只有一个越过叶节点： 此树不对称，因此返回 $false$ ；
  • 当节点 L 值 $\ne$ 节点 R 值： 此树不对称，因此返回 $false$ ；
• 递推工作：
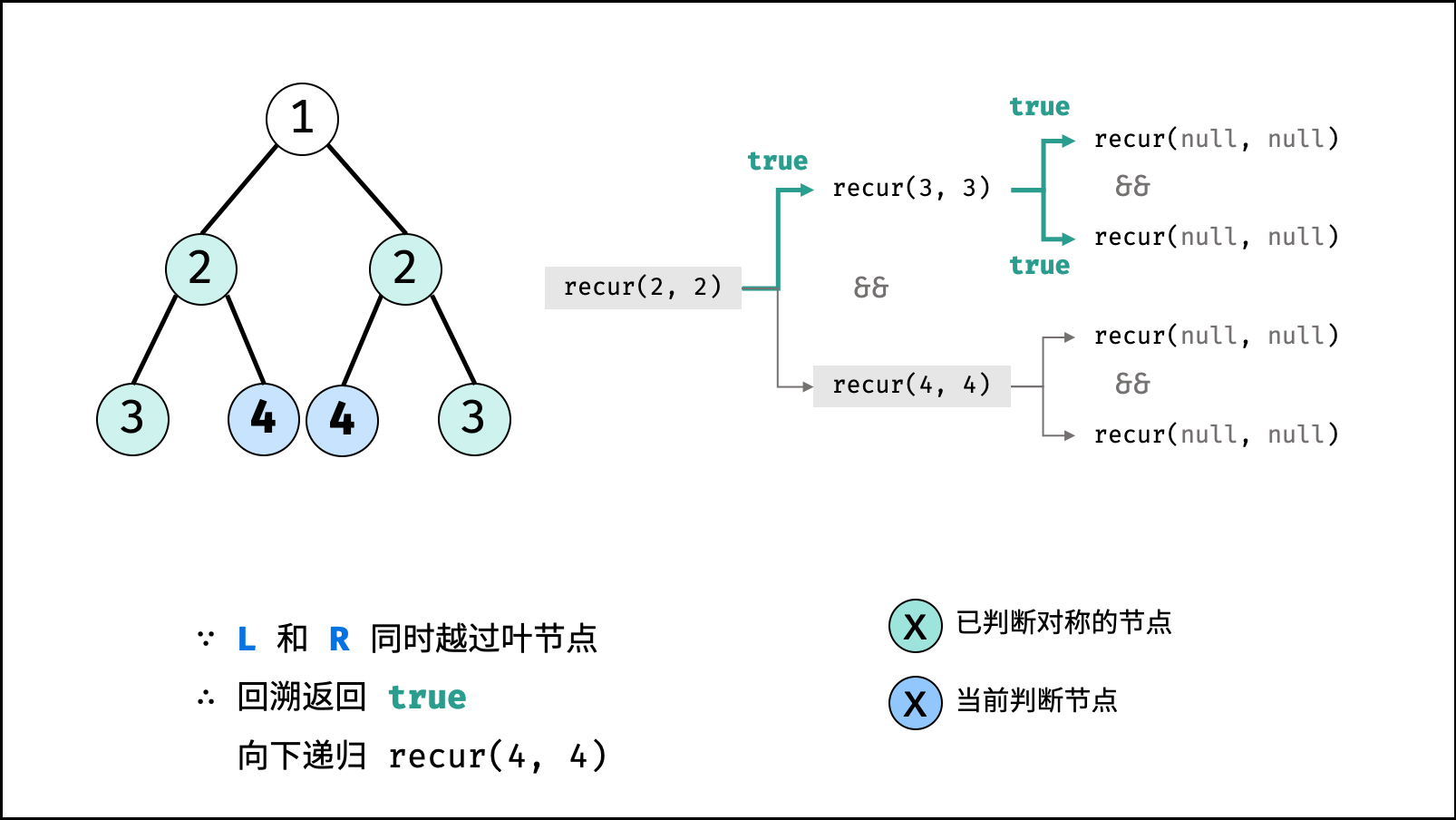
  • 判断两节点 L.left 和 R.right 是否对称，即 recur(L.left, R.right) ；
  • 判断两节点 L.right 和 R.left 是否对称，即 recur(L.right, R.left) ；
• 返回值： 两对节点都对称时，才是对称树，因此用与逻辑符 && 连接。

<,,,,,,,,>

复杂度分析： ​

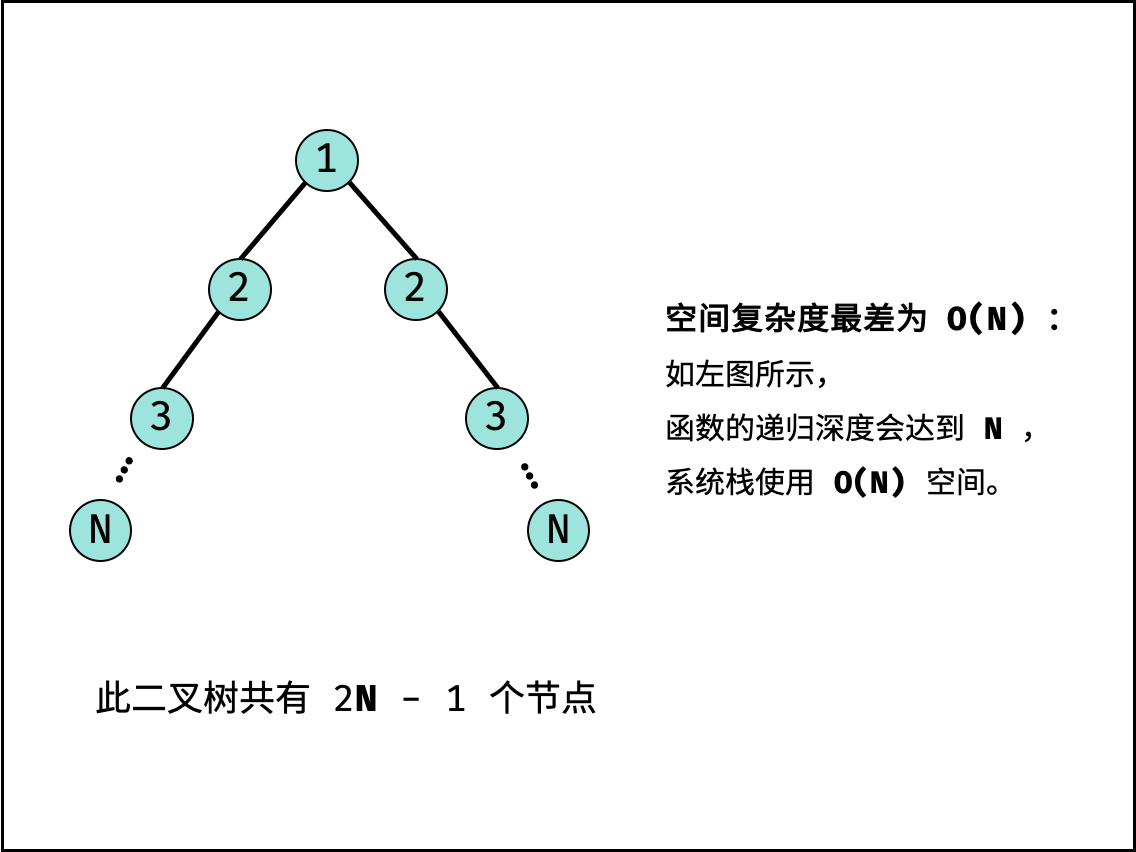
• 时间复杂度 $O(N)$ ： 其中 $N$ 为二叉树的节点数量，每次执行 recur() 可以判断一对节点是否对称，因此最多调用 $N/2$ 次 recur() 方法。
• 空间复杂度 $O(N)$ ： 如下图所示，最差情况下（二叉树退化为链表），系统使用 $O(N)$ 大小的空间。

代码： ​

class Solution:
    def isSymmetric(self, root: TreeNode) -> bool:
        def recur(L, R):
            if not L and not R: return True
            if not L or not R or L.val != R.val: return False
            return recur(L.left, R.right) and recur(L.right, R.left)

        return not root or recur(root.left, root.right)

class Solution {
    public boolean isSymmetric(TreeNode root) {
        return root == null || recur(root.left, root.right);
    }
    boolean recur(TreeNode L, TreeNode R) {
        if(L == null && R == null) return true;
        if(L == null || R == null || L.val != R.val) return false;
        return recur(L.left, R.right) && recur(L.right, R.left);
    }
}

class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        return root == nullptr || recur(root->left, root->right);
    }
private:
    bool recur(TreeNode* L, TreeNode* R) {
        if(L == nullptr && R == nullptr) return true;
        if(L == nullptr || R == nullptr || L->val != R->val) return false;
        return recur(L->left, R->right) && recur(L->right, R->left);
    }
};