解题思路： ​

排序数组中的搜索问题，首先想到 二分法 解决。

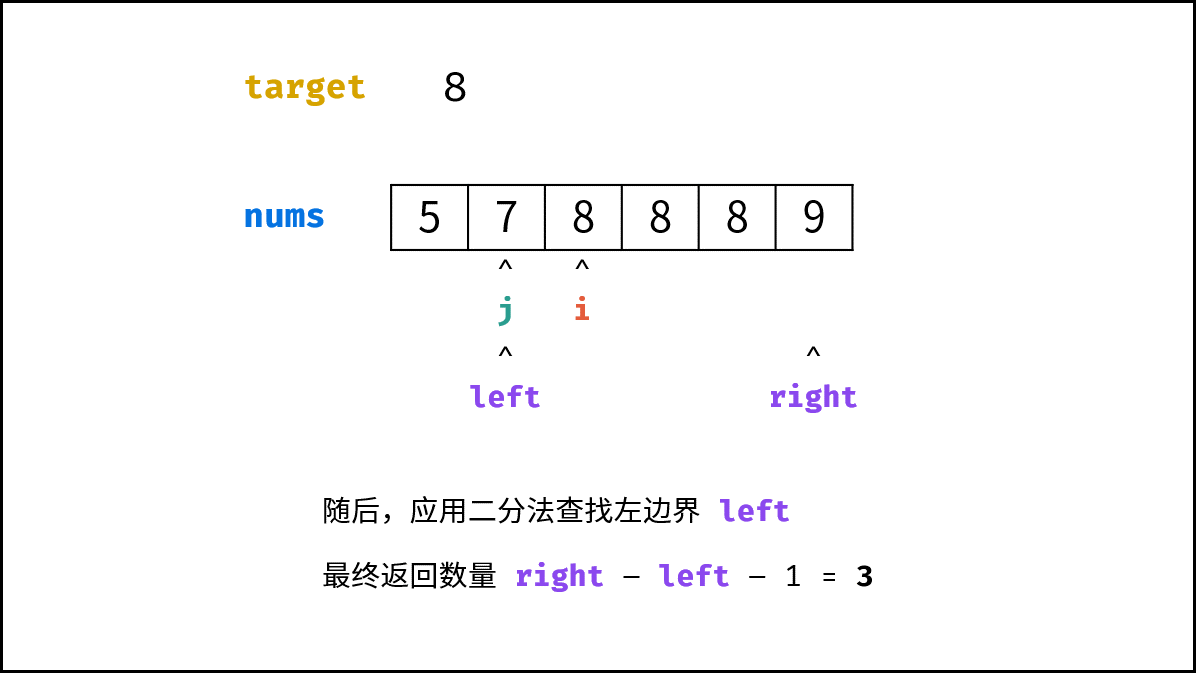
排序数组 $nums$ 中的所有数字 $target$ 形成一个窗口，记窗口的 左 / 右边界 索引分别为 $left$ 和 $right$ ，分别对应窗口左边 / 右边的首个元素。

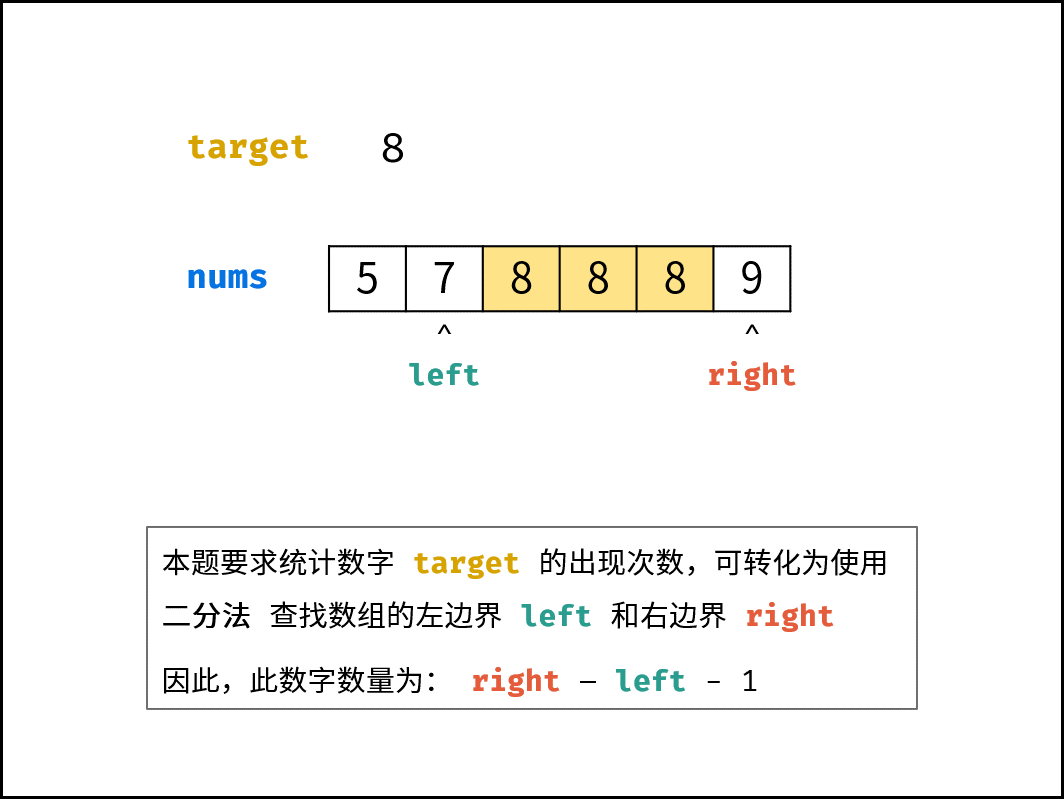
本题要求统计数字 $target$ 的出现次数，可转化为：使用二分法分别找到 左边界 $left$ 和 右边界 $right$ ，易得数字 $target$ 的数量为 $right - left - 1$ 。

算法解析： ​

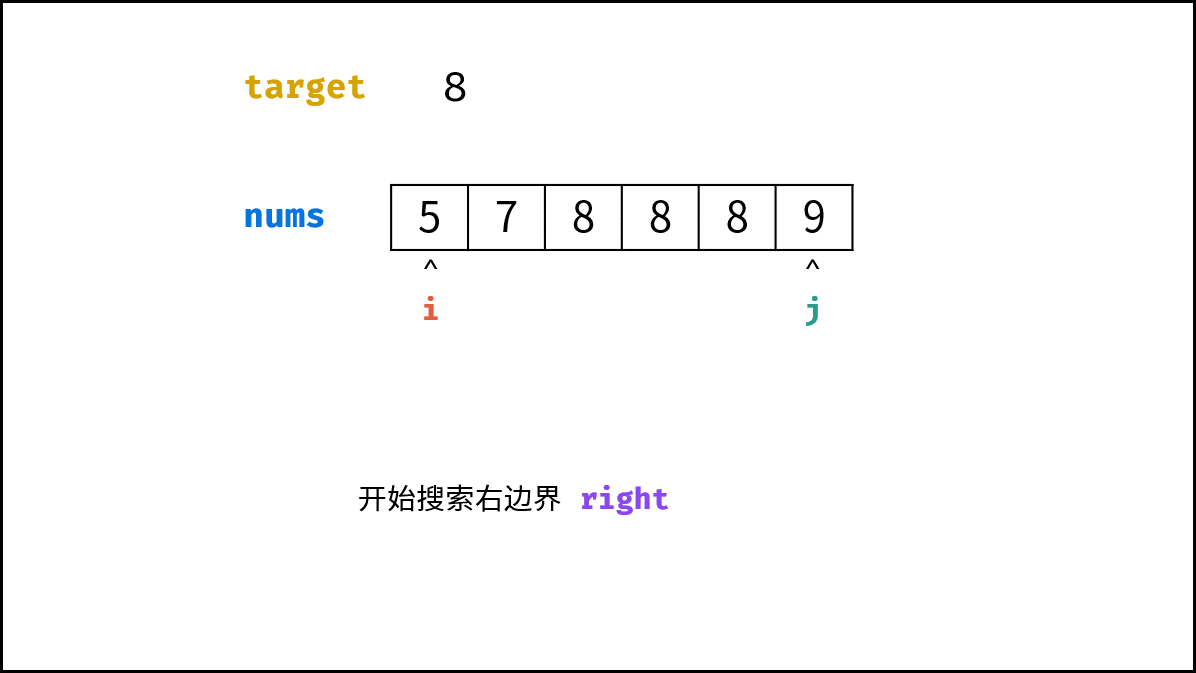
1. 初始化： 左边界 $i = 0$ ，右边界 $j = len(nums) - 1$ 。
2. 循环二分： 当闭区间 $[i, j]$ 无元素时跳出；
   1. 计算中点 $m = (i + j) / 2$ （向下取整）；
   2. 若 $nums[m] < target$ ，则 $target$ 在闭区间 $[m + 1, j]$ 中，因此执行 $i = m + 1$；
   3. 若 $nums[m] > target$ ，则 $target$ 在闭区间 $[i, m - 1]$ 中，因此执行 $j = m - 1$；
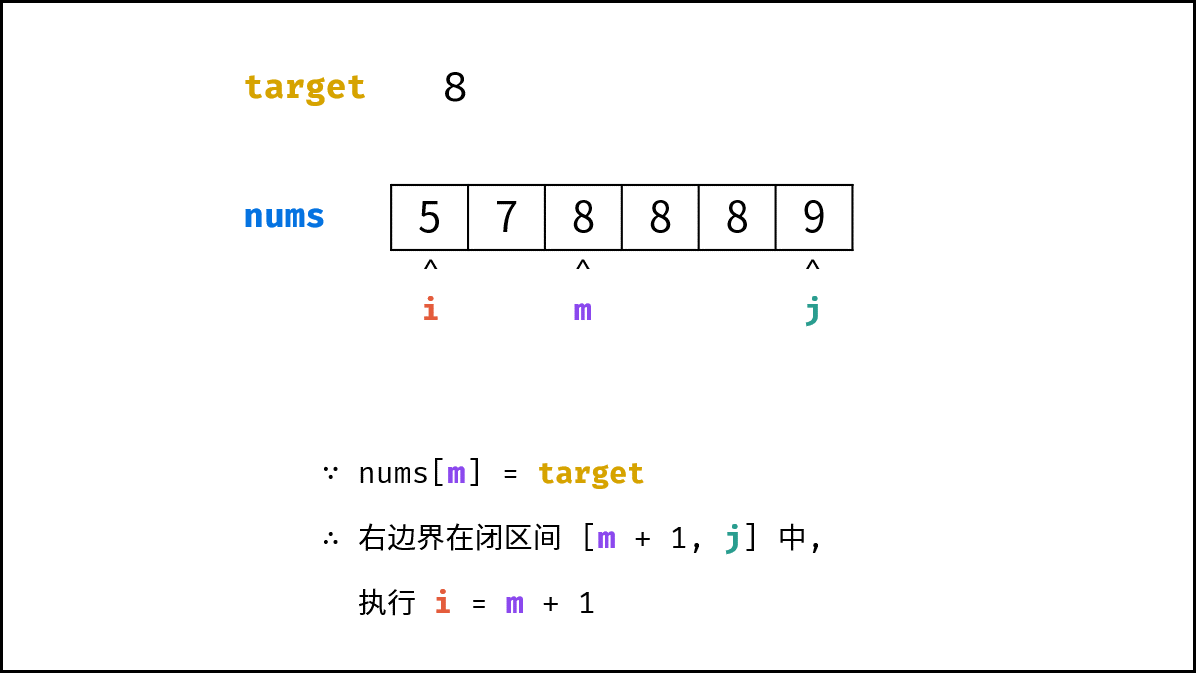
   4. 若 $nums[m] = target$ ，则右边界 $right$ 在闭区间 $[m+1, j]$ 中；左边界 $left$ 在闭区间 $[i, m-1]$ 中。因此分为以下两种情况：
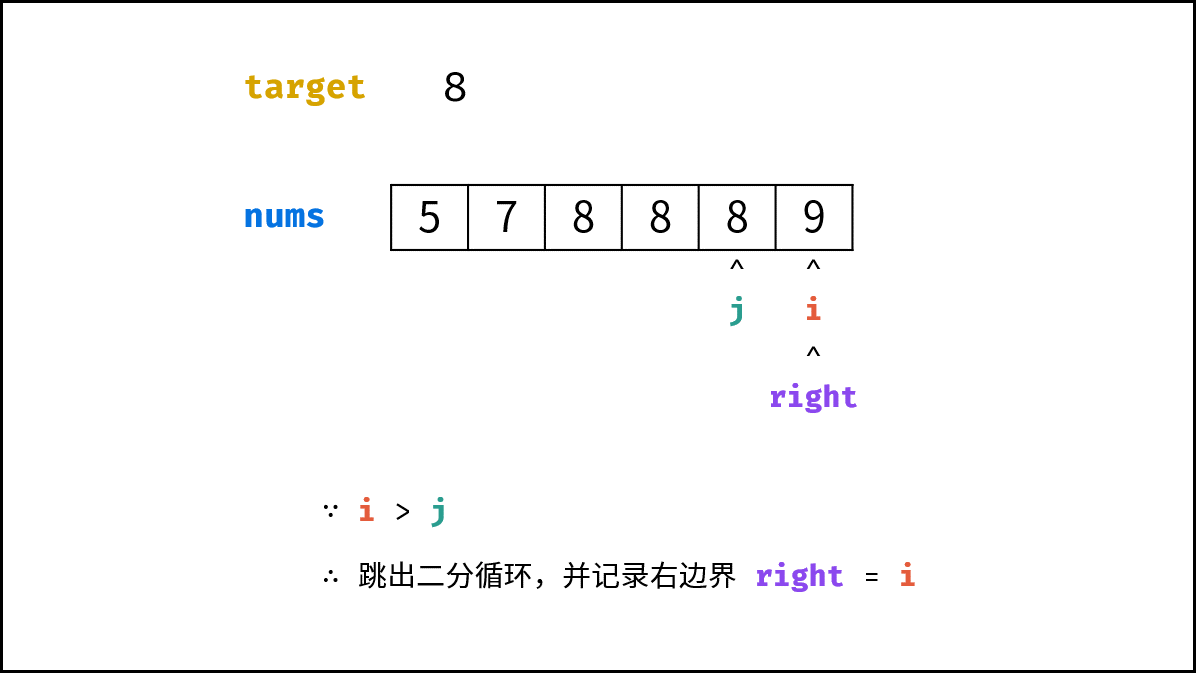
      1. 若查找 右边界 $right$ ，则执行 $i = m + 1$ ；（跳出时 $i$ 指向右边界）
      2. 若查找 左边界 $left$ ，则执行 $j = m - 1$ ；（跳出时 $j$ 指向左边界）
3. 返回值： 应用两次二分，分别查找 $right$ 和 $left$ ，最终返回 $right - left - 1$ 即可。

效率优化： ​

以下优化基于：查找完右边界 $right = i$ 后，则 $nums[j]$ 指向最右边的 $target$ （若存在）。

1. 查找完右边界后，可用 $nums[j] = target$ 判断数组中是否包含 $target$ ，若不包含则直接提前返回 $0$ ，无需后续查找左边界。
2. 查找完右边界后，左边界 $left$ 一定在闭区间 $[0, j]$ 中，因此直接从此区间开始二分查找即可。

<,,,,,>

复杂度分析： ​

• 时间复杂度 $O(\log N)$ ： 二分法为对数级别复杂度。
• 空间复杂度 $O(1)$ ： 几个变量使用常数大小的额外空间。

代码： ​

可将 $nums[m] = target$ 情况合并至其他两种情况中。

class Solution:
    def search(self, nums: [int], target: int) -> int:
        # 搜索右边界 right
        i, j = 0, len(nums) - 1
        while i <= j:
            m = (i + j) // 2
            if nums[m] <= target: i = m + 1
            else: j = m - 1
        right = i
        # 若数组中无 target ，则提前返回
        if j >= 0 and nums[j] != target: return 0
        # 搜索左边界 left
        i = 0
        while i <= j:
            m = (i + j) // 2
            if nums[m] < target: i = m + 1
            else: j = m - 1
        left = j
        return right - left - 1

class Solution {
    public int search(int[] nums, int target) {
        // 搜索右边界 right
        int i = 0, j = nums.length - 1;
        while(i <= j) {
            int m = (i + j) / 2;
            if(nums[m] <= target) i = m + 1;
            else j = m - 1;
        }
        int right = i;
        // 若数组中无 target ，则提前返回
        if(j >= 0 && nums[j] != target) return 0;
        // 搜索左边界 right
        i = 0; j = nums.length - 1;
        while(i <= j) {
            int m = (i + j) / 2;
            if(nums[m] < target) i = m + 1;
            else j = m - 1;
        }
        int left = j;
        return right - left - 1;
    }
}

class Solution {
public:
    int search(vector<int>& nums, int target) {
        // 搜索右边界 right
        int i = 0, j = nums.size() - 1;
        while(i <= j) {
            int m = (i + j) / 2;
            if(nums[m] <= target) i = m + 1;
            else j = m - 1;
        }
        int right = i;
        // 若数组中无 target ，则提前返回
        if(j >= 0 && nums[j] != target) return 0;
        // 搜索左边界 right
        i = 0; j = nums.size() - 1;
        while(i <= j) {
            int m = (i + j) / 2;
            if(nums[m] < target) i = m + 1;
            else j = m - 1;
        }
        int left = j;
        return right - left - 1;
    }
};

以上代码显得比较臃肿（两轮二分查找代码冗余）。为简化代码，可将二分查找右边界 $right$ 的代码 封装至函数 helper() 。 如下图所示，由于数组 $nums$ 中元素都为整数，因此可以分别二分查找 $target$ 和 $target - 1$ 的右边界，将两结果相减并返回即可。

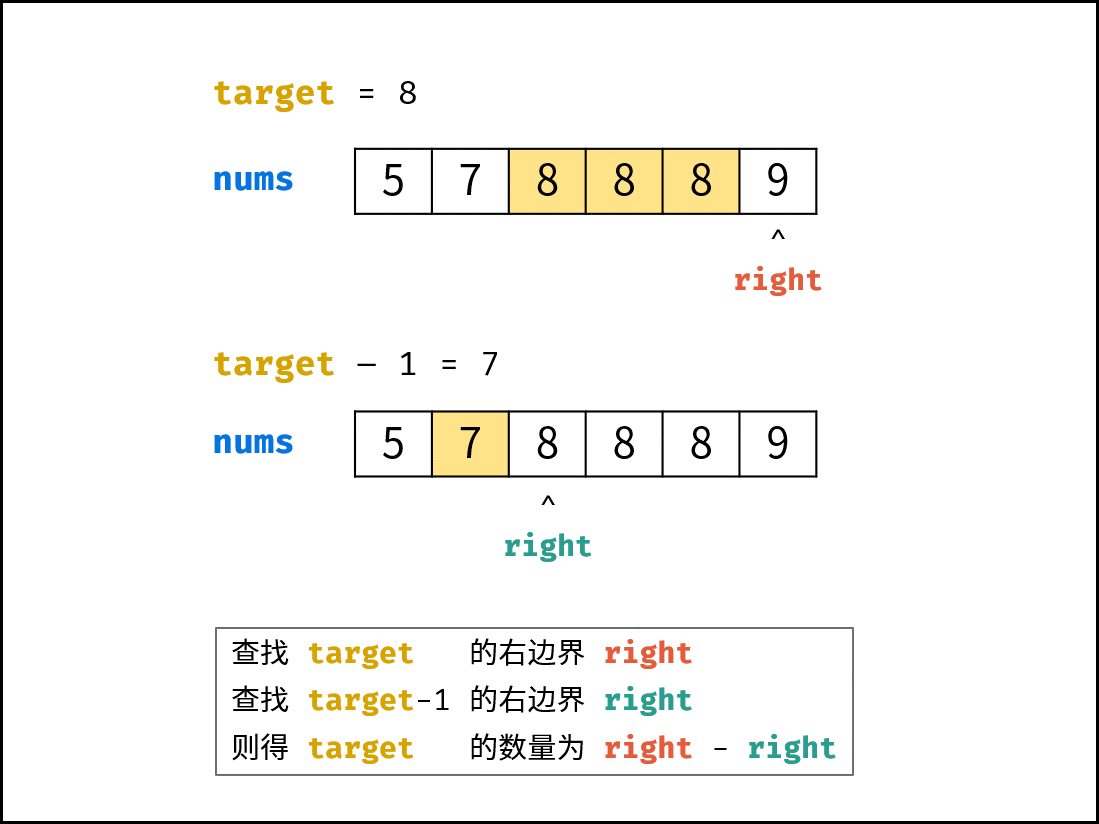
本质上看， helper() 函数旨在查找数字 $tar$ 在数组 $nums$ 中的 插入点 ，且若数组中存在值相同的元素，则插入到这些元素的右边。

class Solution:
    def search(self, nums: [int], target: int) -> int:
        def helper(tar):
            i, j = 0, len(nums) - 1
            while i <= j:
                m = (i + j) // 2
                if nums[m] <= tar: i = m + 1
                else: j = m - 1
            return i
        return helper(target) - helper(target - 1)

class Solution {
    public int search(int[] nums, int target) {
        return helper(nums, target) - helper(nums, target - 1);
    }
    int helper(int[] nums, int tar) {
        int i = 0, j = nums.length - 1;
        while(i <= j) {
            int m = (i + j) / 2;
            if(nums[m] <= tar) i = m + 1;
            else j = m - 1;
        }
        return i;
    }
}

class Solution {
public:
    int search(vector<int>& nums, int target) {
        return helper(nums, target) - helper(nums, target - 1);
    }
private:
    int helper(vector<int>& nums, int tar) {
        int i = 0, j = nums.size() - 1;
        while(i <= j) {
            int m = (i + j) / 2;
            if(nums[m] <= tar) i = m + 1;
            else j = m - 1;
        }
        return i;
    }
};