解题思路： ​

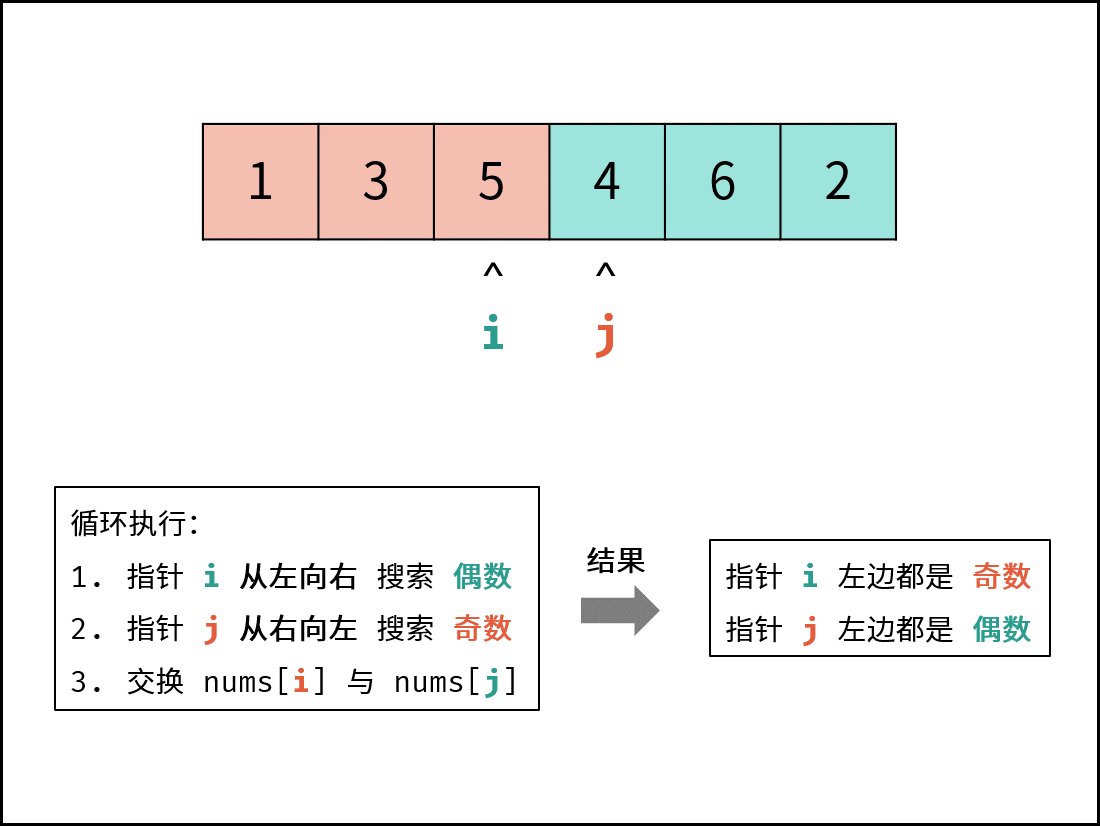
考虑定义双指针 $i$ , $j$ 分列数组左右两端，循环执行：

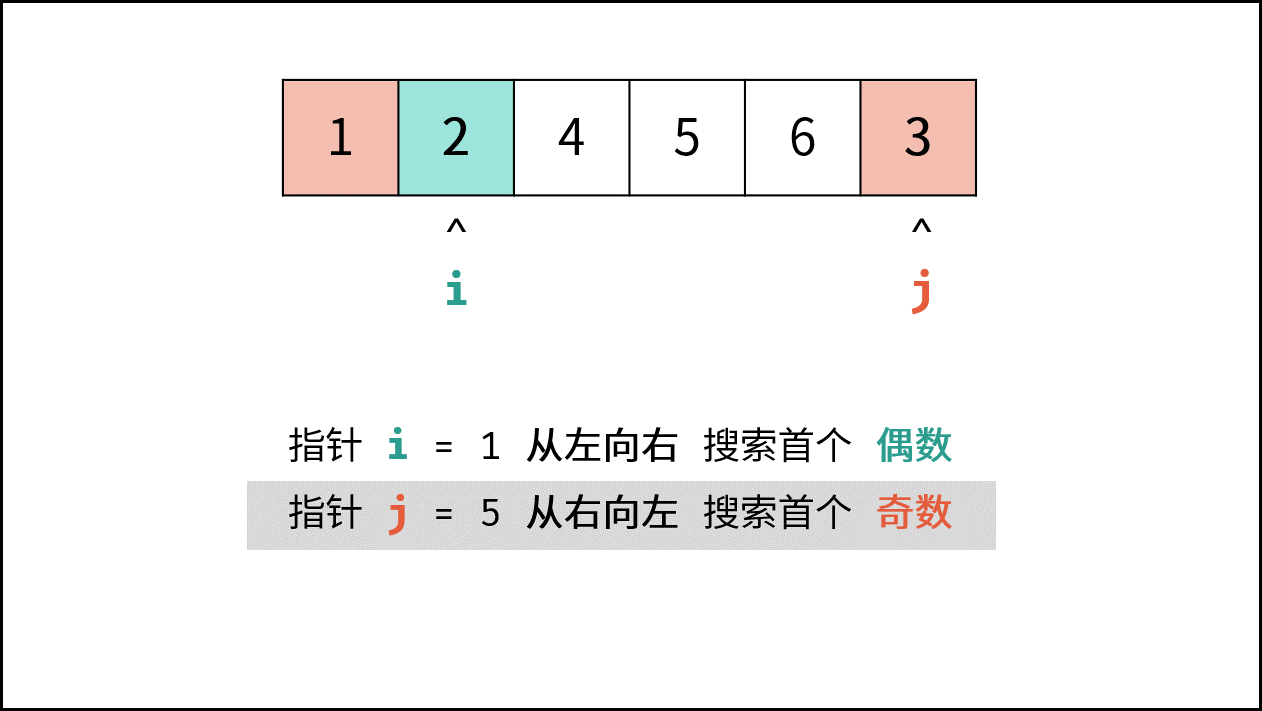
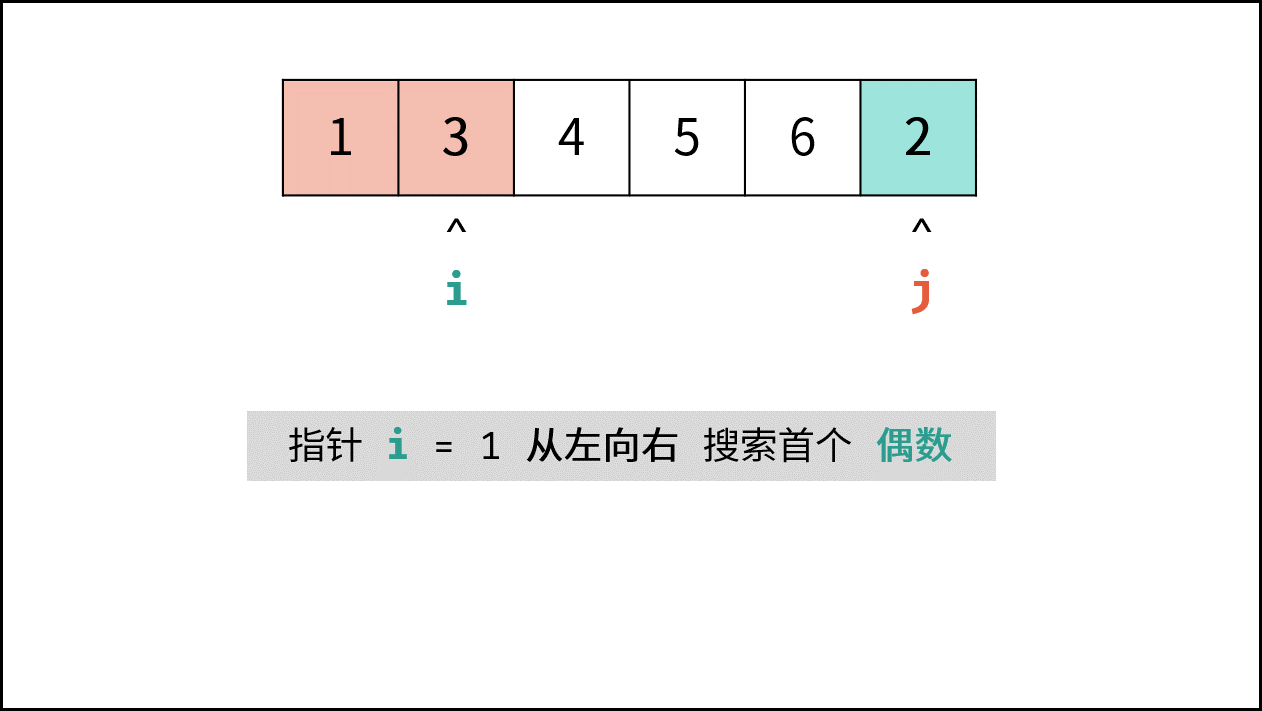
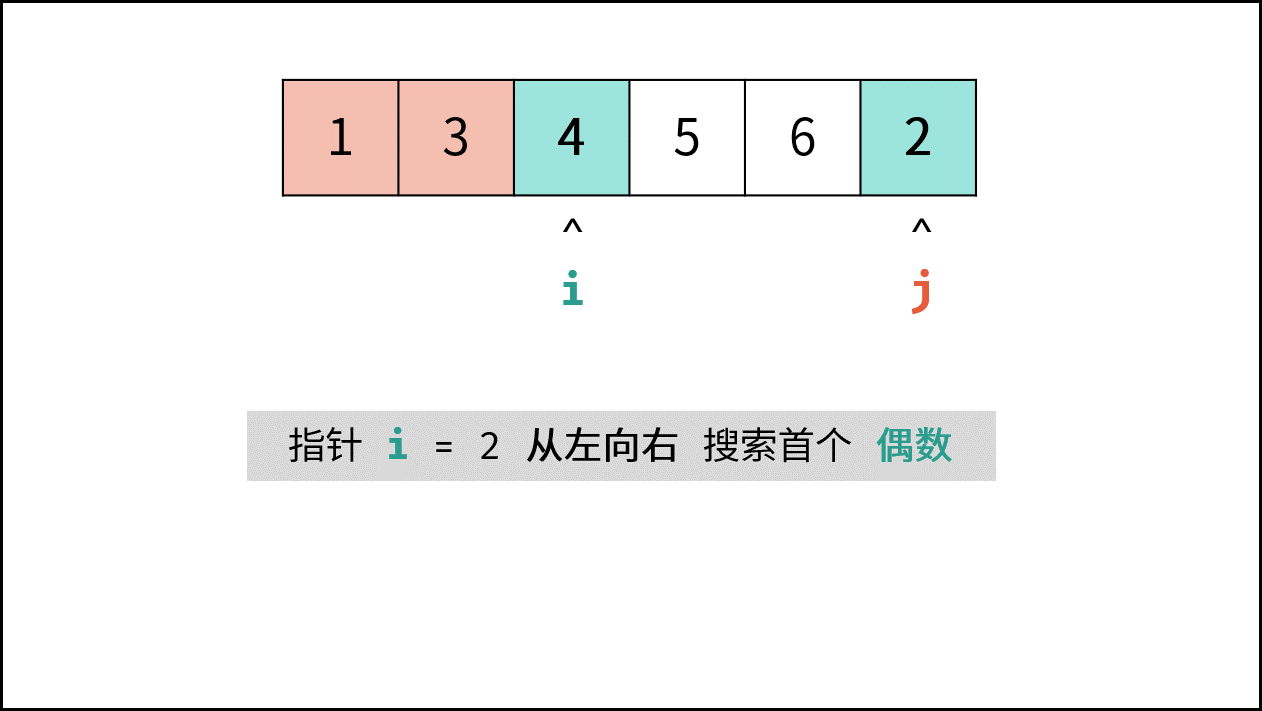
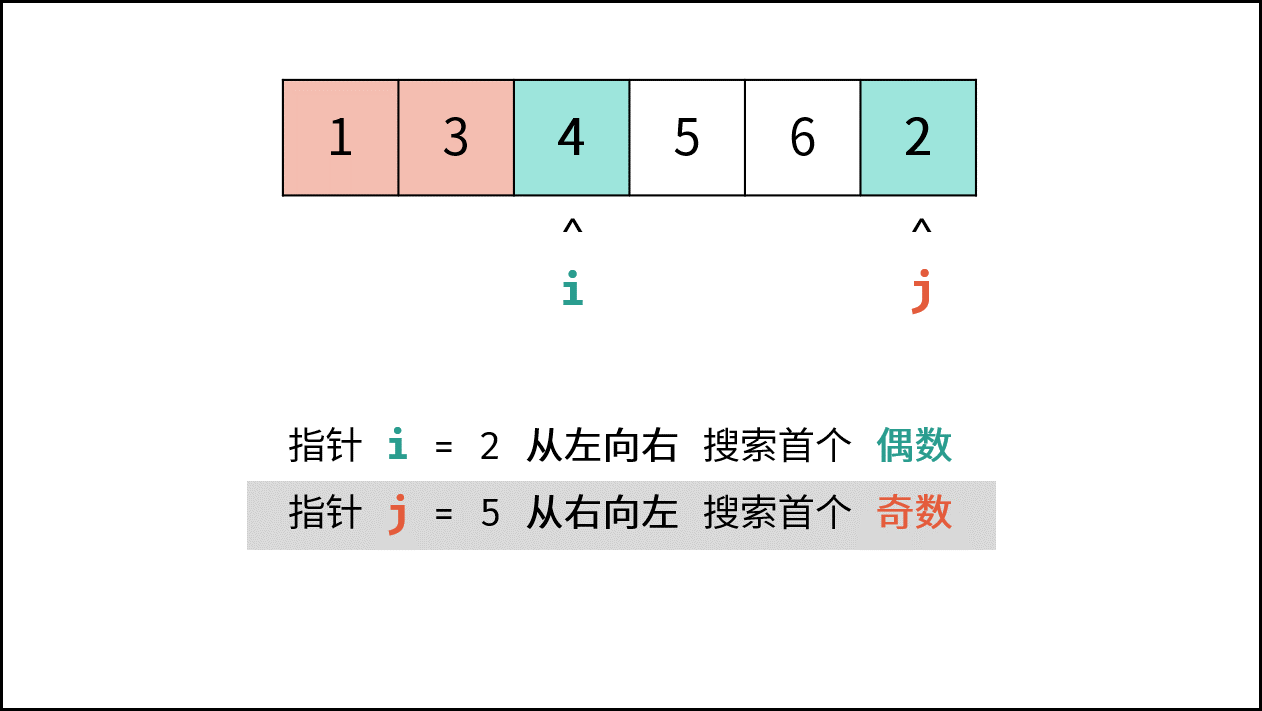
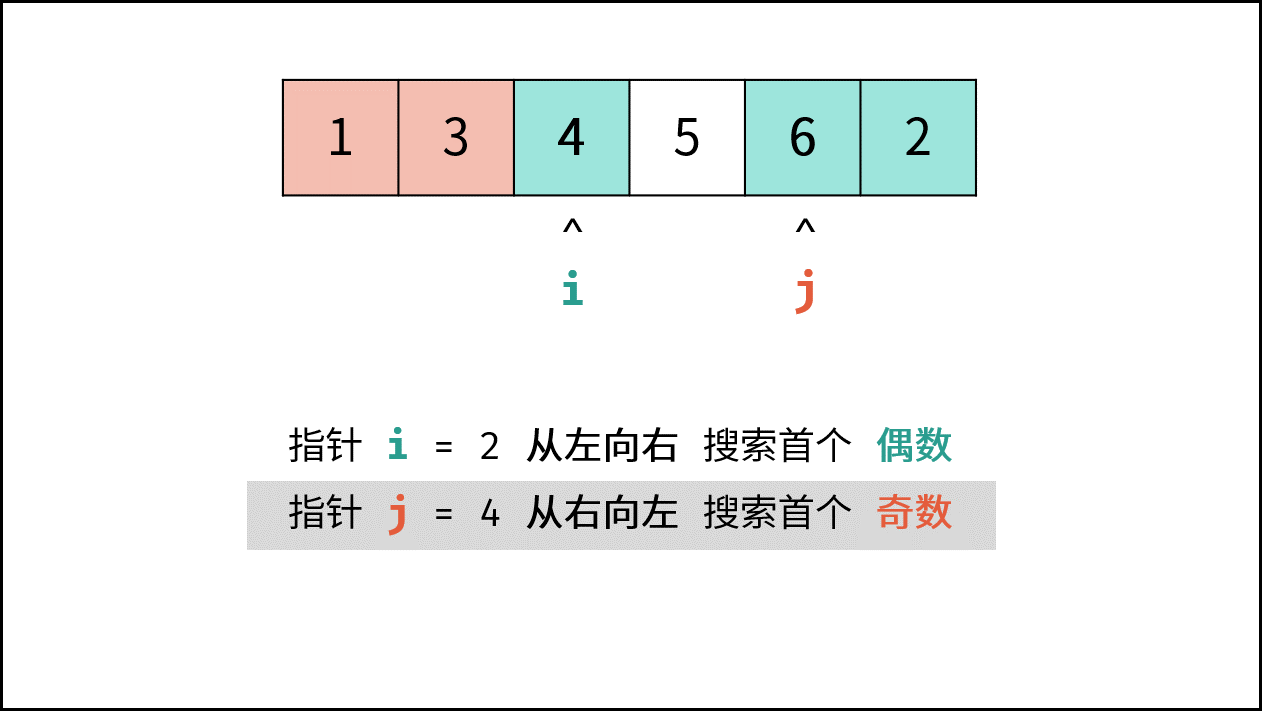
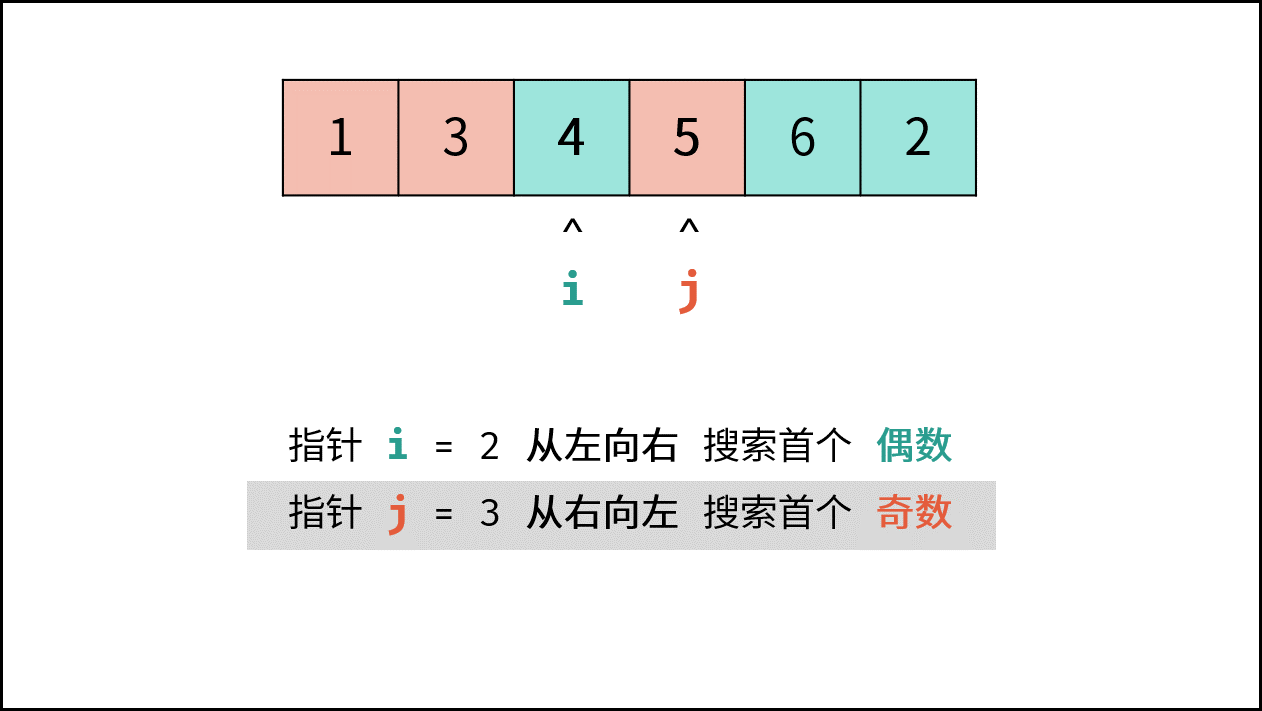
1. 指针 $i$ 从左向右寻找偶数；
2. 指针 $j$ 从右向左寻找奇数；
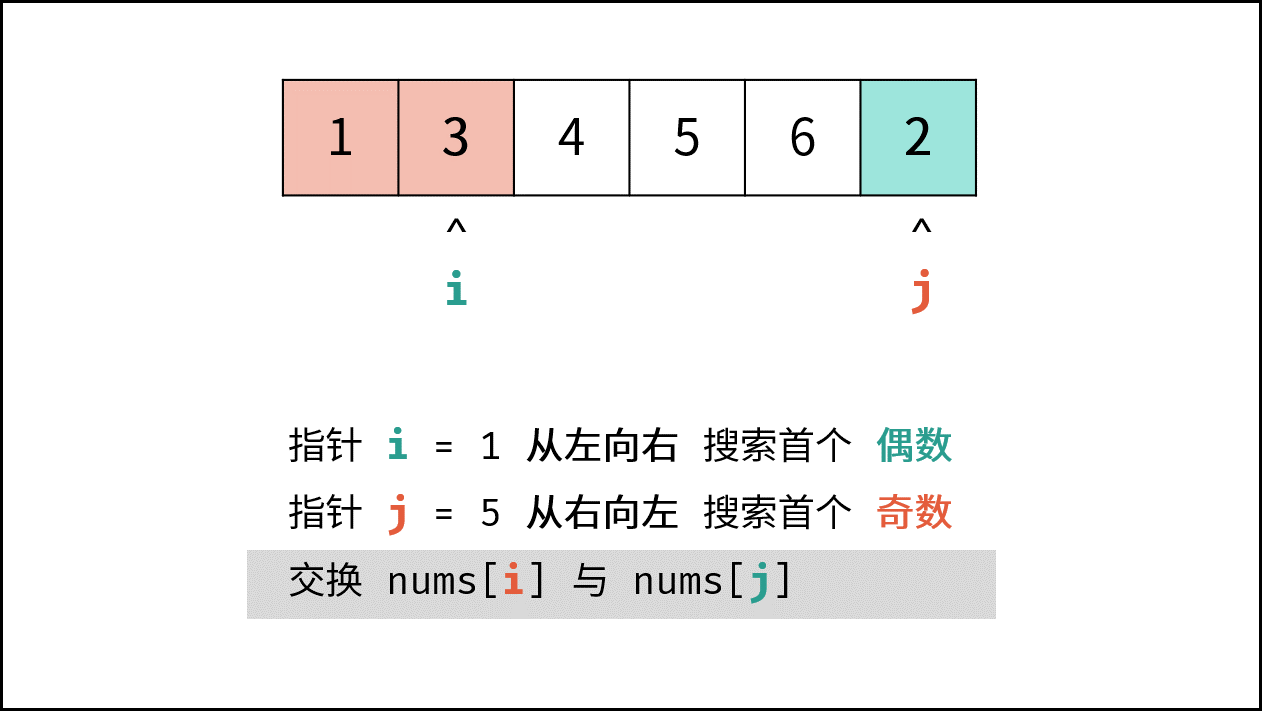
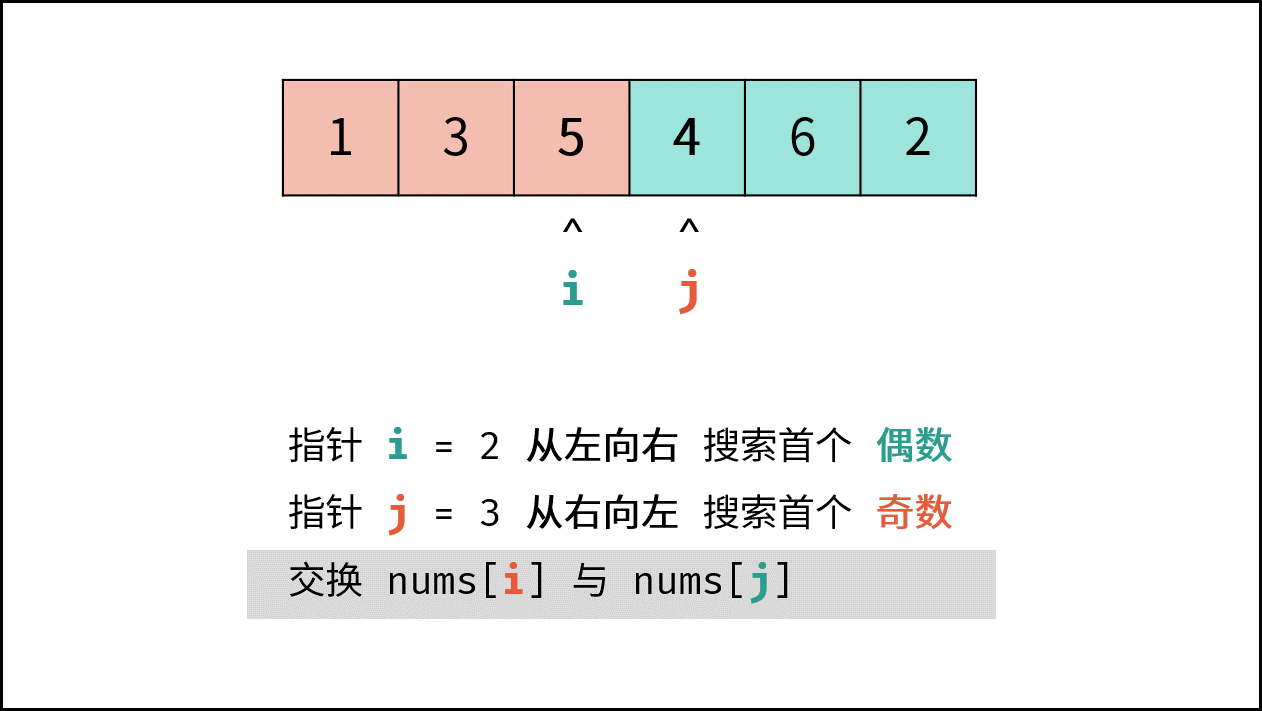
3. 将 偶数 $nums[i]$ 和 奇数 $nums[j]$ 交换。

可始终保证： 指针 $i$ 左边都是奇数，指针 $j$ 右边都是偶数 。

算法流程： ​

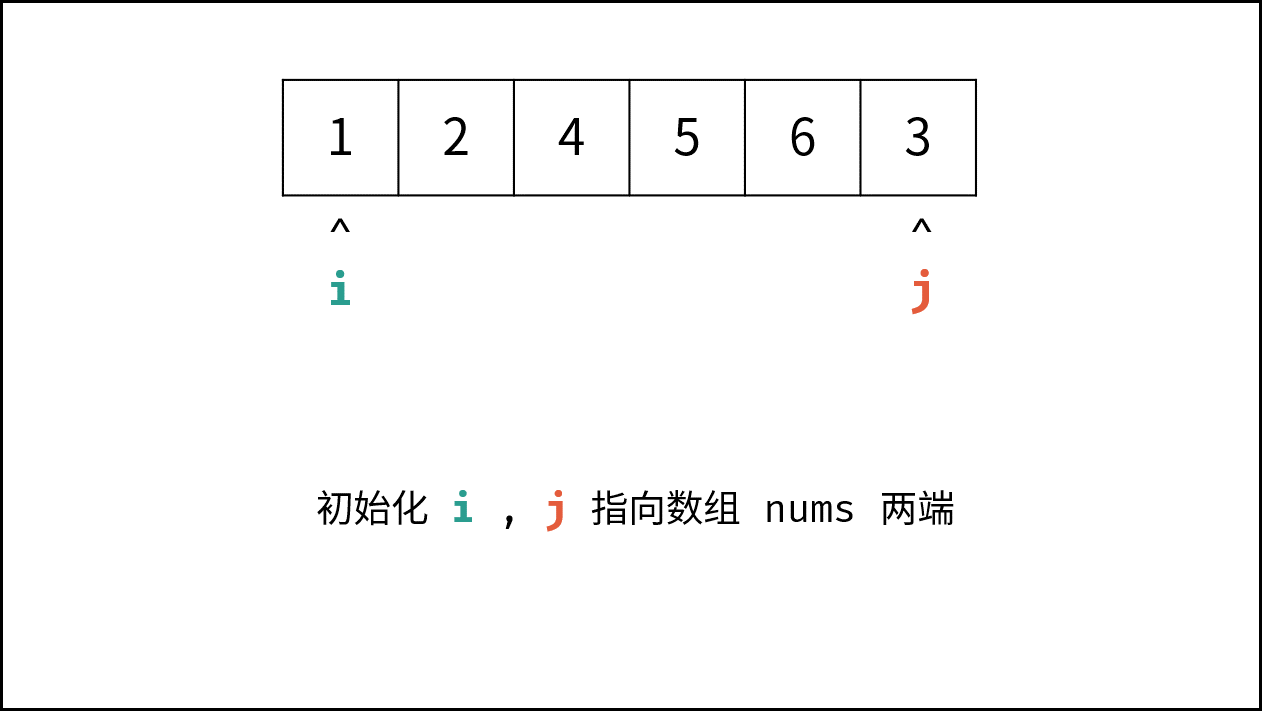
1. 初始化： $i$ , $j$ 双指针，分别指向数组 $nums$ 左右两端；
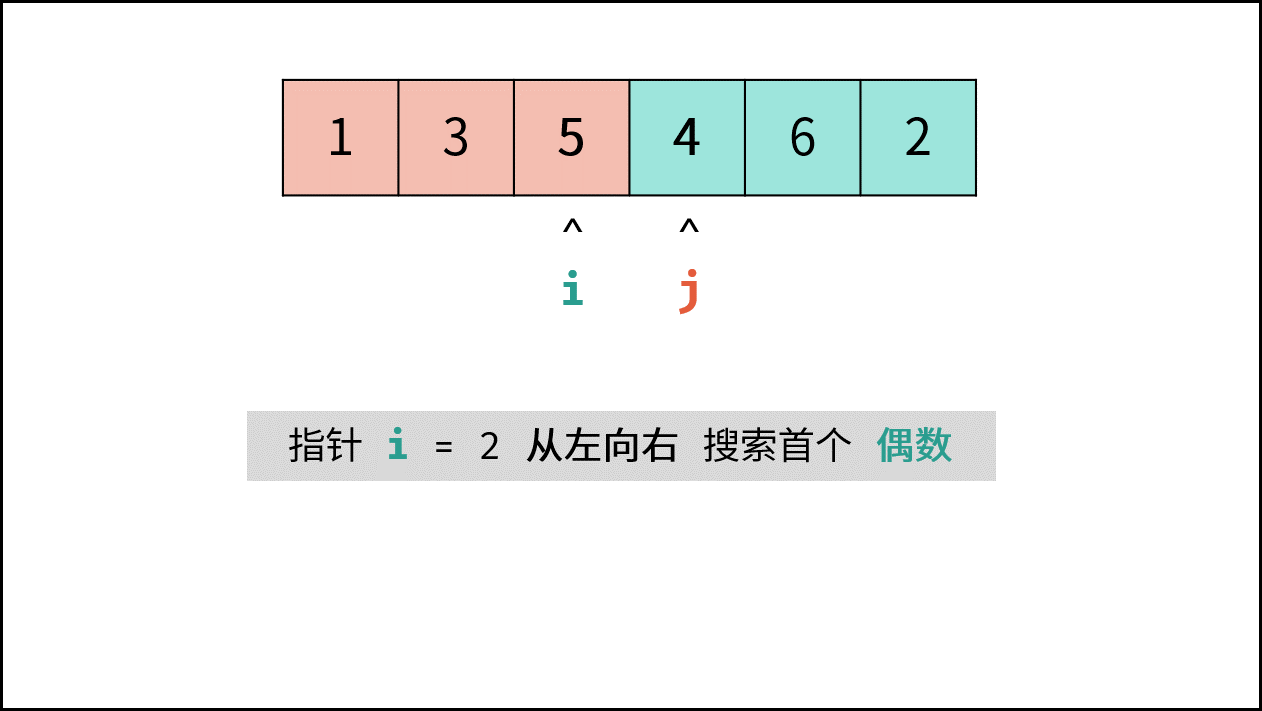
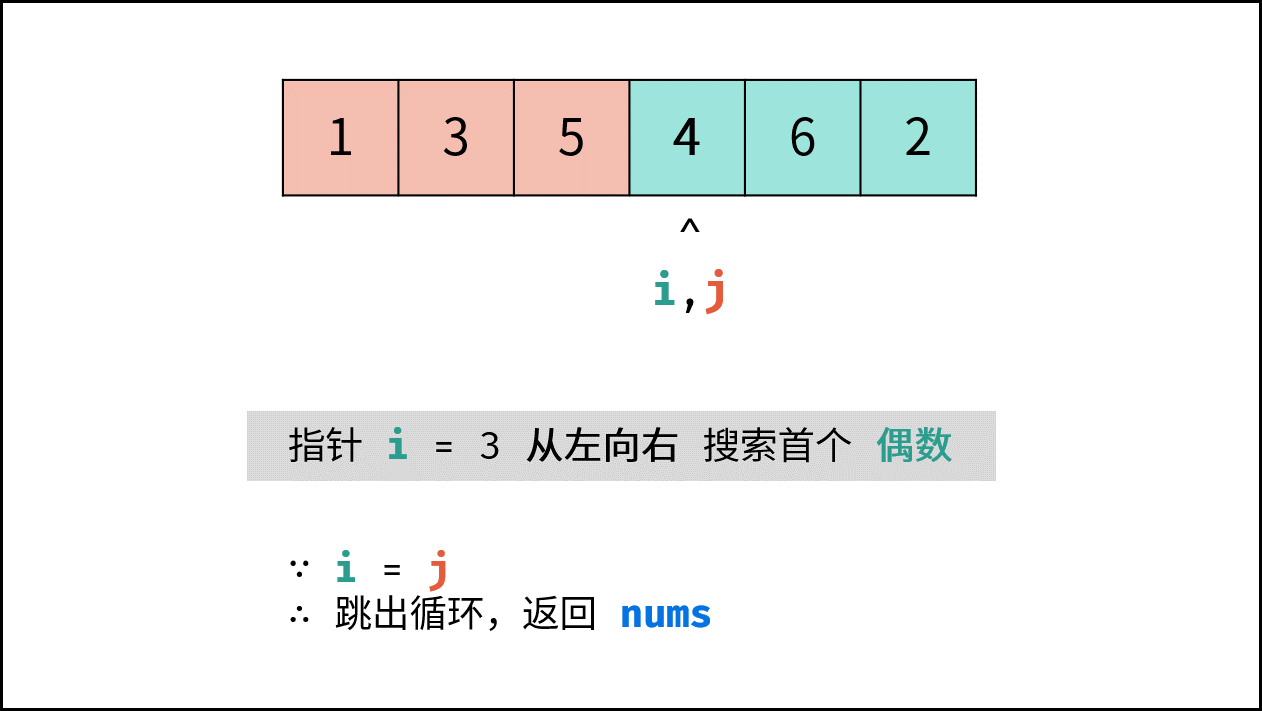
2. 循环交换： 当 $i = j$ 时跳出；
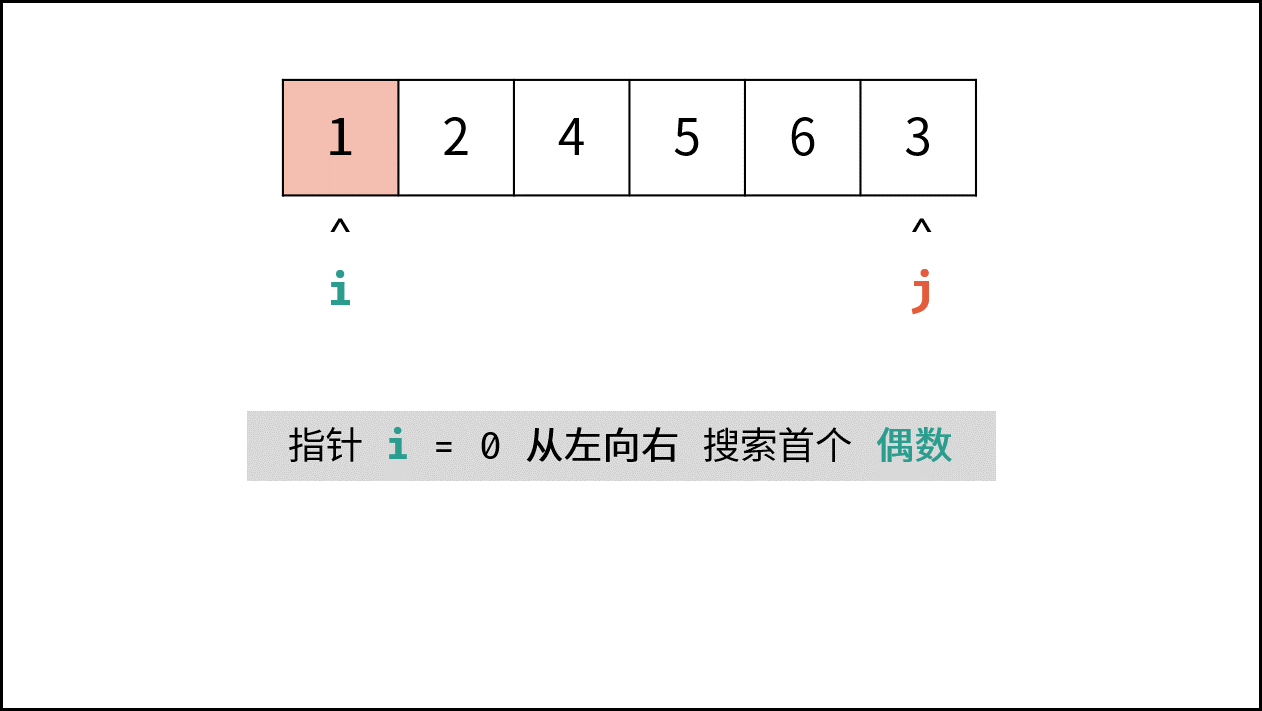
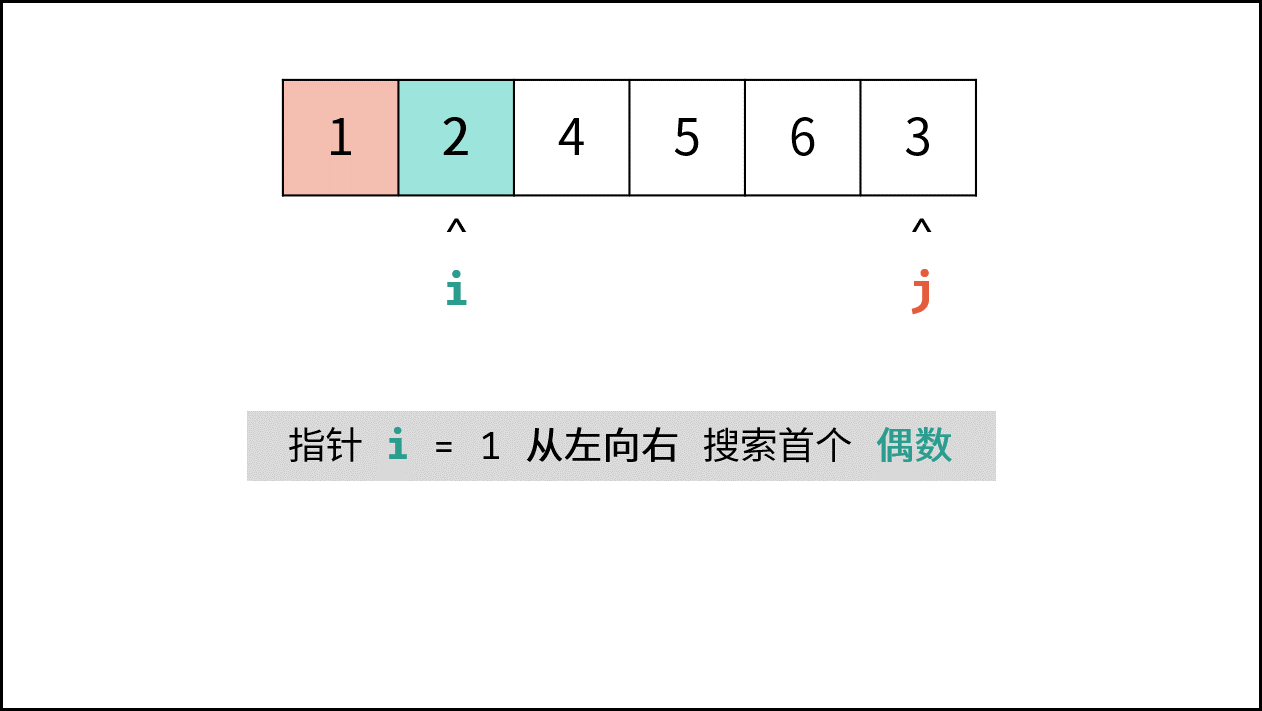
   1. 指针 $i$ 遇到奇数则执行 $i = i + 1$ 跳过，直到找到偶数；
   2. 指针 $j$ 遇到偶数则执行 $j = j - 1$ 跳过，直到找到奇数；
   3. 交换 $nums[i]$ 和 $nums[j]$ 值；
3. 返回值： 返回已修改的 $nums$ 数组。

<,,,,,,,,,,,,>

复杂度分析： ​

• 时间复杂度 $O(N)$ ： $N$ 为数组 $nums$ 长度，双指针 $i$, $j$ 共同遍历整个数组。
• 空间复杂度 $O(1)$ ： 双指针 $i$, $j$ 使用常数大小的额外空间。

代码： ​

$x & 1$ 位运算 等价于 $x % 2$ 取余运算，即皆可用于判断数字奇偶性。

class Solution:
    def exchange(self, nums: List[int]) -> List[int]:
        i, j = 0, len(nums) - 1
        while i < j:
            while i < j and nums[i] & 1 == 1: i += 1
            while i < j and nums[j] & 1 == 0: j -= 1
            nums[i], nums[j] = nums[j], nums[i]
        return nums

class Solution {
    public int[] exchange(int[] nums) {
        int i = 0, j = nums.length - 1, tmp;
        while(i < j) {
            while(i < j && (nums[i] & 1) == 1) i++;
            while(i < j && (nums[j] & 1) == 0) j--;
            tmp = nums[i];
            nums[i] = nums[j];
            nums[j] = tmp;
        }
        return nums;
    }
}

class Solution {
public:
    vector<int> exchange(vector<int>& nums)
    {
        int i = 0, j = nums.size() - 1;
        while (i < j)
        {
            while(i < j && (nums[i] & 1) == 1) i++;
            while(i < j && (nums[j] & 1) == 0) j--;
            swap(nums[i], nums[j]);
        }
        return nums;
    }
};